Abstract
Causal discovery algorithms have the potential to impact many fields of science. However, substantial foundational work on the statistical properties of causal discovery algorithms is still needed. This paper presents what is to our knowledge the first method for conducting power analysis for causal discovery algorithms. The power sample characteristics of causal discovery algorithms typically cannot be described by a closed formula, but we resolve this problem by developing a new power sample analysis method based on standardized in silico simulation experiments. Our procedure generates data with carefully controlled statistical effect sizes in order to enable an accurate numerical power sample analysis. We present that method, apply it to generate an initial power analysis table, provide a web interface for searching this table, and show how the table or web interface can be used to solve several types of real-world power analysis problems, such as sample size planning, interpretation of results, and sensitivity analysis.
Similar content being viewed by others
1 Introduction
Causal discovery is a growing field that develops algorithms for deriving causal model structures from many kinds of data under weak assumptions [1,2,3,4]. It is most known for methods that can learn causal directionality from cross-sectional observational data [2, 5, 6]. There is a large variety of methods within causal discovery, including methods that discover hidden variables and selection bias [2, 7,8,9], methods that orient causal directionality from mere variable pairs data [10,11,12,13,14,15], methods for analyzing data from controlled experiments [16, 17], and methods that guide the sequence of experimentation [18,19,20,21]. Overall, the field has incredible potential to change the way that science is done.
At present, the most widely accepted scientific process for uncovering causal knowledge relies on experimentation, but this has numerous drawbacks such as being costly, lacking scalability, and often being unethical or impossible for many topics [22]. In the future, as high quantities of data become available with increasingly varied modalities, dimensions, sample sizes, measurement technologies, temporality, levels of control or intervention, background knowledge, and so on, data-driven causal analysis methods are likely to have a rapidly growing role in science. Unlike experimentation, this data-driven approach is inexpensive, far more scalable, and can be applied to topics where experimentation is unethical or impossible.
This new paradigm requires foundational work about the properties of existing and future causal discovery algorithms. In order for these methods to be more widely deployed, and in order for the findings of the algorithms to be translated into future work, researchers need to be able to know (A) what kind of performance they can expect from using a particular causal discovery algorithm on a particular data set, and (B) the reliability of published findings where causal discovery algorithms were used. Power analysis is the standard framework for addressing both of these questions [23,24,25,26]; however, no power analysis method has previously been developed for causal discovery algorithms. This is not due to lack of interest, but rather because (1) the statistical power sample characteristics of causal discovery algorithms are not readily described in a closed formula expression and (2) traditional power analysis only considers one model structure at a time, while in causal discovery the model structure is considered unknown and is the learning goal of the causal discovery procedure. For both reasons, a different kind of power analysis method is required.
In this paper, we present a simulation-based power analysis method for answering these and other questions about causal discovery algorithms. For the same reasons mentioned above, power analysis has largely been supplanted by simulation studies in the causal discovery literature. All previous simulations have been severely limited, however, and thus do not serve as an adequate replacement for power analysis. Most importantly, previous simulations have not carefully controlled the causal effect sizes in their data generating models. For example, some studies ensured that effect sizes were varied to be larger or smaller [6], but no studies calculated the specific values of those effect sizes. Effect size can dramatically alter the power of an estimator, and so without knowing the effect sizes of the edges in the data generating models, we cannot make reliable inferences about the method’s real world performance.
One reason for not precisely controlling or examining effect sizes in causal discovery simulation studies is that those studies were only evaluating algorithm performance relative to other algorithms. Under such circumstances, although which methods perform better than others might depend on the effect sizes, the specific effect sizes in the data generating model are not needed for determining that one method is performing better than another. A second reason is that traditional power analysis operates in a hypothesis testing framework. In such a framework, the goal is to determine the power of a particular statistical test for rejecting a predefined null hypothesis. For causal discovery, however, there is no obvious null hypothesis to use. Causal discovery aims to identify a potentially large and complex model structure, and there is a finite, but extremely large, set of alternative structures to consider. In this paper, we resolve this issue by only considering questions about edges, specifically whether the correct edge adjacencies and edge orientations are identified, rather than questions about the entire model structure.
1.1 Our contributions
Our novel contributions presented in this paper include:
-
(1)
We provide the background theory mapping the causal discovery problem into appropriate power analysis concepts. This is necessary to understand what power analysis for causal discovery means. No previous simulation studies address this issue.
-
(2)
We provide a novel and nontrivial method for quickly generating linear Gaussian structural equation models with fixed standardized edge effect sizes and marginal variances. By construction, our models also prevent statistical artifacts such as “varsortability” that some causal discovery methods can use to artificially elevate their performance [27]. Prior DAG simulation methods suffer from these statistical artifacts, so our method is the first to provide a fair standard for method comparison studies.
-
(3)
We provide the results from a large simulation study, which used our model generation method to simulate data. This is only an initial exploration of an extremely large space, but it is the first ever reported power analysis results for causal discovery. These results are navigable through the shared Shiny app or the shared table. They can be used as benchmarks for anyone unwilling or unable to use our method to evaluate the specific algorithm and type of data (number of variables, sample size, etc.) that would be relevant for their own studies.
2 Background
This section covers background material on causal models, causal discovery, and power analysis.
2.1 Causal models
Causal models represent the causal relationships amongst a set of variables [1]. As a consequence, an accurate causal model can be used to solve problems that require causal information, such as predicting the outcome of an intervention, or identifying a promising treatment target. While there are a number of different types of causal models, this paper focuses on causal models that take the form of linear Gaussian structural equation models (SEMs). Let \(G\langle {\textbf {V}},\Gamma ,{\textbf {E}},\Phi \rangle \) be a linear Gaussian SEM with variables \({\textbf {V}}\) each with an independent noise \(\epsilon _V \in \Gamma \), and set of edges \({\textbf {E}}\) each with a corresponding real number \(\beta _E\in \Phi \) representing its linear effect size or “weight.” Let each \(V\in {\textbf {V}}\) be distributed according to \(V\leftarrow \epsilon _V + \sum _{X s.t. (X\rightarrow V)\in {\textbf {E}}}\beta _{X\rightarrow V}X\).
Note that each \(\epsilon _V\) can have different mean \(\mu \) and variance \(\sigma ^2\). As such, the values of the weights (\(\beta \)s) do not directly correspond to standardized statistical effect sizes. This is a hurdle to directly applying power analysis to SEMs, since effect size is a key component of power analysis. We show how we resolve this problem in Sect. 3, by choosing the \(\sigma ^2\) of each \(\epsilon _X\) to ensure that \(\forall X, \sigma ^2(X) = 1\). This ensures that \(\beta _{Y\rightarrow X}=\sqrt{\sigma ^2(\beta _{Y\rightarrow X}Y)/{\sigma ^2(X)}}\), the standardized statistical effect size r.
2.2 Causal discovery
Many different learning problems fall under the umbrella of causal discovery, but this paper focuses on the following: given data \({\textbf {D}}\) generated from a model M, which is a linear SEM with a directed acyclic graph (DAG) structure, learn the structure of M from D. Let \(A({\textbf {D}})\) be a function (embodied in an algorithm) that outputs a set of directed and undirected edges \({\textbf {E}}'\) from a data set \({\textbf {D}}\) sampled from \(G\langle {\textbf {V}},\Gamma ,{\textbf {E}},\Phi \rangle \). The presence of undirected edges in \({\textbf {E}}'\) is due to the existence of Markov Equivalence Classes [3, 28], where the directionality of some edges in E cannot be identified. Then, the specific causal discovery problem that we consider is to minimize the difference between \({\textbf {E}}\) and \({\textbf {E}}'\). Causal discovery algorithms are designed to solve this problem.
It is increasingly being recognized that many scientific fields struggle to infer cause–effect relationships in contexts with large numbers of interacting elements, such as interacting collections of gene expressions, proteins, neurons, or symptoms. Researchers have started to apply causal discovery methods to solve problems like these and successfully discovered important causal relationships [21, 29,30,31,32,33,34,35,36,37]. However, prior to the work presented here, there were no methods for computing the power sample characteristics for causal discovery analysis, which has limited the ability of researchers to plan projects and interpret results.
Previous work on the finite sample performance of causal discovery algorithms has been primarily about comparing different causal discovery algorithms according to their performance on different learning problems rather than assessing questions such as how many samples are required to get adequate performance [6, 38,39,40]. These evaluations have almost exclusively relied on simulation studies, with data generated in silico from either randomly generated causal models or expert-made causal models of real-world processes found in model repositories. There have been some exceptions, however, such as using real-world data measured from processes that have been heavily studied by domain scientists. In these cases, the “gold standard” causal graph is constructed from background knowledge on the topic, and the algorithm’s results on the real-world data are compared to this “gold standard” model rather than a known data-generating model.
The method we present in this paper differs most notably from previous simulation-based methods by having a more advanced simulation procedure. Specifically, this procedure allows us to exactly control the standardized effect size—the variance introduced by the edge relative to the variance of the variable being influenced—of the causal relationships in our data generating models. Effect size, or “signal-to-noise ratio,” is a critical value in power analysis, as finite-sample algorithm performance is drastically impacted by the effect sizes in the data generating model (see Sect. 4).
2.3 Power analysis
Power analysis normally evaluates a specific statistical test of a given hypothesis [23,24,25,26]. The power of a binary hypothesis test is the probability that the statistical test correctly rejects the null hypothesis (\(H_0\)) when a specific alternative hypothesis (\(H_1\)) is true. In other words, power is 1-(type II error rate). The power of a statistical test is generally influenced by: (1) a significance threshold \(\alpha \), which is the acceptable type I error rate or false positive rate, that is, the probably of rejecting \(H_0\) when \(H_1\) is false; (2) effect size; and (3) sample size.
The power analysis for SEM is related to the power analysis for causal structure discovery. There are two types of power analysis done for SEMs [41]. The first is the power of rejecting the SEM model. This is typically done by examining the power of the \(\chi \)-squared goodness of fit test, where the null hypothesis states that the observed data are generated from the specified model [41,42,43,44]. Therefore, the power corresponds to the probability of discovering model mis-specification. It is worth noting that rejecting the Null does not indicate how exactly the model is mis-specified. The second type of power analysis for SEMs is the power of detecting a nonzero coefficient for a particular structural equation. This has some similarity to power analysis for causal structure discovery; however, SEM power analysis assumes the entire structure is known (and specified via structural equations). Many prior methods for computing power for detecting nonzero coefficients additionally require all other model coefficients to be known. A more recent study used simulations to make this process more adaptable and flexible [41].
In contrast with traditional power sample analysis, including that for the SEM, the problem of identifying the entire causal structure from observational data is generally not formulated as a single hypothesis test (although it can be conceptualized as a sequence of statistical tests). Therefore, the power analysis for this task needs to be defined differently from that of traditional hypothesis testing, while aiming to achieve similar goals.
Definition 1
\(\alpha \) for Causal Structure Discovery: the probability of a causal discovery procedure \(\Omega \) claiming the presence of a (directed) causal edge in error, given data D sampled from \(G\langle {\textbf {V}},\Gamma ,{\textbf {E}},\Phi \rangle \) with sample size N, effect size \(\Theta \), and type II error rate (1-power).
Definition 2
Power for Causal Structure Discovery: the probability of a causal discovery procedure \(\Omega \) correctly identifying the presence of a (directed) causal edge given data sampled from \(G\langle {\textbf {V}},\Gamma ,{\textbf {E}},\Phi \rangle \) with sample size N, effect size \(\Theta \), and type I error rate \(\alpha \).
The power for Causal Structure Discovery corresponds to sensitivity. This definition mirrors that of power analysis for traditional statistical tests. However, because the causal structures we observe in many domains are sparse, \(\alpha \) (1-Specificity) might not be very informative. Therefore, we recommend examining the precision in addition to \(\alpha \). The causal discovery procedure can be any procedure that aims to discover causal relationships, such as experimental methods or computational methods. Here we focus on computational causal discovery algorithm with a specific hyperparameter setting. According to this definition, after specifying its hyperparameter(s), each causal discovery procedure has a fixed \(\alpha \) for any given causal discovery task, \(G\langle {\textbf {V}},\Gamma ,{\textbf {E}},\Phi \rangle \) with sample size N. This is different from traditional power analysis, where one can choose an alpha level explicitly for a specific statistical test. However, \(\alpha \) can be adjusted by choosing different hyperparameters for the causal discovery algorithm. For example, the hyperparameter for the PC algorithm is the significance threshold for its conditional independence tests. To avoid confusion, we will refer this hyperparameter as “alpha” instead of \(\alpha \). Increasing this threshold usually increases the sensitivity but decreases the positive predictive value for edge identification (see Sect. 4). In general, there is no closed-form solution for how the threshold relates to the overall discovery performance.
3 Methods of simulation and evaluation
Figure 1 shows the overall structure of the simulation procedure. The procedure is as follows:
-
(1)
Randomly select a directed acyclic graph (DAG), G
-
(2)
Assign weights to the graph edges (for this study we set all weights to the same value)
-
(3)
Compute the independent variance of each node
-
(4)
If the assigned weights prevent the computation of any independent variance value, return to step 1
-
(5)
Generate data from the model
-
(5)
Run a discovery algorithm on the data to generate an estimated graph structure, \(G'\)
-
(6)
Compare \(G'\) to the original DAG G
3.1 Generation of random DAGs
Each structural equation model was generated by first creating a random Directed Acyclic Graph (DAG) with a fixed number of edges over a fixed set of nodes. Pseudocode for this procedure is shown in Algorithm 1.
First, a list of nodes [\(x_1\),\(x_2\),...,\(x_n\)] is shuffled into a random order. Let \(<_T\) be the operator that indicates the order of the nodes, such that \(u <_T v\) indicates u is prior to v in this ordering. This is used as a topological ordering for the DAG, restricting the possible DAGs that can be selected to those where no variable is a parent of another variable that is earlier than it in the ordering. The set of all possible edges, restricted by the topological ordering, is then constructed. Finally, the appropriate number of unique edges is randomly drawn from that set of possible edges.

3.2 Assign \(\beta _{Y\rightarrow X}\) weights
At present, we are assigning the same edge weight values to all edges in a single model. Once we assign the independent noise terms in a particular way, described in Sect. 3.3, these \(\beta \) weights will equal the r effect sizes of these edges. Each edge weight is represented by a \(\beta \) from node i to node j, that is, \(\beta _{i\rightarrow j}\). For example, in the application we present later some models had all \(\beta _{i\rightarrow j}\)’s are set to 0.1, while others had all \(\beta _{i\rightarrow j}=0.3\) or all \(\beta _{i\rightarrow j}=0.5\). Different values could be used if desired. Letting edge weights vary within a single model is an extension left for future work.
3.3 Variance of independent noise
Each variable in the randomly generated SEMs has an independent noise term, \(\epsilon \). These are normally distributed, with mean 0, and a variance that is computed from the structure of the DAG and the value of the edge weights. In order to have the edge weights correspond to r values, the total variance of each variable, including variance from its independent noise term, must be 1. As such, the variances of the independent noise terms are calculated so that they complete the difference between 1 and the variance introduced by the parents of each variable.
Let pa be a function that returns the direct parents of the variable given in its argument. For variable j, the variance due to its parents in the DAG is:
Since all \(\beta \) values are already determined at this stage, and all variance values are 1 by design, the only unknown value in this formula is the covariance of u and v. u and v are linear functions of their parents and their independent noise terms, \(\epsilon _u\) and \(\epsilon _v\). For compactness, let \(pae(x) = pa(x) \cup \{\epsilon _x\)}, and let \(\beta _{\epsilon _x\rightarrow x}=1\) for any variable x. We can then decompose the covariance of u and v further:
This again contains covariance terms that we do not immediately know the value of, specifically the Cov(x, y) terms. These terms are, however, for variables that are strictly prior to u or v in the topological ordering, since all x and y variables are parents of either u or v. As such, if we repeat this decomposition for the Cov(x, y) terms, and assuming that there are a finite number of variables, we will eventually reach cases where either x or y has no parents, terminating the process.
It is thus possible to compute Cov(u, v) using a recursive method, but we opted to implement a more efficient dynamic programming method instead. This procedure starts at the top of the topological order of the variables, computing and storing all covariance values in order. As such, calculating each covariance value requires only querying covariance values that had already been computed. This procedure is described in Algorithm 2.

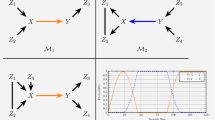
For example, in the simple case shown in Fig. 2, neither u or v has parents, so \(Cov(u,v)=0\). The covariance between w and u is \(Cov(u,w) = \beta _{u\rightarrow w}\). The incoming variance to the child node w from u and v is \(\beta _{u\rightarrow w}^2 Var(u) + \beta _{v\rightarrow w}^2 Var(v) =\beta _{u\rightarrow w}^2 + \beta _{v\rightarrow w}^2\). If \(Var(u)=(Var(v)=1\) and \(\beta _{u\rightarrow w}=\beta _{v\rightarrow w}=0.3\), then the total variance of w due to u and v would be 0.18
In Fig. 3, u and v have a nonzero covariance because they have a common parent t. \(Cov(u,v) = \beta _{t\rightarrow u}\beta _{t\rightarrow v}Cov(t,t) = \beta _{t\rightarrow u}\beta _{t\rightarrow v}\). As such, the total variance of w due to u and v will be different than in Fig. 2, since \(\beta _{u\rightarrow w}\beta _{v\rightarrow w}Cov(u,v)\) will be nonzero. In this case, if all the \(\beta \)s are equal to 0.3 and \(Var(t)= Var(u)=Var(v)=1\), then the total variance of w due to u and v would be 0.36, twice that of the previous example.
3.4 Testing model admissibility
Using the calculated covariance values, we calculate the variance due to a variable’s parents as described in Sect. 3.3. For a standardized model, we assign the variance of that variable’s independent noise term a value equal to 1 minus the variance due to its parents. An error can be encountered here if the variance due to the parents is close to or greater than 1. The independent noise term cannot have negative variance, and to prevent determinism in the model, which could result in a sample covariance matrix that is not positive semi-definite, its variance should be bounded away from 0. As such, if any node in a model would not be able to have an independent noise term with a variance of at least 0.1, then we discard that model and restart at the DAG selection step.
3.5 Generating data
For models that are not discarded, data are generated as follows: in topological order (beginning with nodes that have no parents), we set the value of each node as a sum of the weights (\(\beta \)s) times the value of the parents, plus the independent noise term: \(V \leftarrow \sum _{X\in pa(V)}\beta _{X\rightarrow V}X + \epsilon _V\). This process is repeated for each independent sample. For our demonstration, we generated 102400 total samples from each model.
3.6 Apply causal discovery algorithm
The previous sections detailed the entire process of generating the data generating models and producing data from them. Causal discovery algorithms can then be applied directly to the generated data. Any causal discovery algorithm that operates on continuous data may be used. The results are stored and indexed according to the data generating model, sample size, causal discovery algorithm, and hyperparameters, for use in the evaluation step.
For our application, we used the PC algorithm [2], as implemented in Tetrad causal-cmd\(-\)1.4.1-SNAPSHOT [45]. PC’s alpha value was the only hyperparameter that we varied. The generated data were subsampled at various smaller sample sizes, so that results were produced for sample sizes ranging from 50 to 102400.
3.7 Algorithm performance evaluation
We used common classification metrics of precision and power for evaluating the performance of the causal discovery algorithm with respect to (1) identification of edge adjacencies in the graph, more specifically, identifying which nodes are directly connected to which other nodes without considering directionality, and (2) identification of edge orientations in the graph, that is, identifying whether the exact relationships (for example A causes B rather than B causes A) between variable pairs match those of the data generating graph. We cover adjacency and orientation performance separately. For brevity, let “true” demarcate features of the data generating model; for example, “true edges” are the edges appearing in the data generating model. Figure 4 shows a table summarizing the evaluation of performance metrics for both adjacencies and orientations.
A small portion of the example power analysis table. The complete table is available at: https://osf.io/zmwyb/
3.7.1 Adjacency performance
For each individual data set, we construct a confusion matrix for the algorithm’s adjacency performance on that data set. Adjacency performance reflects the algorithm’s ability to recover the correct adjacencies, ignoring the directionality information in each edge, without making errors. This confusion matrix consists of: (1) true positives (TP), the number of true adjacencies also present in the algorithm’s output graph; (2) false positives (FP), the number of adjacencies in the algorithm’s output that do not correspond to true adjacencies; (3) false negatives (FN), the number of true adjacencies that are not found in the algorithm’s output; (4) true negatives (TN), the number of absent true adjacencies that are also absent in the algorithm’s output.
All of the confusion matrices are stored and can be used to calculate a number of performance measures, including but not limited to sensitivity (TP/[TP + FN]), specificity(TN/[TN + FP]), precision (TP/[TP + FP]), negative predictive value (NPV) (TN/[TN + FN]), and F1 statistic (2TP / [2TP + FP + FN]) for the algorithm, for each hyperparameter value used, data set, and sample size.
3.7.2 Orientation performance
Orientation performance is computed in a similar manner to adjacency performance, but takes directionality into account. The primary difference is that true negatives are not counted for edge orientation, as there is no true orientation that would correspond to a negative state: either \(A \rightarrow B\) or \(B \rightarrow A\), there is no state in the data generating models where A is directly related to B without any directionality.
For orientations, we defined: (1) TP, the number of true edges that are present and oriented correctly in the output graph; (2) FP, the number of oriented edges in the output graph that are absent or given the opposite directionality in the true graph; (3) FN, the number of true edges that are not present or not oriented correctly in the output graph; (4) TN, the number of true edges that are present and oriented opposite of the incorrect orientation in the output graph (this is equal to TP).
Many causal discovery algorithms, including the PC algorithm that we used for demonstration purposes, produce edge types that are more vague than directed arrows. For example, PC can produce undirected edges, where the algorithm does not commit to either the \(A \rightarrow B\) or \(B \rightarrow A\) orientation, instead indicating that both are possible. The definitions for orientation TP, FP, and FN reflect this. In particular, consider the case where the output graph contains an undirected edge that corresponds to a correct adjacency, that is, it correctly identifies that A and B are directly related to each other but does not commit to either directionality for this relationship. For orientation performance, that edge will not count as a TP, since it is not oriented in the correct way, but will also not count as a FP, as it is not oriented in the opposite way. Instead, it will contribute only to the orientation FN count, as it is not oriented correctly.
4 Power analysis simulation for three algorithms
We applied the procedure described above to establish the first ever power analysis results for the PC, FGES, and GRaSP algorithms [2, 46, 47]. Parameters were selected to strike a balance between completeness and computational cost. Simulations were run on graphs with 10, 20, 40, or 100 nodes, with structures sampled uniformly from those with an edge density of 1, 1.5, or 2. In each graph, edges were fixed to have effect sizes of R = 0.1, 0.3, or 0.5. For each combination of parameters, the procedure attempted to randomly simulate 500 models. In order to ensure the simulation concludes in a reasonable amount of time, the algorithm will halt after generating 10 invalid models for any given parameter combination. As a consequence in combinations with higher edge densities and R values, less than 500 models were tested. All parameter combinations with less than 500 complete results were removed prior to forming our summary data. 102400 samples were drawn from each model after checking for model suitability, and smaller data sets were sub-sampled from this larger collection, producing data sets with 50, 100, 200,..., 51200, 102400 samples. All algorithms were run using Tetrad causal-cmd\(-\)1.4.1-SNAPSHOT. PC has an “alpha” hyperparameter that was varied among 0.1, 0.05, 0.01, and 0.001, and otherwise used default settings. FGES and GRaSP have a “penaltydiscount” hyperparameter that was set to 2, and otherwise used default settings.
All of the above results were stored and aggregated into a table, where each row stores the performance found for a particular combination of number of nodes, number of edges, R value, sample size, and alpha value for PC. For R = 0.5, it was found that suitable models were extremely rare or nonexistent for edge density of 1.5 or greater, and so these parts of the table were left empty. Figure 5 shows a small portion of this table. The complete table is available at: https://osf.io/zmwyb/
In addition to the raw data table, we have also created and made public a Shiny App that can be used to filter and sort the table. With it, users can easily answer the most common power analysis questions. Figure 6 shows a screenshot of the Shiny App. It is available for anyone to access and use at: https://kummerfeldlab.shinyapps.io/PowerSim2023-1/
A screenshot of the Shiny app. The app is available at: https://kummerfeldlab.shinyapps.io/PowerSim2023-1/
4.1 Power sample characteristics of PC, FGES, and GRaSP
We encourage interested readers to explore the table and Shiny App at the links provided above, but here we also visualize and evaluate PC’s power sample characteristics under various conditions. Figures 7, 8, 9, and 10 show multiple subplots each. In these figures, each column of plots shows errors for adjacency precision, adjacency sensitivity, orientation precision, and orientation sensitivity. While specificity was also calculated, adjacency specificity is universally high and plotting it is not very informative. Orientation specificity is equal to orientation precision. All of these can range in value from 0 to 1, with higher numbers being preferred because lower numbers indicate higher error rates. The rows show how these error rates change with number of nodes, density of edges, method, and effect size (r), respectively. Each subplot shows how mean error rates change as sample size is varied from 50 to 102400. The shading in each subplot shows the range of error rates from the 5th percentile to the 95th percentile.
Figure 7 shows how FGES [46] responds to different numbers of nodes. It shows only results where the FGES algorithm was used, with density 1.5 and r of 0.3. We can see that increasing the number of nodes from 10 to 100 appears to reduce adjacency precision, while adjacency sensitivity, orientation sensitivity, and orientation precision are increased. There is also a strange behavior where adjacency precision peaks around 200 or 400 samples, depending on the number of nodes, but then decreases as the number of samples increases. For all error types, the variability of the error rate appears to become smaller as the number of nodes increases. This can be explained by the increased number of edges and edge absences when density is fixed but the number of nodes increase, leading to a less noisy estimate of performance at the individual graph level. 100% adjacency sensitivity is achieved for all number of nodes with sufficient sample size, and perhaps counter-intuitively convergence is faster as the number of nodes increases. Orientation precision and sensitivity likewise appear to converge more slowly with fewer nodes than with more nodes. With a fixed hyperparameter, adjacency precision appears to be the only error rate where FGES does worse with higher numbers of nodes.
Regarding edge density, Fig. 8 shows how performance varies when the number of edges per node (density) increases from 1, to 1.5, to 2. Results are shown for both the PC algorithm with alpha = 0.01 and for GRaSP [2, 47]. The plots in this figure are restricted to display results for simulations with 20 variables and edge effect size r = 0.3. Figure 8 suggests that adjacency precision is relatively unresponsive to changes in density within this range, likely a ceiling effect due to performance being universally strong. For adjacency sensitivity, PC appears to converge more slowly as density increases, while GRaSP seems comparatively unaffected by density. This is consistent with previously published simulations that have compared GRaSP with other causal discovery methods at higher graph densities [47]. The orientation precision and sensitivity plots also reveal this distinction between the two methods, with PC converging more slowly than GRaSP. In terms of the shape of convergence, PC’s orientation precision shows a sharp sigmoidal shape at lower density that flattens out and becomes more convex at higher density. In comparison, GRaSP converges stably for all cases. Overall, the plots in Fig. 8 indicate that there can be complicated interactions between some causal discovery methods and the density of edges in the data generating model.
Figure 9 shows how performance varies with different methods. The top four rows of plots show PC’s performance with alpha set to 0.001, 0.01, 0.05, and 0.1, while the bottom two rows of plots show how FGES and GRaSP perform with penaltydiscount = 2. All plots are based only on simulations with 20 nodes, density 1.5, and edge effect size r = 0.3. It provides a more clear comparison of the convergence properties of the implementations of PC, FGES, and GRaSP found in the Tetrad causal-cmd\(-\)1.4.1-SNAPSHOT software package. We emphasize that this is only a comparison of these specific implementations, as implementing causal discovery algorithms is nontrivial and there are many known cases of causal discovery algorithm implementations that contain bugs or have unreasonable default settings.
The primary result of Fig. 9 is that GRaSP appears to have superior convergence speed and shape. All of these methods are correct in the large sample limit, but the short-term performance has dramatic differences. For PC, depending on the selected alpha, there can be strange behavior in its orientation precision convergence. For FGES, we see strange behavior in its adjacency precision. GRaSP lacks these oddities, with adjacency precision and sensitivity performance that rival the best performance of either across the other algorithms, and orientation precision and sensitivity performance that converges more rapidly and smoothly than any of the other tested methods.
Hyperparameter value also appears to play an important role for PC, both in terms of trading between adjacency precision and sensitivity, but also in terms of the shape of convergence for its orientation precision and to a lesser extent sensitivity. With a smaller alpha of 0.001, PC’s orientation precision surprisingly decreases steadily as sample size increases from 50 samples to about 400 samples, where it hits a minimum just above the 50% mark. Following that, it then increases. At 1600 samples, it recovers the same orientation precision it started with at 50 samples, and it continues to converge toward 1 as the sample size increases further. This convex shape is still present but greatly weakened in the orientation precision for alpha = 0.01, and becomes a more well behaved sigmoidal shape as alpha continues to increase to 0.05 and 0.1. A possibly related issue can be found in the adjacency sensitivity plots, where with alpha of 0.001 or 0.01, at 50 samples PC has adjacency sensitivity of only around 0.1 or 0.2. With 30 total true edges in the data generating models, this means that for these simulations PC typically only has about 3 or 6 edges across 20 nodes. This will make it very difficult for PC to discover true unshielded colliders, which is a required step for it to orient any edges. This could also explain the low orientation sensitivity of PC with small alpha.
A comparison of the performance of GRaSP for models with effect size of r = 0.1, r = 0.3, and r = 0.5 is found in Fig. 10. The plots in this figure are restricted to models with 20 variables and 20 edges (density = 1). r = 0.1, 0.3, and 0.5 are considered to be the standard r values for weak, moderate, and strong effects, respectively. The impact of varying r across these values is striking.
For weaker edges at r = 0.1, at sample sizes 400 or below GRaSP with penaltydiscount = 2 struggles to detect any edges at all. Its adjacency sensitivity begins to noticeably rise at sample size 800, passing 0.2, and it rapidly increases until sample size 3200 where its adjacency sensitivity approaches the ceiling of 1. This forms a sigmoidal curve with a high slope, sharply switching from nondetection to perfect detection of these weak edges. As r increases, performance at our minimum sample size of 50 already appears to be in the middle of the slope for r = 0.3, and by r = 0.5 convergence has already almost completed by sample size 50.
Adjacency precision also starts low, with sample size 50 and r = 0.1 showing an adjacency precision of less than 30%; however, there is also enormous variance, likely due to these values being estimated from a very small number of edges. But even for r = 0.1, adjacency precision is near 100% by sample size 400. This is interesting since adjacency sensitivity is still below 10% at sample size 400 and r = 0.1. For r = 0.3, adjacency precision is already at 0.8 for r = 0.3 and approaches 1 at the next sample size of 100.
With r = 0.5, there are some unexpected findings. Adjacency precision and orientation sensitivity in particular indicate lower maximum values than we see for r = 0.3, and adjacency precision for r = 0.5 also shows elevated variance compared to lower r values. This requires further investigation, but we suspect this may be an artificial consequence of our simulation method that requires all edges to have the same r. At r = 0.5, many model structures become excluded from consideration because they cannot support all edges having such a strong effect. In particular, when a variable has multiple parents, and more so when those parents are positively correlated, the variance of that variable can easily be forced to exceed 1. Such models get removed at step 4 of our modeling process (see Fig. 1). As a consequence, the r = 0.5 model structures will in general have fewer colliders, resulting in the sharply decreased orientation sensitivity. This does not provide as clear an explanation for the the adjacency precision at r = 0.5, but it is possibly that this procedure results an in increased overall likelihood of sampling unfaithful models. Since all edges have the precise same effect size, exact unfaithfulness is possible, and GRaSP may respond to unfaithfulness primarily by adding additional edges, resulting in its reduced precision even at sample size 102400.
Orientation precision also shows a stark difference across r values. For weak r = 0.1, there is enormous variance until the adjacency sensitivity reaches a sufficiently high value at 3200 samples. For r = 0.3, we see similar behavior, except that sensitivity is already sufficiently high by 200 samples. With r = 0.5, orientation precision shows almost no change as sample size changes, but still retains substantial variance even at 102400, unlike how the variance vanishes at very high sample size with r = 0.3. This is possibly also due to unfaithful models as discussed above.
5 Example applications
Similar to power sample analysis for traditional statistical analysis, the power sample analysis for causal discovery also requires knowledge or assumptions about the data to be analyzed and the statistical procedure to be applied. If the characteristics of the data specified for power sample calculation deviate from the actual data, the power sample calculation is likely to be inaccurate. The examples below use performance evaluated in terms of specificity and sensitivity (recall) to maintain consistency with how power analysis is traditionally performed. For simplicity, only adjacency performance is considered. Note that (i) causal discovery algorithms almost universally have very good specificity, as an artifact of the large number of absent edges in most models, and (ii) in many real-world applications, precision may be considered no less important than specificity. Especially as the number of variables increases, causal discovery methods can have high specificity but poor precision. Both the table and the shiny app enable the user to limit the findings based on precision in addition to, or instead of, specificity.
5.1 A priori power analysis
In a priori power analysis, the goal is to identify what sample size would be required to obtain a predetermined level of statistical performance. For example, assume that we want to collect data with the intention of using causal discovery to produce a holistic model of how various psychiatric symptoms causally influence each other. We are considering the PC algorithm at various alpha values, or FGES or GRaSP with penaltydiscount = 2. We want to have at least 95% specificity and 90% sensitivity for effect sizes of at least r = 0.3. Our data will have 20 variables, and we anticipate an edge density of 2 (40 edges). How many samples do we need to collect for this analysis? By examining the table (or using the shiny app), we can quickly determine that using GRaSP, 400 samples is enough to achieve 0.994 specificity and 0.947 sensitivity (recall). So, 400 samples would be sufficient.
5.2 Post hoc power analysis
In post-hoc power analysis, the goal is to identify the highest power (recall, sensitivity) that can be achieved for a specific sample size, while maintaining other statistical performance values at or better than a set of preselected values. For example, assume that we have a data set of the physical characteristics of newborn babies, along with medical information about the mother during pregnancy. In total, they amount to 40 variables. We anticipate an edge density of 1. We want to use either PC at various alpha values, or FGES or GRaSP with penaltydiscount = 2. Our goal is to use one of these methods to identify which, if any, of the mother’s medical information might causally influence one or more of the physical characteristics of their newborn baby. We are using data from local birth centers totaling 1600 newborns. We want at least 95% specificity for effect sizes above r = 0.1. What’s the highest recall (power) that we can achieve on this data set (we can pick our hyperparameter to achieve this)? Using either the table or the shiny app, we see that using PC with an alpha of 0.05, PC can achieve 0.968 specificity and 0.966 recall (sensitivity) at sample size 1600, when there are 40 variables and edge density 1. So, 0.966 recall is possible for this data set.
5.3 Criterion power analysis
Criterion power analysis asks us to determine the highest possible precision when sample size and other statistical performance values are fixed. For example, assume that we have a small data set of gene expression values from yeast. We want to learn which gene expressions are most likely to causally influence cell size, as well as how the genes interact with each other. We plan to do knockout gene experiments to confirm any findings, so for us power is more important than precision. We have 200 samples from 40 genes, and expect an edge density of 1.5 (60 edges). In this setting, we want to get at least 90% power for effect sizes of r = 0.3. Is this possible, and what hyperparameter value should we use to also maximize precision? With the table or the shiny app, we find that this it is possible to get recall (power) above 0.9 under these conditions. PC with an alpha value of 0.1 can achieve 0.928 recall while still having 0.98 specificity.
5.4 Sensitivity power analysis
In a sensitivity power analysis, the goal is to determine the lowest effect size for which we can achieve some desired level of statistical performance for a fixed effect size. For example, assume we have a health survey dataset of 20 variables, previously collected from 800 participants. We expect many of these variables are related to each other, so we anticipate an edge density of 2 (40 edges). We are interested in a very accurate model of the causal relationships among physical, psychological, and lifestyle characteristics, and so we want to have at least 95% specificity and 95% recall. What is the minimum effect size for which we can satisfy our criterion? What algorithm and hyper-parameter should we use to achieve that? With the table or the shiny app, we can determine that it is possible to achieve this level of performance for r = 0.3, using GRaSP with penaltydiscount = 2, yielding 0.994 specificity and 0.980 recall.
6 Conclusion
In this paper, we presented what is to our knowledge the first method for doing power analysis for causal discovery algorithms. This method uses simulation, a common technique for evaluating causal discovery algorithms. However, our method differs critically from previous methods due to our development of a random model generation procedure that allows the user to control the model’s standardized effect sizes, specifically r values. We used this new method to generate a large table of results (available at https://osf.io/zmwyb/). Our analysis of the results in this table revealed some unexpected findings in the way that the PC and FGES algorithms converge, as well as other interactions between the algorithms, hyperparameters, and simulation settings that we evaluated. In addition, we created a Shiny app (https://kummerfeldlab.shinyapps.io/PowerSim2023-1/) that allows users to quickly answer the most common power analysis questions, and we provided examples of such solutions as well. The code, results table, and shiny app are all freely available for researchers to use.
The method presented here has some limitations, which we hope to address in future work. All of the edges within each generated graph have the same r values, and this is unrealistic. Real-world systems will almost universally have edge strengths that vary substantially. While we do not know whether incorporating this complexity into the models will change the power analysis results, nevertheless this is something that should be incorporated in future methods. The method currently also only samples from graphs uniformly for a fixed edge density, but other methods for sampling from the space of graphs may better simulate the distribution of graphs we would expect to find in the world, such as graphs with small world (scale-free) structure. This method also does not incorporate any unmeasured variables and as such cannot be used to evaluate the impact of unmeasured variables on statistical performance. All of these modifications can be incorporated into our power analysis framework in the future, however, due to its modular design.
In terms of the table of results, while it is extensive there are still many gaps that we did not consider. For example, we do not have results for sample sizes below 50 or above 102400 and did not test PC with alpha values above 0.1, or FGES and GRaSP at penaltydiscount values other than 2. Similarly, the current table does not cover data with more than 100 variables, or graphs with edge density below 1 or above 2. We also did not evaluate algorithms other than PC, FGES, and GRaSP.
Aside from improving upon the above limitations, we also hope to improve computational performance so that the method can be used more easily and with less computational resources. We also hope to extend these methods to work for algorithms that produce partial ancestral graphs instead of patterns, to allow the incorporation of background knowledge of varying amounts in the search algorithms and to extend to other data types and distributions such as categorical variables, nonlinear relationships, and non-Gaussian noise.
In conclusion, the current study introduced a simulation-based power analysis framework for causal discovery that can be extended and customized to the need of different data types and research needs. This will make causal discovery more accessible to researchers who are not familiar with the formal theory of causal modeling, enable researchers to perform sample size planning for projects where data will be collected specifically for causal discovery analysis, and improve the interpretation of causal discovery results.
Data and Code availability
All data and code have been made freely available, with links provided in the manuscript.
References
Pearl, J.: Causality. Cambridge University Press, UK (2009)
Spirtes, P., Glymour, C.N., Scheines, R., Heckerman, D.: Causation, prediction, and search. MIT press, Cambridge (2000)
Eberhardt, F.: Introduction to the foundations of causal discovery. Int. J. Data Sci. Anal. 3(2), 81–91 (2017)
Spirtes, P.: Introduction to causal inference. J. Mach. Learn. Res. 11(5), 1643–1662 (2010)
Tsamardinos, I., Brown, L.E., Aliferis, C.F.: The max-min hill-climbing Bayesian network structure learning algorithm. Mach. Learn. 65(1), 31–78 (2006)
Aliferis, C.F., Statnikov, A., Tsamardinos, I., Mani, S., Koutsoukos, X.D.: Local causal and Markov blanket induction for causal discovery and feature selection for classification part i algorithms and empirical evaluation. J. Mach. Learn. Res. 11(1), 171–234 (2010)
Kummerfeld, E., Ramsey, J.: Causal clustering for 1-factor measurement models. In: Proceedings of the 22nd ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, pp 1655–1664, (2016)
Bongers, S., Forre, P., Peters, J., Mooij, J.M.: Foundations of structural causal models with cycles and latent variables. Ann. Stat. 49(5), 2885–2915 (2021)
Versteeg, P., Zhang, C., Mooij, JM: Local constraint-based causal discovery under selection bias. arXiv preprint arXiv:2203.01848, (2022)
Guyon, I., Statnikov, A., Batu, B.B.: Cause effect pairs in machine learning. Springer, USA (2019)
Shimizu, S.: Lingam: non-gaussian methods for estimating causal structures. Behaviormetrika 41(1), 65–98 (2014)
Hoyer, P., Janzing, D., Mooij, J.M., Peters, J., Schölkopf, B: Nonlinear causal discovery with additive noise models. In: Advances in Neural Information Processing Systems, 21 (2008)
Zhang, K., Hyvärinen, A: Distinguishing causes from effects using nonlinear acyclic causal models. In: Causality: Objectives and Assessment, PMLR, pp 157–164, (2010)
Janzing, D., Mooij, J., Zhang, K., Lemeire, J., Zscheischler, J., Daniušis, P., Steudel, B., Schölkopf, B.: Information-geometric approach to inferring causal directions. Artif. Intell. 182, 1–31 (2012)
Mooij, J.M., Peters, J., Janzing, D., Zscheischler, J., Schölkopf, B.: Distinguishing cause from effect using observational data: methods and benchmarks. J. Mach. Learn. Res 17(1), 1103–1204 (2016)
Claassen, T., Heskes, T.: Causal discovery in multiple models from different experiments. In: Advances in Neural Information Processing Systems, 23, (2010)
Hyttinen, A., Eberhardt, F., Hoyer, P.O.: Experiment selection for causal discovery. J. Mach. Learn. Res 14, 3041–3071 (2013)
He, Y.-B., Geng, Z.: Active learning of causal networks with intervention experiments and optimal designs. J. Mach. Learn. Res 9, 2523–2547 (2008)
Tong, S., Koller, D: Active learning for structure in Bayesian networks. In: International Joint Conference on Artificial Intelligence, 17: 863–869, (2001)
Statnikov, A., Ma, S., Henaff, M., Lytkin, N., Efstathiadis, E., Peskin, E.R., Aliferis, C.F.: Ultra-scalable and efficient methods for hybrid observational and experimental local causal pathway discovery. J. Mach. Learn. Res. 16(1), 3219–3267 (2015)
Ma, S., Kemmeren, P., Aliferis, C.F., Statnikov, A.: An evaluation of active learning causal discovery methods for reverse-engineering local causal pathways of gene regulation. Sci. Report 6(1), 1–14 (2016)
Frieden, T.R.: Evidence for health decision making-beyond randomized, controlled trials. New England J. Med. 377(5), 465–475 (2017)
Kraemer, H.C., Blasey, C.: How many subjects?: Statistical power analysis in research. Sage Publications, USA (2015)
Cohen, J.: Statistical power analysis. Curr. Dir. Psychol. Sci. 1(3), 98–101 (1992)
Cohen, J.: Statistical power analysis for the behavioral sciences. Routledge, UK (2013)
Thomas, L.: Retrospective power analysis. Conserv. Biol. 11(1), 276–280 (1997)
Reisach, A., Seiler, C., Weichwald, S.: Beware of the simulated dag! causal discovery benchmarks may be easy to game. Adv. Neural. Inf. Process. Syst. 34, 27772–27784 (2021)
Kummerfeld, E.: A simple interpretation of undirected edges in essential graphs is wrong. PLoS ONE 16(4), e0249415 (2021)
Miley, K., Meyer-Kalos, P., Ma, S., Bond, D.J., Kummerfeld, E., Vinogradov, S.: Causal pathways to social and occupational functioning in the first episode of schizophrenia: uncovering unmet treatment needs. Psychol. Med. 53, 2041–2049 (2021)
Rawls, E., Kummerfeld, E., Mueller, B.A., Mas, S., Zilverstand, A.: Executive and attentional resting-state hubs of the human cortical connectome revealed by a causal discovery method for data-driven effective connectivity analysis. BioRxiv 45, 54354 (2021)
Rawls, E., Kummerfeld, E., Zilverstand, A.: An integrated multimodal model of alcohol use disorder generated by data-driven causal discovery analysis. Commun. Biol. 4(1), 1–12 (2021)
Bronstein, M., Kummerfeld, E., Iii, AM., Vinogradov, S: Willingness to vaccinate against sars-cov-2: The role of reasoning biases and conspiracist ideation. Available at SSRN 3908611, (2021)
Kummerfeld, E., Ma, S., Blackman, R.K., DeNicola, A.L., Redish, A.D., Vinogradov, S., Crowe, D.A., Chafee, M.V.: Cognitive control errors in nonhuman primates resembling those in schizophrenia reflect opposing effects of NMDA receptor blockade on causal interactions between cells and circuits in prefrontal and parietal cortices. Biol. Psych. Cognit. Neurosci. Neuroimag 5(7), 705–714 (2020)
Anker, J.J., Kummerfeld, E., Rix, A., Burwell, S.J., Kushner, M.G.: Causal network modeling of the determinants of drinking behavior in comorbid alcohol use and anxiety disorder. Alcohol. Clin. Exp. Res. 43(1), 91–97 (2019)
Shen, Xi., Ma, S., Vemuri, P., Castro, M.R., Caraballo, P.J., Simon, G.J.: A novel method for causal structure discovery from EHR data and its application to type-2 diabetes mellitus. Sci. Reports 11(1), 1–9 (2021)
Saxe, G.N., Ma, S., Morales, L.J., Galatzer-Levy, I.R., Constantin, A., Marmar, C.R.: Computational causal discovery for post-traumatic stress in police officers. Transl. Psychiatr. 10(1), 1–12 (2020)
Attur, M., Statnikov, A., Samuels, J., Li, Z., Alekseyenko, A.V., Greenberg, J.D., Krasnokutsky, S., Rybak, L., Lu, Q.A., Todd, J., et al.: Plasma levels of interleukin-1 receptor antagonist (il1ra) predict radiographic progression of symptomatic knee osteoarthritis. Osteoarthr. Cartil. 23(11), 1915–1924 (2015)
Ramsey, J.D., Malinsky, D., Bui, K.V.: Algcomparison: Comparing the performance of graphical structure learning algorithms with tetrad. J. Mach. Learn. Res. 21(238), 1–6 (2020)
Singh, K., Gupta, G., Tewari, V., Shroff, G.: Comparative benchmarking of causal discovery algorithms. In: Proceedings of the ACM India Joint International Conference on Data Science and Management of Data, pp 46–56, (2018)
Kummerfeld, E., Rix, A.: Simulations evaluating resampling methods for causal discovery: ensemble performance and calibration. In: 2019 IEEE International Conference on Bioinformatics and Biomedicine (BIBM), IEEE, pp 2586–2593, (2019)
Wang, Y.A., Rhemtulla, M.: Power analysis for parameter estimation in structural equation modeling: a discussion and tutorial. Adv. Methods Pract. Psychol. Sci. 4(1), 2515245920918253 (2021)
Wolf, E.J., Harrington, K.M., Clark, S.L., Miller, M.W.: Sample size requirements for structural equation models: An evaluation of power, bias, and solution propriety. Educ. Psychol. Meas. 73(6), 913–934 (2013)
Moshagen, M., Erdfelder, E.: A new strategy for testing structural equation models. Struct. Equ. Modeling 23(1), 54–60 (2016)
Muthén, L.K., Muthén, B.O.: How to use a monte Carlo study to decide on sample size and determine power. Struct. Equ. Model. 9(4), 599–620 (2002)
Ramsey, JD., Zhang, K., Glymour, M., Romero, RS., Huang, B., Ebert-Uphoff, I., Samarasinghe, S., Barnes, EA, Glymour, C.: Tetrad-a toolbox for causal discovery. In: 8th International Workshop on Climate Informatics, (2018)
Ramsey, J., Glymour, M., Sanchez-Romero, R., Glymour, C.: A million variables and more: the fast greedy equivalence search algorithm for learning high-dimensional graphical causal models, with an application to functional magnetic resonance images. Int. J. Data Sci. Anal. 3, 121–129 (2017)
Lam, W-Y., Andrews, B., Ramsey, J.: Greedy relaxations of the sparsest permutation algorithm. In: Uncertainty in Artificial Intelligence, PMLR, pp 1052–1062, (2022)
Funding
This project was supported by funding from grants P50 MH119569 and NCRR 1UL1TR002494-01.
Author information
Authors and Affiliations
Contributions
EK and SM conceived the study. All authors contributed to the design of the study. All code was written and executed by LW. All authors contributed to the writing for the first draft of the manuscript. All authors read and approved the final manuscript.
Corresponding author
Ethics declarations
Conflict of interest
The authors have no conflict of interests to declare.
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Kummerfeld, E., Williams, L. & Ma, S. Power analysis for causal discovery. Int J Data Sci Anal 17, 289–304 (2024). https://doi.org/10.1007/s41060-023-00399-4
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s41060-023-00399-4