1 Introduction

In the past few years, industrial sectors, such as aerospace, automotive and medical, have been attracted by the additive manufacturing (AM) approach to produce high-performance metallic components [1]. In the aerospace and automotive fields, the main driver is the production of lightweight components, integrated parts and high-performance materials with tailored microstructure [2]. For medical applications, the possibility of producing structures with specific design, mass and stiffness has drawn the development of materials and customised implants with better tissue integration [3]. The interconnected porosity of unit cells is the closest structure that mimics trabecular bones [4]. A lattice structure is a 3D open topologically ordered geometry obtained by repeating an elementary cell in a predefined 3D space. The cell is defined by thin elements, called struts, connected in specific nodes and forming a predefined topology [1]. Ashby [5] identified that the characterising parameters of the cellular structure are as follows: material, cell topology and corresponding arrangement, and relative density. The material properties influence the physical behaviour of the structure, particularly for biomedical and structural applications. The cell topology indicates the structural deformation under a specific load. The relative density is defined as the ratio between the density of the lattice structure and the density of a corresponding volume of bulk material. By this parameter, the lattice structure behaves as a homogenised meta-material [6].

Producing such reticular and complex structures is feasible using powder bed fusion (PBF) AM technology [7]. Among AM technologies, the electron beam powder bed fusion process (EB-PBF) is extensively used because it allows the production of such structures without oxygen contamination and supports [8]. Additionally, there is the possibility to nest multiple parts easily in the same build job [8]. However, the high energy involved in the electron beam may cause deviation from the nominal dimensions of such thin structures, and, therefore, the selection of the process parameters may play a key role in determining the actual structure geometries. Cansizoglu et al. [9] showed that the minimum strut dimension was detected when the angle of the struts with respect to the build platform was over 20 degrees. Lower build angles resulted in thinner struts but without structural integrity. On the other hand, the increase in the building angle caused thicker struts. In agreement with Cansizoglu et al. [9], Zhang et al. [10] showed that both the diameter and building angle of the strut affect the final accuracy of the structure. Wu et al. [11] measured the strut dimension in a graded porous structure, remarking a systematic difference between the nominal and manufactured strut dimensions. Epasto et al. [12] found a correlation between cell dimension morphological parameters and strut diameter and length. Béraud et al. [13] attempted to investigate the relationship between the final part thickness, the focus offset and the beam diameter, which is not a parameter set directly in the machine [14]. The focus offset was the most influential process parameter in determining the beam diameter and, therefore, the final part thickness.

In summary, these studies and others on different AM processes (e.g. [15,16,17]) emphasised a relevant effect of the process tuning on the final geometry of the lattice structures regarding the nominal one. In light of those results, it is presumable that if the process conditions vary, the actual structure morphometric parameters significantly change, affecting both the mechanical [16, 18] and the biological performances of the structure [19,20,21].

The mechanical properties (elastic and flexural modulus, compression and bending behaviour) [5, 9, 10, 13, 18, 22,23,24] and the biological quality (influence of cell type and size, material, relative part density) [11, 12, 20, 25, 26] of lattice structures made by EB-PBF have been extensively investigated. In general, when lattice structures are tested at room temperature under compression, they exhibit a typical three stages behaviour (Fig. 1) [18]: an initial elastic behaviour (red line), a progressive collapse of the layers (blue line) and a final collapse with the same trend of the bulk material (green line).

Fig. 1
figure 1

Typical compressive behaviour of a generic lattice structure (adaptation from Fig. 1 [18])

Full size image

All studies on mechanical characterisation refer to the work carried out by Ashby [27], which correlated the mechanical response of the structure (Young’s modulus and yield under compression) and its relative density. Additionally, Murr et al. [24] proved that the lattice properties are greatly influenced by unit cell topology and its dimensions. All works reported in the literature on the mechanical characterisation of lattice structures refer only to the correlation between the mechanical properties and the relative density of the structure (Ashby-Gibson model [28]). To the best of the authors’ knowledge, all studies calculated the mechanical properties from the nominal CAD dimensions of the structure [4, 7, 9, 18, 29]. These approaches exhibit some critical points. Comparing results in literature which used the same material, structures with the same relative density showed remarkably different mechanical properties [18, 30, 31], which was not justified. In addition, the actual morphometric parameters may depend on the processing condition and deviate from nominal designed ones. Consequently, the structure properties will be altered with respect to the ones of the nominal counterparts. Therefore, it is crucial to identify the role that the process parameters play in determining the morphometric parameters of the structure and the relationship with its actual mechanical response.

This paper analyses the variation of the lattice mechanical properties in relation to all morphometric parameters that describe a lattice structure. The same nominal structure is produced by the EB-PBF process and varying the EB-PBF process conditions to observe relevant differences in the final manufactured structure. The beam current, the focus offset and the scan speed were investigated using two designs of experiments (DoE). The first DoE serves as an explorative study, while the second, narrower than the first, is a confirmation run. X-ray computed tomography analyses are used to measure the main morphometric parameters of the structures, such as the struts size, the relative density and the resistant cross-section. Uniaxial compressive tests are performed, and the correlation between the structure morphometry (relative density, resistant cross-section and relative density) and the corresponding mechanical properties is investigated. In addition, the effect of processing conditions on the morphometric parameters of the structure with specific concern to the strut dimension was investigated using descriptive and inferential statistical tools. Models are inferred from the process parameters for forecasting the strut size.

2 Material and methods

2.1 Design of the experiments

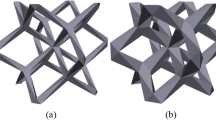
A diamond unit cell lattice structure was selected for the study (Fig. 2), being one of the most commonly used in industry [32]. In addition, this structure is self-supported [4]. The elementary cell has a dimension of 2 mm, with a nominal strut size equal to 0.420 mm. The nominal relative density with respect to the corresponding bulk volume was equal to 20%. The elementary cell was repeated in an ordered manner into a cubic volume of 20 mm edge.

Fig. 2
figure 2

Diamond lattice structure from Materialize Magics database

Full size image

The influence of process parameters on the morphometric features of the structure was investigated by designing two full factorial design of experiments (DoEs) plans. For the EB-PBF process, the most common parameters are the acceleration voltage, the scanning strategy, the layer thickness, the beam current, the scan speed and the spot size [33]. The EB-PBF systems available on the market operate at constant acceleration voltage and, in most cases, cannot be varied. In this work, an Arcam Q10plus was adopted, operating at 60 kV. Only a contour strategy has been used due to the small size of the struts and thus the small sections to be melted. When only contours are used to melt the cross-section, the beam manual current, the spot size, the scan speed, and the distance (offset) between adjacent contours are the most important parameters influencing the melting quality. The manual current (with a constant acceleration voltage) and the scan speed define the amount of energy provided in the unit of time, while the spot size provides information on the dimension of the area in which this energy is distributed. However, in the EB-PBF systems, the spot size cannot be set directly, but it is controlled by jointly varying the beam current and the focus offset. Therefore, the challenging aspect when selecting the level of each experimental design factor is the evaluation of the existing relationship between the manual current, focus offset and actual beam spot size. The exact relationship is unspecified, but it is known that it is not linear. This means that, for example, at a fixed current, increasing focus offset does not always mean bigger spot size and vice versa. As a guideline, the parameters reported in Ref. [18] (manual current 3 mA, focus offset 0 mA and scan speed 450 mm/s), correspond to the Standard Arcam parameters for the Ti6Al4V lattice structures, and the parameters reported in Ref. [14] (manual current 5 mA, focus offset 0 mA and 5 mA and scan speed 450 mm/s, 550 mm/s and 650 mm/s) have been used for the selection. In particular, Galati et al. [14] reported that the obtained width of the melted line for the selected focus offset and beam current values ranged between around 0.400 mm and 0.300 mm, which were considered acceptable with respect to the designed strut dimension in this work (0.420 mm). In that study, higher focus offset values corresponded to larger melt pools and thus larger melted lines [14]. Therefore, to explore the effect on structure morphometric parameters, the focus offset and the scan speed values have been varied remarkably from the standard Arcam parameters while the beam manual current was kept in a narrow, low range to avoid overheating effect. The offset between adjacent contours has been set equal to the default parameter (0.3 mm).

The first DoE (DoE1) consists of two levels for the beam manual current and the beam scan speed and three for the focus offset (Table 1). At least two replicas have been fabricated for each process parameter combination to monitor the replicability of the process (Appendix 1).

Table 1 Process parameters DoE1
Full size table

From the results obtained by DoE1, a second experimental plan has been designed (DoE2), consisting of a narrow range of levels (Table 2) within the variation range of DoE1. In particular, the observations from DoE1 showed only decreasing strut size by increasing the focus offset, meaning that the combination between the selected focus offset and manual current values always corresponded to decreasing spot size (see Sect. 3.2). For this reason, DoE2 considered a variation between positive and negative values of focus offset in a narrow range, closer to the standard value, to obtain the non-linear trend stated in the literature [14]. The manual current, the scan speed and the focus offset have been investigated at two, three and four levels, respectively. At least one replica for each process parameter combination has been fabricated (Appendix 2). The combination of parameters from DoE1, corresponding to manual current 2 mA, scan speed 450 mm/s and focus offset 0 mA, has also been included in DOE2 to make the experiment more robust with respect to the process replicability.

Table 2 Process parameters DoE2
Full size table

Fixing the Z-axis as the build direction, each cubic lattice specimen was tilted by 45 degrees with respect to the X and Y axes to avoid using supports (Fig. 3). In addition, the samples were positioned at 5 mm from the building platform to avoid any thermal effect. The replicas were also equally spaced to avoid any thermal interaction between each other. Figure 3 shows the job design for DoE1, in which spatial randomization of the replicas was proposed to avoid location-dependent influences.

Fig. 3
figure 3

View of the arrangement of the replicas of DoE1 on the building platform. Details on the correspondence between the structure index and the parameters can be found in Appendix 1

Full size image

The production was performed using an Arcam Q10plus, an EB-PBF system. Standard Arcam Ti-6Al-4 V powder was used with a particle size distribution between 45 μm and 106 μm, and the layer thickness was set equal to 50 μm. After the production, the samples were cleaned from sintered powder by shoot blasting using a pressure of 4.5 bar and with the same powder used in the production phase.

2.2 Strut characterization

The strut size of each replica of DoE1 and DoE2 was measured using X-ray computed tomography (CT-scan GE Phoenix v|tome|x s). The scans were performed using a voltage of 240 kV, a current of 150 μA and a voxel size of 0.035 mm. 1001 2D projections were collected for each sample, and the 3D volume was reconstructed using VGStudio Max 3.4. A large portion of the structure, called region of interest (ROI), has been extracted for each sample, and the tool “wall thickness analysis” has been applied to automatically evaluate the average dimension of the strut using the sphere method. The output is a histogram of wall thickness occurrences that provides the mean dimension of the struts with the corresponding deviation. The smaller values were excluded from the subsequent analyses because they referred to the ROI border. On the other hand, the largest values were also excluded because they referred to the connection nodes of the struts. To identify the upper threshold, a preliminary measurement of the node section was performed from the CT extracted cross-sections (see, e.g., Fig. 5). Therefore, the struts dimension and its deviation are obtained as the average of at least 500,000 measurements.

For validation purposes, additional measurements (at least five) were acquired manually in several areas of the 3D reconstructed volume and using the cylinder fitting instrument. The diameter of the fitted cylinder was assumed as the width of the strut.

For each specimen, a second portion of the whole volume, including multiple elementary unit cells, has been considered (e.g., Fig. 4) to compute the effective relative density as the ratio between the volume occupied by the material and the volume of the ROI.

Fig. 4
figure 4

Example of ROI extracted used for calculating the relative density

Full size image

The struts shape has been evaluated in terms of roundness and straightness along its axis using the cylindricity tolerance. With this scope, the cylinder fitting tool present in VGStudio Max 3.4 has been used on at least 10 struts located in different positions of the structure. The obtained tolerances ranged between 0.15 mm and 0.20 mm, independently of the process parameters. Therefore, the process parameters did not affect the strut shape significantly.

2.3 Mechanical characterisation

Uniaxial compression tests have been performed for the samples produced in DoE1 and using an AURA 10 T | EASYDUR ITALIANA with a maximum load capacity equal to 10 tons. During the test, a constant strain rate equal to 1.5 mm/min was applied up to the complete collapse of the structure. The stress/strain curves have been derived from the load/displacement data collected with a 500 Hz sampling frequency.

The data have been referred to the linear elastic law using the analytical approach.

σ = E · ε

where, σ [MPa] = L/A0: load, L, variation referred to the initial section, A0.

ε [−] = (l−l0)/l0: actual length, l, after the compressive test referred to the initial length, l0.

The curve has been computed using the strain deformation function of the stress level, and the elastic region has been interpolated with a linear regression model. The angular coefficient of the linear equation corresponds to the elastic modulus.

To consider the actual geometry of the lattice sample, the sample height, l0, and cross-section, A0, have been extracted from the 3D reconstruction obtained by the CT scan analysis. In particular, the actual resistant cross-section has been evaluated by selecting the cross-section with the minimum area corresponding to the section that includes the structure nodes, and its area has been evaluated by image analysis (e.g., Fig. 5).

Fig. 5
figure 5

Example of resistant cross-section analysis using ImageJ software. The white area is the actual cross-section of the lattice structure

Full size image

3 Results and discussion

The collected morphometric parameters (struts dimension, structure relative density and structure cross-section) have been collected in an open-access database [34].

3.1 CT-scan measurements

Figure 6 compares CT-scan 3D reconstructions of three portions of samples built with different process parameter settings. The wall thickness map was plotted overlapping a part of the illustrated portions for completeness. The warmer colours represent the thicker dimensions, whereas colder colours represent the thinner ones. As observed, a variation of the process parameters significantly caused the structure morphometry variation.

Fig. 6
figure 6

Examples of the variation of strut dimension obtained with different process parameters settings (lattices from DoE2)

Full size image

Figure 7 shows two selected stereomicroscope images for comparing the strut dimensions obtained under two different processing conditions. As it can be observed, the effect on the struts is evident. The thinner strut appears slimmer, while the thicker one is more stocky.

Fig. 7
figure 7

Stereomicroscope images of lattices with different strut dimensions: a index VI DoE2 and b index XXII DoE2

Full size image

3.2 Morphometric parameters and mechanical properties

Figure 8 represents the lattice structure topology behaviour during the uniaxial compression. The stress level progressively increases with increasing strain (region 1 in Fig. 8). At the UCS level, the structure presents the first failure at 45 degrees due to the collapse of an intermediate layer. The increasing strain leads to a failure of the specimen, at the same angle, at several different layers (region 2 in Fig. 8). After those stages, the sample behaviour is similar to a bulk material (region 3 in Fig. 8).

Fig. 8
figure 8

Example of a compression curve (sample process parameter index I (specimen 1) DoE1)

Full size image

The resulting compression curve can be explained by the structure design: when a single strut fails, the load drops rapidly (region 2 in Fig. 8). This result agreed with the literature (e.g., Ref. [18, 35]). The stress level fluctuates by increasing the strain level, and this behaviour can be attributed to a stretch-dominated effect [35, 36]. The recurring twitches of the compression curve represent the subsequent fails on different planes. This behaviour can be compared to a corresponding brittle structure [18].

Figure 9 depicts the average morphometric parameters (cross-section, strut size and relative density) of each structure with the corresponding process parameters and mechanical performance (Young’s modulus (E), strain (ε) and ultimate compressive strength (UCS)).

Fig. 9
figure 9

Mechanical and morphometric properties variation for different process parameters applied to the same nominal CAD geometry

Full size image

Except for samples V and VI, the average strut dimension is always larger than the designed nominal one (0.420 mm). Manual current equal to 4 mA produced the thickest struts. If it is combined with the lowest value of scan speed (samples such as VIII and IX), the strut dimension is almost twice larger than the nominal counterpart, with a strut dimension increasing by increasing the focus offset. Instead, the strut dimensions are comparable at scan speed equal to 750 mm/s and varying the focus offset. At manual current equal to 2 mA, the strut dimensions are closer to the nominal value. For scan speed equal to 750 mm/s and focus offset equal to 0 mA, the deviation between the actual and nominal size is the smallest (7%).

Contrary to the observed results for manual current equal to 4 mA, the strut dimension decreases by fixing the scan speed and increasing focus offset. In particular, at scan speed equal to 750 mm/s, the strut dimension at 9 mA and 15 mA of focus offset are equal and 20% smaller than the nominal one. It is reasonable to suppose that, in this case, the beam diameter decreases by increasing the focus offset; therefore, the measured strut dimension (0.32 mm) value may represent the technological limitation of the system. Overall, the manual current seems to affect the most strut dimension.

The cross-section area (A0), namely the resistant cross-section, follows the strut width. In fact, the connection areas (nodes) are larger when joining larger struts. For example, Fig. 10 compares the samples with indexes V and IX, corresponding to a strut dimension equal to 0.32 mm and 0.80 mm, respectively. Chief among the process parameters for determining the resulting cross-section still seems to be the level of manual current. A variation in the focus offset level for fixed manual current and scan speed levels has a negligible effect on the cross-section area. A remarkable trend is not evident for manual current equal to 2 mA, varying the focus offset. For manual current equal to 4 mA, the larger cross-sections have been detected at the intermediate level of focus offset, 9 mA.

Fig. 10
figure 10

Example from DoE2 of the variation of nodes and strut for different sets of process parameters: a index V: node and strut dimension different due to the smaller strut size b index IX: node and strut dimension are comparable in dimension

Full size image

As a consequence of the strut dimension and cross-section area, the relative density of the structure depends on the process parameters as well. In all cases, the measured value of relative densities was over the nominal value (20%). The highest manual current or lower scan speed produced a more dense structure. The most significant deviation from the nominal relative density was observed for manual current equal to 4 mA and scan speed equal to 450 mm/s, which produced highly dense structures with a relative density of over 60%. The lowest values of relative densities were detected when the strut dimensions fell below the nominal value (samples V, VI).

As can be observed in Fig. 9, the mechanical properties are strictly connected to the morphometric parameters of the structure and, therefore, to the processing condition.

Unlike the literature data based on Ashby and Gibson’s model [28] and reviewed in Ref. [18], no remarkable relationship between the relative density and the mechanical properties has been detected. Therefore, it is presumable that the relative density alone cannot explain the mechanical properties. The strut dimension and relative cross-section should be considered as well. There is a threshold limit of relative density for which the same topological structure behaves mechanically differently. In particular, a systematic variation can be observed between open structure (relative density below 50%) and bulky samples (relative density above 60%). For the open structures, the Young’s modulus follows the variation of the strut width, while for the bulky ones the Young’s modulus follows the variation of the relative density. Bulky samples are described by high value of the relative density due to the thick and stocky struts, with connection nodes approximately of the same dimension (Fig. 10b), that fill the empty spaces of the lattice structure almost completely. Their mechanical behaviour can be roughly approximated by stocky beam, and, therefore, highly resistant to the bending. In the open structure, the strut is thin, with a reasonable ratio between the diameter and its length. The elastic behaviour is therefore more like a slender beam and thus affecting the Young’s modulus. Similarly, the UCS values of bulky samples follows their relative densities, instead the UCS of an open structure is proportional to its cross-section area. Therefore, the effect of the relative density is predominant for the bulky samples. The strain values follow approximately the trend of the strut dimensions up to the technological limit (0.32 mm). This finding is reasonable because the strut geometry may contribute the most to the structure deformation.

Another difference between the open and bulky structure can be noticed regarding the standard deviation of the mechanical properties’ values. In most cases, the values for the open structures are more dispersed. Also, in this case, these results may be explained by the strut geometry. Slender struts may be more sensitive to the presence of process-induced defects due to powder particles attached to the external surface, which, randomly distributed, may jeopardise the mechanical behaviour of the structure for the increased surface roughness (see also Del Guercio et al. [30], Figs. 12 and 13).

The manual current is still the factor producing the most remarkable difference. Practically, a manual current equal to 2 mA always produces open structures, while bulky ones correspond to a manual current of 4 mA. Therefore, at 2 mA, Young’s modulus, strain and UCS values are systematically lower with respect to the corresponding counterpart at 4 mA. Within a specific value of manual current, Young’s modulus and UCS values are higher at lower values of scan speed. For the produced structures, fixing the manual current, at scan speed equal to 750 mm/s, Young’s modulus and the UCS decrease by increasing the focus offset. At 2 mA of manual current and scan speed equal to 450 mm/s, the effect of focus offset on Young’s modulus variation is negligible, while the UCS values follow the decreasing focus offset. The same cannot be affirmed in the scan speed conditions at a manual current equal to 4 mA. Young’s modulus and the UCS assumed a minimum value at 9 mA in this case. The strain values significantly differ between manual current at 2 mA or 4 mA. However, at 2 mA, the strain values vary in an extremely limited range, within the standard deviation of the measurements in most cases. At 4 mA, a significant effect of scan speed is noticeable; higher values produced structures with a lower strain.

The Pearson coefficient (Table 3) and ANOVA (Table 4) have been calculated to quantitatively evaluate the correlation between the morphometric parameters and the mechanical properties. Adjusted R squared (R2 adj in Table 4) has been used as a goodness-of-fit index to identify the percentage of variance in the target field explained by the factors used in the experiments.

Table 3 Quantitative correlation analysis between mechanical properties and morphometric parameters
Full size table
Table 4 ANOVA of mechanical properties as a function of the morphometric parameters of the structure and ANOVA of the estimated regression models for the mechanical properties
Full size table

The Pearson coefficients showed a remarkable positive correlation between the mechanical properties and all morphometric parameters., particularly in the case of E and UCS. In agreement with the discussion reported above, the ANOVA (Table 4) shows that the morphometric parameters of the structure influence the mechanical properties differently. Contrary to the Ashby and Gibson model, the ANOVA test revealed that the significant factors for the variation of E (p-value ≤ 0.05) are the cross-section and the strut measure and their interaction. As detected in Fig. 9, the relative density is significant for the UCS variation, which confirms the categorisation between open and bulky structures. In addition, the UCS values are also influenced by the cross-section and its interaction with the strut measure, which could be considered as an index of the beam shape (stocky or slender). The ANOVA test (Table 4) detected significant factors for the variation of ε, the relative density and its interaction with the structure cross-section. The R2 adj values showed that, in the target field, the investigated parameters explain very well the variation of mechanical properties (70% of the variation of E, 90% of the variation of UCS and 60% of the variation of ε). The residual from the model can be explained by an effect of the cell topology, according to Ref. [24].

Figure 11 compares the discussed experimental results of this study with the results of previous investigations reported in the literature for Ti6Al4V. The mechanical properties, essentially the relative Young’s modulus (ratio between Young’s modulus of the structure, E, and of the material, E0), were reported according to Ashby and Gibson [28] as a function of the relative density (ratio between the density of the structure ρ and the material density of the structure, ρ0). The analysis also considered different topologies, as reported in the graph legend.

Fig. 11
figure 11

Relative Young’s modulus as a function of the relative density where E refers to the structure Young’s modulus and E0 refers to the material Young’s modulus; ρ refers to the structure density and ρ0 refers to the material density

Full size image

As far as the experimental data presented in this work, despite the same topology and material have been used for producing the lattice structure, the experimental data of this study do not fit a linear relationship between the relative Young’s modulus and relative density as proposed by Ashby and Gibson [28]. The data seems to lay on a second-order polynomial in the form E/E0 = a (ρ/ρ0) 2 + b (ρ/ρ0) + c, where the coefficients a, b and c are equal to 0.0989, 0.1308 and -0.0185, respectively.

Comparing cells with similar or same relative density, it can be noticed that the mechanical properties are, in the same case, significantly different. This could depend on the topology of the structure [31]. However, even the same topology and similar relative density (e.g., Ref. [37] vs Ref. [38]) showed different mechanical properties. Previous studies have also detected this discordance, such as [18, 37,38,39,40,41,42,43]. In these cases, therefore, the Ashby and Gibson [28] model fails to comprehensively capture the variation of mechanical properties. These data could be completed with the observations presented in this study, and the variation of such mechanical properties could be better justified if analysed jointly with other morphometric parameters of the structure. However, it should also be noticed that actual Young’s modulus and relative density could differ from the data reported in the literature because only the nominal dimension has been used in those studies.

4 Statistical analysis of the effect of process parameters on the struts dimension

The collected experimental struts dimensions data for DoE1 and DoE2 were statistically analysed using Minitab 17 software. As mentioned above, DoE2 aimed to investigate the effect of process parameters in the range of variation of DoE1.

For both DoEs, the normality of the data distribution has been checked to validate the primary hypothesis for applying the descriptive and inferential statistics. As shown in Fig. 12, the data were normally distributed, indicating the absence of a systematic effect on the measurements. The skewness coefficients equal to 0.30 and -0.34 for DoE1 (Fig. 12a) and DoE2 (Fig. 12b), respectively, indicate nearly symmetric distributions, in which the left limit represents the technological limit of the production process [44].

Fig. 12
figure 12

Data distribution for DoE1 a and DoE2 b and negative skewness

Full size image

Figure 13 shows the main effect plots obtained by grouping the data according to the investigated factor. According to the qualitative analysis reported in the previous section, as far as DoE1 is concerned, all the investigated factors significantly affect the struts dimension. Increasing values of manual current produce larger struts while increasing scan speed and focus offset values generate a thinner strut. This result can be explained by qualitatively considering the melt pool dimension and the heat transfer between the melt pool and the surrounding. Considering a fixed offset between adjacent contours used to melt the strut cross-section, higher values of manual current involve a higher amount of thermal energy supplied during the melting in the same area, which produces a larger melt pool and thus larger contours. On the contrary, a higher scan speed involves less energy supplied in a unit of time, meaning slimmer melt pools and a thinner contour. The monotonic decreasing trend of the strut dimension by varying the focus offset can be explained by the unintentional choice of combination of beam current and focus offset values which produced only decreasing spot size. In fact, the more detailed analysis in a narrow range included in DoE2 showed that the focus offset effect assumed a like-parabolic trend with a maximum strut dimension around 3 mA (Fig. 13). Above this value, the slope became negative in agreement with the observations between 9 and 15 mA in DoE1. This means that in the range of investigated manual current values, the variation of focus offset produced different beam spot diameters and thus variations of the strut dimensions. In a narrow range, the scan speed effect is almost negligible. However, the segment between 550 mm/s and 650 mm/s has a negative sloping according to the results observed in DoE1.

Fig. 13
figure 13

Main effect plots for a DoE1 and b DoE2

Full size image

Figure 14 shows the significance of the interaction among the investigated factors graphically. For DoE1, only a weak interaction between the focus offset and the manual current can be observed. For DoE2, this interaction became more evident. This result is explained because the beam diameter is controlled by the manual current and the focus offset [14] and confirms the above findings. In DoE2, a strong interaction between the focus offset and the scan speed is also noticeable for a fixed beam current value. The significance of this interaction can be explained by considering that the melt pool size and the heat transfer between the melt pool and the surrounding depend on the amount of heat supplied by the beam in the unit of time, and the area on which this heat is distributed.

Fig. 14
figure 14

A plot of the effect of the interactions between the process parameters on the strut dimension

Full size image

Behind the descriptive analysis, ANOVAs were performed under the null hypothesis that the investigated parameters and their interaction do not affect the strut dimension. The ANOVA confirms the findings obtained by the descriptive analysis. Regarding the DoE1, it is possible to affirm, with a risk level equal to 5%, that the null hypothesis is rejected, and all the investigated factors affect the dimensions of the struts (Table 5). In addition, the significance of the interaction between the manual current and the focus offset is confirmed. For DoE2, the statistical test fails to reject the null hypothesis regarding the scan speed (Table 6), meaning a weak effect of the scan speed in the investigated range on the strut dimension. According to Fig. 14, both interactions involving the focus offset are significant and recap the effect of the amount of energy supplied in the unit of time per unit of surface (Scan speed [mm/s] × Focus offset [mA]) and the beam spot (Manual current [mA] × Focus offset [mA]). Furthermore, as the residuals are normally distributed (Fig. 15a and Fig. 15c) and the correspondent distribution (Fig. 15b and Fig. 15d) does not provide evidence of any data clustering.

Table 5 ANOVA of strut dimension as a function of the process parameters (DoE1)
Full size table
Table 6 ANOVA of strut dimension as a function of the process parameters (DoE2)
Full size table
Fig. 15
figure 15

Residual of regression models: a DoE1 and b DoE2

Full size image

4.1 Focus offset and struts dimension modelling

The focus offset is an additional current running through the respective electromagnetic lens. During the process, this additional current operates only a geometrical translation of the focal plane of the electron beam from its zero position [45]. This translation results in beam diameter variations for a fixed value of manual current [33]. As mentioned above, the relationship between the focus offset and manual current, or between the focus offset and beam diameter, is not linear and is not known [33]. Because of that, from a statistical point of view, this parameter must be considered a categorical variable rather than a quantitative one. Practically this means that, in a generic model inferred from experimental data, for example, a manual current equal to 0 mA will correspond to a strut dimension equal to zero because no energy is applied to melt the material, while the same cannot be inferred for focus offset equal to 0 mA. Considering the focus offset as a categoric variable, the experimental data are grouped according to the focus offset, and regression models of the strut dimension are inferred. The models, valid within the investigated range of scan speed and manual current, are reported in Table 7 with the corresponding R-squared (R2), Adjusted R-squared (R2 adj) and the standard error of the regression (S). As can be observed, the models inferred from DoE1 showed a higher R2 adj, meaning that the data fit the obtained models well. The lower values of R2 adj for the DoE2 can be explained by the parabolic effect of the focus effect and the strong interaction between focus offset and the scan speed (Fig. 14). The constant term in the models could presumably be associated with the minimum beam area size at that specific focus offset. According to Fig. 13, an increasing manual current leads to thicker struts, while higher speed produces thinner struts. These results agree with the findings reported by Galati et al. [46], in which the effect of the current and scan speed has been analysed by producing single-line tracks.

Table 7 Regression models inferred from experimental data grouped according to focus offset levels (mc: manual current and ss: scan speed)
Full size table

For focus offset equal to 0 mA analysed in both DoEs, the strut measure was differently affected by the scan speed. The variation in the manual current contribution is marginally affected among the considered ranges, indicating that its energy contribution toward the powder bed is similar for different combinations of process parameters. However, the calculation of strut measure using the obtained models provides similar values within the estimated deviation S.

5 Conclusions

The work presented a study on the effect of EB-PBF processing conditions on the morphometric parameters and, therefore, on the corresponding mechanical proprieties. The same nominal geometry has been produced by varying manual current, scan speed, and focus offset. The morphometric parameters of strut dimension, relative density and cross-section have been measured using X-ray CT-scan analysis. Overall, this work showed a significant effect of the process parameters on the morphometric parameters of the lattice structures. The main findings of the work can be resumed as follows:

  • The process parameters systematically affected the dimensional accuracy of the lattice structure and its morphometric parameters.

  • All mechanical properties are strongly affected by all morphometric parameters of the produced structure. This finding may also answer the open questions in Ref. [18, 37,38,39,40,41,42,43] regarding the incomplete description provided by the Ashby and Gibson model

  • The manual current level is the leading factor in determining the strut dimension. In particular, a threshold of manual current exists for which the structure can be considered open or bulky, according to the relative density. The class of relative density predominantly affects the properties of the structure, and structures with lower values of relative density showed poorer mechanical properties.

  • Within a specific class of relative density, the strut geometry was also a significant parameter to be considered. Young's modulus and UCS values follow relative density variation when the produced struts are large and stocky and the corresponding relative density is above 60% (bulky structure). The Young's modulus and UCS values followed the strut dimension variation for more slender struts, corresponding to relative density below 50%. These findings explain the deviations observed in many literature works (e.g. [18, 30]) from the Ashby-Gibson models [28].

  • At a fixed manual current level, only significant variations of the scan speed produce considerable variations of the strut dimension.

  • The focus offset variation marginally affects the strut dimension.

  • The interaction between manual current and focus offset is significant for the strut dimension, and the variation of the beam diameter may explain this.

  • The results obtained in this work for the effect of the process parameters on the morphometric parameters of a diamond cell are independent of the selected structure. The melt pool formation is crucial. On the other hand, the values of the other morphometric parameters (relative density and the cross-section) depend on the strut dimension and how the struts are combined in the 3D space and, therefore, are specific to the structure topology. The values of E, UCS and ε depend on the material, and the structure topology, but the observed effects are generally independent of the structure. As an example, a larger strut dimension results in a stiffer component. Also, even using other elementary cells, an increase in relative density (e.g. Fig.11) results in an increased relative Young’s modulus.

  • For a given topology, the inferred models in this study could be used to estimate the dimensions of the struts and perform a rapid process tuning and optimisation. Correspondingly, without modifying the nominal geometry, structure for biomedical applications in which a low Young’s modulus is required may be obtained with thin struts (low manual current and high speed); on the contrary, higher structural performance with small deformation may be produced using lower speed or higher beam current, obtaining thicker struts. Similarly, functionalised graded structures with a 3D spatial and localised variation of the inherent properties may be produced directly only by fine-tuning the process parameters and without designing any complex CAD file. On the contrary, the forecasted strut dimension could also be used to modify the nominal CAD geometry and directly calculate the corresponding relative density and cross-section of the structure. This information can be then used to evaluate the mechanical properties qualitatively.

These considerations highlight the need for a new, more complex and comprehensive approach to characterising lattice structures. New models of mechanical structure behaviour should jointly consider the strut dimension, cross-section, and relative density structure. Therefore, the process-aware optimisation for this kind of complex geometries is a critical point for properly tuning the lattice structure properties.