A coupled hydro-thermo-mechanical model based on TLF-SPH for simulating crack propagation in fractured rock mass

Abstract

In this paper, a hydro-thermo-mechanical coupling model based on the smoothed particle hydrodynamics with total Lagrangian formula (HTM-TLF-SPH) is proposed to simulate the crack propagation and instability process of fractured rock mass. TLF-SPH uses the Lagrangian kernel approximation, that is, the kernel function and its gradient need only be calculated once in the initial configuration, which is much more efficient than the smoothed particle hydrodynamics (SPH) based on the Euler kernel approximation. In TLF-SPH, particles interact with each other through virtual link, and the crack propagation path of rock mass is tracked dynamically by capturing the fracture of virtual link. Firstly, the accuracy and robustness of the HTM-TLF-SPH coupling model are verified by a reference example of drilling cold shock, and the simulation results agree well with the analytical solutions. Then, the crack propagation law of surrounding rock and the evolution characteristics of physical fields (displacement, seepage and temperature fields) after excavation and unloading of deep roadway under the coupling condition of hydro-thermo-mechanical are investigated. In addition, the seepage and heat transfer processes of the surrounding rock of Daqiang coal mine under different coupling conditions are successfully simulated. Meanwhile, the effect of the boundary water pressure difference on the temperature and seepage fields under the hydro-thermal coupling condition is quantitatively analyzed.

Article highlights

• A HTM-TLF-SPH model is proposed to simulate crack propagation of fractured rock mass

• The HTM-TLF-SPH model can effectively simulate fissure seepage and thermal diffusion

• Temperature diffusion has little effect on seepage in low permeable rock mass

• The effect of pore water on heat transfer rate mainly depends on the seepage direction

• The pore water pressure at 2 meters in front of the roadway is most affected by temperature

1 Introduction

In recent years, engineering problems such as geothermal energy exploitation, diversion tunnels of hydropower stations and tunnels in cold regions are becoming more and more serious. Surrounding rock damage, instability and crack propagation evolution under the hydro-thermo-mechanical coupling conditions are still key issues to be solved in the field of deep resource mining engineering and rock mass engineering at present (Liu et al. 2006, 2014). In order to reveal the hydro-thermo-mechanical coupling mechanism of rock mass, researchers have carried out a large number of laboratory experiments (Liu et al. 2001; Zhou et al. 2005; He et al. 2018; Zhang et al. 2020a, b; Bai et al. 2020; Zhang et al. 2020a, b) and theoretical derivation (Lai et al. 1999, 2003; Huang 2002; Liu et al. 2015; Yang et al. 2019), and achieved remarkable results. Due to the complexity of mechanical boundary conditions and the limitations of experimental conditions, numerical methods with advantages of low cost, easy operation and high efficiency are favored by many scholars. The multi-field coupling numerical methods commonly used in rock mass engineering mainly include finite element method (FEM), finite difference method (FDM), peridynamics (PD) and smoothed particle hydrodynamics (SPH).

FEM is often used to solve the multi-field coupling problem of engineering rock mass. Liu et al. (2015) established a frost heave solution model considering water migration, and used the equivalent thermal expansion coefficient method to simulate the stress field near the fissure considering the water–ice phase transition. Yang et al. (2019) established a hydro-thermo-mechanical coupling model based on the relationship between pore ice and frost heave rate, and successfully simulated the seepage field, temperature field and stress field of the Musui Tunnel. In order to simulate the water inrush evolution process of coal mine collapse column under complex environment, a coal mine hydro-thermo-mechanical (HTM) multi-field coupling model was established by Zhao et al. (2022). Tang et al. (2007) developed a micromechanical model for simulating rock failure under the hydro-thermo-mechanical coupling conditions, which can well describe the macroscopic failure morphology of rock mass. The hydro-thermo-mechanical coupling model based on FEM has obtained some satisfactory results, but in the multi-field coupling crack propagation simulation, the crack can only propagate along the contact surface between the elements, and the pre-existing defect tip is prone to non-convergence. In particular, each time step during crack propagation needs to be redivided into mesh cells, which is more complicated to realize.

FLAC^3D, belonging to FDM, has the characteristic of easy convergence in nonlinear large deformation analysis, and is widely used in geotechnical engineering. Based on FLAC^3D software, Huang (2014) simulated the deformation law of deep roadway surrounding rock under the hydro-thermo-mechanical coupling conditions. Liu et al. (2011) simulated the water–ice phase transition process of water-rich fissure based on the equivalent thermal expansion coefficient method, and studied the three field distribution characteristics of fractured rock mass under freezing conditions. However, the establishment of the "interface" unit is related to the grid division, and the crack propagation path is determined by the density of the grid division.

PD theory, including bond-based peridynamics (BB-PD) and state-based peridynamics (SB-PD), was first proposed by Silling (2000) to simulate crack propagation in rock mass. In recent years, PD has been developed rapidly in the field of hydro-thermo-mechanical coupling. A hydro-thermo-chemo-mechanical coupling model of fractured rock mass was developed by Wang (2019) based on BB-PD method, and has been successfully applied to hydraulic fracturing and geothermal energy mining projects. However, for two-dimensional plane strain problems, the Poisson's ratio of BB-PD method is usually limited to 1/4. Shou (2017) established a hydro-thermo-mechanical coupling model of fractured rock mass under the the SB-PD framework, and successfully simulated the crack propagation process of surrounding rock after roadway excavation in Daqiang coal mine. Although SB-PD method successfully solves the problem of Poisson's ratio constraint, the variational formula in PD theory does not include tractive force. Therefore, the force acting on the solid boundary is assumed to be the body force acting on the virtual boundary layer, resulting in the application of boundary conditions less accurate than FEM (Wang 2019).

SPH is a grid-free method originally proposed by Ginold and Monaghan (1977) and Lucy (1977) for solving astrophysical problems. In recent years, the SPH method has been used more and more in the fields of crack propagation (Mu et al. 2022a, b; Yu et al. 2023a, b), blasting crack induction, mechanical and hydraulic behavior (Gharehdash et al. 2018, 2019), and thermal cracking (Zhou and Bi 2018). In order to consider the effect of cumulative damage on the interaction between particles, Chakraborty and Shaw (2013) introduced the interaction factor "f" into the SPH governing equation for the first time, and successfully simulated the crack initiation and propagation of solid materials under impact loads. Then, a general particle dynamics (GPD) method was proposed by Zhou's research team (Zhou et al. 2015; Bi et al. 2015; Zhai et al. 2016, 2017; Zhou and Zhang 2017) by introducing the elastic-brittle constitutive model in Chakraborty and Shaw's work, and successfully simulated the crack propagation process of rock or rock-like materials. Gharehdash et al. (2020, 2021) improved the fracture modeling, proposed the selection method of artificial viscosity and tensile instability parameters, and successfully simulated rock cracking induced by blasting combined with variable particle resolution. In order to establish a hydro-mechanical coupling model between the filling medium and pore water, Sun (2016) introduced the osmotic pressure term into the momentum equations of the solid phase and the liquid phase, respectively. Based on the idea of virtual bonds, Bi and Zhou (2017) proposed a new hydro-mechanical coupling model under the framework of GPD, and successfully simulated the crack propagation process of rocks with pre-existing defects under the coupling conditions of compressive load and fracture water pressure. In order to study the coupling mechanism between hydraulic fracture (HF) and natural fracture (NF), Yu et al. (2021) proposed a 2P-IKSPH meshless numerical method based on smoothed particle hydrodynamics method (IKSPH) with improved kernel function. Yu et al. (2022) derived the governing equation of heat conduction under the framework of IKSPH, and developed the thermo-mechanical-damage coupling model (TMD-IKSPH) to solve the thermal cracking problem in engineering. In order to improve the computational efficiency of the traditional SPH thermal cracking model, Mu et al. (2022c) established the TM-BB-SPD model under the TLF-SPH framework, and studied the influence of thermal expansion coefficient and homogeneity on the thermal crack mode of rock disks. Although researchers have achieved satisfactory results in the field of rock crack propagation under two-phase coupling conditions based on SPH, the computational efficiency of SPH is relatively low, which is difficult to solve the multi-field coupling problem of large-scale engineering examples with hundreds of thousands of particles, and the engineering application value is limited.

At present, the TLF-SPH method has not been reported to study the hydro-thermo-mechanical coupling in fractured rock mass. Therefore, this study aims to propose an efficient and accurate hydro-thermo-mechanical coupling model of fractured rock mass under the framework of TLF-SPH to simulate the crack propagation and coalescence process of surrounding rock after roadway excavation. In this work, the SPH discrete scheme of the governing equations of seepage and heat transfer in fractured rock mass under the hydro-thermo-mechanical coupling conditions is proposed first. Then, the hydro-thermo-mechanical coupling constitutive equation is embedded in TLF-SPH program, and the force state function f_k is introduced into the deformation gradient tensor, displacement gradient tensor and hydro-thermo-mechanical coupling momentum equation to realize the macroscopic brittle failure characteristics of the material. Meanwhile, assuming that the adjacent particles interact through the virtual link, and the Cauchy stress on the virtual link can be obtained by averaging that on the two interacting particles. This method effectively avoids the complicated calculation of stress coordinate transformation in the process of solving the Cauchy stress on traditional virtual bonds or pseudo-springs by Riemann solver. In addition, once the Cauchy stress on the virtual link meets the strength criterion, the virtual link breaks. Then, the interaction between the adjacent particles stops transmitting, and the crack starts or propagates from here. The simulation results show that the proposed HTM-TLF-SPH model can effectively reveal the hydro-thermo-mechanical coupling mechanism and crack propagation law of fractured rock mass in roadway surrounding rock, providing important scientific theory and technical support for the stability prediction and disaster prevention of engineering rock mass.

2 Hydro-thermo-mechanical coupling model of fractured rock mass

2.1 Seepage and heat transfer models of fractured rock mass

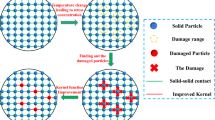
The damage of rock mass particles has a great influence on the seepage of pore water and the heat transfer of porous media. In order to describe the process of seepage (or heat conduction) of fractured rock mass, interpolation functions χ_d (x, D) and χ_s (x, D) were introduced to divide the seepage (or heat conduction) domain of fractured rock mass into three sub-solution domains, namely, storage domain (white area), damage domain (dark yellow area) and transition domain (light orange area) (Lee et al. 2016), as shown in Fig. 1. In addition, the storage domain and fracture domain satisfy χ_s (x, D) = 1 and χ_d (x, D) = 0, χ_s (x, D) = 0 and χ_d (x, D) = 1, respectively.

Fig. 1

Subsolution domain of fractured rock mass

Consequently, the linear expression of the interpolation function in the transition domain is:

$$\left\{ \begin{gathered}\upchi _{d} ({\mathbf{x}},D) = \frac{{D - c_{1} }}{{c_{2} - c_{1} }} \hfill \\\upchi _{s} ({\mathbf{x}},D) = \frac{{c_{2} - D}}{{c_{2} - c_{1} }} \hfill \\ \end{gathered} \right.$$

(1)

where c₁ and c₂ are the upper and lower limits of the damage function, respectively. D is the damage function, given in Sect. 2.3. If D ≤ c₁, χ_d (x, D) = 0 and χ_s (x, D) = 1; If D ≥ c₂, χ_d (x, D) = 1 and χ_s (x, D) = 0. In this work, the values of c₁ and c₂ are 0.5, respectively.

Taking the calculation of seepage as an example, the permeability coefficient of the transition domain of fractured rock mass considering the hydro-thermo-mechanical-damage coupling can be expressed as (Zhou et al. 2018, 2019; Wang 2019; Ni et al. 2020):

$$\kappa_{t} (\sigma ,p,\Theta ) =\upchi _{d} ({\mathbf{x}},D)\kappa_{d} (\sigma ,p,\Theta ) +\upchi _{s} ({\mathbf{x}},D)\kappa_{s} (\sigma ,p,\Theta )$$

(2)

where $\kappa_{d} (\sigma ,p,\Theta )$ and $\kappa_{s} (\sigma ,p,\Theta )$, respectively, represent the permeability coefficients of the damage domain and the storage domain considering the hydro-thermo-mechanical coupling.

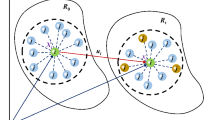
Islam and Peng (2019) established the interaction between particles through virtual links, successfully simulating the crack propagation and brittle fracture process of rocks. In this study, the interactions between adjacent particles are transmitted via virtual links. Different from the previous virtual link, the present virtual link can not only transmit stress waves, but also act as a seepage channel for water (or heat) flow between adjacent particles. Suppose particle i is a reservoir of water (or heat) flow, and pore water (or heat) diffuses freely between particles i and j driven by a pressure (or temperature) gradient, as shown in Fig. 2.

Fig. 2

Adjacent particles transfer water or heat flow through virtual links

In the seepage (or heat transfer) system of fractured rock mass, due to the small distance between adjacent particles, the permeability coefficient of the virtual link can be calculated:

$$\kappa_{t,ij} (\sigma ,p,\Theta ) = \frac{{\kappa_{t,i} (\sigma ,p,\Theta ) + \kappa_{t,j} (\sigma ,p,\Theta )}}{2}$$

(3)

Principal stress and hydrostatic pressure affect the permeability coefficient of fractured rock mass by changing its skeleton. Then, the equivalent continuous permeability coefficient and macroscopic defect permeability coefficient of fractured rock mass under the hydro-mechanical coupling conditions can be expressed as (Mu et al. 2023a, b):

$$\left\{ \begin{gathered} \kappa_{s} (\sigma ,p) = \frac{{g\lambda b_{0}^{3} }}{24u}\exp \left[ { - a(\sigma_{kk} /3 - \alpha p)/H^{\prime}} \right] \hfill \\ \kappa_{d} (\sigma ,p) = \frac{{gb_{0}^{2} }}{12u}\exp \left[ { - a(\sigma_{kk} /3 - \alpha p)/H^{\prime}} \right] \hfill \\ \end{gathered} \right.$$

(4)

where a is the coupling parameter obtained by experiment; α is the effective stress coefficient (between 0 and 1), $\alpha = E/[3(1 - 2v)H^{\prime}]$, and $H^{\prime} = E/3/(1 - 2v)$; σ_kk = σ_x + σ_y + σ_z.

The change of temperature will change the kinematic viscosity of pore water, thus affecting the distribution of seepage. Figure 3 shows the change curve of kinematic viscosity and temperature of pure water at 0–100 °C. As can be seen from Fig. 3, the kinematic viscosity of pore water in rock mass gradually decreases with the increase of temperature. Then, the kinematic viscosity of pore water at any temperature can be calculated according to Hemholtz formula (Yu 2004):

$$u(\Theta ){ = }\frac{{1.775 \times 10^{{{ - }6}} }}{{1 + 0.033\Theta + 0.000221\Theta^{2} }}$$

(5)

Fig. 3

Kinematic viscosity–temperature curve of pure water (0–100 °C) (Yu 2004; Bi 2016)

Since the permeability coefficient is inversely proportional to the kinematic viscosity, the permeability coefficient of rock mass at any temperature can be expressed as:

$$\kappa (\Theta ) = \frac{{u(\Theta_{0} )}}{{u(\Theta )}}\kappa (\Theta_{0} ){ = }\frac{{1 + 0.033\Theta + 0.000221\Theta^{2} }}{{1 + 0.033\Theta_{0} + 0.000221\Theta_{0}^{2} }}\kappa (\Theta_{0} )$$

(6)

where $u(\Theta_{0} )$ is the kinematic viscosity of water at reference temperature $\Theta_{0}$;$\kappa (\Theta_{0} )$ is the permeability coefficient of rock mass at reference temperature $\Theta_{0}$.

By substituting Eq. (6) into Eq. (4), and then the equivalent continuous permeability coefficient and macro-detect permeability coefficient of fractured rock mass considering the hydro-thermo-mechanical coupling are obtained, respectively:

$$\left\{ \begin{gathered} \kappa_{s} (\sigma ,p,\Theta ) = \frac{{g\lambda b_{0}^{3} (1 + 0.033\Theta + 0.000221\Theta^{2} )}}{{4.26 \times 10^{{{ - }5}} }}\exp \left[ { - a(\sigma_{kk} /3 - \alpha p)/H^{\prime}} \right] \hfill \\ \kappa_{d} (\sigma ,p,\Theta ) = \frac{{(1 + 0.033\Theta + 0.000221\Theta^{2} )gb_{0}^{2} }}{{2.13 \times 10^{{ - 5}} }}\exp \left[ { - a(\sigma_{kk} /3 - \alpha p)/H^{\prime}} \right] \hfill \\ \end{gathered} \right.$$

(7)

Similarly, according to the phase field theory, the general expression of thermal conductivity of fractured rock mass is as follows:

$$\lambda_{f}^{t} =\upchi _{d} ({\mathbf{x}},D)\lambda_{f}^{d} +\upchi _{s} ({\mathbf{x}},D)\lambda_{f}^{s}$$

(8)

where $\lambda_{f}^{d}$ is the thermal conductivity of damage domain;$\lambda_{f}^{s}$ = $\lambda_{f}$ is the thermal conductivity of storage domain, where $\lambda_{f}$ is the heat conduction coefficient of rock mass skeleton.

In this work, the thermal conductivity $\lambda_{f}^{d}$ of the damage domain is set to 0, that is, once the particles fail in an insulating state, the heat transfer between particles is no longer carried out, then Eq. (8) can be further simplified as follows:

$$\lambda_{f}^{t} =\upchi _{s} ({\mathbf{x}},D)\lambda_{f}^{s} { = }\upchi _{s} ({\mathbf{x}},D)\lambda_{f}$$

(9)

Consequently, the thermal conductivity of the virtual link can be approximated as:

$$\lambda_{f,ij}^{t} = \frac{{\lambda_{f,i}^{t} + \lambda_{f,j}^{t} }}{2}{ = }\frac{{\upchi _{s,i} ({\mathbf{x}},D)\lambda_{f,i} +\upchi _{s,j} ({\mathbf{x}},D)\lambda_{f,i} }}{2}$$

(10)

According to Darcy's law, the seepage velocity of pore water considering Soret effect is:

$${\mathbf{v}}_{w} = - \kappa (\nabla p - \rho_{w} g) - D_{\Theta } \nabla \Theta$$

(11)

where κ is the permeability coefficient; $\Theta$ is the temperature; ρ_w is the density of water. $D_{\Theta }$ is the diffusivity of water driven by temperature gradient.

The strain rate tensor of rock mass can be expressed by the deformation gradient tensor (Islam and Peng 2019):

$${\dot{\mathbf{\varepsilon }}} = \frac{1}{2}\left[ {{\dot{\mathbf{F}}\mathbf{F}}^{ - 1} + ({\dot{\mathbf{F}}\mathbf{F}}^{ - 1} )^{T} } \right]$$

(12)

Based on continuum mechanics, the deformation gradient tensor can be obtained by:

$${\mathbf{F}} = \frac{{\text{d}{\mathbf{x}}}}{{\text{d}{\mathbf{X}}}}$$

(13)

where x and X are the position vectors of the particles in the deformed configuration and the initial configuration, respectively.

Then, the discrete form of the deformation gradient tensor and its rate at particle i is:

$${\mathbf{F}}_{i} = \sum\limits_{j} {\frac{{m_{j} }}{{\rho_{0j} }}\left( {{\mathbf{x}}_{j} - {\mathbf{x}}_{i} } \right)\nabla_{i} W_{0ij} }$$

(14)

$${\dot{\mathbf{F}}}_{i} = \sum\limits_{j} {\frac{{m_{j} }}{{\rho_{0j} }}\left( {{\mathbf{v}}_{j} - {\mathbf{v}}_{i} } \right)\nabla_{i} W_{0ij} }$$

(15)

where $\nabla_{i} W_{0ij} = \partial W_{0ij} /\partial {\mathbf{X}}_{i}$ is the kernel gradient obtained in the initial configuration.

In this paper, the governing equations for seepage and heat conduction of rock mass considering the hydro-thermo-mechanical coupling (without seepage source) are adopted (Sheng 2006; Li 2011):

$$\left\{ \begin{gathered} \alpha \cdot \frac{{\rho_{w} }}{{\rho_{w0} }}\dot{\varepsilon }_{kk} + n\alpha_{w} \frac{\partial p}{{\partial t}} + n\beta_{w} \frac{\partial \Theta }{{\partial t}} = \nabla \left[ {\frac{{\rho_{w} }}{{\rho_{w0} }}\kappa (\nabla p - \rho_{w} g) + D_{\Theta } \nabla \Theta } \right] \hfill \\ \rho_{f} c_{f} \frac{\partial \Theta }{{\partial t}} + (1 - n)\Theta_{0} ({2}G + {3}\lambda )\beta_{s} \dot{\varepsilon }_{kk} = \nabla (\lambda_{f} \nabla \Theta ) - \rho_{w} c_{w} {\mathbf{v}}_{w} \cdot \nabla \Theta \hfill \\ \end{gathered} \right.$$

(16)

where α is the effective stress coefficient, α = 1;$\Theta_{0}$ is the absolute temperature of rock mass; ρ_w0 is the initial density of water; ρ_f is the density of rock mass, ρ_f = nρ_w + (1–n) ρ_s; c_f is the specific heat capacity of rock mass, c_f = nc_w + (1–n) c_s; λ_f is the thermal conductivity of rock mass, λ_f = nλ_w + (1–n) λ_s; α_w is the compression coefficient of pore water; β_w is the thermal expansion coefficient of pore water; β_s is the thermal expansion coefficient of rock mass skeleton;$\dot{\varepsilon }_{kk}$ is the bulk strain rate, and $\dot{\varepsilon }_{kk} { = }\dot{\varepsilon }_{xx} { + }\dot{\varepsilon }_{yy} { + }\dot{\varepsilon }_{zz}$.

Equation (16) can be further simplified as:

$$\left\{ \begin{gathered} \frac{\partial p}{{\partial t}} = \frac{1}{{n\alpha_{w} }}\left( { - \frac{{\rho_{w} }}{{\rho_{0} }}\nabla {\mathbf{v}}_{w} - n\beta_{w} \frac{\partial \Theta }{{\partial t}} - \alpha \cdot \frac{{\rho_{w} }}{{\rho_{0} }}\dot{\varepsilon }_{kk} } \right) \hfill \\ \frac{\partial \Theta }{{\partial t}} = \frac{1}{{\rho_{f} c_{f} }}\left[ {\lambda_{f} \nabla^{2} \Theta - \rho_{w} c_{w} {\mathbf{v}}_{w} \cdot \nabla \Theta - (1 - n)\Theta_{0} ({2}G + {3}\lambda )\beta_{s} \dot{\varepsilon }_{kk} } \right] \hfill \\ \end{gathered} \right.$$

(17)

References (Chen and Bai 2016; Bai et al. 2018) show that the transfer of water flow or heat flow between particles is only determined by the position relationship between particles. According to Eqs. (4)–(17), combined with the particle approximation method of SPH, the control equations of seepage and heat transfer of fractured rock mass under the hydro-thermo-mechanical coupling can be discretized as follows:

$$\left\{ \begin{gathered}\upchi _{d,i} ({\mathbf{x}},D) = \frac{{D_{i} - c_{1} }}{{c_{2} - c_{1} }},\;\upchi _{s,i} ({\mathbf{x}},D) = \frac{{c_{2} - D_{i} }}{{c_{2} - c_{1} }}\;,C = \frac{{(1 + 0.033\Theta_{i} + 0.000221\Theta_{i}^{2} )gb_{0}^{2} }}{{2.13 \times 10^{{{ - }5}} }} \hfill \\ \kappa_{t,i} (\sigma ,p,\Theta ) = C\left[ {\upchi _{d,i} ({\mathbf{x}},D) + \frac{{\lambda b_{0} }}{2}\upchi _{s,i} ({\mathbf{x}},D)} \right]\exp \left[ {\frac{{ - a(\sigma_{kk,i} /3 - \alpha p_{i} )}}{{H^{\prime}}}} \right] \hfill \\ {\mathbf{v}}_{w,i} = \frac{{\kappa_{t,i} (\sigma ,p,\Theta ) + \kappa_{t,j} (\sigma ,p,\Theta )}}{2}\left[ {\sum\limits_{j} {\frac{{m_{j} }}{{\rho_{j} }}(p_{i} - p_{j} )\frac{{\partial W_{ij} }}{{\partial {\mathbf{x}}_{i} }}} + \rho_{w} g} \right] + D_{\Theta } \sum\limits_{j} {\frac{{m_{j} }}{{\rho_{j} }}(\Theta_{i} - \Theta_{j} )\frac{{\partial W_{ij} }}{{\partial {\mathbf{x}}_{i} }}} \hfill \\ \frac{{\partial \Theta_{i} }}{\partial t} = \frac{{\psi_{s,i} \lambda_{f,i} + \psi_{s,j} \lambda_{f,j} }}{{2\rho_{f} c_{f} }}\sum\limits_{j} {\left[ {\frac{{2m_{j} }}{{\rho_{j} }}\frac{{{\mathbf{x}}_{ij} }}{{r_{ij}^{2} }}(\Theta_{i} - \Theta_{j} )} \right] \otimes \frac{{\partial W_{ij} }}{{\partial {\mathbf{x}}_{i} }}} - \hfill \\ \;\;\;\;\;\;\;\;\;\;\frac{{\rho_{w} c_{w} }}{{\rho_{f} c_{f} }}\sum\limits_{j} {\frac{{m_{j} }}{{\rho_{j} }}\left[ {{\mathbf{v}}_{w,i} (\Theta_{i} - \Theta_{j} )} \right] \otimes \frac{{\partial W_{ij} }}{{\partial {\mathbf{x}}_{i} }}} - \frac{{(1 - n)\Theta_{0} }}{{\rho_{f} c_{f} }}({2}G + {3}\lambda )\beta_{s} \dot{\varepsilon }_{kk,i} \hfill \\ \frac{{\partial p_{i} }}{\partial t} = \frac{1}{{n\alpha_{w} }}\left( {\frac{{\rho_{w} }}{{\rho_{0} }}\sum\limits_{j} {\frac{{m_{j} }}{{\rho_{j} }}({\mathbf{v}}_{w,i} - {\mathbf{v}}_{w,j} )\frac{{\partial W_{ij} }}{{\partial {\mathbf{x}}_{i} }}} - n\beta_{w} \frac{{\partial \Theta_{i} }}{\partial t} - \alpha \cdot \frac{{\rho_{w} }}{{\rho_{0} }}\dot{\varepsilon }_{kk,i} } \right) \hfill \\ \end{gathered} \right.$$

(18)

2.2 Hydro-thermo-mechanical coupling constitutive relation and momentum equation

Smoothed particle hydrodynamics (SPH) is a Lagrangian particle method based on Euler kernel, whose kernel function is defined based on the deformation configuration. However, the kernel function of smoothed particle hydrodynamics with total Lagrangian formula (TLF-SPH) is defined based on the initial configuration, and its conservation and constitutive equations are solved in this configuration. Since the density change of the particles is not involved in the deformation calculation, it is not necessary to solve the continuity equation. Then, the momentum equation of particle i can be expressed as (Lin et al. 2015):

$$\frac{{\text{d}{\mathbf{v}}_{i} }}{{\text{d}t}} = \frac{1}{{\rho_{0i}^{{}} }}\frac{{\partial {\mathbf{P}}_{i} }}{{\partial {\mathbf{X}}_{i} }} + {\mathbf{g}}_{i}$$

(19)

Then, the momentum equation of particle i without considering physical force under the hydro-thermo-mechanical coupling is:

$$\frac{{\text{d}{\mathbf{v}}_{i} ({\mathbf{x}},p{,\Theta ,}t)}}{{\text{d}t}} = \frac{1}{{\rho_{0i}^{{}} }}\frac{{\partial {\mathbf{P}}_{i} ({\mathbf{x}},p{,\Theta ,}t)}}{{\partial {\mathbf{X}}_{i} }}$$

(20)

where ρ_0i is the initial density of particle i;${\mathbf{P}}_{i} ({\mathbf{x}},p{,\Theta ,}t)$ is the first type of Piola–Kirchhoff stress tensor for particle i, which can be converted from the Cauchy stress tensor:

$${\mathbf{P}}_{i} ({\mathbf{x}},p{,\Theta ,}t) = J_{i} {\varvec{\sigma}}_{i} ({\mathbf{x}},p{,\Theta ,}t){\mathbf{F}}_{i}^{ - T}$$

(21)

where J_i is the Jacobian matrix of F_i, and $J_{i} = \det ({\mathbf{F}}_{i} )$. F_i is the deformation gradient tensor of particle i, calculated by Eq. (14).

Considering the effect of thermal stress and pore water pressure on the skeleton deformation of fractured rock mass, the constitutive equation of particle i is as follows:

$${{\varvec{\upsigma}}}_{i} ({\mathbf{x}},p{,\Theta ,}t) = 2G{{\varvec{\upvarepsilon}}}_{i} ({\mathbf{x}},t) + \left\{ {\lambda tr\left[ {{{\varvec{\upvarepsilon}}}_{i} ({\mathbf{x}},t)} \right] + \alpha p_{i} - \frac{{E\beta \Delta\Theta _{i} }}{1 - 2v}} \right\}{\mathbf{I}}$$

(22)

For particle i, the Euler strain tensor can be calculated by:

$${{\varvec{\upvarepsilon}}}_{i} = {\mathbf{F}}_{i}^{ - T} {\mathbf{E}}_{i} {\mathbf{F}}_{i}^{T}$$

(23)

The Greenish-Lagrange strain tensor of particle i can be calculated by:

$${\mathbf{E}}_{i} = \frac{1}{2}({\mathbf{L}}_{i}^{T} + {\mathbf{L}}_{i} + {\mathbf{L}}_{i}^{T} {\mathbf{L}}_{i} )$$

(24)

In continuum mechanics, the displacement gradient tensor can be calculated by:

$${\mathbf{L}}_{i} = \frac{{\text{d}{\mathbf{u}}_{i} }}{{\text{d}{\mathbf{X}}_{i} }}$$

(25)

where u_i is the displacement vector of particle i, u_i = x_i – X_i.

Consequently, the displacement gradient tensor and momentum equation of particle i under the hydro-thermo-mechanical coupling can be discretized as follows:

Based on the particle discrete method in SPH, Eqs. (24) and (25) can be discretized as:

$$\left\{ \begin{gathered} {\mathbf{L}}_{i} = \sum\limits_{j} {\frac{{m_{j} }}{{\rho_{0j}^{{}} }}\left( {{\mathbf{u}}_{j} - {\mathbf{u}}_{i} } \right)\nabla_{i} W_{0ij} } \hfill \\ \frac{{\text{d}{\mathbf{v}}_{i} ({\mathbf{x}},p{,\Theta ,}t)}}{{\text{d}t}} = \sum\limits_{j} {m_{j} \left[ {\frac{{{\mathbf{P}}_{i} ({\mathbf{x}},p{,\Theta ,}t)}}{{\rho_{0i}^{2} }} + \frac{{{\mathbf{P}}_{j} ({\mathbf{x}},p{,\Theta ,}t)}}{{\rho_{0j}^{2} }}{ + }{\mathbf{P}}_{av,i} } \right]\nabla_{i} W_{0ij} } \hfill \\ \end{gathered} \right.$$

(26)

where ${\mathbf{P}}_{av,i} { = }\det ({\mathbf{F}}_{i} )\Pi _{\;ij} {\mathbf{F}}_{i}^{ - T}$ is an additional term to reduce the numerical dissipation and increase the stability of the program. In addition, the expression of artificial viscosity with linear and quadratic terms (Neumann and Richtmyer 1950) proposed by Monaghan and Gingold (1983) is adopted:

$$\Pi _{\;ij} { = }\left\{ {\begin{array}{*{20}l} {\frac{{ - \alpha_{av} \overline{c}_{ij} \phi_{ij} + \beta_{av} \phi_{ij}^{2} }}{{\overline{\rho }_{ij} }},} \hfill & {{\mathbf{v}}_{ij} \cdot {\mathbf{x}}_{ij} < \;0} \hfill \\ {0,} \hfill & {{\mathbf{v}}_{ij} \cdot {\mathbf{x}}_{ij} \ge \;0} \hfill \\ \end{array} } \right.$$

(27)

where $\phi_{ij} { = }\frac{{h_{ij} {\mathbf{v}}_{ij} \cdot {\mathbf{x}}_{ij} }}{{|{\mathbf{x}}_{ij} |^{2} + \varepsilon h_{ij}^{2} }}$, and $h_{ij} = (h_{i} + h_{j} )/2$ is the average smooth length of the interacting particle pair;$\overline{c}_{ij}$ and $\overline{\rho }_{ij}$ are the mean values of the sound velocity and density at particles i and j, respectively, $\overline{c}_{ij} = (c_{i} + c_{j} )/2$ and $\overline{\rho }_{ij} = (\rho_{i} + \rho_{j} )/2$. In addition, the sound speed can be obtained by $c = \sqrt {4G/3\rho_{0} }$, where G and $\rho_{0}$ are the elastic modulus and initial density of the solid material, respectively;${\mathbf{v}}_{ij} = {\mathbf{v}}_{i} - {\mathbf{v}}_{j}$ and ${\mathbf{x}}_{ij} = {\mathbf{x}}_{i} - {\mathbf{x}}_{j}$ are the relative velocity and relative position vectors of particles i and j, respectively.

2.3 Virtual link damage and crack propagation

There are two main failure modes of underground engineering rock mass, namely tensile failure and shear failure. Suitable strength criterion is the key to accurately simulate crack propagation in rock mass. As shown in Eq. (28), the maximum principal stress and Mohr–Coulomb criterion with the characteristics of simple form, few parameters and easy to obtain, have been widely used in engineering practice. In this study, the maximum principal stress criterion is first used to determine the tensile failure of rock mass. If the principal stress on the virtual link does not meet the critical condition, then Mohr–Coulomb criterion is used to test the shear failure of rock mass. The strength criteria involved are defined as follows (Yang et al. 2018):

$$\left\{ \begin{gathered} \sigma_{f} = \sigma_{t} \hfill \\ \tau_{f} = c + \sigma_{f} \tan \varphi \hfill \\ \end{gathered} \right.$$

(28)

where σ_f and τ_f are tensile stress and shear stress on the fracture surface, respectively; σ_t is the maximum tensile strength; φ and c are internal friction angle and cohesion, respectively.

Based on the relative positions between particles i and j, Islam and Peng (2019) redefined the influence domain of the kernel function, that is, particle i (red particle) only interacts with the directly adjacent particle j (orange particle) in the influence domain (see Fig. 4). Once particle j is damaged, the damaged particle (the brown particle) no longer interacts with particle i, resulting in a microcrack. Since the interaction between particles can be controlled by the bell kernel function, a force state function f_k is introduced to characterize the action state of the kernel function. For the virtual link in the initial model, f_k = 1, and once the virtual link is broken, f_k = 0.

Fig. 4

TLF-SPH crack initiation and propagation model

Then, the kernel function introduced into the force state function f_k can be modified to:

$$\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{W}_{0ij} = f_{k} \cdot W_{0ij}$$

(29)

The Cauchy stress on the virtual link can be taken as the average of that on particles i and j:

$$\sigma_{ij} = \frac{1}{2}(\sigma_{i} + \sigma_{j} )$$

(30)

In order to quantitatively describe the damage degree of particles, the damage function D as follows is constructed (Shou 2017; Wang 2019):

$$D({\mathbf{x}},t) = 1 - \frac{{\int_{\Re } {f_{k} dV} }}{{\int_{\Re } {dV} }}$$

(31)

Thus, the Eqs. (14) and (26) introducing modified kernel function can be rewritten as:

$$\left\{ \begin{gathered} {\mathbf{F}}_{i} = \sum\limits_{j} {\frac{{m_{j} }}{{\rho_{0j}^{{}} }}\left( {{\mathbf{x}}_{j} - {\mathbf{x}}_{i} } \right)\nabla_{i} \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{W}_{0ij} } \hfill \\ {\mathbf{L}}_{i} = \sum\limits_{j} {\frac{{m_{j} }}{{\rho_{0j}^{{}} }}\left( {{\mathbf{u}}_{j} - {\mathbf{u}}_{i} } \right)\nabla_{i} \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{W}_{0ij} } \hfill \\ \frac{{\text{d}{\mathbf{v}}_{i} ({\mathbf{x}},p{,\Theta ,}t)}}{{\text{d}t}} = \sum\limits_{j} {m_{j} \left[ {\frac{{{\mathbf{P}}_{i} ({\mathbf{x}},p{,\Theta ,}t)}}{{\rho_{0i}^{2} }} + \frac{{{\mathbf{P}}_{j} ({\mathbf{x}},p{,\Theta ,}t)}}{{\rho_{0j}^{2} }}{ + }{\mathbf{P}}_{av,i} } \right]\nabla_{i} \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{W}_{0ij} } \hfill \\ \end{gathered} \right.$$

(32)

2.4 Implementation strategy of Hydro-thermo-mechanical coupling program

In the hydro-thermo-mechanical coupling program, the virtual link can be used not only for the transfer of interaction between particles, but also as a channel for the transfer of water flow and heat between interacting particles. Then, the virtual link is also endowed with physical properties such as permeability coefficient, flow diffusivity and thermal conductivity. Once the virtual link is broken, the interaction between particles no longer occurs, and the heat flow channel between adjacent particles is blocked. Therefore, the phenomenon of temperature jump can be observed in the previous numerical examples of heat conduction (Wang et al. 2018a, b, 2019). However, the fracture of the virtual link means the expansion of the seepage channel, accelerating the seepage process between the interacting particles. The diffusion process of heat conduction and seepage is relatively slow, while the stress wave transfer is faster. Therefore, the temperature and seepage fields should be iteratively calculated until the steady state is reached, and then the displacement (or stress) load is carried out on the upper end of the model to start the mechanical iterative calculation. In order to more clearly describe the implementation of the algorithm, the specific strategy of the hydro-thermo-mechanical coupling model is as follows:

• 1. Firstly, the geometric boundary and material parameters are input, and the model is discretized into equally spaced particles.

• 2. Secondly, the seepage and temperature fields are calculated iteratively by Eq. (17) until the steady state is reached.

• 3. Subsequently, mechanical iterative calculation is started, and the principal stress of the current step, pore water pressure and temperature solved in the previous step are substituted into Eq. (7) to calculate the permeability coefficient under the hydro-thermo-mechanical coupling.

• 4. Meanwhile, the permeability coefficient and thermal conductivity of fractured rock mass are calculated by Eqs. (1), (2), (7) and (9). Then, the permeability coefficient and thermal conductivity of the virtual link are obtained by using Eqs. (3) and (10).

• 5. Then, the updated permeability coefficient and thermal conductivity of the virtual link are substituted into the governing equations of seepage and heat conduction in Eq. (17), respectively, to obtain the water pressure change rate and temperature change rate considering the coupling effect of body strain, temperature and water pressure.

• 6. Finally, the updated pore water pressure and temperature in the current step are substituted into the constitutive model in Eq. (22) to solve the Cauchy stress of the next time step, and then the principal stress of the next time step is obtained.

After that, the seepage and temperature fields were iterated for the next time step until the sample failed, and the program calculation was completed. In order to describe the implementation strategy of the program more clearly, the program calculation flow of the hydro-thermo-mechanical coupling model of fractured rock mass is shown in Fig. 5.

Fig. 5

Program calculation flow of hydro-thermo-mechanical coupling model for fractured rock mass

3 Numerical simulation of hydro-thermo-mechanical coupling in engineering rock mass

3.1 Benchmark example: cold shock of borehole in square rock mass

The coupling process of hydro-thermo-mechanical in engineering rock mass is very complicated, and the monitoring data of each physical field is difficult to obtain due to the limited test conditions. Therefore, a simplified rectangular saturated granite sample with a size of 1.6 m × 1.6 m and a vertical borehole in the center was selected for simulation to verify the accuracy of the hydro-thermo-mechanical coupling model. In order to better compare with the analytical solution of the mathematical model considering the hydro-thermo-mechanical coupling, the effects of damage on the mechanical, seepage and temperature fields are not considered in this example. Figure 6 shows the geometric model of saturated rock mass under the hydro-thermo-mechanical coupling conditions. As can be seen from Fig. 6, the radius of the drilling hole is r_b = 0.1 m, the initial temperature of the rock sample is 200 °C, and the temperature of hole wall is always maintained at 80 °C. Driven by cold shock, the coupling effect occurs between temperature field, stress field and seepage field of surrounding rock. In order to study the variation characteristics of stress and water pressure caused by temperature, it is considered that the temperature and stress of the far field are 0. The simulation parameters are basically consistent with the numerical parameters used in previous literatures (Li et al. 1998; Ghassemi and Zhang 2004; Zhu et al. 2009), as shown in Table 1.

Fig. 6

Geometric model of saturated rock mass under the hydro-thermo-mechanical coupling conditions

Table 1 Simulation parameters of borehole cold shock in square rock mass

Figure 7 shows the variation curves of temperature, stress and pore water pressure of surrounding rock of borehole with radial distance at different time. As can be seen from Fig. 7a, the temperature of surrounding rock near the borehole decreases rapidly in the initial stage of thermal diffusion. With the passage of heat transfer time, low temperature is gradually transferred to the deep surrounding rock, and the temperature gradient is gradually reduced. The sudden decrease of the temperature at the hole wall causes the surrounding rock to shrink and induce the surrounding rock to produce thermal stress along the circumferential and radial directions. Figure 7c, d show that when t = 1.0 × 10² s, the circumferential tensile stress and radial tensile stress at the hole wall are relatively concentrated, which are 45.8 MPa and 5.58 MPa, respectively. With the increase of radial distance, the circumferential tensile stress decreases rapidly, and the compressive stress begins to appear at 0.15 m. As time goes on, the temperature of the deep surrounding rock decreases further, the circumferential tensile stress and radial tensile stress increase gradually, and the peak value of radial tensile stress moves backward gradually. In addition, the thermal stress of surrounding rock will cause the deformation of rock skeleton, and then change the permeability coefficient of surrounding rock, so the pore water pressure of saturated rock sample will also change. It can be seen from Fig. 7b that when t = 1.0 × 10² s, the pore water pressure at the pore wall drops to 2.0 MPa. In addition, the simulation results agree well with the analytical solutions obtained by the thermoporoelastic model of borehole stability under non-hydrostatic stress field established by Li et al. (1998), verifying that the proposed hydro-thermo-mechanicalc oupling model can accurately simulate some simplified multi-field coupling processes, providing important technical support for the solution of multi-field coupling problems in complex geotechnical engineering.

Fig. 7

Variation curves of temperature, stress and pore water pressure of surrounding rock with radial distance at different times: a Temperature, b Pore water pressure, c Circumferential stress, and d Radial stress

3.2 Simulation of crack propagation in fractured rock mass in roadway excavation

3.2.1 Numerical model and model initialization

In order to study the crack propagation and fracture characteristics of the surrounding rock during excavation and unloading of a deep roadway, a square rock mass with a size of 40 m × 40 m was selected for numerical simulation of hydro-thermo-mechanical coupling. The numerical example is derived from reference (Huang 2014). The size of the model and some of the seepage flow and thermodynamic parameters used are basically consistent with the previous numerical studies. Figure 8 shows the geometric model of roadway excavation. The radius of the top arch is R = 3 m, the height of the side wall is 2 m, and the width of the roadway is 6 m. The red line segments in the model represent six randomly distributed pre-existing defects. Three monitoring points are arranged at the center of the two pre-existing defects on the top arch and side wall, respectively, marked as 1^#, 2^#, and 3^# in turn. Table 2 shows the seepage flow and thermodynamic simulation parameters of the roadway surrounding rock.

Fig. 8

Geometric model of roadway excavation

Table 2 Seepage and thermodynamic simulation parameters of the roadway surrounding rock (Huang 2014)

Under the long-term influence of the crustal movement, deep surrounding rock produces a large tectonic stress, which is also called the initial ground stress. Relevant data (Huang 2014) show that the center of the roadway is located at the –700 m level of the surface, and the initial vertical stress of the surrounding rock is 21 MPa and the lateral pressure coefficient is 1.2. The horizontal displacement is fixed on the left and right boundaries of the model, and the vertical displacement is fixed on the lower boundary. The equivalent load of 21 MPa (the gravity of the overlying rock mass) is applied to the upper boundary for stress loading. The pore water pressure of solid particles at the upper and lower boundaries is 2.0 MPa and 2.4 MPa respectively, and the pore water pressure of solid particles at the roadway boundary is 0 MPa. The temperature of the solid particles at the four boundaries is 50 °C, and the temperature of the solid particles at the boundary of the roadway is 20 °C. The model is discretized with 200 × 200 particles, the particle spacing the is 0.2 m, and the seepage integration time step is Δt^h = 2.0 × 10^–3 s. As shown in Fig. 9, the program prefabricated six defects of varying lengths in the model before tunnel excavation by using prefabricated node segment (PNS) method (Mu et al. 2022a), and the particles on both sides of the pre-existing defects form a new boundary and no longer interact with each other. The cohesive force of rock mass is randomly distributed with a homogeneity of 20, and the cohesive force distribution of model particles is the same under different coupling conditions. In addition, the Weibull distribution function used in the model is (Weibull 1951):

$$W(x) = x_{0} \left( {\frac{x}{{x_{0} }}} \right)^{\omega - 1} \exp \left[ { - \left( {\frac{x}{{x_{0} }}} \right)^{\omega } } \right]$$

(33)

where ω is the homogeneity of rock mass. x is cohesion, and x₀ is the average value of x.

Fig. 9

Numerical model before and after roadway excavation: a Before excavation and b After excavation

According to the actual project, the initial ground stress balance of the model should be carried out before the excavation of the roadway surrounding rock, as shown in Fig. 10. During the mechanical equilibrium, the model particles will cause a small initial displacement. In order to study the influence of excavation unloading on roadway displacement, the initial displacement caused by ground stress balance needs to be zeroed. After that, the steady state seepage calculation is carried out first, and then the excavation simulation of the surrounding rock of the roadway under the hydro-thermo-mechanical coupling is carried out.

Fig. 10

Initial vertical stress distribution (unit: MPa)

Figure 11 shows the seepage process of surrounding rock before tunnel excavation. Driven by hydraulic gradient, pore water flows uniformly from bottom to top. As can be seen from Fig. 11a, b, when t = 0.04 h, pore water seepage occurs from the upper and lower boundaries to the interior of the model. Meanwhile, pore water enrichment occurs first in the pre-existing defect at the bottom of the model, and the seepage velocity of fissure water increases instantaneously. When t = 4 h, more pore water flows into the pre-exsiting defects at the top and bottom of the model, and the seepage velocity of the fissure water along the vertical direction decreases continuously. Meanwhile, it is observed that the three pre-exsiting defects in the middle of the model also gradually begin to seepage, as shown in Fig. 11d. As shown in Fig. 11b, f, when t = 42 h, the maximum seepage velocity of pore water in the pre-exsiting defect along the vertical direction gradually decreases from 1.2 × 10^–6 m/s (t = 0.04 h) to 6.7 × 10^–8 m/s. It can be seen that the seepage field of the roadway surrounding rock has tended to steady state, and the seepage calculation has ended. In addition, Fig. 11c shows that the water pressure at the inflow end of the pre-exsiting defect is significantly smaller than that at other locations of the same water level, while the water pressure at the outflow end of the pre-exsiting defect is significantly larger than that at other locations of the same water level. This is because the fractured virtual link in the pre-exsiting defect significantly increases the seepage channel, resulting in a sudden increase in the seepage velocity of pore water.

Fig. 11

seepage process of surrounding rock before tunnel excavation. a, c, and e: Pore water pressure (unit: MPa); b, d, and f: Vertical seepage velocity (unit: × 10^–7 m/s)

3.2.2 Simulation results and analysis

Figure 12 shows the failure process of surrounding rock after excavation and unloading of deep roadway. When the loading reaches 1000 steps, the maximum shear stress at the top arch and foot of the roadway is concentrated, where crack initiation occurs first driven by the shear stress, as shown in Fig. 12a. When the loading reaches 11,000 steps, obvious shear failure occurs at the foot of the roadway and the shallow surrounding rock of the left top arch and side wall. In addition, a large number of shear cracks spread rapidly and coalesced to form macroscopic cracks, and two macroscopic shear zones formed at the foot of the roadway at 45° from the horizontal direction. When the loading reaches 24,000 steps, the shear cracks on the two sides of the roadway extend further along the horizontal direction towards the depth of the surrounding rock. The pre-existing defect located at the right wall of the roadway forms an inclined shear macroscopic crack along the upper right, which coalesced with the shear crack formed by the expansion of the pre-existing defect at the top arch of the roadway along the lower right. In addition, the maximum shear stress of the other four prefabricated defect tips in the surrounding rock is further concentrated, resulting in sliding shear cracking. When the loading reaches 34,600 steps, the shear cracks continue to expand rapidly to the depth of the surrounding rock, with more shear macroscopic cracks formed.The macroscopic shear zone formed by the pre-existing defect on the right wall of the roadway propagates to the upper right gradually widens, and coalesce with the tip of the pre-existing defect on the upper side (see Fig. 12g). Meanwhile, the upper tip of the pre-existing defect located below the roadway extends along the upper left to form a shear zone, which is connected to the shear zone below the left bottom of the roadway.

Fig. 12

Failure process of load surrounding rock after excavation and unloading of deep roadway. a, c, e, and g: Crack propagation (D = 0 means no damage, D = 1 means complete damage); b, d, f, and h: Maximum shear stress (unit: MPa)

Figure 13 shows the displacement distribution of roadway surrounding rock under different calculation steps. It is worth noting that a positive value indicates that the particle is moving in the positive direction along the x–y axis, and a negative value indicates that the particle is moving in the negative direction along the x–y axis. As can be seen from Fig. 13, after excavation and unloading of the roadway, the surrounding rock has an obvious displacement to the roadway, and the movement direction of the surrounding rock on both sides of the defect is opposite. When the loading reaches 1000 steps, the horizontal and vertical displacements on both sides of the roadway are approximately symmetrical, and the maximum displacements at the side wall, top arch and roadway floor are 25 mm. When the loading reaches 11,000 steps, the crack at the roadway foot propagates obviously, and the horizontal displacement there increases rapidly, as shown in Fig. 13c. When the loading reaches 24,000 steps, the horizontal displacement of the left wall of the roadway increases faster than that of the right wall. This is due to the existence of defects in the right wall, which hinders the transmission of stress waves and inhibits the horizontal deformation of the right wall. In addition, it can be observed that the overlying load of the surrounding rock accelerates the vertical deformation of the top arch, and the heave phenomenon of the roadway floor appears obviously. When the loading reaches 34,600 steps, the stress of the roadway floor is released, but the vertical displacement of the roadway floor changes little. As shown in Fig. 13g–h, the top arch continues to settle downward, with a maximum vertical displacement of 174 mm and a maximum horizontal displacement of 75 mm for the left wall. Therefore, the roadway surrounding rock has the risk of the left wall falling and floor heave, so it is necessary to further strengthen the engineering support and carry out the personnel evacuation in time.

Fig. 13

Displacement distribution of roadway surrounding rock under different calculation steps (unit: mm). a, c, e, and g: Horizontal displacement; b, d, f, and h: Vertical displacement

Figure 14 shows the pore water pressure distribution of roadway surrounding rock under different seepage times. As can be seen from Fig. 14a, driven by hydraulic gradient, pore water flows from shallow surrounding rock to roadway, and pore water pressure in pre-existing defects is significantly lower than that of surrounding rock at the same level. This is caused by the fact that the permeability coefficient of pre-existing defects is much higher than that of fractured rock mass, the seepage rate of pore water in pre-existingd efects is larger, and the water pressure decreases rapidly. When the seepage time reaches 180 s, a uniform pore water pressure zone is formed in the roadway surrounding rock, and the pore water pressure increases gradually from the roadway to the deep surrounding rock. When the seepage time reaches 320 s, the crack propagation of the shallow surrounding rock of the roadway intensifies. Then, more virtual links between interacting particles break, resulting in a sudden increase in the permeability coefficient of rock mass, and the form of seepage field in surrounding rock changes dramatically. When the seepage time reaches 385 s, the damage of surrounding rock is close to steady state. With the seepage velocity of pore water decreasing rapidly, and the shape of the seepage field tends to be stable, as shown in Fig. 14c, d.

Fig. 14

Pore water pressure distribution of roadway surrounding rock under different seepage times (unit: MPa): a 10 s, b 180 s, c 320 s, and d 385 s

Figure 15 shows the temperature field distribution of roadway surrounding rock under different heat transfer times. As can be seen from Fig. 15a, driven by the temperature gradient, heat diffuses from the shallow surrounding rock to the roadway, and a uniform gradient zone with low temperature inside and high temperature outside is formed around the roadway. When the heat transfer time reaches 556 h, the heat transfer occurs only in the shallow surrounding rock of the roadway, and the heat transfer rate of the pre-existing defect is significantly lower than that of the surrounding rock at the same level. This is due to the large seepage rate of pore water in the pre-existing defects, and the pore water brings the heat from the original rock into the pre-existing defects, slowing down the diffusion rate of high temperature heat from the surrounding rock to the roadway. When the heat transfer time reaches 10,000 h, the heat conduction has spread to the deep surrounding rock. Meanwhile, the temperature zone with a gradient from the roadway to the deep surrounding rock has been formed. When the heat transfer time reaches 17,778 h, the temperature field of the shallow surrounding rock of the roadway changes obviously. This is due to the rapid expansion of more macroscopic cracks in the rock mass, and the fracture of the virtual link between interacting particles blocks the heat flow channel, resulting in the heat cannot be effectively transferred from the deep surrounding rock to the roadway. When the heat transfer time reaches 21,389 h, the heat diffusion rate of the shallow surrounding rock to the roadway gradually accelerates, as shown in Fig. 15d. This is because the seepage velocity of pore water in roadway surrounding rock gradually decreases, and the "temperature carrying effect" of pore water gradually weakens during the seepage process.

Fig. 15

Temperature field distribution of roadway surrounding rock under different heat transfer time (unit: °C): a 556 h, b 10,000 h, c 17,778 h, and d 21,389 h

Figure 16 shows the crack propagation of roadway surrounding rock under different coupling conditions. Under the influence of high ground stress, the maximum horizontal principal stress of the roadway surrounding rock is in the state of compressive stress, and the surrounding rock is mainly subjected to shear failure, as shown in Fig. 16a. As can be seen from Fig. 16b, the thermo-mechanical coupling effect intensifies the crack propagation of the shallow surrounding rock of the roadway floor and the crack initiation from the upper tip of the pre-existing defect located on the right wall. Compared with the condition without coupling, the width of shear zone increases obviously under the conditions of thermo-mechanical coupling. However, compared with the thermo-mechanical coupling conditions, the damage range of roadway floor and side wall under the hydro-thermo-mechanical coupling conditions is larger, as shown in Fig. 16c. This is because the seepage of pore water significantly reduces the overall shear strength of surrounding rock, resulting in a rapid decrease in the water pressure of the shallow surrounding rock. Therefore, pore water has a great weakening and destructive effect on deep surrounding rock, while thermal stress mainly causes crack propagation in shallow surrounding rock of roadway. As shown in Fig. 16d, the shear failure of the deep surrounding rock of the roadway is intensified and the crack propagation depth increases significantly under the hydro-thermo-mechanical coupling conditions. The shear zone formed by the expansion of the defects on the right wall and roadway floor coalesces and penetrates the adjacent defects, respectively. The sliding shear failure occurred at both tips of the six defects, resulting in macroscopic shear cracks of varying lengths. As can be seen from Fig. 16, failure forms of surrounding rock under the four coupling conditions are basically the same, and obvious shear failure occurs at the foot of roadway. Thermal stress and pore water pressure both aggravate the crack propagation of roadway floor, and pore water pressure has a greater effect on the damage of roadway floor than thermal stress. Especially for the excavation of deep-buried water-rich roadway, the pore water pressure of roadway floor is large, which is easy to cause water inrush of roadway floor.

Fig. 16

Crack propagation of roadway surrounding rock under different coupling conditions: a No coupling, b Thermo-mechanical coupling, c Hydro-mechanical coupling, and d Hydro-thermo-mechanical coupling

Figure 17 shows the variation curves of the minimum principal stress and vertical settlement displacement at monitoring point 1^# with time under different coupling conditions. As can be seen from Fig. 17a, the minimum principal stress at monitoring point 1^# under the thermo-mechanical coupling condition is less than that without coupling. It shows that the sudden cooling of the roadway causes the roadway surrounding rock to be strained and contracted, and the thermal stress generated is tensile stress. Tensile stress will accelerate the top arch subsidence and floor heave, especially when the temperature of the original rock is high, it is easy to cause the surface crack of surrounding rock. In addition, high temperature will also reduce the mechanical properties of surrounding rock, inducing the surrounding rock to soften and destabilize. Meanwhile, it is found that the minimum principal stress at monitoring point 1^# under the hydro-mechanical coupling condition is greater than that without coupling. It shows that pore water pressure has an obvious expansion and extrusion effect on rock mass, accelerating the subsidence of top arch and creep process of rock mass, triggering the initiation and propagation of macroscopic cracks, inducing water and mud outburst in roadway. As can be seen from Fig. 17b, the vertical settlement displacement at monitoring point 1^# under the thermo-mechanical coupling condition is slightly larger than that without coupling, while the vertical settlement displacement at monitoring point 1^# under the hydro-mechanical coupling condition is much larger than that without coupling. It can be seen that the three coupling conditions all aggravate the settlement of the top arch, and the hydro-thermo-mechanical coupling condition has a more severe settlement on the vertical displacement of the top arch, followed by the water pressure, and the temperature has a relatively small effect. Therefore, for the deep-buried water-rich roadway in complex mechanical environment such as high temperature, high ground stress and high pore water pressure, there is a huge risk of roof falling in the process of engineering excavation, and it is necessary to strengthen the roof support at the later stage of excavation to ensure the safety of construction personnel.

Fig. 17

Variation curves of minimum principal stress and vertical settlement displacement at monitoring point 1^# with time under different coupling conditions: a Minimum principal stress, and b Vertical displacement

Figure 18 shows the seepage rate-time curves at monitoring points 2^# and 3^# under different coupling conditions. As can be seen from Fig. 18c, d, with the passage of seepage time, the seepage rate of monitoring point 3^# decreases first, then increases and then decreases again until it reaches 0. The late change of seepage rate is due to the intensified crack propagation of the pre-existing defects on the right wall, and more virtual links break. Then, the seepage channel at the monitoring point 3^# suddenly increases, resulting in an increase in the vertical seepage rate of pore water. As the seepage time continues to increase, the seepage rate of pore water gradually decreases until it reaches 0. The change of seepage rate at monitoring point 3^# is in good agreement with the engineering practice, which further verifies the effectiveness and feasibility of seepage calculation of fractured rock mass. In addition, since the permeability coefficient of surrounding rock is small, the seepage rate at monitoring points 2^# and 3^# under the hydro-thermo-mechanical coupling condition is slightly lower than that under the hydro-mechanical coupling condition, as shown in Fig. 18. Therefore, for the low permeability rock mass, the seepage rate of pore water is small, and the influence of temperature diffusion on the seepage of surrounding rock can be ignored. In addition, for non-low permeability rock mass, the interaction between temperature diffusion and seepage will be further studied in detail in Sect. 4.

Fig. 18

Seepage rate-time curves at monitoring points 2^# and 3^# under different coupling conditions. a and c: Horizontal seepage rate; b and d: Vertical seepage rate

3.3 Numerical simulation of hydro-thermal coupling of roadway surrounding rock

3.3.1 Control equations for heat transfer and seepage of intact rock mass

Without considering the influence of strain and fissure on temperature diffusion, the governing equation of heat conduction in Eq. (18) can be changed to:

$$\frac{{\partial \Theta_{i} }}{\partial t} = \frac{{\lambda_{f} }}{{\rho_{f} c_{f} }}\sum\limits_{j} {\left[ {\frac{{2m_{j} }}{{\rho_{j} }}\frac{{{\mathbf{x}}_{ij} }}{{r_{ij}^{2} }}(\Theta_{i} - \Theta_{j} )} \right] \otimes \frac{{\partial W_{ij} }}{{\partial {\mathbf{x}}_{i} }}} - \frac{{\rho_{w} c_{w} }}{{\rho_{f} c_{f} }}\sum\limits_{j} {\frac{{m_{j} }}{{\rho_{j} }}\left[ {{\mathbf{v}}_{w,i} (\Theta_{i} - \Theta_{j} )} \right] \otimes \frac{{\partial W_{ij} }}{{\partial {\mathbf{x}}_{i} }}}$$

(34)

According to Darcy's law, considering the effect of temperature on permeability coefficient, the seepage velocity of pore water is:

$${\mathbf{v}}_{w} { = } - \kappa (\Theta )\nabla H$$

(35)

Based on the particle approximation method of SPH, Eq. (35) can be discretized as:

$${\mathbf{v}}_{w,i} = \kappa_{i} (\Theta )\sum\limits_{j} {\frac{{m_{j} }}{{\rho_{j} }}(H_{i} - H_{j} )\frac{{\partial W_{ij} }}{{\partial {\mathbf{x}}_{i} }}}$$

(36)

According to Eqs. (6), (34) and (36), the governing equation for heat conduction of intact rock mass considering the seepage effect is as follows:

$$\left\{ \begin{gathered} {\mathbf{v}}_{w,i} = \frac{{1 + 0.033\Theta + 0.000221\Theta^{2} }}{{1 + 0.033\Theta_{0} + 0.000221\Theta_{0}^{2} }}\kappa_{i} (\Theta_{0} )\sum\limits_{j} {\frac{{m_{j} }}{{\rho_{j} }}(H_{i} - H_{j} )\frac{{\partial W_{ij} }}{{\partial {\mathbf{x}}_{i} }}} \hfill \\ \frac{{\partial \Theta_{i} }}{\partial t} = \frac{{\lambda_{f} }}{{C_{f} }}\sum\limits_{j} {\left[ {\frac{{2m_{j} }}{{\rho_{j} }}\frac{{{\mathbf{x}}_{ij} }}{{r_{ij}^{2} }}(\Theta_{i} - \Theta_{j} )} \right] \otimes \frac{{\partial W_{ij} }}{{\partial {\mathbf{x}}_{i} }}} - \frac{{C_{w} }}{{C_{f} }}\sum\limits_{j} {\frac{{m_{j} }}{{\rho_{j} }}\left[ {{\mathbf{v}}_{w,i} (\Theta_{i} - \Theta_{j} )} \right] \otimes \frac{{\partial W_{ij} }}{{\partial {\mathbf{x}}_{i} }}} \hfill \\ \end{gathered} \right.$$

(37)

In order to simplify the procedure and improve the numerical accuracy, the seepage control equation of the intact rock mass considering temperature effect can be written as follows:

$$\frac{\partial H}{{\partial t}}{ = }\frac{1}{S} \cdot \left[ {\nabla (\kappa \;\nabla H) + \nabla (D_{\Theta } \nabla \Theta )} \right]$$

(38)

According to the discretization method used in Eq. (18), the above equation is discretized as:

$$\frac{{\partial H_{i} }}{\partial t} = \frac{{\kappa_{i} }}{S}\sum\limits_{j} {\left[ {\frac{{2m_{j} }}{{\rho_{j} }}\frac{{{\mathbf{x}}_{ij} }}{{r_{ij}^{2} }}(H_{i} - H_{j} )} \right] \otimes \frac{{\partial W_{ij} }}{{\partial {\mathbf{x}}_{i} }}} + \frac{{D_{\Theta } }}{S}\sum\limits_{j} {\frac{{2m_{j} }}{{\rho_{j} }}\frac{{{\mathbf{x}}_{ij} }}{{r_{ij}^{2} }}(\Theta_{i} - \Theta_{j} ) \otimes \frac{{\partial W_{ij} }}{{\partial {\mathbf{x}}_{i} }}}$$

(39)

By substituting Eq. (6) into Eq. (39), the seepage control equation of the intact rock mass considering temperature effect can be obtained as follows:

$$\begin{aligned} \frac{{\partial H_{i} }}{\partial t} & = \frac{{1 + 0.033\Theta + 0.000221\Theta^{2} }}{{1 + 0.033\Theta_{0} + 0.000221\Theta_{0}^{2} }}\frac{{\kappa_{i} (\Theta_{0} )}}{S}\sum\limits_{j} {\left[ {\frac{{2m_{j} }}{{\rho_{j} }}\frac{{{\mathbf{x}}_{ij} }}{{r_{ij}^{2} }}(H_{i} - H_{j} )} \right] \otimes \frac{{\partial W_{ij} }}{{\partial {\mathbf{x}}_{i} }}} \\ & \quad + \frac{{D_{\Theta } }}{S}\sum\limits_{j} {\frac{{2m_{j} }}{{\rho_{j} }}\frac{{{\mathbf{x}}_{ij} }}{{r_{ij}^{2} }}(\Theta_{i} - \Theta_{j} ) \otimes \frac{{\partial W_{ij} }}{{\partial {\mathbf{x}}_{i} }}} \\ \end{aligned}$$

(40)

3.3.2 Numerical model and boundary conditions

In order to further investigate the coupling effect between the temperature and seepage fields, a roadway surrounding rock with the size of 24 m × 16 m was selected for the hydro-mechanical coupling simulation. As shown in Fig. 19, the roadway geometry consists of a semicircular arch and a rectangle. The radius of the circular arch R = 1.9 m, the height of the vertical wall is 2.6 m, the width of the roadway is 3.8 m, and the distance between the roadway floor and the lower boundary is 3.8 m. The geometric dimensions and simulation parameters of the model are basically consistent with those used in references (Li 2011; Shou 2017).

Fig. 19

Geometric model

According to Wang (2019), the convergence of the model increases as the particle spacing decreases or the radius of the kernel function increases. However, the numerical algorithm needs to take into account the computational efficiency while improving the accuracy. The decrease of particle spacing or the increase of kernel radius will undoubtedly increase the calculation time of the program. In order to ensure the accuracy of the current numerical results and the high computational efficiency of the program, the model is discretized to 57,554 particles with a spacing of 0.08 m (Shou 2017). The radius of the kernel function is δ = 3.015Δx (Shou 2017), the time step of temperature integration is $\Delta \text{t}^{\Theta }$ = 1,000 s, and the time step of seepage integration is Δt^h = 1 s. The simulation parameters of roadway surrounding rock are shown in Table 3.

Table 3 Numerical simulation parameters of roadway rock surrounding (Li 2011; Shou 2017)

Seepage and temperature boundary conditions: The solid particles at the left boundary are subjected to 10 MPa pore water pressure, and the solid particles at the other three boundaries are set as non-permeable boundaries. Meanwhile, the temperature of the solid particles at the four boundaries is set at 46 °C, and the temperature of the solid particles at the boundary of the roadway is set at 25 °C, as shown in Fig. 20.

Fig. 20

Numerical model and boundary conditions: a Seepage boundary and b Temperature boundary

3.3.3 Simulation results

Figure 21 shows the temperature distribution of roadway surrounding rock without coupling. The initial temperature of the roadway surrounding rock is 46 °C. When the temperature of 25 °C is applied to the roadway boundary, the temperature difference between the roadway boundary and the surrounding rock is formed. Driven by the temperature gradient, heat flows uniformly from the surrounding rock to the roadway boundary. When the calculation reaches 278 h, the heat only diffused in the shallow surrounding rock of the roadway and dissipated in time with the airflow in the roadway. When the calculation reaches 1111 h, the heat conduction continues to propagate from the roadway to the deep surrounding rock. When the calculation reaches 5000 h, the roadway surrounding rock forms a uniform temperature gradient zone, and the temperature gradient gradually decreases from the roadway to the deep surrounding rock. Meanwhile, it is observed that the temperature field of the roadway surrounding rock is approximately "hemispherical". When the calculation reaches 10,000 h, the temperature field of surrounding rock changes from "hemispherical" to "rectangular". When the calculation reaches 30,000 h, the diffusion rate of surrounding rock temperature field decreases obviously. Meanwhile, it is found that the temperature gradient zone has spread to the four boundaries of the model, and the temperature field of the surrounding rock has tended to steady state. When the calculation reaches 50,000 h, the temperature field of the roadway surrounding rock has reached the steady state, and the heat is no longer transferred from the deep surrounding rock to the roadway. Figure 22 shows the PD and ANSYS results of temperature field of roadway surrounding rock without coupling. It can be seen from Figs. 21f and 22 that the steady-state results of the surrounding rock temperature field obtained by the present model are in good agreement with the previous PD and ANSYS results, verifying the accuracy of the calculation of heat conduction in roadway surrounding rock.

Fig. 21

Temperature distribution of roadway surrounding rock without coupling: a 278 h, b 1111 h, c 5000 h, d 10,000 h, e 30,000 h, and f 50,000 h

Fig. 22

Peridynamic and ANSYS results of temperature field of roadway surrounding rock without coupling: a PD result (Shou 2017), and b ANSYS result (Li 2011)

Figure 23 shows the pore water pressure of roadway surrounding rock without coupling. When t = 5 h, pore water began to flow around the roadway. Since the water pressure at the roadway boundary is 0, the seepage form changes obviously, and the horizontal seepage velocity gradually decreases from the roadway to the upper and lower boundaries of the model. When t = 10 h, the hydraulic gradient zone is close to the right boundary of the model, and the advanced seepage phenomenon above and below the roadway is more obvious. When t = 15 h, pore water pressure gradually increases clockwise around the roadway. When t = 25 h, the seepage velocity of pore water gradually decreases until the seepage field tends to be stable, and then an obvious local low pressure area is formed in the surrounding rock on the right side of the roadway.

Fig. 23

Pore water pressure of roadway surrounding rock without coupling: a 0.28 h, b 1.11 h, c 5 h, d 10 h, e 15 h, and f 25 h

Figure 24 shows the pore water pressure distribution of roadway surrounding rock without coupling. Figures 23f and 24 show that the present simulation results are in good agreement with the previous PD results and ANSYS solutions, verifying the accuracy of the seepage calculation of the roadway surrounding rock.

Fig. 24

Pore water pressure distribution of roadway surrounding rock without coupling: a PD result (Shou 2017), and b ANSYS solution (Li 2011)

Figure 25 shows the temperature distribution of roadway surrounding rock under the hydro-thermal coupling condition. The initial temperature of surrounding rock and roadway boundary is set at 46 °C and 25 °C respectively. Driven by the temperature gradient, the heat in the surrounding rock is uniformly released through the roadway. When the calculation reaches 278 h, the heat only diffused in the shallow surrounding rock of the roadway and released in time with the airflow in the roadway. With the increase of time step, the heat continues to diffuse from the roadway to the deep surrounding rock. When the calculation reaches 1111 h, the roadway surrounding rock forms a uniform temperature gradient zone, and the temperature gradient decreases from the roadway to the deep surrounding rock. Meanwhile, the temperature of the roadway surrounding rock is less affected by the seepage field, and the distribution is approximately "hemispherical". When the calculation reaches 5000 h, the influence of the temperature field of the roadway surrounding rock on the seepage field begins to appear. The temperature field of the surrounding rock on the left and right sides of the roadway presents an obvious asymmetric distribution, and the diffusion rate of the temperature field on the right side of the surrounding rock is significantly higher than that on the left side. This is because the "temperature carrying effect" of pore water in the seepage process brings the heat in the surrounding rock from the left side of the model to the right side of the model. It can be seen that pore water seepage has an inhibitory effect on the temperature diffusion rate of surrounding rock. Since the seepage rate of the surrounding rock on the left side of the roadway is larger, the temperature diffusion rate there is more significantly affected by the seepage rate. When the calculation reaches 10,000 h, the asymmetry of the temperature field of the surrounding rock on the left and right sides of the roadway is further enhanced. When the calculation reaches 30,000 h, the temperature field of the surrounding rock on the right side of the roadway has been diffused to the right boundary of the model. Meanwhile, the temperature field of surrounding rock tends to steady state, and the diffusion rate of temperature field decreases obviously. When the calculation reaches 50,000 h, the temperature field of roadway surrounding rock has reached steady state.

Fig. 25

Temperature distribution of roadway rock surrounding under the hydro-thermal coupling condition: a 278 h, b 1111 h, c 5000 h, d 10,000 h, e 30,000 h, and f 50,000 h

Figure 26 shows the steady-state distribution of temperature field in roadway surrounding rock under the hydro-thermal coupling condition. As can be seen from Figs. 25f and 26, the simulation results are in good agreement with the previous PD and ANSYS analysis results, which verifies the accuracy of temperature diffusion calculation in roadway surrounding rock under hydro-thermal coupling condition.

Fig. 26

Steady-state distribution of temperature field in roadway surrounding rock under the hydro-thermal coupling condition: a PD result (Shou 2017), and b ANSYS solution (Li 2011)

Figure 27 shows the temperature distribution of roadway surrounding rock under different hydro-thermal coupling conditions at 50,000 h. It can be seen from Fig. 27 that the temperature field of the surrounding rock on the left and right sides of the roadway presents a symmetrical distribution without coupling, while that of the surrounding rock on the left and right sides of the roadway presents an asymmetric distribution under the hydro-thermal coupling conditions. With the increase of the boundary water pressure, the asymmetry of the temperature field of the surrounding rock on the left and right sides of the roadway is gradually enhanced, which shows that the "temperature carrying effect" in the process of pore water seepage has a great influence on the temperature field of the surrounding rock.

Fig. 27

Temperature field of roadway rock surrounding under different hydro-thermal coupling conditions at 50,000 h (unit: °C): a No coupling, b Hydro-thermal coupling (p = 5 MPa), c Hydro-thermal coupling (p = 10 MPa), and d Hydro-thermal coupling (p = 15 MPa)

In order to quantitatively describe the influence of seepage field on the temperature field of surrounding rock, 300 monitoring points were arranged horizontally 6 m away from the upper boundary of the model, as shown in Fig. 19. The temperature monitoring curve of roadway surrounding rock under different hydro-thermal coupling conditions at 50,000 h is given in Fig. 28. As shown in Fig. 28, the temperature monitoring curve of surrounding rock uniformly decreases from the model boundary to the roadway center line without coupling. Compared with no coupling condition, the horizontal position corresponding to the same temperature of the surrounding rock on the left side of the roadway is relatively delayed under the hydro-thermal coupling condition. This numerical observation further indicates that the seepage of pore water slows down the heat transfer process of rock mass, and the higher the water pressure at the left boundary, the slower the heat diffusion of rock mass on the left side of the roadway. With the increase of the water pressure at the left boundary, the "trough" of the temperature curve moves to the right gradually, and the corresponding minimum temperature increases gradually. Therefore, the water pressure at the left boundary has a significant influence on the distribution of temperature field in roadway surrounding rock.

Fig. 28

Temperature monitoring curve of roadway rock surrounding under different hydro-thermal coupling conditions at 50,000 h

Figure 29 shows the distribution of pore water pressure and permeability coefficient of roadway surrounding rock under different hydro-thermal coupling conditions at 10 h. As can be seen from Fig. 29a, when the water pressure of 10 MPa is applied to the left boundary of the model, the seepage rate of pore water in the surrounding rock is larger than that in the case of no coupling. In addition, the pore water in the surrounding rock on the right side of the roadway is in the state of circulation meeting, while the pore water without coupling has not met, as shown in Fig. 29b. This is because the temperature field increases the permeability coefficient of surrounding rock under the hydro-thermal coupling conditions, thus speeding up the seepage process of pore water, as shown in Fig. 29.

Fig. 29

Pore water pressure and permeability coefficient of roadway rock surrounding under different hydro-thermal coupling conditions at 10 h: a Hydro-thermal coupling (p = 10 MPa), and b No coupling

In order to quantitatively describe the influence of temperature field on seepage field, the water pressure monitoring curve of roadway surrounding rock under different hydro-thermal coupling conditions at 10 h was drawn, as shown in Fig. 30. It can be seen from Fig. 30a that the pore water pressure under the hydro-thermal coupling condition is greater than that without coupling. This is due to the increase of permeability coefficient of surrounding rock under the condition of hydro-thermal coupling, more water flows into the same position at the same time, so the pore water pressure increases. As can be seen from Fig. 30b, the absolute water pressure difference of pore water in surrounding rock gradually increases with the equal increase of water pressure at the left boundary, and the increase range gradually decreases. In addition, the absolute water pressure difference-position curve shows that the pore water pressure at 2 m in front of the roadway is most affected by temperature field, while the pore water pressure at the right side of the roadway center line (x = 12 m) is relatively less affected by the temperature field.

Fig. 30

Water pressure monitoring curve of roadway surrounding rock under different hydro-thermal coupling conditions at 10 h: a Pore water pressure, and b Absolute pressure difference

4 Conclusions

An efficient and accurate hydro-thermo-mechanical (HTM) coupling model is proposed to simulate crack propagation in fractured rock mass under TLF-SPH framework. The accuracy of the model is verified by a borehole cold impact numerical test, and the crack propagation and displacement settlement process of roadway surrounding rock under hydro-thermo-mechanical coupling conditions are successfully simulated. Then, the hydro-thermal coupling simulation of the roadway surrounding rock of Daqiang coal mine is carried out, revealing the coupling mechanism between seepage and temperature fields. Meanwhile, some interesting phenomena were observed in the simulation, and the following main conclusions were obtained:

• 1. After excavation and unloading, the surrounding rock of roadway excavation is mainly shear failure, and pore water pressure and thermal stress both aggravate the crack propagation of shallow surrounding rock. Meanwhile, it is found that the damage degree and settlement displacement of surrounding rock under the hydro-thermo-mechanical coupling are the largest, followed by hydro-mechanical coupling, and thermo-mechanical coupling is the least. In addition, temperature diffusion has little effect on pore water seepage and stress distribution of low permeability rock mass, so the multi-field coupling problem can be simplified to hydro-mechanical coupling solution to simplify engineering problems.

• 2. Based on the simplified governing equations of seepage and heat transfer, the coupling mechanism between pore water seepage and thermal diffusion is revealed by the hydro-thermal coupling simulation of roadway surrounding rock of Daqiang coal mine. The simulation results are in good agreement with the previous numerical results, verifying the accuracy of the calculation of seepage flow and heat conduction in the roadway surrounding rock.

• 3. When the direction of heat conduction is opposite to the diffusion direction of seepage, the "temperature carrying effect" of pore water will hinder the rate of heat conduction. With the increase of boundary water pressure difference, the asymmetry of temperature field of surrounding rock is enhanced. In addition, the pore water pressure of surrounding rock under hydro-thermal coupling condition is greater than that without coupling condition, and the difference increases with the increase of boundary water pressure difference.

• 4. Chemical corrosion and particle resolution have significant effects on mechanical parameters and fracture characteristics (brittle or ductile fracture) of rock mass. In the future, it is urgent to establish a hydro-thermo-chemo-mechanical multi-dimension coupling model of fractured rock mass to comprehensively reveal the crack propagation law of underground engineering fractured rock mass under multi-field coupling conditions.