1 Introduction

Natural gas hydrate saturation (NGHS) in reservoirs, generally, serves as a critical parameter for resource reserves calculation (Zhuo et al. 2021). The current evaluation methods of natural gas saturation in reservoirs are usually based on the resistivity or acoustic logging data, by establishing mathematical models in consideration of the characteristics of natural gas reservoirs, such as Archie formula (Azar et al. 2008), Lee weight equation (Lee 2002), Wood equation (Bao et al. 2022). However, due to the major discrepancy between natural gas hydrate reservoirs and conventional natural gas reservoirs, it is difficult to accurately evaluate NGHS in reservoirs using the traditional calculation methods. Therefore, it is of great importance to develop an evaluation method suitable for gas hydrate saturation in reservoirs, further to accurately evaluating the reservoir reserves.

Resistivity log data is commonly used for calculating the natural gas saturation (Sg) in reservoirs. For this method, it is generally considered that the rock pore space consists of only two substances: water and natural gas. The reservoir water saturation (Sw) is calculated by the relationship between the resistivity and water saturation of the reservoir, so as to calculate NGHS of the reservoir (Sh = 1 − Sw). This method was first proposed by Archie (2003) and developed by Poupon et al. (1954), Alger and Raymer (1963), etc., for conventional natural gas reservoirs. The most widely-used calculation models involve Simandoux formula (Simandou 1964), standard Archie formula (Kim et al. 2013), modified Archie formula (Riedel et al. 2013) and Indonesian formula (Amiri et al. 2012). However, Guo and Zhu (2011) pointed out that NGHS in reservoirs calculated by Archie’s formula may pose some discrepancies compared with the actual saturation due to that the geological conditions considered in Archie’s formula are different from those of the actual natural gas hydrate reservoirs. Thus, some novel models were developed with more considerations on the geological conditions for NGHS evaluation, such as the NGHS model considering gas hydrate as pore filling, particle support and separate stratification (Li et al. 2022a), the two-parameter calculation model of resistivity and acoustic interval transit time based on logging data (Li et al. 2022b), and the NGHS prediction method using joint inversion of resistivity and sonic logs (Pandey and Sain 2022). However, these models do not fully consider the natural gas hydrate states of solid as rock matrix, semisolid as filler and fluid during the decomposition process.

Sonic logging data is an effective information for evaluating NGHS in reservoirs (Ding et al. 2020). The most frequently-applied models using sonic logging data are developed via the correlation between rock composition, porosity, density and other parameters of the natural gas hydrate reservoir and the reservoir P-wave velocity. Leclaire et al. (1994) first used the Biot-Type equation to establish the relationship between the elastic wave velocity and reservoir gas saturation. For natural gas hydrates reservoirs, some mathematical models of NGHS in reservoirs based on the sonic velocity were developed in the past few years, such as the time-average equation (Wyllie et al. 1958; Pearson et al. 1983; Arun et al. 2018), the Wood equation (Bao et al. 2022), the BGTL model (Lee 2002), the KT equation (Kuster and Toksoz 1974; Zimmerman and King 1986), and the Frenkle-Gassmann equation (Zillmer 2006). Especially, the equivalent medium theory (Helgerud et al. 1999; Dvorkin et al. 1999), of which natural gas hydrate is considered to be part of the pore fluid when NGHS is low and is considered to be part of the rock matrix when NGHS is high, is mainly suitable for loose, high-porosity sediments. This model is widely accepted by scholars in the area of petroleum engineering (Ecker 2001; Liu et al. 2022). In addition, some empirical formulas were put forward to calculate the porosity of saturated water sediments, NGHS, free gas content, and seismic wave impedance, respectively, using the elastic wave impedance inversion technique based on the logging data (Lu and McMechan 2004). As well as, Zhu et al. (2023) developed a hydrate saturation evaluation according to the cementation factor and saturation index. Although some evaluation methods of NGHS in reservoirs have been developed using the sonic logging data, and some of them have been applied in the field measurement, these methods do not fully consider the characteristics of natural gas hydrate reservoirs, causing practical application to be challenging. Another drawback of these methods is that the parameters used to perform the evaluation are hard to obtain.

Furthermore, a few scholars drew upon mathematical deduction and seismic inversion to calculate NGHS in reservoirs. Shelander et al. (2012) proposed a calculation method for computing NGHS based on seismic inversion, petrophysical models, and stratigraphic sequence in the absence of wells. Although these methods can be used to evaluate NGHS in a larger range of reservoirs, their accuracy are relatively low with little application potential in the accurate evaluation of reservoir reserves or the design of development parameters.

The above methods are mainly developed based on the calculation models used for conventional reservoirs, thus the typical reservoir characteristics of the natural gas hydrate and the easy-to-use calculation parameters have not been well considered in these methods, and the accuracy of the results predicted by these methods is still relatively low. Therefore, this paper, based on the equivalent medium theory, aims to fully consider the occurrence form of natural gas hydrate in the reservoir by two natural gas hydrate occurrence modes: 1) The lower-saturation natural gas hydrate in the reservoir is regarded as fluid (Mode A) whereas 2) the higher-saturation is regarded as matrix (Mode B). Based on the two modes, a calculation model for NGHS in reservoirs using logging data and core-testing data has been established to support and optimize the evaluation of natural gas hydrate resource reserves.

2 Calculation model of NGHS in reservoirs based on the equivalent medium theory

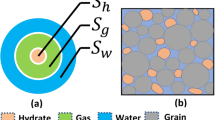
In the practical circumstances, the natural gas hydrate in reservoirs would have two occurrence forms (Helgerud et al. 1999; Ecker 2001; Fang et al. 2022), as shown in Fig. 1: (1) Mode A: moveable natural gas hydrate and, (2) Mode B: immovable natural gas hydrate. The natural gas hydrate of Mode A has not been fixed with the rock matrix and is regarded as a part of the pore fluid in reservoirs. Mode A is suitable for the case where NGHS of the reservoir is low. The natural gas hydrate of Mode B is fixed with the rock matrix, and in this case, natural gas hydrate and rocks form a reservoir rock matrix structure and the porosity of the reservoir will decrease. Mode B is suitable for the situation where NGHS of the reservoir is high. Therefore, according to the situations of two occurrence forms of natural gas hydrate, a new calculation model of NGHS in reservoir can be developed based on the equivalent medium theory and this model is introduced as follows.

Fig. 1
figure 1

Occurrence form schematic diagram of natural gas hydrate in reservoirs with moveable natural gas hydrate particles (a), with immovable natural gas hydrate particles (b), and with bonding natural gas hydrate blocks (c) (modified from Fang et al. 2022)

Full size image

2.1 Calculation model of NGHS in reservoirs for Mode A

The reservoir, including rock, water, gas and NGHS, is regarded as the equivalent medium of Mode A. Thus, based on the equivalent medium theory (Ecker 2001), NGHS in the reservoir can be expressed as:

$$S_{{\rm{h}}} = \frac{{K_{{\rm{w}}} K_{{\rm{h}}} - K_{{\rm{h}}} K_{{\rm{f}}} }}{{K_{{\rm{w}}} K_{{\rm{f}}} - K_{{\rm{h}}} K_{{\rm{f}}} }}$$
(1)

where Sh is the natural gas hydrate saturation (NGHS) in the reservoir, %; Kh is the bulk modulus of natural gas hydrate, GPa, which is 7.7 GPa (Dvorkin et al. 2003); Kw is the bulk modulus of water, GPa, which is 2.29 GPa (Lee 2004); and Kf is the bulk modulus of pore fluid in the reservoir, GPa.

In the Mode A, Kf can be computed by (Ecker 2001):

$$K_{{\rm{f}}} = \frac{{K_{{{\rm{ma}}}} \phi \left( {K_{{{\rm{dry}}}} - K_{{{\rm{sat}}}} } \right)}}{{K_{{{\rm{sat}}}} \left( {1 - \phi } \right) - K_{{{\rm{sat}}}} K_{{{\rm{dry}}}} /K_{{{\rm{ma}}}} - K_{{{\rm{ma}}}} + \left( {1 + \phi } \right)K_{{{\rm{dry}}}} }}$$
(2)

where Ksat is the bulk modulus of the equivalent medium of Mode A, GPa; Kdry is the bulk modulus of dry rock, GPa; ϕ is the porosity of the rock matrix in the reservoir without natural gas hydrate, %; and Kma is the bulk modulus of the solid phase of rock in the reservoir, GPa.

Using the acoustic interval transit time data from well logging, the bulk modulus of the equivalent medium of Mode A (Ksat) can be easily obtained by Eq. (3) (Liu and Luo 2004).

$$K_{{{\rm{sat}}}} = \rho _{{\rm{b}}} \frac{{3\Delta t_{{\rm{s}}}^{2} - 4\Delta t_{{\rm{c}}}^{2} }}{{3\Delta t_{{\rm{s}}}^{2} \Delta t_{{\rm{c}}}^{2} }} \times a_{{\rm{c}}}$$
(3)

where ρb is the volume density of the reservoir, g/cm3, which can be obtained by density logging; Δts and Δtc are the shear wave (S-wave) and longitudinal wave (P-wave) time difference of the reservoir, μs/m; ac is the correction coefficient, ac = 1.0 × 109GPa/(g/cm3).

Generally, only the longitudinal wave time difference of the reservoir can be obtained by well logging, and the shear wave time difference can be calculated by Eq. (4) (Liu and Luo 2004).

$$\Delta t_{{\rm{s}}} = \frac{{\Delta t_{{\rm{c}}} }}{{1 - 1.15\left[ {\frac{{\left( {1/\rho_{{\rm{b}}} } \right) + \left( {1/\rho_{{\rm{b}}} } \right)^{3} }}{{e^{{\left( {1/\rho_{{\rm{b}}} } \right)}} }}} \right]^{1.5} }}$$
(4)

In Eq. (2), Kdry can be obtained by Eq. (5) (Dvorkin et al. 1999).

$$K_{{{\rm{dry}}}} = \left\{ \begin{gathered} \left[ {\frac{{{\raise0.7ex\hbox{$\phi $} \!\mathord{\left/ {\vphantom {\phi {\phi_{{\rm{c}}} }}}\right.\kern-0pt} \!\lower0.7ex\hbox{${\phi_{{\rm{c}}} }$}}}}{{K_{{{\rm{HM}}}} + \frac{4}{3}G_{{{\rm{HM}}}} }} + \frac{{1 - {\raise0.7ex\hbox{$\phi $} \!\mathord{\left/ {\vphantom {\phi {\phi_{c} }}}\right.\kern-0pt} \!\lower0.7ex\hbox{${\phi_{c} }$}}}}{{K_{{{\rm{ma}}}} + \frac{4}{3}G_{{{\rm{HM}}}} }}} \right]^{ - 1} - \frac{4}{3}G_{{{\rm{HM}}}} , \, \phi < \phi_{{\rm{c}}} \hfill \\ \left[ {\frac{{{\raise0.7ex\hbox{${(1 - \phi )}$} \!\mathord{\left/ {\vphantom {{(1 - \phi )} {(1 - \phi_{{\rm{c}}} )}}}\right.\kern-0pt} \!\lower0.7ex\hbox{${(1 - \phi_{{\rm{c}}} )}$}}}}{{K_{{{\rm{HM}}}} + \frac{4}{3}G_{{{\rm{HM}}}} }} + \frac{{{\raise0.7ex\hbox{${(\phi - \phi_{{\rm{c}}} )}$} \!\mathord{\left/ {\vphantom {{(\phi - \phi_{{\rm{c}}} )} {(1 - \phi_{{\rm{c}}} )}}}\right.\kern-0pt} \!\lower0.7ex\hbox{${(1 - \phi_{{\rm{c}}} )}$}}}}{{\frac{4}{3}G_{{{\rm{HM}}}} }}} \right]^{ - 1} - \frac{4}{3}G_{{{\rm{HM}}}} , \, \phi \ge \phi_{{\rm{c}}} \hfill \\ \end{gathered} \right.$$
(5)

where,

$$K_{{{\rm{HM}}}} { = }\left[ {\frac{{r^{2} \left( {1 - \phi_{{\rm{c}}} } \right)^{2} G_{{{\rm{ma}}}}^{{2}} }}{{18{\uppi }^{2} \left( {1 - \nu } \right)^{2} }}P} \right]^{\frac{1}{3}}$$
(6)
$$G_{{{\rm{HM}}}} { = }\frac{5 - 4\nu }{{5\left( {2 - \nu } \right)}}\left[ {\frac{{3r^{2} \left( {1 - \phi_{{\rm{c}}} } \right)^{2} G_{{{\rm{ma}}}}^{{2}} }}{{2{\uppi }^{2} \left( {1 - \nu } \right)^{2} }}P} \right]^{\frac{1}{3}}$$
(7)

where ϕc is the critical porosity of the reservoir, %, generally to be 36–40% (Nur et al. 1998); P is the effective stress applied on the rock in the reservoir, MPa; r is the average number of particles in contact with the unit volume at the critical porosity, generally to be 8–9.5 (Kuster and Toksoz 1974); Gma is the shear modulus of the rock matrix, MPa; and ν is the Poisson’ Ratio of the rock matrix, which can be calculated by Eq. (8) (Dvorkin et al. 1999).

$$\nu { = }\frac{{0.5\left( {K_{{{\rm{ma}}}} - \frac{2}{3}G_{{{\rm{ma}}}} } \right)}}{{K_{{{\rm{ma}}}} + \frac{{G_{{{\rm{ma}}}} }}{3}}}$$
(8)

The effective stress P applied on the rock in the reservoir is calculated by Eq. (9).

$$P{ = }\sigma_{\min } - \alpha P_{{\rm{p}}}$$
(9)

where σmin is the minimum in-situ stress in the vertical and two horizontal directions, MPa; Pp is the formation pore pressure, MPa; α is the Boit elastic coefficient, expressed as (Priestley 1999):

$$\alpha = 1 - \frac{{\rho_{{\rm{b}}} \left( {\frac{3}{{\Delta t_{{\rm{c}}}^{{2}} }} - \frac{4}{{\Delta t_{{\rm{s}}}^{{2}} }}} \right)}}{{\rho_{{\rm{m}}} \left( {\frac{3}{{\Delta t_{{{\rm{mc}}}}^{{2}} }} - \frac{4}{{\Delta t_{{{\rm{ms}}}}^{{2}} }}} \right)}}$$
(10)

where Δtmc and Δtms are the longitudinal wave and shear wave time difference of the rock matrix, respectively, μs/m; ρm is volume density of rock matrix, g/cm3, expressed as:

$$\rho_{{\rm{m}}} = \left( {1 - \phi } \right)\sum\limits_{i = 1}^{m} {f_{i} \rho_{i} }$$
(11)

The in-situ stresses in the three directions are calculated using Huang's model (Yin et al. 2017):

$$\left\{ \begin{gathered} \sigma_{{\rm{v}}} = \rho_{{\rm{b}}} gH \times 10^{ - 3} \hfill \\ \sigma_{{\rm{h}}} = \left[ {\frac{\nu }{1 - \nu } + \beta_{1} } \right] \times \left( {\sigma_{{\rm{v}}} - \alpha P_{{\rm{p}}} } \right) + \alpha P_{{\rm{p}}} \hfill \\ \sigma_{{\rm{H}}} = \left[ {\frac{\nu }{1 - \nu } + \beta_{2} } \right] \times \left( {\sigma_{{\rm{v}}} - \alpha P_{{\rm{p}}} } \right) + \alpha P_{{\rm{p}}} \hfill \\ \end{gathered} \right.$$
(12)

Then σmin is determined as follows:

$$\sigma_{\min } = \min \left( {\sigma_{{\rm{v}}} , \, \sigma_{{\rm{h}}} } \right)$$
(13)

where σv is the vertical stress in reservoir, MPa; H is the formation depth, m; σh is the minimum horizontal stress in the reservoir, MPa; σH is the maximum horizontal stress in the reservoir, MPa; β1 and β2 are the tectonic stress coefficients, determined by the hydraulic fracturing experimental inversion method.

The formation pore pressure Pp is expressed as:

$$P_{{\rm{p}}} = \rho_{{\rm{f}}} gH \times 10^{ - 3}$$
(14)

where ρf is the density of the formation fluid, g/cm3.

In Eqs. (2), (5), (6) and (7), Kma and Gma can be calculated by the following formulas (Ecker et al. 2001):

$$K_{{{\rm{ma}}}} = \frac{1}{2}\left[ {\sum\limits_{i = 1}^{m} {f_{i} K_{i} + \left( {\sum\limits_{i = 1}^{m} {\frac{{f_{i} }}{{K_{i} }}} } \right)^{ - 1} } } \right]$$
(15)
$$G_{{{\rm{ma}}}} = \frac{1}{2}\left[ {\sum\limits_{i = 1}^{m} {f_{i} G_{i} + \left( {\sum\limits_{i = 1}^{m} {\frac{{f_{i} }}{{G_{i} }}} } \right)^{ - 1} } } \right]$$
(16)

where m is the number of minerals in the solid phase of rock, integer; fi is the volume fraction of the i-th mineral in the solid phase of rock, decimal, which can be obtained through the rock mineral composition test; and Ki and Gi are the bulk modulus and shear modulus of the i-th mineral, MPa, which are determined from the literature of Burland et al. (2012).

2.2 Calculation model of NGHS in reservoirs for Mode B

Natural gas hydrate is considered as a part of the rock matrix in Mode B, thus NGHS in reservoirs can be expressed as:

$$S_{{\rm{h}}} = \frac{{\phi - \phi_{{\rm{r}}} }}{\phi }$$
(17)

where ϕr is the reservoir porosity when the natural gas hydrate is regarded as the rock matrix, %.

According to the acoustic velocity data obtained by well logging, Eq. (18) is used to calculate the reservoir porosity (Liu et al. 2013):

$$\phi_{{\rm{r}}} = \frac{{\phi_{{\rm{s}}} }}{{C_{{\rm{p}}} }} = \frac{{\Delta {\rm{t}}_{{\rm{c}}} -\Delta t_{{{\rm{mc}}}} }}{{\Delta t_{{\rm{f}}} -\Delta t_{{{\rm{mc}}}} }} \cdot \frac{1}{{C_{{\rm{p}}} }}$$
(18)

where Δtf is the longitudinal wave time difference of the reservoir fluid, μs/m, generally to be 620 μs/m; ϕs is the sonic porosity before correction, %; Cp is the reservoir compaction correction coefficient, decimal, and Cp, which is widely accepted in petroleum engineering, can be written as the following empirical formula.

$$C_{{\rm{p}}} = \xi - \lambda H$$
(19)

where ξ is the model parameter for Cp, decimal; λ is the correction coefficient for Cp, m−1.

The volume density of the reservoir (ρb) can be expressed as:

$$\rho_{{\rm{b}}} { = }\left( {1 - \phi } \right)\rho_{i} + \left( {\phi - \phi_{{\rm{r}}} } \right)\rho_{{\rm{h}}} + \phi_{{\rm{r}}} \rho_{{\rm{w}}}$$
(20)

where ρi is the density of each mineral in the reservoir rock, g/cm3, which can be obtained by checking the literature of Burland et al. (2012); ρh is the density of pure natural gas hydrate, g/cm3, which is taken as 0.9 g/cm3; ρw is the density of water, g/cm3, which is taken as 1.0 g /cm3.

Thus, according to Eqs. (11) and (20), we have:

$$\phi { = }\frac{{\sum\limits_{i = 1}^{m} {f_{i} \rho_{i} } - \phi_{{\rm{r}}} \rho_{{\rm{h}}} + \phi_{{\rm{r}}} \rho_{{\rm{w}}} - \rho_{{\rm{b}}} }}{{\sum\limits_{i = 1}^{m} {f_{i} \rho_{i} } - \rho_{{\rm{h}}} }}$$
(21)

2.3 Method for selecting Mode A or B

The calculation formulas of NGHS in reservoirs of both Mode A and Mode B are given above. For the actual application, the selection of Mode A or B is carried out through the following steps, as shown in Fig. 2.

  1. (1)

    The parameters of both Mode A and Mode B are obtained for the same rock specimen prepared under different NGHSs.

  2. (2)

    Using the parameters for the same rock specimen prepared under different NGHSs, NGHSs in the rock specimen are calculated by the calculation formulas of both Mode A and Mode B.

  3. (3)

    The predicted results by the calculation formulas of both Mode A and Mode B are compared with the measured values, and the errors of the predicted results by the calculation formulas of both Mode A and Mode B can be obtained.

  4. (4)

    The error curves of the predicted results calculated by Mode A and B are drawn as a figure, and an intersection point for the two curves can be obtained. Thus, we can determine that Mode A calculation formula is selected for NGHS evaluation while the errors of the predicted results calculated by Mode A is below the value of the intersection point, whereas the Mode B calculation formula is selected for NGHS evaluation while the errors of the predicted results calculated by the Mode A is higher than the value of the intersection point.

Fig. 2
figure 2

Flow chart of the selection of Mode A or B for NGHS evaluation

Full size image

The NGHS of the intersection point (Shc) is, therefore, the critical value for selecting whether Model A or Model B to evaluate NGHS in the rock specimen. This critical NGHS is a constant value for rocks no matter how the size or number of rock pores and stress environment vary. This is due to that the ratio of the removable natural gas hydrate in the rock pores, which is the critical NGHS, is the same no matter how the size of rock pores varies.

3 Evaluation of the proposed model

3.1 Other common models for comparison

Two widely-accepted prediction models for natural gas saturation in reservoirs are briefly presented to compare with the proposed model.

3.1.1 Wood equation

The Wood equation has better applicability for evaluating the saturation of the suspended pore fluid filled in the rock pores with higher saturation, and the NGHS model derived by Wood equation is expressed as (Bao et al. 2022):

$$S_{h} = \left(\frac{{\phi_{r} }}{{\rho_{\rm{w}} V_{\rm{w}}^{{2}} }} + \frac{{1 - \phi_{r} }}{{\rho_{\rm{m}} V_{m}^{2} }} - \frac{1}{{\rho_{b} V_{p}^{2} }}\right)\frac{{\rho_{w} \rho_{h} V_{w}^{2} V_{h}^{2} }}{{\phi_{r} (\rho_{h} V_{h}^{2} - \rho_{\rm{w}} V_{w}^{2} )}}$$
(22)

where Vh, Vw, Vm, and Vp are the longitudinal wave velocities of pure natural gas hydrate, pure water, rock matrix, and natural gas hydrate reservoir, respectively, m/s; the longitudinal wave velocity of pure natural gas hydrate (Vh) is 3650 m/s, and the longitudinal wave velocity of pure water (Vw) is 1500 m/s.

3.1.2 Weight equation

Weight equation is developed based on Time-average equation (Lee et al. 1996) and Wood equation (Bao et al. 2022). A weight factor (W) and a constant (n) are used to correct the predicted result to adapt to the actual situation. The expression of Weight equation is as follows:

$$S_{{\rm{h}}} = 1 - \left[ {\frac{{V_{{{\rm{p1}}}} V_{{{\rm{p2}}}} - V_{{\rm{p}}} V_{{{\rm{p1}}}} }}{{W\phi \left( {V_{{\rm{p}}} V_{{{\rm{p2}}}} - V_{{\rm{p}}} V_{{{\rm{p1}}}} } \right)}}} \right]^{\frac{1}{n}}$$
(23)

where Vp1 is the longitudinal wave velocity calculated by Wood equation, m/s; Vp2 is the longitudinal wave velocity calculated by the Time-average equation, m/s; W is the weight factor, dimensionless, generally being equal to 1; and n is the constant related to NGHS, dimensionless, generally equal to 32.

3.2 Criteria for performance comparison

We used three different error measurements to assess the validity of predictions computed by different models: the regression R-square value (R2), the discrepancy percentage or relative difference (Dp), and the average absolute relative error percentage (AAREP). AAREP is preferably used below because it is a simple estimator that provides a direct indication of the prediction error. Their definitions are (Shen et al. 2012a, b, 2014; Zhang et al. 2021a, 2023):

$$R^{2} = 1 - \frac{{\sum\nolimits_{i = 1}^{N} {\left( {S_{{{\rm{h}},i}}^{{{\rm{test}}}} - S_{{{\rm{h}},i}}^{{{\rm{pred}}}} } \right)^{2} } }}{{\sum\nolimits_{i = 1}^{N} {\left( {S_{{{\rm{h}},i}}^{{{\rm{test}}}} - E\left[ {S_{{{\rm{h}},i}}^{{{\rm{test}}}} } \right]} \right)^{2} } }}$$
(24)
$$D_{{{\rm{p}},i}} \left[ {\rm{\% }} \right] = \frac{{S_{{{\rm{h}},i}}^{{{\rm{pred}}}} - S_{{{\rm{h}},i}}^{{{\rm{test}}}} }}{{S_{{{\rm{h}},i}}^{{{\rm{test}}}} }} \times 100{\rm{\% }}$$
(25)
$${\rm AAREP}\left[ \% \right] = \frac{{\sum\nolimits_{{{\rm{i = 1}}}}^{{\rm{N}}} {\left| {{{D}}_{{\rm{p} {\rm{,i}}}} } \right|} }}{{{N}}}$$
(26)

where N is the number of available observations, integer; \(S_{{\rm{h}}}^{{{\rm{test}}}}\) is the observed test results of NGHS, %; \(S_{{\rm{h}}}^{{{\rm{pred}}}}\) is the NGHS predicted by models; and E[‧] denotes the expectation (or statistical mean) operator.

Based on the above definitions, it is clear that a smaller AAREP corresponds to a more reliable model. Meanwhile, R2 increases with the quality of the predictions, so that higher R2 values correspond to models with lower AAREP values. Dp,i, that is needed to compute AAREP, is the relative difference between predicted and observed values for the i-th test.

3.3 Experimental data and model parameters

The experimental data of NGHS and acoustic wave velocity is tested by the SHW-III natural gas hydrate acousto-electricity test device for the specimens of loose natural gas hydrate deposits with different NGHSs. These tests were conducted under triaxial uniform stress (σmin) of 10 MPa, 15 MPa and 20 MPa, respectively. NGHS of the specimen is calculated based on the material balance equation (Sun et al. 2018) and the PVT equation of state (Zhang et al. 2015), and the acoustic wave velocity in the specimen is tested directly by the device. NGHSs and acoustic wave velocities for the same specimen were tested after each gas injection, and the experimental data is shown in Table 1 (Zhao et al. 2018).

Table 1 Experimental data of NGHS and acoustic wave velocity (Zhao et al 2018)
Full size table

According to the test results presented in Table 1 and other rock petrophysics experiments, the parameters of three comparison models can be obtained using the method mentioned in Sect. 2, as shown in Tables 2 and 3. ϕ is measured by the mercury intrusion method using an automatic mercury porosimeter of PoreMaster60 (manufactured by Quantachrome Instruments, USA). Cp is determined by the comparison between ϕ and the porosity determined by the velocity of longitudinal wave, using Eq. (18). The data used for calculating ϕs are the velocities at longitudinal wave of 500.08 μs/m, 395.20 μs/m, 295.25 μs/m for the condition of σmin = 10 MPa, 15 MPa and 20 MPa, respectively. Kma, Gma and ρm of quartz sand are determined from the literature written by Burland et al. (2012). Changes in ρb with the gas injection time are measured by theoretical calculation by the mass of rock, water and gas, as shown in Table 1. ϕc and r are determined from the literature authored by Nur et al. (1998) and Kuster and Toksoz (1974), respectively.

Table 2 Basic model parameters
Full size table
Table 3 Other model parameters
Full size table

3.4 Results and analysis

Experimental data and model parameters mentioned in Sect. 3.3 are substituted into the proposed model of both Mode A and Mode B, and NGHSs of the specimen after different gas injection steps are calculated. The errors of the predicted results for the Mode A and B under the triaxial uniform stress (σmin) of 10 MPa and 15 MPa with measured saturations are shown in Fig. 3. There is an intersection point between the two error curves of Mode A and B predicted results. The prediction errors of the intersection points are 8.09% and 8.11% for the conditions of triaxial uniform stress (σmin) of 10 MPa and 15 MPa, respectively. When the measured saturation is lower than the NGHS of the intersection point, the prediction error of Model A is significantly lower than that of Model B; when the measured saturation is higher than the NGHS of the intersection point, the prediction error of Model B is significantly lower than that of Model A. The similar NGHS of the intersection point can also demonstrate that this value would not change with the size and number of rock pores, as well as the stress condition of rock, as mentioned in Sect. 2.3. Therefore, we can determine the NGHS of the intersection point as 8.10% (average value of 8.09% and 8.11%), that is, if NGHS is lower than 8.10%, the calculation model of Mode A would be used for NGHS evaluation, whereas the calculation model of Mode B would be used when NGHS is higher than 8.10%.

Fig. 3
figure 3

Prediction error and measured saturation curves of Model A and B: a σmin = 10 MPa; b σmin = 15 MPa

Full size image

The errors of the predicted results by the proposed model changed with the measured saturation and the triaxial uniform stress, as shown in Fig. 4. From Fig. 4a, it can be seen that the error of the predicted results changes a lot under σmin = 10 MPa, and the error of the predicted results shows a relatively stable variation under σmin = 15 MPa and 20 MPa. This implies that the prediction accuracy is highly affected by triaxial uniform stress. The error of the predicted results for Mode B generally decreases with increasing measured saturation. For example, the average errors are 9.04%, 14.51%, 7.27%, and 7.49% respectively at the 2nd, 3rd, 4th and 5th injections. The reason for this would be explained as follows: when NGHS is relatively low, some part of the natural gas hydrate with poor bonding strength (as shown in the Fig. 1b) has a weaken propagation capacity in response to the acoustic wave. In this case, the measured acoustic velocity is relatively low. Therefore, some natural gas hydrate particles embedded in rock particles are regarded as water in the model calculation. However, the measured saturation is calculated based on the material balance equation and the PVT equation of state as mentioned in Sect. 3.3, in which situation these natural gas hydrate particles is accurately determined as natural gas hydrate particles. Therefore, considering that the ratio of the natural gas hydrate with poor bonding strength would decrease with increasing gas injection time (increasing NGHS), the accuracy of predicted results for Mode B will increase with increasing NGHS.

Fig. 4
figure 4

Errors of the predicted results by the proposed model changed with the measured saturation (a) and the triaxial uniform stress (b)

Full size image

The error of the predicted results increases with increasing triaxial uniform stress, as shown in Fig. 4b. For example, Dp,i is 0.7–16.4% with an average value of 5.16% for σmin = 10 MPa; Dp,i is 4.18–13.04% with an average value of 10.48% for σmin = 15 MPa; and Dp,i is 8.71–14.73% with an average value of 11.78% for σmin = 20 MPa. The reason can be described as follow. The rock porosity (ϕ) would change with increasing triaxial uniform stress, but this rock porosity (ϕ) is set as a constant value in the proposed model. In this case, a higher triaxial uniform stress would cause a larger change of rock porosity (ϕ), resulting in a bigger error of the predicted results. However, the effect of stress on the rock porosity is negligible due to that the volumetric strain of rock is usually lower than 1.5% before failure (Qiu et al. 2019), resulting in a relatively small change of the errors of the predicted results under different triaxial uniform stress.

The predicted results of the proposed model, Wood equation and Weight equation and the error of the predicted results compared with measured saturations are shown in Table 4. We can clearly find that the predicted results by the proposed model agree better with the measured saturation compared with other two models. This can be verified by the total average errors of 9.14%, 46.84% and 15.70% for the proposed model, Wood equation, and Weight equation, respectively.

Table 4 Natural gas hydrate saturation predicted by the three models and its associated error analysis
Full size table

The comparison of the predicted results of the models and the measured saturations (Fig. 5) also shows that the proposed model has higher prediction accuracy compared with other two models. This can be certified by the following data: AAREP and R2 of the predicted results by the proposed model, Weight equation, Wood equation are 8.90% and 0.968, 15.69% and 0.958, 55.70% and 0.472, respectively. In addition, the error of the predicted results for Weight equation is just a little higher than that for the proposed model and much lower than that for Wood equation. This would be due to that Weight equation is developed based on Time-average equation and Wood equation, and the prediction accuracy of Weight equation has been enhanced by the weight factor (W) and the constant (n) compared with the prediction accuracy of Wood equation.

Fig. 5
figure 5

Comparison of the predicted results of the models and the measured saturations

Full size image

4 Field application

4.1 Background

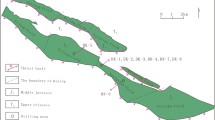
The proposed model is used to evaluate NGHS of a reservoir well section of the DK-1 scientific drilling test well, located in Muli Depression of the permafrost region of Qilian Mountains, northeast of the Qinghai-Tibet Plateau, China. This area can be divided into three tectonic units: the southern Qilian tectonic belt, the northern Qilian tectonic belt and the central Qilian block, as shown in Fig. 6 (Lu et al. 2010). The permafrost region of Qilian Mountains covers an area of 10 × 104 km2, and its annual average ground temperature is 1.5–2.4 °C. The thickness of the frozen formation of the permafrost region is 50–139 m (Zhang et al. 2021b). This implies that the conditions of temperature and pressure are highly suitable for the reservoir-forming natural gas hydrate in permafrost area of Qilian Mountains, especially in Muli Depression (Zhu et al. 2009). As yet, research on natural gas hydrate reservoirs in the permafrost region of Qilian Mountains mainly focus on geological characteristics, gas source characteristics, logging response characteristics, reservoir-forming conditions and thermophysical properties. However, there are few studies on the evaluation of NGHS in this area, and the prediction of NGHS in the reservoir of this area would be of great significance for the evaluation of natural gas hydrate resource reserves.

Fig. 6
figure 6

Sketch map of tectonic units in Qilianshan area, Qinghai Province (Lu et al 2010)

Full size image

The DK-1 scientific drilling test well was drilled on October 18, 2008. Its geographical coordinates are 38°05.591′N, 99°10.260′E, and 4057 m above sea level. The drilling process of this well terminated on November 26, 2008, with a depth of 182.25 m. After that, three new wells of DK-2, DK-3 and DK-4 were drilled in this area, at depths of 645.22 m, 765.01 m, and 466.65 m, respectively, and finally, the total length of the four natural gas hydrate reservoir wells reached 2059.13 m. Among the four wells in Muli Depression of the Qilian Mountains permafrost region, Well DK-1 has the largest hydrate reserves and the most abundant data. We, therefore, chose Well DK-1 to analyze NGHS of this reservoir area using the proposed model. A total of 4 intervals of natural gas hydrate layers were discovered in the entire well section, as listed below: (1) 133.5–135.5 m: natural gas hydrate was found within the pores of fine sandstone, presented as white crystals; (2) 142.9–147.7 m: natural gas hydrate existed in the pores and fissures of argillaceous siltstone as white crystals; (3) 165.3–165.5 m: natural gas hydrate crystals were observed in the fissures of argillaceous siltstone; and (4) 169.0–170.5 m: natural gas hydrate was observed in the pores of siltstone (Zhu et al. 2009).

4.2 Determination of parameters

The 142.9–147.7 m section of Well DK-1, which is the thickest among the four natural gas hydrate layers, is chosen for analysis. The acoustic interval transit time and density of Well DK-1 are collected from the literature written by Guo and Zhu (2011), as shown in Fig. 7. The mineral compositions in this natural gas hydrate reservoir were determined by Wang et al. (2019), as shown in Table 5, indicating that sandstone is the main component in this area.

Fig. 7
figure 7

Logging data, reservoir porosities and natural hydrate saturation for the 142.9–147.7 m well section of Well DK-1 in the permafrost region of Qilian Mountains

Full size image
Table 5 Mineral compositions and the corresponding bulk modulus and shear modulus of the rock in the 142.9–147.7 m section of Well DK-1 in the permafrost region of Qilian Mountains (Wang et al 2019)
Full size table

According to the methods introduced in Sect. 2, the parameters of our proposed model for the 142.9–147.7 m well section of Well DK-1 in the permafrost region of Qilian Mountains are obtained, as shown in Table 6. And the porosity of the reservoir with or without hydrate are shown in Fig. 7.

Table 6 Parameters of the proposed model for the 142.9–147.7 m well section of Well DK-1 in the permafrost region of Qilian Mountains
Full size table

4.3 Predicted results and analysis

According to the data of gas and water extracted from the samples at depths of 142.90 m, 143.25 m, 143.95 m, 144.30 m, 145.00 m, and 146.05 m of the Well DK-1, the measured saturations were determined based on the material balance equation for comparison. The measured saturations of these six samples are 7.5%, 15.8%, 37%, 37.2%, 38.5%, and 40.3%, respectively, as shown in Fig. 7. The measured saturations of the samples at depths of 142.90 m and 143.25 m are much lower than those of the other four samples. This would be due to that these two samples were collected near the upper border of section of Well DK-1in this reservoir. Therefore, according to the Shc of 8.10% for selecting the calculation models of Mode A or B to evaluate natural gas hydrate in reservoir, the calculation model of Mode A is chosen for the NGHS calculation of the 142.9–143.2 m well section and the calculation model of Mode B is used for the 143.2–147.7 m well section. Using the model parameters given in Sect. 4.2, NGHS for the 142.9–147.7 m well section of Well DK-1 in the permafrost region of Qilian Mountains can be calculated by the proposed model, as shown in Fig. 7.

NGHSs predicted by the proposed model for the 142.9–147.7 m well section of Well DK-1 are in the range of 5.3–54.1%. The errors of the predicted results at well depths of 142.90 m, 143.25 m, 143.95 m, 144.30 m, 145.00 m, and 146.05 m of the Well DK-1 are 9.33%, 13.92%, 10.00%, 10.75%, 9.87%, and 9.18%, respectively, with an average error of 10.56%. This indicates that the proposed model can evaluate NGHS in the reservoir of the Qilian Mountains permafrost region with reasonable accuracy. In addition, the error of NGHS predicted by the model of Mode A is generally lower than those predicted by the model of Mode B, and the error of NGHS predicted by the model of Mode B decreases with increasing measured saturation. The change behavior of prediction error with measured saturation are consistent with the results obtained by the experiments, as shown in Fig. 4a. The reason for this would be that some part of the natural gas hydrate is regarded as water for NGHS calculation using the proposed model of Mode B when the NGHS is relatively low, as mentioned in Sect. 3.4. Furthermore, the length of the analyzed well section is only 4.8 m, and the difference of the minimum in-situ stress in the vertical two horizontal directions calculated by this proposed model is lower than 0.113 MPa. Therefore, the effect of the stress difference can be ignored resulting in that there is no relation between the error of the predicted results and the depth.

In general, the errors of the predicted results calculated by the proposed model are all lower than 13.92%, with an average value of 10.51%. This indicates that the predicted results are in good agreement with the measured saturations. In addition, the change behavior of the errors of predicted results compared with the measured saturation agrees well with experiment data, as shown in Sect. 3.4, implying that the proposed model has a good consistency for both experimental analysis and engineering application. So, the satisfying performance of the predicted results by the proposed model shows that this new method developed by the equivalent medium theory is suitable for evaluating the NGHS in the permafrost region reservoir. Furthermore, this method can make full use of field well logging data and does not use too much experimental data for parameter determination, which would highly increase its adaptability.

As what have discussed above, the proposed method would be used as a superior guidance for the accurate evaluation of NGHS. By using the proposed method to obtain an accurate NGHS, the natural gas hydrate reserves can be estimated clearly for the gas reservoir development design, as well as, the exploitation degree of a natural gas hydrate reservoir after production can be monitored effectively. And beyond that, NGHS is also an important parameter for the stability analysis of the wellbore in the formation containing natural gas hydrate. The proposed method of NGHS evaluation is beneficial to the drilling design and operation in the natural gas hydrate reservoir. As well as, it is meaningful for the drilling engineering of other oil and gas development when the well goes through the formation containing natural gas hydrate in high latitude or altitude regions. Furthermore, it is impossible to collect the sediment in natural gas hydrate reservoir without any disturbance. In this case, the original NGHS in the reservoir cannot be tested directly using the sediment sample. Fortunately, NGHS can be calculated by the proposed method using logging data, and the logging data can reflect the original situation of the natural gas hydrate reservoir. In general, the novel evaluation method of NGHS presented in this paper is significative for the geological resource exploitation related to the natural gas hydrate stratum.

5 Conclusions

  1. (1)

    A novel evaluation method of natural gas hydrate saturation (NGHS) in reservoirs is developed in this paper. In light of the equivalent medium theory, the method is derived according to the concept that the natural gas hydrate is regarded as the fluid (Mode A) when NGHS is relatively low, while as the rock matrix (Mode B) when NGHS is high. And if NGHS is no more than 8.10%, the calculation model of Mode A is used for NGHS evaluation, whereas the calculation model of Mode B is used when NGHS is higher than 8.10%.

  2. (2)

    The errors of predicted results by the proposed model are lower than 16.4%. The comprehensive error analysis shows that R2 is 0.968 and AAEPR is 8.90%. And the predictive capability of the proposed model is significantly better than those of Wood equation and Weight equation.

  3. (3)

    The prediction accuracy of the proposed model is highly affected by triaxial uniform stress, showing that the error of the predicted results generally increases with increasing triaxial uniform stress. As well as, the error of the predicted results for Mode B decreases with increasing measured saturation.

  4. (4)

    NGHSs predicted by the proposed model for the 142.9–147.7 m well section of Well DK-1 are in the range of 5.3–54.1%. The errors are 9.18–13.92%, with an average error of 10.56%, compared with the measured saturations determined by the material balance equation. And the error of Mode A is generally lower than those predicted by Mode B.

  5. (5)

    The satisfying performance of the predicted results by the proposed model shows that this method is suitable for evaluating the NGHS of the permafrost region reservoir. This method can make full use of field well logging data and does not use too much experimental data for parameter determination. The novel evaluation method of NGHS presented in this paper is significative for the geological resource exploitation related to the natural gas hydrate stratum.