Towards a Better Understanding of Fractional Brownian Motion and Its Application to Finance

Abstract

The aim of this work is to first build the underlying theory behind fractional Brownian motion and applying fractional Brownian motion to financial market. By incorporating the Hurst parameter into geometric Brownian motion in order to characterize the long memory among disjoint increments, geometric fractional Brownian motion model is constructed to model S &P 500 stock price index. The empirical results show that the fitting effect of fractional Brownian motion model is better than ordinary Brownian motion.

1 Introduction

The main feature of the Black–Scholes market is that the price of a share of stock is given by the exponential Brownian motion. Thus, in particular, the logarithm of the price is a process with independent increments. However, this assumption is quite unrealistic, since the previous history of the market strongly influences its future behaviour. Therefore, there were several attempts to describe a market whose log-price is a stochastic process with dependent increments.

From the point of view of the theory of stochastic processes, the fractional Brownian motion is one of the most studied stochastic processes with dependent increments [1,2,3]. This process is, in particular, a Gaussian process. So, it was natural to study a Black–Scholes market in which the standard Brownian motion is replaced by a fractional Brownian motion. However, it was proved by Shiryaev [4] that such a market admits arbitrage opportunities.

Hu and Øksendal [5] proposed a model of Black–Scholes type which involves fractional Brownian motion and in which usual multiplication is replaced by the so-called Wick product. They proved that such a market has no arbitrage opportunities, which is complete, and there is an analogue of the Black–Scholes pricing formula for a European call option. We also refer to [6] for an extension of the result of Hu and Øksendal.

In recent years, the fractional Brownian model has been widely used in finance, for example, many consider fractional Brownian motion model in option pricing [7,8,9,10,11,12,13,14]. But none of them balance the rigorousness of the theory and application of fractional Brownian motion well. The aim of this study is to make a systematic introduction into the fractional white noise calculus and to explain the main ideas of Hu and Øksendal’s result [5]. In particular, general Gaussian measures on the dual of a nuclear space are studied. Additionally to [5], some existing results from the book by Berezansky and Kondratiev [15] are taken. Moreover, correspondent proofs of the above literature are strongly expanded and the asset price movement is simulated based on fractional Brownian motion.

Our paper is organized as follows: in Sect. 2, some results of fractional white noise calculus are briefly reviewed. In Sect. 3, the fractional Brownian motion is used to model the financial market and a pricing formula for European call option is derived based on fractional Brownian motion. In Sect. 4, empirical analysis between fractional Brownian motion and Brownian motion will be compared using Monte Carlo simulation. In Sect. 5, the results above are concluded. And in “Appendix”, fractional stochastic integral of Itô type is defined using wick product from Gel’fand triple.

2 Review of Fractional White Noise Calculus

In this section, we will shortly review some results of fractional white noise calculus. Some known results and detailed account of the underlying theory can be found in “Appendix”. The following two definitions are taken from [16].

Definition 1

Let $F:S'({\mathbb {R}})\rightarrow {\mathbb {R}}$ and let $\gamma \in S'({\mathbb {R}})$. We say that F has a directional derivative in the direction $\gamma$ if

$$\begin{aligned} D_{\gamma }F(x):=\lim _{\varepsilon \rightarrow 0}\frac{F(x+\varepsilon \gamma )-F(x)}{\varepsilon } \end{aligned}$$

(1)

exists in $({\tilde{S}})'$.

Example 1.1 If $F(x)=\langle x,f\rangle$ for some $f\in S(\mathbb R)$ and $\gamma \in L^2({\mathbb {R}})\subset S'({\mathbb {R}})$ then

$$\begin{aligned} D_{\gamma }F(x)&=\lim _{\varepsilon \rightarrow 0}\frac{1}{\varepsilon }[\langle x+\varepsilon \gamma ,f\rangle -\langle x,f\rangle ]\\&=\lim _{\varepsilon \rightarrow 0}\frac{1}{\varepsilon }[\langle \varepsilon \gamma ,f\rangle ]=\langle \gamma ,f\rangle =\int _{\mathbb R}f(t)\gamma (t)dt. \end{aligned}$$

Definition 2

We say that $F:S'({\mathbb {R}})\rightarrow {\mathbb {R}}$ is differentiable if there exists a map $\Psi :{\mathbb {R}}\rightarrow ({\tilde{S}})'$ such that

$$\begin{aligned} \Psi (t)\gamma (t)=\Psi (t,x)\gamma (t) \end{aligned}$$

is $({\tilde{S}})'$-integrable and

$$\begin{aligned} D_{\gamma }F(x)=\int _{{\mathbb {R}}}\Psi (t,x)\gamma (t)dt \end{aligned}$$

for all $\gamma \in L^2({\mathbb {R}})$. In this case, we put

$$\begin{aligned} D_{t}F(x):=\Psi (t,x) \end{aligned}$$

and call it the Malliavin (or Hida) derivative of F at t.

Remark

In fact, in the above definition one assumes that the product $\Psi (t,x)\gamma (t)$ is well defined.

Example 1.2 Let $F(x)=\langle x,f\rangle$ with $f\in S({\mathbb {R}})$. Then, by Example 7.1 F is differentiable and its stochastic gradient is

$$\begin{aligned} D_{t}F(x)=f(t)\quad for\ a.a. (t,x). \end{aligned}$$

Let ${\mathfrak {F}}^{(H)}_{t}$ be the $\sigma$-algebra generated by $B_{H}(s)$, $0\le s\le t$. Let $\mathfrak L^{1,2}_{\phi }({\mathbb {R}})$ denote the completion of the set of all ${\mathfrak {F}}^{(H)}_{t}$-adapted processes $f(t)=f(t,x)$ such that

$$\begin{aligned} \Vert f\Vert ^2_{{\mathfrak {L}}^{1,2}_{\phi }({\mathbb {R}})}:=\mathbb E_{\mu _{\phi }}\left[ \int _{{\mathbb {R}}}\int _{\mathbb R}f(s)f(t)\phi (s,t)dsdt\right] +{\mathbb {E}}_{\mu _{\phi }}\left[ \left( \int _{\mathbb R}D^{\phi }_{s}f(s)ds\right) ^2\right] <\infty ,\nonumber \\ \end{aligned}$$

(2)

where $D^{\phi }_{s}$ is the $\phi$ derivative defined in [17]. Namely, if $D_{s}F$ denotes the usual Malliavin derivative, then

$$\begin{aligned} D^{\phi }_{s}F=\int _{{\mathbb {R}}}\phi (s,t)D_{t}Fdt. \end{aligned}$$

Then, by [18], Theorem 3.7 we have the following fractional Itô isometry:

$$\begin{aligned} {\mathbb {E}}_{\mu _{\phi }}\left[ \left( \int _{\mathbb R}f(t,x)dB_{H}(t)\right) ^2\right] =\Vert f\Vert ^2_{\mathfrak L^{1,2}_{\phi }({\mathbb {R}})}. \end{aligned}$$

(3)

Moreover, we have

$$\begin{aligned} {\mathbb {E}}_{\mu _{\phi }}\left[ \int _{{\mathbb {R}}}f(t,x)dB_{H}(t)\right] =0\quad for\ f\in {\mathfrak {L}}^{1,2}_{\phi }({\mathbb {R}}). \end{aligned}$$

(4)

Example 1.3 Let $f,g\in H_{\phi }$. Then

$$\begin{aligned}:\langle f,x\rangle :\diamond :\langle g,x\rangle :=:\langle f{\hat{\otimes }}g,x^{\otimes 2}\rangle :. \end{aligned}$$

By Theorem 9(i) in “Appendix” we have

$$\begin{aligned}:\langle f^{\otimes 2},x^{\otimes 2}\rangle :=\Vert f\Vert ^2_{H_{\phi }}H_2(\Vert h\Vert ^{-1}_{H_{\phi }}\langle h,x\rangle ) \end{aligned}$$

and

$$\begin{aligned} H_2(s)=s^2-1. \end{aligned}$$

Therefore, we obtain

$$\begin{aligned}:\langle f^{\otimes 2},x^{\otimes 2}\rangle :=\Vert f\Vert ^2_{H_{\phi }}(\Vert h\Vert ^{-1}_{H_{\phi }}\langle h,x\rangle )^2-1)=\langle h,x\rangle ^2-\Vert f\Vert ^2_{H_{\phi }}. \end{aligned}$$

Moreover, by the polarization identity, we have

$$\begin{aligned}:\langle f{\hat{\otimes }}g,x^{\otimes 2}\rangle :=\langle f,x\rangle \langle g,x\rangle -(f,g)_{H_{\phi }}, \end{aligned}$$

so that

$$\begin{aligned}:\langle f,x\rangle :\diamond :\langle g,x\rangle :=\langle f,x\rangle \langle g,x\rangle -(f,g)_{H_{\phi }}. \end{aligned}$$

Therefore, by Eqs. (5), (6), the standard Wick calculus and finally the fact that

$$\begin{aligned} \langle \chi _{[0,t]},\chi _{[0,t]}\rangle _{H_{\phi }}=\int ^{t}_{0}\int ^{t}_{0}\phi (u,v)dudv=t^{2H}, \end{aligned}$$

we have

$$\begin{aligned} \int ^{t}_{0}B_{H}(s)dB_{H}(s)&=\int ^{t}_{0}B_{H}(s)\diamond W_{H}(s)ds\nonumber \\&=\int ^{t}_{0}B_{H}(s)\diamond \frac{d}{ds}B_{H}(s)ds=\int ^{t}_0\frac{d}{ds}B^{\diamond 2}_{H}(s)ds\nonumber \\&=\frac{1}{2}B^{\diamond 2}_{H}(t)=\frac{1}{2}B^2_{H}(t)-\frac{1}{2}t^{2H}. \end{aligned}$$

(5)

Example 1.4 (Geometric fractional Brownian motion) Consider the fractional stochastic differential equation

$$\begin{aligned} dX(t)=\mu X(t)dt+\sigma X(t)dB_{H}(t),\quad X(0)=x>0, \end{aligned}$$

(6)

where x, $\mu$ and $\sigma$ are constants. By (158), we get:

$$\begin{aligned} dX(t)=\mu X(t)dt+\sigma X(t)\diamond W_{H}(t)dt. \end{aligned}$$

Dividing by dt, we obtain

$$\begin{aligned} \frac{dX(t)}{dt}=\mu X(t)+\sigma X(t)\diamond W_{H}(t). \end{aligned}$$

Since $\mu$ is a constant

$$\begin{aligned} \mu X(t)=\mu \diamond X(t). \end{aligned}$$

Furthermore, since $\diamond$ is commutative,

$$\begin{aligned} X(t)\diamond W_{H}(t)=W_{H}(t)\diamond X(t), \end{aligned}$$

and so

$$\begin{aligned} \frac{dX(t)}{dt}=(\mu +\sigma W_{H}(t))\diamond X(t). \end{aligned}$$

Using Wick calculus, we see that the solution of this equation is

$$\begin{aligned} X(t)=x\exp ^{\diamond }\left( \mu t+\sigma \int ^{t}_{0}W_{H}(s)ds\right) =x\exp ^{\diamond }(\mu t+\sigma B_{H}(t)). \end{aligned}$$

(7)

Here,

$$\begin{aligned} \exp ^{\diamond }F=1+\sum ^{\infty }_{n=1}\frac{1}{n!}\underbrace{F\diamond F\diamond \dots \diamond F}. \end{aligned}$$

(8)

Using (139) in “Appendix” and (5) we have

$$\begin{aligned} X(t)&=\exp ^{\diamond }(\mu t+\sigma B_{H}(t))\nonumber \\&=\exp ^{\diamond }(\mu t)\exp ^{\diamond }(\sigma B_{H}(t))\nonumber \\&=\exp (\mu t)\exp ^{\diamond }(\sigma B_{H}(t))\nonumber \\&=\exp (\mu t)\exp \left( \sigma B_{H}(t)-\frac{\sigma ^2}{2}|\chi _{[0,t]}|^2_{\phi }\right) \nonumber \\&=\exp (\mu t)\exp \left( \sigma B_{H}(t)-\frac{\sigma ^2}{2} t^{2H}\right) \nonumber \\&=x\exp \left( \sigma B_{H}(t)+\mu t-\frac{1}{2}\sigma ^2 t^{2H}\right) . \end{aligned}$$

(9)

The following results we have taken from the paper [5] without proofs.

Theorem 1

(Fractional Girsanov formula) Let $T>0$ and let $\gamma$ be a continuous function with ${\text {supp}}\gamma \subset [0,T]$. Let K be a function with ${\text {supp}}K\subset [0,T]$ and such that

$$\begin{aligned} (K,f)_{H_{\phi }}=(\gamma ,f)_{L^2({\mathbb {R}})},\quad \forall f\in S({\mathbb {R}}),\quad {\text {supp}} f\subset [0,T], \end{aligned}$$

(10)

i.e.

$$\begin{aligned} \int _{{\mathbb {R}}}K(s)\phi (s,t)ds=\gamma (t),\quad 0\le t\le T. \end{aligned}$$

(11)

Define a probability measure $\mu _{\phi ,\gamma }$ on the $\sigma$-algebra ${\mathcal {F}}^{(H)}_{T}$ generated by$\{B_{H}(s):0\le s\le T\}$ by

$$\begin{aligned} \frac{d\mu _{\phi ,\gamma }}{d\mu _{\phi }}=\exp ^{\diamond }\{-\langle x,K\rangle \}. \end{aligned}$$

(12)

Then, ${\hat{B}}_{H}(t)=B_{H}(t)+\int ^{t}_{0}\gamma _{s}ds$, $0\le t\le T$, is a fractional Brownian motion under $\mu _{\phi ,\gamma }$.

Remark 1

Recall that, in the classical case, the Girsanov theorem allows us to find a probability measure which is equivalent to the initial probability measure under which a "shifted" Brownian motion becomes a usual Brownian motion. In the fractional case, the above theorem gives a similar result, under a new probability measure $\mu _{\phi , \gamma }$ (which is equivalent to the initial measure $\mu _{\phi }$) the shifted fractional Brownian motion ${\hat{B}}_{H}(t)=B_{H}(t)+\int ^{t}_{0}\gamma _{s}ds$ becomes a usual fractional Brownian motion.

Remark 2

Since $B_{H}(t)$ is not a martingale, unlike in the standard Brownian motion case, the restriction of $\frac{d\mu _{\phi ,\gamma }}{d\mu _{\phi }}$ to ${\mathcal {F}}^{(H)}_{t}$, $0<t<T$, is in general not given by $\exp ^{\diamond }\{-\langle \omega ,\chi _{[0,t]}K\rangle \}.$

Proposition 1

(Wick products on different white noise spaces) Let $P=\mu _{\phi }$, $Q=\mu _{\phi ,\gamma }$ and ${\hat{B}}_{H}(t)=B_{H}(t)+\int ^{t}_{0}\gamma _{s}ds$ be as in Theorem 1. Let the Wick products corresponding to P and Q be denoted by $\diamond _{p}$ and $\diamond _{Q}$, respectively. Then

$$\begin{aligned} F\diamond _{p}G=F\diamond _{Q}G \end{aligned}$$

for all $F,G\in ({\tilde{S}})'$.

Definition 3

Let $G=:\langle g_{n}, \omega ^{\otimes n}\rangle :$, where $g_n\in H^{\otimes n}_{\phi }$. Then, we define the fractional (or quasi-) conditional expectation of G with respect to ${\mathcal {F}}^{(H)}_{t}$ by

$$\begin{aligned} \tilde{\mathbb E}_{\mu _{\phi }}[G\mid {\mathcal {F}}^{(H)}_{t}]=:\langle g_n 1^{\otimes n}_{[0,t]},\omega ^{\otimes n}\rangle :, \end{aligned}$$

(13)

and we extend $\tilde{\mathbb E}_{\mu _{\phi }}(\cdot |{\mathcal {F}}^{(H)}_{t})$ by linearity.

Remark

In the classical case, this would be indeed the conditional expectation with respect to ${\mathcal {F}}_t$. In the fractional case, this is not so, i.e. $\tilde{{\mathbb {E}}}(\cdot |\mathcal F^{(n)}_{t})\ne {\mathbb {E}}(\cdot |{\mathcal {F}}^{(n)}_{t}).$

Theorem 2

(A fractional Clark–Ocone theorem) Suppose that $G(x)\in L^2(\mu _{\phi })$ is ${\mathcal {F}}^{(H)}_{T}$-measurable. Define

$$\begin{aligned} \Psi (t,x):=\tilde{{\mathbb {E}}}[D_{t}G\mid {\mathcal {F}}^{(H)}_{t}]. \end{aligned}$$

Then $\Psi$ belong to the space $\mathcal L^{1,2}_{\phi }({\mathbb {R}})$ and we have

$$\begin{aligned} G(x)={\mathbb {E}}_{\mu _{\phi }}[G]+\int ^{T}_{0}\tilde{\mathbb E}_{\mu _{\phi }}[D_{t}G\mid {\mathcal {F}}^{(H)}_{t}]dB_{H}(t). \end{aligned}$$

We shall call $\tilde{{\mathbb {E}}}_{\mu _{\phi }}[D_{t}G|\mathcal F^{(H)}_{t}]$ the fractional Clark derivative of G in analogy with the classical Brownian motion case. We will use the notation

$$\begin{aligned} \nabla ^{\phi }_{t}G={\tilde{E}}_{\mu _{\phi }}[D_{t}G\mid {\mathcal {F}}^{(H)}_{t}], \end{aligned}$$

so that

$$\begin{aligned} G(x)={\mathbb {E}}_{\mu _{\phi }}[G]+\int ^{T}_{0}\nabla ^{\phi }_{t}GdB_{H}(t). \end{aligned}$$

Remark 1 By analogy with the classical case, the fractional Clark–Ocone formula gives a representation of a square-integrable random variable G which is defined through the information available up to time T (i.e. ${\mathfrak {F}}^{(H)}_{T}$-measureable) as the expectation of G plus the integral from 0 till T with respect to the fractional Brownian motion in which the integrand for each $t\in [0,T]$ depends only on the information available up to time t (i.e. $\mathfrak F^{(H)}_{t}$-measurable).

3 Fractional Black–Scholes Market

We will now consider the Black–Scholes market with fractional Brownian motion. This market has a bank account or a bond, where the price A(t) at time t is described by the equation

$$\begin{aligned} dA(t)=\rho A(t)dt,\quad A(0)=1,\quad 0\le t\le T, \end{aligned}$$

(14)

where $\rho >0$ is constant, i.e. $A(t)=e^{\rho t}$ and a stock whose price X(t) at time t satisfies the equation

$$\begin{aligned} dX(t)=\mu X(t)dt+\sigma X(t)dB_{H}(t), \quad X(0)=\varkappa >0, \end{aligned}$$

(15)

where $\mu$ and $\sigma \ne 0$ are constants, $0\le t\le T$. By Example 1.4 we have

$$\begin{aligned} X(t)=x\exp \left( \sigma B_{H}(t)+\mu t-\frac{1}{2}\sigma ^2 t^{2H}\right) ,\quad t\ge 0. \end{aligned}$$

(16)

A portfolio or trading strategy $\theta (t)=\theta (t,x)=(u(t),v(t))$ is an ${\mathcal {F}}^{(H)}_{t}$-adapted 2-dimensional process giving the number of units u(t), v(t) held at time t of the bond and the stock, respectively.

We assume that the corresponding value $Z(t)=Z^{\theta }(t,\omega )$ is given by

$$\begin{aligned} Z^{\theta }(t,\omega )=u(t)A(t)+v(t)\diamond X(t). \end{aligned}$$

(17)

Remark

Note that in the above formula, one replaces the usual multiplication by the Wick product. This will later on allow no arbitrage opportunities. However, it is not completely clear whether the above definition is indeed appropriate from the point of view of finance. The same remains in force for some definitions discussed below,

The portfolio is called self-financing if

$$\begin{aligned} dZ^{\theta }(t,\omega )&=u(t)dA(t)+v(t)\diamond dX(t)\nonumber \\&=u(t)dA(t)+\mu v(t)\diamond X(t)dt+\sigma v(t)\diamond X(t)dB_{H}(t);\quad t\in [0,T]. \end{aligned}$$

(18)

We assume that $\theta =(u,v)$ is a self-financing portfolio. Then, by (17) we have

$$\begin{aligned} u(t)=\frac{Z^{\theta }(t)-v(t)\diamond X(t)}{A(t)}. \end{aligned}$$

(19)

Substituting (14) and (146) in “Appendix” into Eq. (18) gives

$$\begin{aligned} dZ^{\theta }(t)=\rho Z^{\theta }(t)dt+\sigma v(t)\diamond X(t)[\frac{\mu -\rho }{\sigma }dt+dB_{H}(t)]. \end{aligned}$$

(20)

By the Girsanov theorem for fractional Brownian motion (Theorem 1) we see that

$$\begin{aligned} {\hat{B}}_{H}(t):=\frac{\mu -\rho }{\sigma }t+B_{H}(t),\quad t\in [0,T], \end{aligned}$$

(21)

is a fractional Brownian motion with respect to the measure ${\hat{\mu }}_{\phi }$ defined on ${\mathcal {F}}^{(H)}_{T}$ by

$$\begin{aligned} d{\hat{\mu }}_{\phi }(x)=\exp \left( -\int ^{T}_{0}K(s)dB_{H}(s)-\frac{1}{2}\Vert K\Vert ^2_{\phi }\right) d\mu _{\phi }(x), \end{aligned}$$

(22)

where $K(s)=K(T,x)$ is defined by the following properties: ${\text {supp}} K\subset [0,T]$ and

$$\begin{aligned} \int ^{T}_{0}K(T,s)\phi (t,s)ds=\frac{\mu -\rho }{\sigma },\quad for\ 0\le t\le T. \end{aligned}$$

(23)

By [5], the solution of (23) is given by

$$\begin{aligned} K(T,s)=\frac{\mu -\rho }{2\sigma H(2H-1)\Gamma (2H-1)\Gamma (2-2H)\cos (\pi (H-\frac{1}{2}))}(Ts-s^2)^{\frac{1}{2}-H}, \nonumber \\ \end{aligned}$$

(24)

where $\Gamma (\cdot )$ denotes the gamma function.

In terms of ${\hat{B}}_{H}(t)$, Eq. (20) can be written as

$$\begin{aligned} dZ^{\theta }(t)=\rho Z^{\theta }(t)dt+\sigma v(t)\diamond X(t)d{\hat{B}}_{H}(s),\quad 0\le t\le T, \end{aligned}$$

(25)

Multiplying by $e^{-\rho t}$ and integrating, we get

$$\begin{aligned} e^{-\rho t}Z^{\theta }(t)=e^{-\rho t}Z^{\theta (t),z}=z+\int ^{t}_{0}e^{-\rho s}\sigma v(s)\diamond X(s)d{\hat{B}}_{H}(s),\quad 0\le t\le T,\nonumber \\ \end{aligned}$$

(26)

where $z=Z^{\theta }(0)$(constant) is the initial fortune.

Definition 4

We say that the portfolio is admissible if it is self-financing and

$$\begin{aligned} v\diamond X\in \hat{\mathfrak {L}}^{1,2}_{\phi }({\mathbb {R}}) \end{aligned}$$

(27)

where $\hat{\mathfrak {L}}^{1,2}_{\phi }({\mathbb {R}})$ is the space defined similarly to $\mathfrak {L}^{1,2}_{\phi }({\mathbb {R}})$(see Eq. (2)), but with $B_{H}(t)$, $\mu _{\phi }$ replaced by ${\hat{B}}_{H}(t)$, ${\hat{\mu }}_{\phi }.$

Definition 5

An admissible portfolio $\theta$ is called an arbitrage if

$$\begin{aligned} Z^{\theta }(0)\le 0,\quad Z^{\theta }(T)\ge 0\quad a.s.\ and\quad \mu _{\phi }({x:Z^{\theta }(T,x)}>0)>0. \end{aligned}$$

(28)

From Eq. (26) we deduce that no arbitrage opportunities can exist. Indeed, by taking the expectation with respect to ${\hat{\mu }}_{\phi }$, we get by Proposition 1 and Eq. (4) applied to ${\hat{\mu }}_{\phi }$:

$$\begin{aligned} {\mathbb {E}}_{{\hat{\mu }}_{\phi }}[e^{-\rho T}Z^{\theta }(T)]=z+\mathbb E\left( \int ^{t}_{0}e^{-\rho s}\sigma v(s)\diamond X(s)d{\hat{B}}_{H}(s)\right) =z=Z^{\theta }(0). \end{aligned}$$

(29)

Thus, if $Z^{\theta }(T)\ge 0$ and $\mu _{\phi }(x: Z^{\theta }(T,x)>0)>0$, then since ${\hat{\mu }}_{\phi }$ is equivalent to $\mu$, ${\mathbb {E}}_{{\hat{\mu }}_{\phi }}(e^{-\rho T}Z^{\theta }(T))>0$ and so $Z^{\theta }(0)>0$.

Definition 6

The market (A(t), X(t)); $t\in [0,T]$ is called complete if for every ${\mathfrak {F}}^{(H)}_{T}$-measurable bounded random variable F(x) there exist $z\in {\mathbb {R}}$ and portfolio $\theta =(u,v)$ such that

$$\begin{aligned} F(x)=Z^{\theta ,z}(T,x)\quad \mu _{\theta }-a.s. \end{aligned}$$

(30)

By Eq. (26), (30) is equivalent to

$$\begin{aligned} e^{-\rho T}F(x)=z+\int ^{T}_{0}e^{-\rho t}\sigma v(t)\diamond X(t)d{\hat{B}}_{H}(t). \end{aligned}$$

(31)

If we apply the fractional Clark–Ocone theorem (Theorem 2) to $G(x)=e^{-\rho T}F(x)$ and with $B_{H}(t)$ replaced by ${\hat{B}}_{H}(t)$, we get

$$\begin{aligned} e^{-\rho T}F(x)={\mathbb {E}}_{{\hat{\mu }}_{\phi }}[e^{-\rho T}F]+\int ^{T}_{0}\tilde{{\mathbb {E}}}_{{\hat{\mu }}_{\phi }}[e^{-\rho T}\hat{D_{t}}|\mathfrak {F}^{(H)}_{t}]d{\hat{B}}_{H}(t), \end{aligned}$$

(32)

where ${\hat{D}}_{t}$ denotes the stochastic gradient with respect to ${\hat{\mu }}_{\phi }$. Note that the $\sigma$-algebra $\hat{\mathfrak F}^{(H)}_{t}$ generated by ${\hat{B}}_{H}(s)$, $s\le t$, is the same as ${\mathfrak {F}}^{(H)}_{t}.$

Comparing (31) and (32), we conclude that our market is indeed complete. Indeed, choose

$$\begin{aligned} z=Z^{\theta }(0)={\mathbb {E}}_{{\hat{\mu }}_{\theta }}[e^{-\rho T}F] \end{aligned}$$

and find v from the equation

$$\begin{aligned} e^{-\rho T}\sigma v(t)\diamond X(t)=\tilde{{\mathbb {E}}}_{{\hat{\mu }}_{\phi }}(e^{-\rho T}F|\mathfrak F^{(H)}_t). \end{aligned}$$

Thus,

$$\begin{aligned} v(t)=e^{\rho T}\sigma ^{-1}\tilde{{\mathbb {E}}}_{\mu _{\phi }}(e^{-\rho T}F|{\mathfrak {F}}^{(H)}_{t})\diamond X(t)^{\diamond (-1)}, \end{aligned}$$

and finally choose u(t) according to (146) in “Appendix”. If F represents a pay-off of the contingent claim at time T, then the time 0 fair price of this claim must be the time 0 value of the trading strategy which replicates this claim, i.e. z. Thus, we have proved the following theorem:

Theorem 3

The fractional Black–Scholes market has no arbitrage opportunities. It is complete and the prize z of a ${\mathfrak {F}}^{(H)}_{T}$-measurable claim $F(x)\in L^2({\hat{\mu }}_{\phi })$ is given by

$$\begin{aligned} z=e^{-\rho T}{\mathbb {E}}_{{\hat{\mu }}_{\phi }}[F], \end{aligned}$$

(33)

where $\mu _{\phi }$ is defined in (22). Moreover, the corresponding replicating portfolio $\theta (t)=(u(t),v(t))$ for the claim F is

$$\begin{aligned} v(t)=e^{-\rho (T-t)}\sigma ^{-1}X^{\diamond (-1)}(t)\diamond \tilde{\mathbb E}_{{\hat{\mu }}_{\phi }}[{\hat{D}}_{t}F\mid {\mathfrak {F}}^{(H)}_t] \end{aligned}$$

(34)

and u(t) is determined by (146).

Let us now consider a European call option [19]:

$$\begin{aligned} F(x)=(X(T,x)-c)^{+}, \end{aligned}$$

(35)

where $c>0$ is a constant (the exercise price). In this case we get:

Corollary 1

(The fractional Black–Scholes formula) The time 0 price of the fractional European call (35) is

$$\begin{aligned} z&=e^{-\rho T}\int _{{\mathbb {R}}}\frac{1}{T^{H}\sqrt{2\pi }}(x\exp [\sigma y+\rho T-\frac{1}{2}\sigma ^2 T^{2H}]-c)^{+}\exp [-\frac{y^2}{2T^{2H}}]dy \end{aligned}$$

(36)

$$\begin{aligned}&=x\varPhi \left( \eta +\frac{1}{2}\sigma T^{H}\right) -ce^{-\rho T}\varPhi \left( \eta -\frac{1}{2}\sigma T^{H}\right) , \end{aligned}$$

(37)

where

$$\begin{aligned} \eta =\sigma ^{-1}T^{-H}\left( {\text {log}}\frac{x}{c}+\rho T\right) \end{aligned}$$

and

$$\begin{aligned} \varPhi (t)=\frac{1}{\sqrt{2\pi }}\int ^{t}_{-\infty }e^{-\frac{s^2}{2}}ds \end{aligned}$$

is the normal distribution function (the error function).

The corresponding replication portfolio $\theta (t)=(u(t),v(t))$ is given by Eq. (146) in “Appendix”, (26), and

$$\begin{aligned} v(t)=\sigma ^{-1}e^{-\rho (T-t)}X^{\diamond (-1)}(t)\diamond \Psi (X(t)), \end{aligned}$$

(38)

where

$$\begin{aligned} \Psi (y)=\frac{1}{\sqrt{2\phi (T^{2H}-t^{2H})}}\int _{\mathbb R}\exp \left( -\frac{({\tilde{y}}-z)^2}{\sqrt{2(T^{2H}-t^{2H})}}\right) h(z)dz. \end{aligned}$$

(39)

Here

$$\begin{aligned} {\tilde{y}}=\frac{\log y-\log x-\rho t+\frac{1}{2}\sigma ^2 t^{2H}}{\sigma }, \end{aligned}$$

(40)

where

$$\begin{aligned} h(z)=\sigma \chi _{[c,\infty ]}(x\exp \left( \sigma z+\rho T-\frac{1}{2}\sigma ^2 T^{2H}\right) . \end{aligned}$$

(41)

Proof

We will only prove the formulas (36) and (37), since the second part of the corollary uses one technical result which requires a long proof.

So, by (16), (21) and (33) we have

$$\begin{aligned} z&=e^{-\rho T}{\mathbb {E}}_{{\hat{\mu }}_{\phi }}[F]\nonumber \\&=e^{-\rho T}{\mathbb {E}}_{{\hat{\mu }}_{\phi }}[(X(T,x)-c)^{+}]\nonumber \\&=e^{-\rho T}{\mathbb {E}}_{{\hat{\mu }}_{\phi }}[(x\exp (\sigma B_{H}(T)+\mu T-\frac{1}{2}\sigma ^2 T^{2H})-c)^{+}]\nonumber \\&=e^{-\rho T}{\mathbb {E}}_{{\hat{\mu }}_{\phi }}[(x\exp (\sigma {\hat{B}}_{H}(T)+\rho T-\frac{1}{2}\sigma ^2 T^{2H})-c)^{+}]\nonumber \\&=e^{-\rho T}{\mathbb {E}}_{\mu _{\phi }}[(x\exp (\sigma B_{H}(T)+\rho T-\frac{1}{2}\sigma ^2 T^{2H})-c)^{+}]\nonumber \\&=e^{-\rho T}\int _{{\mathbb {R}}}\frac{1}{T^{H}\sqrt{2\pi }}(x\exp (\sigma y+\rho T-\frac{1}{2}\sigma ^2 T^{2H})-c)^{+}\nonumber \\&\times \exp [-\frac{y^2}{2T^{2H}}]dy \end{aligned}$$

(42)

which is (36).

Now, let us prove that (36) is equal to (37). Note that

$$\begin{aligned} x\exp [\sigma y+\rho T-\frac{1}{2}\sigma ^2 T^{2H}]-c\ge 0 \end{aligned}$$

if only if

$$\begin{aligned} \exp [\sigma y+\rho T-\frac{1}{2}\sigma ^2 T^{2H}]&\ge \frac{c}{x},\\ \sigma y+\rho T-\frac{1}{2}\sigma ^2 T^{2H}&\ge \log \frac{c}{x},\\ y&\ge \frac{\log \frac{c}{x}+\frac{1}{2}\sigma ^2 T^{2H}-\rho T}{\sigma }=:y_0. \end{aligned}$$

Then,

$$\begin{aligned} z&=e^{-\rho T}\int _{{\mathbb {R}}}\frac{1}{T^{H}\sqrt{2\pi }}\left( x\exp (\sigma y+\rho T-\frac{1}{2}\sigma ^2 T^{2H}\right) -c)^{+}\\&\quad \times \exp \left[ -\frac{y^2}{2T^{2H}}\right] dy\\&=e^{-\rho T}\int ^{\infty }_{y_0}\frac{1}{T^{H}\sqrt{2\pi }}\left( x\exp (\sigma y+\rho T-\frac{1}{2}\sigma ^2 T^{2H})-c\right) \\&\quad \times \exp \left[ -\frac{y^2}{2T^{2H}}\right] dy\\&=e^{-\rho T}\int ^{\infty }_{y_0}\frac{1}{T^{H}\sqrt{2\pi }}(x\exp (\sigma y+\rho T-\frac{1}{2}\sigma ^2 T^{2H}))\\&\quad \times \exp [-\frac{y^2}{2T^{2H}}]dy-c e^{-\rho T}\int ^{\infty }_{y_0}\frac{1}{T^{H}\sqrt{2\pi }}\exp \left[ -\frac{y^2}{2T^{2H}}\right] dy\\&=xe^{-\rho T}\int ^{\infty }_{y_0}\frac{1}{T^{H}\sqrt{2\pi }}\exp (-\frac{(y-\sigma T^{2H})^2}{2T^{2H}}+\rho T)dy\\&\quad -ce^{-\rho T}\int ^{\infty }_{\frac{y_0}{T^{H}}}\frac{1}{\sqrt{2\pi }}\exp [-\frac{y^2}{2}]dy\\&=xe^{-\rho T}\int ^{\infty }_{\frac{y_0-\sigma T^{2H}}{T^{H}}}\frac{1}{\sqrt{2\pi }}\exp (-\frac{y^2}{2}+\rho T)dy-ce^{-\rho T}\int ^{\infty }_{\frac{y_0}{T^{H}}}\frac{1}{\sqrt{2\pi }}\exp [-\frac{y^2}{2}]dy\\&=x\int ^{\infty }_{\frac{y_0-\sigma T^{2H}}{T^{H}}}\frac{1}{\sqrt{2\pi }}\exp (-\frac{y^2}{2})dy-ce^{-\rho T}\int ^{\infty }_{\frac{y_0}{T^{H}}}\frac{1}{\sqrt{2\pi }}\exp [-\frac{y^2}{2}]dy\\&=x\int ^{-\frac{y_0-\sigma T^{2H}}{T^{H}}}_{-\infty }\frac{1}{\sqrt{2\pi }}\exp (-\frac{y^2}{2})dy-ce^{-\rho T}\int ^{-\frac{y_0}{T^{H}}}_{-\infty }\frac{1}{\sqrt{2\pi }}\exp [-\frac{y^2}{2}]dy, \end{aligned}$$

where, in the last equality, we used that the function $\frac{1}{2\pi }e^{-\frac{x^2}{2}}$ is symmetric with respect to the origin. Since $-\frac{y_0-\sigma T^{2\,H}}{T^{H}}=\eta +\frac{1}{2}\sigma T^{H}$ and $-\frac{y_0}{T^{H}}=\eta -\frac{1}{2}\sigma T^{H}$, we reach (37).

Remark 2 Note that z is independent of $\mu$. One may compare this corollary with the standard results for the classical Brownian motion case. We see that we get the fractional Black–Scholes formula from the classical Black–Scholes formula by simply changing the volatility $\sigma$ in the classical formula with $\sigma T^{H-\frac{1}{2}}$.

4 Monte Carlo Simulation and Numerical Results

This section provides the parameter estimation and Monte Carlo simulation of the models under the fractional Geometric Brownian motion and Geometric Brownian motion.

4.1 Parameter Estimation

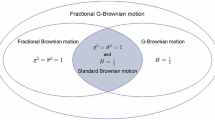
We consider the Hurst index H first. If $H\in (0, \frac{1}{2})$, then the disjoint increments are positively correlated. The process shows the short term dependency. If $H=\frac{1}{2}$, then the process is the classical Brownian motion. If $H\in (\frac{1}{2}, 1)$, the disjoint increments are negatively correlated. The process shows the long-term dependency.

In this study, the R/S analysis (i.e. rescaled range analysis) is implemented to estimate the Hurst parameter, H. Given a time series ${Mi, 1\le i\le M}$ of asset prices. We first transform the time series into logarithmic return series of the length $N=M-1$ through logarithm.

$$\begin{aligned} N_i ={\text {log}} (\frac{M_{i+1}}{M_{i}}), \, i=1,2,\cdots , M-1. \end{aligned}$$

Then, we separate the new series into A subsets of the equal length and the length of every subset is $n=N/A$. The mean value of every subset $e_a$, $a=1,2,\ldots , A$ is

$$\begin{aligned} e_a =\frac{1}{n}\sum ^n_i M_{ai}, \end{aligned}$$

where $M_{ai}$ are the elements of subset a. Next in every subset a, we calculate the total sum of the difference of the first k values $( k=1,2,\ldots , n)$ corresponding to the mean value $e_a$ of the subset:

$$\begin{aligned} X_{k,a}=\sum ^k_{i=1} (N_{i,a} -e_a), \, k=1,2,\ldots , n. \end{aligned}$$

Then, the range $R_a$ of every subset a is

$$\begin{aligned} R_a =\max (X_{k,a} )-\min (X_{k,a} ), \, 1\le k\le n. \end{aligned}$$

And the standard deviation $S_a$ is

$$\begin{aligned} S_a = \sqrt{\frac{1}{n}\sum ^n_{i=1} (M_{ai} - e_a)^2}, \, a=1,2, \ldots , A. \end{aligned}$$

Then, in every subset a, we calculate $\frac{R_a}{S_a}$ and calculate the mean of the rescaled range $\frac{R_a}{S_a}$ of A subsets with time increment n:

$$\begin{aligned} (R/S)_{n}=\frac{1}{A}\sum ^{A}_{a=1} \frac{R_a}{S_a}. \end{aligned}$$

As we increase the value of n, we get the logarithmic asset value series of rescaled range $(R/S)_n$. According to the definition of Hurst index H, $(R/S)_n$ is in proportion to $n^H$, i.e.

$$\begin{aligned} (R/S)_n = C\times n^H, \end{aligned}$$

(43)

where C is the coefficient. Taking the logarithm on both sides of (43), we have

$$\begin{aligned} \ln (R/S)_n = \ln C+H\ln n. \end{aligned}$$

(44)

According to (44), the value of H can be calculated through regression analysis.

We download the S &P 500 data from Yahoo Finance. In this paper, we select the closing index of the 251 trading days for one year from October 31, 2019 to October 30, 2020. Microsoft Excel software is used to do the regression analysis. We get $H=0.6002$. And the goodness of fit is $R^2=0.9591$, which indicates that the fitting effect is good. Therefore, it is reasonable to use the fractional Brownian motion to simulate the movement of the stock index. In the following, in the simulation process, we take the value of H as 0.6, which is rounded to the nearest integer (Fig. 1).

Fig. 1

Rescales range analysis of the S &P 500 from 31 October 2019 to 30 October 2020

We consider again Eq. (15) satisfied by the stock price process $\lbrace X_t, t\ge 0\rbrace$:

$$\begin{aligned} dX_t=\mu X_t dt+\sigma X_t dB_H (t), \end{aligned}$$

where $\mu$ and $\sigma$ are the expected return of stocks and the volatility of stock prices, respectively. $B_H (t)$ in Eq. (15) represents the fractional Brownian motion, which is further expressed as

$$\begin{aligned} dB_H (t)=\epsilon \sqrt{2Ht^{2H-1}dt}, \end{aligned}$$

(45)

where $\epsilon \sim N(0,1)$. If we set $G_t=\ln X_t$, then by Eqs. (15), (45), and (16), we get

$$\begin{aligned} dG_t&=\frac{\partial G_t}{\partial t}dt+\frac{\partial G_t}{\partial X_t}dX_t +\frac{1}{2}\frac{\partial ^2 G_t}{\partial X^2_t}(dX_t)^2\\&=\frac{1}{X_t} (\mu X_t dt+\sigma X_t dB_H (t))-\frac{1}{2X_t^2}\sigma _t^2 X_t^2 d(t^{2H})\\&=\mu dt+\sigma _t dB_H (t)-\frac{1}{2}\sigma _t^2 2Ht^{2H-1}dt\\&=(\mu -\sigma _t^2 Ht^{2H-1} )dt+\sigma _t\epsilon \sqrt{2Ht^{2H-1}dt}. \end{aligned}$$

By discretization, we have

$$\begin{aligned} \Delta G_t&=\ln X_{t+\Delta t}-\ln X_t=\ln \frac{X_{t+\Delta t}}{X_t}\\&=(\mu -\sigma _t^2 Ht^{2H-1} )\Delta t+\sigma _t\epsilon \sqrt{2Ht^{2H-1}\Delta t}. \end{aligned}$$

It is trivial to see that

$$\begin{aligned} \frac{\ln \frac{X_{t+\Delta t}}{X_t}-(\mu -\sigma _t^2 Ht^{2H-1} )\Delta t}{\sqrt{\sigma _t^2 2Ht^{2H-1}\Delta t}}\sim N(0,1), \end{aligned}$$

and

$$\begin{aligned}{} & {} {\text {E}}(\ln \frac{X_{t+\Delta t}}{X_t})=(\mu -\sigma _t^2 Ht^{2H-1} )\Delta t,\\{} & {} {\text {Var}}(\ln \frac{X_{t+\Delta t}}{X_t})=\sigma _t^2 2Ht^{2H-1}\Delta t. \end{aligned}$$

Solving the above equations, we have

$$\begin{aligned} \mu= & {} \frac{{\text {E}}(\ln \frac{X_{t+\Delta t}}{X_t})}{\Delta t}+\frac{1}{2}\frac{{\text {Var}}(\ln \frac{X_{t+\Delta t}}{X_t})}{\Delta t}, \end{aligned}$$

(46)

$$\begin{aligned} \sigma _t^2= & {} \frac{{\text {Var}}(\ln \frac{X_{t+\Delta t}}{X_t})}{2Ht^{2H-1}\Delta t}. \end{aligned}$$

(47)

Equations (46) and (47) will be used in the following simulation process to estimate the mean value $\mu$ and the standard deviation $\sigma$ of the stock logarithmic return.

4.2 Numerical Results

In the following, we simulate the trend of the stock prices. The following are the concrete steps:

Step 1 Using the closing index of the 251 trading days from October 31, 2019 to October 30, 2020, and the closing index of October 30, 2019, which is rounded to 3048, we get the estimates of the mean value $\mu$ and the standard deviation $\sigma$ of the S &P 500 index logarithmic return by Eqs. (46) and (47).

Step 2 Discretizing the S &P 500 price Index, we have

$$\begin{aligned} \Delta X_{t_i}=X_{t_i+\Delta t} - X_{t_i}=\mu X_{t_i} \Delta t +\epsilon _{t_i +\Delta t} \sigma _{t_i+\Delta t} X_{t_i} \sqrt{2H t_i^{2H-1}\Delta t}. \end{aligned}$$

Let $t_i =i\Delta t$ and $\Delta t=1$, it becomes

$$\begin{aligned} X_{i} -X_{i-1} =\mu X_{i-1}+\epsilon _{i}\sigma _{i} X_{i-1}\sqrt{2H(i-1)^{2H-1}}, \end{aligned}$$

where $\epsilon _i$ and $\sigma _i$ indicate the standard normal random variable and corresponding standard deviation generated the ith time. Namely, when $i=1$, it is

$$\begin{aligned} X_1=(\mu +1)X_0. \end{aligned}$$

When $i=2$, it is

$$\begin{aligned} X_2 = (\mu +1)X_1 +\epsilon _2 \sigma _2 X_1 \sqrt{2H}, \end{aligned}$$

where $\epsilon _2$ and $\sigma _2$ indicate the standard normal random variable and the second standard deviation generated the second time. When $i=3$, it is

$$\begin{aligned} X_3 = (\mu +1)X_2 +\epsilon _3 \sigma _3 X_2 \sqrt{2H 2^{2H-1}}, \end{aligned}$$

where $\epsilon _3$ and $\sigma _3$ indicate the standard normal random variable and the third standard deviation generated the third time. Likewise, we can obtain the 251 simulation values.

Step 3 Using the Microsoft Excel, we simulate the movement of S &P 500 index. Then, we compare the real movement with simulated movement to determine whether the price of S &P 500 index obeys the fractional Brownian motion. The results are shown in Figs. 2, 3, and 4. In the graphs, the blue track represents the real movement, and the red track represents the corresponding fractional Brownian motion simulated movement. It is easy to observe the simulation effect is quite ideal.

Fig. 2

First simulation of the S &P 500 from 31 October 2019 to 30 October 2020

Fig. 3

Second simulation of the S &P 500 from 31 October 2019 to 30 October 2020

Fig. 4

Third simulation of the S &P 500 from 31 October 2019 to 30 October 2020

Furthermore, we need a measurement to evaluate the results of our simulation. Here, we use root mean square error (RMSE). The root mean square error is defined as

$$\begin{aligned} R=\sqrt{\frac{1}{N}\sum ^n_{i=1} (Y_i -{\hat{Y}}_i)^2}. \end{aligned}$$

where N is the number of the samples. In our Monte Carlo simulations, $N=251$. $Y_i$ and ${\hat{Y}}_i$ are the actual price and the Monte Carlo simulated price of the S &P 500 index, respectively. Therefore, R value corresponding to the simulated movement in Figs. 2, 3, and 4 are 225.252, 220.420, and 243.65. It can be seen that the second simulation is the highest and the third simulation is the lowest. In addition, in order to compare the fitting goodness between the fractional Brownian motion method and the Brownian motion simulation method, we use the previous data, and we get that Brownian motion simulation’s R value is 282.408. It is concluded that the proposed method is superior to the ordinary standard Brownian motion method. Therefore, it verifies the theory we construct in the previous chapters.

5 Conclusion

In this paper, we systematically study the fractional Brownian motion theory based on Gel’fand triples and apply the fractional Brownian motion to financial markets. During the simulation of S& P 500 index, unknown parameters need to be estimated and the goodness of fit of the models are compared between fractional Brownian motion and traditional Brownian motion. The results show that fractional Brownian motion model is more accurate than Brownian motion model.

Future work can consider simulate the fractional Gaussian noise using more factors like mean-reverting jump-type model and seasonality model. Moreover, data-driven methods can also be used to replicate the financial markets more closely.

Appendices

Appendix

Gel’fand Triples

The notions of a nuclear space and its dual space with respect to a centre Hilbert space will be introduced.

1.1 Rigging by Hilbert Spaces

First, let us consider the notion of a space with negative norm. Let $H_0$ be a real Hilbert space with scalar product $\left( \cdot ,\cdot \right) _{H_0}$ and norm $\Vert \cdot \Vert _{H_0}$ and we suppose that

$$\begin{aligned} H_+\subseteq H_0, \end{aligned}$$

where $H_+$ is a dense subset of $H_0$. We suppose that $H_+$ is a Hilbert space with respect to another scalar product $\left( \cdot ,\cdot \right) _{H_+}$ and that the norm $\Vert \cdot \Vert _{H_+}$ in $H_+$ is such that

$$\begin{aligned} \Vert \cdot \Vert _{H_0}\le \Vert \cdot \Vert _{H_+},\quad u\in H_+. \end{aligned}$$

(48)

Each element $f\in H_0$ generates a linear continuous functional $\langle f,\cdot \rangle$ on $H_+$ by the formula

$$\begin{aligned} \langle f,u\rangle :=(f,u)_{H_0},\quad u\in H_+ \end{aligned}$$

(49)

Let us show that this is indeed so. Let us first check the linearity: Let $\alpha _1,\alpha _2\in {\mathbb {R}}$, then using the linearity of inner product, we have

$$\begin{aligned} \langle f,\alpha _1u_1+\alpha _2u_2\rangle&=(f,\alpha _1u_1+\alpha _2u_2)_{H_0}\\&=\alpha _1(f,u_1)_{H_+}+\alpha _2(f,u_2)_{H_+}\\&=\alpha _1\langle f,u_1\rangle +\alpha _2\langle f,u_2\rangle . \end{aligned}$$

Next, let us check that the map (49) is continuous. We suppose that $u_n\rightarrow u_0$ in $H_0$ as $n\rightarrow \infty$. Then, by (48),

$$\begin{aligned} |\langle f,u_n\rangle -\langle f,u_0\rangle |&=|(f,u_n-u_0)_{H_0}|\\&\le \Vert f\Vert _{H_0}\Vert u_n-u_0\Vert _{H_0}\\&\le \Vert f\Vert _{H_0}\Vert u_n-u_0\Vert _{H_+}\rightarrow 0. \end{aligned}$$

We introduce a new norm on $H_0$, denoted by $\Vert \cdot \Vert _{H_-}$ by taking the norm of f as the norm of the functional $\langle f,\cdot \rangle$:

$$\begin{aligned} \Vert f\Vert _{H_-}:=\sup \left\{ \frac{|(f,u)_{H_0}|}{\Vert u\Vert _{H_+}}\mid u\in H_+,\ u\ne 0\right\} . \end{aligned}$$

(50)

Since the right hand side of (50) is a norm of a linear functional, to check that $\Vert \cdot \Vert _{H_-}$ is indeed a norm on $H_0$, it is sufficient to check that $\Vert f\Vert _{H_-}=0$ implies that $f=0$.

Indeed, if $\Vert f\Vert _{H_-}=0$, then $(f,u)_{H_0}=0$ for all $u\in H_+$ and $u\ne 0$. Since $H_+$ is dense in $H_0$, it follows that $f=0$.

Let X be a normed linear space with norm $\Vert \cdot \Vert$. If any Cauchy sequence $\{x_n\}^{\infty }_{n=1}$ in X has a limit, then X is called complete, and thus X becomes a Banach space. In fact, if X is not complete, then one can always construct a so-called completion of this space, which is a Banach space containing X as a dense subset and the norm of the completion restricted to X coincides with the original norm on X. (Recall that the completion of X is constructed by taking all possible Cauchy sequences in X and identifying those Cauchy sequences $\{x_n\}^{\infty }_{n=1}$ and $\{x'_n\}^{\infty }_{n=1}$ in X for which for any $\varepsilon >0$ there exists $N\in {\mathbb {N}}$ such that $\Vert x_n-x'_m\Vert <\varepsilon$ for all $n,m\ge N$.)

Now we complete $H_0$ in the norm (50) and obtain a Banach space $H_-$, which is called the space with negative norm. Thus, we have constructed the chain

$$\begin{aligned} {H_+}\subseteq {H_0}\subseteq {H_-} \end{aligned}$$

(51)

of spaces with positive, zero and negative norms.

Each element $\alpha \in H_-$ is clearly a linear continuous functional on $H_+$, so that

$$\begin{aligned} H_-\subseteq (H_+)' \end{aligned}$$

(52)

where $(H_+)'$ denotes the dual space of $H_+$. We will write $(\alpha ,u)_{H_0}$ or $\langle \alpha ,u\rangle$ for the action of the functional $\alpha$ on an element $u\in H_+$. It is obvious that

$$\begin{aligned} | (\alpha ,u)_{H_0}|\le \Vert \alpha \Vert _{H_-}\Vert u\Vert _{H_+},\quad \alpha \in H_-,\ u\in H_+, \end{aligned}$$

(53)

which is a generalization of the Cauchy inequality.

Let us prove that the space $H_-$ is, in fact, a Hilbert space.

Theorem 4

The negative space $H_-$ is a Hilbert space.

Proof

Let $O:H_+\rightarrow H_0$ be a continuous imbedding operator, i.e. $Ou=u,\ u\in H_+$, and u on the right hand side of the last equality is treated as an element of $H_0$. By (48), for each $u\in H_+$

$$\begin{aligned} \Vert Ou\Vert _{H_0}=\Vert u\Vert _{H_0}\le \Vert u\Vert _{H_+}, \end{aligned}$$

so that O is a bounded operator. We define $I=O^*: H_0\rightarrow H_+$. We have

$$\begin{aligned} (f,u)_{H_0}=(f,Ou)_{H_0}=(If,u)_{H_+},\quad f\in H_0,\ u\in H_+. \end{aligned}$$

(54)

We introduce on $H_-$ a quasi-scalar product (i.e. we do not yet know whether $(f,f)_{H_-}=0$ implies $f=0$) as follows:

$$\begin{aligned} (f,g)_{H_-} :&=(If,Ig)_{H_+}=(f,OIg)_{H_0}\nonumber \\&=(f,Ig)_{H_0}=(If,g)_{H_0},\quad f,g\in H_0, \end{aligned}$$

(55)

By (50) and (54) we then have, for $f\in H_0$

$$\begin{aligned} \Vert f\Vert _{H_-}:&=\sup \left\{ \frac{|(f,u)_{H_0}|}{\Vert u\Vert _{H_+}} \mid u\in {H_+},\ u\ne 0\right\} \\&=\sup \left\{ \frac{\Vert (f,Ou)_{H_0}\Vert }{\Vert u\Vert _{H_+}}\mid u\in H_+,\ u\ne 0\right\} \\&=\sup \left\{ \frac{|(If,u)_{H_+}|}{\Vert u\Vert _{H_+}}\mid u\in {H_+},\ u\ne 0\right\} . \end{aligned}$$

By the Riesz representation theorem, we therefore have, by (55),

$$\begin{aligned} \Vert f\Vert _{H_-}=\Vert If\Vert _{H_+}=\sqrt{(If,If)_{H_+}}=\sqrt{(f,f)_{H_-}},\quad f\in H_0. \end{aligned}$$

Since $\Vert \cdot \Vert$ as in Eq. (50) is a norm in $H_-$, the $(\cdot ,\cdot )_{H_-}$ is indeed a scalar product and not a quasi-scalar product. By completing $H_0$ with respect to the norm $\Vert \cdot \Vert _-$, we extend the scalar product $(\cdot ,\cdot )_{H_-}$ to the whole space $H_-$, and hence $H_-$ becomes a Hilbert space.

Since $\Vert I\Vert =\Vert O\Vert \le 1$, it follows that

$$\begin{aligned} \Vert f\Vert _{H_-}=\Vert If\Vert _{H_+}\le \Vert f \Vert _{H_0},\quad f\in {H_0}. \end{aligned}$$

(56)

By the first equality of (55), I is an isometric operator from $H_-$ into $H_+$, defined on the dense subset $H_0$ of $H_-$. Extending it by continuity, we obtain an isometric operator $\mathbb I: H_-\rightarrow H_+$, ${\mathbb {I}}\restriction _ {H_0}=I$.

Lemma 1

${\mathbb {I}}$ is a unitary operator between the whole of $H_-$ and the whole of $H_+$ (i.e. the range ${\text {Ran}}({\mathbb {I}})=H_+$).

Proof

Let $u\in H_+$ be such that $u\bot {\text {Ran}}(\mathbb I)$. Then, for all $f\in H_0$ we have by (55) that

$$\begin{aligned} 0=(If,u)_{H_+}=(f,u)_{H_0} \end{aligned}$$

Therefore, since $H_+$ is dense in $H_0$, $u=0$.

Furthermore, ${\text {Ran}}({\mathbb {I}})$ is closed in $H_+$ as the range of an isometric operator, therefore ${\text {Ran}}({\mathbb {I}})=H_+$. $\square$

Lemma 2

We have:

$$\begin{aligned} (\alpha ,u)_{H_0}=({\mathbb {I}}\alpha ,u)_{H_+}, \quad \alpha \in H_-, u\in H_+ \end{aligned}$$

Proof

Let $\alpha \in H_-$ and let us suppose that $f_n\in H_0$ and $f_n\rightarrow \alpha$ as $n\rightarrow \infty$ in $H_-$. From the continuity of ${\mathbb {I}}$ and from (2.7), (2.8) it follows that

$$\begin{aligned} (\alpha ,u)_{H_0}= \lim _{n\rightarrow \infty } (f_n,u)_{H_0}=\lim _{n\rightarrow \infty } (If_n,u)_{H_+}=(I\alpha ,u)_{H_+}. \end{aligned}$$

$\square$

We will now derive the main result of this section stating that the Hilbert space $H_-$ is the dual space of $H_+$ with respect to the centre space $H_0$.

Theorem 5

We have $H_-=(H_+)'$, i.e. $H_-$ can be thought of as the dual space of $H_+$.

Proof

We have to show that any functional $l\in (H_+)'$ is of the form $l(u)=(\alpha ,u)_{H_0}$, $u\in {H_+}$ for some $\alpha \in {H_0}$. By the Riesz theorem, there exists $a\in {H_+}$ such that $l(u)=(a,u)_{H_+}, u\in {H_+}$. Since ${\text {Ran}}({\mathbb {I}})=H_+$, we set $\alpha ={{\mathbb {I}}^{-1}}a\in {H_-}$ and by Lemma 2, it follows then

$$\begin{aligned} l(u)&=(a,u)_{H_+}=({\mathbb {I}}\,{\mathbb {I}}^{-1}a,u)_{H_+}\\&=({\mathbb {I}}^{-1}a,u)_{H_0}=(\alpha ,u)_{H_0}, \quad u\in H_+. \end{aligned}$$

$\square$

Hence, the pairing between the space $H_+$ and its dual space $(H_+)^\prime ={H_-}$ is determined by means of the space $H_0$.

Definition 7

A rigging ${H_+} \subseteq {H_0}\subseteq {H_-}$ is called quasi-nuclear if the inclusion operator $O: H_+\rightarrow H_0$ is quasi-nuclear (or Hilbert–Schmidt) operator, i.e. $\sum ^{\infty }_{n=1} \Vert Oe_n \Vert ^2_{H_0}<{\infty }$, where $(e_n)^{\infty }_{n=1}$ is an orthonormal basis (ONB) of $H_+$.

Example A.1. For any ${\tau }=(\tau _k)^{\infty }_{k=1},\ {\tau _k}>0$, we define

$$\begin{aligned} \ell _2(\tau ):=\left\{ (f_k)^{\infty }_{k=1}\in {\mathbb {R}}^{{\mathbb {N}}} \mid \sum ^{\infty }_{k=1} f^2_k\tau _k<{\infty }\right\} \end{aligned}$$

(57)

and for any $f=(f_k)^{\infty }_{k=1}$, $g=(g_k)^{\infty }_{k=1}\in \ell _2(\tau )$ we define

$$\begin{aligned} (f,g)_{l_2(\tau )}:=\sum ^{\infty }_{k=1} {f_k}{g_k}{\tau _k}. \end{aligned}$$

(58)

Suppose that ${\tau _k}\ge 1,\ k\in {\mathbb {N}}$. Denote by $\ell _{2,0}$ all finite sequences

$$\begin{aligned} (f_1,f_2,\dots ,f_N,0,0,\dots ), \end{aligned}$$

where $f_1,\dots ,f_N\in {\mathbb {R}}$, $N\in {\mathbb {N}}$. Clearly, $\ell _{2,0}\subset \ell _2(\tau )$ and $\ell _{2,0}$ is dense in $\ell _2$. Therefore, $\ell _2(\tau )$ is dense in $\ell _2$. Furthermore, by the definition of $\ell _2(\tau )$, for each $f\in \ell _2(\tau )$, $\Vert f\Vert _{\ell _2}\le \Vert f\Vert _{\ell _2(\tau )}$. Therefore, we may set $H_0=\ell _2$ and $H_+=\ell _2(\tau )$. Let $I: H_0\rightarrow H_+$ be as in the proof of Theorem 5. Then, for $f\in \ell _2$, $u\in \ell _2(\tau )$,

$$\begin{aligned} (f,u)_{\ell _2}&=\sum ^{\infty }_{k=1} {f_k}{u_k}=(If,u)_{\ell _2(\tau )}= \sum ^{\infty }_{k=1} (If)_k{u_k}{\tau _k}. \end{aligned}$$

(59)

Therefore, $(If)_k=\frac{f_k}{\tau _k}$. Hence, for all $f,g\in \ell _2$, we have

$$\begin{aligned} (f,g)_{H_-}=(If,Ig)_{H_+}=\sum ^{\infty }_{k=1}\frac{f_k}{\tau _k}\frac{g_k}{\tau _k}{\tau _k}=\sum ^{\infty }_{k=1}f_k{g_k}\frac{1}{\tau _k}. \end{aligned}$$

(60)

Thus,

$$\begin{aligned} H_-=\ell _2(\tau ^{-1}),\quad \tau ^{-1}:=(\tau ^{-1}_k)^{\infty }_{k=1}. \end{aligned}$$

Lemma 3

The inclusion $\ell _2(\tau )\subseteq \ell _2$ is quasi-nuclear if and only if

$$\begin{aligned} \sum ^{\infty }_{k=1} \frac{1}{\tau _k}<{\infty }. \end{aligned}$$

Proof

Let

$$\begin{aligned} e_k=(0,\dots ,0,\underbrace{1}_{k\text {th place}},0,\dots ). \end{aligned}$$

Then $(e_k\frac{1}{\sqrt{\tau _k}})^{\infty }_{k=1}$ is an ONB in $H_+$. Next,

$$\begin{aligned} \bigg \Vert e_k\frac{1}{\sqrt{\tau _k}}\bigg \Vert ^2_{H_0}=\frac{1}{\tau _k}\Vert e_k\Vert ^2_{H_0}=\frac{1}{\tau _k}. \end{aligned}$$

Hence,

$$\begin{aligned} \sum ^{\infty }_{k=1}\Vert e_k\frac{1}{\sqrt{\tau _k}}\Vert ^2_{H_0}=\sum ^{\infty }_{k=1}\frac{1}{\tau _k} \end{aligned}$$

which implies the statement.$\square$

Example A.2. Let $H_0=L^2(R, d\mu (x))=L^2(R,\mathfrak {R},\mu ),$ where R is a space with a measure $\mu$ given on a certain $\sigma$-algebra $\mathfrak {R}$ of subsets of R and such that $\mu (R)\le \infty$. We set ${H_+}=L^2(R, p(x)d\mu (x))$, where $p(x)\ge 1, x\in R$, is some measurable weight function which is finite almost everywhere. Analogously to Example 2.1, one can easily show that the chain now takes the form

$$\begin{aligned} H_-=L^2(R, p^{-1}(x), d\mu (x))\supset L^2(R, d\mu (x))=H_0\supset L^2(R,p(x)d\mu (x))=H_+.\nonumber \\ \end{aligned}$$

(61)

Example A.3. Let $C^{\infty }_b({\mathbb {R}})$ denote the set of all bounded infinite differentiable functions on ${\mathbb {R}}$ with bounded derivatives. The Sobolev space $W^{l}_2({\mathbb {R}}, p(x)dx)$, $l\in {{\mathbb {N}}}$, $p(x)\ge 1$, $x\in {\mathbb {R}}$, measurable, a.e. finite, is defined as the completion of $C^{\infty }_b({\mathbb {R}})$ with respect to scalar product

$$\begin{aligned} (\varphi ,\psi )_{W^{\ell }_2(\mathbb R)}=\sum ^{\ell }_{k=0}\int _{\mathbb R}{\varphi ^{(k)}(x)}{\psi ^{(k)}(x)}p(x)\,dx, \end{aligned}$$

(62)

where $\varphi ^{(k)}(x)$ denotes the kth derivative of $\varphi$ ($\varphi ^{(0)}:=\varphi$). Then, we may set $H_+=W^{l}_2({\mathbb {R}}, p(x)dx)$ for $l\in {\mathbb {N}}$, and $H_0=L^2({\mathbb {R}},dx)$. Then, $H_-$ is called a Sobolev space with negative index $-l$ and is denoted by $W^{-l}_2(\mathbb R,p^{-1}(x)dx)$.

1.2 Rigging by a Nuclear Space

Let $\varPhi$ be a linear topological space, $\varPhi \subseteq H_0$, and we suppose that the embedding operator $O:\varPhi \hookrightarrow H_0$ is continuous. As in Sect. A.1, any element $f\in H_0$ generates a linear continuous functional $l_f$ on $\varPhi$ by the formula $l_f(u):=(f,u)_{H_0},\ u\in \varPhi$. We identify f with $l_f$ and obtain the inclusion $H_0\subseteq {\varPhi '}$, so that $\varPhi \subseteq {H_0}\subseteq {\varPhi '}$. In what follows, we will only consider the case where $\varPhi$ is a nuclear space (generated by a countable family of Hilbert spaces). So, let $(H_n)_{n\in {\mathbb {N}}}$ be a family of Hilbert spaces. We suppose that the set $\varPhi :=\bigcap _{n\in {\mathbb {N}}} H_n$ is dense in each $H_n$, and that

$$\begin{aligned} \forall n\in {\mathbb {N}}\quad H_{n+1}\subset H_n \end{aligned}$$

and the inclusions are quasi-nuclear. On $\varPhi$ we introduce the topology of a projective limit. As a basis of this topology, we take all possible open balls,

$$\begin{aligned} {\mathcal {U}}(\psi ,n,\varepsilon )=\{\phi \in \varPhi \mid \Vert \phi -\psi \Vert _{H_n}<\varepsilon \}, \quad \psi \in \varPhi ,\ n\in {\mathbb {N}},\ \varepsilon >0. \end{aligned}$$

(63)

In other words, the topology on $\varPhi$ is the weakest topology on $\varPhi$ with respect to which all inclusions $O_n:\varPhi \hookrightarrow H_n$ become continuous. Then, $\varPhi$ is called the projective limit of Hilbert spaces $(H_n)_{n\in {\mathbb {N}}}$, and one writes

$$\begin{aligned} {\varPhi }=\projlim _{n\in {\mathbb {N}}} H_n. \end{aligned}$$

(64)

Such a space $\varPhi$ is called a nuclear space.

Suppose now that for some Hilbert space $H_0$, we have $H_1\subset H_0$ densely and continuously. We can now construct the riggings

$$\begin{aligned} H_n\subseteq H_0\subseteq H_{-n},\quad n\in {\mathbb {N}}\\ \varPhi \subseteq H_0\subseteq {\varPhi '}. \end{aligned}$$

Notice that since $H_{n+1}\subseteq H_{n}$, we have

$$\begin{aligned} H_{-n}\subseteq H_{-(n+1)}. \end{aligned}$$

(65)

Theorem 6

(Schwartz) We have

$$\begin{aligned} \varPhi '=\bigcup _{n\in N} {H_n'}=\bigcup _{n\in N}{H_{-n}}. \end{aligned}$$

This equality should be understood as follows: $\forall l\in \varPhi '\ \exists n\in {\mathbb {N}}$ such that l may be extended by continuity from $\varPhi$ to a linear continuous functional on $H_n$ and vice versa if $l\in H_{-n}$ for some $n\in {\mathbb {N}}$, then $l\restriction \varPhi \in \varPhi '$.

Proof

Each element of $H_{-n}$ is a linear continuous functional on $H_n$. Since $\varPhi \subset H_n$ continuously, every element of $H_{-n}$ generates a linear continuous functional on $\varPhi$, so that we get the inclusion $H_{-n}\subset \varPhi '$.

Let now $l\in \varPhi '$. Since l is continuous at 0, there exists a basic neighbourhood of 0 in $\varPhi$, ${\mathcal {U}}(0,n,\delta )$, such that $|l(\varphi )|<1$ for all $\varphi \in {\mathcal {U}}(0,n,\delta )$. Consider the space $H_n$. Then, l determines a linear functional defined on a dense set $\varPhi$ in $H_n$ and bounded by 1 on the intersection of $\varPhi$ with the ball $\{\Vert u\Vert _{H_n}<\delta , u\in H_n\}$. Therefore, l is bounded on $\varPhi$ equipped with the norm $\Vert \cdot \Vert _{H_n}$. Extending l by continuity, we obtain a continuous functional on $H_n$, i.e. an element of $H_{-n}$. $\square$

Since $\varPhi '=\bigcup _{n\in {\mathbb {N}}} H_{-n}$, we can introduce on $\varPhi '$ the topology of the inductive limit of Hilbert spaces $(H_{-n})_{n\in {\mathbb {N}}}$. This topology is defined by basic open sets

$$\begin{aligned} {\mathcal {U}}(\xi ,-n,\varepsilon (\cdot ))={\text {c.l.s.}}\bigg (\bigcup _{n\in N}\{{{\Vert \xi -\xi '\Vert }_{H_{-n}}}<{\varepsilon (n) \mid \xi '\in \varPhi ', \xi -\xi '\in H_{-n}}\}\bigg )\nonumber \\ \end{aligned}$$

(66)

where c.l.s. denotes the convex linear span, $\xi \in \varPhi '$ and ${\mathbb {N}}\in n\mapsto {\varepsilon (n)}>0$. Now, one writes $\varPhi '=\text {ind lim}_{n\in {\mathbb {N}}} {H_{-n}}$. Thus, we have

$$\begin{aligned} \varPhi =\projlim _{n\in {\mathbb {N}}} H_n\subseteq H_0\subseteq \text {ind lim}_{n\in {\mathbb {N}}} H_{-n}=\varPhi ', \end{aligned}$$

(67)

which is called a Gel’fand (standard) triple.

1.3 Schwartz Triple

First, consider the real space $\ell _2$ of square summable sequences $(x_j)^{\infty }_{j=0}$.

Recall Example A.1. Consider the weight $\tau ^{(n)}=(\tau ^{(n)}_j)^{\infty }_{j=0}$ given by

$$\begin{aligned} \tau ^{(n)}_j=(2j+2)^{2n}. \end{aligned}$$

We have $\tau ^{(n)}_j\ge 1$. Furthermore,

$$\begin{aligned} \sum ^{\infty }_{j=0}{\frac{1}{(2j+2)^2}}<{\infty }, \end{aligned}$$

and therefore by Lemma 3, the embedding of the space $\ell _2(\tau ^{(n)})$ into $\ell _2$ is quasi-nuclear. Analogously, we may conclude that, for each $n\ge 2$, the embedding $\ell _2(\tau ^{(n-1)})$ into $\ell _2(\tau ^{(n)})$ is also quasi-nuclear.

We set

$$\begin{aligned} \varPhi =\projlim _{n\rightarrow \infty }\ell _2(\tau ^{(n)}) \end{aligned}$$

which is a nuclear space, being densely and continuously embedded into $\ell _2$. Thus, we get the Gel’fand triple

$$\begin{aligned} \varPhi =\projlim _{n\rightarrow \infty }\ell (\tau ^{(n)})\subset {\ell _2}\subset \text {ind lim}_{n\rightarrow \infty }\ell _2({\tau ^{(n)}}^{-1})={\varPhi '}. \end{aligned}$$

(68)

(Note that ${\tau ^{(n)}}^{-1}=((2j+2)^{-2n})^{\infty }_{j=0}$.) Let now $H_0=L^2({\mathbb {R}},dx)$. For each $j=0,1,2,\dots ,$ the jth Hermite function $e_j$ is defined by

$$\begin{aligned} e_j=e_j(x)=(\sqrt{\pi }{2^j}j!)^{-\frac{1}{2}}{(-1)^j}e^{\frac{x^2}{2}}{(\frac{d}{dx})^j}e^{-x^2},\quad x\in {\mathbb {R}}. \end{aligned}$$

It is known that $(e_j)^{\infty }_{j=0}$ is an orthonormal basis of $L^2({\mathbb {R}},dx)$. Through this basis one gets that $L^2({\mathbb {R}},dx)$ is unitarily isomorphic to $\ell _2$. Thus, using this isomorphism, we get the following Gel’fand triple (being isomorphic to (68))

$$\begin{aligned} S({\mathbb {R}})=\projlim _{n\rightarrow \infty }S_n({\mathbb {R}})\subset L^2(\mathbb R)\subset \text {ind lim}_{n\rightarrow \infty }S_{-n}(\mathbb R)=S'({\mathbb {R}}). \end{aligned}$$

Thus, for each $n\in {\mathbb {N}}$, $S_n({\mathbb {R}})$ consists of all functions of the form

$$\begin{aligned} f(x)=\sum ^{\infty }_{j=0}{f_j}{e_j(x)} \end{aligned}$$

such that

$$\begin{aligned} \sum ^{\infty }_{j=0}f^2_j(2j+2)^{2n}<\infty \end{aligned}$$

and the inner product of $f,g\in S_n({\mathbb {R}}),$ is given by

$$\begin{aligned} (f,g)_{S_n({\mathbb {R}})}=\sum ^{\infty }_{j=0}{f_j}{g_j}(2j+2)^{2n}, \end{aligned}$$

where $g(x)=\sum ^{\infty }_{j=0}{g_j}{e_j(x)}$. (Note that all these series converge in the Hilbert space $L^2({\mathbb {R}})$, and therefore in the Lebesgue measure). Furthermore, the dual space $S_{-n}({\mathbb {R}})$ may be interpreted as the Hilbert space consisting of formal series

$$\begin{aligned} \xi (x)=\sum ^{\infty }_{j=0}{\xi _j}e_j(x) \end{aligned}$$

such that

$$\begin{aligned} \sum ^{\infty }_{j=0}{\xi ^2_j}(2j+2)^{-2n}<{\infty } \end{aligned}$$

and the dual pairing between $\xi$ and $f\in S_n({\mathbb {R}})$ is given by

$$\begin{aligned} \langle \xi ,f\rangle =\sum ^{\infty }_{j=0}{\xi _j}f_j. \end{aligned}$$

In fact, one can give an explicit description of all functions from the space $S({\mathbb {R}})$. This space consists of all smooth (infinitely differentiable) functions on ${\mathbb {R}}$ which satisfy the following condition for each $m=0,1,2,\dots$, $k\in {\mathbb {N}},$

$$\begin{aligned} \frac{|f^{(m)}|}{(1+|x|)^k}\rightarrow 0\quad \text {as}\quad x\rightarrow \pm \infty . \end{aligned}$$

In other words, the function f, together with all its derivatives, converges at infinite to zero quicker than any function $(1+|x|)^{-k}.$ The space $S({\mathbb {R}})$ is called the Schwartz space of smooth rapidly decreasing functions. The dual space $S'({\mathbb {R}})$ is called the Schwartz space of tempered distributions.

1.4 Minlos Theorem

Let

$$\begin{aligned} \varPhi \subseteq H_0\subseteq \varPhi ' \end{aligned}$$

be a Gel’fand triple. We first need a $\sigma$-algebra on $\varPhi '$. Take any $f_1,\dotsc , f_n\in \varPhi$, $n\in {\mathbb {N}}$ and any Borel set $A\in {\mathcal {B}}{({{\mathbb {R}}}^n)}$. We define a cylinder set in $\varPhi '$ as

$$\begin{aligned} {{\mathcal {C}}}(f_1,\dotsc , f_n,A):=\{\xi \in \varPhi ': (\langle \xi , f_1\rangle , \dotsc , \langle \xi , f_n\rangle )\in A\}. \end{aligned}$$

(69)

We denote by ${\mathcal {C}}(\varPhi ')$ all cylinder sets in $\varPhi '$ and it is easy to see that ${\mathcal {C}}(\varPhi ')$ is an algebra. Furthermore, by ${\mathcal {C}}_{\sigma }(\varPhi ')$ we denote the $\sigma$-algebra which is generated by ${\mathcal {C}}(\varPhi ')$. One can show that ${\mathcal {C}}_{\sigma }(\varPhi ')$ coincides with the Borel $\sigma$-algebra ${\mathcal {B}}(\varPhi ')$, the space $\varPhi '$ being endowed with the inductive limit topology. The following theorem is an infinite-dimensional generalization of the classical Bochner theorem on the Fourier transform of a probability measure.

Theorem 7

(Minlos) Suppose $F:\varPhi \rightarrow {\mathbb {C}}$. Then F is the Fourier transform of a unique probability measure $\mu$ on $(\varPhi ', {\mathcal {C}}_{\sigma }(\varPhi '))$, i.e.

$$\begin{aligned} F(f)=\int _{\varPhi '} e^{i\langle x,f\rangle }d\mu (x),\quad f\in \varPhi , \end{aligned}$$

(70)

if and only if:

$\bullet$ $F(0)=1$,

$\bullet$ F is positive definite, i.e. $\forall c_1,\dotsc , c_n\in {\mathbb {C}},\ n\in {\mathbb {N}},\ y_1,\dotsc , y_n\in \varPhi$:

$$\begin{aligned} \sum ^n_{i,j=1}{c_i}{\overline{c_j}}F(y_i-y_j)\ge 0, \end{aligned}$$

$\bullet$ F is continuous on $\varPhi$.

Remark

Let $H_0={{\mathbb {R}}}^d$ with the usual Euclidian inner product. Since the space $H_0$ is finite-dimensional (i.e. it has exactly d elements in its orthonormal basis), the identity operator in $H_0$ is of Hilbert–Schmidt class. Therefore, we can set $H_n=H_0$, $n\in {\mathbb {N}}$, and thus, ${\mathbb {R}}^d$ is also a nuclear space, which is dual to itself. Then, the Fourier transform (70) becomes

$$\begin{aligned} F(f)=\int _{{\mathbb {R}}^d}e^{\langle x,f\rangle }\mu (dx),\quad f\in {\mathbb {R}}^d, \end{aligned}$$

i.e. the usual Fourier transforms of a probability measure on ${\mathbb {R}}^d$. Recall that the classical Bochner theorem states that a function $F:{\mathbb {R}}^d\rightarrow {\mathbb {C}}$ is the Fourier transform of a unique probability measure $\mu$ on ${\mathbb {R}}^d$ if and only if $F(0)=1$ and F is positive definite, i.e. $\forall c_1,\dots ,c_n\in {\mathbb {C}}$, $y_1,\dots ,y_n\in {\mathbb {R}}^d,$

$$\begin{aligned} \sum ^n_{i,j=1}{c_i}{\bar{c_j}}F(y_i-y_j)\ge 0. \end{aligned}$$

Thus, in the finite-dimensional case, that condition that F be continuous on ${\mathbb {R}}^d$ is automatically satisfied. However, in infinite dimensions, this condition is crucial, and one can give examples of functions $F:\varPhi '\rightarrow {\mathbb {C}}$ which satisfy $F(0)=1$ and positive definiteness, which are not continuous on $\varPhi$ and for which there is no probability measure on $\varPhi '$ whose Fourier transform is F.

Gaussian Measures

1.1 Definition and Moments of a Gaussian Measure

Let

$$\begin{aligned} \varPhi =\projlim _{n\in {\mathbb {N}}} H_n\subseteq H_0\subseteq \text {ind lim} H_{-n}=\varPhi ' \end{aligned}$$

(71)

be a rigging of a Hilbert space $H_0$ by a nuclear space $\varPhi$. Let $C:\varPhi \rightarrow \varPhi '$ be a linear operator. We suppose that there exists $n\in {\mathbb {N}}$ such that C acts continuously from $H_n$ into $H_{-n}$. Furthermore, we suppose that C is positive, i.e. for any $f\in \varPhi$, $f\ne 0$, we have

$$\begin{aligned} \langle Cf,f\rangle >0. \end{aligned}$$

(72)

We define

$$\begin{aligned} \Vert f\Vert _{H_{C}}:=\langle Cf,f\rangle ^{\frac{1}{2}},\quad f\in \varPhi . \end{aligned}$$

(73)

As easily seen

$$\begin{aligned} (f_1,f_2)_{H_C}:=\langle Cf_1,f_2\rangle ,\quad f_1,f_2\in \varPhi , \end{aligned}$$

is an inner product on $\varPhi$. Indeed, for every $f\in \varPhi$,

$$\begin{aligned} (f,f)_{H_C}=\langle Cf,f\rangle \ge 0, \end{aligned}$$

$(f,f)_{H_C}=\langle Cf,f\rangle =0$ if and only if $f=0$ (see (72)), for any $\alpha \in {\mathbb {R}}$, $f_1,f_2,g\in \varPhi$

$$\begin{aligned} (\alpha f_1+f_2,g)&=\langle C(\alpha f_1+f_2),g\rangle \\&=\alpha \langle Cf_1,g\rangle +\langle Cf_2,g\rangle \\&=\alpha (f_1,g)_{H_C}+(f_2,g)_{H_C} \end{aligned}$$

and for any $f_ 1$, $f_2\in \varPhi$

$$\begin{aligned} (f_1,f_2)_{H_C}=\langle Cf_1,f_2\rangle =\langle f_1,Cf_2\rangle =\langle Cf_2,f_1\rangle =(f_2,f_1)_{H_C}. \end{aligned}$$

(Note that C is symmetric since C is positive, which can be proved by analogy with the case of real Hilbert spaces). Therefore, $\Vert \cdot \Vert _{H_C}$ is a norm on $\varPhi$.

Define the Hilbert space $H_{C}$ as the completion of $\varPhi$ with respect to the norm $\Vert \cdot \Vert _{H_{C}}$.

We define

$$\begin{aligned} F(f):=\exp (-{\frac{1}{2}}\Vert f\Vert ^2_{H_{{\mathcal {C}}}}),\quad f\in \varPhi . \end{aligned}$$

(74)

Proposition 2

The mapping F(f) satisfies conditions of the Minlos theorem, and therefore there exists a probability measure $\mu _C$ on $(\varPhi ',C_{\sigma }(\varPhi '))$ such that

$$\begin{aligned} \int _{\varPhi '}e^{i\langle x,f\rangle }d\mu _C(x)=\exp (-\frac{1}{2}\Vert f\Vert ^2_{H_C}). \end{aligned}$$

Proof

Evidently $F(0)=1$. Since the operator C is continuous, the mapping $\varPhi \ni f\mapsto \langle Cf,f\rangle =\Vert f\Vert _{H_C}\in \mathbb R$ is continuous. Therefore, the mapping $\varPhi \ni f\mapsto F(f)\in {\mathbb {R}}$ is continuous. Thus, it only remains to prove that F is positive definite. To this end, let us first fix arbitrary $f_1,\dots ,f_n\in \varPhi$. Define

$$\begin{aligned} C_{ij}=\langle Cf_i,f_j\rangle ,\quad i,j=1,\dots ,n, \end{aligned}$$

(75)

and define

$$\begin{aligned} C=(C_{ij})^n_{i,j=1}. \end{aligned}$$

(76)

Since the operator C is positive, the matrix C is positive definite. Therefore, there exists a centred Gaussian measure on ${\mathbb {R}}^n$ with correlation operator C. This measure is given by

$$\begin{aligned} \gamma (A)&=\pi ^{-\frac{n}{2}}({\text {Det}} C)^{-\frac{1}{2}}\int _{A}\exp [-\frac{1}{2}(C^{-1}x,x)_{\mathbb R^n}]dx. \end{aligned}$$

(77)

The Fourier transform of $\gamma ^{(n)}$ is given by

$$\begin{aligned} F_{\gamma }(u)=\int _{{\mathbb {R}}^n}e^{{i(u,y)}_{\mathbb R^n}}d\gamma (y)=\exp [-\frac{1}{2}(Cu,u)_{{\mathbb {R}}^n}],\quad u\in {\mathbb {R}}^n. \end{aligned}$$

(78)

Choose

$$\begin{aligned} u_1=(1,0,\dots ,0), u_2=(0,1,0,\dots ,0),\dots ,u_n=(0,\dots ,0,1), \end{aligned}$$

and choose arbitrary $c_1,\dots ,c_n\in {\mathbb {C}}$. Since $F_{\gamma }(\cdot )$ is the Fourier transform of a probability measure on ${\mathbb {R}}^n$, it is positive definite, and so

$$\begin{aligned} \sum ^n_{i,j=1}c_i{\bar{c_j}}F_{\gamma }({u_i}-{u_j})\ge 0. \end{aligned}$$

(79)

We note that, for any $i,j\in \{1,\dots ,n\}$, by (2),

$$\begin{aligned} (Cu_i,u_j)_{{\mathbb {R}}^n}=C_{ij}=\langle Cf_i,f_j\rangle . \end{aligned}$$

Therefore,

$$\begin{aligned} \sum ^n_{i,j=1}c_i{\bar{c_j}}F_{\gamma }(u_i-u_j)&=\sum ^n_{i,j=1}c_i{\bar{c_j}}\exp [-\frac{1}{2}(C(u_i-u_j),u_i-u_j)_{{\mathbb {R}}^n}]\nonumber \\&=\sum ^n_{i,j=1}c_i{\bar{c_j}}\exp [-\frac{1}{2}((Cu_i,u_i)_{{\mathbb {R}}^n}-(Cu_j,u_i)_{{\mathbb {R}}^n}\nonumber \\&\quad -(Cu_j,u_i)_{{\mathbb {R}}^n}+(Cu_j,u_j)_{{\mathbb {R}}^n})]\nonumber \\&=\sum ^n_{i,j=1}c_i{\bar{c_j}}\exp [-\frac{1}{2}(\langle Cf_i,f_i\rangle -\langle Cf_j,f_i\rangle \nonumber \\&\quad -\langle Cf_j,f_i\rangle +\langle Cf_j,f_j\rangle )]\nonumber \\&=\sum ^n_{i,j=1}c_{i}\bar{c_{j}}\exp [-\frac{1}{2}\langle C(f_{i}-f_{j}), f_{i}-f_{j}\rangle ]\nonumber \\&=\sum ^n_{i,j=1}c_i{\bar{c_j}}F(f_i-f_j). \end{aligned}$$

(80)

Thus, by (79) and (80), we have

$$\begin{aligned} \sum ^n_{i,j=1}c_i{\bar{c_j}}F(f_i-f_j)\ge 0. \end{aligned}$$

$\square$

Remark

Let $f_1,\dots ,f_n\in \varPhi$. Consider the measurable mapping

$$\begin{aligned} \varPhi '\ni x\mapsto (\langle x,f_1\rangle ,\dots ,\langle x,f_2\rangle )\in {\mathbb {R}}^n, \end{aligned}$$

Let $\mu ^{(f_1,\dots ,f_n)}_C$ be the image of the measure $\mu _C$ under this mapping. Then, $\mu ^{(f_1,\dots ,f_n)}_C$ coincides with the Gaussian measure $\gamma$ given by (77), with the correlation operator C defined by (75) and (76). Indeed, let us calculate the Fourier transform of $\mu ^{(f_1,\dots ,f_n)}_{C}$. For any $u_1,\dots ,u_n\in {\mathbb {R}}$, we have

$$\begin{aligned}&\int _{{{\mathbb {R}}}^n}e^{i({u_1}{x_1}+\dots +{u_n}{x_n})}d{\mu ^{(f_1,\dots ,f_n)}_C}{(x_1,\dots ,x_n)}\\&=\int _{\varPhi '}e^{i(u_1\langle x,f_1\rangle +\dots +u_n\langle x,f_n\rangle )}d\mu _C(x)\\&=\int _{\varPhi '}e^{i\langle x,u_1{f_1}+\dots +u_n{f_n}\rangle }d\mu _C(x). \end{aligned}$$

Since $u_1{f_1}+\dots +u_n{f_n}\in \varPhi$, we continue as follows:

$$\begin{aligned}&=\exp (-\frac{1}{2}\Vert u_1{f_1}+\dots +u_n{f_n}\Vert ^2_{H_C})\\&=\exp (-\frac{1}{2}\langle C(u_1{f_1}+\dots +u_n{f_n}),u_1{f_1}+\dots +u_n{f_n}\rangle )\\&=\exp (-\frac{1}{2}\sum ^n_{i,j=1}u_i{u_j}\langle C{f_i},f_j\rangle )\\&=\exp (-\frac{1}{2}\sum ^n_{i,j=1}u_i{u_j}C_{ij})\\&=\exp (-\frac{1}{2}(Cu,u)_{{\mathbb {R}}^n}). \end{aligned}$$

Now the statement follows from (78).

Therefore, the measure $\mu$ is called Gaussian measure with correlation operator C.

Then, the nth moment of $\mu$ is defined by

$$\begin{aligned} C_n(f_1,\dots ,f_n):=\int _{\varPhi '}\langle x,f_1\rangle \dots \langle x,f_n\rangle d\mu (x),\quad f_1,\dots ,f_n\in \varPhi , \end{aligned}$$

(81)

if the integral exists.

Now for $t\in {\mathbb {R}}$

$$\begin{aligned} \int _{\varPhi '} e^{it\langle x,f\rangle } d\mu _{C}(x)=\exp (-{\frac{t^2}{2}}\Vert f\Vert ^2_{H_{C}}). \end{aligned}$$

(82)

We take the first derivative in t at zero, i.e. $(\frac{d}{dt})|_{t=0}$ in order to get the first moment of the Gaussian measure:

$$\begin{aligned} \frac{d}{dt}{\int _{\varPhi '}e^{it\langle x,f\rangle } d{\mu _{C}}(x)}&=\int _{\varPhi '} i\langle x,f\rangle e^{it\langle x,f\rangle }d{\mu _{C}(x)}\\&=(-t){\Vert f\Vert ^2_{H_{C}}}\exp (-\frac{t^2}{2}\Vert f\Vert _{H_{C}}), \end{aligned}$$

then we insert $t=0$ and get

$$\begin{aligned} i\int _{\varPhi '}{\langle x,f\rangle d{\mu _{C}(x)}}=0. \end{aligned}$$

(83)

Therefore, $\mu _{C}$ is a centred measure.

We now take the second derivative in order to get the second moment of the Gaussian measure:

$$\begin{aligned}&(\frac{d}{dt})^2{\int _{\varPhi '} e^{it\langle x,f\rangle }d{\mu _{C}(x)}} ={\int _{\varPhi '} i^2\langle x,f\rangle ^2e^{it\langle x,f\rangle }d{\mu _{C}(x)}}\\&=-\Vert f\Vert ^2_{H_{C}}\exp (-\frac{t^2}{2}\Vert f\Vert ^2_{H_{C}})+((-t)\Vert f\Vert ^2_{H_{C}})^2\exp (-{\frac{t^2}{2}}\Vert f\Vert ^2_{H_{C}}) \end{aligned}$$

and inserting $t=0$ we have

$$\begin{aligned} \int _{\varPhi '}{\langle x,f\rangle }^2 d{\mu _{C}(x)}=\Vert f\Vert ^2_{H_{C}}={\langle Cf,f\rangle }, \end{aligned}$$

(84)

and hence

$$\begin{aligned} \int _{\varPhi '}\bigg (\langle x,f\rangle -\int _{\varPhi '}\langle x,f\rangle d\mu _{C}(x)\bigg )^2 d\mu _{C}(x)={\langle Cf,f\rangle }. \end{aligned}$$

(85)

Thus, we get the following formula for the covariance of $\langle \cdot , f\rangle$:

$$\begin{aligned} {\text {Cov}}_{\mu _{C}}(\langle \cdot ,f\rangle )=\langle Cf,f\rangle . \end{aligned}$$

(86)

This is the reason why the operator C is called the covariance operator.

We define the operator I by

$$\begin{aligned} H_{C}\supseteq \varPhi \ni f\mapsto If:=\langle \cdot ,f\rangle \in L^2(\varPhi ',d\mu _{C}). \end{aligned}$$

By Eq. (84), we get

$$\begin{aligned} \Vert If\Vert _{L^2(\varPhi ',d\mu _{C})}=\Vert f\Vert ^2_{H_{C}}. \end{aligned}$$

(87)

Let $f\in H_{C}$ and we approximate f by $f_n\in \varPhi$, $n\in {\mathbb {N}}$, in $\Vert \cdot \Vert _{H_{C}}$. Then,

$$\begin{aligned} \Vert {\langle x,f_n\rangle }-{\langle x,f_m\rangle }\Vert _{L^2(\varPhi ',d\mu _{C})}&=\Vert \langle x,f_n-f_m\rangle \Vert _{L^2(\varPhi ',d\mu _{C})}\\&=\Vert f_n-f_m\Vert _{H_{C}}\rightarrow 0\quad as\ n,m\rightarrow \infty . \end{aligned}$$

Hence, $(\langle x,f_n\rangle )_{n\in {\mathbb {N}}}$ is a Cauchy sequence in $L^2(\varPhi ',d\mu _{C})$. Therefore, there exists $F\in L^2(\varPhi ',d\mu _{C})$, such that $\langle x,f_n\rangle \rightarrow F(x)$ in $L^2(\varPhi ',d\mu _{C})$. We set $\langle x,f\rangle :=F(x)$. It follows also that we can extend the operator I by continuity to the whole of $H_{C}$ and I then becomes an isometric operator between $H_{C}$ and $L^2(\varPhi ',d\mu _{C})$.

It can be easily shown by approximation that, for each $f\in H_C$, we have

$$\begin{aligned} \int _{\varPhi '}e^{i\langle x,f\rangle }d\mu _C(x)=\exp [-\frac{1}{2}\Vert f\Vert ^2_{H_C}]. \end{aligned}$$

Lemma 4

(Moments of Gaussian measures) For $\mu _{C}$, we have

$$\begin{aligned} C_{2n+1}(f_1,\dots ,f_{2n+1})&=0,\end{aligned}$$

(88)

$$\begin{aligned} C_{2n}(f_1,\dots ,f_{2n})&=\sum (f_{k_1},f_{l_1})_{H_{C}},\dots ,(f_{k_n},f_{l_n})_{H_{C}} \end{aligned}$$

(89)

where $f_1,\dots ,f_{n+1}\in H_C$ and the summation is over all possible $\frac{(2n)!}{2^n n!}$ pairings of the numbers $\{1,\dots .2n\}$, i.e. all possible partitions of $\{1,2,\dots ,2n\}$ into n pairs $\{k_1,l_1\},\dots ,\{k_n,l_n\}$.

Proof

We first consider the special case when $f_1=\dots =f_n=f$.

$$\begin{aligned} \int _{\varPhi '}{{\langle x,f\rangle }^n}d{\mu _{C}(x)}&=i^{-n}{(\frac{d}{dt})^n}|_{t=0}\int _{\varPhi '}e^{i\langle x,f\rangle t}d\mu _{C}(x)\\&=i^{-n}(\frac{d}{dt})^n|_{t=0}\exp (-{\frac{1}{2}}t^2\Vert f\Vert ^2_{H_{C}}),\quad n\in {\mathbb {N}}. \end{aligned}$$

For a smooth function $f:{\mathbb {R}}\rightarrow {\mathbb {R}}$, we have the following formula,

$$\begin{aligned} \frac{d^n}{d{t^n}} e^{f(t)}=\sum _{\begin{array}{c} m_1,\dots ,m_k\in {\mathbb Z_+}\\ m_1+2m_2+\dots +km_k=n \end{array} }\frac{n!(f^{(1)}(t))^{m_1}(f^{(2)}(t))^{m_2}\dots (f^{(n)}(t))^{m_k}}{m_1!(2!)^{m_2}m_2!\dots (k!)^{m_k}m_k!} e^{f(t)}.\nonumber \\ \end{aligned}$$

(90)

Setting

$$\begin{aligned} f(t)=-\frac{1}{2}t^2\Vert f\Vert ^2_{H_{C}} \end{aligned}$$

(91)

we have,

$$\begin{aligned} f'(t)&=-t{\Vert f\Vert ^2_{H_{{\mathcal {C}}}}}&f'(0)&=0,\\ f''(t)&=-{\Vert f\Vert ^2_{H_{{\mathcal {C}}}}}&{f^{(n)}}(t)&=0,\ n\ge 3. \end{aligned}$$

Thus, now (90) reduces to

$$\begin{aligned} \frac{d^n}{dt^n}e^{f(t)}|_{t=0}=\sum _{m_2\in {\mathbb {Z}}_+:2m_2=n}\frac{n!(-\Vert f\Vert ^2_{H_C})^{m_2}}{(2!)^{m_2}{m_2}!}. \end{aligned}$$

Therefore, it follows now that

$$\begin{aligned} C_{2n+1}(f,\dots ,f)=0,\ C_{2n}(f,\dots ,f)=\frac{(2n)!}{{2^n}n!}\Vert f\Vert ^{2n}_{H_{C}}. \end{aligned}$$

We now consider the general case by using the polarization identity: For $a_1,\dots ,a_m\in {\mathbb {R}}$ we have

$$\begin{aligned} \prod ^m_{k=1}a_k=\frac{1}{m!}\sum ^m_{p=1}(-1)^{m-p}\sum _{1\le k_1<k_2<\dots <k_p\le m}( a_{k_1}+a_{k_2}+\dots +a_{k_p})^m. \end{aligned}$$

i.e. we represent the product of $a_1,\dots ,a_n$ through a linear combination of powers of their sums. This classical formula may be proved by induction, but we will skip the proof. Now, substituting $a_k=\langle x,f_k\rangle , \ i=1,\dots ,m,\ f_1,\dots ,f_m\in \varPhi ,$ we have:

$$\begin{aligned} \prod ^m_{k=1}\langle x,f_k\rangle =\frac{1}{m!}\sum ^m_{p=1}(-1)^{m-p}\sum _{1\le k_1<k_2<\dots <k_p\le m}\langle x, f_{k_1}+\dots +f_{k_p}\rangle ^m. \end{aligned}$$

Therefore, we have that

$$\begin{aligned} C_n(f_1,\dots ,f_n)&=\int _{\varPhi '}\prod ^m_{k=1}\langle x,f_k\rangle d{\mu _{C}(x)}\nonumber \\&=\int _{\varPhi '}\frac{1}{m!}\sum ^m_{p=1}(-1)^{m-p} \sum _{k_1<\dots<k_p}{{\langle x,f_{k_1}+\dots +f_{k_p}\rangle }^m}d\mu _{C}(x)\nonumber \\ {}&=\frac{1}{m!}\sum ^m_{p=1}(-1)^{m-p}\sum _{1\le k_1<\dots <k_p\le m}\int _{\varPhi '}{\langle x,f_{k_1}+\dots +f_{k_p}\rangle }^m d\mu _{C}(x). \end{aligned}$$

(92)

We note that the mapping

$$\begin{aligned} \varPhi ^n\ni (f_1,\dots ,f_n)\mapsto C_n(f_1,\dots ,f_n)\in {\mathbb {R}},\quad n\in {\mathbb {N}} \end{aligned}$$

is linear.

It follows from (92) that this mapping is uniquely identified by its diagonal values, i.e. by $C_n(f_1,\dots ,f_n)$, $f\in H_C.$ Now, formulas on the right hand side of (88) and (89) are also linear in $f_i$’s and they coincide with $C_n(f,\dots ,f).$ Therefore, they are true for different $f_1,\dots ,f_n\in H_C$. $\square$

1.2 White Noise and Fractional White Noise

We will now discuss two examples of Gaussian measures. We consider the Schwartz triple

$$\begin{aligned} {\mathcal {S}}({\mathbb {R}})\subseteq L^2({\mathbb {R}})\subseteq {\mathcal {S}}'({\mathbb {R}}) \end{aligned}$$

and we set C to be the identical operator ${\textbf{1}}$, which evidently satisfies conditions of a correlation operator. Let us recall the definition of a standard Brownian motion.

Definition 8

A continuous-time stochastic process ${B_t:0\le t<+\infty }$ is called a standard Brownian Motion starting at zero if it has the following four properties:

• (i) $B_0=0$.

• (ii) The increments of $B_t$ are independent; that is, for any finite set of times $0\le t_1<t_2<\dots <t_n$ the random variables

  $$\begin{aligned} B_{t_1}, B_{t_2}-B_{t_1}, B_{t_3}-B_{t_2}, \dots , B_{t_n}-B_{t_{n-1}} \end{aligned}$$

  are independent.

• (iii) For any $0\le s\le t<T$ the increment $B_t-B_s$ has the Gaussian distribution with mean 0 and variance $t-s$.

• (iv) For all $\omega$ in a set of probability one, $B_t(\omega )$ is a continuous function of t.

For each $t\ge 0$, we now set

$$\begin{aligned} X_t(x):=\langle x,\chi _{[0,t]}\rangle , \end{aligned}$$

(93)

where $\chi _{[0,t]}$ denotes the indicator function of [0, t]. Evidently $\chi _{[0,t]}\in L^2({\mathbb {R}})$, so that $X_t\in L^2({\mathcal {S}}'({\mathbb {R}}),\mu _1)$. Thus, we have the stochastic process $(X_t)_{t\ge 0}$. For a fixed $t\ge 0$ and $u\in {{\mathbb {R}}}$ we have

$$\begin{aligned} \int _{{{\mathcal {S}}'}({\mathbb R})}e^{iu{X_t}(x)}d\mu _1(x)&=\int _{{{\mathcal {S}}'}(\mathbb R)}{e^{i\langle x,u\chi _{[0,t]}\rangle }}d\mu _1(x)\nonumber \\ {}&=\exp (-{\frac{{u^2}t}{2}}), \end{aligned}$$

(94)

and therefore $X_t$ is a Gaussian random variable. Furthermore,

$$\begin{aligned} \int _{{{\mathcal {S}}'}({\mathbb {R}})} X(t)d{\mu _{1}}(x)=\int _{{\mathcal {S}}'({\mathcal {R}})}{\langle x,\chi _{[0,t]}\rangle } d{\mu _1}(x)=0 \end{aligned}$$

(95)

and for any $0<s<t$, we have

$$\begin{aligned} \int _{{\mathcal {S}}'({\mathbb {R}})}X(s)X(t)d\mu _1(x)&=\int _{\mathcal S'({\mathbb {R}})}\langle x,\chi _ {[0,s]}\rangle \langle x,\chi _{[0,t]}\rangle dx\nonumber \\ {}&=\int _{\mathbb R}\chi _{[0,s]}(u)\chi _{[0,t]}(u)\nonumber \\ {}&=\min {\{s,t\}}. \end{aligned}$$

(96)

By (94)-(96), one can conclude that $(X_t)_{t\ge 0}$ is a version of Brownian motions, i.e. $(X_t)_{t\ge 0}$ satisfies the properties $(i)-(iii)$ in Definition 3.1. It is known from the general theory of Brownian motion that one can take a version of each $X_t$ so that $(X_t)_{t\ge 0}$ becomes a proper Brownian motion, i.e. condition (iv) is satisfied as well. Calculating informally, we next have

$$\begin{aligned} \frac{d}{dt}X(t)&=\lim _{{\varepsilon }\rightarrow 0} \frac{X(t+\varepsilon )-X(t)}{\varepsilon }\\ {}&=\lim _{\varepsilon \rightarrow 0}\frac{\langle x,\chi _{[0,t+\varepsilon ]}\rangle -\langle x,\chi _{[0,t]}\rangle }{\varepsilon }\\ {}&=\lim _{\varepsilon \rightarrow 0}\frac{1}{\varepsilon }({\int ^{t+\varepsilon }_0}x(s)ds-\int ^t_0 x(s)ds)\\ {}&=\lim _{\varepsilon \rightarrow 0}\frac{1}{\varepsilon }\int ^{t+\varepsilon }_t x(s)ds=x(t),\end{aligned}$$

where $\delta _t$ denotes the delta function at t. Therefore, x(t) is the derivative of the Brownian motion, i.e. white noise. The measure $\mu$ is called (Gaussian) white noise measure.

Let us now consider the case of a fractional white noise. We again consider the Schwartz triple

$$\begin{aligned} {\mathcal {S}}({\mathbb {R}})\subseteq L^2({\mathbb {R}})\subseteq {\mathcal {S}}'({\mathbb {R}}) \end{aligned}$$

and we fix a so-called Hurst parameter $H\in (\frac{1}{2},1)$. Define

$$\begin{aligned} \phi (s,t)=H(2H-1)|s-t|^{2H-2},\quad s,t\in {\mathbb {R}}, \end{aligned}$$

(97)

and let

$$\begin{aligned} (C_{\phi }f)(s)=\int _{{\mathbb {R}}}\phi (s,t)f(t)dt,\quad s\in \mathbb R, \end{aligned}$$

(98)

(as easily seen the integral above exists). Let us show that the operator $C_{\phi }$ can serve as a correlation operator of a Gaussian measure. Let us first show that $C_{\phi }$ is a continuous operator from ${\mathcal {S}}({\mathbb {R}})$ into $\mathcal S'(\mathbb R)$. We have, for any $f,g\in {\mathcal {S}}({\mathbb {R}})$

$$\begin{aligned} \biggl |\int _{\mathbb R}(Cf)(s)g(s)ds\biggl |&=\biggl |\int _{{\mathbb {R}}}\int _{\mathbb R}\phi (s,t)f(t)g(s)dtds\biggl |\\ {}&\le H(2H-1)\int _{\mathbb R}\int _{{\mathbb {R}}}|s-t|^{2H-2}|f(t)||g(s)|dtds, \end{aligned}$$

by changing the variables $u=s$ and $v=s-t$, we obtain

$$\begin{aligned}&\bigg |\int _{{\mathbb {R}}}({ C_{\phi }}f)(s)g(s)ds\bigg |\\&\le H(2H-1)\int _{{\mathbb {R}}}\int _{{\mathbb {R}}}|v|^{2H-2}|f(u-v)||g(u)|dudv\\&=H(2H-1)\int _{{\mathbb {R}}}du\int _{[-1,1]}dv\, v^{2H-2}|f(u-v)||g(u)|\\&\quad +H(2H-1)\int _{{\mathbb {R}}}du\int _{{[-1,1]}^c}dv v^{2H-2}|f(u-v)||g(u)| \\&\le H(2H-1)\Vert f\Vert _{L^{\infty }({\mathbb {R}})}\Vert g\Vert _{L^1({\mathbb {R}})}\int _{[-1,1]}v^{2H-2}dv\\&\quad +H(2H-1)\int _{{\mathbb {R}}}\int _{{\mathbb {R}}}|f(u-v)||g(u)|dudv \\&=H(2H-1)\Vert f\Vert _{L^{\infty }({\mathbb {R}})}\Vert g\Vert _{L^1({\mathbb {R}})}\int _{[-1,1]}|v|^{2H-2}dv+H(2H-1)\Vert f\Vert _{L^1({\mathbb {R}})}\Vert g\Vert _{L^1({\mathbb {R}})}. \end{aligned}$$

It is known that

$$\begin{aligned} \max \{\Vert f\Vert _{L^1({\mathbb {R}})},\Vert f\Vert _{L^{\infty }(\mathbb R)}\}\le \Vert f\Vert _{{\mathcal {S}}_1({\mathbb {R}})},\quad f\in \mathcal S({\mathbb {R}}). \end{aligned}$$

(99)

Hence,

$$\begin{aligned} \bigg |\int _{{\mathbb {R}}}(C_{\phi }f)(s)g(s)ds\bigg |\le 2H(2H-1)\int _{[-1,1]}|v|^{2H-2}dv\Vert f\Vert _{{\mathcal {S}}_1(\mathbb R)}{\Vert g\Vert _{{\mathcal {S}}_1({\mathbb {R}})}}, \end{aligned}$$

which implies that

$$\begin{aligned} \Vert C_{\phi }f\Vert _{{\mathcal {S}}_{-1}({\mathbb {R}})}\le 2H(2H-1)\int _{[-1,1]}|v|^{2H-2}dv\Vert f\Vert _{{\mathcal {S}}_1({\mathbb {R}})}, \end{aligned}$$

i.e.

$$\begin{aligned} \Vert C_{\phi }\Vert _{{\mathcal {L}}({\mathcal {S}}_1({\mathbb {R}}),\mathcal S_{-1}({\mathbb {R}}))}\le 2H(2H-1)\int _{[-1,1]}|v|^{2H-2}dv. \end{aligned}$$

Therefore, $C_{\phi }$ is a continuous operator. Furthermore, it is known the operator $C_{\phi }$ is positive, i.e. for any $f\in {\mathcal {S}}({\mathbb {R}}), f\ne 0$, we have

$$\begin{aligned} \langle C_{\phi }f,f\rangle >0, \end{aligned}$$

(100)

Therefore, we can consider the Gaussian measure $\mu _{C_{\phi }}$, which we will denote by $\mu _{\phi }$. We will also denote the Hilbert space $H_{C_{\phi }}$ just by $H_{\phi }$. As easily seen, there exists a sequence $(f_n)_{n\in {\mathbb {N}}}\subseteq \mathcal S({\mathbb {R}})$ such that $f_n(x)\rightarrow \chi _{[0,t]}(x)$ as $n\rightarrow \infty$ for each $x\in {\mathbb {R}}$ and

$$\begin{aligned} |f_n(x)|\le \chi _{[-1,t+1]}(x),\quad n\in {\mathbb {N}},\quad x\in {\mathbb {R}}. \end{aligned}$$

Furthermore, we have

$$\begin{aligned} {\int _{{\mathbb {R}}}}{\int _{\mathbb R}}H(2H-1){\frac{1}{|s-t|^{2H-2}}}\chi _{[-1,t+1]}(s)\chi _{[-1,t+1]}(t)dsdt\nonumber \\ =\int ^{t+1}_{-1}\int ^{t+1}_{-1}H(2H-1)\frac{1}{|s-t|^{2H-2}}dsdt. \end{aligned}$$

(101)

Making the change of variables $s'=s$ and $t'=s-t$, we get

$$\begin{aligned} \int ^{t+1}_{-1}\int ^{t+1}_{-1}H(2H-1)\frac{1}{|s-t|^{2H-2}}dsdt\\=\int _{\Delta }\int H(2H-1)\frac{1}{t^{2H-2}}dsdt, \end{aligned}$$

where ${\Delta }$ is a bounded set in ${{\mathbb {R}}}^2$. Hence,

$$\begin{aligned} {\int _{{\mathbb {R}}}}{\int _{\mathbb R}}H(2H-1){\frac{1}{|s-t|^{2H-2}}}{\chi _{[-1,t+1]}(s)}{\chi _{[-1,t+1]}(t)}dsdt<{\infty }. \end{aligned}$$

(102)

From (102), by the dominated convergence theorem, we conclude that $(f_n)_{n\in {\mathbb {N}}}$ is a Cauchy sequence in $H_{\phi }$. Therefore, there exists an $f\in H_{\phi }$ such that $f_n\rightarrow f$ as $n\rightarrow \infty$ in $H_{\phi }$, and we can evidently identify this f with $\chi _{[0,t]}$. Hence,

$$\begin{aligned} B_H(t):=\langle x,\chi _{[0,t]}\rangle ,\quad t\ge 0, \end{aligned}$$

(103)

is well defined and $(B_H(t))_{t\ge 0}$ is a stochastic process. Informally, we have that $x(t)=B'_H(t)$.

Let us prove that $(B_H(t))_{t\ge 0}$ is a version of a fractional Brownian motion with Hurst parameter $H\in (\frac{1}{2},1))$. Indeed, for $u\in {\mathbb {R}}$

$$\begin{aligned} \int _{{\mathcal {S}}'(\mathbb R)}e^{iu{B_H(t)}}d\mu _{\phi }=\exp (-{\frac{1}{2}}u^2{\int ^t_0}{\int ^t_0}\frac{1}{|s'-t'|^{2H-2}}ds'dt'). \end{aligned}$$

(104)

From (104), it follows that $B_H(t)$ is a Gaussian random variable. Furthermore, we have that

$$\begin{aligned} \int _{{\mathcal {S}}'({\mathbb {R}})}B_H(t)d\mu _{\phi }=0, \end{aligned}$$

and for any $s,t>0$,

$$\begin{aligned} \int _{{\mathcal {S}}'(\mathbb R)}B_H(t)B_H(s)d\mu _{\phi }&=(\chi _{[0,t]},\chi _{[0,s]})_{H_{\phi }}\\ {}&={\int ^t_0}{\int ^s_0}H(2H-1)|s'-t'|^{2H-2}ds'dt'. \end{aligned}$$

Since the integral is symmetric in t and s, it is sufficient to consider only the case $s\le t$. By changing the variables $t=t'$ and $t-s=s'$ we obtain,

$$\begin{aligned} {\int ^t_0}{\int ^s_0}(s'-t')^{2H-2}H(2H-1)ds'dt'&={\int ^t_0}dt'{\int ^s_0}ds'H(2H-1)|s'-t'|^{2H-2}\\ {}&=H(2H-1){\int ^t_0}dt'{\int ^s_0}ds'(s'-t')^{2(H-1)}\\ {}&=\frac{H(2H-1)}{2H-2+1}{\int ^t_0}dt'(s'-t')^{2H-1}|^{s'=s}_{s'=0}\\ {}&=H\int ^t_0 dt'[(s-t')^{2H-1}-(t')^{2H-1}]\\ {}&=\frac{H}{2H}[(s-t')^{2H}|^{t'=t}_{t'=0}-(t')^{2H}|^{t'=t}_{t'=0}]\\ {}&=\frac{1}{2}[(t-s)^{2H}-s^{2H}-t^{2H}]. \end{aligned}$$

Hence, we see that $B_H(t)$ is a Gaussian process with

$$\begin{aligned} {{\mathbb {E}}}_{\mu _{C}}[B_H(t)]=0,\quad \mathbb E_{\mu _{C}}[B_H(s)B_H(t)]=\frac{1}{2}(t^{2H}+s^{2H}-|t-s|^{2H}) \end{aligned}$$

(105)

Therefore, $(B_H(t))_{t\ge 0}$ is a version of a fractional Brownian motion.

Wick Calculus

1.1 Fock Space

1.1.1 Tensor Product of Hilbert Spaces

Assume that $(H_k)^n_{k=1}$ is a finite sequence of real separable Hilbert spaces, and that $(e^{(k)}_j)^{\infty }_{j=0}$ is some orthonormal basis in $H_k$. We now construct a formal product as follows

$$\begin{aligned} e_{\alpha }=e^{(1)}_{\alpha _1}\otimes \dots \otimes e^{(n)}_{\alpha _n}, \end{aligned}$$

(106)

where $\alpha =(\alpha _1,\dots ,\alpha _n)\in {\mathbb {Z}}^n_{+}=\mathbb Z^1_+\times \dots \times {\mathbb {Z}}^1_+$(n times). Let us consider the ordered sequence $(e^{(1)}_{\alpha _1},\dots ,e^{(n)}_{\alpha _n})$ and span a real Hilbert space by the formal vectors (106), assuming that they form the orthonormal basis of this space. The separable Hilbert space obtained as a result is called a tensor product of the spaces $H_1,\dots ,H_n$ and is denoted by $H_1\otimes \dots \otimes H_n=\bigotimes ^n_{k=1}H_k$. Its vectors have the form

$$\begin{aligned} f=\sum _{\alpha \in {\mathbb {Z}}^n_+}f_{\alpha }e_{\alpha } (f_{\alpha }\in {\mathbb {R}}^1),\quad \Vert f\Vert ^2_{\bigotimes ^n_{k=1}H_k}=\sum _{\alpha \in \mathbb Z^n_+}|f_{\alpha }|^2<\infty , \quad \nonumber \\ (f,g)_{\otimes ^n_{k=1}H_k}=\sum _{\alpha \in \mathbb Z^n_+}f_{\alpha }g_{\alpha },\quad g=\sum _{\alpha \in \mathbb Z^n_+}g_{\alpha }e_{\alpha }\in \bigotimes ^n_{k=1}H_k. \end{aligned}$$

(107)

Let $f^{(k)}=\sum ^{\infty }_{j=0}{f^{(k)}_j}e^{(k)}_j\in H_k(k=1,\dots ,n)$ be some vectors. We define

$$\begin{aligned} f=f^{(1)}\otimes \dots \otimes f^{(n)}:=\sum _{\alpha \in \mathbb Z^n_+}f^{(1)}_{\alpha _1}\dots f^{(n)}_{\alpha _n}e_{\alpha }. \end{aligned}$$

(108)

The coefficients $f_{\alpha }=f^{(1)}_{\alpha _1}\dots f^{(n)}_{\alpha _n}$ of decomposition (108) satisfy (107). Therefore, the vector (108) belongs to $\bigotimes ^n_{k=1}H_k$ and moreover,

$$\begin{aligned} \Vert f\Vert _{\bigotimes ^n_{k=1}H_{k}}=\prod ^n_{k=1}\Vert f_k\Vert _{H_k}. \end{aligned}$$

(109)

We can easily see that this definition of a tensor product depends on the choice of the orthonormal basis $(e^{(k)}_j)^{\infty }_{j=0}$ in each factor $H_k$. However, one can easily understand that after changing the bases, we obtain a tensor product isomorphic to the initial one and preserving its structure.

1.1.2 Fock Space and Its Basis

Let H be a real Hilbert space. For every $n\in {\mathbb {N}}$ we denote by $H^{\otimes n}=H\otimes \dots \otimes H$ the nth tensor power of H. We put our emphasis on a subspace of symmetric elements from $H^{\otimes n}$. So as to define this subspace, we think about the unitary operator $U_{\sigma ,n}$ in $H^{\otimes n}$, introduced by the formula

$$\begin{aligned} U_{\sigma ,n}(h_1\otimes \dots \otimes h_n)=h_{\sigma (1)}\otimes \dots \otimes h_{\sigma (n)} \end{aligned}$$

on a total set of elements of the form $h_1\otimes \dots \otimes h_n\in H^{\otimes n}$, with each permutation $\sigma =(\sigma (1),\dots ,\sigma (n))$ from the set ${\mathfrak {G}}_{n}$ of all permutations of $\{1,\dots ,n\}$. We define the operator

$$\begin{aligned} P_n=\frac{1}{n!}\sum _{\gamma \in {\mathfrak {G}_n}}U_{\sigma ,n}. \end{aligned}$$

We have $P^2_n=P_n$, $P^*_n=P_n$ which implies that it is an orthogonal projector in $H^{\otimes n}$. The closed subspace of $H^{\otimes n}$ onto which $P_n$ projects is denoted by $\mathfrak {F}_n(H)$. It is called the nth symmetric tensor power of H. Moreover, we set $\mathfrak {F}_0(H)={\mathbb {R}}^1$. The Fock space (symmetric or Bose) $\mathfrak {F}(H)$ is defined as a Hilbert orthogonal sum

$$\begin{aligned} \mathfrak {F}(H)=\bigoplus ^{\infty }_{n=0}{\mathfrak {F}_n(H)} \end{aligned}$$

(110)

Hence, it consists of sequences $f=(f_n)^{\infty }_{n=0} (f_n\in {\mathfrak {F}_n(H)}$ for which

$$\begin{aligned} \Vert f\Vert _{\mathfrak {F}(H)}^2=\sum ^{\infty }_{n=0}\Vert f_n\Vert ^2_{H^{\otimes n}}<{\infty }. \end{aligned}$$

The subspaces ${\mathfrak {F}}_n(H)$ are often called n-particle subspaces, and $\mathfrak {F}_0(H)$ is called the vacuum subspace.

Let us introduce a series of objects in the Fock space which are relevant in what follows. We define $\mathfrak {F}_{fin}(H)$ the subset of finite vectors from $\mathfrak {F}(H)$, i.e. vectors of the form $f=(f_0,\dots ,f_n,0,0,\dots )$. Clearly, $\mathfrak {F}_{fin}(H)$ is dense in ${\mathfrak {F}}(H)$. For $h\in H$, we set

$$\begin{aligned} h^{\otimes n}=h\otimes \dots \otimes h\in {{\mathfrak {F}}_n(H)}. \end{aligned}$$

The vectors

$$\begin{aligned} \Gamma (h)=(1,(1!)^{-\frac{1}{2}}h,\dots ,(n!)^{-\frac{1}{2}}h^{\otimes n},\dots ) \end{aligned}$$

are called coherent states. It is easy to get that, for different $h\in H$, they are linearly independent and form a total set in ${\mathfrak {F}}(H)$ (i.e. the linear span of this set is dense in $\mathfrak {F}(H)$). From the definition of ${\mathfrak {F}}(H)$, we have

$$\begin{aligned} (\Gamma (h_1),\Gamma (h_2))_{{\mathfrak {F}}(H)}=\exp (h_1,h_2)_H,\\ \Vert {\Gamma (h)}\Vert _{{\mathfrak {F}}(H)}=\exp (\frac{1}{2}\Vert h\Vert ^2_H)\quad (h_1,h_2,h\in H). \end{aligned}$$

The vector $\Gamma (0)=(1,0,0,\dots )$ is called a vacuum.

We now construct a special basis in the Fock space which is often called the occupation numbers basis. We start from the orthonormal basis $(e_j)^{\infty }_{j=1}$ in H. Let $\mathbb Z^{\infty }_{+,0}\subset {\mathbb {Z}}^{\infty }_+=\mathbb Z_+\times {\mathbb {Z}}_+\times \dots$ be a set of finite multi-indices $\alpha =(\alpha _1,\dots ,\alpha _v,0,0,\dots )$ with integer nonnegative coordinates; here $v=v(\alpha )$ is the length of the multi-index $\alpha$, i.e. the minimal $k\in {\mathbb {N}}$ for which $\alpha _{k+1}=\alpha _{k+2}=\dots =0$. For each $\alpha \in \mathbb Z^{\infty }_{+,0}$ such that $|\alpha |=\alpha _1+\dots +\alpha _v=n\in {\mathbb {N}}$, the vector

$$\begin{aligned} e^{(n)}_{\alpha }=\bigg (\frac{n!}{\alpha _1!\dots \alpha _v!}\bigg )^{\frac{1}{2}}P_n(e^{\otimes \alpha _1}_1\otimes \dots \otimes e^{\otimes \alpha _v}_v) \end{aligned}$$

belongs to $\mathfrak {F}_n(H)$ (in the case where $\alpha _k=0$, the vector $e_k$ is absent in the tensor product, and 0!=1). The vectors $e^{(n)}_{\alpha }$, where $\alpha \in \mathbb Z^{\infty }_{+,0},\ |\alpha |=n$, form an orthonormal basis in ${\mathfrak {F}}_n(H)$. This follows from the fact that vectors of the type $e_{j_1}\otimes \dots \otimes e_{j_n}(j_k\in {\mathbb {N}})$ form an orthonormal basis in $H^{\otimes n}$, and the numerical coefficient in the expression for $e^{(n)}_{\alpha }$ is chosen so that the equality $\Vert e^{(n)}_{\alpha }\Vert _{H^{\otimes n}}=1$ holds. Therefore, the vectors

$$\begin{aligned} e_{\alpha }=(\underbrace{0,\dots ,0}_{|\alpha |-1},e^{(n)}_{\alpha },0,0,\dots )\quad (\alpha \in {\mathbb {Z}}^{\infty }_{+,0}, |\alpha |>0),\\ e_{(0,0,\dots )}=(1,0,0,\dots )=\Gamma (0) \end{aligned}$$

form an orthonormal basis in $\mathfrak {F}(H)$. This is exactly the occupation numbers basis.

1.2 Continuous Polynomials on $\varPhi '$

We define the Hermite polynomials $(H_n(x))^{\infty }_{n=0}$ on ${\mathbb {R}}$ as the polynomials with the leading coefficient 1 which are obtained by the procedure of orthogonalization of monomials $x^n$ with respect to the standard Gaussian measure $\mu _1$,

$$\begin{aligned} \mu _1(dx)=(2\pi )^{-\frac{1}{2}}\exp (-\frac{x^2}{2})dx. \end{aligned}$$

(111)

In other words, $H_n(x)={(-1)^n}e^{x^2}\frac{d^n}{dx^n}(e^{-x^2})$. Moreover, one can prove that these polynomials satisfy the following recursion relation:

$$\begin{aligned} xH_n(x)=H_{n+1}(x)+nH_{n-1}(x). \end{aligned}$$

(112)

We also define the normalized Hermite polynomials as follows:

$$\begin{aligned} h_n(x):=\frac{1}{\Vert H_n\Vert _{L^2({\mathbb {R}},\mu _1)}}H_n(x). \end{aligned}$$

(113)

Then, $(h_n)^{\infty }_{n=0}$ is an orthonormal basis in $L^2(\mathbb R,d\mu _1)$. As is known $\Vert H_n\Vert _{L^2({\mathbb {R}},\mu _1)}=\sqrt{n!}$, so that

$$\begin{aligned} h_n(x)=\frac{1}{\sqrt{n!}}H_n(x), \end{aligned}$$

(114)

and by (112), $(h_n)^{\infty }_{n=0}$ satisfy the following relation:

$$\begin{aligned} xh_n(x)=\sqrt{n+1}h_{n+1}(x)+\sqrt{n}h_{n-1}(x),\quad h_0(x)=1. \end{aligned}$$

(115)

Now, we fix a Gel’fand triple $\varPhi \subseteq H_0\subseteq \varPhi '$ and consider polynomials on $\varPhi '$. We denote by $P_{cyl}(\varPhi ')$ the set of cylinder polynomials on $\varPhi '$, i.e. functions on $\varPhi '$ of the form

$$\begin{aligned} c+\langle x,f_{11}\rangle +\langle x,f_{21}\rangle \langle x,f_{22}\rangle +\dots +\langle x,f_{n1}\rangle \times \cdots \times \langle x,f_{nn}\rangle , \end{aligned}$$

(116)

where $c\in {\mathbb {R}}$ and $f_{ij}\in \varPhi$, $1\le i,j\le n.$ For a Hilbert space H, let $H^{{\hat{\otimes }}n}$ denote the symmetric tensor power, i.e. ${\mathfrak {F}}_{n}(H)$. If $\varPhi =\projlim _{n\in {\mathbb {N}}}H_n$, we denote

$$\begin{aligned} \varPhi ^{{\hat{\otimes }}n}=\projlim _{n\in {\mathbb {N}}}H^{{\hat{\otimes }}n}_n \end{aligned}$$

(117)

and

$$\begin{aligned} (\varPhi ')^{{\hat{\otimes }}n}=\text {ind lim}_{n\in \mathbb N}H^{{\hat{\otimes }}n}_{-n}, \end{aligned}$$

(118)

where $H_{-n}$ is the dual space of $H_n$ with respect to the zero space $H_0$. Then,

$$\begin{aligned} \varPhi ^{{\hat{\otimes }}n}\subseteq H^{{\hat{\otimes }}n}_0\subseteq (\varPhi ')^{{\hat{\otimes }}n} \end{aligned}$$

(119)

is again a Gel’fand triple.

We define the set of continuous polynomials on $\varPhi '$, denoted by $P(\varPhi ')$, as the set of functions on $\varPhi '$ of the form

$$\begin{aligned} c+\langle x,f^{(1)}\rangle +\langle x^{\otimes 2},f^{(2)}\rangle +\cdots +\langle x^{\otimes n},f^{(n)}\rangle ,\quad c\in {\mathbb {R}},\ f^{(i)}\in \varPhi ^{{\hat{\otimes }}i},\ n\in {\mathbb {N}}. \end{aligned}$$

(120)

We can easily see that every element of $P(\varPhi ')$ is indeed a continuous function on $\varPhi '$. Furthermore, since for any $f_1,...,f_n\in \varPhi$

$$\begin{aligned} \langle x,f_1\rangle \dots \langle x,f_n\rangle&=\langle x^{\otimes n},f_1\otimes \cdots \otimes f_n\rangle \\&=\langle x^{\otimes n},f_1{\hat{\otimes }}...{\hat{\otimes }}f_n\rangle , \end{aligned}$$

we have that

$$\begin{aligned} P_{cyl}(\varPhi ')\subset P(\varPhi '). \end{aligned}$$

(121)

The following theorem holds:

Theorem 8

Let $\mu$ be a probability measure on $(\varPhi ',\mathcal C_{\sigma }(\varPhi '))$. Suppose that there exists $C>0$ and $p\in {\mathbb {N}}$ such that

$$\begin{aligned} \int _{\varPhi '}|\langle x,f\rangle |^n d\mu (x)\le C^n n!\Vert f\Vert ^n_p,\quad f\in \varPhi . \end{aligned}$$

(122)

Then, $P_{cyl}(\varPhi ')$ is dense in $L^2(\varPhi ',d\mu )$.

Let $\mu _C$ be the Gaussian measure on $\varPhi '$ with a correlation operator C.

Proposition 3

$P_{cyl}(\varPhi ')$ is dense in $L^2(\varPhi ',d\mu _C).$

Proof

For any $f\in \varPhi$, using the Cauchy inequality and Lemma 3.1 we have:

$$\begin{aligned} \int _{\varPhi '}|\langle x,f\rangle |^n d\mu _C(x)\le (\int _{\varPhi '}\langle x,f\rangle ^{2n}d\mu _C(x))^{\frac{1}{2}}=(\frac{(2n)!}{2^n n!}\Vert f\Vert ^{2n}_{H_C})^{\frac{1}{2}}. \end{aligned}$$

Since

$$\begin{aligned} (2n)!=1\cdot ...\cdot 2n&=(1\cdot 3\cdot 5...(2n-1))(2\cdot 4\cdot ...\cdot 2n)\\&\le (2\cdot 4\cdot 6\cdot ...\cdot 2n)^2=(2^n n!)^2, \end{aligned}$$

we have

$$\begin{aligned} \int _{\varPhi '}|\langle x,f\rangle |^n d\mu _C(x)&\le \left( \frac{(2^{n}n!)^2}{2^{n}n!}\Vert f\Vert ^{2n}_{H_C}\right) ^{\frac{1}{2}}\\&= (\sqrt{2})^n\sqrt{n!}\Vert f\Vert ^{n}_{H_C}\\&\le (\sqrt{2}\Vert f\Vert _{H_C})^{n}n! \end{aligned}$$

and then from Theorem 8, the proposition follows. $\square$

1.3 Orthogonal Polynomials

We define $P_n(\varPhi ')$ as the set of all continuous polynomials on $\varPhi$ of order less than or equal to n. Furthermore, we define $P_{\mu _C,n}(\varPhi ')$ to be the closure of the set $P_n(\varPhi ')$ in $L^2(\varPhi ',d\mu _C)$. We set

$$\begin{aligned} \Gamma _n(\varPhi ',\mu _C)&:=P_{\mu _C,n}(\varPhi ')\circleddash P_{{\mu _C},n-1}(\varPhi '),\ n\in {\mathbb {N}},\end{aligned}$$

(123)

$$\begin{aligned} \Gamma _0(\varPhi ',\mu _C)&=\{constants\}, \end{aligned}$$

(124)

We evidently have

$$\begin{aligned} P_{\mu _C,n}(\varPhi ')=\bigoplus ^n_{k=0}\Gamma _k(\varPhi ',\mu _C). \end{aligned}$$

(125)

By Proposition 3 it is known that the continuous polynomials $P(\varPhi ')$ are dense in $L^2(\varPhi ',\mu _C)$. Since

$$\begin{aligned} P(\varPhi ')=\bigcup _{n\in \mathbb N}P_n(\varPhi ')\subseteq \bigoplus ^{\infty }_{n=0}\Gamma _n(\varPhi ',\mu _C), \end{aligned}$$

(126)

it follows that $\bigoplus ^{\infty }_{n=0}\Gamma _n(\varPhi ',\mu _C)$ is dense in $L^2(\varPhi ',\mu _C)$. Furthermore,$\bigoplus ^{\infty }_{n=0}\Gamma _n(\varPhi ',\mu _C)$ is closed in $L^2(\varPhi ',\mu _C)$. Therefore, by the definition of dense set, we have

$$\begin{aligned} \bigoplus ^{\infty }_{k=0}\Gamma _k(\varPhi ',\mu _C)=L^2(\varPhi ',\mu _C). \end{aligned}$$

(127)

Let $P_{\Gamma _n(\varPhi ',\mu _C)}$ denote the orthogonal projection of $L^2(\varPhi ',\mu _C)$ onto $\Gamma _n(\varPhi ',\mu _C)$.

For any $a_n\in \varPhi ^{\otimes n}$, we define

$$\begin{aligned} :(a_n,x^{\otimes n})_{H^{\otimes n}_0}:=P_{\Gamma _n(\varPhi ',\mu _C)}((a_n,x^{\otimes n})_{H_0}). \end{aligned}$$

(128)

For a polynomial $p(x)=\sum ^n_{k=0}(a_k,x^{\otimes k})_{H^{\otimes k}_0}$, we define a Wick polynomial

$$\begin{aligned} :p(x):=\sum ^{n}_{k=0}:(a_k,x^{\otimes k})_{H^{\otimes k}_0}:,\quad :a_0:=a_0. \end{aligned}$$

(129)

Theorem 9

(i) $\forall h\in \varPhi ,\ n\in {\mathbb {N}}$, we have $\mu _C$-a.s.

$$\begin{aligned} :(h,x)^n_{H_0}:=\Vert h\Vert ^n_{H_C}H_n(\Vert h\Vert _{H_C}^{-1}(h,x)_{H_0}). \end{aligned}$$

(130)

(ii) For $h_1,\dots ,h_n\in \varPhi$, which are mutually orthogonal in $H_C$ and for fixed $n_1,\dots ,n_m\in {\mathbb {N}}$, we have in $L^2(\varPhi ',\mu _C)$ that

$$\begin{aligned} :\prod ^m_{k=1}(h_k,x)^{n_k}_{H_0}:=\prod ^m_{k=1}:(h_k,x)^{n_k}_{H_0}:. \end{aligned}$$

(131)

(iii) For $h_k,g_k\in \varPhi ,\ k=1,\dots ,n,$ we have

$$\begin{aligned} \int _{\varPhi '}:\prod ^n_{k=1}(h_k,x)_{H_0}::\prod ^n_{k=1}(g_k,x)_{H_0}:d{\mu _C}(x)\nonumber \\ =\sum _{\sigma \in \mathfrak {G}_n}(h_{\sigma (1)},g_1)_{H_C}\cdots (h_{\sigma (n)},g_n)_{H_C}. \end{aligned}$$

(132)

where $\mathfrak {G}_n$ denotes the group of permutations of n numbers.

Proof

(i) Consider

$$\begin{aligned} (h,x)^n_{H_C}-\Vert h\Vert ^n_{H_C}H_n(\Vert h\Vert ^{-1}_{H_C}{{(h,x)}_{H_0} }). \end{aligned}$$

(133)

Then,

$$\begin{aligned} H_{n}(\Vert h\Vert ^{-1}_{H_C}(h,x)_{H_0})=H_{n}(\Vert h\Vert ^{-1}_{H_C}h,x)_{H_0}) \end{aligned}$$

is a cylindrical polynomial of x. Therefore, (133) is a continuous polynomial. Clearly, it belongs to $P_{n}(\varPhi ')$. But $H_n(\cdot )$ has the leading coefficient 1, and therefore the coefficient by $(h,x)^n_{H_0}$ in (133) is 0. Therefore, (133) belongs to $P_{n-1}(\varPhi ').$

Hence,

$$\begin{aligned}:(h,x)^n_{H_0}-\Vert h\Vert ^n_{H_C}P_{\Gamma _n(\varPhi ',\mu _{C})}H_n(\Vert h\Vert ^{-1}_{H_C}(h,x)_{H_0})=0, \end{aligned}$$

so that

$$\begin{aligned}:(h,x)^n_{H_0}:=\Vert h\Vert ^n_{H_C}P_{\Gamma _n(\varPhi ',\mu _{C})}H_n(\Vert h\Vert ^{-1}_{H_C}(h,x)_{H_0}). \end{aligned}$$

Therefore, we need to prove that

$$\begin{aligned} P_{{\Gamma _n}(\varPhi ',\mu _C)}H_n(\Vert h\Vert ^{-1}_{H_C}(h,x)_{H_0})=H_n(\Vert h\Vert ^{-1}_{H_C}(h,x)_{H_0}). \end{aligned}$$

But $H_n(\Vert h\Vert ^{-1}_{H_C}(h,x)_{H_0})\in P_n(\varPhi ').$ So the aim is to prove

$$\begin{aligned} H_n(\Vert h\Vert ^{-1}_{H_C}(h,x)_{H_0})\perp P_{n-1}(\varPhi '). \end{aligned}$$

(134)

In order to show (134), it is sufficient to show that

$$\begin{aligned} H_n((h_1,x)^n_{H_0})\perp \{ (g,x)^q_{H_0}\mid g\in \varPhi ,\ q=0,\dots ,n-1\}, \end{aligned}$$

where $h_1={\frac{1}{\Vert h\Vert _{H_C}}}h$. For a fixed $g\in \varPhi$, $g=c_1{h_1}+g_1$ and $g_1\perp h_1$ in $H_{C}$, we have that

$$\begin{aligned} (g,x)^q_{H_0}=\sum ^q_{j=1}\left( {\begin{array}{c}q\\ j\end{array}}\right) c^j_1(h_1,x)^j_{H_0}(g_1,x)^{q-j}_{H_0}. \end{aligned}$$

Furthermore, it follows from Lemma 3.1

$$\begin{aligned}&\int _{\varPhi '}H_n({(h_1,x)}_{H_0})(h_1,x)^j_{H_0}(g_1,x)^{q-j}_{H_0}d\mu _C(x)\\&=\int _{\varPhi '}H_n((h_1,x)_{H_0})(h_1,x)^j_{H_0})d\mu _C(x)\int _{\varPhi '}(g_1,x)^{q-j}_{H_0}d\mu _C(x). \end{aligned}$$

By the remark in section 3.1 the distribution of $(h,\cdot )_{H_0}$ under $\mu _{C}$ is the standard Gaussian distribution with mean 0 and variance 1. Hence, we set $a=\int _{\varPhi '}{(g_1,x)}^{q-j}_{H_0}d\mu _C{(x)}$ and get

$$\begin{aligned}&\int _{\varPhi '}H_n({(h_1,x)}_{H_0}){(h_1,x)}^j_{H_0}d\mu _C{(x)}\int _{\varPhi '}(g_1,x)^{q-j}_{H_0}d\mu _C(x)\\&=a\int _{\mathbb R}{t^j}H_n(t)\frac{1}{\sqrt{2\pi }}e^{-\frac{t^2}{2}}dt=0. \end{aligned}$$

(ii) By (i), we have that

$$\begin{aligned} \prod ^m_{k=1}(h_k,x)^{n_k}_{H_0}-\prod ^m_{k=1}:(h_k,x)^{n_k}_{H_0}:\in P_{\mu _C,n_1+\dots +n_k-1}(\varPhi '), \end{aligned}$$

(135)

Hence, it

$$\begin{aligned} P_{\Gamma _{n_1+\dots +n_k}(\varPhi ',\mu _{C})}(\prod ^m_{k=1}(h_k,x)^{n_k}_{k_0})=P_{\Gamma _{n_1+\dots +n_k}(\varPhi ',\mu _{C})}(\prod ^{m}_{k=1}:(h_k,x)^{n_k}_{k_0}). \end{aligned}$$

But, by definition

$$\begin{aligned} P_{\Gamma _{n_1+\dots +n_k}(\varPhi ',\mu _{C})}(\prod ^{m}_{k=1}(h_k,x)^{n_k}_{H_0})=:\prod ^{m}_{k=1}(h_k,x)^{n_k}_{H_0}:. \end{aligned}$$

Thus, we need to prove that

$$\begin{aligned} P_{\Gamma _{n_1+\dots +n_k}(\varPhi ',\mu _{C})}(\prod ^{m}_{k=1}:(h_k,x)^{n_k}_{k_0})=\prod ^{m}_{k=1}:(h_k,x)^{n_k}_{H_0}:. \end{aligned}$$

But $\prod ^{m}_{k=1}:(h_k,x)^{n_k}_{H_0}:\in P_{n_1+\dots +n_k}(\varPhi ')$. Hence, it suffices to prove that $\prod ^{m}_{k=1}:(h_k,x)^{n_k}_{H_0}:$ is orthogonal to $P_{l}$, where $l=n_1+n_2+\dots +n_k-1,$ or equivalently, it suffices to prove that $\prod ^{m}_{k=1}:(h_k,x)^{n_k}_{H_0}:$ is orthogonal to each monomial. $(g,x)^q_{H_0}$, $q\in \varPhi$, $q=0,\dots ,l$. We have that $g=\sum ^m_{k=1}c_k h_k+g_0$ and $g_0\perp h_n$, with $n=1,\dots ,m.$ Hence,

$$\begin{aligned} (g,x)^q_{H_0}=\sum _{a_0+\dots +a_m=q}c^{\alpha _1}_1\dots c^{\alpha _m}_m(h_1,x)^{\alpha _1}_{H_0}\dots (h_m,x)^{\alpha _m}_{H_0}(g_0,x)^{\alpha _0}_{H_0}, \end{aligned}$$

and therefore by (i) and Lemma 3.1

$$\begin{aligned} \int _{\varPhi '}(g,x)^q_{H_0}\prod ^m_{k=1}:(h_k,x)^{n_k}_{H_0}:d\mu _{C}(x)&=\sum _{\alpha _0+\dots +\alpha _m=q}\prod ^m_{k=1}c^{\alpha _k}_{k}\int _{\varPhi '}(h_k,x)^{\alpha _{k}}_{H_0}\\&\times :(h_k,x)^{n_k}_{H_0}: d\mu _C(x)\\&\times \int _{\varPhi '}(g_0,x)^{\alpha _0}_{H_0}d\mu _C(x)=0, \end{aligned}$$

since there exists $k_0$ such that $\alpha _{k_0}<n_{k_0}$.

(iii) We first take $g_k=h_k=h\in \varPhi$, for $k=1,\dots ,n$. Then, we have that

$$\begin{aligned} \int _{\varPhi '}:(h,x)^n_{H_0}:^2 d\mu _C(x)=\int _{\mathbb R}\Vert h\Vert ^{2n}_{H_C}H^2_n(t)d\mu _1(t)=\Vert h\Vert ^{2n}_{H_C}n!. \end{aligned}$$

The general case follows from the polarization identity in $L^2(\varPhi ',\mu _C):$

$$\begin{aligned}:\prod ^n_{k=1}(h_k,x)_{H_0}:=\frac{1}{n!}\sum ^n_{k=1}(-1)^{n-k}\sum _{j_1<\dots <j_k}:(h_{j_1}+\dots +h_{j_k},x)^n_{H_0}:, \end{aligned}$$

for $h_1,\dots ,h_n\in H_C$ and $x\in \varPhi '.$ $\square$

We consider the mapping $I_C:{\mathfrak {F}}(H_C)\rightarrow L^2(\varPhi ',\mu _C)$ defined on the total set $\{h_1{\hat{\otimes }}\dots {\hat{\otimes }}h_n, h_k\in H_C\}$ by

$$\begin{aligned} I_C h_1{\hat{\otimes }}\dots {\hat{\otimes }}h_n=(n!)^{-\frac{1}{2}}:\prod ^n_{k=1}(h_k,x)_{H_0};, \end{aligned}$$

$I_C \Gamma (0)=1$ and then extend $I_C$ by linearity. By Theorem 9(iii), we have that

$$\begin{aligned} \int _{\varPhi '}I_C(h_1{\hat{\otimes }}\dots {\hat{\otimes }}h_n)I_C(g_1{\hat{\otimes }}\dots {\hat{\otimes }}g_n)d\mu _C(x)=(h_1{\hat{\otimes }}\dots {\hat{\otimes }},g_1{\hat{\otimes }}\dots {\hat{\otimes }}g_n)_{{\mathfrak {F}}_n(H_C)}. \end{aligned}$$

Hence, $I_C$ is an isometric mapping, and therefore, we can extend it by continuity to the whole ${\mathfrak {F}}(H_C)$.

Theorem 10

The image of the operator $I_C$ is the whole of $L^2(\varPhi ',\mu _C)$ and hence $I_C$ is a unitary operator between ${\mathfrak {F}}(H_C)$ and $L^2(\varPhi ',\mu _C).$

Proof

Since $I_C$ is an isometry, it is sufficient to show that ${\text {Im}}(I_C)$ is dense in ${\mathfrak {F}}(H_C)$. We have that for any $h\in H$, $H_n((h,x)_{H_0})\in {\text {Im}}(I_C)$. Hence, by linearity, we have $(h,x)^n_{H_0}\in Im(I_C)$ for each $n\in {\mathbb {N}}$. It follows that $P_{cyl}(\varPhi ')\in Im(I_C)$, but $P_{cyl}(\varPhi ')$ is dense in $L^2(\varPhi ',\mu _C).$ $\square$

For any $f^{(n)}\in {\mathfrak {F}}_n(H)$, we define

$$\begin{aligned} :(f^{(n)},x^{\otimes n})_{H_0}:=I_C(\sqrt{n!}f^{(n)}), \end{aligned}$$

(136)

which in the case $f^{(n)}\in \varPhi ^{{\hat{\otimes }}n}$ coincides with the definition of $:(f^{(n)},x^{\otimes n})_{H_0}$. Thus, the unitary $I_C$ can be written down in the form

$$\begin{aligned} f=(f^{(n)})^{\infty }_{n=0}\mapsto I_C f=\sum ^{\infty }_{n=0}(n!)^{-\frac{1}{2}}:(f_n,x^{\otimes n})_{H^{\otimes n}_0}:\in L^2(\varPhi ',\mu _C). \end{aligned}$$

(137)

Example 5.1 We have for $h\in H_C$ that

$$\begin{aligned} (I_C\Gamma (h))(x)=\sum ^{\infty }_{n=0}\frac{1}{n!}:(h,x)^n_{H_0}:=\sum ^{\infty }_{n=0}\frac{1}{n!}\Vert h\Vert ^n_{H_C}H_n(\Vert h\Vert ^{-1}_{H_C}(h,x)_{H_0}), \end{aligned}$$

where the second equality follows from theorem 9(i). Recall the well-known formula of the Hermite polynomials:

$$\begin{aligned} \sum ^{\infty }_{n=0}\frac{1}{n!}z^n H_n(t)=\exp (tz-\frac{z^2}{2}). \end{aligned}$$

(138)

If we set $z=\Vert h\Vert _{H_C}$ and $t=\Vert h\Vert ^{-1}_{H_C}(h,x)_{H_0}$, we then get by Eq. (138)

$$\begin{aligned} \sum ^{\infty }_{n=0}\frac{1}{n!}:(h,x)^n_{H_0}:=\exp \bigg ((h,x)_{H_0}-\frac{\Vert h\Vert ^2_{H_C}}{2}\bigg ). \end{aligned}$$

(139)

We also set

$$\begin{aligned} :\exp (h,x)_{H_0}:=\sum ^{\infty }_{n=0}\frac{1}{n!}:(h,x)^{\otimes n}_{H_0}:, \end{aligned}$$

(140)

so that

$$\begin{aligned}:\exp (h,x)_{H_0}:=\exp ((h,x)_{H_0}-\frac{\Vert h\Vert ^2_{H_{C}}}{2}). \end{aligned}$$

Example 5.2 For the basis of occupation numbers, we have

$$\begin{aligned} I_C e_{\alpha }=I_C[(\frac{|\alpha |!}{\alpha _1!\dots \alpha _{\nu }!})^{\frac{1}{2}}e^{\otimes \alpha _1}_1{\hat{\otimes }}\dots {\hat{\otimes }}e^{\otimes \alpha _{\nu }}_{\nu }], \end{aligned}$$

where $|\alpha |=\alpha _1+\dots +\alpha _{\nu }.$ The vector $e_1,\dots , e_{\nu }$ are by construction orthogonal in $H_C$ and therefore

$$\begin{aligned} I_C e_{\alpha }&=(\frac{|\alpha |!}{\alpha _1!\dots \alpha _{\nu }!})^{\frac{1}{2}}(\frac{1}{|\alpha !|})^{\frac{1}{2}}:(e_1,x)^{\alpha _1}_{H_0}\dots (e_{\nu },x)^{\alpha _{\nu }}_{H_0};\\&=(\frac{1}{\alpha _1!\dots \alpha _{\nu }!})^{\frac{1}{2}}:(e_1,x)^{\alpha _1}_{H_0}:\dots :(e_{\nu },x)^{\alpha _{\nu }}_{H_0}:\\&=(\frac{1}{\alpha _1!\dots \alpha _{\nu }!})^{\frac{1}{2}}H_{\alpha _1}((e_1,x)_{H_0})\dots H_{\alpha _{\nu }}((e_{\nu },x)_{H_0})\\&=h_{\alpha _1}((e_1,x)_{H_0})\dots h_{\alpha _{\nu }}((e_{\nu },x)_{H_0}, \end{aligned}$$

which forms an orthogonal basis in $L^2(\varPhi ',\mu _C).$

1.4 Fractional Stochastic Calculus of Itô Type

Let us recall that in “Appendix A” we have constructed the Schwartz triple

$$\begin{aligned} S({\mathbb {R}})=\projlim _{p\in {\mathbb {N}}}S_{p}({\mathbb {R}})\subseteq L^2({\mathbb {R}})\subseteq \text {ind lim}_{p\in \mathbb N}S_{-p}({\mathbb {R}})=S'({\mathbb {R}}), \end{aligned}$$

(141)

Let

$$\begin{aligned} (\Gamma _{\phi }f)(u)=c_{H}\int ^{\infty }_{u}(t-u)^{H-\frac{3}{2}}f(t)dt, \end{aligned}$$

where

$$\begin{aligned} c_{H}=(\frac{H(2H-1)\Gamma (\frac{3}{2}-H)}{\Gamma (H-\frac{1}{2})\Gamma (2-2H)})^{\frac{1}{2}} \end{aligned}$$

(142)

and $\Gamma$ denotes the gamma function. By Lemma 2.1 in [5], $\Gamma _{\phi }$ is a unitary operator between $H_{\phi }$ and $L^2({\mathbb {R}})$. Therefore,

$$\begin{aligned} \Gamma ^{-1}_{\phi }:L^2({\mathbb {R}})\mapsto H_{\phi } \end{aligned}$$

is a unitary operator.

Let

$$\begin{aligned} {\tilde{S}}_{p}({\mathbb {R}})=\Gamma ^{-1}_{\phi }(S_{p}(\mathbb R)),\quad p\in {\mathbb {N}}, \end{aligned}$$

(143)

and define the scalar product in ${\tilde{S}}_{p}({\mathbb {R}})$ by

$$\begin{aligned} (f,g)_{{\tilde{S}}_p(\mathbb R)}:=(\Gamma _{\phi }f,\Gamma _{\phi }g)_{S_{p}({\mathbb {R}})}. \end{aligned}$$

(144)

Evidently,

$$\begin{aligned} {\tilde{S}}({\mathbb {R}})=\projlim _{p\in \mathbb N}{\tilde{S}}_{p}({\mathbb {R}}) \end{aligned}$$

(145)

is a nuclear space. Let also ${\tilde{S}}_{-p}({\mathbb {R}})$ be the dual space of ${\tilde{S}}_{p}({\mathbb {R}})$ with respect to zero space $L^2({\mathbb {R}})$. Thus, we get the Gel’fand triple

$$\begin{aligned} {\tilde{S}}({\mathbb {R}})=\projlim _{p\in \mathbb N}{\tilde{S}}_{p}({\mathbb {R}})\subseteq H_{\phi }\subseteq \text {ind lim}_{p\in \mathbb N}{\tilde{S}}_{-p}({\mathbb {R}})={\tilde{S}}'({\mathbb {R}}). \end{aligned}$$

(146)

Let us now consider an abstract Gel’fand triple

$$\begin{aligned} \varPhi =\projlim _{n\in {\mathbb {N}}}H_{p}\subseteq H_0\subseteq \text {ind lim}_{p\in {\mathbb {N}}}H_{-p}=\varPhi '. \end{aligned}$$

Denote

$$\begin{aligned} {\mathfrak {F}}(\varPhi )=\projlim _{n\in {\mathbb {N}}}{\mathfrak {F}}(H_{p}). \end{aligned}$$

One can show that ${\mathfrak {F}}(\varPhi )$ is a nuclear space. Furthermore, ${\mathfrak {F}}(H_{-p})$ is the dual space of $\mathfrak F(H_{p})$ with respect to the space ${\mathfrak {F}}(H)$. Therefore,

$$\begin{aligned} {\mathfrak {F}}(\varPhi ')=\text {ind lim}_{p\in {\mathbb {N}}}{\mathfrak {F}}(H_{-p}) \end{aligned}$$

is the dual space of ${\mathfrak {F}}(\varPhi )$ with respect to zero space ${\mathfrak {F}}(\varPhi )$. Thus we get the Gel’fand triple

$$\begin{aligned} {\mathfrak {F}}(\varPhi )=\projlim _{p\in {\mathbb {N}}}\mathfrak F(H_{p})\subseteq {\mathfrak {F}}(H_0)\subseteq \text {ind lim}_{p\in {\mathbb {N}}}{\mathfrak {F}}(H_{-p})={\mathfrak {F}}(\varPhi '). \end{aligned}$$

(147)

Applying this general construction to the Schwartz triple (141) to (146), we get the Gel’fand triples

$$\begin{aligned} {\mathfrak {F}}(S({\mathbb {R}}))&=\projlim _{p\in {\mathbb {N}}}{\mathfrak {F}}(S_{p}({\mathbb {R}}))\subseteq {\mathfrak {F}}(L^2({\mathbb {R}}))\nonumber \\&\subseteq \text {ind lim}_{p\in {\mathbb {N}}}\mathfrak F(S_{-p}({\mathbb {R}}))={\mathfrak {F}}(S'({\mathbb {R}})) \end{aligned}$$

(148)

and

$$\begin{aligned} {\mathfrak {F}}({\tilde{S}}({\mathbb {R}}))&=\projlim _{p\in {\mathbb {N}}}{\mathfrak {F}}({\tilde{S}}_{p}({\mathbb {R}}))\subseteq {\mathfrak {F}}(H_{\phi })\nonumber \\&\subseteq \text {ind lim}_{p\in {\mathbb {N}}}\mathfrak F({\tilde{S}}_{-p}({\mathbb {R}}))=\mathfrak F({\tilde{S}}'({\mathbb {R}})). \end{aligned}$$

(149)

Recall that we have unitary operators

$$\begin{aligned}{} & {} I_1:{\mathfrak {F}}(L^2({\mathbb {R}})\mapsto L^2(S'({\mathbb {R}}),\mu _1))\end{aligned}$$

(150)

$$\begin{aligned}{} & {} I_{\phi }:{\mathfrak {F}}(H_{\phi })\mapsto L^2(S'(\mathbb R),\mu _{\phi })), \end{aligned}$$

(151)

where we used the notation $I_{\phi }=I_{C_{\phi }}$. Applying (150), respectively (6.11), to the Gel’fand triple (148), respectively (6.9), we get the following Gel’fand triples

$$\begin{aligned} (S)=\projlim _{p\in {\mathbb {N}}}(S)_{p}\subseteq L^2(S'(\mathbb R),\mu _1)\subseteq \text {ind lim}_{p\in \mathbb N}(S)_{-p}=(S') \end{aligned}$$

(152)

and

$$\begin{aligned} ({\tilde{S}})=\projlim _{p\in {\mathbb {N}}}({\tilde{S}})_{p}\subseteq L^2({\tilde{S}}'({\mathbb {R}}),\mu _1)\subseteq \text {ind lim}_{p\in {\mathbb {N}}}({\tilde{S}})_{-p}=({\tilde{S}}'). \end{aligned}$$

(153)

The space (S) is called the space of the Hida test functions, and $(S)'$ is called the space of Hida distributions. Therefore, $({\tilde{S}})$ is called the space of fractional Hida test functions and $({\tilde{S}})'$ is called the space of fractional Hida distributions.

Let us again consider an abstract triple

$$\begin{aligned} {\mathfrak {F}}(\varPhi )\subseteq {\mathfrak {F}}(H_0)\subseteq \mathfrak F(\varPhi '). \end{aligned}$$

For any $f^{(n)}\in \varPhi '^{{\hat{\otimes }}n}$ and $g^{(m)}\in \varPhi '^{{\hat{\otimes }}m}$, we define

$$\begin{aligned} f^{(n)}\diamond g^{(m)}:=\sqrt{\frac{(n+m)!}{n!m!}}f^{(n)}{\hat{\otimes }}g^{(m)}\in \varPhi '^{{\hat{\otimes }}(n+m)}. \end{aligned}$$

(154)

This mapping can be extended by linearity and continuity to the bilinear, continuous mapping

$$\begin{aligned} \diamond :{\mathfrak {F}}(\varPhi ')\times \mathfrak F(\varPhi ')\mapsto {\mathfrak {F}}(\varPhi '), \end{aligned}$$

which is called the Wick product. Furthermore, restricting to ${\mathfrak {F}}(\varPhi )$, we get a bilinear continuous mapping

$$\begin{aligned} \diamond :{\mathfrak {F}}(\varPhi )\times {\mathfrak {F}}(\varPhi )\mapsto \mathfrak F(\varPhi ), \end{aligned}$$

(155)

Realizing $\diamond$ on $F(S'({\mathbb {R}}))$, respectively, $F({\tilde{S}}'({\mathbb {R}}))$, and mapping $\diamond$ onto $(S)'$, respectively, $({\tilde{S}})'$, we get a Wick product on $(S)'$ (as well as on (S)) and on $({\tilde{S}})'$ (as well as on $({\tilde{S}})$). We note that for any $f^{(n)}\in S'(\mathbb R)^{{\hat{\otimes }}n}$ (respectively, ${\tilde{S}}'(\mathbb R)^{{\hat{\otimes }}n})$ and $g^{(m)}\in S'(\mathbb R)^{{\hat{\otimes }}m}$ (respectively, ${\tilde{S}}'(\mathbb R)^{{\hat{\otimes }}m}$), we get

$$\begin{aligned}:\langle f^{(n)}, x^{\otimes n}\rangle :\diamond :\langle g^{(m)},x^{\otimes m}\rangle :=:\langle f^{(n)}{{\hat{\otimes }}}g^{(m)}, x^{\otimes (n+m)}\rangle : \end{aligned}$$

(where we used a natural notation $:\langle f^{(n)}, x^{\otimes n}\rangle :$ for a generalized function $f^{(n)}$). Before giving an application of the Wick calculus, let us state a lemma as below: (see [5])

Lemma 5

There exists an ONB $\{e_{i}\}^{\infty }_{i=1}$ of $H_{\phi }$ such that

$$\begin{aligned} \bigg |\int _{\mathbb R}e_{n}(s)\phi (s,t)ds\bigg |<C_{t}n^{\frac{1}{6}},\quad C_t>0, \end{aligned}$$

(156)

$e_{i}$’s are smooth and

$$\begin{aligned} t\mapsto \int _{{\mathbb {R}}}e_n(s)\phi (s,t)ds \end{aligned}$$

is continuous for each n.

In what follows, let $\{e_i\}^{\infty }_{i=1}$ be as in Lemma 5. The fractional white noise $W_{H}(t)$ is defined by

$$\begin{aligned} W_{H}(t)=\sum ^{\infty }_{i=1}[\int _{{\mathbb {R}}}e_{i}(v)\phi (t,v)dv]\langle e_i,x\rangle . \end{aligned}$$

We see that for $q\le 2$ we have

$$\begin{aligned} \Vert W_{H}(t)\Vert ^2_{{\tilde{S}}_{-q}({\mathbb {R}})}=\sum ^{\infty }_{i=1}[\int _{\mathbb R}e_{i}(v)\phi (t,v)dv]^2(2i)^{-q}<\infty , \end{aligned}$$

by inequality (156). Hence, $W_{H}(t)\in ({\tilde{S}})'$ for all t. Moreover, by (113) it follows that $t\rightarrow W_{H}(t)$ is a continuous function from ${\mathbb {R}}$ into $({\tilde{S}})'$. We define

Definition 9

Suppose $Z:{\mathbb {R}}\rightarrow ({\tilde{S}})'$ is a given function with the property that

$$\begin{aligned} \langle Z(t),\Psi \rangle \in L^1({\mathbb {R}})\quad \forall \Psi \in ({\tilde{S}}). \end{aligned}$$

Then, the integral $\int _{{\mathbb {R}}}Z(t)dt$ is defined to be the unique element of $({\tilde{S}})'$ such that

$$\begin{aligned} \langle \int _{{\mathbb {R}}}Z(t)dt,\Psi \rangle =\int _{{\mathbb {R}}}\langle Z(t),\Psi \rangle dt\quad \forall \Psi \in ({\tilde{S}}). \end{aligned}$$

Since $t\rightarrow W_{H}(t)$ is continuous, $W_{H}(t)$ is integrable in $({\tilde{S}})'$ for $0\le s\le t$ and

$$\begin{aligned} \int ^{t}_{0}W_{H}(s)ds=\sum ^{\infty }_{i=1}[\int ^{t}_{0}(\int _{{\mathbb {R}}}e_{i}(v)\phi (t,v)dv)du]\langle x,e_i\rangle =\langle \chi _{[0,t]},x\rangle =B_{H}(t). \end{aligned}$$

Therefore, $t\rightarrow B_{H}(t)$ is differentiable in $({\tilde{S}})'$ and

$$\begin{aligned} \frac{d}{dt}B_{H}(t)=W_{H}(t)\quad in ({\tilde{S}})'. \end{aligned}$$

(157)

This justifies the name fractional white noise for $W_{H}(t)$.

We finally want to introduce an (Itô-type) stochastic integral

$$\begin{aligned} \int ^{\infty }_{0}Y(t)dB_{H}(t), \end{aligned}$$

or since informally $dB_{H}(t)=W_{H}(t)dt$ we have to define

$$\begin{aligned} \int ^{\infty }_{0}Y(t)W_{H}(t)dt. \end{aligned}$$

Since the multiplication $Y(t)W_{H}(t)$ is pointwisely not well defined, we replace it with the Wick multiplication $Y(t)\diamond W_{H}(t)dt.$

Definition 10

Suppose $Y:{\mathbb {R}}\rightarrow ({\tilde{S}})$ is a given (generalized) function such that $Y(t)\diamond W_{H}(t)$ is integrable in $({\tilde{S}})'$. Then, we define its fractional stochastic integral of Itô type, $\int _{{\mathbb {R}}}Y(t)dB_{H}(t)$ by

$$\begin{aligned} \int _{{\mathbb {R}}}Y(t)dB_{H}(t)=\int _{{\mathbb {R}}}Y(t)\diamond W_{H}(t)dt \end{aligned}$$

(158)

Remark 6.1 In the case of the standard Brownian motion, the usual Itô integral $\int _{{\mathbb {R}}}Y(t)dB(t)$ coincides with $\int _{{\mathbb {R}}}Y(t)\diamond W(t)dt$, which is one of the central results of classical white noise analysis.