Magnetic Characterization of Ferromagnetic Shape Memory Components Under Defined Mechanical Loading

Abstract

The present paper introduces a novel test procedure for the quasistatic magnetic characterization of FSMA (ferromagnetic shape memory alloy) components under mechanical loading for the use in actuator-level modeling. Its development was necessary due to certain requirements coming from the twin structure and shape of typical FSMA components which are not met by the presented test setups up to now. The measurements carried out in the developed test setup are verified by a reference sample and FE simulations. Error sources are discussed and the main systematic error is calculated. After correcting the remaining error, the acquired data correspond well to data from the literature and show a physical consistency. The developed test procedure is hence able to measure effective but absolute magnetization behavior of FSMA components under mechanical loading. These data can directly be applied to any kind of actuator-level models.

Introduction

Ferromagnetic shape memory alloys (FSMA) are metallic single crystals with twinned lattice structure of reduced symmetry and high magnetocrystalline anisotropy. By means of an extrinsically induced magnetization, martensitic variants reorient and twin boundary motion induces a strong magneto-mechanic coupling. Common NiMnGa alloys with 5M modulation exhibit maximum strains of 6% under compressive loads up to 2 MPa at applied magnetic fields below 1 MA/m. FSMA are considered to be promising actuator materials for compact electromagnetic drives as used in switches, latches or valves, as shown in [1, 2].

However, due to the energy barrier to overcome for displacing twin boundaries, the coupling is associated with a strong nonlinearity and a distinct hysteresis. This particular behavior needs to be considered in the design process of FSMA drives in order to make use of the specific advantages of the material. Numerous models have been presented for this purpose in the past, varying from micromechanical to actuator level. From the point of view of a system designer, macroscopic material or even scalar component models are desired. Especially lumped element network models have been proven to support the design process of FSMA drive systems [1, 3].

Regardless of the underlying simulation approach, a sufficient amount of data on the coupling behavior is required. These data are needed to parametrize and fit models on the one hand and to evaluate their prediction accuracy on the other. Especially data on magnetic behavior are necessary for magnetic circuit design. Compared to the number of published models, only little experimental data are available which consider the load-dependent magnetic behavior of FSMA. Most of the remaining published data on magnetic behavior cannot directly be used for modeling.

The aim of the present study is to introduce a procedure for the macroscopic magnetic characterization of FSMA components under mechanical loading providing appropriate data for simulation models. Starting from general considerations and a review on published measurement techniques, the present paper analyses the measurement techniques applied up to now and evaluates their applicability for the abovementioned demands. Based on the findings, we introduce a novel test procedure allowing the simultaneous measurement of magneto-mechanical coupling and magnetization process generating a macroscopically almost uniform magnetization within the investigated sample. Subsequently, test setup and procedure are experimentally validated with a sample of known magnetic properties and then applied to a FSMA component. Finally, the results of the procedure are discussed.

Review on Measurement Techniques

Preliminary Considerations

Prior to a review on published experimental techniques, some general considerations on material characterization and particular characteristics of FSMA are useful. Although different procedures allow the determination of material properties on the micro-scale, the measurement of bulk material properties relevant for actuation is usually carried out on components (material samples). In order to make these data generalizable and transferable to other components, both test setup and sample geometry must ensure a macroscopically uniform loading, i.e., uniform magnetic field and stress distributions. Since this approach assumes a homogenous material, one needs to further account for the microstructure of the material, i.e., its characteristic length must be small compared to the investigated component size. A discussion about how these lengths scale to each other has rarely been conducted in the literature so far, and could not be found at all in the context of experimental characterization. If a uniform loading or a homogenization is not possible, effective internal fields might be derived from measurement.

Typical FSMA components for both macroscopic experiments and use in actuators are slim rectangular cuboids, sometimes called “sticks,” exhibiting dimensions of a few tens of mm³ (typ. size 15 mm × 3 mm × 2 mm) [4]. It is generally recognized that the magnetization $\mathbf{M}$ in rectangular prismatic bodies is nonuniform when exposed to uniform external fields ${\mathbf{H}}_{0}$ as a result of its nonuniform demagnetizing field ${\mathbf{H}}_{\mathrm{d}}$ and its nonlinear magnetization characteristics $\mathbf{M}(\mathbf{H})$ [5]. The investigation of magnetically more favorable geometries, like ellipsoids [6] or disks [7], has been published rarely and is associated with mechanical issues like cracking [7] and preparing such shapes from a single crystal appears to be challenging.

Furthermore, the macroscopic shape change needs to be considered as well, occurring in two dimensions while the volume remains constant. In this regard, either effective quantities need to be measured or the test setup must force a macroscopically uniform field in the sample. Since shape change and magnetization are associated mechanisms, the average magnetic flux density $B$ depends not only on the magnetic field $H$ but also on the volume fraction of twin variants $\xi$:

$$B=B(\xi ,H).$$

(1)

While the volume fraction of twins can be derived from strain, their distribution cannot. The number of macroscopic twin boundaries depends strongly on treatment during fabrication, for example shown in [8]. Average twin size may vary from a few tens of µm to the mm range [9], but a single boundary structure is possible as well [8]. Even if a fine twin structure is present, local defects in the crystal can lead to a lower mobility and to broad twins [10]. Reference [11] reported an influence of twin boundary evolution on pinning phenomena, on local obstacles as well as on load history. Furthermore, twin variant width and evolution changes with magnetic field intensity and frequency [12].

Although experimentally possible, e.g., shown in [12], the twin structure of the investigated sample is usually not observed during magneto-mechanical experiments. Hence, distribution, size, and number of twins are practically unknown and hardly to predict.

Obviously, twin variant width and distribution cannot be neglected for typical components sizes. For the sake of illustration, consider a qualitative two-dimensional magnetic flux density distribution plot shown in Fig. 1 gained with a magnetostatic finite element (FE) simulation with a linear anisotropic material formulation (see “Evaluation of the Review” section) for a FSMA crystal sample with intentionally rough chosen twin structure. The internal magnetic field distribution is strongly nonuniform suggesting that a loading in the desired way is not possible. This effect has been reported elsewhere [9, 13], but consequences on measurement have not yet been discussed.

Fig. 1

Simulated qualitative two-dimensional magnetic flux density distribution and field line plot of a sample with rough twin structure (intentionally chosen here), magnetized in the air gap of an electromagnet

The variance in material behavior, even within one ingot slice [4], and the load dependency of the evolution of microstructure necessitate that magnetic and mechanical measurements are carried out on the same sample in the same setup, simultaneously at the best. Loading conditions should be chosen similar to the ones in application. In summary, the following requirements might be used for evaluating the subsequent literature review, independent of the applied principle:

• I. The measured quantities should correspond to average or effective internal fields.

• II. The magnetic field inhomogeneities within the investigated sample due to the setup need to be reduced to an insignificant level.

• III. An application-oriented setup and loading should be considered. Magnetic behavior should be measured under mechanical loading.

• IV. Local stray fields resulting from the twinned microstructure need to be averaged.

Published Macroscopic Measurement Procedures

Bulk magnetic measurements can be performed with the so-called magnetic open- and closed-circuit methods [5]. In principle, both can be applied to straight extrusion bodies like typical FSMA samples and are able to measure volume average magnetic quantities. Among the former, vibrating sample magnetometers (VSM) are widely used [14]. In order to prevent variant reorientation, the investigated FSMA sample is usually constrained mechanically, e.g., by clamping or molding with resin. Although this open-circuit method is well established and relatively easy to perform, the interpretation of its results is challenging when applied to prismatic FSMA components for some reasons:

• I. the magnetization is nonuniform due to the sample geometry and the material’s nonlinear anisotropic magnetic properties, even in single-variant state,

• II. the measured induced voltage depends on the coil arrangement and leads to relative magnetization data if not calibrated and

• III. only the applied magnetic field is measured and a demagnetizing correction is necessary [5] if magnetization data depending on internal fields are desired.

The first point is inherent in principle, as outlined in the last section. The second one can be overcome by calibration with a sample of identical geometry and known saturation magnetization in order to measure an absolute magnetization [15]. However, strictly speaking, this calibration is only valid for a saturated sample, since for the present sample geometry the demagnetizing field—and so is the demagnetizing factor ${N}_{\mathrm{d}}$—is not only shape-dependent but also a function of the magnetic permeability ${\mu }_{\mathrm{r}}$ [16]. This fact also influences the third point, i.e., the demagnetizing correction of the applied magnetic field ${H}_{0}$. Moreover, in a multi-variant state size and distribution of twin variants will strongly affect the internal field distribution, as shown in Fig. 1. In this regard, the application of an effective and constant scalar demagnetizing factor is, although common practice, disputable. Recently, this has been investigated for FSMA samples in a model-based study [17]. By assuming a homogenized isotropic material ($\xi =0.5$), the authors found out that if the applied field is measured at the right location, the use of a constant demagnetizing factor is feasible. However, this conclusion results from the fact that the sample is magnetically saturated at most of the investigated magnetic operation points. Whenever the effective ${\mu }_{\mathrm{r}}>1$, higher errors occurred, as to be expected due to the dependence of ${N}_{\mathrm{d}}({\mu }_{\mathrm{r}})$ shown in [16]. In this regard, the application of a constant demagnetizing factor is limited to homogenizable weak magnetic FSMA samples. Among others, Haldar et al. [18] proposed an inverse problem solution for the demagnetizing correction using finite element (FE) simulations by assuming a homogenized material model. However, as indicated in the last section, the actual twin distribution is difficult to predict and practically unknown. Furthermore, the computed solution might not be unique. Without an experimental or simulation-based proof, an inverse problem solution assuming a homogenized material model is limited to single-variant samples and cannot be considered as a general method. The described issues might be the reason why most publications using VSM only present relative magnetization curves $M/{M}_{\mathrm{s}\mathrm{a}\mathrm{t}}$ as a function of ${H}_{0},$ mostly in a macroscopic single-variant state or mechanically unconstrained. These data may support material development by comparing different alloys with the same setup and sample shape. However, they give neither relevant information for material modeling nor device design.

A few other research groups use DC hysteresigraphs for hard magnetic materials or similar setups [19, 20]. In those closed-circuit configurations, no demagnetizing field is present as long as certain geometric conditions are fulfilled [21]. The sample is clamped between ferromagnetic poles or inserted with a small gap compared to the sample thickness. A pick-up coil, closely wound around the sample or concentrically on a form in its proximity (sometimes called surrounding coil), is used to measure the magnetic flux. In the former case (see Fig. 2a), the coil either constrains the sample mechanically due to contact pressure or the coil will be deformed plastically itself due to the shape change, leading to an undefined coil area. In the latter case, the sample is usually entirely surrounded by coil and pole faces (see Fig. 2b). A simultaneous mechanical load application perpendicular to the magnetized axis is thus practically not realizable. Results are therefore usually gained either in macroscopically single-variant or discrete (mechanically constrained) states. In the cited references [19, 20], sample shape and loading direction, respectively, were further different to practical load cases.

Fig. 2

Two different options for flux measurement for FSMA components in DC hysteresigraphs: a coil closely wound around the sample (a) and so-called “surrounding coil” enclosing the sample (b). The desired mechanical loading for magneto-mechanical characterization is also indicated

Different topologies for a combined magneto-mechanical characterization of FSMA have been presented in the past, explained in [14]. However, for the application of arbitrary magnetic and mechanic load paths, a particular setup, schematically depicted in Fig. 3, is widely used [22,23,24]. These setups are mostly combinations of standard laboratory equipment. On the magnetic side, a field is created in a laboratory-scale electromagnet whose air gap volume and total air gap length ${d}_{\mathrm{g}\mathrm{a}\mathrm{p}}$ are much larger than the sample volume and the magnetically loaded sample dimension $d$, respectively. Either the applied magnetic field ${H}_{0}$ or the stray field $H^{\prime}$ close to the sample is measured with a magnetic sensor, mostly by a uniaxial Hall probe. On the mechanical side, a universal test machine or similar equipment is used. A compressive force $F$ is applied with a push rod and usually measured with a load cell while the displacement $u$ of the rod is measured with a position sensor.

Fig. 3

Schematic structure of a typical test setup for the magneto-mechanical characterization of FSMA devices according to the literature

Due to the physical size of the magnetic sensor and the need for a mechanical sample guidance, an open magnetic circuit is formed in this manner, causing the same principle issues as outlined for VSM. Since the measured stray field has no predictable relation to the average internal magnetic flux density, it is hardly possible to derive absolute magnetization data thereof. Some authors [25, 26] published relative changes of the measured stray field. In a more complex biaxial open-circuit setup, analytical calculations were used to compute average internal magnetization and field strength from measured stray fields, assuming a uniformly magnetized sample [27]. Another approach was presented in [7], where a vibrating coil magnetometer was included into a test apparatus described above. Magnetic field $H$ was determined by demagnetizing correction with constant factor. Still both approaches suffer from the same problems of nonuniform magnetic loading and as outlined for VSM.

Evaluation of the Review

Concluding the review, it can be stated that the test procedures presented up to now do not fulfill the requirements formulated in “Preliminary Considerations” section for an adequate component characterization. Open-circuit setups can neither apply uniform magnetic fields nor measure effective magnetic quantities within the sample. The practically unknown twin structure of the material prohibits an inverse problem solution except for single-variant samples unless the correctness of the approach is verified. As indicated in the last section, closed-circuit test setups in principle fulfill all the requirements except the unwanted constraining and the impossibility to apply mechanical loads and the constraining of lateral faces, due to the pick-up coil and the poles, respectively. A modification is hence necessary.

For closed-circuit setups, several conditions to attain low measurement errors are described in the corresponding standard [21]. In essence, the magnetically loaded sample width, $d$ here, must be much smaller than the diameter of the poles and much larger than the sum of both residual air gaps ${d}_{\mathrm{r}\mathrm{e}\mathrm{s}}$ between sample and poles. While the former condition can usually be fulfilled, the latter cannot. The resulting relative measurement error in magnetic field strength can be estimated with

$$\frac{\Delta H}{H}\approx \frac{2{d}_{\mathrm{r}\mathrm{e}\mathrm{s}}}{d}=\frac{{d}_{\mathrm{g}\mathrm{a}\mathrm{p}}-d}{d}\cdot {\mu }_{\mathrm{r}}.$$

(2)

Due to the necessary clearance between sample and poles for mechanical loading, the typical device aspect ratio as well as its lateral strain, magnetic field strength cannot be measured directly. With realistic dimensions (d = 2 mm, d_gap = 2.1 mm), the relative error exceeds 10% already with magnetic permeabilities of ${\mu }_{\mathrm{r}}>2$. In this regard, even the dimensional change due to lateral strain is crucial.

Furthermore, a different flux measurement technique needs to be applied. While the evaluation of the excitation coil current and the total flux through the magnetic core results in large errors, it is possible to exploit the continuity of the magnetic flux density normal to the component surface.

Thin induction coil sensors or Hall sensors, as recently published Graphene-based sensors [28], allow for maintaining small residual air gaps on principle. Inevitably, application of thin sensors is related to the fourth requirement from “Preliminary Considerations” section, which is the influence of local stray fields resulting from the twin structure of the sample, as visible from Fig. 1. It must be ensured that the sensor signal corresponds to an average field instead of an arbitrary stray field component around a twin boundary. Since this cannot be considered in a qualitative way, we propose an estimation of the maximum possible error by means of a numerical solution of the corresponding magnetostatic field problem, e.g., by FEA, as performed by the authors here. The results are summarized in Fig. 4 and described in the following.

Fig. 4

Simulation of the stray field influence on magnetic flux density measurement close to the sample surface: schematic of the simulated geometry (a), measured and approximated magnetic curves from [29] of easy and hard axis (b), resulting normalized errors along $z$ for a selected parameter combination (c) and maximum errors from evaluated spatial field distribution depending on normalized input parameters at constant twin boundary length ${l}_{\mathrm{t}\mathrm{w}}^{{\prime}}=0.1 \mathrm{m}\mathrm{m}$ (d)

A schematic of the chosen geometry and boundary conditions are depicted in Fig. 4a. It shows a periodic cut-out of a magnetically loaded FSMA sample surrounded by two magnetic poles of large magnetic permeability ${\mu }_{\mathrm{r}}\gg 1$ and separated by a residual air gap of width ${d}_{\mathrm{r}\mathrm{e}\mathrm{s}}$. For the sake of simplicity, fields along the third sample axis (y-axis in Fig. 3) were ignored for a first estimation and a two-dimensional treatment of the problem is proposed. Depending on the sample width w (see "Proposed Measurement Procedure" section), the magnitude of the flux density is expected to be different in the 3D case. However, the qualitative relationship between the local and averaged field is maintained in principle and is of main interest at this point. Since only the effective range of a stray field around a twin boundary is from interest, it is sufficient to consider a minimum number of them and useful to apply periodic boundary conditions. The problem can further advantageously be formulated based on the magnetic scalar potential. The twin structure within a FSMA sample with width $d$ is considered, as shown elsewhere [9, 13], with two twin variants tilted at 45° with complementary perpendicular magnetization axes (i.e., easy and hard axis) of projected width ${l}_{\mathrm{t}\mathrm{w}}^{{\prime}}=\sqrt{2}{l}_{\mathrm{t}\mathrm{w}}$. The assumed orthotropic, complementary relative magnetic permeabilities ${\mu }_{\mathrm{r},\mathrm{1,2}}$ of both variants 1 and 2 read in Cartesian coordinates

Fig. 5

Underlying load case, corresponding quantities on component level and relevant dimensions of the FSMA component

$${\mu }_{\mathrm{r},1}=\left(\begin{array}{cc}{\mu }_{\mathrm{r},\mathrm{e}}& 0\\ 0& {\mu }_{\mathrm{r},\mathrm{h}}\end{array}\right),{ \mu }_{\mathrm{r},2}=\left(\begin{array}{cc}{\mu }_{\mathrm{r},\mathrm{h}}& 0\\ 0& {\mu }_{\mathrm{r},\mathrm{e}}\end{array}\right).$$

(3)

With regard to the magnetic characteristics of FSMA, it is obvious that the maximum error will occur in the magnetic curve region with the highest difference of magnetic permeability (denoted as region I in Fig. 4b). In order to make the results comparable through normalization, a bilinear approximation is chosen for the anisotropic magnetic characteristics (data from [29]) of the FSMA sample (see Fig. 4b). Input parameter sets were chosen according to the literature and typical values (see Table 1). Regarding typical sensor dimensions, certain parameter combinations are not possible at all, but are included for the sake of completeness.

Table 1 Chosen parameter values and ranges for simulation input

With the geometry acc. to Fig. 4a, certain parameter combinations lead to geometric similar field problems with identic results when normalized. Since the ratio of the input values is of importance, the number of parameter variations can be reduced. In our case, the projected twin variant width ${l}_{\mathrm{t}\mathrm{w}}^{{\prime}}$ was held constant, while the other parameters were varied. Furthermore, the evaluation with an equal volume fraction of twin variants (ratio 1:1, $\xi =0.5$) is sufficient, since the maximum error is evaluated. The simulations were carried out using the COMSOL Multiphysics AC/DC package. An exemplary progression of the measurement error of the measured flux density $\Delta {B}_{x}={B}_{x}\left(z\right)-{\overline{B}}_{x}$ along the $z$-axis is shown in Fig. 4c, computed for a fixed ratio between residual air gap and twin boundary length and varying sensor distances displayed within the diagram. The results of $\Delta {B}_{x}$ were normalized average of the applied uniaxial magnetic flux density $\overline{B}_{x}$. The influence of the stray fields on the magnitude of close to the sample is visible. With increasing distance, the deviation from the average value decays. For the evaluation of more parameter combinations, consider Fig. 4d. The absolute values of the maximum relative measurement errors

$$e=\mathrm{max}\left[\left|\frac{\mathrm{max}\left({B}_{x}\left(z\right)\right)-\overline{B}_{x}}{\overline{B}_{x}}\right| ,\left|\frac{\overline{B}_{x}-\mathrm{min}\left({B}_{x}\left(z\right)\right)}{\overline{B}_{x}}\right|\right]$$

(4)

are shown. For the sake of a better comparability, results are displayed in normalized form. On the abscissa, ${d}_{\mathrm{s}\mathrm{e}\mathrm{n}\mathrm{s}}$ was normalized to the projected twin variant width ${l}_{\mathrm{t}\mathrm{w}}^{{\prime}}$. The same applies for the residual air gap ${d}_{\mathrm{r}\mathrm{e}\mathrm{s}}$ in the family of curves. Note that these results only estimate the geometrical conditions for a local flux density measurement. The nonuniform magnetization, which additionally occurs with increasing air gap, is not considered in the shown simulation approach.

From the results, the following conclusions can be derived: the relation between projected twin variant width ${l}_{\mathrm{t}\mathrm{w}}^{{\prime}}$ and sensor distance ${d}_{\mathrm{s}\mathrm{e}\mathrm{n}\mathrm{s}}$ determines if a stray field of a single-variant or the averaged sample stray field is measured. For narrow air gaps, whose length is small compared to the twin variant width, the resulting error is unacceptable, since ${d}_{\mathrm{s}\mathrm{e}\mathrm{n}\mathrm{s}}<{l}_{\mathrm{t}\mathrm{w}}^{{\prime}}$. The stray field influence decreases with increasing sensor distance and air gap width. For a rule of thumb, the sensor distance must be at least equal to the expected maximum twin variant width. Since the actual size twin variant is unknown, a local measurement of the magnetic flux density is not possible. Hence, a different measurement procedure is necessary, overcoming the aforementioned issues in measurement within closed magnetic circuits.

Proposed Measurement Procedure

Approach and Quantities at Component Level

Since the unknown twin structure and the sample shape both lead to a nonuniform magnetization in practical (closed-circuit) setups, we propose to measure magnetic component quantities instead of localized field quantities. Consequently, the internal twin structure is neglected by treating the sample as a lumped element. This approach seems to be appropriate with regard to the intended use of the characterization data for actuator-level modeling. In addition, this approach consistently transfers the measurement procedure from the mechanical domain to the magnetic domain. In other words, such as force $F$ and displacement $u$, both corresponding to component quantities in the mechanical domain, the equivalent component quantities in the magnetic domain, namely magnetic flux $\Phi$ and magnetic voltage ${V}_{\mathrm{m}}$ are measured.

In this work, they are derived for a particular load case having the most relevance for actuation [30], depicted in Fig. 5, including the relevant component dimensions. The component is loaded magnetically along its shortest (x-axis here) and mechanically along its longest dimension (z-axis here). The corresponding effective stress ${\tilde{\sigma}}$ and strain ${\tilde{\varepsilon}},$ are computed in the following manner (with ${A}_{\mathrm{F}}$ —loaded component surface and ${l}_{0}$—initial component length):

$${\tilde{\sigma}}=\frac{F}{{A}_{\mathrm{F}}},$$

(5)

$${\tilde{\varepsilon}}=\frac{u}{{l}_{0}}.$$

(6)

In this load case, only the magnetic flux through the surface ${A}_{\Phi }$ is assumed to be relevant for coupling and can be expressed by the surface integral of the magnetic flux density normal to that surface

$$\Phi ={\iint }_{A}\mathbf{B}\cdot \mathrm{d}\mathbf{A}\approx {B}_{x}{A}_{\Phi }.$$

(7)

As long as the area $A$ remains spacial- and time-invariant, the expression can be simplified to a scalar equation. By splitting up Ampère's law in sections, the magnetic voltage ${V}_{\mathrm{m}}$ can be defined as line integral between two points P₁ and P₂ [31], assuming equipotential surfaces on either end side:

$${V}_{\mathrm{m}}={\int }_{{P}_{1}}^{{P}_{2}}\mathbf{H}\cdot \mathrm{d}\mathbf{s}\approx {H}_{x}d.$$

(8)

As a result, the magnetic flux becomes a function of magnetic voltage and displacement.

A conceptual schematic of the corresponding setup is shown in Fig. 6. Its principle mechanical structure is similar to the magneto-mechanical setups published in the literature, shown in Fig. 3, but with a closed-circuit structure. The proposed measurement might be understood as an adapted hysteresigraph with a simultaneous mechanical load application. Further details are explained in the following subsections.

Fig. 6

Setup concept for the proposed measurement principle

Measurement of Magnetic Flux

The magnetic flux $\Phi$ passing through the surface ${A}_{\Phi }$ can advantageously be measured with a thin induction coil sensor close to the component surface. Depending on the chosen technology, residual air gaps in the range of 0.1 mm and below are possible in this way. Both coil contour and surface area should match well with those of the sample surface since, unlike as for hard magnetic materials, flux contributions around edges cannot be corrected. In this regard, single turn coils are required. However, using a coil on either side increases sensitivity by factor two and allows for equalizing small geometrical inaccuracies. By integrating the induced electric voltage ${V}_{\mathrm{i}\mathrm{n}\mathrm{d}}$ over time, the magnetic flux through the coil can be determined by

$${\Phi }_{\mathrm{C}\mathrm{o}\mathrm{i}\mathrm{l}}=\frac{1}{N}\int {V}_{\mathrm{i}\mathrm{n}\mathrm{d}} \mathrm{d}t.$$

(9)

We assume that the average magnetic flux density ${\tilde{B}}$ passing through the coil surface ${A}_{\mathrm{C}\mathrm{o}\mathrm{i}\mathrm{l}}$ is equal to the average magnetic flux density through the sample surface ${A}_{\Phi },$

$${\tilde{B}} =\frac{{\Phi }_{\mathrm{C}\mathrm{o}\mathrm{i}\mathrm{l}}}{{A}_{\mathrm{C}\mathrm{o}\mathrm{i}\mathrm{l}}}\approx \frac{\Phi }{{A}_{\Phi }\left(u\right)}.$$

(10)

In this regard, the corresponding flux needs to be corrected by the actual component geometry. Due to axial displacement, the permeated surface ${A}_{\Phi }$ needs to be considered:

$$\Phi ={\tilde{B}}{A}_{\Phi }\left(u\right)={\tilde{B}}\cdot {l}_{0}\left(1+u\right)\cdot w.$$

(11)

Unlike as in typical closed-circuit setups, the investigated component is mechanically unconstrained on its lateral faces. A magnetic measurement under axial mechanical loading or constraining is therefore possible.

Measurement of Magnetic Voltage

As outlined, the average magnetic field ${\tilde{H}}$ in the sample cannot be measured directly. Due to the relatively low maximum permeability ${\mu }_{\mathrm{r},\mathrm{m}\mathrm{a}\mathrm{x}}\approx 40$ of the investigated FSMA components (cf. Fig. 4b), the pole faces of the electromagnet can be assumed as equipotential surfaces of constant scalar magnetic potential $\psi$ [21]. This assumption is valid as long as their physical size is large compared to the magnetically loaded sample dimension $d,$ and its magnetic permeability is high compared to the sample. The last condition implies that the core material of the magnetic poles remains unsaturated, even if the FSMA component saturates. For the present case, this condition is fulfilled, since the core material (electrical steel) exhibits a higher saturation magnetic flux density than the FSMA component.

The magnetic potential difference between the pole faces (magnetic voltage ${V}_{\mathrm{m},\mathrm{g}\mathrm{a}\mathrm{p}}$) can be computed from the applied magnetic field ${H}_{0},$ measured by a Hall probe, and the total air gap length ${d}_{\mathrm{g}\mathrm{a}\mathrm{p}}.$ In absence of any currents, the magnetic field is a conservative field ($\oint \mathbf{H}\cdot \mathrm{d}\mathbf{s}=0$) and the magnetic voltage drop across the component is equal to

$${V}_{\mathrm{m}}={V}_{\mathrm{m},\mathrm{g}\mathrm{a}\mathrm{p}}-2{V}_{\mathrm{m},\mathrm{r}\mathrm{e}\mathrm{s}}={H}_{0}{d}_{\mathrm{g}\mathrm{a}\mathrm{p}}-2\frac{{\tilde{B}}}{{\mu }_{0}}{d}_{\mathrm{r}\mathrm{e}\mathrm{s}}\left(u\right),$$

(12)

where $2{V}_{\mathrm{m},\mathrm{r}\mathrm{e}\mathrm{s}}$ is the sum of the magnetic voltages across the two remaining residual air gaps on either side. For its computation, its width ${d}_{\mathrm{r}\mathrm{e}\mathrm{s}}$ as well as the average flux density ${\tilde{B}}$ are necessary. While the latter quantity is known from the measurement of $\Phi$ (see Eq. (10)), the former changes depending on the sample state. Assuming a volume constancy during the twin boundary motion, the length ${d}_{\mathrm{r}\mathrm{e}\mathrm{s}}$ can be expressed as a function of axial displacement:

$${d}_{\mathrm{r}\mathrm{e}\mathrm{s}}\left(u\right)=\frac{1}{2}{d}_{\mathrm{g}\mathrm{a}\mathrm{p}}-\frac{1}{2}\underset{d}{\underbrace{{{d}_{0}\left(1-\frac{u}{{l}_{0}}\right)}}}.$$

(13)

Hence, the measurement of the magnetic voltage is traced to a dimensional measurement. The average magnetic field strength ${\tilde{H}}$ might be computed from

$${\tilde{H}}=\frac{{V}_{\mathrm{m}}}{d}.$$

(14)

Magneto-Mechanical Test Setup

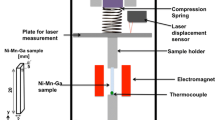
A schematic of the used magneto-mechanical test setup developed and built by the authors is depicted in Fig. 7. Main elements are a laboratory-scale electromagnet for the generation of the exciting magnetic field, a dedicated sample holder, sensors and respective signal conditioners for magnetic and mechanical loads, an assembly for the mechanical load application and an automated computer-based data acquisition and control system (not shown here) implemented in LabVIEW. An in-house build electromagnet with laminated core generates a magnetic field in the air gap and is energized by a bipolar current source using a power amplifier (NF 4520A). The coil current I is measured using a precision 4-wire Manganin shunt (Isabellenhütte PBV 0.005) and an isolated signal conditioner (Dataforth SCM5B40). For the narrow air gaps as applied in the following experiments, magnetic flux densities up to 2 T can be attained in air. The sample is held in place with a machined nonmagnetic sample holder made of aluminum. The pole faces of the electromagnet, together with two polyimide foil assemblies, form a sample guidance and carry the field coil at the same time. Each foil assembly consists of two layers of adhesive polyimide tape enclosing a single turn induction coil sensor (Ø0.05-mm enameled copper wire) and has a thickness of approx. 120 µm. The overall air gap due to sample holder and induction coil sensors was determined to 2.3 ± 0.05 mm in mounted state using a feeler gauge. Both search coils are connected electrically in series.

Fig. 7

Schematic structure of the used test setup for the presented magneto-mechanical characterization procedure

The magnetic flux through these search coils is measured by a digital fluxmeter (M-Pulse M-Flux 1000). A slot in the sample holder allows for the measurement of the applied uniaxial magnetic flux density ${B}_{0}={\mu }_{0}{H}_{0}$ with a commercial Hall probe (Projekt Elektronik AS-NTP). The assembly for mechanical loading consists of a linear voice coil motor rigidly coupled to a strain gauge load cell (ME Meßsysteme KD24s) and a nonmagnetic push rod made of a titanium alloy. Displacement is measured with an optical triangulation displacement sensor (MicroEpsilon ILD 2300-2) on the motor mover. Depending on the chosen feedback for the motor controller (Galil DMC-31012), either force or displacement can be controlled. All measured quantities are put out by the respective signal conditioner as analog signals. They are captured with low latency compared to the applied excitation signal frequency using a PC-based 16-bit data acquisition system (Measurement Computing USB-1616HS-4). The same system provides analog set points for both motor controller and power amplifier.

Experimental Verification and Application

Investigated Samples and Test Procedure

A NiMnGa sample from Goodfellow (alloy composition Ni₅₀Mn₂₈Ga₂₂, original manufacturer ETO Magnetic) with dimensions of (14.63 × 2.97 × 1.90) mm³ in compressed and (15.51 × 2.97 × 1.78) mm³ in extended state was investigated. As magnetic reference, a Nickel sample of high purity was prepared with dimensions close to FSMA component (15.21 × 3.11 × 1.85) mm³. The components were magnetized along the axis of their shortest dimension.

Each magnetic test procedure started with a mechanical resetting of the FSMA sample with an average compressive stress of ${\tilde{\sigma}}=5$ MPa in order to generate a macroscopic single-variant sample. While maintaining this load, a degaussing (sinusoidal excitation field with decreasing magnitude) was performed in order to remove remanence in core and sample. By resetting the integrator subsequently, an eventual offset in the flux measurement is removed. Afterwards, the prestress was decreased to 0.5 MPa which is the approximate twinning stress. This position represents the reference position for the following measurement since the contribution of elastic displacement is expected to be low. The excitation signal frequency was chosen to be below 1 Hz. At this frequency, no dynamic effects of the involved components are to be expected and the measurements can be considered as quasistatic.

Verification of the Proposed Measurement Procedure

The verification of the magnetic measurement procedure is a necessary precondition for its application to FSMA. It is divided into two subsequent steps:

• I. Calibration of the flux measurement system and

• II. Comparison of measured quantities with a reference sample of known magnetic properties.

Besides calibrating the electronic fluxmeter with its internal voltage–time reference, the effective coil surface area needs to be determined. Therefore, sample holder and a Hall probe were put into the air gap of the electromagnet without a sample. Due to the small width of the air gap, the field uniformity within the volume of interest is assumed to be sufficiently high. The electromagnet was excited with a sinusoidal current of fixed frequency and both magnetic flux $\Phi$ through the coils and flux density ${B}_{0}$ in the center of the volume were measured.

An overall coil surface area $N{A}_{\mathrm{Coil}} = 93\,\mathrm{mm}^{2}$ was determined by matching both curves (solid lines in Fig. 8). This result was confirmed optically by analyzing micrographs of both coils using an image processing software (Olympus Stream Essentials) captured with the corresponding light microscope (Olympus SZX12). The relative error between the optically and electrically determined areas was found to be below 1% indicating that contributions of parasitic wire loops are low. Hence, a proper function of the flux measurement system was confirmed.

Fig. 8

Comparison between simulated and measured magnetic flux density ${B}_{0}$ measured in the center of the sample volume and the surface magnetic flux density $\Phi /{A}_{\Phi }$ in air (without sample)

The second step involves a verification of the measurement principle by calibrating the measured magnetic flux and the applied magnetic field by a sample of known magnetic properties. Unlike twinned NiMnGa, Nickel can be considered as homogenous and isotropic. Since the sample geometry are known, a comparison between the measured effective ${\tilde{B}}({\tilde{H}})$ curves and material curve $B(H)$ from the literature is feasible. The results are shown in Fig. 9 in the first two curves. The main error between these curves is the error in magnitude of saturation magnetic flux density of about 10%. Another error in the slope is visible in the range between 0 and 30 kA/m which will be explained below. In order to determine the error source, an FEA of the corresponding magnetostatic field problem was performed. The three-dimensional FE model considers sample, poles, magnetic yoke and excitation coils. Since the magnetic hysteresis of both Nickel and core material is rather small and the core is reasonably sheared, their magnetic hysteresis can be neglected. Furthermore, since core saturation starts at much higher currents (cf. Fig. 8) it is possible to assume a constant magnetic permeability for the core material within the FE model, drastically reducing the computation time. For the calibration of the model, the measured ${B}_{0}(I)$ curves in air, shown in Fig. 8, were compared to those in a model without a Nickel sample at slightly varied air gaps (dashed lines in Fig. 8). A main air gap of 2.3 mm and parasitic air gaps of 50 µm between yoke and pole shoes showed good agreement to measurement corresponding well with the physical dimensions of the sample holder and the expected surface roughness of the laser-cut laminated sheet core, respectively. Due to the good agreement, the model was then extended with the Nickel sample. The $B(H)$ material curve of Nickel was derived from Ref. [32] (digitized data from [33]). A comparison between measured and simulated characteristics for the resulting effective ${\tilde{B}}({\tilde{H}})$ curves is also visible from Fig. 9. Good agreement in terms of saturation magnetic flux density was observed, verifying that the flux is captured correctly. However, this flux does not correspond to the effective flux through the sample and the main error source are flux contributions through the other sample faces. Further discussion on this error can be found in “Error Discussion” section. The differences in slope $\mathrm{d}{\tilde{B}}/\mathrm{d}{\tilde{H}}$ is likely caused by the uncertainty of the measured total air gap length ${d}_{\mathrm{g}\mathrm{a}\mathrm{p}}$, since for high magnetic permeabilities, the slope of the ${\tilde{B}}({\tilde{H}})$ curve is strongly affected by slight deviations in the range of a few hundredths of mm, corresponding to the mechanical measurement accuracy. Furthermore, the assumed material curve $B(H)$ from the literature may differ from the one of the investigated sample.

Fig. 9

Comparison between reference material curve $B(H)$ for Nickel, measured effective ${\tilde{B}}\left({\tilde{H}}\right)$ curve, and simulated ${\tilde{B}}\left({\tilde{H}}\right)$ and for the investigated Nickel sample. Reference data are derived from the literature [32] (digitized data from [33])

Application of the Measurement Principle to FSMA

After calibration and validation, the measurement principle was applied to the FSMA component. Below, two different load cases are presented. For the sake of a better interpretation, the effective material curves are depicted rather than component quantities. Firstly, a set of curves ${\tilde{B}}\left({\tilde{H}}, {\tilde{\varepsilon}}=\mathrm{c}\mathrm{o}\mathrm{n}\mathrm{s}\mathrm{t}.\right)$ for a constrained component at different strains is shown in Fig. 10. Secondly, a set of curves ${\tilde{B}}\left({\tilde{H}}, {\tilde{\sigma}}=\mathrm{c}\mathrm{o}\mathrm{n}\mathrm{s}\mathrm{t}.\right)$ for a constant loading is shown in Fig. 11. A discussion of the results follows in the subsequent section.

Fig. 10

Measured effective magnetic characteristics ${\tilde{B}}\left({\tilde{H}}\right)$ for the investigated FSMA sample at different effective strain levels (averaged over two cycles)

Fig. 11

Measured effective magnetic characteristics ${\tilde{B}}\left({\tilde{H}}\right)$ for the investigated FSMA sample for two constant compressive loadings (averaged over two cycles)

Discussion

Error Discussion

Regarding the simulation results for Nickel, the major error source for ${\tilde{B}}$ and hence for $\Phi$ is the field nonuniformity in the component caused by flux concentration, i.e., the flux ${\Phi }_{\mathrm{s},1}$ and ${\Phi }_{\mathrm{s},2}$ passing through the side faces of the component which is not captured by the induction coil sensor (see subfigure in Fig. 12a). In comparison, the difference between surface and measured flux is only a minor error source. Due to the unknown microstructure, an error estimation for FSMA is only possible in the absence of twin boundaries, i.e., for single-variant states. For an error estimation for the FSMA components, the three-dimensional FE model introduced in the last section used for Nickel was adapted. A magnetic scalar potential problem solution was used in order to simplify the problem solution in favor for a finer meshing. The model considers sample and magnetic poles, but neither the excitation coils nor the back iron. Instead of a piecewise linear approximation, as shown in Fig. 4b a global numerical approximation function for the magnetic permeabilities ${\mu }_{\mathrm{r}}(H)$ was implemented here, derived from simple approximation functions of easy and hard axis:

Fig. 12

Simulation results of relative errors of $\Delta \Phi /{\Phi }_{\mathrm{e}\mathrm{f}\mathrm{f}}$ (a) and ${\Delta V}_{\mathrm{m}}/{V}_{\mathrm{m},\mathrm{e}\mathrm{f}\mathrm{f}}$ (b) depending on volume average magnetic flux density $\overline{B}_{x}$ and magnetic field strength ${\overline{H}}_{x},$ respectively. Data were gained in a FEA with the assumed FSMA material curves according to Eq. (15). The subfigure in (a) indicates the side faces of additional (not tracked) flux contributions. The subfigure in (b) shows the simulation results for ${\tilde{B}}\left({\tilde{H}}\right)$ and $\overline{B}_{x}({\overline{H}}_{x})$

$${B}_{\mathrm{e},\mathrm{h}}\left(H\right)={\mu }_{0}H+{J}_{\mathrm{s}\mathrm{a}\mathrm{t}}\mathrm{tanh}\left(\frac{H}{{H}_{\mathrm{s}\mathrm{a}\mathrm{t},\mathrm{e},\mathrm{h}}}\right).$$

(15)

Parameters were chosen to ${J}_{\mathrm{s}\mathrm{a}\mathrm{t}}=0.68 \mathrm{T},\;{H}_{\mathrm{s}\mathrm{a}\mathrm{t},\mathrm{e}}=10.8 \mathrm{k}\mathrm{A}/\mathrm{m}$ and ${H}_{\mathrm{s}\mathrm{a}\mathrm{t},\mathrm{h}}=270 \mathrm{k}\mathrm{A}/\mathrm{m},$ corresponding to typical magnetic characteristics to be expected. An orthotropic magnetic behavior was considered, as done in [34] where the y-axis is always assumed to be magnetically hard. In compressed ($\xi =0$ and $c\parallel z$) and elongated state ($\xi =1$ and $c\parallel x$), the corresponding magnetic permeability tensors read in Cartesian coordinates:

$$ \begin{gathered} {\varvec{\upmu}}^{{{\text{comp}}}} = \mu _{0} \left( {\begin{array}{*{20}c} {\mu _{{\text{h}}} } & 0 & 0 \\ 0 & {\mu _{{\text{h}}} } & 0 \\ 0 & 0 & {\mu _{{\text{e}}} } \\ \end{array} } \right){\text{and}} \hfill \\ {\varvec{\upmu}}^{{{\text{elong}}}} = \mu _{0} \left( {\begin{array}{*{20}c} {\mu _{{\text{e}}} } & 0 & 0 \\ 0 & {\mu _{{\text{h}}} } & 0 \\ 0 & 0 & {\mu _{{\text{h}}} } \\ \end{array} } \right). \hfill \\ \end{gathered} $$

(16)

For the sake of simplicity, the shape change was not considered here. As a measure for the error, the effective flux ${\Phi }_{\mathrm{e}\mathrm{f}\mathrm{f}}$ and the effective magnetic voltage ${V}_{\mathrm{m},\mathrm{e}\mathrm{f}\mathrm{f}}$ are defined as

$${\Phi }_{\mathrm{e}\mathrm{f}\mathrm{f}}=\overline{B}_{x}\cdot {A}_{\Phi },$$

(17)

$${V}_{\mathrm{m},\mathrm{e}\mathrm{f}\mathrm{f}}={\overline{H}}_{x}\cdot d,$$

(18)

where $\overline{B}_{x}$ and ${\overline{H}}_{x}$ are the volume average of $\mathbf{B}$ and $\mathbf{H}$ along the magnetic loaded direction (x-axis here). The respective relative errors $\Delta \Phi =\Phi -{\Phi }_{\mathrm{e}\mathrm{f}\mathrm{f}}$ and $\Delta {V}_{\mathrm{m}}={V}_{\mathrm{m}}-{V}_{\mathrm{m},\mathrm{e}\mathrm{f}\mathrm{f}}$ are displayed normalized in Fig. 12, representing the margins of error for both extreme cases of single-variant samples (compressed and elongated). The average magnetic flux in the sample is underestimated and an average error of approx. 10% is visible. However, for the most interesting curve region (beyond the effective saturation flux density of the easy axis), the relative error band of $\Phi$ becomes narrow and almost independent on sample state. The same applies for the relative error in ${V}_{\mathrm{m}},$ which is very large for the region of high permeability, but strongly decreasing above the effective saturation field strength of the easy axis. Its effect on the difference between ${\tilde{B}}\left({\tilde{H}}\right)$ and $\overline{B}_{x}\left({\overline{H}}_{x}\right)$ is therefore rather low, as visible from the inset in Fig. 12b. Hence, the main error source remains the flux contributions through the side faces.

Besides these principle errors, it is worth noting that the measurement resolution is a limiting factor. Since only the use of single turn coils are possible, the induced voltage is on a very low absolute level. Even small input voltage fluctuations, e.g., due to thermoelectric voltages, may affect the measurement significantly in terms of drift and cannot be compensated. Furthermore, noise level is high. There are a few other systematic and random error sources which cannot be addressed in this paper. Among others, this includes deviations in coil position, shape and size, the influence of a nonideal sample shape, exact values of lateral strain and effects due to sample tilting. A dedicated study with a sensitivity analysis would be necessary in order to determine margins of error.

Option of Error Correction

Considering again Fig. 12, it turns out that the flux contributions on the side faces remain almost constant relative to measured flux and almost independent from the sample state (and hence from the volume fraction of variants). This is especially true for ${\tilde{H}}>50 \mathrm{k}\mathrm{A}/\mathrm{m}.$ In this regard, a fudge factor might be used, although the authors are aware of the frequent misuse of such factors. However, in our case the factor is motivated physically and can directly derived from magnetostatic simulations whose results are in accordance with measurements. The “corrected” effective magnetic flux density can be computed in the following manner:

$${{\tilde{B}}}^{{{\prime}}}={\tilde{B}}\cdot {f}_{\mathrm{c}}.$$

(19)

Note that for the computation of ${\tilde{H}},\;{\tilde{B}}$ must not be corrected since in Eq. (12), the air gap flux density is taken into account. The measured effective material curves shown in Fig. 10, ${{\tilde{B}}}_{\mathrm{e}}\left({\tilde{H}}\right)$ and ${{\tilde{B}}}_{\mathrm{h}}\left({\tilde{H}}\right)$ for easy and hard axis, respectively, were both corrected by the fudge factor ${f}_{\mathrm{c}}=1.075$ corresponding to an average error in magnetic flux (see Fig. 12a). The results were compared to single-variant measurements from the literature, as can be seen from Fig. 13. A good agreement was attained, indicating that the correction of an almost constant flux through the side faces is feasible. Note that the significance of this comparison is limited to measurements in a single-variant state.

Fig. 13

Comparison between the measured effective magnetic characteristics ${{\tilde{B}}}^{{\prime}}\left({\tilde{H}}\right)$ from Fig. 10 corrected by a fudge factor of ${f}_{c}=1.075$ of the investigated FSMA sample in single-variant state and $B(H)$-curves from the literature [29]

The fudge factor needs to be understood as a component behavior, individually determined by simulation. It depends on component aspect ratio, residual air gap width, pole geometry and weakly on magnetic properties, which is the basic assumption beyond the correction. In theory, for components whose dimensions $l,w\gg d,$ the side faces might be small compared to ${A}_{\Phi }$ and the corresponding flux might be ignored, hence ${f}_{\mathrm{c}}\approx 1.$ For the practically used sample sizes, however, the fudge factor is expected to be greater than 1.

Interpretation and Application of Results

It should be emphasized that the results need to be understood as effective, quasistatic component characteristics. They are only valid for the applied load case and the particular component investigated.

Since the purpose of the presented measurement method is to provide valid data for actuator-level modeling, their physical interpretability is important. Different arguments support this interpretability: Firstly, good agreement in terms of the saturation magnetic flux could be observed, independent from the loading or constraining condition. Secondly, a linear scalar superposition of magnetic characteristics between single-variant states on volume fraction of variants,

$${\tilde{B}}\left({\tilde{H}},\xi \right)={{\tilde{B}}}_{\mathrm{h}}\left({\tilde{H}}\right)+\xi \left({{\tilde{B}}}_{\mathrm{e}}\left({\tilde{H}}\right)-{{\tilde{B}}}_{\mathrm{h}}\left({\tilde{H}}\right)\right),$$

(20)

as published by different authors [20, 35], could be confirmed. Thirdly, the measured difference in magnetic energy, if the flux error is corrected by the fudge factor (${f}_{\mathrm{c}}=1.075$) found in the last section and taking into account the sample volume of ${V}_{\mathrm{F}\mathrm{S}\mathrm{M}\mathrm{A}}=82.5 {\mathrm{m}\mathrm{m}}^{3},$ the measured value corresponds to a magnetic anisotropy constant of $\Delta {w}_{\mathrm{m}\mathrm{a}\mathrm{g}}\approx {K}_{\mathrm{U}}=166\, \mathrm{kJ}/{\mathrm{m}}^{3},$ agreeing well with values for similar alloy compositions in the literature [36].

Summary

In this paper, a novel procedure for the macroscopic magnetic characterization of FSMA under mechanical loading was introduced. Its development was necessary since the measurement procedures presented up to now do not consider the requirements coming from the microstructure of the material and the typical sample shape. The presented method fulfills the requirements specified in “Preliminary Considerations” section in the following manner:

• I. Effective absolute quantities are measured: the magnetic flux $\Phi$ through the sample surface and the magnetic voltage ${V}_{\mathrm{m}}$ across the sample.

• II. A macroscopically almost uniform field is applied by a closed magnetic circuit setup with a narrow air gap. Changes of sample geometry are considered.

• III. Magnetic measurement under mechanical load is enabled in a setup which corresponds to the typical magnetic load case in actuators.

• IV. By evaluating the magnetic flux and voltage, an averaging over all occurring twin variants, independent from their size and distribution, is achieved.

The presented measurement approach is consistent to the one used for mechanical quantities and delivers effective component data which can directly be used for modeling. In contrast to other experimental techniques, a transferability of results gained in a laboratory-scale test setup to typical narrow air gap systems is feasible. Even the test method itself is transferable, it allows to measure effective magnetic component characteristics within drive units. The main error source presented in the last section is the flux contribution through the side faces which are not captured by the test method. This error is physically caused by the sample shape and is approx. 10%. By using the proposed correction method, good agreement to data in the literature for single-variant samples is achieved. The data are considered to be physically consistent.