Efficiency Comparison of Quaternions and Spherical Trigonometry Formulas for 3D Rotations

Abstract

There are several methods to perform rotations in space. That is, rotate a vector ${\vec{\text{v}}}$ and an angle θ around an axis in the direction of a vector ${\vec{\text{u}}}$, resulting in the rotated vector ${{\vec{v}^{\prime}}}$. Quaternions are generally used to solve rotation problems because they are considered to have the best computational complexity. However, this work shows that when the data is given in spherical coordinates, the use of spherical trigonometry formulas to solve a rotation, can offer better computational complexity than the quaternion method which is systematically used. Additionally, sometimes when the data is given in spherical coordinates, an abacus is used to solve the rotation problems. The use of abacus makes it possible to observe intermediate results as the rotation goes. Also, the use of spherical trigonometry formulas allows this, however it is not possible to do so using quaternions.

Appendix: Obtaining angles ZUV′ and \({{\varvec{\lambda}}}_{\varvec{v}{^{\prime}}}\)

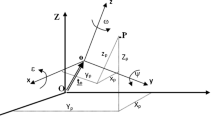
The accounts to be made to obtain the angle $ZUV$ from and of the angle $ZUV$ depend on the location of the triangles formed by points $Z, U$ and $V$ and $Z, U$ and V′. In particular, if divide the unit sphere into two hemispheres from the $\overline{ZU }$ meridian, we can separate the cases depending on whether the triangle formed by $Z, U$ and $V$ is to the left or to the right of the meridian $\overline{ZU }$, and in turn if the triangle formed by $Z$, $U$ and V′ is on the same side (it is saying, in the same hemisphere) or the other.

In the case where the triangle formed by $Z, U$ and $V$ is formed to the right of the $\overline{ZU }$ meridian, the triangle formed by $Z, U$ and V′ will form on the opposite side (as is the case in Fig. 2) if meets the condition

$$ 0 < \theta - ZUV < \pi . $$

(16)

In this case you have:

$$ ZUV^{\prime} = \theta - ZUV, $$

(17)

$$ \lambda_{v^{\prime}} = \lambda_{u} - UZV^{\prime}. $$

(18)

If, on the contrary, the triangle formed by $Z, U$ and $V$ is formed on the same side as the formed by $Z, U$ and V′ (that is, to the right of the $\overline{ZU }$ meridian), which will happen if the condition is not met given by Eq. (16), you have the relationships:

$$ ZUV^{\prime} = ZUV - \theta ;\quad if \quad \theta - ZUV < 0, $$

(19)

$$ ZUV\prime = ZUV + \left( {2\pi - \theta } \right);\quad if \quad\theta - ZUV > \pi , $$

(20)

$$ \lambda_{v^{\prime}} = \lambda_{u} + UZV^{\prime}. $$

(21)

The other possible case for the triangle formed by $Z, U$ and $V$ is that it forms to the left of the $\overline{ZU }$ meridian. In that case, the triangle formed by $Z, U$ and V′ will form a on the opposite side if complies that:

$$ \pi < \theta + ZUV < 2\pi , $$

(22)

in which case we have:

$$ ZUV^{\prime} = 2\pi - \left( {ZUV + \theta } \right), $$

(23)

$$ \lambda_{v^{\prime}} = \lambda_{u} + UZV^{\prime}. $$

(24)

If the condition given by Eq. (22) is not fulfilled (which implies that the triangle formed by $Z, U$ and V′ it is formed on the left side of the $\overline{ZU }$ meridian, just like the triangle formed by $Z, U$ and $V$), the relationships are:

$$ ZUV^{\prime} = ZUV + \theta ;\,if\,\,\theta + ZUV < \pi , $$

(25)

$$ ZUV^{\prime} = ZUV + \left( {\theta + 2\pi } \right);\,if\,\,\theta + ZUV > 2\pi , $$

(26)

$$ \lambda_{v^{\prime}} = \lambda_{u} - UZV^{\prime}. $$

(27)