Computational Analysis of Magnetohydrodynamic Free Convection Flow and Heat Transfer of Non-Newtonian Tangent Hyperbolic Fluid from a Horizontal Circular Cylinder with Partial Slip

Abstract

An analysis is presented for the nonlinear steady boundary layer flow and heat transfer of an incompressible tangent hyperbolic non-Newtonian fluid from horizontal circular cylinder in the presence of thermal and hydrodynamic slip condition. The transformed conservation equations are solved numerically subject to physically appropriate boundary conditions using a second-order accurate implicit finite-difference Keller Box technique. The numerical code is validated with previous studies. The influence of a number of emerging non-dimensional parameters, namely Weissenberg number $(W_{e})$, power law index $(n)$, velocity slip parameter $(\hbox {S}_\mathrm{f})$, thermal jump parameter $(\hbox {S}_\mathrm{T})$, Prandtl number (Pr), magnetic parameter $(M)$ and dimensionless tangential coordinate $(\xi )$ on velocity and temperature evolution in the boundary layer regime are examined in detail. Furthermore, effects of these parameters on surface heat transfer rate and local skin friction are also investigated. Validation with earlier Newtonian studies is presented and excellent correlation achieved. It is observed that velocity, skin friction and heat transfer rate are reduced with increasing Weissenberg number ($W_{e}$), whereas, temperature increases slightly. Increasing power law index ($n$) increases velocity and heat transfer rate but decreases temperature and skin friction. An increase in $S_{f}$, is observed to enhance velocity and heat transfer rate but decreases temperature and local skin friction. Whereas, increasing $S_{T}$, is found to decrease velocity, temperature, skin friction and Nusselt number. The study is relevant to chemical materials processing applications.

Introduction

Analysis of non-Newtonian fluids has been the focus of several investigations during the past few decades because of its extensive engineering and industrial applications. Especially, flow and heat transfer of non-Newtonian fluids play central role in food engineering, petroleum production, power engineering and in polymer solutions and in polymer melt in the plastic processing industries. In nature there are non-Newtonian fluids with different characteristics and consequently various constitutive equations of non-Newtonian fluids have been presented. The use of such constitutive equations leads to more complicated and highly nonlinear systems. The analytic/numerical solutions of such equations present exciting challenges to the mathematicians, physicists, numerical simulists and modelers. Significant attention has been directed at mathematical and numerical simulation of non-Newtonian fluids. Recent investigations have implemented, respectively the Casson model [1], second-order Reiner-Rivlin differential fluid models [2], power-law nanoscale models [3] and Jefferys viscoelastic model [4].

The study of magnetohydrodynamic (MHD) flows is quite interesting and useful because it is used in magnetic wound or cancer tumour treatment causing hypothermia, bleeding reduction during surgeries, targeted transport of drugs using magnetic particles as drug carries and MRI (magnetic resonance imaging) to diagnose the disease. Magnetohydrodynamic refers to the study of the mutual interaction of fluid flow with magnetic fields. MHD viscous flows with heat and mass transfer has emerged as an important field of study in recent times due to its application in several different fields of engineering and technology as well as in astrophysics, geophysics and nuclear sciences [5]. Numerous studies of both an experimental and numerical nature have been communicated regarding magnetohydrodynamic flow in chemical engineering [6–8].

Slip effects have shown to be significant in certain industrial thermal problems and manufacturing fluid dynamics systems. Sparrow et al. [9] presented the first significant investigation of laminar slip-flow heat transfer for tubes with uniform heat flux. Inman [10] further described the thermal convective slip flow in a parallel plate channel or a circular tube with uniform wall temperature. These studies generally indicated that velocity slip acts to enhance heat transfer whereas temperature jump depresses heat transfer. Many studies have appeared in recent years considering both hydrodynamic and thermal jump effects. Interesting articles of relevance to process mechanical engineering include Larrode et al. [11] who studied thermal/velocity slip effects in conduit thermal convection. Spillane [12] who examined sheet processing boundary layer flows with slip boundary conditions and Crane and McVeigh [13] who studied slip hydrodynamics on a micro-scale cylindrical body. Further studies in the context of materials processing include Yu and Ameel [14], Crane and McVeigh [15]. Studies of slip flows from curved bodies include Bég et al. [16] who examined using network numerical simulation the magneto-convective slip flow from a rotating disk, Wang and Ang [17] who studied using asymptotic analysis the slip hydrodynamics from a stretching cylinder. Results assuming that the slip solution was a perturbation of the no-slip solution predicted that the slip conditions would not affect shear stress, boundary-layer thickness, or heat transfer [18]. In addition semi-analytic results suggested that heat transfer would change in the presence of slip flow [19]. Additional computations proved that shear stress would as well change [20]. Several explanations were offered for the contradictory results. The solutions to other viscous flows considered similar to boundary layer flows, such as Couette, Poiseuille, and Rayleigh flows, showed a change in heat transfer and shear stress [21]. This led to the suggestion that the mathematical and experimental techniques available at the time lacked the accuracy necessary to capture the result. The suggestion was also made that the boundary-layer equations were not valid for slip flows. Two separate arguments were made. The first was that the second-order slip boundary condition was of the same order as the terms that were discarded from the Navier–Stokes equations to create the boundary-layer equations [22]. A second problem was the Reynolds number scaling of the boundary-layer equations. Using the definitions of viscosity and the speed of sound, the Knudsen number can be found as a function of the Mach number and Reynolds number [23]:

$$\begin{aligned} Kn_x \alpha \frac{M}{\mathrm{Re}_x} \end{aligned}$$

(I)

This scaling indicates that an incompressible boundary layer, with a Reynolds number of 500 or greater and a Mach number of less than 0.3, is unlikely to have a Knudsen number large enough for slip to appear. Several decades after these initial results, the development of microelectromechanical systems led to a renewed interest in slip flows [24]. The correct scaling of boundary-layer slip was shown to be based on the boundary-layer thickness and was computed as

$$\begin{aligned} Kn_\delta \alpha \frac{M}{\mathrm{Re}_x} \end{aligned}$$

(II)

This scaling does allow an incompressible boundary layer with a Reynolds number of 500 or greater and a Mach number of less than 0.3 to have a large enough Knudsen number for slip to appear.

An interesting non-Newtonian model developed for chemical engineering systems is the Tangent Hyperbolic fluid model. This rheological model has certain advantages over the other non-Newtonian formulations, including simplicity, ease of computation and physical robustness. Furthermore it is deduced from kinetic theory of liquids rather than the empirical relation. Several communications utilizing the Tangent Hyperbolic fluid model have been presented in the scientific literature. There is no single non-Newtonian model that exhibits all the properties of non-Newtonian fluids. Among several non-Newtonian fluids, hyperbolic tangent model is one of the non-Newtonian models presented by Pop and Ingham [25]. Nadeem et al. [26] made a detailed study on the peristaltic transport of a hyperbolic tangent fluid in an asymmetric channel. Nadeem and Akram [27] investigated the peristaltic flow of a MHD hyperbolic tangent fluid in a vertical asymmetric channel with heat transfer. Very recently, Akbar et al. [28] analyzed the numerical solutions of MHD boundary layer flow of tangent hyperbolic fluid on a stretching sheet.

In many chemical engineering and nuclear process systems, curvature of the vessels employed is a critical aspect of optimizing thermal performance. Examples of curved bodies featuring in process systems include torus geometries, wavy surfaces, cylinders, cones, ellipses, oblate spheroids and in particular, spherical geometries. A number of theoretical and computational studies have been communicated on transport phenomena from cylindrical bodies, which frequently arise in polymer processing systems. Zueco et al [29] examined the multi-physical and chemical transport from cylindrical bodies. Further, non-Newtonian models employed in analyzing convection flows from cylinders include micropolar liquids [30], viscoelastic materials [31], micropolar nanofluids [32] and Casson fluids [1].

The objective of the present study is to investigate the laminar boundary layer flow and heat transfer of a Tangent Hyperbolic non-Newtonian fluid from horizontal circular cylinder. The non-dimensional equations with associated dimensionless boundary conditions constitute a highly nonlinear, coupled two-point boundary value problem. Keller’s implicit finite difference “box” scheme is implemented to solve the problem [33]. The effects of the emerging thermophysical parameters, namely Weissenberg number $(W_{e})$, power law index ($n$), magnetic parameter ($M$), thermal jump $(S_{T})$, velocity slip $(S_{f})$ and Prandtl number (Pr), on velocity, temperature, skin friction number, and heat transfer rate characteristics are studied. The present problem has to the authors’ knowledge not appeared thus far in the scientific literature and is relevant to polymeric manufacturing processes in chemical engineering.

Non-Newtonian Constitutive Tangent Hyperbolic Fluid Model

In the present study a subclass of non-Newtonian fluids known as Tangent Hyperbolic fluid is employed owing to its simplicity. The Cauchy stress tensor, in Tangent Hyperbolic non-Newtonian fluid [25] takes the form:

$$\begin{aligned} \overline{\tau } =\left[ {\mu _\infty +\left( {\mu _0 +\mu _\infty } \right) \tanh \left( {\Gamma \overline{\dot{\gamma }}} \right) ^{n}} \right] \overline{\dot{\gamma }} \end{aligned}$$

(1)

where $\bar{\tau }$ is extra stress tensor, $\mu _\infty$ is the infinite shear rate viscosity, $\mu _0$ is the zero shear rate viscosity, $\Gamma$ is the time dependent material constant, n is the power law index i.e. flow behaviour index and $\bar{\dot{\gamma }}$ is defined as

$$\begin{aligned} \overline{\dot{\gamma }} =\sqrt{\frac{1}{2}\sum _i {\sum _j {\overline{\dot{\gamma }} _{ij} \overline{\dot{\gamma }} _{ji} } } }=\sqrt{\frac{1}{2}\Pi }, \end{aligned}$$

(2)

where $\Pi =\frac{1}{2}trac\left( {gradV+\left( {gradV} \right) ^{T}} \right) ^{2}.$ We consider Eq. (1), for the case when $\mu _\infty = 0$ because it is not possible to discuss the problem for the infinite shear rate viscosity and since we considering tangent hyperbolic fluid that describing shear thinning effects so $\Gamma \bar{\dot{\gamma }}<< 1$. Then Eq. (1) takes the form

$$\begin{aligned} \overline{\tau }= & {} \mu _0 \left[ {\left( {\Gamma \overline{\dot{\gamma }}} \right) ^{n}} \right] \overline{\dot{\gamma }} \nonumber \\= & {} \mu _0 \left[ {\left( {1+\Gamma \overline{\dot{\gamma }}-1} \right) ^{n}} \right] \overline{\dot{\gamma }} \nonumber \\= & {} \mu _0 \left[ {1+n\left( {\Gamma \overline{\dot{\gamma }}-1} \right) } \right] \overline{\dot{\gamma }} \end{aligned}$$

(3)

The introduction of the appropriate terms into the flow model is considered next. The resulting boundary value problem is found to be well-posed and permits an excellent mechanism for the assessment of rheological characteristics on the flow behaviour.

Mathematical Flow Model

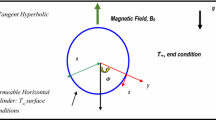
Steady, laminar, two-dimensional, electrically-conducting, incompressible flow of a Tangent Hyperbolic fluid from a horizontal circular cylinder, is considered, as illustrated in Fig. 1. We assume that the fluid is subject to a constant transverse magnetic field, $B_0$, which acts radially i.e. normal to the cylinder surface. The $x$-coordinate (tangential) is measured along the circumference of the horizontal cylinder from the lowest point and the $y$-coordinate (radial) is directed perpendicular to the surface, with $a$ denoting the radius of the horizontal cylinder. $\Phi =x/a$ is the angle of the $y$-axis with respect to the vertical $0\le \Phi \le \pi$. The gravitational acceleration g, acts downwards. Magnetic Reynolds number is assumed to be small enough to neglect the induced magnetic field. When the fluid moves into the magnetic fluid, two major physical effects arise. The first one is that an electric field E is induced in the flow. We assume that the flow is 2D, and $B_0 .\left( {\nabla \times V} \right) =0.$ the current density J is given by Ohm’s law as $J=\sigma \left( {E+V\times B_0 } \right)$. From the charge conservation law, we have $\nabla .J=\sigma \nabla .E+\sigma \nabla .\left( {V\times B_0 } \right) =\sigma \nabla .E+\sigma B_0 .\left( {\nabla \times V} \right) =0$, and $\nabla . E=0$ is satisfied. Neglecting the induced magnetic field also implies $\nabla \times E=0$. Because both of the divergence and the curl of the electric fled are zero, the electric field is zero, and the current density J is given by Ohm’s law as $J=\sigma \left( {V\times B_0 } \right)$. The second effect is dynamic in nature, i.e., a Lorentz force $J\times B_0$, which acts on the fluid and modifies its motion. This results in the transfer of energy from the electromagnetic field to the fluid. Hall current and ionslip effects are also neglected since the magnetic field is weak. We also assume that the Boussineq approximation holds i.e. that density variation is only experienced in the buoyancy term in the momentum equation. Additionally the electron pressure (for weakly conducting fluids) and the thermoelectric pressure are negligible. The radial magnetic field $B_0$ is generated by passing a steady electric current along the longitudinal parallel to the cylinder, where the cylinder edges terminate at perfect electrodes that are connected via a load. The magnetic field, therefore, acts radially to the external boundary layer flow. This has been studied by Nath [34] and Makinde et al. [35]. An alternative technique to achieve the desired magnetic field is through the implementation of a permeable core within the cylinder and a permeable cylinder shell. As such, the magnetic flux lines would close via these circular paths at significant distances from the regime of interest. The “source” of the magnetic flux would be discs of permanently magnetized material between the cylinder and the external flow. In either case, the magnetic field is radial and external to the boundary layer flow regime on the surface of the cylinder. For the hydromagnetic body force term, we follow the standard assumptions that the magnetic field acts transverse to the streamwise direction (the length of the cylinder). An order of magnitude analysis leads to the final linear drag force term for magnetohydrodynamic effects. Such an approach is further discussed by Aleksandrova [36], Ishak et al. [37] and EL-Hakiem [38].

Fig. 1

Physical model and coordinate system

Both horizontal cylinder and the Tangent Hyperbolic fluid are maintained initially at the same temperature. Instantaneously they are raised to a temperature $T_w >T_\infty$, the ambient temperature of the fluid which remains unchanged. In line with the approach of Yih [39] and introducing the boundary layer approximations, the equations for mass, momentum, and energy, can be written as follows:

$$\begin{aligned}&\frac{\partial u}{\partial x}+\frac{\partial v}{\partial y}=0\end{aligned}$$

(4)

$$\begin{aligned}&u\frac{\partial u}{\partial x}+v\frac{\partial u}{\partial y}=\nu \left( {1-n} \right) \frac{\partial ^{2}u}{\partial y^{2}}+\sqrt{2}\nu n\Gamma \left( {\frac{\partial u}{\partial y}} \right) \frac{\partial ^{2}u}{\partial y^{2}}+g\beta \sin \left( {\frac{x}{a}} \right) \left( {T-T_\infty } \right) -\frac{\sigma B_0^2 }{\rho }u\nonumber \\ \end{aligned}$$

(5)

$$\begin{aligned}&u\frac{\partial T}{\partial x}+v\frac{\partial T}{\partial y}=\alpha \frac{\partial ^{2}T}{\partial y^{2}} \end{aligned}$$

(6)

where ${u}$ and ${v}$ are the velocity components in the ${x}$- and $y$- directions respectively, $\nu =\frac{\mu }{\rho }$ is the kinematic viscosity of the tangent hyperbolic fluid, $\beta$ is the coefficient of thermal expansion, $\alpha$ is the thermal diffusivity, $T$ is the temperature, $\uprho$ is the density of the fluid, $\sigma$ is the electrical conductivity, $B_0$ is the externally imposed radial magnetic field (i.e. applied in the y-direction), $\rho$ is the density. The Tangent Hyperbolic fluid model therefore introduces a mixed derivative (second order, first degree) into the momentum boundary layer equation (5). The non-Newtonian effects feature in the shear terms only of Eq. (5) and not the convective (acceleration) terms. The third term on the right hand side of Eq. (5) represents the thermal buoyancy force and couples the velocity field with the temperature field equation (6). The fourth term on the right hand side of Eq. (5) represents the hydromagnetic drag.

$$\begin{aligned} \begin{aligned} {\text {At}}\,y&= 0,\quad u = {N_0}\frac{{\partial u}}{{\partial y}},\quad v = 0,\quad T = {T_w} + {K_0}\frac{{\partial T}}{{\partial y}} \\{\text {As}}\,y&\rightarrow \infty ,\quad u \rightarrow 0,\quad T \rightarrow {T_\infty }\, \\\end{aligned} \end{aligned}$$

(7)

Here $N_{0}$ is the velocity slip factor, $K_{0}$ is the thermal slip factor and $T_\infty$ is the free stream temperature. For $N_{0} = 0 = K_{0}$, one can recover the no-slip case.

The stream function $\psi$ is defined by $u=\frac{\partial \uppsi }{\partial y}$ and $v=-\frac{\partial \uppsi }{\partial x}$, and therefore, the continuity equation is automatically satisfied. In order to render the governing equations and the boundary conditions in dimensionless form, the following non-dimensional quantities are introduced.

$$\begin{aligned} \begin{aligned} \xi&= \frac{x}{a},\quad \eta = \frac{y}{a}Gr^{{1/4}},\quad f = \frac{\psi }{{\nu \xi }}Gr^{{ - 1/4}} ,\quad \theta \left( {\xi ,\eta } \right) = \frac{{T - T_{\infty } }}{{T_{w} - T_{\infty } }} \\ \Pr&= \frac{\nu }{\alpha },\quad Gr = \frac{{g\beta _{1} \left( {T_{w} - T_{\infty } } \right) a^{3} }}{{\nu ^{2} }},\quad W_{e} = \frac{{\sqrt{2} \nu \Gamma xGr^{{3/4}} }}{{a^{3} }},\quad M = \frac{{\sigma B_{0}^{2} a^{2} }}{{\rho \nu \sqrt{Gr} }} \end{aligned} \end{aligned}$$

(8)

All terms are defined in the nomenclature. In view of the transformation defined in Eq. (8), the boundary layer equations (5)–(7) are reduced to the following coupled, nonlinear, dimensionless partial differential equations for momentum and energy for the regime:

$$\begin{aligned}&\left( {1-n} \right) f^{{\prime }{\prime }{\prime }} +ff^{{\prime }{\prime }}-\left( {f^{\prime }} \right) ^{2}+nW_e f^{{\prime }{\prime }}f^{{\prime }{\prime }{\prime }} +\theta \frac{\sin \xi }{\xi }-Mf^{\prime }= \xi \left( {f^{\prime }\frac{\partial f^{\prime }}{\partial \xi }-f^{{\prime }{\prime }}\frac{\partial f}{\partial \xi }} \right) \qquad \end{aligned}$$

(9)

$$\begin{aligned}&\frac{\theta ^{{\prime }{\prime }}}{\hbox {Pr}}+f\theta ^{\prime }=\xi \left( {f^{\prime }\frac{\partial \theta }{\partial \xi }-\theta ^ {\prime }\frac{\partial f}{\partial \xi }} \right) \end{aligned}$$

(10)

The transformed dimensionless boundary conditions are:

$$\begin{aligned} \begin{aligned}&At\quad \eta = 0,\quad f = 0,\quad f' = S_{f} f''\left( 0 \right) ,\quad \theta = 1 + S_{T} \theta '\left( 0 \right) \\&As\quad \eta \rightarrow \infty ,\quad f' \rightarrow 0,\quad \theta \rightarrow 0 \end{aligned} \end{aligned}$$

(11)

Here primes denote the differentiation with respect to $\eta ,\, S_f =\frac{N_0 Gr^{1/4}}{a}$ and $S_T =\frac{K_0 Gr^{1/4}}{a}$ are the non-dimensional velocity and thermal jump parameters respectively. The skin-friction coefficient (shear stress at the cylinder surface) and Nusselt number (heat transfer rate) can be defined using the transformations described above with the following expressions.

$$\begin{aligned} Gr^{-3/4}C_f= & {} \left( {1-n} \right) \xi f^{{\prime }{\prime }}(\xi ,0)+\frac{n}{2}W_e \xi \left( {f^{{\prime }{\prime }}(\xi ,0)} \right) ^{2}\end{aligned}$$

(12)

$$\begin{aligned} Gr^{-1/4}Nu= & {} -\theta ^{\prime }(\xi ,0) \end{aligned}$$

(13)

The location, $\xi \sim 0$, corresponds to the vicinity of the lower stagnation point on the cylinder.

Since $\frac{\sin \xi }{\xi } \rightarrow 0/0$ i.e. 1. For this scenario, the model defined by eqns. (9) and (10) contracts to an ordinary differential boundary value problem:

$$\begin{aligned} \left( {1-n} \right) f^{{\prime }{\prime }{\prime }}+ff^{{\prime }{\prime }}-\left( {f^{\prime }} \right) ^{2}+nW_e f^{{\prime }{\prime }}f^{{\prime }{\prime }{\prime }}+\theta -Mf^{\prime }=0 \end{aligned}$$

(14)

$$\begin{aligned} \frac{1}{\Pr }\theta ^{{\prime }{\prime }}+f\theta ^{\prime }=0 \end{aligned}$$

(15)

The general model is solved using a powerful and unconditionally stable finite difference technique introduced by Keller [40]. The Keller-box method has a second order accuracy with arbitrary spacing and attractive extrapolation features.

Numerical Solution with Keller Box Implict Method

The Keller-box implicit difference method is implemented to solve the nonlinear boundary value problem defined by Eqs. (9)–(10) with boundary conditions (11). This technique, despite recent developments in other numerical methods, remains a powerful and very accurate approach for parabolic boundary layer flows. It is unconditionally stable and achieves exceptional accuracy [40]. This method has been deployed in resolving many challenging, multi-physical fluid dynamics problems. These include hydromagnetic Sakiadis flow of non-Newtonian fluids [41], radiative rheological magnetic heat transfer [42], waterhammer modelling [43], and magnetized viscoelastic stagnation flows [44]. The Keller-box discretization is fully coupled at each step which reflects the physics of parabolic systems—which are also fully coupled. Discrete calculus associated with the Keller-box scheme has also been shown to be fundamentally different from all other mimetic (physics capturing) numerical methods, as elaborated by Keller [40]. The Keller box scheme comprises four stages.

• 1) Decomposition of the $N$th order partial differential equation system to $N$ first order equations.

• 2) Finite difference discretization.

• 3) Quasilinearization of non-linear Keller algebraic equations and finally.

• 4) Block-tridiagonal elimination solution of the linearized Keller algebraic equations

Stability and Convergence of Keller Box Method

In laminar boundary layer calculations, the wall shear stress parameter $v\left( {x,0} \right)$, is commonly used as the convergence criterion [45]. This is probably because in boundary layer calculations, it is found that the greatest error usually appears in the wall shear stress parameter. Different criterion is used for turbulent flows problem. Throughout the study of this paper, the convergence criterion is used as it is efficient, suitable and the best. Calculations are stopped when

$$\begin{aligned} \left| {\delta v_0^{(i)} } \right| <\varepsilon _1 \end{aligned}$$

where $\varepsilon _1$ is a small prescribed value.

Numerical Results and Interpretation

Comprehensive solutions have been obtained and are presented in Tables 1, 2, 3, 4 and 5 and Figs. 2, 3, 4, 5, 6, 7, 8, 9, 10, 11 and 12. The numerical problem comprises two independent variables $(\xi ,\eta )$, two dependent fluid dynamic variables $(f,\theta )$ and five thermo-physical and body force control parameters, namely, $W_\mathrm{e},\, n,\, \hbox {S}_\mathrm{f},\, \hbox {S}_\mathrm{T},\, \hbox {M},\, \hbox {Pr},\, \xi$ . The following default parameter values i.e. $W_{e}= 0.3,\, \hbox {n} = 0.3,\, \hbox {S}_\mathrm{f}, = 0.5,\, \hbox {S}_\mathrm{T}=1.0,\, \hbox {M} = 0.5,\, \hbox {Pr} = 7.0, \xi = 1.0$ are prescribed (unless otherwise stated). Furthermore the influence of stream-wise (transverse) coordinate on heat transfer characteristics is also investigated.

Table 1 Values of the local heat transfer coefficient $-\theta ^{\prime }\left( {\xi ,0} \right)$ for various values of $\xi$ with $\hbox {W}_{e} =0.0,\, \hbox {n} = 0.0,\, \hbox {M} = 0.0,\, \hbox {S}_\mathrm{f} = 0.0,\, \hbox {S}_\mathrm{T} = 0.0$

Table 2 Values of ${f}''(\xi ,0)$ and $-{\theta }'(\xi ,0)$ for different values of $\hbox {S}_\mathrm{f},\, \hbox {S}_\mathrm{T}$ and M $(\hbox {Pr} = 7.0,\, \hbox {W}_\mathrm{e}= 0.3,\, \hbox {n} = 0.3, \xi = 1.0)$

Table 3 Values of ${f}''(\xi ,0)$ and $-{\theta }'(\xi ,0)$ for different values of $\hbox {S}_\mathrm{f},\, \hbox {S}_\mathrm{T}$ and M $(\hbox {Pr} = 7.0,\, \hbox {W}_\mathrm{e}= 0.3,\, \hbox {n} = 0.3,\, \xi = 1.0)$

Table 4 Values of ${f}''(\xi ,0)$ and $-{\theta }'(\xi ,0)$ for different values of We, n and Pr $(\hbox {S}_\mathrm{f} = 0.5,\, \hbox {S}_\mathrm{T} = 1.0,\, \hbox {M} = 1.0)$

Table 5 Values of ${f}''(\xi ,0)$ and $-{\theta }'(\xi ,0)$ for different values of $\hbox {W}_\mathrm{e}$, n and Pr $(\hbox {S}_\mathrm{f} = 0.5, \hbox {S}_\mathrm{T} = 1.0$, M = 1.0)

Fig. 2

a Influence of $\hbox {W}_\mathrm{e}$ on velocity profiles. b Influence of $\hbox {W}_\mathrm{e}$ on temperature profiles

Fig. 3

a Influence of n on velocity profiles. b Influence of n on temperature profiles

Fig. 4

a Influence of $\hbox {S}_\mathrm{f}$ on velocity profiles. b Influence of $\hbox {S}_\mathrm{f}$ on temperature profiles

Fig. 5

a Influence of $\hbox {S}_\mathrm{T}$ on velocity profiles. b Influence of $\hbox {S}_\mathrm{T}$ on temperature profiles

Fig. 6

a Influence of M on velocity profiles. b Influence of M on temperature profiles

Fig. 7

a Influence of $\xi$ on velocity profiles. b Influence of $\xi$ on temperature profiles

Fig. 8

a Influence of $\hbox {W}_\mathrm{e}$ on skin friction coefficient result. b Influence of $\hbox {W}_\mathrm{e}$ on Nusselt number result

Fig. 9

a Influence of n on skin friction coefficient result. b Influence of n on Nusselt number result

Fig. 10

a Influence of $\hbox {S}_\mathrm{f}$ on skin friction coefficient result. b Influence of $\hbox {S}_\mathrm{f}$ on Nusselt number result

Fig. 11

a Influence of $\hbox {S}_\mathrm{T}$ on skin friction coefficient result. b Influence of $\hbox {S}_\mathrm{T}$ on Nusselt number result

Fig. 12

a Influence of M on skin friction coefficient result. b Influence of M on Nusselt number result

Table 1 presents the values of heat transfer coefficient for different values of $\xi$ and are compared with those of Merkin [46] and Nazar et al. [47] and are found to be in excellent correlation.

Tables 2 and 3 document results for the influence of the velocity slip $(\hbox {S}_\mathrm{f})$ and the thermal jump $(\hbox {S}_\mathrm{T})$ on skin friction and heat transfer rate along with a variation in the Magnetic parameter (M). It has been observed that increasing $\hbox {S}_\mathrm{f}$ reduces skin friction but increases heat transfer rate (Nusselt numbers). Also increasing $\hbox {S}_\mathrm{T}$ is found to decrease both the skin friction and heat transfer rate (Nusselt number). These tables also show that an increase in M is found to decrease both skin friction and heat transfer rate.

Tables 4 and 5, we present the influence of the Weissenberg number (We) and power law index (n), on skin friction and heat transfer rate (Nusselt number), along with a variation in the Prandtl number (Pr). It is observed that, increasing We, decreases both Skin friction and heat transfer rate. Furthermore, an increase in power law index (n) decreases skin friction but increases heat transfer rate. As increasing Pr is found to reduce skin friction but enhances heat transfer rate.

Figure 2a, b depict the velocity $\left( {f^{\prime }} \right)$ and temperature $\left( \theta \right)$ distributions with increasing Weissenberg number, $W_{e}$ . Very little tangible effect is observed in Fig. 2a, although there is a very slight decrease in velocity with increase in We. Conversely, there is only a very slight increase in temperature magnitudes in Fig. 2b with a rise in We. The mathematical model reduces to the Newtonian viscous flow model as $W_\mathrm{e} \rightarrow 0$ and $\hbox {n} \rightarrow 0$. The momentum boundary layer equation in this case contracts to the familiar equation for Newtonian mixed convection from a cylinder, viz. $f^{{\prime }{\prime }{\prime }}+ff^{{\prime }{\prime }}-f^{/2}+\theta \frac{\sin \xi }{\xi }-Mf^{\prime }=\xi \left( {f^{\prime }\frac{\partial f^{\prime }}{\partial \xi }-f^{{\prime }{\prime }}\frac{\partial f}{\partial \xi }} \right)$. The thermal boundary layer equation (10) remains unchanged.

Figure 3a, b illustrate the effect of the power law index, $n$, on velocity $\left( {f^{\prime }} \right)$ and temperature $\left( \theta \right)$ distributions through the boundary layer regime. It is observed that increasing $n$, increases velocity significantly. Conversely temperature is consistently reduced with increasing values of $n$.

Figure 4a, b depict the evolution of velocity $\left( {f^{\prime }} \right)$ and temperature $\left( \theta \right)$ functions with a variation in velocity slip parameter, $\hbox {S}_\mathrm{f}$. Dimensionless velocity component (Fig. 4a) at the wall is considerably enhanced with increasing $\hbox {S}_\mathrm{f}$. There will be a corresponding increase in the momentum (velocity) boundary layer thickness. The influence of $\hbox {S}_\mathrm{f}$ is evidently more pronounced closer to the cylinder surface $(\eta = 0)$. Further from the surface, there is a transition in velocity slip effect, and the flow is found to be accelerated markedly. Smooth increase of the velocity profiles are observed into the free stream demonstrating excellent convergence of the numerical solution. These trends in the response of velocity field in external thermal convection from a cylinder were also observed by Wang and Ang [17] and Wang [48]. Furthermore, the acceleration near the wall with increasing velocity slip effect has been computed by Crane and McVeigh [15] using asymptotic methods, as has the retardation in flow further from the wall. The switch in velocity slip effect on velocity evolution has also been observed for the case of a power-law rheological fluid by Ajadi et al. [49]. Figure 4b shows that an increase in $\hbox {S}_\mathrm{f}$, significantly reduces temperature in the flow flied and thereby decreases thermal boundary layer thickness. Temperature profiles consistently decay monotonically from a maximum at the cylinder surface to the free stream. All profiles converge at large value of radial coordinate, again showing that convergence has been achieved in the numerical computations. A similar pattern of thermal response to that computed in Fig. 4b who has indicated also that temperature is enhanced since stresses and this permits a more effective transfer of heat from the wall to the fluid regime.

Figure 5a, b depict the evolution of velocity $\left( {f^{\prime }} \right)$ and temperature $\left( \theta \right)$ functions with a variation in thermal jump parameter, $\hbox {S}_\mathrm{T}$. The response of velocity is much more consistent than for the case of changing velocity slip parameter (Fig. 4a). It is strongly decreased for all locations in the radial direction. The peak velocity accompanies the case of no thermal jump $(S_{T} = 0)$. The maximum deceleration corresponds to the case of strongest thermal jump $(S_{T} = 3)$. Temperatures (Fig. 5b) are also strongly depressed with increasing thermal jump. The maximum effect is observed at the wall. Further into the free stream, all temperature profiles converge smoothly to the vanishing value. The numerical computations correlate well with the results of Larrode et al. [11], who also found that temperature is strongly lowered with increasing thermal jump and that this is attributable to the decrease in heat transfer from the wall to the fluid regime, although they considered only a Newtonian fluid.

Figure 6a, b depict the profiles for velocity $\left( {f^{\prime }} \right)$ and temperature $\left( \theta \right)$ for various values of the magnetic parameter, M. An increase in M from 0 (non-magnetic case) to 2, strongly decelerates the flow i.e., reduces velocity values. In all profiles a peak arises near the surface of the cylinder and this peak is displaced progressively closer to the wall with an elevation in M values. Here $M=\frac{\sigma B_0^2 a^{2}}{\rho \nu \sqrt{Gr}}$ and embodies the relative effect of hydrodynamic (Lorentzian) drag force to the viscous hydrodynamic force in the regime. It is a form of Hartmann number familiar from MHD. Clearly, higher M values correspond to stronger applied magnetic field $\left( {B_0 } \right)$ acting normal to the cylinder longitudinal axis. The linear magnetic drag force,$-Mf^{\prime }$, featured in the non-dimensional momentum boundary equation (9), is directly proportional to M and, in turn, M is directly proportional to $B_0$ for constant electrical conductivity $\left( \sigma \right)$, cylinder radius $\left( a \right)$, fluid density $\left( \rho \right)$, kinematic viscosity $\left( \nu \right)$ and Grashof number $\left( {Gr} \right)$. Therefore, a greater retarding effect is generated in the flow with greater M values (i.e., stronger magnetic field strengths), which causes the prominent depression in velocities. For M = 1 the magnetic drag force will be of the same order of magnitude as the viscous hydrodynamic force. For $\hbox {M} > 1$, hydromagnetic drag will dominate and vice versa for $\hbox {M} < 1$. Therefore, in magnetic materials processing the flow can be very effectively controlled with a magnetic field. However, increasing M is found to accelerate the temperature.

Figure 7a, b depict the velocity $( {f^{\prime }}$ and temperature $(\theta )$ distributions with dimensionless radial coordinate, for various transverse (stream wise) coordinate values, $\xi$. Generally velocity is noticeably lowered with increasing migration from the leading edge i.e. larger $\xi$ values (Fig. 7a). The maximum velocity is computed at the lower stagnation point $(\xi \sim 0)$ for low values of radial coordinate $(\eta )$. The transverse coordinate clearly exerts a significant influence on momentum development. A very strong increase in temperature $(\theta )$, as observed in Fig. 7b, is generated throughout the boundary layer with increasing $\xi$ values. The temperature field decays monotonically. Temperature is maximized at the surface of the spherical body ($\eta = 0$, for all $\xi$) and minimized in the free stream $(\eta = 25)$. Although the behaviour at the upper stagnation point $(\xi \sim \pi )$ is not computed, the pattern in Fig. 7b suggests that temperature will continue to progressively grow here compared with previous locations on the cylinder surface (lower values of $\xi$).

Figure 8a, b show the influence of Weissenberg number, $W_{e}$, on the dimensionless skin friction coefficient $\left( {\left( {1-n} \right) \xi {f}''\left( {\xi ,0} \right) +\frac{nW_e }{2}\xi \left( {f^{{\prime }{\prime }}\left( {\xi ,0} \right) } \right) ^{2}} \right)$ and heat transfer rate $\left( {\theta ^{\prime }\left( {\xi ,0} \right) } \right)$ at the cylinder surface. It is observed that the dimensionless skin friction is decreased with the increase in $W_e$ i.e. the boundary layer flow is accelerated with decreasing viscosity effects in the non-Newtonian regime. The surface heat transfer rate is also substantially decreased with increasing $W_e$ values.

Figure 9a, b illustrate the influence of the power law index, n, on the dimensionless skin friction coefficient and heat transfer rate. The skin friction (Fig. 9a) at the cylinder surface is reduced with increasing $n,$ however only for very large values of the transverse coordinate, $\xi$. However, heat transfer rate (local Nusselt number) is enhanced with increasing n, again at large values of $\xi$, as computed in Fig. 9b.

Figure 10a, b present the influence of the velocity slip, $\hbox {S}_\mathrm{f}$, on the dimensionless skin friction coefficient and heat transfer rate at the cylinder surface. With an increase in $\hbox {S}_\mathrm{f}$, wall shear stress is consistently reduced. This trend was observed by Wang and Ang [17] and Wang [48] using asymptotic methods. There is a progressive migration in the peak shear stress locations further from the lower stagnation point, as wall slip parameter is increased. The impact of wall slip is therefore significant on the boundary layer characteristics of the fluid flow from a cylinder. With an increasing $\hbox {S}_\mathrm{f}$, the local Nusselt number considerably increased and the profiles are generally monotonically increasing. The minimum local Nusselt number arises at the cylinder surface and is maximised with proximity to the lower stagnation point i.e. greater distance from the upper stagnation point.

Figure 11a, b present the effect of thermal jump, $\hbox {S}_\mathrm{T}$, on the dimensionless skin friction coefficient and heat transfer rate at the cylinder surface. Increasing $S_{T}$, is found to decrease both skin friction coefficient and local Nusselt number.

Figure 12a, b show the influence of the magnetic parameter, M, on the dimensionless skin friction coefficient and heat transfer rate at the cylinder surface. It is observed from these figures that both skin friction coefficient and heat transfer rate decreases considerably owing to the retarding effects of magnetic field on the fluid flow. Intense amount of magnetic field inside the boundary layer literally increase the Lorentz force which significantly opposes the flow in the reverse direction. Thus, skin friction coefficient and heat transfer rate diminishes.

Conclusions

Numerical solutions have been presented for the buoyancy-driven flow and heat transfer of Tangent Hyperbolic flow external to a horizontal cylinder. The Keller-box implicit second order accurate finite difference numerical scheme has been utilized to efficiently solve the transformed, dimensionless velocity and thermal boundary layer equations, subject to realistic boundary conditions. Excellent correlation with previous studies has been demonstrated testifying to the validity of the present code. The computations have shown that:

• 1. Increasing Weissenberg number, We, decreases velocity, skin friction (surface shear stress) and heat transfer rate (Nusselt number), whereas increases temperature.

• 2. Increasing power law index, $n$, increases velocity and heat transfer rate, for all values of radial coordinate i.e., throughout the boundary layer regime whereas, decreases temperature and skin friction.

• 3. Increasing velocity slip, $\hbox {S}_\mathrm{f}$, increases velocity and heat transfer rate but decreases temperature and skin friction.

• 4. Increasing thermal jump, $\hbox {S}_\mathrm{T}$, decreases all the four i.e., velocity, temperature, skin friction and hear transfer rate.

• 5. Increasing magnetic parameter, M, decreases velocity, skin friction and heat transfer rate but increases temperature.

• 6. Increasing transverse coordinate $(\upxi )$ generally decelerates the flow near the cylinder surface and reduces momentum boundary layer thickness whereas it enhances temperature and therefore increases thermal boundary layer thickness in Tangent Hyperbolic non-Newtonian fluids.

Generally very stable and accurate solutions are obtained with the present finite difference code. The numerical code is able to solve nonlinear boundary layer equations very efficiently and therefore shows excellent promise in simulating transport phenomena in other non-Newtonian fluids.