Improved CoCoSo Method Based on Frank Softmax Aggregation Operators for T-Spherical Fuzzy Multiple Attribute Group Decision-Making

Abstract

In this article, a novel CoCoSo (Combined compromise solution) method based on Frank operational laws and softmax function is investigated to handle multiple attribute group decision-making problems for T-spherical fuzzy sets. We extend Frank operations in T-spherical fuzzy environment and develop a series of aggregation operators, including T-spherical fuzzy Frank softmax (T-SFFS) average and geometric operators, and their weighted forms, i.e., T-SFFS weighted averaging (T-SFFSWA) and T-SFFS weighted geometric (T-SFFSWG) operators. Some of their basic properties and particular cases are discussed. Meanwhile, the monotonicity of proposed operators is also analyzed, and it is discussed that how they indicate the decision-makers’ optimistic and pessimistic decision attitudes with risk preference. Furthermore, a novel CoCoSo method based on Hamming distance measure is proposed, which considers both decision-maker’s decision attitude and attribute priority, and a multiple attribute group decision-making framework with two independent and parallel T-spherical fuzzy information processing processes are designed. Lastly, a real case of spent power battery recycling technology (SPBRT) selection is presented to show the practicability of the proposed method. Also sensitivity and comparative analyses are carried out to prove the reliability, effectiveness, and superiority of our proposed method.

1 Introduction

The multi-attribute group decision-making (MAGDM) integrates the alternative preference information given by multiple decision-makers (DMs) into group preference information, and the constructed theory is used to select the best of limited options [1]. Recently, the MAGDM has turn into a hot topic in modern decision-making field. However, the actual group decision-making problems have become more complicated with the rapid development of economy and society. Many scholars face great challenges in depicting the ambiguity, uncertainty, and personality preference of individual opinions and views in the evaluation process.

For MAGDM problems, the expression of evaluation information and the determination of optimal alternative are the two most critical topics. In the expression of evaluation information, there may be three types of uncertainty in the evaluation information. It may be caused by fuzziness, randomness, and incomplete information. In order to deal with such uncertainty of evaluation information, scholars have proposed many theories to express and process, such as classical fuzzy set (CFS) [2], intuitionistic fuzzy set (IFS) [3], Pythagorean fuzzy set (PyFS) [4], q-rung orthopair fuzzy sets (q-ROFSs) [5], picture fuzzy set (PFS) [6], spherical fuzzy set (SFS) [7], and T-spherical fuzzy (T-SF) set (T-SFS) [7], and so forth. In contrast, the T-SFS is the most novel generalized fuzzy set, and it has greater expression space and freedom. In terms of methods for determining the optimal alternative, in addition to various aggregation operators, many alternative ranking techniques are prevailing in literature, such as TOPSIS (technique for order of preference by similarity to ideal solution) [8], VIKOR (VlseKriterijumska Optimizacija I Kompromisno Resenje) [9], MULTIMOORA (Multi-objective optimization based on the ratio analysis with the full multiplicative form) [10], TODIM (Portuguese acronym meaning Interactive Multi-Criteria Decision Making) [11], and CoCoSo [12]. Although these methods can solve the alternatives ranking problem, the most suitable one must depend on the structure of the decision-making problem.

Yazdani et al. [12] introduced and developed a decision-making technique named the CoCoSo. The traditional CoCoSo method uses a comparison based on the weighted average of the values in the initial decision matrix. The weighted average is performed by multiplying the standard value of the alternatives by the standard weight in two ways. The first method involves applying a weighted sum model (WSM) in which each weight of the standard is multiplied by the normalized value of the initial decision matrix. The second method means that the weighted product model (WPM) is used to calculate the overall relative importance of alternatives. After defining the weighted values of the criterion functions of the alternatives, their aggregation is performed in order to obtain a unique ranking index. Aggregation is performed by implementing three pooling strategies applied to each given alternative. Each strategy defines its own internal ranking, and the final ranking index further improves the ranking. Finally, aggregation is performed by using the cumulative equation that defines the final rank of the alternatives [12]. The procedure of this method is based on the combination of trade-off strategies. Its calculation is simple and the results obtained are reliable. However, the WSM and WPM in the existing CoCoSo methods fail to cope with the MAGDM problems by considering the DMs’ decision-making attitude with risk preference. Therefore, keeping the advantages of T-SFS and CoCoSo, it is of great significance to realize an improvement of CoCoSo method in T-SF environment for determining the priorities of alternatives in MAGDM.

Against the analysis above, the aim of this paper is to develop an improved CoCoSo method within the environment of T-SFSs for handling MAGDM problems. To this end, we give an overall system framework of this paper, as shown in Fig. 1. The main contributions of this paper are summarized as follows:

• (1) We extend FOLs in T-SF environment and propose some AOs based on FOLs and softmax function, and the basic properties and particular cases of these AOs are also explored. We make clear the important meaning that the monotonicity of proposed AOs can reflect the DMs’ decision attitudes with risk preference.

• (2) In the T-SF environment, we extend the DEMATEL (Decision-making trial and evaluation laboratory) method which considering the association of attributes to determine the subjective weights of attributes, and utilize the similarity measure to calculate the attributes’ objective weights. Then, we obtain the attributes’ combination weights.

• (3) We build the MAGDM framework based on improved CoCoSo method. This framework is divided into two processes of independent and parallel information processing: optimistic and pessimistic; The T-SFFSWA and T-SFFSWG operators are used to replace WSM and WPM in traditional CoCoSo method; The performance values of alternatives are defuzzified by distance measure to calculate the relative closeness.

• (4) The practicability of the proposed method is verified by solving a real case of the SPBRT selection problem, and then we demonstrate the effectiveness and superiority of the improved CoCoSo method through sensitivity analysis and comparative study.

Fig. 1

The overall system framework of this research

The rest segments are arranged. In Sect. 2, the literature review is presented. In Sect. 3, we briefly review some related notions. We extend T-SFNs’ Frank operations and propose some AOs for T-SFSs, the properties and special cases are discussed and the monotonicity of the proposed AOs is analyzed. Then, we construct the MAGDM framework with T-SFNs based on improved CoCoSo method. In Sect. 4, we present a real case of SPBRT selection to illustrate the effectiveness and application. The managerial implications are presented in Sect. 5. In Sect. 6, the conclusion is remarked and direction is given for future work.

2 Literature Review

The literature analysis presented is related to three main streams: generalization of fuzzy sets, Frank t-norms and softmax function, and CoCoSo method.

2.1 Generalization of Fuzzy Sets

The CFS [2] proved to be an effective means for evaluation information description and is widely used to deal with information modeling problems, but CFS is not competent to describe the uncertainty of human cognition of things, because there is only membership degree (MD) τ(x) (0 ≤ τ(x) ≤ 1) in CFS. Atanassov [3] proposed a binary form composed of MD τ(x) and non-membership degree (ND) ϑ(x) (0 ≤ ϑ(x) ≤ 1) with the condition that the sum of both the degrees must lies in the unit interval [0, 1], and called it intuitionistic fuzzy set (IFS). As compared with CFS, the IFS can describe more detailed assessment information but it was observed that the condition τ(x) + ϑ(x) ≤ 1 creates problems for the decision makers, because it is possible that τ(x) + ϑ(x) > 1. To handle this drawback, Yager [4] initiated the notion of Pythagorean fuzzy set (PyFS), whose τ(x) and ϑ(x) meet the conditions: τ²(x) + ϑ²(x) ≤ 1. Later on to facilitate the decision makers, Yager [5] further designed more generalized notion of q-rung orthopair fuzzy sets (q-ROFSs) based on the PyFSs to meet τ^q(x) + ϑ^q(x) ≤ 1 (q ≥ 1). Obviously, the q-ROFSs have lager decision scope and more free to express views than IFSs and PyFSs.

Although the above discussed notions of IFSs, PyFSs, and that of q-ROFSs attained great achievements but they can handle only the cases involving only either “yes” and “no,” but in real life there are many cases, like voting, where these theories fail [6]. To handle this issue the notion of picture fuzzy set (PFS) was introduced by Cuong [6], which is a triplet composed of MD (τ(x)), ND(ϑ(x)), and abstinence degree (AD) ψ(x) (0 ≤ ψ(x) ≤ 1), and meets τ(x) + ψ(x) + ϑ(x) ≤ 1. The 3D description of information by PFSs is obviously more powerful than the 2D description of IFS and its generalizations like PyFSs and q-ROFSs. In 2019, Mahmood et al. [7] proposed a new concept of spherical fuzzy set (SFS) to solve the decision problem with τ(x) + ψ(x) + ϑ(x) > 1. The SFS is characterized (τ(x))² + (ψ(x))² + (ϑ(x))² ≤ 1. Meanwhile, a generalized concept of T-spherical fuzzy (T-SF) set (T-SFS) ( (τ(x))^q + (ψ(x))^q + (ϑ(x))^q ≤ 1 (q ≥ 1)) was advanced by Mahmood, et al. [7] The “Yes,” “Abstain,” “No,” and “Refuse” in DMs’ opinions are expressed with higher freedom. Obviously, the T-SFS has generalizability, and the CFS, IFS, PyFS, q-ROFS, PFS, and SFS are special cases of this concept under certain conditions, and a comparison of these fuzzy sets is listed in Table 1. Recently, many scholars have developed numerous aggregation operators (AOs) and some ranking techniques in the T-SF environment. The aggregation technology of T-SFS has been considered by many scholars. Some scholars have proposed some T-SF AOs based on Algebraic operational laws (AOLs) [7, 13,14,15]. For example, the Maclarurin symmetric mean, Muirhead mean, and the power average operators have been all extended for T-SFSs. As the characteristics of AOLs cannot reflect the flexibility and generality of operational rules, several scholars further proposed some T-SF AOs based on the Dombi [10], Einstein [16], and Hamacher [17] operational laws. In addition, the AOs based on the interactive operational laws were investigated for the interactive relationship between three functions in T-SF numbers (T-SFNs) to elude counterintuitive phenomena in process of information fusion [11, 18,19,20]. There are a few relevant studies on T-SF ranking methods. For example, Mahmood et al. [10] proposed the T-SF Dombi prioritized weighted arithmetic (T-SFDPWA) and T-SF Dombi prioritized weighted geometric (T-SFDPWG) operators and improved the MULTIMOORA method for T-SFSs. Ju et al. [11] advanced some interactive AOs and extended the traditional TODIM method with T-SFNs. Ullah et al. [21] developed some new dice similarity measures to modify the method.

Table 1 Comparison of existing fuzzy sets

2.2 Frank t-Norms and Softmax Function

It is worth noting that Frank t-norm and s-norm [22] is the only operational form with compatibility characteristics in above operations, which has better generality, flexibility, and robustness in dealing with information aggregation to overcome the defects of AOLs. Since the Frank t-norm and s-norm can be degenerated into Lukasiewicz and Algebraic operations under special conditions, it has been applied to define the operational laws in various fuzzy theories, such as IFSs [23], Hesitant fuzzy sets [24], PyFSs [25], q-ROFSs [26], PFSs [27], and single-value neutrosophic sets [28]. Combined with the previous T-SF AOs review, we find that there is no research on developing new AOs based on Frank operations in the T-SF environment. Therefore, it is necessary to extend the existing Frank operational laws (FOLs) and develop some novel T-SF AOs based on the T-SFNs’ FOLs.

The prioritized averaging operator (PAO) was first introduced by Yager [29] to solve the information fusion problems when there is a priority relationship between arguments. As it can make the decision-making process more realistic, it has been widely used by many scholars [30,31,32,33]. However, the PAO can represent the priority relationships between arguments, but it can neither describe the degree of priority relationship nor flexibly adjust the level of priority relationship according to the actual decision facts. In other words, the existing PAO lacks flexibility and generality. Therefore, we introduce the softmax function to remedy this defect. The softmax function is the extension of Logistic regression model on multiple classification problems, which has been widely used on deep learning [34], decision analysis [35, 36] and other fields. The softmax function can effectively depict the priority relationship between decision variables in different decision-making environments [35]. For example, Torres et al. [36] first extended softmax function to hesitant fuzzy sets and developed some AOs. Yu [35] developed two AOs based on the softamx function in IFSs. Thus, since the softmax function contains exponential function and a modulation parameter, it not only has the characteristics of non-linearity, monotonicity and boundedness [35], but also can show stronger generalization and decision-making flexibility than the existing PAOs. Currently, there is no relevant study on softmax function in T-SF environment.

2.3 CoCoSo Method

It is very important to determine the optimal alternative in decision analysis. The CoCoSo [12] is a decision-making method based on combination and compromise perspectives, which has the advantages of avoiding decision-making compensatory problems and realizing internal equilibrium of final utility, as well as relatively low computational complexity. At present, this method has been extended and applied to different decision environments, such as CFSs [37], PyFSs [38, 39], q-ROFSs [40], rough sets [41], PFSs [42], SFSs [43], and interval type-2 fuzzy sets [44]. Obviously, the CoCoSo method has attracted extensive attention from scholars. The existing CoCoSo methods are studied in MAGDM problems, as shown in Table 2. However, these methods still have some shortcomings: (1) the traditional CoCoSo method has not been promoted to T-SF environment for research and application; (2) The weighted sum model (WSM) and weighted product model (WPM) in existing CoCoSo methods do not consider the priority relationship between input arguments; (3) The evaluation information of alternatives is basically processed by WSM and WPM based on AOLs, which can neither reflect the flexibility and generality of the decision nor depict the decision attitude or risk preference of the DMs; (4) Although the CoCoSo method has a compromise decision-making mechanism, there is still a lack of research on the compromise of DMs’ opposite decision attitudes or risk preferences. Therefore, to remedy the above defects, it is necessary to improve the traditional CoCoSo method under T-SF environment.

Table 2 Research on existing CoCoSo methods in MAGDM problems

2.4 2.4 Research Gaps

The following research gaps have been identified.

• (1) T-SFSs are an advanced type of fuzzy technique, which can handle higher levels of vagueness or indeterminacy and provide freedom in expressing decision-making preferences. However, there are few ranking methods with T-SF information in solving MAGDM problems. As a result, it is necessary to extend appropriate ranking technique in T-SF environment, such as CoCoSo method, to enrich T-SFS decision-making theory system.

• (2) The FOLs and softmax function have not been studied in the T-SF environment, but combining their advantages, we can integrate the FOLs and softmax function in T-SF context and develop T-SF average and geometric operators, so as to highlight the ability of these operators in the aspect of generalization of information processing, decision flexibility and monotonicity of DM’s decision attitude.

• (3) The CoCoSo method, which is a very popular and influential decision-making tool, has not been extended before using T-SFSs. Meanwhile, the existing WSM and WPM have no flexibility, ignore priority of argument and do not consider the attitude or preference of DMs. Thus, a new aggregation operator is needed to replace WSM and WPM to improve the CoCoSo method in T-SF context.

• (4) How to effectively solve the T-SF MAGDM problems? We need to build a novel T-SF methodological framework based on the improved CoCoSo with decision attitude as well as approve its effectiveness in the real-world context of selecting SPBRT.

3 Preliminaries

3.1 T-Spherical Fuzzy Sets

Definition 1

[7] Let X be a universe set, then the form of T-SFS is described as below:

$$ \Im { = }\left\{ {\left\langle {x,\left( {\tau_{\Im } (x),\psi_{\Im } (x),\vartheta_{\Im } (x)} \right)} \right\rangle |x \in X} \right\} $$

(1)

where $\tau_{\Im } (x),\psi_{\Im } (x),\vartheta_{\Im } (x)$ are, respectively, the MD, AD, and ND of element x ∈ $\Im$ in X, that is, $\tau_{\Im } (x),\psi_{\Im } (x),\vartheta_{\Im } (x) \in [0,1]$, and meeting $0 \le \tau_{\Im }^{q} (x) + \psi_{\Im }^{q} (x) + \vartheta_{\Im }^{q} (x) \le 1$, q ≥ 1 for ∀x ∈ X. In addition, $\pi_{\Im } (x) = \sqrt[q]{{1 - \tau_{\Im }^{q} (x) - \psi_{\Im }^{q} (x) - \vartheta_{\Im }^{q} (x)}}$ is called the degree of refusal. For simplicity, the T-SFN is represented as a triplet ofτ, ψ andϑ, and denoted as δ = (τ, ψ, ϑ).

Definition 2

[11] For a T-SFN δ = (τ, ψ, ϑ), the score function sc(δ) and accuracy function ac(δ) are defined as:

$$ sc(\delta ) = \frac{{1 + \tau^{q} - \psi^{q} - \vartheta^{q} }}{2} $$

(2)

$$ ac(\delta ) = \tau^{q} + \psi^{q} + \vartheta^{q} $$

(3)

To compare the two T-SFNs δ₁ = (τ₁, ψ₁, ϑ₁) and δ₂ = (τ₂, ψ₂, ϑ₂), the comparative rules are as follows:

• (1) If sc(δ₁) > sc(δ₂), then δ₁ is greater than δ₂, namely, δ₁ > δ₂;

• (2) If sc(δ₁) = sc(δ₂), then (i) if ac(δ₁) > ac(δ₂), then δ₁ is greater than δ₂, namely, δ₁ > δ₂; (ii) if ac(δ₁) = ac(δ₂), then δ₁ is equal to δ₂, namely, δ₁ = δ₂.

Definition 3

[7] Let δ = (τ, ψ, ϑ), δ₁ = (τ₁, ψ₁, ϑ₁), and δ₂ = (τ₂, ψ₂, ϑ₂) be three arbitrary T-SFNs, then their operational rules are described as below:

• (1) $\delta_{1} \oplus \delta_{2} = \left( {\sqrt[q]{{\tau_{1}^{q} + \tau_{2}^{q} - \tau_{1}^{q} \tau_{2}^{q} }},\psi_{1} \psi_{2} ,\vartheta_{1} \vartheta_{2} } \right)$;

• (2) $\delta_{1} \otimes \delta_{2} = \left( {\tau_{1} \tau_{2} ,\sqrt[q]{{\psi_{1}^{q} + \psi_{2}^{q} - \psi_{1}^{q} \psi_{2}^{q} }},\sqrt[q]{{\vartheta_{1}^{q} + \vartheta_{2}^{q} - \vartheta_{1}^{q} \vartheta_{2}^{q} }}} \right)$;

• (3) $\eta \cdot \delta = \left( {\sqrt[q]{{1 - (1 - \tau^{q} )^{\eta } }},\psi^{\eta } ,\vartheta^{\eta } } \right)$, η > 0;

• (4) $\delta^{\eta } = \left( {\tau^{\eta } ,\sqrt[q]{{1 - (1 - \psi^{q} )^{\eta } }},\sqrt[q]{{1 - (1 - \vartheta^{q} )^{\eta } }}} \right)$, η > 0.

Definition 4

[10] For two T-SFNs δ₁ = (τ₁, ψ₁, ϑ₁) and δ₂ = (τ₂, ψ₂, ϑ₂), the Hamming distance between them is defined as:

$$ D_{H} (\delta_{1} ,\delta_{2} ) = \frac{1}{2}\left( {\left| {\tau_{1}^{q} - \tau_{2}^{q} } \right| + \left| {\psi_{1}^{q} - \psi_{2}^{q} } \right| + \left| {\vartheta_{1}^{q} - \vartheta_{2}^{q} } \right| + \left| {\pi_{1}^{q} - \pi_{2}^{q} } \right|} \right) $$

(4)

Definition 5

[45] For two T-SFNs δ₁ = (τ₁, ψ₁, ϑ₁) and δ₂ = (τ₂, ψ₂, ϑ₂), their similarity measure is defined as:

$$ S(\delta_{1} ,\delta_{2} ) = \frac{{\tau_{1}^{q} \tau_{2}^{q} + \psi_{1}^{q} \psi_{2}^{q} + \vartheta_{1}^{q} \vartheta_{2}^{q} }}{{\sqrt {(\tau_{1}^{q} )^{2} + (\psi_{1}^{q} )^{2} + (\vartheta_{1}^{q} )^{2} } \cdot \sqrt {(\tau_{2}^{q} )^{2} + (\psi_{2}^{q} )^{2} + (\vartheta_{2}^{q} )^{2} } }} $$

(5)

3.2 T-Spherical Fuzzy Frank Softmax Aggregation Operators

In this section, we first extend some FOLs for T-SFNs, then we develop a series of AOs based on the FOLs and softmax function to fuse the T-SFNs, and further a family of particular cases is analyzed. We also analyze the monotonicity of the AOs with respect to the parameter.

3.2.1 T-Spherical Fuzzy Frank Operational Laws

Definition 6

[22] For any two real numbers a, b ∈ [0,1], Frank product and Frank sum are described as below:

$$ t\left( {a,b} \right) = a \otimes_{F} b = \log_{\theta } \left( {1 + \frac{{\left( {\theta^{a} - 1} \right)\left( {\theta^{b} - 1} \right)}}{\theta - 1}} \right); \, s\left( {a,b} \right) = a \oplus_{F} b = 1 - \log_{\theta } \left( {1 + \frac{{\left( {\theta^{1 - a} - 1} \right)\left( {\theta^{1 - b} - 1} \right)}}{\theta - 1}} \right) $$

(6)

where θ ∈ (1, + ∞). The Frank operations have two particular cases: (1) If θ → 1, the Frank product and Frank sum are reduced to the Algebraic operations, namely t(a, b) = xy and s(a, b) = a + b-ab. (2) If θ →  + ∞, the Frank product and Frank sum are reduced to the Lukasiewicz operations, namely t(a, b) → max (0, a + b-1) and s(a, b) → min (a + b, 1).

We extend the FOLs of T-SFNs based on the Definition 6.

Definition 7

For two T-SFNs δ₁ = (τ₁, ψ₁, ϑ₁) and δ₂ = (τ₂, ψ₂, ϑ₂), with q ≥ 1 and η > 0, the FOLs of T-SFNs are described as below:

• (1) $\delta_{1} \oplus_{F} \delta_{2} = \left( {\sqrt[q]{{1 - \log_{\theta } \left( {1 + \frac{{(\theta^{{1 - \tau_{1}^{q} }} - 1)(\theta^{{1 - \tau_{2}^{q} }} - 1)}}{\theta - 1}} \right)}},\sqrt[q]{{\log_{\theta } \left( {1 + \frac{{(\theta^{{\psi_{1}^{q} }} - 1)(\theta^{{\psi_{2}^{q} }} - 1)}}{\theta - 1}} \right)}},\sqrt[q]{{\log_{\theta } \left( {1 + \frac{{(\theta^{{\vartheta_{1}^{q} }} - 1)(\theta^{{\vartheta_{2}^{q} }} - 1)}}{\theta - 1}} \right)}}} \right)$;

• (2) $\delta_{1} \otimes_{F} \delta_{2} = \left( {\sqrt[q]{{\log_{\theta } \left( {1 + \frac{{(\theta^{{\tau_{1}^{q} }} - 1)(\theta^{{\tau_{2}^{q} }} - 1)}}{\theta - 1}} \right)}},\sqrt[q]{{1 - \log_{\theta } \left( {1 + \frac{{(\theta^{{1 - \psi_{1}^{q} }} - 1)(\theta^{{1 - \psi_{2}^{q} }} - 1)}}{\theta - 1}} \right)}},\sqrt[q]{{1 - \log_{\theta } \left( {1 + \frac{{(\theta^{{1 - \vartheta_{1}^{q} }} - 1)(\theta^{{1 - \vartheta_{2}^{q} }} - 1)}}{\theta - 1}} \right)}}} \right)$;

• (3) $\eta \cdot_{F} \delta_{1} = \left( {\sqrt[q]{{1 - \log_{\theta } \left( {1 + \frac{{(\theta^{{1 - \tau_{1}^{q} }} - 1)^{\eta } }}{{(\theta - 1)^{\eta - 1} }}} \right)}},\sqrt[q]{{\log_{\theta } \left( {1 + \frac{{(\theta^{{\psi_{1}^{q} }} - 1)^{\eta } }}{{(\theta - 1)^{\eta - 1} }}} \right)}},\sqrt[q]{{\log_{\theta } \left( {1 + \frac{{(\theta^{{\vartheta_{1}^{q} }} - 1)^{\eta } }}{{(\theta - 1)^{\eta - 1} }}} \right)}}} \right)$;

• (4) $(\delta_{1} )^{{ \wedge_{F} \eta }} = \left( {\sqrt[q]{{\log_{\theta } \left( {1 + \frac{{(\theta^{{\tau_{1}^{q} }} - 1)^{\eta } }}{{(\theta - 1)^{\eta - 1} }}} \right)}},\sqrt[q]{{1 - \log_{\theta } \left( {1 + \frac{{(\theta^{{1 - \psi_{1}^{q} }} - 1)^{\eta } }}{{(\theta - 1)^{\eta - 1} }}} \right)}},\sqrt[q]{{1 - \log_{\theta } \left( {1 + \frac{{(\theta^{{1 - \vartheta_{1}^{q} }} - 1)^{\eta } }}{{(\theta - 1)^{\eta - 1} }}} \right)}}} \right)$.

It is easy to prove that the above calculation results are still T-SFNs, which is omitted.

Theorem 1

Let δ = (τ, ψ, ϑ), δ₁ = (τ₁, ψ₁, ϑ₁), and δ₂ = (τ₂, ψ₂, ϑ₂) be three T-SFNs, η₁, η₂, η ≥ 0. Then their operational properties are as below:

• (1) $\delta_{1} \oplus_{F} \delta_{2} = \delta_{2} \oplus_{F} \delta_{1}$;

• (2) $\delta_{1} \otimes_{F} \delta_{2} = \delta_{2} \otimes_{F} \delta_{1}$;

• (3) $\eta \cdot_{F} (\delta_{1} \oplus_{F} \delta_{2} ) = \eta \cdot_{F} \delta_{2} \oplus_{F} \eta \cdot_{F} \delta_{1}$;

• (4) $\eta_{1} \cdot_{F} \delta \oplus_{F} \eta_{2} \cdot_{F} \delta = (\eta_{1} + \eta_{2} ) \cdot_{F} \delta$;

• (5) $\delta^{{ \wedge_{F} \eta_{1} }} \otimes_{F} \delta^{{ \wedge_{F} \eta_{2} }} = \delta^{{ \wedge_{F} (\eta_{1} + \eta_{2} )}}$;

• (6) $\delta_{1}^{{ \wedge_{F} \eta }} \otimes_{F} \delta_{2}^{{ \wedge_{F} \eta }} = (\delta_{1} \otimes_{F} \delta_{2} )^{{ \wedge_{F} \eta }}$.

3.2.2 Some T-Spherical Fuzzy Frank Softmax Aggregation Operators

Definition 8

[35] As a generalized form of logistic function, the softmax function is defined as:

$$ \phi^{\kappa } (i,T_{1} ,T_{2} , \ldots ,T_{n} ) = \phi_{i}^{\kappa } = \frac{{\exp \left( {{{T_{i} } \mathord{\left/ {\vphantom {{T_{i} } \kappa }} \right. \kern-\nulldelimiterspace} \kappa }} \right)}}{{\sum\nolimits_{i = 1}^{n} {\exp \left( {{{T_{i} } \mathord{\left/ {\vphantom {{T_{i} } \kappa }} \right. \kern-\nulldelimiterspace} \kappa }} \right)} }} \, \kappa > 0 $$

(7)

where κ is modulation parameter. For a set of T-SFNs, the sc(δ_i) is the score function of T-SFN δ_i, and the T_i is obtained by the following Eq. (6):

$${{T}_{i}}=\left\{ \begin{matrix} \prod\nolimits_{l=1}^{i-1}{sc({{\delta }_{l}})}\quad i=2,3,\ldots ,n \\ 1\quad \quad i=1 \\\end{matrix} \right.$$

(8)

We can find that the value of softmax function is in the range of [0, 1] and satisfies $\sum\nolimits_{i = 1}^{n} {\phi_{i}^{\kappa } = 1}$. Yu [35] and Torres et al. [36] both believe that it has the properties of nonlinearity, monotonicity, and boundedness.

Definition 9

Suppose δ_i = (τ_i, ψ_i, ϑ_i) (i = 1,2,..,n) is a family of T-SFNs, then the T-spherical fuzzy Frank softmax averaging (T-SFFSA) is defined as:

$$ T - SFFSA\left( {\delta_{1} ,\delta_{2} , \ldots ,\delta_{n} } \right) = \mathop { \oplus_{F} }\limits_{i = 1}^{n} \left( {\phi_{i}^{\kappa } \cdot_{F} \delta_{i} } \right) $$

(9)

where $\phi_{i}^{\kappa } = \frac{{\exp \left( {{{T_{i} } \mathord{\left/ {\vphantom {{T_{i} } \kappa }} \right. \kern-\nulldelimiterspace} \kappa }} \right)}}{{\sum\nolimits_{i = 1}^{n} {\exp \left( {{{T_{i} } \mathord{\left/ {\vphantom {{T_{i} } \kappa }} \right. \kern-\nulldelimiterspace} \kappa }} \right)} }}$ satisfies $\phi_{i}^{\kappa } \in [0,1]$ $\sum\nolimits_{i = 1}^{n} {\phi_{i}^{\kappa } = 1}$, κ is modulation parameter and κ > 0. $T_{i} = \prod\nolimits_{l = 1}^{i - 1} {sc(\delta_{l} )}$(i = 2,3,…n), T₁ = 1, and sc(δ_i) is the score function of T-SFN δ_i.

Theorem 2

Suppose δ_i (i = 1, 2,…, n) is a collection of T-SFNs, q ≥ 1, θ > 1. Then the aggregation result of T-SFFSA operator in Eq. (9) is still a T-SFN, i.e.,

$$ T - SFFSA\left( {\delta_{1} ,\delta_{2} , \ldots ,\delta_{n} } \right) = \left( {\sqrt[q]{{1 - \log_{\theta } \left( {1 + \prod\limits_{i = 1}^{n} {\left( {\theta^{{1 - \tau_{i}^{q} }} - 1} \right)^{{\phi_{i}^{\kappa } }} } } \right)}},\sqrt[q]{{\log_{\theta } \left( {1 + \prod\limits_{i = 1}^{n} {\left( {\theta^{{\psi_{i}^{q} }} - 1} \right)^{{\phi_{i}^{\kappa } }} } } \right)}},\sqrt[q]{{\log_{\theta } \left( {1 + \prod\limits_{i = 1}^{n} {\left( {\theta^{{\vartheta_{i}^{q} }} - 1} \right)^{{\phi_{i}^{\kappa } }} } } \right)}}} \right) $$

(10)

Proof

The Eq. (10) is easily proved to be a T-SFN, we omitted it. The Eq. (10) is proved for n by mathematical induction.

When n = 2, by Definition 7, we have:

$$ \phi_{1}^{\kappa } \cdot_{F} \delta_{1} { = }\left( {\sqrt[q]{{1 - \log_{\theta } \left( {1 + \frac{{(\theta^{{1 - \tau_{1}^{q} }} - 1)^{{\phi_{1}^{\kappa } }} }}{{(\theta - 1)^{{\phi_{1}^{\kappa } - 1}} }}} \right)}},\sqrt[q]{{\log_{\theta } \left( {1 + \frac{{(\theta^{{\psi_{1}^{q} }} - 1)^{{\phi_{1}^{\kappa } }} }}{{(\theta - 1)^{{\phi_{1}^{\kappa } - 1}} }}} \right)}},\sqrt[q]{{\log_{\theta } \left( {1 + \frac{{(\theta^{{\vartheta_{1}^{q} }} - 1)^{{\phi_{1}^{\kappa } }} }}{{(\theta - 1)^{{\phi_{1}^{\kappa } - 1}} }}} \right)}}} \right) $$

$$ \phi_{2}^{\kappa } \cdot_{F} \delta_{2} { = }\left( {\sqrt[q]{{1 - \log_{\theta } \left( {1 + \frac{{(\theta^{{1 - \tau_{2}^{q} }} - 1)^{{\phi_{2}^{\kappa } }} }}{{(\theta - 1)^{{\phi_{2}^{\kappa } - 1}} }}} \right)}},\sqrt[q]{{\log_{\theta } \left( {1 + \frac{{(\theta^{{\psi_{2}^{q} }} - 1)^{{\phi_{2}^{\kappa } }} }}{{(\theta - 1)^{{\phi_{2}^{\kappa } - 1}} }}} \right)}},\sqrt[q]{{\log_{\theta } \left( {1 + \frac{{(\theta^{{\vartheta_{2}^{q} }} - 1)^{{\phi_{2}^{\kappa } }} }}{{(\theta - 1)^{{\phi_{2}^{\kappa } - 1}} }}} \right)}}} \right) $$

Then

$$ \begin{gathered} T - SFFSA(\delta_{1} ,\delta_{2} ) = \phi_{1}^{\kappa } \cdot_{F} \delta_{1} \oplus_{F} \phi_{2}^{\kappa } \cdot_{F} \delta_{2} \hfill \\ = \left( \begin{gathered} \sqrt[q]{{1 - \log_{\theta } \left( {1 + \frac{{\left( {\theta^{{1 - 1 + \log_{\theta } \left( {1 + \frac{{(\theta^{{1 - \tau_{1}^{q} }} - 1)^{{\phi_{1}^{\kappa } }} }}{{(\theta - 1)^{{\phi_{1}^{\kappa } - 1}} }}} \right)}} - 1} \right)\left( {\theta^{{1 - 1 + \log_{\theta } \left( {1 + \frac{{(\theta^{{1 - \tau_{2}^{q} }} - 1)^{{\phi_{2}^{\kappa } }} }}{{(\theta - 1)^{{\phi_{2}^{\kappa } - 1}} }}} \right)}} - 1} \right)}}{\theta - 1}} \right)}},\sqrt[q]{{\log_{\theta } \left( {1 + \frac{{\left( {\theta^{{\log_{\theta } \left( {1 + \frac{{(\theta^{{\psi_{1}^{q} }} - 1)^{{\phi_{1}^{\kappa } }} }}{{(\theta - 1)^{{\phi_{1}^{\kappa } - 1}} }}} \right)}} - 1} \right)\left( {\theta^{{\log_{\theta } \left( {1 + \frac{{(\theta^{{\psi_{2}^{q} }} - 1)^{{\phi_{2}^{\kappa } }} }}{{(\theta - 1)^{{\phi_{2}^{\kappa } - 1}} }}} \right)}} - 1} \right)}}{\theta - 1}} \right)}}, \hfill \\ \sqrt[q]{{\log_{\theta } \left( {1 + \frac{{\left( {\theta^{{\log_{\theta } \left( {1 + \frac{{(\theta^{{\vartheta_{1}^{q} }} - 1)^{{\phi_{1}^{\kappa } }} }}{{(\theta - 1)^{{\phi_{1}^{\kappa } - 1}} }}} \right)}} - 1} \right)\left( {\theta^{{\log_{\theta } \left( {1 + \frac{{(\theta^{{\vartheta_{2}^{q} }} - 1)^{{\phi_{2}^{\kappa } }} }}{{(\theta - 1)^{{\phi_{2}^{\kappa } - 1}} }}} \right)}} - 1} \right)}}{\theta - 1}} \right)}} \hfill \\ \end{gathered} \right) \hfill \\ = \left( {\sqrt[q]{{1 - \log_{\theta } \left( {1 + \frac{{(\theta^{{1 - \tau_{1}^{q} }} - 1)^{{\phi_{1}^{\kappa } }} (\theta^{{1 - \tau_{2}^{q} }} - 1)^{{\phi_{2}^{\kappa } }} }}{{(\theta - 1)^{{\phi_{1}^{\kappa } + \phi_{2}^{\kappa } - 1}} }}} \right)}},\sqrt[q]{{\log_{\theta } \left( {1 + \frac{{(\theta^{{\psi_{1}^{q} }} - 1)^{{\phi_{1}^{\kappa } }} (\theta^{{\psi_{2}^{q} }} - 1)^{{\phi_{2}^{\kappa } }} }}{{(\theta - 1)^{{\phi_{1}^{\kappa } + \phi_{2}^{\kappa } - 1}} }}} \right)}},\sqrt[q]{{\log_{\theta } \left( {1 + \frac{{(\theta^{{\vartheta_{1}^{q} }} - 1)^{{\phi_{1}^{\kappa } }} (\theta^{{\vartheta_{2}^{q} }} - 1)^{{\phi_{2}^{\kappa } }} }}{{(\theta - 1)^{{\phi_{1}^{\kappa } + \phi_{2}^{\kappa } - 1}} }}} \right)}}} \right) \hfill \\ \end{gathered} $$

Since $\phi_{1}^{\kappa } + \phi_{2}^{\kappa } = 1$, so we get

$$ T - SFFSA(\delta_{1} ,\delta_{2} ) = \left( {\sqrt[q]{{1 - \log_{\theta } \left( {1 + \prod\limits_{i = 1}^{2} {(\theta^{{1 - \tau_{i}^{q} }} - 1)^{{\phi_{i}^{\kappa } }} } } \right)}},\sqrt[q]{{\log_{\theta } \left( {1 + \prod\limits_{i = 1}^{2} {(\theta^{{\psi_{i}^{q} }} - 1)^{{\phi_{i}^{\kappa } }} } } \right)}},\sqrt[q]{{\log_{\theta } \left( {1 + \prod\limits_{i = 1}^{2} {(\theta^{{\vartheta_{i}^{q} }} - 1)^{{\phi_{i}^{\kappa } }} } } \right)}}} \right) $$

Which means that the Eq. (10) holds for n = 2.

If the Eq. (10) holds for n = m, i.e.,

$$ T - SFFSA(\delta_{1} ,\delta_{2} , \ldots ,\delta_{m} ) = \left( {\sqrt[q]{{1 - \log_{\theta } \left( {1 + \prod\limits_{i = 1}^{m} {(\theta^{{1 - \tau_{i}^{q} }} - 1)^{{\phi_{i}^{\kappa } }} } } \right)}},\sqrt[q]{{\log_{\theta } \left( {1 + \prod\limits_{i = 1}^{m} {(\theta^{{\psi_{i}^{q} }} - 1)^{{\phi_{i}^{\kappa } }} } } \right)}},\sqrt[q]{{\log_{\theta } \left( {1 + \prod\limits_{i = 1}^{m} {(\theta^{{\vartheta_{i}^{q} }} - 1)^{{\phi_{i}^{\kappa } }} } } \right)}}} \right) $$

When n = m + 1, we can obtain

$$ \begin{gathered} T - SFFSA(\delta_{1} ,\delta_{2} , \ldots ,\delta_{m} ,\delta_{m + 1} ) = T - SFFSA(\delta_{1} ,\delta_{2} , \ldots ,\delta_{m} ) \oplus_{F} \phi_{m + 1}^{\kappa } \cdot_{F} \delta_{m + 1} \hfill \\ = \left( {\sqrt[q]{{1 - \log_{\theta } \left( {1 + \prod\limits_{i = 1}^{m} {(\theta^{{1 - \tau_{i}^{q} }} - 1)^{{\phi_{i}^{\kappa } }} } } \right)}},\sqrt[q]{{\log_{\theta } \left( {1 + \prod\limits_{i = 1}^{m} {(\theta^{{\psi_{i}^{q} }} - 1)^{{\phi_{i}^{\kappa } }} } } \right)}},\sqrt[q]{{\log_{\theta } \left( {1 + \prod\limits_{i = 1}^{m} {(\theta^{{\vartheta_{i}^{q} }} - 1)^{{\phi_{i}^{\kappa } }} } } \right)}}} \right) \hfill \\ \, \oplus_{F} \left( {\sqrt[q]{{1 - \log_{\theta } \left( {1 + \frac{{(\theta^{{1 - \tau_{m + 1}^{q} }} - 1)^{{\phi_{m + 1}^{\kappa } }} }}{{(\theta - 1)^{{\phi_{m + 1}^{\kappa } - 1}} }}} \right)}},\sqrt[q]{{\log_{\theta } \left( {1 + \frac{{(\theta^{{\psi_{m + 1}^{q} }} - 1)^{{\phi_{m + 1}^{\kappa } }} }}{{(\theta - 1)^{{\phi_{m + 1}^{\kappa } - 1}} }}} \right)}},\sqrt[q]{{\log_{\theta } \left( {1 + \frac{{(\theta^{{\vartheta_{m + 1}^{q} }} - 1)^{{\phi_{m + 1}^{\kappa } }} }}{{(\theta - 1)^{{\phi_{m + 1}^{\kappa } - 1}} }}} \right)}}} \right) \hfill \\ = \left( {\sqrt[q]{{1 - \log_{\theta } \left( {1 + \frac{{\left( {\prod\limits_{i = 1}^{m} {(\theta^{{1 - \tau_{i}^{q} }} - 1)^{{\phi_{i}^{\kappa } }} } } \right)(\theta^{{1 - \tau_{m + 1}^{q} }} - 1)^{{\phi_{m + 1}^{\kappa } }} }}{{(\theta - 1)^{{(\sum\nolimits_{i = 1}^{m + 1} {\phi_{i}^{\kappa } } ) - 1}} }}} \right)}},\sqrt[q]{{\log_{\theta } \left( {1 + \frac{{\left( {\prod\limits_{i = 1}^{m} {(\theta^{{\psi_{i}^{q} }} - 1)^{{\phi_{i}^{\kappa } }} } } \right)(\theta^{{1 - \psi_{m + 1}^{q} }} - 1)^{{\phi_{m + 1}^{\kappa } }} }}{{(\theta - 1)^{{(\sum\nolimits_{i = 1}^{m + 1} {\phi_{i}^{\kappa } } ) - 1}} }}} \right)}},\sqrt[q]{{\log_{\theta } \left( {1 + \frac{{\left( {\prod\limits_{i = 1}^{m} {(\theta^{{\vartheta_{i}^{q} }} - 1)^{{\phi_{i}^{\kappa } }} } } \right)(\theta^{{1 - \vartheta_{m + 1}^{q} }} - 1)^{{\phi_{m + 1}^{\kappa } }} }}{{(\theta - 1)^{{(\sum\nolimits_{i = 1}^{m + 1} {\phi_{i}^{\kappa } } ) - 1}} }}} \right)}}} \right) \hfill \\ \end{gathered} $$

Since $\sum\nolimits_{i = 1}^{m + 1} {\phi_{i}^{\kappa } } = 1$, we can obtain

$$ T - SFFSA(\delta_{1} ,\delta_{2} , \ldots ,\delta_{m} ,\delta_{m + 1} ) = \left( {\sqrt[q]{{1 - \log_{\theta } \left( {1 + \prod\limits_{i = 1}^{m + 1} {(\theta^{{1 - \tau_{i}^{q} }} - 1)^{{\phi_{i}^{\kappa } }} } } \right)}},\sqrt[q]{{\log_{\theta } \left( {1 + \prod\limits_{i = 1}^{m + 1} {(\theta^{{\psi_{i}^{q} }} - 1)^{{\phi_{i}^{\kappa } }} } } \right)}},\sqrt[q]{{\log_{\theta } \left( {1 + \prod\limits_{i = 1}^{m + 1} {(\theta^{{\vartheta_{i}^{q} }} - 1)^{{\phi_{i}^{\kappa } }} } } \right)}}} \right) $$

So, which means that the Eq. (10) holds for n = m + 1.

Hence, the Eq. (10) holds for all n. Therefore, the proof of Theorem 2 is complete.

According to Theorem 1 and Theorem 2, we can easily prove that the T-SFFSA operator has the following properties:

Theorem 3

Suppose δ_i (i = 1, 2,…, n) is a family of T-SFNs,

• (1) (Idempotency). If δ_i = δ, then $T - SFFSA(\delta_{1} ,\delta_{2} , \ldots ,\delta_{n} ) = \delta$.

• (2) (Monotonicity). If δ^*_i (i = 1, 2,…, n) is also a set of T-SFNs, and δ_i ≤ δ_i^*, then

$$ T - SFFSA(\delta_{1} ,\delta_{2} , \ldots ,\delta_{n} ) \le T - SFFSA(\delta_{1}^{ * } ,\delta_{2}^{ * } , \ldots ,\delta_{n}^{ * } ) $$

• (3) (Boundedness). If

$P^{ - } = \min \delta_{i} = (\mathop {\min }\limits_{i} (\tau_{i} ),\mathop {\max }\limits_{i} (\psi_{i} ),\mathop {\max }\limits_{i} (\vartheta_{i} ))$, $P^{ + } = \max \delta_{i} = (\mathop {\max }\limits_{i} (\tau_{i} ),\mathop {\min }\limits_{i} (\psi_{i} ),\mathop {\min }\limits_{i} (\vartheta_{i} ))$, then. $P^{ - } \le T - SFFSA(\delta_{1} ,\delta_{2} , \ldots ,\delta_{n} ) \le P^{ + }$.

Definition 10

Suppose δ_i (i = 1, 2,…, n) is a family of T-SFNs, w = (w₁,w₂,…,w_n)^T is weight vector, and $\sum\nolimits_{i = 1}^{n} {w_{i} = 1}$, w_i ≥ 0. The T-SFFSWA operator is defined as:

$$ T - SFFSWA\left( {\delta_{1} ,\delta_{2} , \ldots ,\delta_{n} } \right) = \mathop { \oplus_{F} }\limits_{i = 1}^{n} \left( {\Phi_{i}^{\kappa } \cdot_{F} \delta_{i} } \right) $$

(11)

where $\Phi_{i}^{\kappa } = \frac{{w_{i} \exp \left( {{{T_{i} } \mathord{\left/ {\vphantom {{T_{i} } \kappa }} \right. \kern-\nulldelimiterspace} \kappa }} \right)}}{{\sum\nolimits_{i = 1}^{n} {w_{i} \exp \left( {{{T_{i} } \mathord{\left/ {\vphantom {{T_{i} } \kappa }} \right. \kern-\nulldelimiterspace} \kappa }} \right)} }}$ (κ > 0) satisfies $\Phi_{i}^{\kappa } \in [0,1]$ $\sum\nolimits_{i = 1}^{n} {\Phi_{i}^{\kappa } = 1}$. $T_{i} = \prod\nolimits_{l = 1}^{i - 1} {sc(\delta_{l} )}$(i = 2,3,…n), T₁ = 1, and sc(δ_l) is the score function of T-SFN δ_l.

Theorem 4

Suppose δ_i (i = 1, 2,…, n) is a collection of T-SFNs, q ≥ 1, θ > 1. Then the result by applying the Eq. (11) is also a T-SFN, and even.

$$ T - SFFSWA\left( {\delta_{1} ,\delta_{2} , \ldots ,\delta_{n} } \right) = \left( {\sqrt[q]{{1 - \log_{\theta } \left( {1 + \prod\limits_{i = 1}^{n} {\left( {\theta^{{1 - \tau_{i}^{q} }} - 1} \right)^{{\Phi_{i}^{\kappa } }} } } \right)}},\sqrt[q]{{\log_{\theta } \left( {1 + \prod\limits_{i = 1}^{n} {\left( {\theta^{{\psi_{i}^{q} }} - 1} \right)^{{\Phi_{i}^{\kappa } }} } } \right)}},\sqrt[q]{{\log_{\theta } \left( {1 + \prod\limits_{i = 1}^{n} {\left( {\theta^{{\vartheta_{i}^{q} }} - 1} \right)^{{\Phi_{i}^{\kappa } }} } } \right)}}} \right) $$

(12)

Similar to the proof of Theorem 2, which we omit here.

Definition 11

Suppose δ_i = (τ_i, ψ_i, ϑ_i) (i = 1,2,..,n) is a collection of T-SFNs, then the T-spherical fuzzy Frank softmax geometric (T-SFFSG) operator is defined as:

$$ T - SFFSG\left( {\delta_{1} ,\delta_{2} , \ldots ,\delta_{n} } \right) = \mathop { \otimes_{F} }\limits_{i = 1}^{n} \left( {\delta_{i} } \right)^{{ \wedge_{F} \phi_{i}^{\kappa } }} $$

(13)

where $\phi_{i}^{\kappa } = \frac{{\exp \left( {{{T_{i} } \mathord{\left/ {\vphantom {{T_{i} } \kappa }} \right. \kern-\nulldelimiterspace} \kappa }} \right)}}{{\sum\nolimits_{i = 1}^{n} {\exp \left( {{{T_{i} } \mathord{\left/ {\vphantom {{T_{i} } \kappa }} \right. \kern-\nulldelimiterspace} \kappa }} \right)} }}$ satisfies $\phi_{i}^{\kappa } \in [0,1]$ $\sum\nolimits_{i = 1}^{n} {\phi_{i}^{\kappa } = 1}$, κ is modulation parameter and κ > 0. $T_{i} = \prod\nolimits_{l = 1}^{i - 1} {sc(\delta_{l} )}$(i = 2,3,…n), T₁ = 1, and sc(δ_l) is the score function of T-SFN δ_l.

Theorem 5

Suppose δ_i (i = 1, 2,…, n) is a set of T-SFNs, q ≥ 1, θ > 1. Then the aggregation result of T-SFFSG operator is still a T-SFN, i.e.,

$$ T - SFFSG\left( {\delta_{1} ,\delta_{2} , \ldots ,\delta_{n} } \right) = \left( {\sqrt[q]{{\log_{\theta } \left( {1 + \prod\limits_{i = 1}^{n} {\left( {\theta^{{\tau_{i}^{q} }} - 1} \right)^{{\phi_{i}^{\kappa } }} } } \right)}},\sqrt[q]{{1 - \log_{\theta } \left( {1 + \prod\limits_{i = 1}^{n} {\left( {\theta^{{1 - \psi_{i}^{q} }} - 1} \right)^{{\phi_{i}^{\kappa } }} } } \right)}},\sqrt[q]{{1 - \log_{\theta } \left( {1 + \prod\limits_{i = 1}^{n} {\left( {\theta^{{1 - \vartheta_{i}^{q} }} - 1} \right)^{{\phi_{i}^{\kappa } }} } } \right)}}} \right) $$

(14)

Similar to the proof of Theorem 2, it is omitted in here.

According to Theorem 1 and Theorem 5, we can easily prove that the T-SFFSG operator has the following properties:

Theorem 6

Suppose δ_i (i = 1, 2,…, n) is a family of T-SFNs,

• (1) (Idempotency). If δ_i = δ, then $T - SFFSG(\delta_{1} ,\delta_{2} , \ldots ,\delta_{n} ) = \delta$.

• (2) (Monotonicity). If δ^*_i (i = 1, 2,…, n) is also a family of T-SFNs, and δ_i ≤ δ_i^*, then.

$T - SFFSG(\delta_{1} ,\delta_{2} , \ldots ,\delta_{n} ) \le T - SFFSG(\delta_{1}^{ * } ,\delta_{2}^{ * } , \ldots ,\delta_{n}^{ * } )$.

• (3) (Boundedness). If.

$P^{ - } = \min \delta_{i} = (\mathop {\min }\limits_{i} (\tau_{i} ),\mathop {\max }\limits_{i} (\psi_{i} ),\mathop {\max }\limits_{i} (\vartheta_{i} ))$, $P^{ + } = \max \delta_{i} = (\mathop {\max }\limits_{i} (\tau_{i} ),\mathop {\min }\limits_{i} (\psi_{i} ),\mathop {\min }\limits_{i} (\vartheta_{i} ))$, then.

$P^{ - } \le T - SFFSG(\delta_{1} ,\delta_{2} , \ldots ,\delta_{n} ) \le P^{ + }$.

Definition 12

Suppose δ_i = (τ_i, ψ_i, ϑ_i) (i = 1, 2,…, n) is a family of T-SFNs, w = (w₁,w₂,…,w_n)^T is the weight vector, and $\sum\nolimits_{i = 1}^{n} {w_{i} = 1}$, w_i ≥ 0. Then the T-SFFSWG operator is defined as:

$$ T - SFFSWG\left( {\delta_{1} ,\delta_{2} , \ldots ,\delta_{n} } \right) = \mathop { \otimes_{F} }\limits_{i = 1}^{n} \left( {\delta_{i} } \right)^{{ \wedge_{F} \Phi_{i}^{\kappa } }} $$

(15)

where $\Phi_{i}^{\kappa } = \frac{{w_{i} \exp \left( {{{T_{i} } \mathord{\left/ {\vphantom {{T_{i} } \kappa }} \right. \kern-\nulldelimiterspace} \kappa }} \right)}}{{\sum\nolimits_{i = 1}^{n} {w_{i} \exp \left( {{{T_{i} } \mathord{\left/ {\vphantom {{T_{i} } \kappa }} \right. \kern-\nulldelimiterspace} \kappa }} \right)} }}$(κ > 0) satisfies $\Phi_{i}^{\kappa } \in [0,1]$ $\sum\nolimits_{i = 1}^{n} {\Phi_{i}^{\kappa } = 1}$. $T_{i} = \prod\nolimits_{l = 1}^{i - 1} {sc(\delta_{l} )}$(i = 2, 3,…n), T₁ = 1, and sc(δ_l) is the score function of T-SFN δ_l.

Theorem 7

Suppose δ_i (i = 1, 2,…, n) is a collection of T-SFNs, q ≥ 1, θ > 1. Then the aggregation result of T-SFFSG operator in Eq. (15) is still a T-SFN, i.e.,

$$ \begin{gathered} T - SFFSWG\left( {\delta_{1} ,\delta_{2} , \ldots ,\delta_{n} } \right) = \hfill \\ \left( {\sqrt[q]{{\log_{\theta } \left( {1 + \prod\limits_{i = 1}^{n} {\left( {\theta^{{\tau_{i}^{q} }} - 1} \right)^{{\Phi_{i}^{\kappa } }} } } \right)}},\sqrt[q]{{1 - \log_{\theta } \left( {1 + \prod\limits_{i = 1}^{n} {\left( {\theta^{{1 - \psi_{i}^{q} }} - 1} \right)^{{\Phi_{i}^{\kappa } }} } } \right)}},\sqrt[q]{{1 - \log_{\theta } \left( {1 + \prod\limits_{i = 1}^{n} {\left( {\theta^{{1 - \vartheta_{i}^{q} }} - 1} \right)^{{\Phi_{i}^{\kappa } }} } } \right)}}} \right) \hfill \\ \end{gathered} $$

(16)

The proof emulates from Theorem 2.

3.3 The Family Analysis of Proposed AOs

We can obtain the following several particular cases under different decision scenarios.

Theorem 8

Suppose δ_i = (τ_i, ψ_i, ϑ_i) (i = 1, 2,…, n) is a family of T-SFNs, w = (w₁,w₂,…,w_n)^T is the weight vector, and $\sum\nolimits_{i = 1}^{n} {w_{i} = 1}$, w_i ≥ 0. Then.

• (1) If q = 1, ψ_i = 0, θ → 1, then the T-SFFSWA and T-SFFSWG operators are reduced to the softmax intuitionistic fuzzy weight averaging and geometric operators, i.e., SIFWA and SIFWG [35].

$$ \mathop {\lim }\limits_{\theta \to 1} T - SFFSWA_{q = 1} (\delta_{1} ,\delta_{2} , \ldots ,\delta_{n} ) = SIFWA(\delta_{1} ,\delta_{2} , \ldots ,\delta_{n} ) = \left( {1 - \prod\limits_{i = 1}^{n} {\left( {1 - \tau_{i} } \right)^{{\frac{{w_{i} \exp \left( {{{T_{i} } \mathord{\left/ {\vphantom {{T_{i} } \kappa }} \right. \kern-\nulldelimiterspace} \kappa }} \right)}}{{\sum\nolimits_{i = 1}^{n} {w_{i} \exp \left( {{{T_{i} } \mathord{\left/ {\vphantom {{T_{i} } \kappa }} \right. \kern-\nulldelimiterspace} \kappa }} \right)} }}}} } ,\prod\limits_{i = 1}^{n} {\left( {\vartheta_{i} } \right)^{{\frac{{w_{i} \exp \left( {{{T_{i} } \mathord{\left/ {\vphantom {{T_{i} } \kappa }} \right. \kern-\nulldelimiterspace} \kappa }} \right)}}{{\sum\nolimits_{i = 1}^{n} {w_{i} \exp \left( {{{T_{i} } \mathord{\left/ {\vphantom {{T_{i} } \kappa }} \right. \kern-\nulldelimiterspace} \kappa }} \right)} }}}} } } \right) $$

(17)

$$ \mathop {\lim }\limits_{\theta \to 1} T - SFFSWG_{q = 1} (\delta_{1} ,\delta_{2} , \ldots ,\delta_{n} ) = SIFWG(\delta_{1} ,\delta_{2} , \ldots ,\delta_{n} ) = \left( {\prod\limits_{i = 1}^{n} {\left( {\tau_{i} } \right)^{{\frac{{w_{i} \exp \left( {{{T_{i} } \mathord{\left/ {\vphantom {{T_{i} } \kappa }} \right. \kern-\nulldelimiterspace} \kappa }} \right)}}{{\sum\nolimits_{i = 1}^{n} {w_{i} \exp \left( {{{T_{i} } \mathord{\left/ {\vphantom {{T_{i} } \kappa }} \right. \kern-\nulldelimiterspace} \kappa }} \right)} }}}} } ,1 - \prod\limits_{i = 1}^{n} {\left( {1 - \vartheta_{i} } \right)^{{\frac{{w_{i} \exp \left( {{{T_{i} } \mathord{\left/ {\vphantom {{T_{i} } \kappa }} \right. \kern-\nulldelimiterspace} \kappa }} \right)}}{{\sum\nolimits_{i = 1}^{n} {w_{i} \exp \left( {{{T_{i} } \mathord{\left/ {\vphantom {{T_{i} } \kappa }} \right. \kern-\nulldelimiterspace} \kappa }} \right)} }}}} } } \right) $$

(18)

• (2) If q = 1, ψ_i = 0, κ →  + ∞, θ → 1, then the T-SFFSWA and T-SFFSWG operators are reduced to the intuitionistic fuzzy weighted averaging and geometric operators, i.e., IFWA and IFWG [46].

$$ \mathop {\lim }\limits_{\begin{subarray}{l} \theta \to 1 \\ \kappa \to + \infty \end{subarray} } T - SFFSWA_{q = 1} (\delta_{1} ,\delta_{2} , \ldots ,\delta_{n} ) = IFWA(\delta_{1} ,\delta_{2} , \ldots ,\delta_{n} ) = \left( {1 - \prod\limits_{i = 1}^{n} {\left( {1 - \tau_{i} } \right)^{{w_{i} }} } ,\prod\limits_{i = 1}^{n} {\left( {\vartheta_{i} } \right)^{{w_{i} }} } } \right) $$

(19)

$$ \mathop {\lim }\limits_{\begin{subarray}{l} \theta \to 1 \\ \kappa \to + \infty \end{subarray} } T - SFFSWG_{q = 1} (\delta_{1} ,\delta_{2} , \ldots ,\delta_{n} ) = IFWG(\delta_{1} ,\delta_{2} , \ldots ,\delta_{n} ) = \left( {\prod\limits_{i = 1}^{n} {\left( {\tau_{i} } \right)^{{w_{i} }} } ,1 - \prod\limits_{i = 1}^{n} {\left( {1 - \vartheta_{i} } \right)^{{w_{i} }} } } \right) $$

(20)

• (3) If q = 2, ψ_i = 0, κ →  + ∞, θ → 1, then the T-SFFSWA and T-SFFSWG operators are reduced to the Pythagorean fuzzy weighted averaging and geometric operators, i.e., PyFWA and PyFWG [47].

$$ \mathop {\lim }\limits_{\begin{subarray}{l} \theta \to 1 \\ \kappa \to + \infty \end{subarray} } T - SFFSWA_{q = 2} (\delta_{1} ,\delta_{2} , \ldots ,\delta_{n} ) = PyFWA(\delta_{1} ,\delta_{2} , \ldots ,\delta_{n} ) = \left( {\sqrt {1 - \prod\limits_{i = 1}^{n} {\left( {1 - \tau_{i}^{2} } \right)^{{w_{i} }} } } ,\prod\limits_{i = 1}^{n} {\left( {\vartheta_{i} } \right)^{{w_{i} }} } } \right) $$

(21)

$$ \mathop {\lim }\limits_{\begin{subarray}{l} \theta \to 1 \\ \kappa \to + \infty \end{subarray} } T - SFFSWG_{q = 2} (\delta_{1} ,\delta_{2} , \ldots ,\delta_{n} ) = PyFWG(\delta_{1} ,\delta_{2} , \ldots ,\delta_{n} ) = \left( {\prod\limits_{i = 1}^{n} {\left( {\tau_{i} } \right)^{{w_{i} }} } ,\sqrt {1 - \prod\limits_{i = 1}^{n} {\left( {1 - \vartheta_{i}^{2} } \right)^{{w_{i} }} } } } \right) $$

(22)

• (4) If ψ_i = 0, κ →  + ∞, θ → 1, then the T-SFFSWA and T-SFFSWG operators are reduced to the q-rung orthopair fuzzy weighted averaging and geometric operators, i.e., q-ROFWA and q-ROFWG [48].

$$ \mathop {\lim }\limits_{\begin{subarray}{l} \theta \to 1 \\ \kappa \to + \infty \end{subarray} } T - SFFSWA(\delta_{1} ,\delta_{2} , \ldots ,\delta_{n} ) = q - ROFWA(\delta_{1} ,\delta_{2} , \ldots ,\delta_{n} ) = \left( {\sqrt[q]{{1 - \prod\limits_{i = 1}^{n} {\left( {1 - \tau_{i}^{q} } \right)^{{w_{i} }} } }},\prod\limits_{i = 1}^{n} {\left( {\vartheta_{i} } \right)^{{w_{i} }} } } \right) $$

(23)

$$ \mathop {\lim }\limits_{\begin{subarray}{l} \theta \to 1 \\ \kappa \to + \infty \end{subarray} } T - SFFSWG(\delta_{1} ,\delta_{2} , \ldots ,\delta_{n} ) = q - ROFWG(\delta_{1} ,\delta_{2} , \ldots ,\delta_{n} ) = \left( {\prod\limits_{i = 1}^{n} {\left( {\tau_{i} } \right)^{{w_{i} }} } ,\sqrt[q]{{1 - \prod\limits_{i = 1}^{n} {\left( {1 - \vartheta_{i}^{q} } \right)^{{w_{i} }} } }}} \right) $$

(24)

• (5) If q = 1, κ →  + ∞, θ → 1, then the T-SFFSWA and T-SFFSWG operators are reduced to the picture fuzzy weighted averaging and geometric operators, i.e., PFWA and PFWG [49].

$$ \mathop {\lim }\limits_{\begin{subarray}{l} \theta \to 1 \\ \kappa \to + \infty \end{subarray} } T - SFFSWA_{q = 1} (\delta_{1} ,\delta_{2} , \ldots ,\delta_{n} ) = PFWA(\delta_{1} ,\delta_{2} , \ldots ,\delta_{n} ) = \left( {1 - \prod\limits_{i = 1}^{n} {\left( {1 - \tau_{i} } \right)^{{w_{i} }} } ,\prod\limits_{i = 1}^{n} {\left( {\psi_{i} } \right)^{{w_{i} }} } ,\prod\limits_{i = 1}^{n} {\left( {\vartheta_{i} } \right)^{{w_{i} }} } } \right) $$

(25)

$$ \mathop {\lim }\limits_{\begin{subarray}{l} \theta \to 1 \\ \kappa \to + \infty \end{subarray} } T - SFFSWG_{q = 1} (\delta_{1} ,\delta_{2} , \ldots ,\delta_{n} ) = PFWG(\delta_{1} ,\delta_{2} , \ldots ,\delta_{n} ) = \left( {\prod\limits_{i = 1}^{n} {\left( {\tau_{i} } \right)^{{w_{i} }} } ,1 - \prod\limits_{i = 1}^{n} {\left( {1 - \psi_{i} } \right)^{{w_{i} }} } ,1 - \prod\limits_{i = 1}^{n} {\left( {1 - \vartheta_{i} } \right)^{{w_{i} }} } } \right) $$

(26)

• (6) If q = 2, κ →  + ∞, θ → 1, then the T-SFFSWA and T-SFFSWG operators are reduced to the spherical fuzzy weighted averaging and geometric operators, i.e., SFWA and SFWG [50, 51].

$$ \mathop {\lim }\limits_{\begin{subarray}{l} \theta \to 1 \\ \kappa \to + \infty \end{subarray} } T - SFFSWA_{q = 2} (\delta_{1} ,\delta_{2} , \ldots ,\delta_{n} ) = SFWA(\delta_{1} ,\delta_{2} , \ldots ,\delta_{n} ) = \left( {\sqrt {1 - \prod\limits_{i = 1}^{n} {\left( {1 - \tau_{i}^{2} } \right)^{{w_{i} }} } } ,\prod\limits_{i = 1}^{n} {\left( {\psi_{i} } \right)^{{w_{i} }} } ,\prod\limits_{i = 1}^{n} {\left( {\vartheta_{i} } \right)^{{w_{i} }} } } \right) $$

(27)

$$ \mathop {\lim }\limits_{\begin{subarray}{l} \theta \to 1 \\ \kappa \to + \infty \end{subarray} } T - SFFSWG_{q = 2} (\delta_{1} ,\delta_{2} , \ldots ,\delta_{n} ) = SFWG(\delta_{1} ,\delta_{2} , \ldots ,\delta_{n} ) = \left( {\prod\limits_{i = 1}^{n} {\left( {\tau_{i} } \right)^{{w_{i} }} } ,\sqrt {1 - \prod\limits_{i = 1}^{n} {\left( {1 - \psi_{i}^{2} } \right)^{{w_{i} }} } } ,\sqrt {1 - \prod\limits_{i = 1}^{n} {\left( {1 - \vartheta_{i}^{2} } \right)^{{w_{i} }} } } } \right) $$

(28)

• (7) If κ →  + ∞, θ → 1, then the T-SFFSWA and T-SFFSWG operators are reduced to the T-spherical fuzzy weighted averaging and geometric operators, i.e., T-SFWA and T-SFWG [52].

$$ \mathop {\lim }\limits_{\begin{subarray}{l} \theta \to 1 \\ \kappa \to + \infty \end{subarray} } T - SFFSWA(\delta_{1} ,\delta_{2} , \ldots ,\delta_{n} ) = T - SFWA(\delta_{1} ,\delta_{2} , \ldots ,\delta_{n} ) = \left( {\sqrt[q]{{1 - \prod\limits_{i = 1}^{n} {\left( {1 - \tau_{i}^{2} } \right)^{{w_{i} }} } }},\prod\limits_{i = 1}^{n} {\left( {\psi_{i} } \right)^{{w_{i} }} } ,\prod\limits_{i = 1}^{n} {\left( {\vartheta_{i} } \right)^{{w_{i} }} } } \right) $$

(29)

$$ \mathop {\lim }\limits_{\begin{subarray}{l} \theta \to 1 \\ \kappa \to + \infty \end{subarray} } T - SFFSWG(\delta_{1} ,\delta_{2} , \ldots ,\delta_{n} ) = T - SFWG(\delta_{1} ,\delta_{2} , \ldots ,\delta_{n} ) = \left( {\prod\limits_{i = 1}^{n} {\left( {\tau_{i} } \right)^{{w_{i} }} } ,\sqrt[q]{{1 - \prod\limits_{i = 1}^{n} {\left( {1 - \psi_{i}^{2} } \right)^{{w_{i} }} } }},\sqrt[q]{{1 - \prod\limits_{i = 1}^{n} {\left( {1 - \vartheta_{i}^{2} } \right)^{{w_{i} }} } }}} \right) $$

(30)

• (8) If κ →  + ∞, then the T-SFFSWA and T-SFFSWG operators are reduced to the T-spherical Frank weighted averaging and geometric operators, i.e., T-SFFWA and T-SFFWG [53].

$$ \begin{gathered} \mathop {\lim }\limits_{\kappa \to + \infty } T - SFFSWA\left( {\delta_{1} ,\delta_{2} , \ldots ,\delta_{n} } \right){ = }T - SFFWA\left( {\delta_{1} ,\delta_{2} , \ldots ,\delta_{n} } \right) \hfill \\ \, = \left( {\sqrt[q]{{1 - \log_{\theta } \left( {1 + \prod\limits_{i = 1}^{n} {\left( {\theta^{{1 - \tau_{i}^{q} }} - 1} \right)^{{w_{i} }} } } \right)}},\sqrt[q]{{\log_{\theta } \left( {1 + \prod\limits_{i = 1}^{n} {\left( {\theta^{{\psi_{i}^{q} }} - 1} \right)^{{w_{i} }} } } \right)}},\sqrt[q]{{\log_{\theta } \left( {1 + \prod\limits_{i = 1}^{n} {\left( {\theta^{{\vartheta_{i}^{q} }} - 1} \right)^{{w_{i} }} } } \right)}}} \right) \hfill \\ \end{gathered} $$

(31)

$$ \begin{gathered} \mathop {\lim }\limits_{\kappa \to + \infty } T - SFFSWG\left( {\delta_{1} ,\delta_{2} , \ldots ,\delta_{n} } \right) = T - SFFWG\left( {\delta_{1} ,\delta_{2} , \ldots ,\delta_{n} } \right) \hfill \\ \, = \left( {\sqrt[q]{{\log_{\theta } \left( {1 + \prod\limits_{i = 1}^{n} {\left( {\theta^{{\tau_{i}^{q} }} - 1} \right)^{{w_{i} }} } } \right)}},\sqrt[q]{{1 - \log_{\theta } \left( {1 + \prod\limits_{i = 1}^{n} {\left( {\theta^{{1 - \psi_{i}^{q} }} - 1} \right)^{{w_{i} }} } } \right)}},\sqrt[q]{{1 - \log_{\theta } \left( {1 + \prod\limits_{i = 1}^{n} {\left( {\theta^{{1 - \vartheta_{i}^{q} }} - 1} \right)^{{w_{i} }} } } \right)}}} \right) \hfill \\ \end{gathered} $$

(32)

• (9) If q = 1, κ →  + ∞, θ →  + ∞, then the T-SFFSWA and T-SFFSWG operators are reduced to the picture fuzzy traditional arithmetic weighted mean operator, i.e.,

$$ \mathop {\lim }\limits_{\begin{subarray}{l} \theta \to + \infty \\ \kappa \to + \infty \end{subarray} } T - SFFSWA_{q = 1} (\delta_{1} ,\delta_{2} , \ldots ,\delta_{n} ) = \mathop {\lim }\limits_{\begin{subarray}{l} \theta \to + \infty \\ \kappa \to + \infty \end{subarray} } T - SFFSWG_{q = 1} (\delta_{1} ,\delta_{2} , \ldots ,\delta_{n} ) = \left( {\sum\limits_{i = 1}^{n} {w_{i} \tau_{i} } ,\sum\limits_{i = 1}^{n} {w_{i} \psi_{i} } ,\sum\limits_{i = 1}^{n} {w_{i} \vartheta_{i} } } \right) $$

(33)

• (10) If q = 2, κ →  + ∞, θ →  + ∞, then the T-SFFSWA and T-SFFSWG operators are reduced to the spherical fuzzy traditional arithmetic weighted mean operator, i.e.,

$$ \mathop {\lim }\limits_{\begin{subarray}{l} \theta \to + \infty \\ \kappa \to + \infty \end{subarray} } T - SFFSWA_{q = 2} (\delta_{1} ,\delta_{2} , \ldots ,\delta_{n} ) = \mathop {\lim }\limits_{\begin{subarray}{l} \theta \to + \infty \\ \kappa \to + \infty \end{subarray} } T - SFFSWG_{q = 2} (\delta_{1} ,\delta_{2} , \ldots ,\delta_{n} ) = \left( {\sqrt {\sum\limits_{i = 1}^{n} {w_{i} \tau_{i}^{2} } } ,\sqrt {\sum\limits_{i = 1}^{n} {w_{i} \psi_{i}^{2} } } ,\sqrt {\sum\limits_{i = 1}^{n} {w_{i} \vartheta_{i}^{2} } } } \right) $$

(34)

Remark 1

It is worth noting that parameter κ (κ > 0) can reflect the priority relationship among decision variables, which means that DMs can flexibly choose the value of κ according to the actual decision situation. The smaller the κ value is, the more obvious the priority relationship between decision variables is; otherwise, the less obvious the priority relationship between decision variables is. When κ →  + ∞, the priority relationship between decision variables is not considered, i.e., T-SFFWA and T-SFFWG, see Eqs. (31, 32).

3.4 Monotonicity Analysis on Parameter θ

In this subsection, we analyze the influence of parameter θ on the monotonicity of the T-SFFSWA and T-SFFSWG operators. Furthermore, we also analyze the relationship between the two operators.

Theorem 9

For a set of T-SFNs, the score value of aggregation result calculated by T-SFFSWA operator decreases monotonically with θ, while the score value of aggregation result calculated by T-SFFSWG operator increases monotonically with θ.

Proof

We first prove that the score function of the aggregation result calculated by T-SFFSWA operator decreases monotonically with θ. From Definition 2, the score function of Eq. (12) can be obtained.

$$ \begin{gathered} sc(T - SFFSWA(\delta_{1} ,\delta_{2} , \ldots ,\delta_{n} )) = f(\theta ) \hfill \\ = \frac{1}{2}\left( {2 - \log_{\theta } \left( {1 + \prod\limits_{i = 1}^{n} {\left( {\theta^{{1 - \tau_{i}^{q} }} - 1} \right)^{{\Phi_{i}^{\kappa } }} } } \right) - \log_{\theta } \left( {1 + \prod\limits_{i = 1}^{n} {\left( {\theta^{{\psi_{i}^{q} }} - 1} \right)^{{\Phi_{i}^{\kappa } }} } } \right) - \log_{\theta } \left( {1 + \prod\limits_{i = 1}^{n} {\left( {\theta^{{\vartheta_{i}^{q} }} - 1} \right)^{{\Phi_{i}^{\kappa } }} } } \right)} \right) \hfill \\ \end{gathered} $$

Let $f(\theta ){ = }\frac{1}{2}\left( {2 - g(\theta )} \right)$, $g(\theta ) = \log_{\theta } \left( {1 + \prod\limits_{i = 1}^{n} {\left( {\theta^{{1 - \tau_{i}^{q} }} - 1} \right)^{{\Phi_{i}^{\kappa } }} } } \right) + \log_{\theta } \left( {1 + \prod\limits_{i = 1}^{n} {\left( {\theta^{{\psi_{i}^{q} }} - 1} \right)^{{\Phi_{i}^{\kappa } }} } } \right) + \log_{\theta } \left( {1 + \prod\limits_{i = 1}^{n} {\left( {\theta^{{\vartheta_{i}^{q} }} - 1} \right)^{{\Phi_{i}^{\kappa } }} } } \right)$.

We take the first-order derivative of f(θ) with respect to θ, then

$$ \frac{dg(\theta )}{{d\theta }} = \frac{{\prod\limits_{i = 1}^{n} {\left( {\theta^{{1 - \tau_{i}^{q} }} - 1} \right)^{{\Phi_{i}^{\kappa } }} \cdot \sum\limits_{i = 1}^{n} {\frac{{\Phi_{i}^{\kappa } (1 - \tau_{i}^{q} )\theta^{{ - \tau_{i}^{q} }} }}{{\theta^{{\tau_{i}^{q} }} - 1}}} } }}{{\left( {1 + \prod\limits_{i = 1}^{n} {\left( {\theta^{{1 - \tau_{i}^{q} }} - 1} \right)^{{\Phi_{i}^{\kappa } }} } } \right)\ln \theta }} + \frac{{\prod\limits_{i = 1}^{n} {\left( {\theta^{{\psi_{i}^{q} }} - 1} \right)^{{\Phi_{i}^{\kappa } }} \cdot \sum\limits_{i = 1}^{n} {\frac{{\Phi_{i}^{\kappa } \psi_{i}^{q} \theta^{{\psi_{i}^{q} - 1}} }}{{\theta^{{1 - \psi_{i}^{q} }} - 1}}} } }}{{\left( {1 + \prod\limits_{i = 1}^{n} {\left( {\theta^{{\psi_{i}^{q} }} - 1} \right)^{{\Phi_{i}^{\kappa } }} } } \right)\ln \theta }} + \frac{{\prod\limits_{i = 1}^{n} {\left( {\theta^{{\vartheta_{i}^{q} }} - 1} \right)^{{\Phi_{i}^{\kappa } }} \cdot \sum\limits_{i = 1}^{n} {\frac{{\Phi_{i}^{\kappa } \vartheta_{i}^{q} \theta^{{\vartheta_{i}^{q} - 1}} }}{{\theta^{{1 - \vartheta_{i}^{q} }} - 1}}} } }}{{\left( {1 + \prod\limits_{i = 1}^{n} {\left( {\theta^{{\vartheta_{i}^{q} }} - 1} \right)^{{\Phi_{i}^{\kappa } }} } } \right)\ln \theta }} $$

Since θ > 1, 0 ≤ τ_i, ψ_i, ϑ_i, $\Phi_{i}^{\kappa }$ ≤ 1, then $(\theta^{{1 - \tau_{i}^{q} }} - 1)^{{\Phi_{i}^{\kappa } }} \ge 0$, $1 - \tau_{i}^{q} \ge 0$, $\theta^{{ - \tau_{i}^{q} }} \ge 0$, $\theta^{{\tau_{i}^{q} }} - 1 \ge 0$; $(\theta^{{\psi_{i}^{q} }} - 1)^{{\Phi_{i}^{\kappa } }} \ge 0$, $\theta^{{\psi_{i}^{q} - 1}} \ge 0$, $\theta^{{1 - \psi_{i}^{q} }} - 1 \ge 0$; $(\theta^{{\vartheta_{i}^{q} }} - 1)^{{\Phi_{i}^{\kappa } }} \ge 0$, $\theta^{{\vartheta_{i}^{q} - 1}} \ge 0$, $\theta^{{1 - \vartheta_{i}^{q} }} - 1 \ge 0$.

So, $\frac{dg(\theta )}{{d\theta }} \ge 0$, and since $f(\theta ){ = }\frac{1}{2}\left( {2 - g(\theta )} \right)$.

Hence, f(θ) decreases monotonically with θ, namely, the score function of the aggregation result calculated by the T-SFFSWA operator decreases monotonically with θ. In the same way, the score function of T-SFFSWG operator increases monotonically with θ can also be proved to be true. Therefore, the Theorem 9 holds.

Remark 2

The T-SFFSWA and T-SFFSWG operators have monotonicity with respect to parameter θ (θ > 1), which indicates that DMs can choose the value of parameter θ flexibly to express their risk preference. In the actual decision-making situation, if θ → 1, the T-SFFSWA operator means that the DMs seek to get positive results (i.e., risk seeking), while the T-SFFSWG operator means that the DMs averse to obtain negative results (i.e., risk aversion). On the contrary, if θ →  + ∞, the T-SFFSWA operator indicates that the DMs have the preference of risk aversion, while the T-SFFSWG operator show that the DMs have the preference of risk seeking.

Theorem 10

If δ_i (i = 1, 2,…, n) is a family of T-SFNs, then the T-SFFSWA operator is greater than the T-SFFSWG operator, i.e., T-SFFSWA (δ₁, δ₂,…, δ_n) > T-SFFSWG (δ₁, δ₂,…, δ_n), (θ > 1, κ > 0, q ≥ 1).

Proof

Let the score function of T-SFFSWA (δ₁, δ₂,…, δ_n) be sc(A) and the score function of T-SFFSWG (δ₁, δ₂,…, δ_n) be sc(G). According to Eq. (2), we have.

$$ sc(A) = \frac{1}{2}\left( {2 - \log_{\theta } \left( {1 + \prod\limits_{i = 1}^{n} {\left( {\theta^{{1 - \tau_{i}^{q} }} - 1} \right)^{{\Phi_{i}^{\kappa } }} } } \right) - \log_{\theta } \left( {1 + \prod\limits_{i = 1}^{n} {\left( {\theta^{{\psi_{i}^{q} }} - 1} \right)^{{\Phi_{i}^{\kappa } }} } } \right) - \log_{\theta } \left( {1 + \prod\limits_{i = 1}^{n} {\left( {\theta^{{\vartheta_{i}^{q} }} - 1} \right)^{{\Phi_{i}^{\kappa } }} } } \right)} \right) $$

$$ sc(G) = \frac{1}{2}\left( {\log_{\theta } \left( {1 + \prod\limits_{i = 1}^{n} {\left( {\theta^{{\tau_{i}^{q} }} - 1} \right)^{{\Phi_{i}^{\kappa } }} } } \right) + \log_{\theta } \left( {1 + \prod\limits_{i = 1}^{n} {\left( {\theta^{{1 - \psi_{i}^{q} }} - 1} \right)^{{\Phi_{i}^{\kappa } }} } } \right) + \log_{\theta } \left( {1 + \prod\limits_{i = 1}^{n} {\left( {\theta^{{1 - \vartheta_{i}^{q} }} - 1} \right)^{{\Phi_{i}^{\kappa } }} } } \right) - 1} \right) $$

Then,

$$ \begin{gathered} sc(A) - sc(G) \hfill \\ = \frac{1}{2}\left( {2 - \log_{\theta } \left( {1 + \prod\limits_{i = 1}^{n} {\left( {\theta^{{1 - \tau_{i}^{q} }} - 1} \right)^{{\Phi_{i}^{\kappa } }} } } \right) - \log_{\theta } \left( {1 + \prod\limits_{i = 1}^{n} {\left( {\theta^{{\psi_{i}^{q} }} - 1} \right)^{{\Phi_{i}^{\kappa } }} } } \right) - \log_{\theta } \left( {1 + \prod\limits_{i = 1}^{n} {\left( {\theta^{{\vartheta_{i}^{q} }} - 1} \right)^{{\Phi_{i}^{\kappa } }} } } \right)} \right) \hfill \\ - \frac{1}{2}\left( {\log_{\theta } \left( {1 + \prod\limits_{i = 1}^{n} {\left( {\theta^{{\tau_{i}^{q} }} - 1} \right)^{{\Phi_{i}^{\kappa } }} } } \right) + \log_{\theta } \left( {1 + \prod\limits_{i = 1}^{n} {\left( {\theta^{{1 - \psi_{i}^{q} }} - 1} \right)^{{\Phi_{i}^{\kappa } }} } } \right) + \log_{\theta } \left( {1 + \prod\limits_{i = 1}^{n} {\left( {\theta^{{1 - \vartheta_{i}^{q} }} - 1} \right)^{{\Phi_{i}^{\kappa } }} } } \right) - 1} \right) \hfill \\ = \frac{1}{2}\left\{ \begin{gathered} 1 + \hfill \\ \left( {1 - \log_{\theta } \left( {1 + \prod\limits_{i = 1}^{n} {\left( {\theta^{{1 - \tau_{i}^{q} }} - 1} \right)^{{\Phi_{i}^{\kappa } }} } } \right) - \log_{\theta } \left( {1 + \prod\limits_{i = 1}^{n} {\left( {\theta^{{\psi_{i}^{q} }} - 1} \right)^{{\Phi_{i}^{\kappa } }} } } \right) - \log_{\theta } \left( {1 + \prod\limits_{i = 1}^{n} {\left( {\theta^{{\vartheta_{i}^{q} }} - 1} \right)^{{\Phi_{i}^{\kappa } }} } } \right)} \right) + \hfill \\ \left( {1 - \log_{\theta } \left( {1 + \prod\limits_{i = 1}^{n} {\left( {\theta^{{\tau_{i}^{q} }} - 1} \right)^{{\Phi_{i}^{\kappa } }} } } \right) - \log_{\theta } \left( {1 + \prod\limits_{i = 1}^{n} {\left( {\theta^{{1 - \psi_{i}^{q} }} - 1} \right)^{{\Phi_{i}^{\kappa } }} } } \right) - \log_{\theta } \left( {1 + \prod\limits_{i = 1}^{n} {\left( {\theta^{{1 - \vartheta_{i}^{q} }} - 1} \right)^{{\Phi_{i}^{\kappa } }} } } \right)} \right) \hfill \\ \end{gathered} \right\} \hfill \\ \end{gathered} $$

Since the T-SFFSWA and T-SFFSWG operators are T-SFNs according to Theorems 4 and 7, and they satisfy the condition in Definition 1, that is, $0 \le \tau_{\Im }^{q} (x) + \psi_{\Im }^{q} (x) + \vartheta_{\Im }^{q} (x) \le 1$.

So we can obtain $Sc(A) - Sc(G) \ge \frac{1}{2} > 0$.

Therefore, we have proved that T-SFFSWA (δ₁, δ₂,…, δ_n) > T-SFFSWG (δ₁, δ₂,…, δ_n).

Remark 3

The T-SFFSWA operator is always greater than the T-SFFSWG operator, which means that the T-SFFSWA operator is suitable for DMs with optimistic attitude, and parameter θ can describe the level of optimistic decision attitude, while the T-SFFSWA operator is suitable for DMs with pessimistic attitude, and parameter θ can describe the level of pessimistic decision attitude.

In summary, we can find that different values of θ contained in the AOs proposed in this paper can indicate the type and degree of DMs’ risk preference from the monotonicity in the Theorem 9. The score function of T-SFFSWA operator shows a decreasing trend in the range of θ values. When the DM is risk aversion, a larger parameter value is taken. When the DM is risk seeking, the smaller parameter value is taken. However, the score function of T-SFFSWG operator shows an overall increasing trend within the θ value range. According to the type of risk preference of DMs, the method for taking θ value is opposite to the parameter value rule in the T-SFFSWA operator. In addition, the size relationship between two AOs in Theorem 10 shows that the T-SFFSWA operator has a higher comprehensive evaluation value and is suitable for optimistic DMs. The θ also can describe the level of optimism of DMs, while the T-SFFSWG operator is suitable for pessimistic DMs, and the DMs’ pessimistic level is represented by the θ. Therefore, when the individual assessment information is fused by the T-SFFSWA or T-SFFSWG operator, the aggregated result indicates that DMs with decision attitude (optimistic or pessimistic) can flexibly adjust the type of risk preference (seeking or aversion) through θ.

3.5 An Improved CoCoSo Method for MAGDM with T-SFNs

As illustrated in Fig. 2, this paper proposes a T-SF MAGDM framework based on the improved CoCoSo method, in it, we establish two independent and parallel calculation processes according to the characteristics of proposed AOs in sub-Sect. 3.4, namely the information processing of optimistic and pessimistic decision attitude with risk preference. There are three stages here. The first stage is to collect experts’ evaluation data and construct T-SF decision matrix (T-SFDM) and T-SF direct relation matrix (T-SFDRM). In the second stage (steps 1 ~ 4), the T-SFFSWA and T-SFFSWG operators are utilized to fuse experts’ individual evaluation information, and the extended DEMATEL and similarity measure to determine the subjective and objective combined weight of attribute. In the third stage (steps 5 ~ 8), the T-SFFSWA and T-SFFSWG operators are applied to calculate the performance values of alternatives, and the T-SF Hamming distance is employed to de fuzzy (calculate the relative closeness degree of alternative).

Fig. 2

The flowchart of improved CoCoSo method for T-SFMAGDM

For an T-SF MAGDM problem, there are m alternatives s_i (i = 1, 2,…,m) to form the alternative set as S = {s₁, s₂, …, s_m}. The attribute set is composed of n attributes h_j (j = 1, 2,…, n), which is H = {h₁, h₂,…, h_n}, and the weight vector is ω = (ω₁, ω₂,…, ω_n)^T, with $\omega_{j} \in [0,1]$, $\sum\nolimits_{j = 1}^{n} {\omega_{j} = 1}$. The expert set E = {e₁, e₂,…, e_z} is composed of z experts e_t (t = 1, 2,…, z), λ = (λ₁,λ₂,…,λ_z)^T is the weight vector of expert set E, and satisfies $\lambda_{t} \in [0,1]$, $\sum\nolimits_{t = 1}^{z} {\lambda_{t} = 1}$. Experts evaluate alternative s_i (i = 1, 2,…,m) according to attribute h_j (j = 1, 2,…, n), and then the individual T-SFDM of expert e_t is $D^{t} = \left[ {d_{ij}^{t} } \right]_{m \times n}$, $d_{ij}^{t} = (\tau_{ij}^{t} ,\psi_{ij}^{t} ,\vartheta_{ij}^{t} )$ ( i = 1, 2,…, m; j = 1, 2,…, n; t = 1, 2,…, z), meeting $0 \le \tau_{ij}^{t} ,\psi_{ij}^{t} ,\vartheta_{ij}^{t} \le 1$ and $(\tau_{ij}^{t} )^{q} + (\psi_{ij}^{t} )^{q} + (\vartheta_{ij}^{t} )^{q} \le 1$(q ≥ 1). Generally, we usually need to normalize D^t and transform it from Eq. (35) to obtain the normalized T-SFDM R^t = [r_ij^t]_m×n ( i = 1, 2,…, m; j = 1, 2,…, n; t = 1, 2,…, z).

$$ r_{ij}^{t} = \left\{ {\begin{array}{*{20}c} {d_{ij}^{t} = (\tau_{ij}^{t} ,\psi_{ij}^{t} ,\vartheta_{ij}^{t} ){ , }h_{j} \in \Psi_{1} } \\ {(d_{ij}^{t} )^{c} = (\vartheta_{ij}^{t} ,\psi_{ij}^{t} ,\tau_{ij}^{t} ), \, h_{j} \in \Psi_{2} } \\ \end{array} } \right. $$

(35)

where $(d_{ij}^{t} )^{c}$ is the complement set of T-SFN $d_{ij}^{t}$, Ψ₁ and Ψ₂ represent benefit and cost attributes, respectively. Meanwhile, expert e_t evaluates the correlation degree between attributes and constructs the individual initial T-SFDRM $\aleph^{t} = \left[ {\gamma_{jl}^{t} } \right]_{n \times n}$, $\gamma_{jl}^{t} = (\tau_{jl}^{t} ,\psi_{jl}^{t} ,\vartheta_{jl}^{t} ,)$(j, l = 1, 2,…,n; t = 1, 2,…,z), if j = l, then $\gamma_{jl}^{t} = (0,0,0)$.

Next, the detailed steps of the improved CoCoSo method are summarized.

Step 1: We used the Eqs. (36, 37) to calculate the priority weight $\varpi_{jl}^{t}$ _and $\varpi_{ij}^{t}$ of experts for T-SFDRMs ℵ^t and T-SFDMs R^t (t = 1,2,…,z), respectively.

$$ \varpi_{jl}^{t} = \frac{{\lambda_{t} \exp \left( {{{T_{jl}^{t} } \mathord{\left/ {\vphantom {{T_{jl}^{t} } \kappa }} \right. \kern-\nulldelimiterspace} \kappa }} \right)}}{{\sum\nolimits_{t = 1}^{z} {\lambda_{t} \exp \left( {{{T_{jl}^{t} } \mathord{\left/ {\vphantom {{T_{jl}^{t} } \kappa }} \right. \kern-\nulldelimiterspace} \kappa }} \right)} }} $$

(36)

$$ \varpi_{ij}^{t} = \frac{{\lambda_{t} \exp \left( {{{T_{ij}^{t} } \mathord{\left/ {\vphantom {{T_{ij}^{t} } \kappa }} \right. \kern-\nulldelimiterspace} \kappa }} \right)}}{{\sum\nolimits_{t = 1}^{z} {\lambda_{t} \exp \left( {{{T_{ij}^{t} } \mathord{\left/ {\vphantom {{T_{ij}^{t} } \kappa }} \right. \kern-\nulldelimiterspace} \kappa }} \right)} }} $$

(37)

where $T_{jl}^{t} = \prod\nolimits_{p = 1}^{t - 1} {sc(\gamma_{jl}^{p} )}$, $T_{ij}^{t} = \prod\nolimits_{p = 1}^{t - 1} {sc(r_{ij}^{p} )}$(t = 2,3,…,z), T_ij¹ = 1. λ_t is the weight of expert and κ is the modulation parameter, κ > 0.

Step 2: We adopt the T-SFFSWA and T-SFFSWG operators to fuse the individual assessment information from experts in the individual initial T-SFDRMs ℵ^t (t = 1, 2,…,z), and we can use the Eqs. (38, 39) to form the group initial T-SFDRMs $\aleph^{(1)} = \left[ {\gamma_{jl}^{(1)} } \right]_{n \times n}$ and $\aleph^{(2)} = \left[ {\gamma_{jl}^{(2)} } \right]_{n \times n}$, respectively. In the same way, we use the Eqs. (40, 41) obtain the two group T-SFDMs $M^{(1)} = \left[ {g_{ij}^{(1)} } \right]_{m \times n}$ and $M^{(2)} = \left[ {g_{ij}^{(2)} } \right]_{m \times n}$.

$$ \begin{gathered} \gamma_{jl}^{(1)} = T - SFFSWA(\gamma_{jl}^{1} ,\gamma_{jl}^{2} , \ldots ,\gamma_{jl}^{z} ) \hfill \\ = \left( {\sqrt[q]{{1 - \log_{\theta } \left( {1 + \prod\limits_{t = 1}^{z} {\left( {\theta^{{1 - (\tau_{jl}^{t} )^{q} }} - 1} \right)^{{\varpi_{jl}^{t} }} } } \right)}},\sqrt[q]{{\log_{\theta } \left( {1 + \prod\limits_{t = 1}^{z} {\left( {\theta^{{(\psi_{jl}^{t} )^{q} }} - 1} \right)^{{\varpi_{jl}^{t} }} } } \right)}},\sqrt[q]{{\log_{\theta } \left( {1 + \prod\limits_{t = 1}^{z} {\left( {\theta^{{(\vartheta_{jl}^{t} )^{q} }} - 1} \right)^{{\varpi_{jl}^{t} }} } } \right)}}} \right) \hfill \\ \end{gathered} $$

(38)

$$ \begin{gathered} \gamma_{jl}^{(2)} = T - SFFSWG(\gamma_{jl}^{1} ,\gamma_{jl}^{2} , \ldots ,\gamma_{jl}^{z} ) \hfill \\ = \left( {\sqrt[q]{{\log_{\theta } \left( {1 + \prod\limits_{t = 1}^{z} {\left( {\theta^{{(\tau_{jl}^{t} )^{q} }} - 1} \right)^{{\varpi_{jl}^{t} }} } } \right)}},\sqrt[q]{{1 - \log_{\theta } \left( {1 + \prod\limits_{t = 1}^{z} {\left( {\theta^{{1 - (\psi_{jl}^{t} )^{q} }} - 1} \right)^{{\varpi_{jl}^{t} }} } } \right)}},\sqrt[q]{{1 - \log_{\theta } \left( {1 + \prod\limits_{t = 1}^{z} {\left( {\theta^{{1 - (\vartheta_{jl}^{t} )^{q} }} - 1} \right)^{{\varpi_{jl}^{t} }} } } \right)}}} \right) \hfill \\ \end{gathered} $$

(39)

and

$$ \begin{gathered} g_{ij}^{(1)} = T - SFFSWA(r_{ij}^{1} ,r_{ij}^{2} , \ldots ,r_{ij}^{z} ) \hfill \\ = \left( {\sqrt[q]{{1 - \log_{\theta } \left( {1 + \prod\limits_{t = 1}^{z} {\left( {\theta^{{1 - (\tau_{ij}^{t} )^{q} }} - 1} \right)^{{\varpi_{ij}^{t} }} } } \right)}},\sqrt[q]{{\log_{\theta } \left( {1 + \prod\limits_{t = 1}^{z} {\left( {\theta^{{(\psi_{ij}^{t} )^{q} }} - 1} \right)^{{\varpi_{ij}^{t} }} } } \right)}},\sqrt[q]{{\log_{\theta } \left( {1 + \prod\limits_{t = 1}^{z} {\left( {\theta^{{(\vartheta_{ij}^{t} )^{q} }} - 1} \right)^{{\varpi_{ij}^{t} }} } } \right)}}} \right) \hfill \\ \end{gathered} $$

(40)

$$ \begin{gathered} g_{ij}^{(2)} = T - SFFSWG(r_{ij}^{1} ,r_{ij}^{2} , \ldots ,r_{ij}^{z} ) \hfill \\ = \left( {\sqrt[q]{{\log_{\theta } \left( {1 + \prod\limits_{t = 1}^{z} {\left( {\theta^{{(\tau_{ij}^{t} )^{q} }} - 1} \right)^{{\varpi_{ij}^{t} }} } } \right)}},\sqrt[q]{{1 - \log_{\theta } \left( {1 + \prod\limits_{t = 1}^{z} {\left( {\theta^{{1 - (\psi_{ij}^{t} )^{q} }} - 1} \right)^{{\varpi_{ij}^{t} }} } } \right)}},\sqrt[q]{{1 - \log_{\theta } \left( {1 + \prod\limits_{t = 1}^{z} {\left( {\theta^{{1 - (\vartheta_{ij}^{t} )^{q} }} - 1} \right)^{{\varpi_{ij}^{t} }} } } \right)}}} \right) \hfill \\ \end{gathered} $$

(41)

Step 3: In this step, we extend T-SFDMs, calculate the objective weight of attribute by T-SF similarity measure and obtain the subjective weight of attribute by T-SF DEMEATEL method.

Step 3.1: We construct the extended group T-SFDM EM^(ϒ) (ϒ = 1, 2).

$$ EM^{(\Upsilon )} = \begin{array}{*{20}c} {} & {\begin{array}{*{20}c} {Y_{1} , \, } & {Y_{2} , \, } & { \cdots ,} & {Y_{n} } \\ \end{array} } \\ {\begin{array}{*{20}c} {NIS} \\ {P_{1} } \\ \vdots \\ {\begin{array}{*{20}c} {P_{m} } \\ {PIS} \\ \end{array} } \\ \end{array} } & {\left[ {\begin{array}{*{20}c} {\begin{array}{*{20}c} {g_{1}^{(\Upsilon )NIS} } \\ {g_{11}^{(\Upsilon )} } \\ \vdots \\ {\begin{array}{*{20}c} {g_{m1}^{(\Upsilon )} } \\ {g_{1}^{(\Upsilon )PIS} } \\ \end{array} } \\ \end{array} } & {\begin{array}{*{20}c} {g_{2}^{(\Upsilon )NIS} } \\ {g_{12}^{(\Upsilon )} } \\ \vdots \\ {\begin{array}{*{20}c} {g_{m2}^{(\Upsilon )} } \\ {g_{2}^{(\Upsilon )PIS} } \\ \end{array} } \\ \end{array} } & {\begin{array}{*{20}c} \cdots \\ \cdots \\ \ddots \\ {\begin{array}{*{20}c} \cdots \\ \cdots \\ \end{array} } \\ \end{array} } & {\begin{array}{*{20}c} {g_{n}^{(\Upsilon )NIS} } \\ {g_{1n}^{(\Upsilon )} } \\ \vdots \\ {\begin{array}{*{20}c} {g_{mn}^{(\Upsilon )} } \\ {g_{n}^{(\Upsilon )PIS} } \\ \end{array} } \\ \end{array} } \\ \end{array} } \right]} \\ \end{array} $$

(42)

where the NIS and PIS mean the negative ideal solution (NIS) and positive ideal solution (PIS) of the group T-SFDM M^(ϒ), respectively, that is $g_{j}^{(\Upsilon )NIS} = \left( {\mathop {\min }\limits_{i} (\tau_{ij} ),\mathop {\max }\limits_{i} (\psi_{ij} ),\mathop {\max }\limits_{i} (\vartheta_{ij} )} \right)$ and $g_{j}^{(\Upsilon )PIS} = \left( {\mathop {\max }\limits_{i} (\tau_{ij} ),\mathop {\min }\limits_{i} (\psi_{ij} ),\mathop {\min }\limits_{i} (\vartheta_{ij} )} \right)$.

Step 3.2: According to the Definition 5, we use the Eq. (43) to calculate the objective weight for each attribute $w_{oj}^{(\Upsilon )}$, (ϒ = 1, 2).

$$ w_{oj}^{(\Upsilon )} = \frac{{\frac{1}{m - 1}\sum\limits_{i = 1}^{m} {\sum\limits_{\varsigma = 1,\varsigma \ne i}^{m} {\left( {1 - S(g_{ij}^{(\Upsilon )} ,g_{\varsigma j}^{(\Upsilon )} )} \right)} } }}{{\sum\limits_{j = 1}^{n} {\left( {\frac{1}{m - 1}\sum\limits_{i = 1}^{m} {\sum\limits_{\varsigma = 1,\varsigma \ne i}^{m} {\left( {1 - S(g_{ij}^{(\Upsilon )} ,g_{\varsigma j}^{(\Upsilon )} )} \right)} } } \right)} }} $$

(43)

Step 3.3: Inspired by Gül [54], we extend DEMATEL method in T-SF environment. The specific steps are as follows:

• (1) Based on the matrix operation, the group initial T-SFDRMs ℵ^(ϒ) (ϒ = 1, 2) are separated into MD sub-matrix ℵ^M(ϒ), AD sub-matrix ℵ^A(ϒ), and ND sub-matrix ℵ^N(ϒ). We employ the Eq. (44) to normalize the three sub-matrices, respectively, and the normalized MD sub-matrix X^M(ϒ), AD sub-matrix X^A(ϒ), and ND sub-matrix X^N(ϒ).

$$ x_{jl} = \frac{{y_{jl} }}{{\max \left\{ {\mathop {\max }\limits_{l} \sum\nolimits_{j = 1}^{n} {y_{jl} ,} \mathop {\max }\limits_{j} \sum\nolimits_{l = 1}^{n} {y_{jl} } } \right\}}} $$

(44)

• (2) We apply the Eq. (45) to obtain three total relation sub-matrices. Due to the form of $t_{jl}^{(\Upsilon )} = \left( {t_{jl}^{M(\Upsilon )} ,t_{jl}^{A(\Upsilon )} ,t_{jl}^{N(\Upsilon )} } \right)$, we transform the three sub-matrices into total relation matrix $T^{(\Upsilon )} = \left[ {t_{jl}^{(\Upsilon )} } \right]_{n \times n}$.

  $$ \left[ {t_{jl}^{M(\Upsilon )} } \right] = X^{M(\Upsilon )} \times \left( {1 - X^{M(\Upsilon )} } \right)^{ - 1} ; \, \left[ {t_{jl}^{A(\Upsilon )} } \right] = X^{A(\Upsilon )} \times \left( {1 - X^{A(\Upsilon )} } \right)^{ - 1} ; \, \left[ {t_{jl}^{N(\Upsilon )} } \right] = X^{N(\Upsilon )} \times \left( {1 - X^{N(\Upsilon )} } \right)^{ - 1} $$

  (45)

• (3) Furthermore, we use the T-SFWA operator [52] (see Eq. (29)) to sum the rows and columns of the total influence matrix T^(ϒ) by $\Gamma_{l}^{(\Upsilon )}$($\Gamma_{j}^{(\Upsilon )}$) and $\Lambda_{j}^{(\Upsilon )}$ (Eq. (46)), respectively, and the weights are all equal. Then, we utilize the Eq. (2) to compute the score value for $\Gamma_{j}^{(\Upsilon )}$ and $\Lambda_{j}^{(\Upsilon )}$ to obtain $sc(\Gamma_{j}^{(\Upsilon )} )$ and $sc(\Lambda_{j}^{(\Upsilon )} )$. So, the attribute’s subjective weight is computed by Eq. (47).

  $$ \Gamma_{l}^{(\Upsilon )} = \sum\limits_{j}^{n} {t_{jl}^{(\Upsilon )} } = T - SFWA(t_{1l}^{(\Upsilon )} ,t_{2l}^{(\Upsilon )} , \ldots ,t_{nl}^{(\Upsilon )} ), \, \Lambda_{j}^{(\Upsilon )} = \sum\limits_{l = 1}^{n} {t_{jl}^{(\Upsilon )} } = T - SFWA(t_{j1}^{(\Upsilon )} ,t_{j2}^{(\Upsilon )} , \ldots ,t_{jn}^{(\Upsilon )} ) $$

  (46)
  $$ w_{sj}^{(\Upsilon )} = \frac{{\sqrt {\left( {sc(\Gamma_{j}^{(\Upsilon )} ) + sc(\Lambda_{j}^{(\Upsilon )} )} \right)^{2} + \left( {sc(\Gamma_{j}^{(\Upsilon )} ) - sc(\Lambda_{j}^{(\Upsilon )} )} \right)^{2} } }}{{\sum\nolimits_{j = 1}^{n} {\sqrt {\left( {sc(\Gamma_{j}^{(\Upsilon )} ) + sc(\Lambda_{j}^{(\Upsilon )} )} \right)^{2} + \left( {sc(\Gamma_{j}^{(\Upsilon )} ) - sc(\Lambda_{j}^{(\Upsilon )} )} \right)^{2} } } }} $$

  (47)

Step 4: The Eq. (48) is adopted to compute the subjective and objective combined weight $w_{cj}^{(\Upsilon )}$, and then calculate attribute priority weight values $\omega_{ij}^{(\Upsilon )}$,$\omega_{\Theta j}^{(\Upsilon )}$ with Eq. (49).

$$ w_{cj}^{(\Upsilon )} = \varphi w_{oj}^{(\Upsilon )} + (1 - \varphi )w_{sj}^{(\Upsilon )} $$

(48)

$$ \omega_{ij}^{(\Upsilon )} = \frac{{w_{cj}^{(\Upsilon )} \exp \left( {{{T_{ij}^{(\Upsilon )} } \mathord{\left/ {\vphantom {{T_{ij}^{(\Upsilon )} } \kappa }} \right. \kern-\nulldelimiterspace} \kappa }} \right)}}{{\sum\nolimits_{j = 1}^{n} {w_{cj}^{(\Upsilon )} \exp \left( {{{T_{ij}^{(\Upsilon )} } \mathord{\left/ {\vphantom {{T_{ij}^{(\Upsilon )} } \kappa }} \right. \kern-\nulldelimiterspace} \kappa }} \right)} }}; \, \omega_{\Theta j}^{(\Upsilon )} = \frac{{w_{cj}^{(\Upsilon )} \exp \left( {{{T_{\Theta j}^{(\Upsilon )} } \mathord{\left/ {\vphantom {{T_{\Theta j}^{(\Upsilon )} } \kappa }} \right. \kern-\nulldelimiterspace} \kappa }} \right)}}{{\sum\nolimits_{j = 1}^{n} {w_{cj}^{(\Upsilon )} \exp \left( {{{T_{\Theta j}^{(\Upsilon )} } \mathord{\left/ {\vphantom {{T_{\Theta j}^{(\Upsilon )} } \kappa }} \right. \kern-\nulldelimiterspace} \kappa }} \right)} }} $$

(49)

where φ is the adjustment parameter, we set this parameter φ = 0.5. ϒ = 1, 2, “Θ”denotes NIS and PIS, respectively, and $T_{ij}^{(\Upsilon )} = \prod\nolimits_{p = 1}^{j - 1} {sc(g_{ip}^{(\Upsilon )} )}$,$T_{\Theta j}^{(\Upsilon )} = \prod\nolimits_{p = 1}^{j - 1} {sc(g_{\Theta p}^{(\Upsilon )} )}$(j = 2,3,…,n), $T_{i1}^{(\Upsilon )} = T_{\Theta 1}^{(\Upsilon )} = 1$.

Step 5: The T-SFNs of all attributes h_j in the extended group T-SFDM are aggregated by Eqs. (50, 51) to obtain the performance values of all alternatives.

$$ \left\{ {\begin{array}{*{20}c} \begin{gathered} \wp_{i}^{(1)} = T - SFFSWA(g_{i1}^{(1)} ,g_{i2}^{(1)} , \ldots ,g_{in}^{(1)} ) \hfill \\ \, = \left( {\sqrt[q]{{1 - \log_{\theta } \left( {1 + \prod\limits_{j = 1}^{n} {\left( {\theta^{{1 - (\tau_{ij}^{(1)} )^{q} }} - 1} \right)^{{\omega_{ij}^{(1)} }} } } \right)}},\sqrt[q]{{\log_{\theta } \left( {1 + \prod\limits_{j = 1}^{n} {\left( {\theta^{{(\psi_{ij}^{(1)} )^{q} }} - 1} \right)^{{\omega_{ij}^{(1)} }} } } \right)}},\sqrt[q]{{\log_{\theta } \left( {1 + \prod\limits_{j = 1}^{n} {\left( {\theta^{{(\vartheta_{ij}^{(1)} )^{q} }} - 1} \right)^{{\omega_{ij}^{(1)} }} } } \right)}}} \right) \hfill \\ \end{gathered} \\ \begin{gathered} \wp_{\Theta }^{(1)} = T - SFFSWA(g_{\Theta 1}^{(1)} ,g_{\Theta 2}^{(1)} , \ldots ,g_{\Theta n}^{(1)} ) \hfill \\ \, = \left( {\sqrt[q]{{1 - \log_{\theta } \left( {1 + \prod\limits_{j = 1}^{n} {\left( {\theta^{{1 - (\tau_{\Theta j}^{(1)} )^{q} }} - 1} \right)^{{\omega_{\Theta j}^{(1)} }} } } \right)}},\sqrt[q]{{\log_{\theta } \left( {1 + \prod\limits_{j = 1}^{n} {\left( {\theta^{{(\psi_{\Theta j}^{(1)} )^{q} }} - 1} \right)^{{\omega_{\Theta j}^{(1)} }} } } \right)}},\sqrt[q]{{\log_{\theta } \left( {1 + \prod\limits_{j = 1}^{n} {\left( {\theta^{{(\vartheta_{\Theta j}^{(1)} )^{q} }} - 1} \right)^{{\omega_{\Theta j}^{(1)} }} } } \right)}}} \right) \hfill \\ \end{gathered} \\ \end{array} } \right. $$

(50)

and

$$ \left\{ {\begin{array}{*{20}c} \begin{gathered} \wp_{i}^{(2)} = T - SFFSWG(g_{i1}^{(2)} ,g_{i2}^{(2)} , \ldots ,g_{in}^{(2)} ) \hfill \\ { = }\left( {\sqrt[q]{{\log_{\theta } \left( {1 + \prod\limits_{j = 1}^{n} {\left( {\theta^{{(\tau_{ij}^{(2)} )^{q} }} - 1} \right)^{{\omega_{ij}^{(2)} }} } } \right)}},\sqrt[q]{{1 - \log_{\theta } \left( {1 + \prod\limits_{j = 1}^{n} {\left( {\theta^{{1 - (\psi_{ij}^{(2)} )^{q} }} - 1} \right)^{{\omega_{ij}^{(2)} }} } } \right)}},\sqrt[q]{{1 - \log_{\theta } \left( {1 + \prod\limits_{j = 1}^{n} {\left( {\theta^{{1 - (\vartheta_{ij}^{(2)} )^{q} }} - 1} \right)^{{\omega_{ij}^{(2)} }} } } \right)}}} \right) \hfill \\ \end{gathered} \\ \begin{gathered} \wp_{\Theta }^{(2)} = T - SFFSWG(g_{\Theta 1}^{(2)} ,g_{\Theta 2}^{(2)} , \ldots ,g_{\Theta n}^{(2)} ) \hfill \\ { = }\left( {\sqrt[q]{{\log_{\theta } \left( {1 + \prod\limits_{j = 1}^{n} {\left( {\theta^{{(\tau_{\Theta j}^{(2)} )^{q} }} - 1} \right)^{{\omega_{\Theta j}^{(2)} }} } } \right)}},\sqrt[q]{{1 - \log_{\theta } \left( {1 + \prod\limits_{j = 1}^{n} {\left( {\theta^{{1 - (\psi_{\Theta j}^{(2)} )^{q} }} - 1} \right)^{{\omega_{\Theta j}^{(2)} }} } } \right)}},\sqrt[q]{{1 - \log_{\theta } \left( {1 + \prod\limits_{j = 1}^{n} {\left( {\theta^{{1 - (\vartheta_{\Theta j}^{(2)} )^{q} }} - 1} \right)^{{\omega_{\Theta j}^{(2)} }} } } \right)}}} \right) \hfill \\ \end{gathered} \\ \end{array} } \right. $$

(51)

Step 6: Combined with the T-SF Hamming distance measure, the Eqs. (52, 53) are used to calculate the closeness degree $\partial_{i}^{(1)}$ and $\partial_{i}^{(2)}$.

$$ \partial_{i}^{(1)} = \frac{{D_{H} (\wp_{i}^{(1)} ,\wp_{NIS}^{(1)} )}}{{D_{H} (\wp_{i}^{(1)} ,\wp_{NIS}^{(1)} ) + D_{H} (\wp_{i}^{(1)} ,\wp_{PIS}^{(1)} )}} $$

(52)

$$ \partial_{i}^{(2)} = \frac{{D_{H} (\wp_{i}^{(2)} ,\wp_{NIS}^{(2)} )}}{{D_{H} (\wp_{i}^{(2)} ,\wp_{NIS}^{(2)} ) + D_{H} (\wp_{i}^{(2)} ,\wp_{PIS}^{(2)} )}} $$

(53)

In Eq. (52), $D_{H} (\wp_{i}^{(1)} ,\wp_{NIS}^{(1)} )$ represents the T-SF Hamming distance measure between $\wp_{i}^{(1)}$ and $\wp_{NIS}^{(1)}$. The closeness degree $\partial_{i}^{(1)}$ and $\partial_{i}^{(2)}$ are the results of information processing of experts’ optimistic and pessimistic decision attitudes with risk preference.

Step 7: Three aggregated strategies for each option are calculated to indicate the relative importance of each option.

$$ K_{ia} = \frac{{\partial_{i}^{(1)} + \partial_{i}^{(2)} }}{{\sum\nolimits_{i = 1}^{m} {\left( {\partial_{i}^{(1)} + \partial_{i}^{(2)} } \right)} }};K_{ib} = \frac{{\partial_{i}^{(1)} }}{{\min_{i} (\partial_{i}^{(1)} )}} + \frac{{\partial_{i}^{(2)} }}{{\min_{i} (\partial_{i}^{(2)} )}};K_{ic} = \frac{{\rho \partial_{i}^{(1)} + (1 - \rho )\partial_{i}^{(2)} }}{{\rho \max_{i} (\partial_{i}^{(1)} ) + (1 - \rho )\max_{i} (\partial_{i}^{(2)} )}} $$

(54)

where K_ia means the additive normalization of $\partial_{i}^{(1)}$ and $\partial_{i}^{(2)}$. K_ib indicates the sum of the relative relations of $\partial_{i}^{(1)}$ and $\partial_{i}^{(2)}$. K_ic represents the tradeoff of alternatives of $\partial_{i}^{(1)}$ and $\partial_{i}^{(2)}$. In K_ic, ρ is the compromise coefficient, ρ ∈ [0,1], and its value is determined by DMs. Meanwhile, ρ indicates the flexibility and stability of improved CoCoSo method.

Step 8: The comprehensive utility value K_i (i = 1, 2,…,m) of each alternative is calculated, and the final compromise order of the alternatives is determine, that is, the larger K_i is, the better.

$$ K_{i} = \left( {K_{ia} \cdot K_{ib} \cdot K_{ic} } \right)^{\frac{1}{3}} + \frac{1}{3}(K_{ia} + K_{ib} + K_{ic} ) $$

(56)

4 Case Study: SPBRT Selection

In this segment, a real case of SPBRT selection in China is presented to explain the application and validity of the proposed method. Then, the flexibility and superiority are examed by sensitivity analysis and comparative study.

At present, the first wave of spent power battery has appeared around 2020 in China according to the service life of new energy vehicle power battery is 5–8 years. Some companies can extract cobalt, nickel, lithium, manganese, iron, aluminum, and other metals from spent power batteries. It is estimated that by 2030, the total mass of recyclable iron phosphate, lithium carbonate, nickel sulfate, cobalt sulfate, and manganese sulfate in the whole industry will reach 1,039,000 tons, 193,000 tons, 696,000 tons, 290,000 tons, and 154,000 tons, respectively. By then, the total scale of China’s power battery recycling industry will reach more than ¥ 100 billion yuan. The recycling of spent power battery plays an important role in reducing environment pollution, alleviating resource shortage and promoting the sustainable development of power battery industry, which has profound social and economic significance. Therefore, evaluation and selection of existing SPBRT has become a key link in investment and operation of spent power battery recycling companies. From the perspective of circular economy, SPBRT selection needs to consider environmental, economic, social, and other factors as well as the impact of individual interests and risk preference behavior of many stakeholders. Therefore, the SPBRT selection is essentially a MAGDM problem in uncertain environment.

Jiangxi Ruida New Energy Technology Co., Ltd (Ruida for short) is a technology enterprise focusing on the research and development, production and sales of lithium cathode materials, precursors, and other new materials. It was founded in 2014 and is located in Wanzai County, Jiangxi Province. Nearly three years, the COVID-19 epidemic has affected the global supply chain of raw materials, resulting in a sharp rise in the prices of lithium battery metals such as lithium, cobalt, and nickel in China, and a tight supply pattern in the future. In this context, Ruida plans to invest in spent power lithium battery comprehensive utilization project, mainly engaged in spent power lithium battery dismantling, power battery precursor, and cathode material regeneration business. Due to the pressure from the market and environment, the selection of SPBRT has become the core challenge of this enterprise’s investment project. At present, there are four existing SPBRTs in this industry, including Pyro-metallurgy (s₁), Hydrometallurgy (s₂), Bio-metallurgy (s₃), and Electrochemical extraction (s₄) [55, 56]. This enterprise invited five experts from government department, research institute, technical department of this enterprise, downstream enterprise, industry association, and to form an expert group E = (e₁, e₂,…, e₅), the corresponding weight vector is λ = (0.15, 0.20, 0.30, 0.20, 0.15)^T. All the members of the expert group have strong decision-making ability and at least 6 years of work experience, and their priority relationship is e₁ > e₂ > e₃ > e₄ > e₅. Seven attributes are determined by the experts from the perspective of circular economy: h₁: investment and operational cost, h₂: recycling efficiency, h₃: technical reliability, h₄: pollution control investment, h₅: long-term risk level, h₆: jobs, h₇: public acceptance. h₁, h₄, and h₅ are cost type attributes, while other attributes are benefit type. The experts identify the priority relationship of the seven attributes as h₁ > h₅ > h₂ > h₄ > h₃ > h₆ > h₇. Due to the vagueness and uncertainty of the decision-making process, the alternative s_i rating of attribute h_j is expressed by T-SFNs. To determine the most appropriate recycling technology, experts evaluate each recycling technology option based on seven attributes. Table 3 lists the evaluation information of alternative based on the attributes provided by the experts. The T-SFNs in Table 3 are normalized according to Eq. (35), as shown in Table 4. For the degree of association between attributes, experts evaluated the direct influence relationship between any two attributes and expressed it with T-SFN. Therefore, 5 experts provide the individual initial T-SFDRMs ℵ^t (t = 1, 2,…, 5), see Table 5.

Table 3 Evaluation information provided by experts

Table 4 Normalized individual T-SFDMs

Table 5 Individual initial T-SFDRMs provided by five experts

4.1 Decision Procedure

Step 1: We utilize the Eqs. (36–37) to calculate the experts’ priority weights $\varpi_{jl}^{t}$ and $\varpi_{ij}^{t}$. See Tables 6, 7.

Table 6 The priority weight $\varpi_{ij}^{t}$ of experts

Table 7 The priority weight $\varpi_{jl}^{t}$ of experts

Step 2: The T-SFFSWA and T-SFFSWG operators (Eqs. 38–41) are utilized to aggregate individual evaluation information, so as to obtain group T-SFDM M⁽¹⁾, M⁽²⁾ and group initial T-SFDRM ℵ⁽¹⁾ and ℵ⁽²⁾. See the Tables 8, 9, respectively.

Table 8 Aggregated T-SFDM M⁽¹⁾ and M⁽²⁾

Table 9 Aggregated initial T-SFDRM ℵ⁽¹⁾ and ℵ⁽²⁾

Step 3: The extended group T-SFDMs EM⁽¹⁾ and EM⁽¹⁾ are obtained by Eq. (42), as shown in Table 10. Meanwhile, we can determine the attributes’ objective and subjective weights by the T-SF similarity measure (Eq. (43)) and T-SF DEMATEL method (Eqs. (44–47)), respectively. they are listed as below:

Table 10 The extended group T-SFDM EM⁽¹⁾ and EM⁽²⁾

w_s⁽¹⁾ = (0.177, 0.145, 0.141, 0.146, 0.149, 0.127, 0.116)^T; w_s⁽²⁾ = (0.209, 0.145, 0.136, 0.150, 0.159, 0.111, 0.009)^T;

w_o⁽¹⁾ = (0.056, 0.156, 0.069, 0.147, 0.244, 0.201, 0.127)^T;

w_o⁽²⁾ = (0.031, 0.100, 0.090, 0.293, 0.034, 0.285, 0.168)^T.

Step 4: The combination weight vector $w_{c}^{(\Upsilon )}$(ϒ = 1, 2) of attributes is calculated by Eq. (48), the parameter φ = 0.5, we can get w_c⁽¹⁾ = (0.117, 0.150, 0.105, 0.147, 0.196, 0.164, 0.121)^T; w_c⁽²⁾ = (0.120, 0.123, 0.113, 0.222, 0.096, 0.198, 0.129)^T. Then, the attributes’ priority weights $\omega_{ij}^{(\Upsilon )}$ and $\omega_{\Theta j}^{(\Upsilon )}$(ϒ = 1, 2) are computed by Eq. (49), as shown in Table 11.

Table 11 The attributes’ priority weights $\omega_{ij}^{(\Upsilon )}$ and $\omega_{\Theta j}^{(\Upsilon )}$(ϒ = 1, 2)

Steps 5–6: The Eqs. (50, 51) are used to aggregate the evaluation information under each attribute, and the alternatives’ performance values ℘_i⁽¹⁾ and℘_i⁽²⁾ are obtained. Then, we use Eqs. (52, 53) to calculate the relative closeness degree $\partial_{i}^{(1)}$ and $\partial_{i}^{(2)}$(i = 1, 2, 3, 4). The results are shown in Table 12.

Table 12 The performance values and relative closeness degrees under two decision attitudes

Step 7: The three aggregation strategies K_ia, K_ib, and K_ic (i = 1, 2, 3, 4) of alternatives are calculated according to Eq. (54), in which the ρ = 0.5.

K_1a = 0.249, K_2a = 0.205, K_3a = 0.290, K_4a = 0.256;

K_1b = 2.559, K_2b = 2.092, K_3b = 2.017, K_4b = 2.707;

K_1c = 0.853, K_2c = 0.702, K_3c = 0.994, K_4c = 0.877.

Step 8: The Eq. (55) is utilized to compute the comprehensive utility values K₁ = 2.036, K₂ = 1.670, K₃ = 2.389, K₄ = 2.127. Hence, we determine the alternatives’ ranking s₃ > s₄ > s₁ > s₂. Obviously, the Bio-metallurgy (s₃) is the optimal alternative.

4.2 Sensitivity Analysis

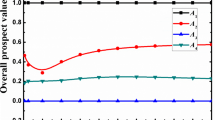
The influence of parameters ρ, κ, and θ on the final alternative ranking are mainly explored in this sub-section. Firstly, when ρ ∈ [0.0, 1.0], and other parameters are fixed values φ = 0.5, κ = 1, and θ = 2, the rankings of alternatives are shown in Table 13. We can find that although the order of s₁ and s₄ changes slightly when ρ = 0.9 and ρ = 1.0, and the s₃ is always the best. So, the alternative ranking is relatively stable on the whole.

Table 13 The alternative ranking results on ρ

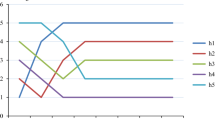
Next, when κ ∈ [1, 10] and the other parameters are set to fixed values φ = 0.5, ρ = 0.5, and θ = 2, we can get the rankings of alternative. The results are shown in Table 14. From Table 14, s₃ is the best option and remained unchanged in κ ∈ [1, 10], while other options change from s₄ > s₁ > s₂ to s₂ > s₄ > s₁. In Fig. 3, the parameter κ value increases, the comprehensive utility value K₁, K₃, and K₄ decrease continuously, while K₂ increases gradually. Then all the alternatives tend to stabilize gradually. According to the Remark 1, the priority relationship between the attributes decrease with the increase of κ. Furthermore, when κ →  + ∞, the priority relationship between attributes is not considered, that is, The T-SFFSWA and T-SFFSWG operators are reduced into the T-SFFWA and T-SFFWG operators (Eqs. (35–36)). These operators are applied into CoCoSo method, and the ranking of the alternative is s₂ > s₃ > s₁ > s₄, the optimal alternative is s₂. Obviously, the priority relationship between attributes and the prioritized degree can affect the final ranking of alternatives, which is more consistent with the actual situation of decision-making problems.

Table 14 The alternative ranking results on κ

Fig. 3

The change of alternatives ranking on κ

Furthermore, when θ ∈ (1,1000], and fixed values φ = 0.5, ρ = 0.5, and κ = 1 are used. We obtain the rankings of alternatives and the results are presented in Table 15. From Table 15, the variation of parameter θ has no influence on the alternative ranking (s₃ > s₄ > s₁ > s₂), which indicates that the ranking has certain stability with respect to different parameter θ. The reason is that the θ in the T-SFFSWA operator can represent DMs’ pessimistic attitude with risk. The two kinds of opposite decision attitudes with risk preference can obtain a relatively stable alternative ranking under the compromise decision mechanism of CoCoSo method.

Table 15 The alternative ranking results on θ

4.3 Discussion

In this subsection, two groups of methods are organized to verify the rationality of the proposed method, that is, the aggregation results obtained from AOs with T-SFNs are first compared and analyzed, including the T-SFWA [52], T-SFWG [52], T-SF weighted average interaction (T-SFWAI) [11], T-SF weighted geometric interaction (T-SFWGI) [11], T-SFDPWA [10], T-SFDPWG [10], and T-SF weighted generalized Maclarurin symmetric mean (T-SFWGMSM) [13] operators. Then, it is compared with the existing alternative ranking approaches in T-SF environment, such as MULTIMOORA [10], TOPSIS [21], and TODIM [11].

We first discuss the comparison with AOs. The caveat here is that the average value of two combination weight vectors of attributes obtained in this paper is adopted, i.e., w_c = (0.167, 0.144, 0.141, 0.147, 0.147, 0.131, 0.122)^T. The T-SFWA, T-SFWG, T-SFWAI, T-SFWGI, T-SFDPWA, and T-SFDPWG operators are applied to aggregate normalized data in Table 3. For the T-SFWGMSM operator, we adopt the average value of two objective weight vectors of attributes, i.e., w_o = (0.142,0144, 0.144, 0.147, 0.140, 0.143, 0.141)^T, and given the generalized coefficient λ₁ = λ₂ = … = λ₇ = 1 and the combination coefficient k = 2. These AOs’ results of all alternatives are obtained, as listed in Table 16. An intuitive comparison of ranking results is shown in Fig. 4.

Table 16 The comparison of the proposed method with different AOs

Fig. 4

Comparison of alternative rankings with different AOs

From Table 16, the alternative ranking results obtained by existing AOs are different from those in this paper. This difference is caused by the existing AOs processing mechanism form evaluation information.

• (1) The T-SFWA, T-SFWG, T-SFWAI, and T-SFWGI operators perform rigid information fusion based on the AOLs and IOLs, respectively. While T-SFFSWA and T-SFFSWG operators used in our proposed method can aggregate information based on the FOLs, and the aggregation process can be made more flexible by adjusting the parameters.

• (2) The T-SFDPWA and T-SFDPWG operators are based on the DOLs and also consider the priority relationship of input arguments, but these two AOs can neither adjust the priority degree nor obtain the optimal balanced alternative through compromise mechanism. Instead, they determine the alternative ranking according to the value of score function.

• (3) The T-SFWGMSM operator ignores the priority relationship between attributes, although the interrelationship between attributes is considered as the method in this paper. In this AO, the degree of interrelationship between attributes can be adjusted by the combination coefficient k. However, if the number of attributes n increases, then the value of binomial coefficient $C_{n}^{k}$ is larger, which increases the computational complexity of this AO. At the same time, we find that the final ranking of alternative obtained by the T-SFWGMSM operator is the same as our result presented in Table 14 in the case of κ →  + ∞, which also indicates that the method presented in this paper is generalized in terms of priority relationship.

In addition, we can find from Table 16 that the results of the alternatives obtained by the existing AOs are all converted into crisp values by the score function (Eq. (2)) for comparison and ranking. The proposed method applies the Hamming distance measure (Eq. (5)) to defuzzy. However, the score function cannot completely and effectively distinguish T-SFNs. For example, let h₁ = (0.5, 0.3, 0.4), h₂ = (0.6, 0.48, 0.36), h₃ = (0.2, 0.5, 0.7), and h_NIS = (0,0,1) be the comprehensive values of three alternatives and a negative ideal solution, then h₁, h₂, and h₃ are calculated by the score function and ranked as sc(h₁)_(0.5) = sc(h₂)_(0.5) > sc(h₃)_(0.15). It can be seen that we cannot distinguish between the optimal alternatives h₁ and h₂. We measure the Hamming distance between h₁, h₂, h₃, and h_NIS, and rank as D_H(h₂)_(0.87) > D_H(h₁)_(0.84) > D_H (h₃)_(0.51) according to the calculation results, that is, h₁ is the best option. Obviously, our method is more reasonable and effective than the above AOs.

We further adopted the existing ranking approaches to solve the MAGDM problem in this case, and the results are listed in Table 17. From Table 17, the results obtained by different existing methods are completely different from our method. The main reasons are not only the difference in the evaluation information aggregation and attribute weight, but also the parallel calculation and the compromise two decision attitudes of the final results. The detailed comparison is described as follows:

• (1) Compare with T-SF TOPSIS method. Ullah et al. [21] used entropy measure to determine the objective weight of attributes, and introduced generalized dice similarity measure to calculate the deviation between each alternative and the ideal solution, so as to determine the relative closeness degree of the alternative. In this process, the TOPSIS method neither considered the correlation and priority relationship among attributes, nor reflected the decision attitude or risk preference. However, multiple attributes often have correlation and priority relationship in the actual decision-making process. Meanwhile, the evaluation information of different experts hides the pessimistic or optimistic decision attitude of DMs and their risk preference. Therefore, the proposed method is more suitable for solving decision-making problems in real life.

• (2) Compare with T-SF MULTIMOORA method. Mahmood et al. [10] developed the T-SFDPWA and T-SFDPWG operators based on DOLs, and were used in the MULTIMOORA method to determine the utility value of each alternative. The ratio system, reference point and Multiplicative form were determined and the final ranking of alternative was determined by the dominance theory. Firstly, although this method considers the priority relationship of attributes, the relationship level is not adjustable compared with our method, that is, the PAO does not have the generality of softmax function adopted in this article. Secondly, the DOLs contain parameters like FOLs, which can make the decision process more flexible. However, Mahmood et al. [10] did not explain whether the T-SFDPWA and T-SFDPWG operators can reflect DMs’ decision attitude or risk preference. In addition, the T-SFDPWA and T-SFDPWG operators (see Eqs. 58–59) cannot handle T-SFN where MD or AD or ND is zero, because the denominator in Eqs. (58, 59) cannot be zero. In contrast, the proposed AOs are more reasonable and comprehensive, and more suitable for aggregating evaluation information in actual decision-making problems.

$$ \begin{gathered} T - SFDPWA(P_{1} ,P_{2} , \ldots ,P_{\sigma } ) = \hfill \\ \left( {\sqrt[q]{{1 - \frac{1}{{1 + \left\{ {\sum\nolimits_{\xi = 1}^{\sigma } {\left( {\tfrac{{w_{\xi } \chi_{\xi } }}{{\sum\nolimits_{\xi = 1}^{t} {\chi_{\xi } } }}} \right)\left( {\frac{{\tau_{\xi }^{q} }}{{1 - \tau_{\xi }^{q} }}} \right)^{\Xi } } } \right\}^{1/\Xi } }}}},\sqrt[q]{{\frac{1}{{1 + \left\{ {\sum\nolimits_{\xi = 1}^{\sigma } {\left( {\tfrac{{w_{\xi } \chi_{\xi } }}{{\sum\nolimits_{\xi = 1}^{t} {\chi_{\xi } } }}} \right)\left( {\frac{{1 - \psi_{\xi }^{q} }}{{\psi_{\xi }^{q} }}} \right)^{\Xi } } } \right\}^{1/\Xi } }}}},\sqrt[q]{{\frac{1}{{1 + \left\{ {\sum\nolimits_{\xi = 1}^{\sigma } {\left( {\tfrac{{w_{\xi } \chi_{\xi } }}{{\sum\nolimits_{\xi = 1}^{t} {\chi_{\xi } } }}} \right)\left( {\frac{{1 - \vartheta_{\xi }^{q} }}{{\vartheta_{\xi }^{q} }}} \right)^{\Xi } } } \right\}^{1/\Xi } }}}}} \right) \hfill \\ \end{gathered} $$

(58)

$$ \begin{gathered} T - SFDPWG(P_{1} ,P_{2} , \ldots ,P_{\sigma } ) = \hfill \\ \left( {\sqrt[q]{{\frac{1}{{1 + \left\{ {\sum\nolimits_{\xi = 1}^{\sigma } {\left( {\tfrac{{w_{\xi } \chi_{\xi } }}{{\sum\nolimits_{\xi = 1}^{t} {\chi_{\xi } } }}} \right)\left( {\frac{{1 - \tau_{\xi }^{q} }}{{\tau_{\xi }^{q} }}} \right)^{\Xi } } } \right\}^{1/\Xi } }}}},\sqrt[q]{{1 - \frac{1}{{1 + \left\{ {\sum\nolimits_{\xi = 1}^{\sigma } {\left( {\tfrac{{\lambda_{\xi } \chi_{\xi } }}{{\sum\nolimits_{\xi = 1}^{t} {\chi_{\xi } } }}} \right)\left( {\frac{{\psi_{\xi }^{q} }}{{1 - \psi_{\xi }^{q} }}} \right)^{\Xi } } } \right\}^{1/\Xi } }}}},\sqrt[q]{{1 - \frac{1}{{1 + \left\{ {\sum\nolimits_{\xi = 1}^{\sigma } {\left( {\tfrac{{\lambda_{\xi } \chi_{\xi } }}{{\sum\nolimits_{\xi = 1}^{t} {\chi_{\xi } } }}} \right)\left( {\frac{{\vartheta_{\xi }^{q} }}{{1 - \vartheta_{\xi }^{q} }}} \right)^{\Xi } } } \right\}^{1/\Xi } }}}}} \right) \hfill \\ \end{gathered} $$

(59)

Table 17 The alternative ranking results of different methods

where Ξ is operational parameter and Ξ > 0. P_ξ = (τ_ξ,ψ_ξ,ϑ_ξ) (ξ = 1, 2,…, σ) is a set of T-SFNs, and w_ξ is the corresponding weight value and $\sum\nolimits_{\xi = 1}^{\sigma } {w_{\xi } = 1}$,λ_ξ > 0. $\chi_{\xi } = \prod\nolimits_{i = 1}^{\xi - 1} {sc(P_{i} )}$ and χ₁ = 1. sc(P_ξ) is the value of score function.

• 1) Compare with T-SF TODIM method. Ju et al. [11] proposed some T-SF interaction AOs based on IOLs for the MAGDM problem with incomplete weight information, and used them to aggregate individual evaluation information, then extended the TODIM method considering DMs’ psychological behaviors in the T-SF environment. Firstly, Ju et al. [11] determined the objective weight of attribute based on the maximizing deviation method, while the combination weight of attribute is determined by the DEMATEL and similarity measure methods in T-SF environment in our proposed method, where the T-SF DEMATEL method considers the interrelationship between attributes, which Ju et al. [11] did not consider. Secondly, although the AOs proposed by Ju et al. [11] considered the interaction among MD, AD, and ND of T-SFNs, it ignored the priority relationship between attributes. Thirdly, the dominance function in TODIM method contains loss attenuation coefficient, which can be adjusted according to the risk preference of DMs. The proposed AOs can describe the DMs’ optimistic and pessimistic decision attitudes with risk preference. For this purpose, a processing of independent and parallel calculation of the two decision attitudes is designed, and the optimal alternative is obtain through the compromise mechanism of CoCoSo method. Therefore, our proposed method can process the evaluation information more comprehensively and dig out the decision attitude and risk preference of DMs. Meanwhile, the optimal alternative can be determined by adjusting the compromise coefficient according to the actual decision problems. Obviously, the proposed method is more flexible, effective, and reasonable.

From the features analysis of different methods in Table 18, the proposed method has more advantages than the existing methods can be found intuitively.

Table 18 The features analysis of different methods

5 Managerial Implications

The notion of circular economy has become a popular word in today’s commercial market. In the field of spent power battery recycling management, the government and enterprises pay more and more attention to the resource reuse of rare and precious materials. According to the existing literature, many practices of circular economy have been completed to improve the sustainable development of enterprises, but there is a lack of recycling technology evaluation practice. As a consequence, the evaluation of recycling technology from the perspective of circular economy will become an important topic for enterprise managers. To this end, the main goal of this paper is to introduce a new group decision-making model for resource recycling enterprises to implement recycling technology management practice in a highly uncertain environment, which has some enlightenment for enterprise managers.

The results show that there are some important insights into attributes and recycling technology alternatives: the new weight determination model developed in this paper, which can reflect the decision attitude of DMs, can help managers of resource recycling enterprises to determine the importance rating of attributes from the perspective of circular economy. The combined model of objective and subjective weights based on these attributes makes the decision results more consistent. The weight shows that under the optimistic attitude, long-term risk level h₅ (0.196) is the most important attribute, followed by jobs h₆ (0.164), and technical reliability h₃ (0.105) has the lowest significant value; under the pessimistic attitude, pollution control investment h₄ (0.222) is the most important attribute, followed by jobs h₆ (0.198) and the attribute with the lowest value is long-term risk level h₅ (0.096). In this study, the improved CoCoSo technology can make a compromise decision on the SPBRT selection from the two dimensions of optimism and pessimism. Moreover, the developed method is suitable for practical complex group decision-making problems from the perspective of practical application. The results of this study will help resource recycling enterprises understand the impact of various attributes on the evaluation of recycling technology from the perspective of circular economy, and provide a clear picture of how to make correct decisions.

6 Conclusion

In this article, some new AOs are proposed and a new MAGDM framework for T-SFSs is designed based on the improved CoCoSo method considering the decision attitude of DMs and the priority relationship of input arguments. The main work of this article is summarized as below:

• (1) We extend the Frank operations in the T-SF environment, and develop some AOs based on the FOLs and softmax function, such as T-SFFSA, T-SFFSWA, T-SFFSG, and T-SFFSWG operators. Some basic properties and special cases are discussed. At the same time, the monotonicity of the proposed AOs on parameter θ is analyzed.

• (2) In the T-SF MAGDM problem, we extend the DEMATEL method to determine the subjective weight of attribute, and employ the similarity measure to calculate the objective weight of attribute, so as to obtain the combination weight of attribute.

• (3) Further, according to the monotonicity analysis results of the proposed AOs, an independent and parallel information processing process with optimistic and pessimistic decision attitudes with risk preference is designed. Meanwhile, the T-SFFSWA and T-SFFSWG operators are used to replace WSM and WPM in traditional CoCoSo method, and the performance value of alternative is defuzzied by distance measure to calculate the relative closeness.

• (4) We solve a real case of SPBRT selection by applying the MADGM framework proposed. The results show that the comprehensive utility value of Bio-metallurgy (s₃) (2.389) is the largest, while that of Hydrometallurgy (s₂) (1.607) is the smallest. So s₃ is the best option.

• (5) For the validation of the obtained results, sensitivity analysis and comparative studies are also carried out. The results of both confirmed the applicability of the developed method.

In the T-SF environment, our method not only considers the attributes’ interrelationship and determines the combination weight, but also reflects the decision attitude of DMs with risk preference and the generalization of attribute priority relationship level. Therefore, the proposed method is generalized and flexible, which makes the decision result is closer to the practical decision problems. In future work, we will pay more attention to developing new AOs and modifying existing methods (e.g., MARCOS [57] and WASPAS [58]) for complex T-SFSs [59].