1 Introduction

Over the last decade, fractional calculus has emerged as one of the best innovative tools for modelling and controlling dynamic systems. Including fractional order (FO) operators in design adds an extra degree of freedom, providing flexibility and superior performance. Therefore, the application of fractional differ-integral operators in controllers has gained recent research thrust in the field of control of motor [1], renewable energy [2, 3], process control [4, 5], power system [6, 7], robotics [8,9,10,11], tumour growth control [12, 13], and automatic voltage regulation [14]. Moreover, it is widely utilised with advanced intelligent techniques for the design and control of real-world systems.

Intelligent techniques such as fuzzy logic and its variants have been effectively used in security design for the networked control system, autonomous vehicles, and control of time-varying, non-linear systems [15,16,17,18]. Fuzzy logic is the branch of artificial intelligence (AI) that provides excellent control of the uncertain and imprecise system through expert knowledge-based reasoning and cognitive abilities [19]. This feature motivated researchers across the globe to incorporate fuzzy logic-based intelligence into conventional controllers and enhance its capabilities. Different fuzzy logic controller (FLC) structures based on classical proportional integral-derivative (PI/PD/PID) have been proposed in the literature. The controller design proposed in [20] is based on analytical formulae that provide self-tuning capability and preserve PI/PD/PID linear structure. The closed-loop system stability is analysed using the small gain theorem, and the bounded input bounded output (BIBO) stability condition is established [19,20,21,22,23,24,25,26,27,28].

In recent years, fuzzy logic-based linear PID controller performance has been improved by replacing integer order operators with fractional operators. Literature reveals the applicability of fractional FLC in the field of control problems [29,30,31,32,33,34,35,36,37]. Das et al. introduced the family of fractional order fuzzy PID controllers by utilising fractional differ-integral operators on error and control signals. Input and output scaling gains and fractional operators are optimised with a genetic algorithm, and their performance is compared for FO processes with dead time [29]. Das et al. also presented the application of FO fuzzy PID for control of the nuclear reactor and the unstable process. The controller design variables are tuned with the genetic algorithm, and its performance proved superior to conventional fuzzy PID controllers [30, 31]. A different type of fractional order fuzzy PD plus conventional I controller is proposed by Jesus et al. [32], in which a basic genetic algorithm is utilised to optimise its parameters. Due to efficient and robust control offered by fractional order fuzzy PID controllers, its implementation is found in diverse fields such as load frequency control of interconnected systems [33], smart seismic isolated structures [34], automatic generation control of power systems [35], hydrometallurgy [36], hybrid power system [37], bioreactor [38].

The above discussed fractional order fuzzy PID controllers are designed based on expert knowledge rather than the analytical method. Consequently, desirable properties of a controller such as controllability, stability, and reliability become significant concerns. Therefore, a design methodology based on the precise mathematical model of fractional order fuzzy controllers needs to be explored to deal with these problems. The present work aims to design the fractional order fuzzy controller by using fragmented fractional order PID control structure. A novel FO fuzzy PID (FOFPI + D) control law is derived mathematically from the conventional fractional order PID controller, exhibited in Fig. 1. The structure of FOFPI + D is the combination of FO fuzzy proportional-integral (FOFPI) and FO fuzzy derivative (FOFD) action. The designed scheme shows self-tuning control capability, as the gains vary nonlinearly besides retaining the properties and advantages of traditional non-integer PID controllers. The required BIBO stability conditions are analytically derived for the closed-loop system using two straight line method.

Fig. 1
figure 1

Control schematic of FO PID controller

Full size image

Further, the performance of the proposed control scheme is examined on the two-link robotic manipulator, which is non-linear and exhibits multi-input multi-output coupled behaviour. The parameters associated with membership functions, input and output scaling factors, and FO operators of the FOFPI + D controller are optimised with non-dominated sorting genetic algorithm-II (NSGA-II) for getting minimum variations in manipulating signal and sum of absolute error. The comprehensive simulation study is done to validate the robustness of the designed controller over its integer order counterpart for trajectory tracking, parametric uncertainties, tracking for varying boundary conditions of reference trajectory, and disturbance rejection. The results obtained demonstrate that the FO fuzzy PI + D controller performs better than its integer order equivalent in all case studies. Incorporating a non-integer operator in design adds an extra degree of freedom, thereby providing better design performance over its integer order equivalent. The significant contribution of this work is summarised as.

  1. 1.

    Precise analytical formulae of the proposed FOFPI + D controller are derived from the FO PID controller. A mathematically derived simple fuzzy technique is fused with derived PID action to obtain intelligent and adaptive FOPID.

  2. 2.

    The proposed controller preserves the linearity of traditional FO PID and has self-tuning capabilities.

  3. 3.

    Stability requirements for the closed-loop control structure are ascertained methodically using the graphical approach.

  4. 4.

    The performance of the designed controllers is adequate and robust compared to its integer order equivalent while addressing different operating conditions such as parameter uncertainty, disturbance, and altering reference trajectory for the highly non-linear two-link robot.

The structure of the paper is as follows. A brief literature review is presented in Sect 1 and the problem formulation is discussed in Sect. 2. The design methodology of FOFPI + D control, stability conditions, and the implementation of the NSGA-II algorithm are outlined in Sect. 3. The performance analysis of FOFPI + D for controlling the two-link robotic manipulator is presented in Sect. 4. This section also presents the comparative study of the proposed controller with its integer order variant for trajectory tracking, parametric uncertainty, and disturbance rejection. Finally, the concluding notes are discussed in Sect. 5.

2 Problem Formulation

In recent years, FO fuzzy controllers have been extensively utilised to control dynamical systems. These controllers are designed and implemented by replacing the integer operators with fractional operators in fuzzy structures. As a demonstration, the basic integer order fuzzy PI and FO fuzzy PI controller structures are depicted in Fig. 2. The mathematical expression of the FO fuzzy PI controller is given as

$${u = K_{3} \frac{{d^{ - \beta } }}{{dt^{ - \beta } }}\left[ {f\left( {K_{1} e\left( t \right), K_{2} \frac{{d^{\alpha } }}{{dt^{\alpha } }}e\left( t \right)} \right)} \right]}$$
(1)

where \(f\) is the mapping among the input and output of the fuzzy controller. The method of linear approximation suggested by Jantzen [39] is utilised to simplify the FO fuzzy PI controller as

$$u = K_{3} \frac{{d^{ - \beta } }}{{dt^{ - \beta } }}\left( {K_{1} e\left( t \right) + K_{2} \frac{{d^{\alpha } }}{{dt^{\alpha } }}e\left( t \right)} \right)$$
$$\begin{array}{*{20}c} {u = K_{1} K_{3} \frac{{d^{ - \beta } }}{{dt^{ - \beta } }}e\left( t \right) + K_{2} K_{3} \frac{{d^{\alpha - \beta } }}{{dt^{\alpha - \beta } }}e\left( t \right)} \\ \end{array}$$
(2)
Fig. 2
figure 2

Schematic block diagram of controllers a Fuzzy PI, and b FO fuzzy PI

Full size image

The approximation reduces the complexity of the controller while retaining its properties. The Eq. (2) is directly considered FOPI control action, whereas the control action generated is not only PI, but it depends on the values of \(\alpha\) and \(\beta .\) The actual control action generated by \(u\) depending on \(\alpha\) and \(\beta\) is as follows

$$u = \left\{ {\begin{array}{*{20}c} {Fractional\,order\,I + D\,action\,\,\,\,\,\,\,if\,\alpha > \beta } \\ {Fractional\,order\,I + I\,action\,\,\,\,\,\,\,if\,\alpha < \beta } \\ {Fractional\,order\,P + I\,action\,\,\,\,\,\,if\,\alpha = \beta } \\ \end{array} } \right.{\text{ }}$$
(3)

Hence, analytically the control signal \(u\) generates FO fuzzy PI action if and only if \(\alpha =\beta\). It is revealed from the literature [29,30,31,32,33,34,35,36,37] that various authors have considered \(\alpha \ne \beta\) and claimed the structure as FO fuzzy PI controller, which conflicts with mathematical formulation. This work proposes the design of the FO fuzzy PID controller based on precise mathematical derivation. The designed control structure preserves the features and properties of FOPID and the additional benefit of self-regulatory control. Also, the issues related to the stability of the fuzzy controller are addressed by deriving sufficient BIBO stability conditions for the proposed fuzzy controller. The controller performs its best with the proper tuning of its parameters. Therefore, an AI-based metaheuristic algorithm is implemented to find the design parameters of the controller according to the requirement of the system.

3 Design of FOFPI + D Controller

The derivation of FO fuzzy PI + D controller action is obtained in three stages as follows:

  1. 1.

    The FO fuzzy PI control action is formulated from the traditional FO PI controller.

  2. 2.

    The FO fuzzy D output is derived from the FO derivative action.

  3. 3.

    The overall action of FOFPI + D is the combination of FOFPI and FOFD controller output collectively in a suitable way, and is discussed in the next sub-sections.

3.1 Derivation of FO Fuzzy PI Control Law

The traditional FO PI control law in the Laplace domain is expressed as

$$\begin{array}{*{20}c} {U_{PI} \left( s \right) = \left( {K_{P}^{c} + K_{I}^{c} \frac{1}{{s^{\lambda } }}} \right)E\left( s \right)} \\ \end{array}$$
(4)

where, \({K}_{P}^{c}\) and \({K}_{I}^{c}\) are the proportional and integral gains, respectively. \(E(s)\) is the tracking error signal, and \(\lambda\) is the order of fractional operator. The above equation can be changed into the discrete domain by using backward transformation \(s\backsimeq \frac{(1-{z}^{-1})}{T}\), Where \(T>0\) is the step time.

$$\begin{array}{*{20}c} {U_{PI} \left( z \right) = \left( {K_{P}^{c} + K_{I}^{c} \frac{{T^{\lambda } }}{{\left( {1 - z^{ - 1} } \right)^{\lambda } }}} \right)E\left( z \right)} \\ \end{array}$$
(5)
$$\begin{array}{*{20}c} {\Delta U_{PI} \left( z \right) = \left( {K_{P}^{c} \left( {1 - z^{ - 1} } \right)^{\lambda } + K_{I}^{c} T^{\lambda } } \right)E\left( z \right)} \\ \end{array}$$
(6)

where

$$\begin{array}{*{20}c} {\Delta U_{PI} \left( z \right) = U_{PI} \left( z \right)\left( {1 - z^{ - 1} } \right)^{\lambda } } \\ \end{array}$$
(7)

Using power series expansion [40] on Eq. (6), yields

$$\begin{array}{*{20}c} {\Delta U_{PI} \left( z \right) = K_{P}^{c} \mathop \sum \limits_{k = 0}^{\infty } \left( { - 1} \right)^{k} \left( {\begin{array}{*{20}c} \lambda \\ k \\ \end{array} } \right)z^{ - k} E\left( z \right) + K_{I}^{c} T^{\lambda } E\left( z \right)} \\ \end{array}$$
(8)

Taking inverse Z-transform for Eq. (8), obtains

$$\begin{array}{*{20}c} {\Delta u_{PI} \left( {nT} \right) = K_{I}^{c} T^{\lambda } e\left( {nT} \right) + K_{P}^{c} \mathop \sum \limits_{k = 0}^{\infty } \left( { - 1} \right)^{k} \left( {\begin{array}{*{20}c} \lambda \\ k \\ \end{array} } \right)e\left( {\left( {n - k} \right)T} \right)} \\ \end{array}$$
(9)

The second term on the R.H.S. of Eq. (9) is analogous to the formulation proposed by Lubich for the FO differ-integral with order \(\Omega\) for any function \(g(nT)\) as [41]:

$$\begin{array}{*{20}c} {D^{ \mp \Omega } g\left( {nT} \right) = T^{ \pm \Omega } \mathop \sum \limits_{k = 0}^{\infty } \left( { - 1} \right)^{k} \left( {\begin{array}{*{20}c} { \mp \Omega } \\ k \\ \end{array} } \right)g\left( {\left( {n - k} \right)T} \right)} \\ \end{array}$$
(10)

Merging, Eq. (9) and Eq. (10) yields

$$\begin{array}{*{20}c} {\Delta u_{PI} \left( {nT} \right) = K_{I}^{c} T^{\lambda } e\left( {nT} \right) + K_{P}^{c} T^{\lambda } D^{\lambda } e\left( {nT} \right)} \\ \end{array}$$

or simply

$$\begin{array}{*{20}c} {\Delta u_{PI} \left( {nT} \right) = K_{I} e\left( {nT} \right) + K_{P} e_{r} \left( {nT} \right)} \\ \end{array}$$
(11)

where, \({K}_{P}={K}_{P}^{c}{T}^{\lambda }\), \({K}_{I}={K}_{I}^{c}{T}^{\lambda }\), \({e}_{r}\left(nT\right)={D}^{\lambda }e\left(nT\right)\). Moreover, solving Eq. (7) for control action gives

$$\begin{array}{*{20}c} {U_{PI} \left( z \right) = \mathop \sum \limits_{k = 0}^{\infty } \left( { - 1} \right)^{k} \left( {\begin{array}{*{20}c} { - \lambda } \\ k \\ \end{array} } \right)\Delta U_{PI} \left( z \right)z^{ - k} } \\ \end{array}$$
(12)
$$\begin{array}{*{20}c} {u_{PI} \left( {nT} \right) = \mathop \sum \limits_{k = 0}^{\infty } \left( { - 1} \right)^{k} \left( {\begin{array}{*{20}c} { - \lambda } \\ k \\ \end{array} } \right)\Delta u_{PI} \left( {\left( {n - k} \right)T} \right)} \\ \end{array}$$
(13)
$$\begin{array}{*{20}c} {u_{PI} \left( {nT} \right) = T^{ - \lambda } D^{ - \lambda } \left( {\Delta u_{PI} \left( {nT} \right)} \right)} \\ \end{array}$$
(14)

Replacing the term \({T}^{-\lambda }\) by gain \({K}_{uPI}\) and \(\Delta {u}_{PI}\left(nT\right)\) by FO fuzzy PI control action, such that

$$\begin{array}{*{20}c} {u_{PI} \left( {nT} \right) = K_{uPI} D^{ - \lambda } \left( {\Delta u_{PI} \left( {nT} \right)} \right)} \\ \end{array}$$
(15)

The structure of FOFPI is designed using Eq. (11) with \({K}_{I}e\left(nT\right)\) and \({K}_{P}{e}_{r}\left(nT\right)\) as inputs and \(\Delta {u}_{PI}\left(nT\right)\) as control action of the FOFPI component. Where \({K}_{uPI}\) is the scaling gain of the FOFPI control action.

3.2 Derivation of FO Fuzzy D Control Law

The conventional FO derivative control action for input as \(x\) and action as \({u}_{D}\) is described in Eq. (16) as

$$\begin{array}{*{20}c} {U_{D} \left( s \right) = K_{D}^{c} s^{\lambda } X\left( s \right)} \\ \end{array}$$
(16)

Applying the backward transformation, \(s \simeq \frac{{(1 - z^{{ - 1}} )}}{T}\)

$$\begin{array}{*{20}c} {U_{D} \left( z \right) = \frac{{K_{D}^{c} \left( {1 - z^{ - 1} } \right)^{\lambda } X\left( z \right)}}{{T^{\lambda } }}} \\ \end{array}$$
(17)
$$\begin{array}{*{20}c} {\Delta U_{D} \left( z \right) = K_{D}^{c} \mathop \sum \limits_{k = 0}^{\infty } \left( { - 1} \right)^{k} \left( {\begin{array}{*{20}c} \lambda \\ k \\ \end{array} } \right)X\left( z \right)z^{ - k} } \\ \end{array}$$
(18)

where

$$\begin{array}{*{20}c} {\Delta U_{D} \left( z \right) = T^{\lambda } U_{D} \left( z \right)} \\ \end{array}$$
(19)

Applying inverse Z- transform to Eq. (18) yields

$$\begin{array}{*{20}c} {\Delta u_{D} \left( {nT} \right) = K_{D}^{c} \mathop \sum \limits_{k = 0}^{\infty } \left( { - 1} \right)^{k} \left( {\begin{array}{*{20}c} \lambda \\ k \\ \end{array} } \right)x\left( {\left( {n - k} \right)T} \right)} \\ \end{array}$$
(20)
$$\begin{array}{*{20}c} {\Delta u_{D} \left( {nT} \right) = K_{D}^{c} T^{\lambda } D^{\lambda } x\left( {nT} \right)} \\ \end{array}$$
(21)
$$\begin{array}{*{20}c} {\Delta u_{D} \left( {nT} \right) = K_{D} D^{\lambda } x\left( {nT} \right)} \\ \end{array}$$
(22)

It is difficult to generate meaningful fuzzy control action depending on a single input. Therefore, the control law of Eq. (22) is modified by adding a signal \(Kx\left( {nT} \right)\) to its right-hand side as an input of the FOFD component.

$$\begin{array}{*{20}c} {\Delta u_{D} \left( {nT} \right) = Kx\left( {nT} \right) + K_{D} x_{r} \left( {nT} \right)} \\ \end{array}$$
(23)

where \(K_{D} = K_{D}^{c} T^{\lambda }\),\(x\left( {nT} \right) = - e\left( {nT} \right) = y\left( {nT} \right) - y_{d} \left( {nT} \right)\), \(x_{r} \left( {nT} \right) = D^{\lambda } x\left( {nT} \right)\) and solving the Eq. (19) for control action

$$\begin{array}{*{20}c} {U_{D} \left( z \right) = T^{ - \lambda } \Delta U_{D} \left( z \right)} \\ \end{array}$$
(24)
$$\begin{array}{*{20}c} {u_{D} \left( {nT} \right) = T^{ - \lambda } \Delta u_{D} \left( {nT} \right)} \\ \end{array}$$
(25)

When \({\Delta U}_{D}\left(nT\right)\) is converted to FOFD control law, and the term \({T}^{-\lambda }\) is replaced by gain \({K}_{uD}\), then Eq. (25) can be rewritten as

$$\begin{array}{*{20}c} {u_{D} \left( {nT} \right) = K_{uD} \Delta u_{D} \left( {nT} \right)} \\ \end{array}$$
(26)

The structure of the FOFD component is modelled by Eq. (23) with \({\Delta u}_{D}\left(nT\right)\) as control action and \(Kx\left(nT\right)\) and \({K}_{D}{x}_{r}\left(nT\right)\) as inputs of the FOFD component.

3.3 Inclusive FO Fuzzy PI + D Control Law

At last, overall FOFPI + D controller action is achieved by subtracting the action of FOFD component Eq. (26) from FOFPI component Eq. (15) collectively as

$$\begin{array}{*{20}c} {u_{PID} \left( {nT} \right) = u_{PI} \left( {nT} \right) - u_{D} \left( {nT} \right)} \\ \end{array}$$
(27)

Or

$$\begin{array}{*{20}c} {u_{PID} \left( {nT} \right) = K_{uPI} D^{ - \lambda } \left( {\Delta u_{PI} \left( {nT} \right)} \right) - K_{uD} \Delta u_{D} \left( {nT} \right)} \\ \end{array}$$
(28)

Based on the mathematical model described above, the generalised control structure of the FOFPI + D controller for the non-linear dynamic system is shown in Fig. 3.

Fig. 3
figure 3

Generalised control structure of FOFPI + D for dynamic system

Full size image

3.4 Implementation of Fractional Operators

Fractional calculus has become integral to various engineering applications in the past decade. Several methods for realising fractional operators are recorded in the literature [42, 43]. This work uses a digital approximation of the fractional operator defined by Lubich [41]. The implementation in a discrete domain involves the binomial expansion of backward transformation in \({s}^{\pm \mu }\) as follows

$$\begin{array}{*{20}c} {s^{ \pm \mu } = \left( {\frac{{1 - z^{ - 1} }}{T}} \right)^{ \pm \mu } } \\ \end{array}$$
(29)
$$\begin{array}{*{20}c} {s^{ \pm \mu } = T^{ \mp \mu } \mathop \sum \limits_{k = 0}^{\infty } \left( { - 1} \right)^{k} \frac{{\left( { \pm \mu } \right)\left( { \pm \mu - 1} \right)\left( { \pm \mu - 2} \right) \ldots \ldots \left( { \pm \mu - k + 1} \right)}}{k!}z^{ - k} } \\ \end{array}$$
(30)

Denoting discrete-time differ-integral operator as ‘\(D\)’, the designed fractional differentiator/integrator in the discrete domain is represented as

$$\begin{array}{*{20}c} {D^{ \mp \mu } = T^{ \pm \mu } \mathop \sum \limits_{k = 0}^{\infty } \left( { - 1} \right)^{k} \left( {\begin{array}{*{20}c} { \mp \mu } \\ k \\ \end{array} } \right)z^{ - k} } \\ \end{array}$$
(31)

Practical realisation of the Eq. (31) requires the calculation of the infinite number of coefficients. Hence, the short memory principle is implemented to design fractional operators as

$$\begin{array}{*{20}c} {D^{ \mp \mu } g\left( {nT} \right) = T^{ \pm \mu } \mathop \sum \limits_{k = 0}^{M} \left( { - 1} \right)^{k} \left( {\begin{array}{*{20}c} { \mp \mu } \\ k \\ \end{array} } \right)g\left( {\left( {n - k} \right)T} \right)} \\ \end{array}$$
(32)

where \(g\left(nT\right)\) is an arbitrary discrete function, \(\alpha\) is the order of operator, \(M\) is memory size, and its value is 100.

3.5 The Analytical Design of Fuzzy Control

This section presents the design of fuzzy systems using standard methodology, which includes fuzzification, creating rule base, and defuzzification procedure.

3.5.1 Fuzzification

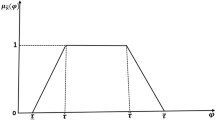
The FOFPI and FOFD components of the FOFPI + D controller are fuzzified separately. Then, the rule base of both the components is combined by considering the FOFPI + D control law in Eq. (27). FOFPI component utilises 2 inputs: error signal \(\widetilde{e}\left(nT\right)={K}_{I}e\left(nT\right)\) and fractional rate of error \({\widetilde{e}}_{r}\left(nT\right)={K}_{P}{e}_{r}\left(nT\right)\). Similarly, the FOFD component of the controller has inputs \(\widetilde{x}\left(nT\right)=Kx\left(nT\right)\) and \({\widetilde{x}}_{r}\left(nT\right)={K}_{D}{x}_{r}\left(nT\right)\). For each input, two triangular membership functions denoted as \(n\): negative and \(p\): positive are designated. FOFPI and FOFD blocks have single control output \(\Delta {u}_{PI}\left(nT\right)\) and \(\Delta {u}_{D}\left(nT\right)\) respectively, which are fuzzified using three singleton membership functions. Figure 4 portrays the membership functions for input and output of FOFPI and FOFD components, where \(L>0\) and its value is obtained through optimisation.

Fig. 4
figure 4

Membership functions for a Inputs & b Output of FOFPI and FOFD

Full size image

3.5.2 Formulation of Control Rules for FOFPI and FOFD

The rule base for the fuzzy inference system is designed based on either expert experience or control system knowledge. This work establishes four fuzzy control rules based on control system knowledge for each FOFPI and FOFD controller. Depending on membership functions, the following control rule base is framed for the FOFPI controller:

$$({\text{Cr}}_{{1}} ) - {\text{If}}\,\tilde{e} = \tilde{e}.n\,{\text{and}}\,\tilde{e}_{r} = \tilde{e}_{r} .n\,{\text{then}}\,\Delta u_{PI} = o.n$$
$$({\text{Cr}}_{{2}} ) - {\text{If}}\,\tilde{e} = \tilde{e}.n\,{\text{and}}\,\tilde{e}_{r} = \tilde{e}_{r} .p\,{\text{then}}\,\Delta u_{PI} = o.z$$
$$({\text{Cr}}_{{3}} ) - {\text{If }}\tilde{e} = \tilde{e}.p\,{\text{and}}\,\tilde{e}_{r} = \tilde{e}_{r} .n\,{\text{then}}\,\Delta u_{PI} = o.z$$
$$({\text{Cr}}_{{4}} ) - {\text{If}}\,\tilde{e} = \tilde{e}.p\,{\text{and}}\,\tilde{e}_{r} = \tilde{e}_{r} .p\,{\text{then}}\,\Delta u_{PI} = o.p$$

where \(\widetilde{e}={K}_{I}e={K}_{I}({y}_{d}-y)\) is the error, \({\widetilde{e}}_{r}={K}_{P}{e}_{r}\left(nT\right)={K}_{P}({D}^{\lambda }{y}_{d}-{D}^{\lambda }y)\) is the fractional rate of error and \(\Delta {u}_{PI}\) is the output of the FOFPI component. '\(\widetilde{e}.n\)' signifies error negative, ' \({\widetilde{e}}_{r}.p\)' implies the fractional derivative of error is positive, and '\(o.z\)' is output zero. Similarly, control rules for FOFD controller are framed as follows:

$$({\text{Cr}}_{{5}} ) - {\text{If}}\,\tilde{x} = \tilde{x}.p\,{\text{and}}\,\tilde{x}_{r} = \tilde{x}_{r} .p\,{\text{then}}\,\Delta u_{P} = o.z$$
$$({\text{Cr}}_{{6}} ) - {\text{If}}\,\tilde{x} = \tilde{x}.p\,{\text{and}}\,\tilde{x}_{r} = \tilde{x}_{r} .n\,{\text{then}}\,\Delta u_{P} = o.p$$
$$({\text{Cr}}_{{7}} ) - {\text{If}}\,\tilde{x} = \tilde{x}.p\,{\text{and}}\,\tilde{x}_{r} = \tilde{x}_{r} .n\,{\text{then}}\,\Delta u_{P} = o.n$$
$$({\text{Cr}}_{{8}} ) - {\text{If}}\,\tilde{x} = \tilde{x}.n\,{\text{and}}\,\tilde{x}_{r} = \tilde{x}_{r} .n\,{\text{then}}\,\Delta u_{P} = o.z$$

In these control rules:\(\widetilde{x}=Kx=K(y-{y}_{d})\), \({\widetilde{x}}_{r}={K}_{D}{x}_{r}={K}_{D}{D}^{\lambda }x\), \({\Delta u}_{D}\) is the output of the FOFD component. The set of eight rules together determines the overall control law of the FOFPI + D controller. The significance of control rules is explained as.

In control rule 1 (Cr1): condition \(\widetilde{e}.n\) (error negative) implies that output \(y\) of the system is above the desired output \({y}_{d}\), & \({\widetilde{e}}_{r}.n\) (a fractional derivative of error is negative) infers \({D}^{\lambda }y>{D}^{\lambda }{y}_{d}\) (means system output is moving upwards faster than desired output). Therefore, to keep output \(y\) close to the desired signal \({y}_{d}\), the output of the FOFPI component \(\Delta {u}_{PI}\) is set as negative. In the case of the FOFD component, control rule 5 (Cr5) is fired corresponding to Cr1, and its output \({\Delta u}_{D}\) is set to be zero. Thus, by Cr1 and Cr5 of both components, the overall control law as given in Eq. (27) drives the output of the system downwards. The system output can also be driven faster if the FOFD component output is positive. But both component outputs being non-zero simultaneously, complicates controller design.

In control rule 2 (Cr2), the system output is above the desired output but moves downwards faster than the desired output. So, \(\Delta {u}_{PI}\) is set zero and \({\Delta u}_{D}\) is made positive to bring the system output down by combining Cr2 and Cr6. Similarly, other rules can also be explained.

3.5.3 Defuzzification

Defuzzification is converting the fuzzy value to a crisp value; several methods are available in the literature to defuzzify the fuzzy output. The selection of the defuzzification method for a specific problem is a critical and challenging task. Driankov et al. [44] evaluated and compared the performance of different defuzzification methods for control applications. The study suggested that the centroid/centre of mass defuzzification method proved more efficient than other techniques. Therefore, in this work centre of mass formula to defuzzify FOFPI and FOFD components is used [19]. The control action \(\Delta {u}_{PI}\) and \(\Delta {u}_{D}\) based on the defuzzification method is described as

$$\begin{array}{*{20}c} {\Delta u = \frac{{\sum \left( {{\text{output corresponding to membership value of input}} \times {\text{membership value of input}}} \right)}}{{\sum {\text{membership value of input}}}}} \\ \end{array} .$$
(33)

e FOFPI inputs, i.e. error and fractional error rate, are divided into 20 input combination (IC) regions and are graphically depicted in Fig. 5. The horizontal axis represents the membership functions of the error \({K}_{I}e\left(nT\right)\) and that of the fractional rate of error \({K}_{P}{e}_{r}\left(nT\right)\) is represented on the vertical axis. The control rules (Cr1 to Cr4), membership functions, and the IC regions are used to evaluate each region's fuzzy control law of the FOFPI controller. Considering region IC1 and Cr1, the value of \(\widetilde{e}.n<0.5\) and \({\widetilde{e}}_{r}.n>0.5\) from Fig. 4a, therefore by using Zadeh's logic [45]

Fig. 5
figure 5

Input combination region for both FOFPI and FOFD components

Full size image

\(\widetilde{e}=\widetilde{e}.n\) and \({\widetilde{e}}_{r}={\widetilde{e}}_{r}.n\) implies \(min\){\(\widetilde{e}.n, {\widetilde{e}}_{r}.n\)} = \(\widetilde{e}.n\)

Therefore, from Cr1,

$$({\text{Cr}}_{1} )\left\{ {\begin{array}{*{20}c} {{\text{The chosen input membership function is }} \tilde{e}.n } \\ {{\text{The membership value of output is o.n}} } \\ \end{array} } \right.$$

Similarly, other rules and Zadeh's logic yields

$$({\text{Cr}}_{2} )\left\{ {\begin{array}{*{20}c} {{\text{The}}\,{\text{chosen}}\,{\text{input}}\,{\text{membership}}\,{\text{function}}\,{\text{is}}\,\tilde{e}.n} \\ {{\text{The}}\,{\text{membership}}\,{\text{value}}\,{\text{of}}\,{\text{output}}\,{\text{is}}\,o.z} \\ \end{array} } \right.$$
$$({\text{Cr}}_{3} )\left\{ {\begin{array}{*{20}c} {{\text{The}}\, {\text{chosen}}\, {\text{input}}\, {\text{membership}}\, {\text{function}}\, {\text{is}}\, \tilde{e}_{r} .n } \\ {{\text{The}}\, {\text{membership}}\, {\text{value}}\, {\text{of}}\, {\text{output}}\, {\text{is}} o.z } \\ \end{array} } \right.$$
$$({\text{Cr}}_{4} )\left\{ {\begin{array}{*{20}c} {{\text{The}}\,{\text{chosen}}\,{\text{input}}\,{\text{membership}}\,{\text{function}}\,{\text{is}}\,\tilde{e}_{r} .p} \\ {{\text{The}}\,{\text{membership}}\,{\text{value}}\,{\text{of}}\,{\text{output}}\,{\text{is}}\,o.p} \\ \end{array} } \right.$$

The values of \(o.p=L,o.n=-L, o.z=0\) are from Fig. 4b, and by applying the geometry of straight line to the membership functions of input, following formula are derived [27]:

$$e.p = \frac{{K_{I} e\left( {nT} \right) + L}}{2L}, e.n = \frac{{ - K_{I} e\left( {nT} \right) + L}}{2L}$$
$$e_{r} .p = \frac{{K_{P} e_{r} \left( {nT} \right) + L}}{2L}, e_{r} .n = \frac{{ - K_{P} e_{r} \left( {nT} \right) + L}}{2L}$$

Now, substituting the above formulae and values in Eq. (33), the output \(\Delta {u}_{PI}(nT)\) in region IC1 is obtained as,

$$\begin{array}{*{20}c} {\Delta u_{PI} \left( {nT} \right) = \frac{{L\left( {K_{I} e\left( {nT} \right) + K_{P} e_{r} \left( {nT} \right)} \right)}}{{2\left( {2L - K_{I} e\left( {nT} \right)} \right)}}} \\ \end{array}$$

Rearranging the above equation yields

$$\begin{array}{*{20}c} {\Delta u_{{PI}} \left( {nT} \right) = \left[ {\frac{{LK_{I} }}{{2\left( {2L - K_{I} e\left( {nT} \right)} \right)}}} \right]e\left( {nT} \right) + \left[ {\frac{{LK_{P} }}{{2\left( {2L - K_{I} e\left( {nT} \right)} \right)}}} \right]e_{r} \left( {nT} \right)} \\ \end{array}$$
(34)

The control law Eq. (34) follows the linearity property of classical controller with the difference that its gains vary nonlinearly as the function of input signals \(e\left(nT\right).\) These non-linear gains provide adaptive/self-regulatory features to the controller. Similarly, all the control laws for FOFPI and FOFD components for each \(IC\) region are obtained and listed in Table 1. The following section establishes sufficient stability conditions for the control loop using the two straight lines method (graphical approach).

Table 1 Formulae for \(\Delta {\mathrm{u}}_{\mathrm{PI}}\) and \(\Delta {\mathrm{u}}_{\mathrm{D}}\) for all regions of \(\mathrm{IC}\)
Full size table

3.6 Stability Analysis Using a Graphical Approach

The sufficient stability condition for fuzzy PI/PD/PID controller has been determined using the acclaimed small gain theorem. For a BIBO stable system, the output of the system is bounded at all times in the case of bounded input. The obtained conditions by the analysis help design a safe fuzzy control and provide guaranteed closed-loop stability. The BIBO stability of FO fuzzy PI + D controller in a closed-loop is investigated analytically using a graphical approach [23, 28].

Now by considering Fig. 3, it is clear that \(x\left(nT\right)\) and \({x}_{r}\left(nT\right)\) have an opposite sign as compared to \(e\left(nT\right)\) and \({e}_{r}\left(nT\right)\), respectively. Thus, overall control action \({u}_{PID}\left(nT\right)\) of closed-loop control, the structure depends on \(e\left(nT\right)\) and \({e}_{r}\left(nT\right)\). In the discrete domain, let

$$a\left( z \right) = \frac{e\left( z \right)}{{u_{PID} \left( z \right)}}\,{\text{and}}\,b\left( z \right) = \frac{{e_{r} \left( z \right)}}{{u_{PID} \left( z \right)}}$$

where

$$a\left( z \right) = a_{0} + a_{1} z^{ - 1} + a_{2} z^{ - 2} + \ldots$$
$$b\left( z \right) = b_{0} + b_{1} z^{ - 1} + b_{2} z^{ - 2} + \ldots$$

Here coefficients are unknown. In the same way,

$$e\left( z \right) = e_{0} + e_{1} z^{ - 1} + e_{2} z^{ - 2} + \ldots$$
$$e_{r} \left( z \right) = e_{{r_{0} }} + e_{{r_{1} }} z^{ - 1} + e_{{r_{2} }} z^{ - 2} + \ldots$$
$$u_{PID} \left( z \right) = u_{{{\text{PID0}}}} + u_{{{\text{PID1}}}} z^{ - 1} + u_{{{\text{PID2}}}} z^{ - 2} + \ldots$$

Let

$$A = \mathop \sum \limits_{i = 0}^{\infty } \left| {a_{i} } \right|,\,and\,B = \mathop \sum \limits_{i = 0}^{\infty } \left| {b_{i} } \right|$$
$$E = \sum\limits_{{i = 0}}^{\infty } {\left| {e_{i} } \right|} ,\,R = \sum\limits_{{i = 0}}^{\infty } {\left| {e_{{r_{i} }} } \right|} \,and\,U = \sum\limits_{{i = 0}}^{\infty } {\left| {u_{{PIDi}} } \right|} ,$$

Now for the closed-loop system to be BIBO stable, both \(\Vert A\Vert\) and \(\Vert B\Vert\) must be finite, thus

$$\left\| A \right\| = \alpha_{1}$$
$$\left\| B \right\| = \alpha_{2}$$

where \({\alpha }_{1}\) and \({\alpha }_{2}\) are constants. Also, we have

$$\begin{array}{*{20}c} {\left\| E \right\| \le \alpha_{1} \left\| U \right\|} \\ \end{array}$$
(35)
$$\left\| R \right\|\begin{array}{*{20}c} { \le \alpha_{2} \left\| U \right\|} \\ \end{array}$$
(36)

Suppose that

$$y\left( {nT + T} \right) = \aleph \left( {y\left( {nT} \right)} \right) + H_{1} \left( {u_{PID} \left( {nT} \right)} \right) + H_{2} \left( {w\left( {nT} \right)} \right)$$

where, \(\aleph\) is an operator of a closed-loop scheme, \(w(nT)\) are corresponding disturbances in the system (\({H}_{2}=0\) if it does not exist), and \(\aleph\), \({H}_{1}\), \({H}_{2}\) are bounded non-linear functions (in norm operator), such that:

$$\left\| \aleph \right\| < \infty ,\,\left\| {H_{1} } \right\| < \infty ,\, \left\| {H_{2} } \right\| < \infty$$

Then, it follows that

$$\left\| {H_{1} \left( {u_{PID} \left( {nT} \right)} \right)} \right\| = \left\| {y\left( {nT + T} \right) - \aleph \left( {y\left( {nT} \right)} \right) - H_{2} \left( {w\left( {nT} \right)} \right)} \right\|$$
$$\left\| {H_{1} \left( {u_{PID} \left( {nT} \right)} \right)} \right\| \le \left\| {y\left( {nT + T} \right)} \right\| + \left\| \aleph \right\| \times \left\| {y\left( {nT} \right)} \right\| + \left\| {H_{2} } \right\| \times \left\| {w\left( {nT} \right)} \right\|$$

Also, \(\left\| {H_{1} \left( {u_{PID} \left( {nT} \right)} \right)} \right\| \le \left\| {H_{1} } \right\| \times \left\| {\left( {u_{PID} \left( {nT} \right)} \right)} \right\|\) to assure that LHS be bounded, then

$$\left\| {H_{1} } \right\| \times \left\| {\left( {u_{PID} \left( {nT} \right)} \right)} \right\| \le \left\| {y\left( {nT + T} \right)} \right\| + \left\| \aleph \right\| \times \left\| {y\left( {nT} \right)} \right\| + \left\| {H_{2} } \right\| \times \left\| {w\left( {nT} \right)} \right\|$$

Or, still more conventionally as

$$\left\| {\left( {u_{PID} \left( {nT} \right)} \right)} \right\|\begin{array}{*{20}c} { \le \beta_{1} + \beta_{2} \left\| E \right\| + \beta_{3} \left\| R \right\|} \\ \end{array}$$
(37)

where

$$\beta_{1} \le \frac{1}{{\left\| {H_{1} } \right\|}}\left( {\left\| {y\left( {nT + T} \right)} \right\| + \left\| \aleph \right\| \times \left\| {y\left( {nT} \right)} \right\| + \left\| {H_{2} } \right\| \times \left\| {w\left( {nT} \right)} \right\|} \right)$$
$$\beta_{2} \le {\text{max}}\left\{ {\left\| {K_{I} } \right\|, \,\left\| K \right\|} \right\}$$
$$\beta_{3} \le {\text{max}}\{ \left\| {K_{P} } \right\|,\,\left\| {K_{D} } \right\|\}$$

Substituting, Eq. (37) in Eqs. (35) and (36) yields

$$\left\| E \right\| \le \alpha_{1} \left( {\beta_{1} + \beta_{2} \left\| E \right\| + \beta_{3} \left\| R \right\|} \right)$$

Explicitly,

$$\begin{array}{*{20}c} {\left\| R \right\| \ge \frac{1}{{\alpha_{1} \beta_{3} }}\left[ {\left( {1 - \alpha_{1} \beta_{2} } \right)\left\| E \right\| - \alpha_{1} \beta_{1} } \right]} \\ \end{array}$$
(38)

and

$$\begin{array}{*{20}c} {\left\| R \right\| \le \frac{1}{{1 - \alpha_{2} \beta_{3} }}\left[ {\alpha_{2} \beta_{2} \left\| E \right\| + \alpha_{2} \beta_{1} } \right]} \\ \end{array}$$
(39)

Comparing the above Eqs. (38) and (39) with the general equation of the straight line (i.e. \(\Vert R\Vert =\) slope \(*\Vert E\Vert +\) constant) in \(\Vert E\Vert\)-\(\Vert R\Vert\) the plane provides information about the slope and constant. The sufficient condition for the closed-loop system to be stable is achieved by examining the four cases as. Case 1. When \({\alpha }_{1}{\beta }_{2}>1\) and \({\alpha }_{2}{\beta }_{3}<1\):

Under this condition, the slope of Eq. (38) is negative, and Eq. (39) is positive. The intersection region produced by plotting both the lines is shown in Fig. 6a. In this case, there exists an unbounded region in the first quadrant of \(\Vert E\Vert\)-\(\Vert R\Vert\) plane. Thus, the closed-loop system is unbounded; and the case is avoided.

Fig. 6
figure 6

Intersection region of two straight lines in \(\Vert E\Vert\)-\(\Vert R\Vert\) plane a Case 1 b Case 2 c Case 3 d Case 4

Full size image

Case 2. When \({\alpha }_{1}{\beta }_{2}>1\) and \({\alpha }_{2}{\beta }_{3}>1\)

In this condition, the slope and constant of both the straight lines are negative; therefore, no bounded region exists in the first quadrant of \(\Vert E\Vert\)-\(\Vert R\Vert\) plane, as shown in Fig. 6b. Therefore, this case does not provide the condition of stability and should be abolished.

Case 3. When \({\alpha }_{1}{\beta }_{2}<1\) and \({\alpha }_{2}{\beta }_{3}>1\)

The slope and constant of Eq. (38) are positive and negative, respectively, and for Eq. (39) both are negative. In this situation, there is an empty region in the first quadrant, as shown in Fig. 6c. Therefore this case is also discarded.

Case 4. When \({\alpha }_{1}{\beta }_{2}<1\) and \({\alpha }_{2}{\beta }_{3}<1\)

In this case slope of both lines are positive, with constants having the opposite sign. Therefore, the lines intersect in the first quadrant with a common region, as shown in Fig. 6d. The common region is bounded within the first quadrant of \(\Vert E\Vert\)-\(\Vert R\Vert\) plane. Thus, a sufficient stability condition exists and is derived by equating the Eqs. (38) and (39).

$$\frac{1}{{\alpha_{1} \beta_{3} }}\left[ {\left( {1 - \alpha_{1} \beta_{2} } \right)\left\| {E_{Q} } \right\| - \alpha_{1} \beta_{1} } \right] = \frac{1}{{1 - \alpha_{2} \beta_{3} }}\left[ {\alpha_{2} \beta_{2} \left\| {E_{Q} } \right\| + \alpha_{2} \beta_{1} } \right],$$

where \(\left\| {E_{Q} } \right\|\) is the value of \(\left\| E \right\|\) at the point of intersection of two lines. Solving for \(\left\| {E_{Q} } \right\|\) gives

$$E_{Q} = \frac{{\alpha_{1} \beta_{1} }}{{1 - \left( {\alpha_{1} \beta_{2} + \alpha_{2} \beta_{3} } \right)}}$$

Similarly, \(\Vert {R}_{Q}\Vert\) is obtained as

$$\left\| {R_{Q} } \right\| = \frac{{\alpha_{2} \beta_{1} }}{{1 - \left( {\alpha_{1} \beta_{2} + \alpha_{2} \beta_{3} } \right)}}$$

Hence, the lines intersect at a point,

$$\left( {\left\| {E_{Q} } \right\|, \left\| {R_{Q} } \right\|} \right) = \left( {\frac{{\alpha_{1} \beta_{1} }}{{1 - \left( {\alpha_{1} \beta_{2} + \alpha_{2} \beta_{3} } \right)}}, \frac{{\alpha_{2} \beta_{1} }}{{1 - \left( {\alpha_{1} \beta_{2} + \alpha_{2} \beta_{3} } \right)}}} \right)$$

The coordinate of the point is finite and bounded; when \(\alpha_{1} \beta_{2} + \alpha_{2} \beta_{3} < 1\).

Lemma 1

The sufficient condition of stability for FOFPI + D in the control loop are summarised as

  1. (a)

    \(\left\| E \right\| \le \alpha_{1} \left\| U \right\|, \left\| R \right\| = \le \alpha_{2} \left\| U \right\|\)

  2. (b)

    \(\alpha_{1} \beta_{2} + \alpha_{2} \beta_{3} < 1\)

  3. (c)

    \(\beta_{1} \le \frac{1}{{\left\| {H_{1} } \right\|}}\left( {\left\| {y\left( {nT + T} \right)} \right\| + \left\| \aleph \right\| \times \left\| {y\left( {nT} \right)} \right\| + \left\| {H_{2} } \right\| \times \left\| {w\left( {nT} \right)} \right\|} \right)\)

  4. (d)

    \(\beta_{2} \le {\text{max}}\left\{ {\left\| {K_{I} } \right\|, \left\| K \right\|} \right\}\)

  5. (e)

    \(\beta_{3} \le {\text{max}}\{ \left\| {K_{P} } \right\|, \,\left\| {K_{D} } \right\|\)

  6. (f)

    \(\alpha_{1} \beta_{2} < 1, \alpha_{2} \beta_{3} < 1\)

Finally, the norm \(\Vert y\Vert\) in statement c) of lemma1 needs not to be finite when validating term \({\beta }_{1}\), if \(\Vert y\Vert =\infty\) at that moment, statement c) is trivially fulfilled. Nevertheless, if all the remaining statements are satisfied concurrently, then \(\Vert y\Vert\) undoubtedly will be finite as an outcome of the stability of closed-loop configuration.

3.7 Multiobjective Optimisation and NSGA-II

The proposed FOFPI + D controller has additional design parameters associated with fuzzy logic and fractional order operators, thereby increasing the computational complexity. The design of the controller requires a large amount of calculation and the controller performs its best with fine tuning only. There are different methods to find the controller parameters; nevertheless, with the advancement in artificial intelligence, the optimum parameters can be found easily using AI-based metaheuristics algorithms. In this work, an efficient multiobjective evolutionary optimisation algorithm is utilised to deal with the large computations required for tuning the controller. The main goal of evolutionary algorithms is to find the optimum result by minimising the objective through the survival of the fittest criterion. The system considered in this work has conflicting objectives, and optimisation by a single objective genetic algorithm (GA) can compromise the performance. Also, these optimisation algorithms generate the final best solution to a problem, so there is no chance of obtaining a trade-off among divergent objectives. On the other hand, multiobjective optimisation minimises several objectives simultaneously besides satisfying (optional) constraints. A vector of conflicting objectives is considered for optimisation is expressed as

$$\begin{array}{*{20}c} {F\left( \zeta \right) = \left\{ {f_{1} \left( \zeta \right). f_{2} \left( \zeta \right), \ldots , f_{m} \left( \zeta \right)} \right\}} \\ \end{array}$$

Subject to:

$$\begin{array}{*{20}c} {q_{j} \left( \zeta \right) = 0 \forall j \in \left[ {1, v} \right]} \\ \end{array}$$
$$\begin{array}{*{20}c} { c_{j} \le h_{j} \left( \zeta \right) \le d_{j} \forall j \in \left[ {1, s} \right]} \\ \end{array},$$

where \({c}_{j}\) and \({d}_{j}\) are constants, \(\zeta\) is the number of variables in the problem, \(\zeta \in \gamma\), with \(\gamma\) being decision space, and \({R}^{n}\) is objective space, also \(F:\gamma \to {R}^{n}\) contains \(m\) objective functions. \({h}_{j}\left(.\right)\) and \({q}_{j}\left(.\right)\) are optional \(s\) inequality and \(v\) equality constraints on the problem, respectively. The objectives \({f}_{1}\left(\zeta \right), {f}_{2}\left(\zeta \right), \dots , {f}_{m}\left(\zeta \right)\) are usually conflicting. Therefore, the principle of Pareto optimality is used for simultaneous optimisation of objectives, providing acceptable solutions with the trade-off between various objectives [46].

Non-dominated sorting genetic algorithm-II (NSGA-II) is a vastly utilised multiobjective optimisation algorithm inspired by biological evolution. The supremacy of NSGA-II lies in converting multiple objectives into a single measure by generating a set of Pareto fronts, sorted on the basis of non-domination. To solve multiple objectives problems in engineering fields, NSGA-II is implemented because of its efficiency, simplicity, and elitism [9, 10, 13, 47, 48]. NSGA-II performs all the computations in this work and finds the controller parameters for its optimum performance. The design steps for implementing NSGA-II are given in [38]. In subsequent sections, the performance of the NSGA-II optimised FOFPI + D and FPI + D controllers is evaluated for control of a non-linear robotic system.

4 Results and discussion

The performance of the proposed controllers is critically inspected for position control of the two-link robotic manipulator. This system exhibits highly non-linear characteristics and is a benchmark problem for testing the efficacy of new control designs. Therefore, the non-linear dynamics of the two-link robotic arm is simulated in a closed-loop configuration with FOFPI + D and FPI + D controllers. The control signal generated by the designed controllers provides the required torque for the angular movement of the links. Simulations are performed in MATLAB using a fourth-order Runge–Kutta differential equation solver with a sampling time of \(\mathrm{T}=1\) ms. The dynamics of the two-link robotic manipulator under consideration is described [49] as

$$\tau _{1} = m_{2} l_{2}^{2} \left( {\mathop \theta \limits_{1}^{{ \cdot \cdot }} + \mathop \theta \limits_{2}^{{ \cdot \cdot }} } \right) + \left( {m_{1} + m_{2} } \right)l_{1}^{2} \mathop \theta \limits_{1}^{{ \cdot \cdot }} + m_{2} l_{1} l_{2} c_{2} \left( {2\mathop \theta \limits_{1}^{{ \cdot \cdot }} + \mathop \theta \limits_{2}^{{ \cdot \cdot }} } \right) - m_{2} l_{1} l_{2} s_{2} \mathop \theta \limits^{{ \cdot _{2}^{2} }} - 2m_{2} l_{1} l_{2} s_{2} \mathop \theta \limits_{1}^{ \cdot } \mathop \theta \limits_{2}^{ \cdot } + \left( {m_{1} + m_{2} } \right)l_{1} gc_{1} + m_{2} l_{2} gc_{{12}}$$
$$\tau _{2} = m_{2} l_{1} l_{2} c_{2} \ddot{\theta }_{1} + m_{2} l_{1} gc_{{12}} + m_{2} l_{2}^{2} \left( {\ddot{\theta }_{1} + \ddot{\theta }_{2} } \right) + m_{2} l_{1} l_{2} s_{2} \ddot{\theta }_{1}^{2},$$

where \({c}_{1}=cos{\theta }_{1}, {c}_{2}=cos{\theta }_{2}, {c}_{12}=\mathit{cos}({\theta }_{1}+{\theta }_{2}), {s}_{1}=sin{\theta }_{1}\) and \({s}_{2}=sin{\theta }_{2}\). Subscripts \(1\) and \(2\) represent the parameters of link1 and link2, respectively. The angular position of link1 (\({\theta }_{1}\)) is measured w.r.t \(X\)-axis of the reference frame, whereas angular position (\({\theta }_{2}\)) for link2 is measured w.r.t link1. The torque \({\tau }_{1}\) and \({\tau }_{2}\) are applied at the base (starting point) of link1 and link2, respectively. The corresponding structure of the robot is depicted in Fig. 7. The value of the associated parameters of the robotic manipulator is recorded in Table 2.

Fig. 7
figure 7

Structure of the two-link robot

Full size image
Table 2 Description and value of parameters for robotic manipulator [50]
Full size table

The closed-loop configuration for position control of the robotic manipulator with the FOFPI + D controller is shown in Fig. 8. Constraints applied on \({\tau }_{1}\) and \({\tau }_{2}\) for controlling the angular position of links are taken as \([-5, 5]\) Nm to avoid the manipulator wear and tear. The designed controllers are tested for trajectory tracking with and without varying boundary conditions, model parametric uncertainties, and disturbance rejection.

Fig. 8
figure 8

Schematic block diagram of FOFPI + D controller for robotic manipulator

Full size image

4.1 Trajectory Tracking Performance

Generally, to perform any task, the links of the manipulator should track a predefined desired trajectory. In this regard, the desired trajectory is considered as a cubic polynomial of time 't' as [50]:

$$\theta_{{d_{i} }} \left( t \right) = a_{0i} + a_{1i} t + a_{2i} t^{2} + a_{3i} t^{3}$$

Satisfying the boundary condition

$$\left[ {\left. {\theta_{{d_{i} }} \left( t \right)} \right|_{t = 2 s} , \left. {\dot{\theta }_{{d_{i} }} \left( t \right)} \right|_{t = 2 s} ,\left. {\theta_{{d_{i} }} \left( t \right)} \right|_{t = 4 s} ,\left. {\dot{\theta }_{{d_{i} }} \left( t \right)} \right|_{t = 4 s} } \right],$$

where \(\mathrm{i}=1, 2\) specifies link1 and link2, respectively,\({\uptheta }_{{\mathrm{d}}_{\mathrm{i}}}\) is desired position and \({\dot{\uptheta }}_{{\mathrm{d}}_{\mathrm{i}}}\) is the corresponding velocity. Initial boundary condition for desired trajectory is chosen as \([1, 0, 0.5, 0]\) for link1 and \([2, 0, 4, 0]\) for link2. The search space for the controller parameter is restricted to \([0, 200]\) for \({K}_{{I}_{i}} \& {K}_{i}\); \([0, 50]\) for \({L}_{i}, {K}_{{P}_{i}} \& {K}_{{D}_{i}}\); [0, 500] for \({K}_{{uPI}_{i}} \& {K}_{{uD}_{i}}\) and [0, 1] for fractional operator \({\lambda }_{i}\).

The controller parameters are optimised using multiobjective NSGA-II with maximum iterations of 100. The problem for optimisation is formulated by defining objectives regarding absolute position error and torque variations for the two-link robotic manipulator. Their mathematical formulation is given in Eqs. (40) and (41). These objectives are contrary and conflicting (i.e., reducing objective results in increasing the other). The multiobjective optimisation offers promising solutions by trading off these objectives.

$$\begin{array}{*{20}c} {f_{1} = \sum \left| {\theta_{{d_{1} }} \left( {nT} \right) - \theta_{1} \left( {nT} \right)} \right| + \left| {\theta_{{d_{2} }} \left( {nT} \right) - \theta_{2} \left( {nT} \right)} \right|} \\ \end{array}$$
(40)
$$\begin{array}{*{20}c} {f_{2} = \sum \left| { \tau_{1} \left( {nT + T} \right) - \tau_{1} \left( {nT} \right)} \right| + \left| { \tau_{2} \left( {nT + T} \right) - \tau_{2} \left( {nT} \right)} \right|} \\ \end{array}$$
(41)

The time elapsed in optimising FOFPI + D is 10981.4 s, whereas for FPI + D, it is 9380.1 s. Fractional order operators are additional design variables that need tuning in the FOFPI + D controller, thus needing more time than the FPI + D controller. It makes the optimisation process more computationally complex, but it does not affect the time to generate the control signal. The control signal generation from both the controllers is unaffected by the complexity of the controllers. Figure 9 shows the Pareto front obtained for optimising the FOFPI + D and FPI + D controllers for the defined objectives. Associated optimised parameters values, objectives, and integral absolute error (IAE) for both the controllers are given in Table 3. These parameters of both controllers were kept unchanged throughout the entire simulation study.

Fig. 9
figure 9

Trade-off between objectives \({f}_{1}\) and \({f}_{2}\) a FOFPI + D b FPI + D with selected solution dotted black colour

Full size image
Table 3 Optimum parameters of controllers for link1 and link2
Full size table

The trajectory tracking performance of the controllers is shown in Fig. 10a, and their corresponding variations in torque, error, and end effector position in XY- plane with time are shown in Fig. 10b, c, and d, respectively. The IAE values of link1 and link2 in the FOFPI + D controller are almost 1/3 and 1/17 times that of the FPI + D controller, respectively. The improvement in IAE value is because the introduction of fractional operators in the FPI + D controller adds extra design variables. Moreover, gains of controllers vary nonlinearly, thereby providing automated control action to the system. Thus FOFPI + D offers tight trajectory tracking over the FPI + D controller.

Fig. 10
figure 10

Tracking response of the system with FOFPI + D and FPI + D controller a Links position b Control effort c Error and d End effector position in XY- plane

Full size image

Further, the effectiveness of the incorporated AI technique in the proposed controllers is analysed by comparing its performance with other non-AI controllers. Various controllers such as primary PID, fractional order PID (FO-PID), non-linear PID (NL-PID), and non-linear fractional order PID (NLF-PID) are designed in the literature [11] for the control of two-link robotic manipulator with identical parameters. These controllers are also optimised by NSGA-II, making the evaluation fair. Table 4 shows the comparison of the performance of controllers in trajectory tracking based on IAE value. It can be seen from the table that the controller that has AI incorporated through fuzzy logic performs better as compared to other controllers. Later, in the subsequent section, the robustness of the controller is tested for varying boundary conditions of trajectory, model parametric uncertainties, and disturbance rejection with and without uncertainties.

Table 4 Tracking response of the system for link1 and link2 by different controllers
Full size table

4.2 Trajectory Tracking for Varying Boundary Conditions

In actual situations, the robot end effector follows different trajectories in the workspace to perform various tasks. Variations in the trajectory are modelled by simultaneously varying the boundary conditions of link1, link2, and both links. The performance of control techniques is assessed based on IAE for all cases. The trajectory tracking performance and the corresponding variations in torque, position error, and position in XY-plane with time for boundary condition of \(\left[-2, 1, 3, 2\right]\) and \(\left[2, -1, -3, 1\right]\) for link1 and link2, respectively, are shown in Fig. 11. IAE values of both the controllers for varying boundary conditions of reference trajectory of link1, link2, and both links simultaneously are listed in Table 5. The results show that IAE in link position by FOFPI + D is lesser than the FPI + D controller for all boundary conditions. Better performance of FOFPI + D is achieved due to the FO operator, which provides an additional parameter to the controller. Thus FOFPI + D is more robust for changes in the desired trajectory than the FPI + D controller

Fig. 11
figure 11

Tracking response of the system with FOFPI + D and FPI + D controller a Links position b Control effort c Error and d XY-plane movement of the end effector with time for boundary condition of \(\left[-2, 1, 3, 2\right]\) and \(\left[2, -1, -3, 1\right]\) for link1 and link2, respectively

Full size image
Table 5 IAE values for varying boundary conditions of the desired trajectory of link1, link2, and both links
Full size table

4.3 Model Uncertainty

The physical systems are extraordinarily complex and ill-defined, so it is pretty tedious to determine their mathematical model. Such systems always have model uncertainties. Therefore the handling of uncertainties becomes a critical issue for any controller. Including parametric uncertainties, the model of the robotic manipulator is described as:

$${\tau }_{1}={(m}_{2}+\delta {m}_{2}){({l}_{2}+\delta {l}_{2})}^{2}\left({\ddot{\theta }}_{1}+{\ddot{\theta }}_{2}\right)+\left({m}_{1}+{m}_{2}+\delta {m}_{1}+\delta {m}_{2}\right){({l}_{1}+\delta {l}_{1})}^{2}{\ddot{\theta }}_{1}+{(m}_{2}+\delta {m}_{2})\left({l}_{1}+\delta {l}_{1}\right)({l}_{2}+\delta {l}_{2}){c}_{2}\left(2{\ddot{\theta }}_{1}+{\ddot{\theta }}_{2}\right)-{(m}_{2}+\delta {m}_{2})\left({l}_{1}+\delta {l}_{1}\right)({l}_{2}+\delta {l}_{2}){s}_{2}{\dot{\theta }}_{2}^{2}-2{(m}_{2}+\delta {m}_{2})\left({l}_{1}+\delta {l}_{1}\right)({l}_{2}+\delta {l}_{2}){s}_{2}{\dot{\theta }}_{1}{\dot{\theta }}_{2}+\left({m}_{1}+{m}_{2}+\delta {m}_{1}+\delta {m}_{2}\right)({l}_{1}+\delta {l}_{1})g{c}_{1}+{(m}_{2}+\delta {m}_{2})\left({l}_{2}+\delta {l}_{2}\right)g{c}_{12}$$
$${\tau }_{2}={(m}_{2}+\delta {m}_{2})\left({l}_{1}+\delta {l}_{1}\right)({l}_{2}+\delta {l}_{2}){c}_{2}{\ddot{\theta }}_{1}+{(m}_{2}+\delta {m}_{2})\left({l}_{1}+\delta {l}_{1}\right)g{c}_{12}+{(m}_{2}+\delta {m}_{2}){({l}_{2}+\delta {l}_{2})}^{2}\left({\ddot{\theta }}_{1}+{\ddot{\theta }}_{2}\right)+{(m}_{2}+\delta {m}_{2})\left({l}_{1}+\delta {l}_{1}\right)({l}_{2}+\delta {l}_{2}){s}_{2}{\dot{\theta }}_{1}^{2},$$

where

$$\left| {\delta m_{1} } \right| \le \frac{b}{100} \times m_{1} ,\,\left| {\delta m_{2} } \right| \le \frac{b}{100} \times m_{2}$$
$$\left| {\delta l_{1} } \right| \le \frac{b}{100} \times l_{1} ,\,\left| {\delta l_{2} } \right| \le \frac{b}{100} \times l_{2}$$

\(b\) is uncertainty in mass and length of links of the system. The uncertainties ' \(b\)' of \(\pm\) 5% to \(\pm\) 35% are introduced in the mass and length of link1 and link2, from their nominal values.

The designed FOFPI + D and FPI + D controllers are then employed to control the movement of the links. The performance of both the controllers in dealing with the uncertainty is compared on the basis of IAE in the angular position of the links. Table 6 records IAE values in the position of link1 and link2 for FOFPI + D and FPI + D controller, and a graphical depiction is represented in Fig. 12. The potentially robust FOFPI + D controller has an almost no or minor change in IAE value for every case of uncertainty in parameters. It is also evident from Fig. 12 that IAE in the position of links is relatively lower by FOFPI + D controller than FPI + D controller. The fuzzy inference technique in the FOFPI + D controller resembles human decision-making expertise. It provides the designed controller with a solid framework to handle imprecise system information and uncertainty. The control action generated by FLC is not dependent on system dynamics, thus effectively handling the uncertainty by its reasoning. It is found from the outcomes that IAE for FOFPI + D controller is intact and lesser than its integer order counterpart for all the situations of uncertainty.

Table 6 IAE in link position for \(b\%\) uncertainty in parameters \({{m}_{1},{m}_{2},l}_{1}\& {l}_{2}\)
Full size table
Fig. 12
figure 12

Variation of IAE in link position with varying uncertainty for a link1 and b link2

Full size image

4.4 Disturbance Rejection

The unexpected disturbances generated internally or externally in practical systems are critical issues because they can deviate system output from their actual value. Thus, there is a requirement for an efficient controller which can discard such disturbances, so that response of the system accurately tracks the desired output. Therefore, disturbance rejection plays a vital role in testing the robustness of the designed controllers. Two separate studies for the disturbance rejection are performed to examine the controller's robustness. In the first study, disturbance rejection with the nominal values of system parameters is tested, and disturbance rejection with uncertain system parameters is tested in the second study.

4.4.1 Disturbance Rejection with Nominal Parameters of the System

The performance of designed controllers is investigated for disturbance rejection without model uncertainty by introducing a sinusoidal disturbance of different amplitudes (Table 7) for the entire time in \(d1\), \(d2,\) and simultaneously in both \(d1\) & \(d2\) as shown in Fig. 8. Disturbance rejection response for the case of \(10Sin50t\) Nm disturbance is shown in Fig. 13, including tracking response, control effort, position error and XY coordinates of the end effector with time. The IAE from the reference position of link1 and link2 in case of the disturbance rejection is listed in Table 7. For comparative analysis, variations in IAE are plotted and depicted in Fig. 14. It is observed from graphical and quantitative analysis that the IAE value variations are significantly less for FOFPI + D than for the FPI + D controller. Hence, it can be emphasised that FOFPI + D controller performance is superior to its integer order counterpart in the rejection of disturbance.

Table 7 IAE in link position by FOFPI + D and FPI + D controller for added disturbance
Full size table
Fig. 13
figure 13

Tracking response with FOFPI + D and FPI + D controller a Links position b Control effort c Error and d End effector position in XY- plane by adding \(10Sin50t\) Nm disturbance in both \(d1\)& \(d2\)

Full size image
Fig. 14
figure 14

Variation in IAE by FOFPI + D and FPI + D controller a link1 with added disturbance in \(d1\) b link2 with added disturbance in \(d1\) c link1 with added disturbance in \(d2\) d link2 with added disturbance in \(d2\) e link1 with added disturbance in both \(d1\) &\(d2\) f link2 with added disturbance in both \(d1\) & \(d2\)

Full size image

4.4.2 Disturbance Rejection with an Uncertain System

In this section, the controller's intense robustness testing is carried out by incorporating model uncertainty and disturbance. The complete study is accomplished by considering ± 35% model uncertainty with the boundary condition of trajectory as \(\left[-4, -1, -7, 5\right]\) &\([3, 1, 5, -5]\) for link1 and link2, respectively. Moreover, IAE values for added disturbance of \(10Sin50t\) Nm in \(d1\), \(d2\), and both \(d1 \,\& \,d2\) simultaneously are recorded in Table 8. The trajectory tracking performance of FOFPI + D and FPI + D controllers and their corresponding variations in torque, position error, and end effector position in XY-plane versus time with added disturbance in both \(d1 \,\&\, d2\) are shown in Fig. 15. Further, the bar graphs in Fig. 16 are also used to depict the quantitative performance analysis. It is observed that IAE value of FOFPI + D for link1 and link2 are approximately (33% & 33%), (20% & 0.8%) and (25% & 8%) of FPI + D controller for all the three cases i.e. \(d1, d2\) and both \(d1 \,\&\, d2\) respectively. Thus, the FOFPI + D controller offers robust, effective, and better control than FPI + D.

Table 8 IAE values of FOFPI + D and FPI + D controller by incorporating ± 35% parameter uncertainties with added disturbance of \(10Sin50t\) Nm in \(d1\), \(d2\) and simultaneously in \(d1\, \& \,d2\)
Full size table
Fig. 15
figure 15

Tracking response of the system with FOFPI + D and FPI + D controller a Links position b Control effort c Error and d End effector position in XY- plane by incorporating ± 35% parameter uncertainties with added disturbance of \(10Sin50t\) in both \(d1\) & \(d2\)

Full size image
Fig. 16
figure 16

Quantitative analysis of FOFPI + D and FPI + D controller based on IAE value for a link1 and b link2 by incorporating ± 35% parameter uncertainties with added disturbance of \(10Sin50t\) Nm in \(d1\), \(d2\) and simultaneously in \(\mathrm{d}1\, \&\, d2\)

Full size image

5 Conclusion

A framework for the fractional fuzzy proportional integral plus derivative (FOFPI + D) controller is demonstrated in this paper. The proposed controller (FOFPI + D) is derived mathematically as a FOFPI and FOFD controller combination. It retains the simple linear structure in PI and D portions but has non-linear gains, enhancing its self-tuning control ability. The analytical formulae for the proposed FOFPI + D controller, fuzzification, rule base setup, and defuzzification are presented. Also, the condition for stability of the closed-loop system using the graphical method is established. Thus, providing assured reliability, stability, and adaptability to the resulting control scheme (FOFPI + D). The proposed controller also exhibits intelligence in making decisions and computations based on a metaheuristic algorithm.

A detailed study of the performance of the proposed FOFPI + D design for the control of a non-linear robotic manipulator is discussed. The controller parameters are optimally tuned through NSGA-II by minimising control signal and error variation. The simulation results show the effectiveness of the FOFPI + D controller for trajectory tracking, robustness against parametric variation, tracking for varying boundary conditions of reference trajectory, and disturbance rejection. Further, the quantitative comparative analysis based on IAE is performed to prove the advantages of AI-based controllers over conventional controllers. The controller could be further advanced by implementing techniques such as neural networks, type 3 fuzzy logic and algorithms.