Abstract
We present a comprehensive review of the optical response of graphene, in both the linear and nonlinear regime. This will serve as a reference for both beginners and more experienced researchers in the field. We introduce, derive, and extensively discuss the Dirac–Bloch equations framework, central to describing electron–photon interaction in nonperturbative, gapless materials. We use this model to re-derive several known results in the linear regime, such as the universal absorption law, and to describe the nonlinear interaction of ultrashort pulses with graphene. We compare the validity of the Dirac–Bloch equations model with the traditional Semiconductor-Bloch equations and point out advantages and shortcomings of the two models. Lastly, we present a cutting-edge model for describing the nonlinear optical response of graphene when bending becomes important, a situation that deeply affects the output spectra, and can provide insight to a novel, effective way to manipulate light in two-dimensional media.
Similar content being viewed by others
1 Introduction
It is hard to believe that any well-rounded scientist or science enthusiast, up-to-date with the latest developments in Physics and technology, has not heard of the word “graphene” in some form or another. “Graphene is the name given to a single layer of carbon atoms densely packed into a benzene-ring structure”, as was described in the seminal paper reporting its experimental realisation [1].
As an atom-thick layer of carbon atoms arranged in a hexagonal structure, graphene provides the basis of many nanostructures of carbon (known by the jargon allotropes): carbon nanotubes can be thought as rolled-up sheets of graphene; graphite can be construed as a particular stacking of such layers, and Buckminsterfullerene C\(_{60}\), also known as a “buckyball”, can also be thought of a spherical version of graphene.
These structures can now be produced in the laboratory, but this was not the case until very recently. Long theoretically predicted by Wallace [2], who determined the energy spectrum of a single electron in graphene in 1947, graphene was thought to be an abstract artefact of Solid State Physics, never to be produced in the laboratory. Most notably, Physics heavyweights, such as Landau [3], Peierls [4] and, later, Mermin [5] invoked thermodynamical arguments to dispute the notion that two-dimensional crystals can be stable, due to a divergent contribution of thermal fluctuations in low-dimensional crystal lattices. The rest is history—Geim and Novoselov [1] were successful in producing the first sample that would be unequivocally characterised as graphene in 2004. For those efforts, they won the Nobel prize in Physics in 2010.
The physics of graphene and related materials, such as black transition metal dichalcogenides (TMDs) [6], black phosphorous [7], and hexagonal boron nitride [8], to name a few, has attracted an ardent interest since the initial experimental realisation of graphene monolayers [1]. What exactly is so special about this particular material? How come is the research output concerning graphene still so abundant so many years after its physical realisation?
Firstly, the electronic structure displayed by the carriers is remarkable: at relative low energies, graphene shows a unique Dirac-like band structure and this implies that quasielectrons behave as if they were massless Dirac fermions [9], akin to charged photons or neutrinos.
It is not surprising that under certain conditions, quasiparticles may also be pseudorelativistic. Electrons in graphene are ballistic in the sense that their Fermi velocity is about \(0.3 \%\) of the speed of light. While it is true that they do not attain velocities compared to the speed of light, where relativistic effects take place, the absence of both a gap, a crucial aspect of semiconductors, and curvature in the energy dispersion for low-lying electronic states, suggest this tempting analogy, namely to model them with a relativistic equation.
Due to this special property, graphene electronics is quite different from conventional semiconductor electronics, and holds the promise of revolutionising the technological landscape in many different ways [9]. It is no surprise that graphene has been the spotlight in Material Science research and, involuntarily, shaped the direction of two-dimensional crystals research in many unrelated directions.
Furthermore, on the technological side, a tremendous effort to link novel effects and properties to new devices and related applications have reached so far as to use graphene as an “atomic sieve” and as a biosensor [10, 11]. Its mechanical properties truly are amazing. Reports that “establish graphene as the strongest material ever measured” [12] motivate this claim.
For the theorist, graphene provides a joyful playground for studying and idealising a myriad of theoretical concepts. Given its quasirelativistic nature, graphene is expected to show signatures of features found in (high-energy) Quantum Electrodynamics, such as Klein tunneling [13], or Zitterbewegung [14]. Furthermore, graphene eventually led the research community to a true paradigm change in an abundant scope of areas: a deeper understanding of universal electronic properties through a topological analysis of the underlying Hamiltonian, leading to the discovery of many novel topological states [15, 16]. With this understanding, the Quantum Hall effect has been established alongside experimental observations [17]. Astonishing reports of superconductivity in twisted bilayer graphene have been recently published [18]. Graphene has prominently kicked off a whole new ambition in Condensed Matter Physics to engineer systems with generalised topological properties to new realms [19]. Examples of this are given by the observation of (three-dimensional) Dirac semimetals [20, 21], Weyl semimetals [22, 23] and, very recently, to startling new quasiparticles known as type-II Dirac fermions, which seem to break Lorentz invariance [24, 25], and to possess an intriguing nonlinear optical response [26]. The future seems promising for the field.
This work is concerned with understanding the optical properties of Dirac fermions and it relies on a particular employment of methods to predict optical phenomena of graphene and, at large, two-dimensional quasirelativistic materials. It begs the question: In what way are these quasirelativistic features present in the optical interactions? Apart from their noteworthy electronic properties, massless Dirac fermions, the term used to describe the carriers in monolayer graphene, have already been shown extraordinary optical features [27] which have already been employed in photonics for ultrafast photodetectors [28], optical modulation [29], molecular sensing [30], and several nonlinear applications [31, 32].The conical dispersion itself is known to induce highly nonlinear dynamics for light [33]. Graphene’s optical response is characterised by a highly-saturated absorption at rather modest light intensities [34], a remarkable property which has already been exploited for mode-locking in ultrafast fiber-lasers [35]. The high nonlinear response of graphene leads to the efficient generation of higher harmonics [36, 37].
The understanding of how these fermions interact with light in extreme and ultrashort conditions remains, to a large extent, incomplete. The work presented in this Review tries to address this point with the aid of a set of equations, termed the Dirac–Bloch Equations (DBEs), which will be derived precisely and analysed with realistic probing parameters typical of intense (high electric field amplitudes) and short (few pulse optical cycles) electromagnetic pulses.
For the sake of completeness, it is worth mentioning that the DBE approach is not the only possibility, when tackling the problem of calculating the nonlinear optical response of graphene. There are, in fact, other methods available, such as the random phase approximation, the time-dependent density functional theory and other quantum chemistry methods [38]. These are in general more complex and resource-demanding, but provide an answer beyond the simple two-band model of graphene implicitly assumed in DBEs. An extensive discussion and comparison of these methods, their advantages and disadvantages compared to more traditional two-bands model is presented in a recent review [39]. Moreover, analytical solutions for the nonlinear susceptibility of graphene, within the framework of quantum mechanics, have been recently proposed. We refer the interested reader to, for example, the work of Mikhailov [40].
1.1 Review structure
This review is organised as follows: in Sect. 2 we present the general theoretical framework commonly used to describe electron dynamics in graphene. Here, we derive the usual tight-binding Hamiltonian from its crystal lattice structure, discuss its linearised dispersion relation in the vicinity of the Dirac points, and the correspondent density of states. Section 3 is instead dedicated to providing a continuum model for electrons in graphene, based on the massless Dirac equation. In Sect. 4, we then discuss in detail the optical properties of graphene; in particular, we construct a semiclassical framework for light–matter interaction encompassing both linear and nonlinear effects, and then discuss in detail the electric dipole approximation for graphene, and some consequences of the linear optical response, such as universal absorption, and the linear conductivity—with a numerical and computer simulation approach in mind. Sections 5 and 6 represent the core of this review, where the analytical and numerical methods used to calculate the optical response of graphene are analysed in detail, and sample solutions to known problems, such as third-harmonic generation, are discussed. In particular, Sect. 5 reviews the well-known framework of semiconductor Bloch equations and guides the reader on how to apply them to the case of graphene. Section 6, instead, generalises this method to the case of the so-called Dirac–Bloch equations, which proves more useful to handle light–matter interaction in graphene, and 2D materials in general. Then, the two methods are compared in Sect. 7, and advantages and disadvantages of both methods are discussed in a comparative manner. To conclude the review, Sect. 8 presents recent developments concerning the role of artificial gauge fields, emerging from bending and strain applied to graphene flakes, in their nonlinear optical response, with particular attention to their role in the high-harmonic generation spectrum of graphene. Finally, conclusions and outlook are drawn in Sect. 9.
To add value to this Review, actually making it useful not only for experts in the field, but also, and most importantly, to readers approaching this research field for the first time, we will re-derive many of the main linear properties found in the theoretical and experimental literature, including the law of universal absorption and the behaviour of transmitted and reflected fields (using the Dirac–Bloch equations framework), with the hope that presenting the details of these calculations will help the reader in gaining more insight on the physics of graphene and its theoretical models.
2 The physics of graphene
2.1 Overview
Graphene is simply a layered structure of carbon atoms. From this point of view, the standard theory of crystals and solids may be used to understand it as a quantum mechanical system. In this section, the basic theory that underpins most of how the electronic properties of crystals in a particular lattice arrangement are understood is introduced. Most tools to study such condensed matter systems revolve around the tight-binding approximation, introduced in Sect. 2.4.
With it, it will be shown that, for the particular case of a graphene monolayer, the conduction and valence bands depend linearly on the magnitude of the crystal momentum, touching each other at two special points in reciprocal space. Tied to this observation, a reduction of the usual scalar wavefunction describing the carriers, determined from the Schrödinger equation, to the two-component spinor described by a (2+1)-dimensional Dirac equation, is presented.
To fully appreciate the physicochemical reasons behind this unusual property, a brief explanation underlying the process of orbital hybridisation is given in Sect. 2.3. Ultimately, the orbital hybridisation leads to the rather strong hexagonal arrangement—known as a honeycomb lattice—that is responsible for its structural stability.
The consequences of such a geometrical disposition are deep. Such a real-space lattice is not a Bravais lattice although it can be decomposed into two Bravais triangular sublattices. As will be seen, this fact will allow such a decomposition to play the role of a degree of freedom, in turn allowing the quasiparticles describing the unhybridised electrons to be written in a relativistic fashion, leading to the celebrated Dirac Equation.
Once the relativistic analogy is set up, mimicking the electronic features of the carriers in the low-momentum regime, this framework yields startling features. For instance, the density of states of a graphene monolayer is, contrary to what is predicted of usual two-dimensional semiconductors, shown to be linear in Sect. 3.1, as a consequence of the linearity of the dispersion. Not surprisingly, its optical properties are expected to differ from a conventional semiconductor. A brief exposition of the tools and concepts necessary to understand them is given in Sect. 4. With them, the law of universal absorption, another astonishing feature of graphene, is derived. As will be discussed, this consideration leads to deep conclusions about the non-perturbative nature of graphene.
2.2 Electronic band structure
To start off, the concept of a quasiparticle must be framed. Dynamical phenomena in condensed matter systems, owing much to the system intrinsic geometrical configuration, may sometimes be idealised with the aid of particles. Depending on whether these obey fermionic or bosonic rules, they are termed quasiparticles or collective excitations, respectively. Examples of such dynamical phenomena may be a transfer of charge, energy, momentum or spin and are obviously a result of often complicated and intricate many-body interactions across the system.
The quasiparticle picture is particularly helpful precisely because it can reduce these phenomena to effective free-like single-particle excitations. For these reasons, one must distinguish conceptually the idea of an electron dispersing in free space, and of one constrained in a particular atomic arrangement, interacting with many other constituent parts of the system (including other electrons). For brevity purposes, the mouthful “quasielectron”, used to describe electronic quasiparticles, will not be used throughout this Review. Any subsequent description of “electrons” are meant in this way.
2.3 Hybridisation
Before engaging in discussions about the structure of graphene, it is enlightening to understand how those particular geometric arrangements make themselves manifest. In the jargon of Chemical Physics (or Physical Chemistry), the quasiparticles of interest in graphene are known as \(\pi \) electrons. The fundamental reason why such electrons may be represented by 2-component states is related to the geometrical arrangements, which arises from the \(sp^2\) hybridisation of the outer shell electrons of the carbon ions—conceptualised through its hexagonal, honeycomb lattice.
A carbon atom has six electrons in a configuration \(1\,s^{2} 2\,s^{2} 2p^{2}\). The first shell is normally irrelevant to chemical bonding, leaving the second shell, containing 2 electrons in the 2s orbital and another 2 in the \({|{2p_{x}}\rangle },{|{ 2p_{y}}\rangle }, {|{2p_{z}}\rangle }\), available to participate in bonding. As intuition tells, the 2s orbital is energetically more favourable than the remaining energy-degenerate 2p orbitals, being 4 eV lower. A comprehensive discussion of the chemical properties of carbon can be found, for example, in the lecture notes by Fuchs and Goerbig [41].
However, while bonding with other elements, namely carbon itself, this argument breaks down. The energy gain can be even higher if one 2s electron is promoted to one of the 2p orbitals, so that the three of them have one unpaired electron. This entails the basic idea behind hybridisation: the electrons are to be understood as a superposition of the \({|{2s}\rangle }\) and \({|{2p}\rangle }\) states. It turns out that the planar configuration of the layer is obtained through \(sp^{2} \) hybridisation, resulting in three new orbitals \({|{sp^{2}_{i}}\rangle }\) (\(i = 1,2,3\)) comprised of linear combinations of the \({|{2s}\rangle }\) and two p orbitals, arbitrarily taken as \({|{2p_{x}}\rangle }\) and \({|{2p_{y}}\rangle }\).
Through this process, all orbitals in the \(n=2\) shell—the \({|{sp^{2}_{i}}\rangle }\) and the remaining \({|{2p}\rangle }\)—have one unpaired electron. The geometric shape of these new hybridised orbitals indeed reveals three (\(\sigma \)) carbon bonds along the horizontal plane, which are \(120^{\circ }\) apart and hence organise the atoms in a hexagonal, honeycomb arrangement. Moreover, the separation between the carbon atoms, dictated by these orbitals, is the lattice constant \(a = 0.142\) nm. The unhybridised (\(\pi \)) orbital, \({|{2p_{z}}\rangle }\) has upper and lower symmetrical lobes and is perpendicular to the plane. The chemically-reactive electrons are the ones belonging to these orbitals and, any mention of “electrons” in graphene will be meant to denote these. \(\pi \) bonding between close-by \(\pi \) electrons is at the heart of the production of surface currents in graphene.
Even though all lattice sites, located at the corners of the hexagons, are composed of identical carbon atoms, it is clear that the honeycomb lattice arrangement does not represent a Bravais lattice \(\varvec{T}\), a type of geometric arrangements where all lattice sites can be obtained through a suitable linear combination of a particular set of of vectors \(\varvec{a}_{i}\):
where the basis of this space is known as the primitive vectors. The minimal area spanned by the basis is known as the unit cell.
This is a relevant observation. To see why the honeycomb lattice is not Bravais, consider Fig. 1. The vectors \(\varvec{\delta }_{i}\) connecting the nearest neighbours, all purple, to the blue site would have to also connect any purple site to all surrounding blue ones. However, it is clear that these vectors would have to be rotated by \(60^{\circ }\). The blue and purple sites are hence not physically equivalent. If only alternate sites are considered, i.e. only the blue or purples sites, it can now be seen that the underlying triangular lattice \(\varvec{T}\) is indeed Bravais, leading to all sites to be related by a unique set of translational vectors and hence a Bravais lattice defined as Eq. (1) requires by taking, for instance, the primitive vectors \(\varvec{a}_{1} = \sqrt{3}a(1,0)\) and \(\varvec{a}_{2} = \frac{\sqrt{3}a}{2}(1, \sqrt{3})\).
This construction holds for either colour of sites separately. This distinction of “species” is not made aimlessly: it is now clear that the honeycomb lattice can be decomposed into two Bravais sublattices, blue and purple, each containing one site per unit cell. Given that there is only one \(\pi \) electron per lattice site, the unit cell contains two valence electrons. This leads to the conclusion that the underlying lattice of graphene is a triangular with two sites per unit cell, which is depicted as the turquoise rhombus in Fig. 1. As will be seen shortly, the physical meaning behind this decomposition is vital to understand the electronics of the \(\pi \) electrons.
These triangular sublattices are normally denoted by A and B. In this case, they are not too different: one is simply shifted by \(\pm \varvec{\delta }_{3}\) with respect to the other. Therefore, for a sublattice index \(j \ (j = A,B)\), a shift vector \(\varvec{\delta }_{j}\) can associate any point of the honeycomb lattice to a point on that particular triangular sublattice j. Many choices for such shift vectors can be found although a rather simple choice is to fix one sublattice j with the honeycomb lattice (leading to \(\varvec{\delta }_{j} = 0\)) and describe any other point in the other sublattice \(i \ne j\) with a shift of \(\varvec{\delta }_{i} =\varvec{\delta }_{3}\).
The reciprocal lattice of each triangular sublattice is also a triangular sublattice, but now spanned by the vectors \(\varvec{b}_{1} = 2 \pi /(\sqrt{3}a)(1,- 1/\sqrt{3})\) and \(\varvec{b}_{2} = 4 \pi /(3a)(1,0)\). If only inequivalent vectors are considered, i.e. vectors which cannot be obtained by a shift of any other vector in the reciprocal lattice, are considered, the Brillouin zone (BZ) is obtained. This region defines the crystal momentum: all possible lattice excitations must therefore be identifiable with one such vector.
Figure 2 depicts the reciprocal lattice, with the Brillouin zone. It resembles a hexagon, bounded by six corners. These points cannot all belong to the interior, since four of them are related to the other two by a reciprocal vector shift. The two remaining, inequivalent points are termed the Dirac points and noted by \({\textbf{K}}\) and \({\textbf{K}}'\). Importantly, there is one unfilled \(\pi \) electron state per atom, as the three \(\sigma \) bonds that resulted from the \(sp^{2}\) hybridisation of the orbitals leave the remaining \(\pi \) electron available for pairing. Therefore, the relevant dispersion to understand the electronic properties of graphene is the \(\pi \) bands, composed of the chemically and physically reactive \(\pi \) electrons.
Depiction of the reciprocal lattice of the honeycomb lattice. Given the sublattice decomposition, two non-equivalent points in momentum space appear \({\textbf{K}}\) and \({\textbf{K}}'\), contained in the reciprocal unit cell, the blue rhombus. All non-equivalent points are contained within the first Brillouin zone, depicted in orange
As will be shortly seen, the Dirac points are crucial in understanding the low-energy properties of the \(\pi \) electrons in graphene, i.e. far from the \(\Gamma \) point, located exactly in the centre of the hexagon. The next section will introduce methodologies to describe the electronic band of such electrons.
2.4 Tight-binding approximation
To calculate the electronic bands of the \(\pi \) electrons, the tight-binding formalism is used. In this method, the wavefunction of the overall many-body system is assumed to be a linear superposition of atomic wavefunctions, localised at a particular lattice site. The latter is calculated without any reference to the lattice, i.e. without accounting for any environmental interaction. For this reason, the atomic wavefunction is not a true eigenstate of the system. This difference is assumed to stem from overlaps of neighbouring atomic wavefunctions at different sites. Furthermore, the overlap is assumed to decay quickly given the localisation of the electron on its site—hence why it is “tightly-bound”.
To see this, an atomic Hamiltonian at a lattice site l in position \({\textbf{R}}_{l}\) is considered:
where \(\nabla ^2\) is the Laplacian, m the mass of the free electron and \(V_{l}({\textbf{r}}- {\textbf{R}}_{l})\) is the potential at site l. The electron wavefunction at that site is the eigenfunction of the atomic Hamiltonian, satisfying:
where n is an index labelling the different orbitals composing the atom at site l and \(\epsilon _{n}\) their energy. In a mean-field approach, the full Hamiltonian is composed of the single-particle contributions \(H_{l}\), leading to an effective potential that may be treated as a perturbation \(\Delta V({\textbf{r}})\):
At this stage, the goal is to find the n eigenstates \(\psi _{{\textbf{k}}}({\textbf{r}})\) and their respective eigenvalues \(\epsilon _{n}\) of this Hamiltonian. Before one attempts to calculate them, an Ansatz that solves Eq. (4) must be found. The symmetries of the underlying lattice constraint the wavefunction across the lattice itself.
The technicalities of such statement lie deep in what is known as Bloch’s theorem. Given the physical invariance of the lattice sites in a Bravais lattice, the wavefunction must not behave differently when shifted by any lattice vector \({\textbf{R}}\). In particular, this means that a suitable translation operator \({\mathcal {T}}({\textbf{R}})\) must commute with the Hamiltonian. Consequently, both operators share the same eigenfunctions:
Given the Bravais decomposition of the honeycomb lattice just discussed, the wavefunction must in general be written as a linear combination of two components, one describing amplitudes from each sublattice:
In this fashion, each component satisfies Bloch’s Theorem, whenever \({\textbf{R}}\) is a vector of each underlying triangular sublattice. The coefficients \(\alpha ({\textbf{k}})\) and \(\beta ({\textbf{k}})\) naturally quantify the probability of finding the electron in each sublattices.
Given the alternate nature of the lattice sites, the essence of the tight-binding philosophy becomes clear: an electron of momentum \({\textbf{k}}\) is initially assumed to be fairly localised at an atomic site, belonging to a particular sublattice. The local site is itself composed of its atomic orbitals, dependent on the atomic character of the site. However, due to the overlap of the wavefunction sitting this particular lattice site with another electron wavefunction sitting on an adjacent lattice site, a non-zero probability of a transition into adjacent sites. Quantities pertaining to this mechanism are usually not easily reachable given the intrinsic complexities of the orbitals in question. In this instance, the p orbitals are not inherently challenging.
The Bloch functions \(\psi ^{(j)}_{{\textbf{k}}}({\textbf{r}})\) of either sublattice are too general to compute. To attain an Ansatz which satisfies Bloch’s Theorem, the tight-binding assumption relies on constructing them using atomic wavefunctions \(\phi ^{(j)}\), eigenfunctions of the atomic Hamiltonian:
where the sum is performed over all Bravais lattice vectors. In the present case, these correspond to the \({|{p_{z}}\rangle }\) orbitals at each site. The connection to the sublattice index is now clear: the primitive unit cell in graphene contains two atoms (one per sublattice), as seen in Fig. 1.
Precisely because the wavefunction \(\Psi _{{\textbf{k}}} ({\textbf{r}})\) must comply with Bloch’s Theorem, itself not warranted if the underlying lattice is not Bravais, a decomposition into Bravais sublattice must be found. This consideration alone leads to a decomposition of the wavefunction into two independent components, each pertaining to the different sublattices A and B and individually.
To obtain a matrix representation of the tight-binding Hamiltonian that will allow for the energy dispersion to be obtained, one must solve the Schrödinger equation \(H \psi _{{\textbf{k}}} = \epsilon _{{\textbf{k}}} \psi _{{\textbf{k}}}\). In the sublattice basis chosen in Eq. (6), the matrix elements must read:
Given the expansion of each sublattice wavefunction in terms of the atomic orbitals of Eq. (7), this is generally a hugely difficult task. However, after a rather lengthy derivation which can be found in the lecture notes by Fuchs and Goerbig [41], the Hamiltonian elements are calculated more easily if the following decomposition of the Hamiltonian is performed:
In it, the first part contains the on-site energy \(\epsilon ^{i}\) of the orbital i, multiplied by what is known as the overlap matrix \(s^{ij}_{{\textbf{k}}} \equiv \psi ^{(i)*}_{{\textbf{k}}}\psi ^{(j)}_{{\textbf{k}}}\). This matrix accounts for the orthogonality between the orbital bases of each individual sublattice species:
Given the usual normalisation condition of the atomic orbitals, the diagonal entries of the overlap matrix are unity. The perturbation to the potential energy of Eq. ( 4) is fully expressed in the hopping matrix t which, not surprisingly, is related to the expectation value of the perturbation \(\Delta V\) between sites i and j:
The factor of N accounts for the number of atoms per unit cell. As previously discussed, if one fixes the relative shifts as \(\varvec{\delta }_{B} = \varvec{\delta }_{3}\) and \(\varvec{\delta }_{A} = \varvec{0}\), the sum over the Bravais lattice vectors \({\textbf{R}}_{l}\) is performed on the sublattice which has \(\varvec{\delta }_{i} = \varvec{0}\). Keeping the convention, the sublattice A is chosen as such. The space integrals in each matrix yield the amplitude of the process and are assumed a constant. Finally, the decomposition just presented allows for the energy dispersion \(\epsilon ^{\lambda }_{{\textbf{k}}}\) to be obtained by solving the secular equation:
leading to exactly N bands (\(\lambda = 1,\ldots ,N\)). With the sublattice basis, two bands are thus predicted.
Considering that the hopping matrix involves a challenging integral in space, summed over all lattice vectors, it is not surprising that the underlying calculation of its elements presents many difficulties. Further simplifications are often taken given the particular system.
Since both sublattices are comprised of the same atomic orbitals, the out-of-plane, vertically-oriented \(p_{z}\) orbitals contribute the same amount to the on-site energy and would yield an irrelevant shift in the dispersion given in Eq. (12). Furthermore, since it can be reasonably assumed that contributions from neighbouring atoms are more relevant, the sum over the lattice vectors may be performed by first considering the nearest neighbours, followed by the next-nearest neighbours and so on.
Given the alternate nature of the disposition of the sublattices, the nearest neighbours are always located at different sublattices. The amplitude of this particular element is known as the (nearest neighbour) hopping factor:
For graphene, it has a value \(t = 2.8\) eV [8]. To compute the remaining phases in the hopping matrix t given in Eq. (11), the associated phases to each hopping are simply given by the appropriate triangular Bravais lattice vectors that connect an arbitrary A site, at position r, to the nearest B sites—\(B_{1},B_{2},B_{3}\), illustrated in Fig. 1. To find the shift in the position argument of the wavefunction at those points, one can use \(\varvec{a}_{2} - \varvec{\delta }_{3}\) for \(B_{1}\), \(\varvec{a}_{3} - \varvec{\delta }_{3}\) for \(B_{2}\) and \(\varvec{0} - \varvec{\delta }_{3}\) for \(B_{3}\). Therefore, the off-diagonal entries of the hopping matrix are simply \(t^{AB}_{{\textbf{k}}} = t^{BA ~*}_{{\textbf{k}}} = t \gamma _{{\textbf{k}}}\), where the phase acquired by each hopping is \(\gamma _{{\textbf{k}}}\):
The nearest-neighbour approximation assumes that the contribution to the atomic potential does not need to consider interactions between lattice sites farther away than the second smallest distance. Given the alternate nature of the honeycomb lattice, any contribution will come from sites separated by \(\Vert \varvec{a}_{1,2} \Vert \). This approximation already yields satisfactory results for most solids for which the tight-binding treatment applies and depends on the type of orbitals.
The addition of further sites to the calculation is similar in style: the next-nearest neighbours (nnn) are now of the same sublattice type:
where \(\varvec{a}_1\) is the vector connecting the amplitude of this nnn-hopping was obtained using the A sublattice but the B sublattice produces the same hopping factor. Again, from an arbitrary A sublattice site, six connections to other A sites are found, with the overall phase \(\gamma '_{{\textbf{k}}}\):
Gathering all hopping terms leads to the hopping matrix:
As one may expect, the contributions from the the overlap matrix s tend to be very small in comparison to their hopping counterparts. Going up to nearest-neighbours only, the sum is performed exactly like was performed for t. The normalisation of each sublattice Bloch wavefunction leads to the diagonal entries being 1. As for its off-diagonal entries, their amplitude is given by:
and the overall phase exactly equal to t i.e. equal to \(\gamma _{{\textbf{k}}}\), leading to a matrix:
finally allowing the tight-binding dispersion to be written to a great accuracy as:
where the secular equation of Eq. (12) was used. Given that the overlap amplitude s is much smaller than the others, the denominator can be Taylor-expanded as
\(1/(1+x) \approx 1 - x\), leading to:
where the last step assumes \(t'<< t\). A bit of algebra yields a relation between the phases as \(\gamma '_{{\textbf{k}}} = |\gamma _{{\textbf{k}}}|^2 - 3\), which allows the dispersion to be written as:
The factor \(3t'\) corresponds to a constant shift and is therefore irrelevant. What is interesting is that the inclusion of the overlaps leads to a renormalisation of the nnn hopping amplitude. This effect is incredibly feeble in graphene, since \(t'\) is measured to be \(t' \approx 0.01t = 0.028\) eV. As for the overlap amplitude, it is impossible to obtain given that measurements cannot differentiate \(t'\) from \(t'_{\textrm{eff}}\).
It is now clear that if only the nn hoppings are considered, the dispersion is simply:
where the explicit components of \(\varvec{a}_{i}\) were used. \(\varvec{a}_{3}\) is not part of the basis that was previously chosen: it is the combination \(\varvec{a}_{3} = \varvec{a}_{2} - \varvec{a}_{1}\). If this dispersion of Eq. (23) is now Taylor-expanded, for small \({\textbf{k}}\), it becomes linear with the momentum, leading to the famous Dirac cones:
where the constant \(v_{\textrm{F}} \equiv 3 t a /(2 \hbar )\) is known as the Fermi velocity and plays a crucial role in the reduction of the \(\pi \) electrons to two-dimensional Dirac spinors.
The applicability of this approximation holds up to energies of \(\approx 1\) eV, where a bending naturally arises so a peak is reached at the \(\Gamma \) point, as illustrated in Fig. 3 from [8].
This regime is nonetheless intriguing. Firstly, it indicates that graphene behaves like a zero-gap semiconductor. The positive and negative signs of Eq. (24) imply the existence of two symmetrical bands, naturally interpreted as the conduction and valence bands, respectively. Furthermore, this symmetry implies something deeper, namely the equivalence between electron and hole states occupying each band. The Fermi energy lies at the band-touching.
In principle, the introduction of a next-nearest neighbour interactions breaks such symmetry, as seen in Eq. (22). The rather strong covalent bonding of the nearest neighbour corrections in graphene absolutely dominate the overall perturbation expansion. Indeed, as was previously discussed, measurements of the nnn hopping amplitude put this figure as \(t' \approx 0.01\) eV, compared to its nn amplitude counterpart of \(t \approx 2.8\) eV [8].
3 Massless Dirac fermions
The previous section offered insightful clues to the adequacy of thinking of the carriers in graphene as massless Dirac fermions. In particular, the linear dispersion provides an exciting result since it mimics the dispersion found for massless quasiparticles notably neutrinos and photons, which are known to be ultra-relativistic. Many in the research community ponder the implication of such a connection. Is it possible to probe high-energy physics concepts, adequate for such relativistic particles in a low-energy framework?
In this section, the quasirelativistic nature of the carriers is formalised. The connection between the Dirac equation in \((3+1)\) dimensions will be shown to model the plane-confined carriers in \((2+1)\) dimensions, allowing interesting analogies to be presented between both models. The material presented in this Section can be found in many different standard textbooks on quantum mechanics, such as the book by Dirac [42], and in the book by M. I. Katsnelson on graphene physics [44], and it is intended to be a concise introduction to the topic. We refer the interested reader to these books for mode details about Dirac equation and its role in graphene physics.
The Dirac Equation was formulated by Dirac in 1928 [43] in the hope of reconciling Special Relativity with the then short-lived Quantum Mechanics for a spin 1/2 fermion. The particle, of rest mass m, is described with the aid of a 4-dimensional spinor \(\Psi \) and, in free-space, must satisfy:
where c is the speed of light. The \(\gamma \) matrices are 4-dimensional objects and not uniquely defined. A suitable representation for them must however satisfy the Clifford algebra:
where \(\{ \cdot , \cdot \}\) denotes the anti-commutator and \({\mathbb {I}}_{4}\) the identity operator. Additionally, they must satisfy the Hermiticity condition:
If Eq. (25) is left-multiplied by \(\gamma ^{0}\) and the definition \(\alpha ^{\mu } \equiv \gamma ^{0} \gamma ^{\mu }\) defined:
The metric tensor is taken as \(\eta ^{\mu \nu } = \text {diag}(1,-1,-1,-1)\). The differential 4-vector has covariant components \( \partial _{\mu } = \{(1/c) \partial _{t}, \varvec{\nabla } \}\) and contravariant components \( \partial ^{\mu } = \{(1/c) \partial _{t}, -\varvec{\nabla } \}\). The remaining dot product thus takes the form:
where \(\alpha ^{0} = (\gamma ^{0})^2 = {\mathbb {I}}\) by the anticommutation relation.
This is a partial differential equation, depending on space. However, through the canonical relation \({\textbf{p}} = -i \hbar \varvec{\nabla }\), the equation is Fourier-transformed, becoming an ordinary differential equation in time. This form is, of course, reminiscent of the Schrödinger equation.
The operator on the right-hand side becomes associated to the (Dirac) Hamiltonian \(H_{D}\). For a massless fermion, \(m=0\) and \(\gamma _{0}\) becomes irrelevant. As for \(a_{i}\), and consequently \(\gamma _{i}\), the Dirac representation can be constructed with the aid of the two-dimensional Pauli matrices:
The Dirac representation of \(\gamma \) matrices is simply taken as:
In such representation, the Dirac Hamiltonian in the Dirac representation:
The analogy is now clear: if c is replaced with \(v_{\textrm{F}}\), the (3+1) Dirac Equation for a massless fermion is composed of two 2-dimensional equivalent blocks of the form:
This Hamiltonian measures the energy from the \({\textbf{K}}\) point. For the purpose of this section, only one such valley will be considered given their symmetric role in the physics of ungapped graphene. In it, \(\varvec{\sigma }\) is known as the pseudospin and characterises many important properties of the quasiparticles [44].
The dot product is to be taken as \(\varvec{\sigma } \cdot {\textbf{k}}= \sigma _{x} k_{x} + \sigma _{y}k_{y}\) over the in-plane wavevector, where \(\sigma _{\mu }\) (\(\mu = 1,2\)) are the Pauli matrices. In matrix form, the Hamiltonian of Eq. (34) reads:
where the phase is given by \(\phi _{{\textbf{k}}} = \arctan \left( \frac{k_{y}}{k_{x}}\right) \). As expected, this model accounts for the linearity of the dispersion calculated from first principles, that resulted in Eq. (24). The eigenvalues of \(H({\textbf{k}})\) in Eq. (35) are:
with two symmetric branches \(\lambda = 1,-1\). Its associated normalised eigenstates may be obtained as:
The wavefunction of each band \(\lambda \), represented by \(\Psi ^{\lambda }_{{\textbf{k}}}({\textbf{r}})\), is a solution of the Time-Independent Schrödinger Equation:
and simply is the \({\textbf{r}}\)-representation of the ket states:
where A is the area of the sample. The splitting of the upper and lower components in this fashion is beneficial for future calculations. Consider the normalisation of such wavefunctions:
As for the spinor normalisation, it reads:
Evidently, for \({\textbf{k}}' = {\textbf{k}}\), one obtains \(\langle \lambda ' {\textbf{k}}'| \lambda {\textbf{k}}\rangle = \delta _{\lambda ' \lambda }\). With the knowledge of the wavefunction, many properties and features of the system may be unravelled.
3.1 Density of states
The density of states plays a particularly important role in the dynamics and interactions of electrons within a condensed matter system. It can be seen as a degree of degeneracy, accounting for the number of available quantum states for a given fixed energy interval.
Unlike an electron in two dimensions modelled by the Schrödinger Equation, which admits a constant density of states (per unit volume per unit energy) [45], the linearity of the dispersion of low-momentum electrons just discussed leads, by extension, to another interesting result—the density of states of the carriers in graphene is also linearly proportional to their energy.
The calculation for a then-hypothetical graphene monolayer in 1952, a mere five years after the dispersion had been obtained by Wallace, was already well established [46], by a direct calculation of the specific heat using a Debye frequency distribution. In addition to that, the appearance of non-differentiable points in the density of states leads to fascinating phenomena, such as enhancement in the electric resistance and optical conductivity of the material [47]. For more physically-relevant graphene flakes, the effect of geometry, size and edge terminations have been reported to create various van Hove singularities which in turn affect the optical response of the flake [48].
Before engaging in this particular calculation, the general definition is given, where \(g(\epsilon )\) denotes the density of states of the states in the interval \([\epsilon - \delta \epsilon , \epsilon + \delta \epsilon ]\):
Since the dispersion of Eq. (24) is not dependent on which Dirac point the Hamiltonian is measured from nor on the spin contributions, since they do not appear in the quasirelativistic model so far developed, one must introduce the valley and spin degeneracy factors, respectively given by \(g_{v}\) and \(g_{s}\). These are \(g_{v} = g_{s}=2\), respectively for the \({\textbf{K}}\) and \({\textbf{K}}'\) valleys and for the spin up and down contributions.
The calculation of the density of states, as dictated by Eq. (42) is in general rarely obtained through analytical methods, given the intrinsic complexity of general dispersions. However, in the linear regime of the dispersion, the general definition of Eq. (42) can be simplified using the continuum approximation:
where A is the area of the monolayer sample and the sum performed over momentum. Using the energy dispersion of Eq. (24) and integrating with polar coordinates \(k \equiv \Vert {\textbf{k}}\Vert \), \(\phi \equiv \arctan \left( k_{y}/k_{x} \right) \), it becomes:
where the integration in both variables is independent given the dispersion is purely radial. The evaluation of the integrand is performed using the following identity of the Dirac-\(\delta \) distribution:
where the sum is performed over the zeroes of f(k), \(k_{i}\). Letting \(f(k):= \epsilon - \epsilon (k)\), and given that k is necessarily non-negative, a unique solution \(k_{0}\) arises for a fixed \(\epsilon \), namely whenever \(k_{0} =\epsilon /(\hbar v_\textrm{F})\), hence the density of states becomes:
Finally, the sifting property of the \(\delta \) distribution:
implies that, for \(f(k) \equiv k\), \(g(\epsilon )\) takes the form:
where the modulus sign arises from the equivalence of \(k_{0}\) for either a positive or negative energy.
It can then be seen that the density of states is piecewise linear. This result is surprising for a two-dimensional system and to be contrasted with a Fermi gas in two-dimensions, which admits a constant density of states. The neutrality point occurs at the Dirac point i.e. when \(\epsilon = 0\), where \(g(\epsilon )\) becomes non-differentiable. From a QFT point of view, the linearity of the spectrum is unique in that it implies the Coulomb interactions between the carriers are not screened [49]. As will be seen throughout this work, the Dirac points really are remarkable and dictate much of the physics observed in graphene.
4 The optics of graphene
4.1 Overview
To understand how matter behaves optically, an obvious ingredient is missing—light. Throughout this work, a semiclassical approach will be used to describe any light–matter interactions. This is to say that any electromagnetic field are taken as classical fields, while the carriers in the crystal are treated quantum mechanically. Maxwell Equations provide the fundamental relationship between electromagnetic fields and matter.
This relationship is not easy to quantify for most part: it is a feedback-based hierarchy of external and induced fields which act as a response to the external disturbance on their charge configuration. Finding macroscopic quantities that describe these two different types of contributions is at best challenging.
Light is classically understood, at the macroscopic level, by the specification of the electric field \({\textbf{E}}({\textbf{r}},t)\) and the magnetic field \({\textbf{B}}({\textbf{r}},t)\). Depending on the coupling profile, matter will respond to the perturbation. In the simplest picture, a charge distribution will take place, leading to the medium polarisation. Dynamical charge distributions create electric currents in the sample. The harmonic composition of such currents acts in many ways as a means to probe the light–matter interactions. However intuitive, this picture completely overlooks the difficulty of obtaining reliable estimates of such quantities.
To further complicate the task, these estimates depend hugely on which optical excitation regime is chosen. A rough separation of affairs concerns the electric field intensity. If the macroscopic polarisation responds linearly to the electric field, the system is said to be excited in the linear optical regime. Otherwise, it is known as nonlinear. It is known, and somewhat expected, that there is a remarkable qualitative departure from the linear regime when the field intensity becomes large, leading to a modification of the optical properties of the material itself when probed. Therefore, these properties are field-dependent and thus frequency-dependent, in highly nontrivial ways.
The features are also strictly dependent on the features of the medium and a generalisation of the principles is not easy to achieve. The advancement of highly-coherent laser devices, with which intense monochromatic beams can be created reliably in the femtoscale has revolutionised the field, has provided to be a reliable platform to study intense excitation regimes. The field of Nonlinear Optics has been irrevocably linked to the methods and mechanisms that provide the framework for understanding harmonic generation, sum and difference-frequency generation, saturable absorption, self-induced transparency [50] and many other concepts not found in the more usual, linear branch of Optics [51, 58] and has inspired more general treatments such as Quantum Optics [59], where full quantum-mechanical properties of both matter and light fields are taken into account.
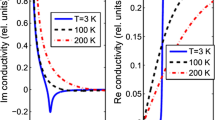
Not surprisingly, the linearity of the spectrum of massless Dirac fermions makes graphene an interesting platform to probe many optical phenomena. For instance, diffusive electron transport and temperature-dependent resistivity and conductivity vary from what is expected of a conventional semiconductor [60, 61].
As will be showed in Sect. 4.3, when excited with a weak electromagnetic field, a graphene monolayer absorbs all frequencies with the same efficiency of approximately \(2.3 \%\). Fascinatingly, this rate is not dependent on any excitation parameter, rendering it universal, given by the fundamental constants:
where \(\alpha _{rm QED}\) is the fine-structure constant in Quantum Electrodynamics. Related to this behaviour is the conductivity of a graphene sheet, which is also a constant [62] and related to the quantum of conductance \(2e^{2}/h\), as:
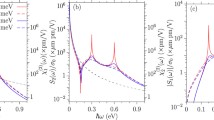
The frequency-dependent character of the conductivity as the excitation energy is increased may be appreciated in [63]. Despite the existence of defects and other environmental factors, the universal optical conductivity has been been experimentally verified in the spectral range of 0.2–1.2 eV [64].
In this section, a brief review of the necessary main optical and optoelectronic properties of graphene is given. The techniques needed to introduce light interactions within the formalism just exposed will also be presented. With them, a calculation of the electric dipole moment induced by photon absorption is presented and used to compare the same quantity that is found for semiconductors. To make sense of what is meant by a weak field, a rather brief review of the concepts of linear optics will be given here and used in later sections to retrieve results pertaining to this regime.
4.2 Semiclassical light–matter interactions
4.2.1 Nonlinear susceptibility
For simplicity, a space-independent electric field E(t) is considered for now. The (macroscopic) polarisation P(t) is normally obtained through expansion in powers of the field, as explained in detail in the book by Boyd [51],
where \(\epsilon _{0}\) is the permittivity of free space. The quantity \(\chi ^{(i)}\) denotes the ith order of the electric susceptibility. The information about the optical properties of the material is encoded in it. Since the electric field is input as a scalar, the susceptibility is a constant, dependent on the material.
Given the nature of the expansion, each order of the polarisation \(P^{(i)} \equiv \epsilon _{0} \chi ^{(i)}E^{i}\) only makes sense if subsequent terms become smaller i.e. \(P^{(i)}>P^{(i+1)}\). Field intensities for which this expansion is broken are exceedingly high. For instance, an estimation of the susceptibility of a hydrogen atom leads to a second-order susceptibility \(\chi ^{(2)} \approx 1.94 \times 10^{-12}\) mV\(^{-1}\) and a third-order susceptibility \(\chi ^{(3)} \approx 3.78 \times 10^{-24}\) m\(^2\)V\(^{-2}\) [51]. A critical electric field intensity is then:
leading to a critical intensity \(I_{\textrm{crit}}\) estimation of the order:
a rather large value. It is therefore generally safe to assume the expansion is meaningful. If the electric field is now a vector field \({\textbf{E}}= (E_{x}, E_{y}, E_{z})\), the susceptibility is much more complicated. Each expansion of it, \(\chi ^{(i+1)}\), becomes a rank-\((i+1)\) tensor. Anisotropic media need to be necessarily treated in this fashion.
The \(j^{\textrm{th}}\) component of the polarisation is now expressed as [65]:
This formula assumes an instantaneous response: that the polarisation at a time t only depends on the susceptibility at that instant. In reality, the response depends on past times \(t'< t\) too, leading to a more general form for the polarisation:
where \(\varvec{\tau }\) denotes a vector \(\varvec{\tau } = (\tau _{1},\tau _{2},\tau _{3},\ldots )\), with its differential being \(d \varvec{\tau } = {\text {d}} \tau _{1} {\text {d}} \tau _{2} {\text {d}} \tau _{3}\ldots \).
In this fashion, the linear and nonlinear contributions can be retrieved easily. In particular, the first-order susceptibility tensor \(\chi ^{(1)}\) is a matrix that describes the linear part of the polarisation. If only the linear contribution is considered, Eq. (55) allows a simple decomposition to be made:
If Eq. (56) is Fourier-transformed, i.e. by obtaining the frequency-dependent polarisation and electric field:
one can see that a non-instantaneous response leads to a frequency-dependent susceptibility \(\chi ^{(1)}(\omega )\), a phenomenon that leads to a particular dispersion profile of the medium. It can be simply obtained by the Convolution Theorem:
This equation defines the linear response of the system to the electric field. Interestingly, the first nonlinearity in most materials is found when considering the third-order term in the expansion i.e. the second-harmonic susceptibility contribution is null.
The condition for this phenomenon to occur is related to the centrosymmetry of the material: whether the lattice has the property for which the mapping \({\textbf{r}}\mapsto -{\textbf{r}}\) preserves its structure. To appreciate the role of centrosymmetry in second-order susceptibility, one must simply consider a simple homogeneous instantaneously-polarised medium [51]. Then, from Eq. (51), its corresponding second-order contribution to the polarisation is simply:
It can now be seen that if \(E \mapsto -E\), then \(P^{(2)} \mapsto P^{(2)}\). However, if the system is centrosymmetric, \(P^{(2)}\) must also change sign when the electric field does. This leads to the conclusion that \(P^{(2)}\) must vanish. Since both \(\epsilon _{0}\) and E(t) do not vanish, it follows that \(\chi ^{(2)}\) does i.e. \(\chi ^{(2)} = 0\).
This conclusion has deep consequences. For graphene, in particular, this means that \(\epsilon _{{\textbf{k}}}=-\epsilon _{-{\textbf{k}}}\), since graphene is a centrosymmetric material and, therefore, doesn’t exhibit any second order nonlinearity, i.e., \(\chi ^{(2)}_\textrm{graphene}=0\). A more detailed discussion, involving crystal symmetry and group theory, on the reason and justification of this for materials with the same symmetry class of graphene can be found in the book by Lax [52].
4.2.2 Minimal substitution
To couple light to electrons in a crystal structure, an accurate scheme to introduce the light contributions into the Schrödinger equation, the equation which models the dynamics of the carriers, must be found. Simple gauge arguments suffice and lead to the establishment of two additional fields: the electromagnetic vector potential \({\textbf{A}}\) and the electromagnetic (scalar) potential U. These arguments are briefly presented in this Section, but further details on them can be found in any standard textbook on electrodynamics, such as the excellent book by Jackson [53] or Stratton [54]. Semiclassically, the interaction of radiation with matter may be appropriately obtaining by applying the minimal substitution—a change of the electronic momentum through the vector electromagnetic potential as given by:
where \(q = -e\) is the electron charge. The relevance of these fields can be understood by symmetry considerations: a free electron in the lattice is described by the time-dependent Schrödinger equation:
where \(V({\textbf{r}})\) is the lattice potential introduced in Eq. (2). If a physically irrelevant phase \(\chi ({\textbf{r}},t)\) is applied to one of its solutions in the form of the local gauge transformation \(\Psi ({\textbf{r}},t) \mapsto \Psi ({\textbf{r}},t) e^{i \chi ({\textbf{r}},t)}\), the Schrödinger equation must be changed to:
To comply with the invariance of the probability density \(|\Psi ({\textbf{r}},t)|^{2}\). In this fashion, the equation was made gauge-invariant under such gauge transformation. Consequently, the potentials must transform as:
meaning both potentials are gauge-dependent and not physical. The physical electromagnetic fields can be unambiguously defined via:
with the identification to the momentum operator \({\textbf{p}}\equiv - i \hbar \nabla \) was used, the minimally-coupled Hamiltonian takes the form:
The electromagnetic four-potential \(a^{\mu } \equiv (U, {\textbf{A}})\), where \({\textbf{A}}\) denotes the three Cartesian components of the electromagnetic vector potential \({\textbf{A}}\), is not uniquely defined given the constraints of Eq. (63). A useful complete gauge choice, and one that will be extensively used in all theory and simulations developed in this work, is known as the radiation gauge, achieved by the requirements that \(\varvec{\nabla }\cdot {\textbf{A}}=0\). The scalar electromagnetic potential can be set to \(U({\textbf{r}},t)=0\). In this way, \({\textbf{E}}({\textbf{r}},t)\) is related to \({\textbf{A}}({\textbf{r}},t)\) simply as:
4.2.3 Dipole approximation
Another assumption that simplifies subsequent calculations is given by the dipole approximation. The details of this approximation can be found in the book by Jackson [53], or in more advanced textbooks, like the book on quantum optics by Loudon [55] or Cohen-Tannoudji [56]. The electric field \({\textbf{E}}({\textbf{r}},t)\) associated with light, under some circumstances, may be assumed to be a function of time only. This results in no spatial dependence when considering the effects of light on the dynamics of an electron. The optical fields (both applied and induced) are supposed to have characteristic wavelengths much larger than the next-neighbour separation and the atom diameter. For instance, the applied electric field \({\textbf{E}}({\textbf{r}},t)\), here taken in the form of a continuous wave, remains uniform throughout the whole carbon atom since, for an atom sitting at \({\textbf{r}}=\mathbf {r_{0}}\):
where the approximation \({\textbf{k}}\cdot {\textbf{r}}\ll 1\) was explicitly used. The same reasoning can be applied to the electromagnetic vector potential \({\textbf{A}}({\textbf{r}},t)\).
4.2.4 Slowly varying envelope approximation
In general, and in the context of pulsed excitations, \({\textbf{E}}({\textbf{r}},t)\) is a fast-oscillating wave over many optical cycles, bounded by an envelope \({\mathcal {E}}({\textbf{r}},t)\). This field configuration does not admit, in general, analytical solutions to dynamical equations which depend on it. Therefore, it becomes impractical—if not impossible—to retrieve \({\textbf{E}}\) from its primitive, \({\textbf{A}}\), as Eq. (66) suggests.
To find a method to relate \({\textbf{E}}({\textbf{r}},t)\) to \({\textbf{A}}({\textbf{r}},t)\), the Slowly Varying Envelope Approximation (SVEA) allows a huge deal of complexity to be removed from many models, while keeping the same physical information of the pulse. This of course is contingent on excitation conditions.
Generally, an electric field \({\textbf{E}}({\textbf{r}},t)\), of optical frequency \(\omega _{0}\) may be decomposed through its envelope \({\mathcal {E}}({\textbf{r}},t)\):
and likewise for \({\textbf{A}}({\textbf{r}},t)\) with envelope \({\mathcal {A}}({\textbf{r}},t)\):
Inserting Eqs. 68 and 69 into Eq. 66 yields
which leads to the following relation between the field envelopes (Fig. 3):
The Slowly Varying Envelope Approximation may now be used: one may assume that the temporal rate of change of the envelope is negligible, i.e. \(\left| \partial _{t} {\mathcal {A}} \right| \ll \omega _{0}\left| {\mathcal {A}} \right| \). Then:
4.2.5 Optical absorption
As the field penetrates the medium, the intensity of its corresponding electric field will decay. This decay can be associated with the sample’s absorption. To quantify this process, the refractive index \(n(\omega )\) is defined as:
where the dielectric function \(\varepsilon (\omega )\) quantifies the electric permittivity of the material when excited at a frequency \(\omega \). At this point, the reader should be warned, that assigning a refractive index to a 2D material in not formally correct, as by nature, the refractive index is a concept associate to the bulk of a material, and not its surface. Nevertheless, we can imagine associating, by analogy, a refractive index to graphene, so that we can continue using standard optical techniques to describe its reflection, transmission, and absorption properties. This is possible, for example, by depositing a single layer of graphene onto a substrate and then calculate the effective refractive index of the graphene+substrate compound with the so-called transfer matrix method, described in the book by Born and Wolf [57]. For the case of two-dimensional materials without a substrate, the background contributions to these two quantities will not be considered. If they were, they would lead to a renormalisation of the field speed and the dielectric function [61]. In this case, however, the concept of refractive index should be taken more as an analogy, than a real physical concept, that allows one to use the standard techniques of optics to evaluate the linear light–matter interaction at the macroscopic level, using standard optics tools.
Also notice that in general, both the permittivity \(\epsilon (\omega )\) and the susceptibility \(\chi ^{(1)}(\omega )\) are tensorial quantities (to be precise, they are both rank 2 tensors). However, in this work we deliberately use scalar quantities, corresponding to optically isotropic graphene, to keep the description simple and focus on the physical meaning, rather than on the general formalism. The interested reader can find more information on both the nature of the refractive index and the tensorial nature of permittivity and susceptibility of materials in any standard book of nonlinear optics, such as that of Boyd [51] or Shen [58].
As the pulse propagates throughout the sample, the field wavevector, which is not to be confused with the electronic wavevector \({\textbf{k}}\), will satisfy a dispersion relation, determined by the medium’s frequent-dependent properties:
The field will have its intensity decreased as it penetrates the material. If this decay is exponential, then:
where the refractive index has been split in its real and imaginary parts \(n(\omega ) \equiv n'(\omega ) + i n''(\omega )\). The damping is consequently related to the imaginary part of the refractive index.
Assuming the wave only propagates in the direction perpendicular to the plane occupied by the sample, its intensity may be computed as the average of the Poynting vector \({\textbf{S}}({\textbf{r}},t)\):
and therefore proportional to \(|{\textbf{E}}|^2\). The auxiliary magnetic field \({\textbf{H}}\) is simply proportional to the magnetic field density \({\textbf{B}}\) since no magnetisation is present. If the time-dependent term is averaged, the spatial dependence on the intensity may be written as \(I(z) = I_{0}e^{-\alpha (\omega ) z}\) given that:
In this way, and attending to the definition in Eq. (73) and Taylor-expanding it up to first-order, the absorption coefficient \(\alpha (\omega )\) is:
where the susceptibility was also written as \(\chi ^{(1)}(\omega ) \equiv \chi ^{(1)'}(\omega ) + i \chi ^{(1)''}(\omega )\). This result will be used for Eq. (157), where the explicit evaluation of the linear susceptibility leads to the prediction of the law of universal absorption of graphene.
4.3 Optical response
With all these ingredients presented, the light–matter coupling can be included in the Hamiltonian describing massless Dirac fermions. To do this, the minimal substitution that was given in Eq. (60) is applied to the Hamiltonian of Eq. (34):
naturally yielding the explicit interaction term \(H_{\textrm{int}}\). In SVEA conditions, Eq. 72 allows the interaction operator to be expressed in terms of the electric field envelope:
which, if compared to the standard electric dipole moment operator \(\varvec{\mu }\), satisfying \(H_{\textrm{int}}(t) = -{\varvec{\mu }} \cdot {\varvec{E}}(t)\), allows one to find the following representation of the electric dipole operator for massless Dirac fermions:
4.3.1 Electric dipole moment
With a representation of the interaction, the associated electric dipole moment, the observable of this operator, is simply its expectation value. Conveniently, the calculation of expectations of a position-independent operator \(\hat{{\mathcal {Q}}}\) is easily achieved due to the orthogonality of the plane waves associated with different \({|{\lambda {\textbf{k}}}\rangle }\) states, since (Fig. 4):
where the following identity for the p-dimensional Dirac \(\delta \) function was used:
the expectation value of Eq. (82) vanishes for \({\textbf{k}}' \ne {\textbf{k}}\), implying that only transitions where the initial and final states have the same momentum are allowed (vertical transitions i.e. \({\textbf{k}}= {\textbf{k}}'\):
Furthermore, two kinds of transitions at \({\textbf{k}}\) can be differentiated: interband transitions, satisfying \(\lambda ' = -\lambda \) and intraband transitions, satisfying \(\lambda ' = \lambda \). The matrix elements of the dipole moment operator \(\hat{\varvec{\mu }}\) for a Cartesian component j are thus simply:
with the knowledge of the SVEA representation of Eq. (81), the contribution to both in-plane coordinates x, y can be obtained.
For instance, the x component satisfies:
Similarly, the y component has:
This quantity has dimensions  as expected since classically, one has \(\varvec{\mu }= - e \cdot {\textbf{r}}\).
as expected since classically, one has \(\varvec{\mu }= - e \cdot {\textbf{r}}\).
How to interpret the effects of the interaction Hamiltonian on the eigenstates? In the picture that has been developed so far, electronic excitations can be collected according to their energy, giving rise to bands. In suitable resonant conditions, photon absorption leads to a change of the charge distribution throughout the sample, conceptualised as the creation of a polarisation field. To quantify this change at a fundamental level, the mechanism of photon absorption can be thought of as the creation of a dipole between the newly-promoted valence electron to the conduction band and the vacant state in the valence band, since they carry opposite charges. This dipole thus create an attractive Coulomb interaction. In the quasiparticle picture, a photon of energy \(\hbar \omega _{0}\) may, given a vertical energy separation between a valence and conduction bands \(\Delta \epsilon < \hbar \omega _{0}\) induce an electronic excitation of that electron. This process is thus equivalent to the creation of a hole in the valence band and an electron in the conduction band.
Given the gapless nature of the spectrum, a spectrally-distributed pulse will have a frequency component resonant with some two-level system of a fixed momentum \({\textbf{k}}\). In this setting, graphene is idealised as an infinite, non-interacting two-level system. This is a central concept throughout this work and will be dealt with in more detail in Sect. 5.2.
4.3.2 Fine structure constant \(\alpha _{\textrm{G}}\)
Without the machinery of linear optics which was just introduced, the law of universal absorption can be obtained using Fermi’s golden rule. If the light–matter interaction described by the dipole-field term in the Hamiltonian of Eq. 34 is treated as perturbation, Fermi’s golden rule may be used to estimate the transition rate of valence to conduction electronic eigenstates.
The application of this approach is well justified as all calculations have been performed in the low field limit
The transition rate from \({|{-\lambda , {\textbf{k}}}\rangle }\) to \({|{\lambda , \mathbf {k'}}\rangle }\) is:
Here, \(g(\epsilon _{{\textbf{k}}'})\) is the density of states at the energy of the final state \({|{\lambda , {\textbf{k}}'}\rangle }\). The optical dipole matrix M for vertical transitions in \({\textbf{k}}\) is diagonal. Using the symmetry of the treatment in either the x or y components, one may, without loss of generality, consider \(\mu _{x, {\textbf{k}}}\), given in Eq. (86). Again, considering the interband transitions \(\lambda ' = -\lambda \) and \(\mathbf {k'}={\textbf{k}}\), M reads:
This quantity is now angle-averaged i.e. \({\langle {f(\phi )}\rangle } \equiv 1/(2 \pi )\int _{0}^{2 \pi }f(\phi ) {\text {d}} \phi \):
In perfect resonance, at a transition energy \(\epsilon _{0}\) exactly equal to the difference energy between the initial and final states of \(\delta \epsilon _{{\textbf{k}}}= 2 \epsilon _{{\textbf{k}}}\), one has \(\epsilon _{0}= \epsilon _{{\textbf{k}}}/2\) and the density of final states is therefore:
At this energy, the transition probability, the transition happens at \({\textbf{k}}={\textbf{k}}_{0}\) (the wavevector of the external electromagnetic wave), \(T_{\omega _{0}}\) takes the form:
Therefore, the power of the absorbed radiation is \(P_{\textrm{ABS}}= T_{\omega _{0}}\epsilon _{0}= T_{\omega _{0}} \hbar \omega _{0}\), whereas the total power input by the radiation field is \(P_{\textrm{IN}}= \frac{c}{4 \pi }|{\mathscr {E}}|^2\). The optical absorption \(\alpha (\omega _{0})\) is given by their ratio:
where \(\alpha _{\textrm{QED}}\) is the fine-structure constant from Quantum Electrodynamics (QED). Measurements of the universal absorption have been reported in Fig. 1 of [66]. Two features are prominent: (i) the decrease in the light transmittance is \(\pi \alpha \approx 2.3 \%\) and (ii) this value is a constant for all wavelengths. This result explains why graphene, unlike its related allotrope graphite, is optically transparent. The inset on the right shows how the number of graphene layers impacts the absorbance. Naturally, by around five layers the overall absorption is far greater and, for such a reduced number of layers, this decrease occurs in units of the monolayer absorbance \(\alpha _\textrm{G}\).
This constant also leads to other fundamental considerations regarding the nature of quantum field theories applied to graphene. This discussion will be made in Sect. 5.6.1. In Sect. 5.11, this same result will be obtained via a rather different method, wherein the Semiconductor Bloch Equations will provide a numerical validation of this result.
4.3.3 A qualitative comparison to semiconductors
The dipole moment calculated in the last section is vastly different to what is normally expected of semiconductors. It is therefore instructive to see the qualitative difference between their optical transitions. For the case of a simple free-electron in a semiconductor the optical dipole matrix element changes depend on the modulus of \({\textbf{k}}\). For a quadratic dispersion, with bands separated by \(\Delta \) at \({\textbf{k}}= 0\), it can be written as a Lorentzian curve [60]:
where \(m_{e}\) and \(m_{h}\) correspond respectively to the electron and hole masses of each band. Unlike the electrons in graphene, the electron and hole states in a semiconductor have a non-zero effective mass, determined by the curvature of their dispersion branch:
For graphene, the dipole moment can be seen to be inversely proportional to the optical frequency and hence the electron–hole separation \(r = \mu /e\), for a fixed \({\textbf{k}}\). Importantly, this quantity is not-well defined for \({\textbf{k}}= 0\), i.e. at the Dirac points. In fact, the terms \(\cos \phi _{{\textbf{k}}} = k_{x}/|{\textbf{k}}|\) and \(\sin \phi _{{\textbf{k}}} = k_{y}/|{\textbf{k}}|\) defining the eigenstates in Eq. (86)–(87), are undefined at \({\textbf{k}}=0\). This is easily understandable since the two-level system becomes degenerate there, given the band-touching. Charge separation may be inferred from measurements of the dipole moment. For instance, for a pulse of frequency \(\omega _{0} = 484\) THz (visible, red radiation), the optical dipole moment is determined to be \(|\mu | \approx 6.88 \times 10^{-8}\) e cm, corresponding to a separation of \(r = 6.88\) Å= 2.88a.
5 The semiconductor Bloch equations
5.1 Overview
The previous section was mainly concerned with the electronic properties of a general condensed matter system, in the presence of of an underlying lattice configuration. Subsequently, the two bands of the \(\pi \) electrons in graphene predicted in tight-binding conditions were obtained in Sect. 2.2. These lead to two valleys, located at two special points termed Dirac points, where the dispersion is linearly proportional to the crystal momentum.
Having exposed the treatment underlying electrons in a lattice and a classical electromagnetic field, this section focuses on how to couple both elements. This task will be implemented using the framework of a two-level system, a ubiquitous concept permeating many areas of Physics. In particular, this section is devoted to one such implementation, which became known as the Semiconductor Bloch Equations (SBEs).
The modus operandi behind the SBEs stems from well-established equations, known as the Optical Bloch Equations (OBEs) or sometimes the Maxwell–Bloch Equations which describe the dynamics of a single two-level system when coupled to light, in particularly useful conditions. The first realisations of such systems came from Atomic Physics, where energy levels in particular atomic systems can be manipulated to achieve population inversion, leading to the first successful physical realisation of the laser [67].
The notion that a many-body quantum system like a semiconductor, encoding numerous complex scattering and responses when excited with light, may be described with two-level systems is perhaps unanticipated. It turns out that the versatility of a two-level treatment is excellently suited to treat light–matter interactions in many condensed matter systems. The SBEs offer a striking and revolutionary application of these principles in the realms of condensed matter physics.
Research within this formalism has been intensively applied to semiconductors [60, 69,70,71] and it has been extremely successful in explaining many phenomena such as dipole-dipole effects in dense media [72, 73], Rabi oscillations [74, 75] and optical bistability [76], self-induced transparency [50] and even single-mode inhomogenously broadened lasers [77]. The effect of ultrashort pulses on dense semiconducting media was studied not long after the SBEs were formulated [76]. The scope of the SBEs can be expanded to allow various incoherent and scattering contributions in the carrier dynamics to be considered [78].
Theoretical approaches to model the nonlinear dynamics of graphene typically rely on the Boltzmann transport equation, accounting only for intraband electron dynamics [33]. As a zero-gap semiconductor, the SBEs have been applied to graphene [79] by adapting the conical dispersion to the usual dispersion of a semiconductor in order to account for the interband dynamics only.
Not surprisingly, the main goal of this section is thus to present results concerning the application of the SBEs to monolayer graphene. To achieve that, the OBEs shall be derived and discussed as a means of introducing the necessary jargon and concepts to obtain the SBEs, whose predictions are analysed in Sect. 5.10. The main success of the SBEs lies on the linear optical regime, wherein many well-established results in the literature may be retrieved, providing a validation of these models to model light–matter interactions accurately in such regime. In particular, the direct proportionality between the absorption and the fine structure constant in graphene, discussed in Sect. 4.3.2, may be retrieved. Conveniently, this regime also allows for analytical solutions of the SBEs to be obtained in special probing conditions, which are derived in Sect. 5.7.
5.2 The theory of two-level systems
The building blocks of any of the models that will be presented throughout this Review are what physicists like to term ’two-level systems’. Many realisations of this concept may be obtained in various branches of both Physics and Mathematics, varying from qbits, extensively exploited for Quantum Computing and Information, both theoretically [80] and experimentally [81], to the dynamics of a spin-1/2 particle interacting with a time-dependent magnetic field, for instance by Rabi as early as 1937 [82]. In the realm of Condensed Matter Physics, a myriad of systems display features that can be understood in such a framework. An excellent starting point for studying the physics of two level systems is the excellent book by Allen and Eberly [67]. For the more quantum-information-oriented reader, good introductions to two-level systems can be found in the books by Gruska [80] and Nielsen and Chuang [68].
It is surprising how many physical systems can be adequately described by two-level systems, given how simple it can be understood mathematically. A two-level system refers to a quantum system whose features can be fully captured by a superposition of two independent states, here denoted by the lower ket \({|{1}\rangle }\) and upper ket \({|{2}\rangle }\). The representation in which states from the underlying two-dimensional Hilbert space are presented is irrelevant at this level. For most applications to quantum systems, one would choose the space representation \({|{\psi _{\mu }({\textbf{r}})}\rangle } \equiv {\langle {{\textbf{r}}|i}\rangle }\), with \(i = 1,2\).
In this framework, the system dynamics can always be described, in this basis, with the aid of a ket-state \({|{\psi (t)}\rangle }\)
i.e., a linear combination of two states, described by a column vector, determined by suitable coefficients \(c_{i}(t)\). The element \(|c_{i}(t)|^{2}\) will evidently return the probability per unit time of observing the system in the state \({|{i}\rangle }\). The basis is now assumed to be comprised of the eigenstates of the Hamiltonian of the system, \({\mathcal {H}}_{0}\), with energies as given by \({\mathcal {H}}_{0}{|{i}\rangle } = \epsilon _{i} {|{i}\rangle }\). The general state of Eq. (96) must therefore solve the Time-Dependent Schrödinger Equation:
whose solution is straightforwardly given by:
where \(\psi _{i}({\textbf{r}})\) are eigenstates of \({\mathcal {H}}_{0}\) and \(c_{i}\) the weight of such eigenstates in the linear superposition.
An important consequence of the existence of such a basis is that an Hermitian \({\hat{Q}}\) operator acting on the state space may always be written in the form:
provided \(\alpha , \beta , \gamma \ \text {and} \ \theta \in {\mathbb {R}}\). Clearly, \({\hat{Q}} = {\hat{Q}}^{\dagger }\). Such operators are obviously of importance since their eigenvalues are real. To obtain a matrix representation of such operator in this particular basis, one may exploit the fact that there must be \(2 \times 2\) linearly independent operators, the projectors, acting on the ket-space and defined as the outer product \({|{i}\rangle } {\langle {j}|}\), \((i,j=1,2)\), with the aid of the completeness relation \(\sum _{i} {|{i}\rangle } {\langle {i}|} = {\mathbb {I}}\), \({\mathbb {I}}\) being the identity operator.
The Hamiltonian \({\mathcal {H}}_{0}\) is thus easily found to be:
The system thus far does not seem very interesting: each state of Eq. (98) will oscillate sinusoidally at its particular frequency \(\omega _{i} = \epsilon _{i}/\hbar \). The Hamiltonian \({\mathcal {H}}_{0}\) is interpreted as being determined and known—after all this is why one may assume that the energies of such states are known. What if the two-level system is now coupled to a perturbation that modifies such energies and perhaps even the basis? In that instance, the dynamics could in principle become exceedingly complex, in turn leading to a much more challenging task of computing the time evolution of the coefficients \(c_{i}(t)\).
A feasible way to incorporate interactions with the two-level system is to write the Hamiltonian of the system as a sum of a Hamiltonian known for a particular regime and a perturbation part as \({\mathcal {H}} = {\mathcal {H}}_{0} + {\mathcal {H}}_{\textrm{I}}\). The expected value of such a perturbation is then:
This interaction will be assumed to only induce a perturbation between the two states, meaning that \(\langle i|{\mathcal {H}}_{\textrm{I}}|i\rangle = 0\). This assumption is generally warranted, as will be seen in Sect. 5.4, when the interaction Hamiltonian will be explicitly given. In the same fashion, the matrix form of such a general interaction Hamiltonian may be obtained as:
Naturally, since \({\mathcal {H}}_{\textrm{I}}\) must be hermitian, one has \(\epsilon ^{\textrm{I}}_{12}= {\epsilon ^{\textrm{I}}_{21}}^{*}\) and a polar representation \(\epsilon ^{\textrm{I}}_{ij} \equiv |\epsilon ^\textrm{I}_{ij}|e^{i \phi }\) is possible, leading to a full Hamiltonian in the general form of Eq. (99):
This step is exactly what allows light–matter interactions to be obtained between an external optical field and the two-level system. The two-level system is a mathematical realisation of matter, as was developed in Sect. 2.2, whereas the interaction Hamiltonian allows an external parameter to drive its dynamics. An appropriate form of \({\mathcal {H}}_{\textrm{I}}\) is of course necessary to ultimately solve the Schrödinger equation encompassing the full dynamics and that is achieved in the next section.
5.3 The optical Bloch equations
A first step to solve the dynamics of the full Hamiltonian is now given, following the explanations provided in the book on quantum optics by Scully [59]. Another excellent reference for optical Bloch equations is represented by the book by Koch on semiconductor physics [60]. If the field is assumed constant in space and only varies in time, the interaction between the atom and the field is classically written as a dipole-like interaction:
where both vectors are given in their Cartesian coordinates. For the sake of simplicity, the field is now assumed to be linearly polarised in the \({\hat{x}}\) direction. In this dipole-type interaction, diagonal entries in the interaction Hamiltonian would imply a permanent dipole moment and so for this treatment one shall assume that these vanish.
From Eq. (101), it can thus be seen that the system will have zero dipole moment if the product \(c_{1}c_{2}^{*}(t) \ne 0\) i.e. whenever the atom is in a superposition of both states. In accordance with the expansion in the equation, the interaction Hamiltonian elements may be split as \(\epsilon ^{\textrm{I}}_{ij} = - E(t) \mu _{ij}\), where \(\mu _{ij} = e {\langle {i|{\hat{x}}|j}\rangle }\).
Finally, the Hamiltonian matrix of Eq. (103) is applied to the general state of Eq. (96) using the TDSE (Eq. (97)). At this stage, and for simplicity purposes, the electric field is taken to be a monochromatic plane wave of frequency \(\omega _{0}\), of the form \(E(t) = {\mathscr {E}} \cos (\omega _{0}t)\), where \({\mathscr {E}}\) is its amplitude. Splitting the magnitude and phase of the dipole moment \(\mu _{12}= |\mu _{12}|e^{i \phi }\), the following system of differential equations is obtained:
The parameter \(\Omega _{\textrm{R}} = |\mu _{12}| {\mathscr {E}}/\hbar \) is the Rabi frequency and describes the driving frequency at which the populations will oscillate when coupled to the field.
However neatly expressed, this set of differential equations is in general not possible to be solved analytically given the fast oscillation of the coefficients. One reasonable way out is to express the coefficients \(c_{i}\) in terms of their slowly-varying amplitudes \({\tilde{c}}_{i} = c_{i}e^{i \omega _{i}t}\). If the transition frequency is denoted by \(\Delta \omega \equiv \omega _{2}-\omega _{1}\), the equations become:
The Rotating Wave Approximation (RWA) is now applied, by only keeping the coherent terms i.e. terms close to resonance. Terms proportional to \(\exp \left( \pm i (\Delta \omega + \omega _{0} \right) )\) are therefore ignored. This is in general a good assumption for many systems. However, as will be seen in the next section, these terms are important in dealing with ultrashort pulses, where the notion of a slow-varying oscillation is often ill-defined, if the frequency of the pulse is comparable with the inverse pulse duration.
Solving this set of equations leads to the Optical Bloch Equations (also known as the Maxwell–Bloch Equations). These were derived as far as 1965 [83] and provide a way to describe the dynamics of a single two-level system when coupled with a classical electromagnetic field of a single frequency mode:
The coefficients \(a_{1/2}\) and \(b_{1/2}\) are determined by the system’s initial conditions and provide no insight into the physics. What is remarkable is that the two-level system is described by two characteristic frequencies, namely the detuning frequency \(\Delta = \Delta \omega - \omega _{0}\) and the generalised Rabi frequency \(\Omega = \sqrt{\Omega _{\textrm{R}} + \Delta ^2}\).
A sensible boundary condition is given as \(c_{2}(0) = 0\) and \(c_{1}(0) = 1\), meaning that the two-level system is initially in the ground state. It is customary to introduce more physically relevant dynamical variables than the coefficients themselves. Equation (102) already hinted at a definition: the polarisation \(p(t) = {\tilde{c}}^{*}_{1} {\tilde{c}}_{2} \mu _{12} + {\tilde{c}}_{1} {\tilde{c}}_{2}^{*} \mu ^{*}_{12} \) and takes the form:
The inversion of a two-level system is defined as the difference of the occupation probabilities and may be expressed as:
Interestingly, the polarisation oscillates with the same frequency as the field. As for the inversion, different detunings yield different Rabi cycles, reflecting different oscillations profiles between the ground and excited states. For a vanishing detuning, the system is said to be on resonance and the inversion is total—\(w(t) = \cos (\Omega _{\textrm{R}}t)\), meaning that the populations will shift sinusoidally between the lower and upper states. For extremely detuned systems, the interaction is minimal and the inversion does not change much from its initial conditions, leading to an inversion \(w(t) \approx -1\).
5.4 Derivation
To understand the philosophy of the SBEs, their derivation is now shown, following the outline presented in [60]. The main elements in it are conceptually very close to what was presented in the previous section. The notation will nonetheless be more suited for a condensed matter system. In particular, the variables needed to describe the system’s evolution will be chosen to be physically more transparent. Despite such similarities, the density matrix of the two-level system will be used instead. The convenience of it relies on the fact that at no point of the derivation neither the knowledge of the eigenstates nor the Time-Dependent Schrödinger equation are needed.
Electronic transitions in semiconductors are adequately understood with the aid of the electronic bands that originate as an aggregate of reactive orbitals. Since the bands are functions of the crystal momentum, it is convenient to take the two levels as the eigenstates of the free Hamiltonian for fixed momentum \({\textbf{k}}\)—here denoted by \({|{v, {\textbf{k}}}\rangle }\) and \({|{c, {\textbf{k}}}\rangle }\). The energy of each state \({|{c/v, {\textbf{k}}}\rangle }\) will be denoted as \(\epsilon _{c/v, {\textbf{k}}}\). The wavefunction in direct space of such states can be simply obtained by taking the scalar product \(\psi _{{\textbf{k}}}({\textbf{r}}) = {\langle {{\textbf{r}}| \lambda , {\textbf{k}}}\rangle }\).
As usual, the two-level system may be generally represented as:
It is natural to associate the coefficients \(\eta _{v}\) and \(\eta _{c}\) to the valence and conduction bands, respectively, given the considerations that led to Eq. (96). The density matrix of the two-level system is simply given by the general definition:
Similarly to the OBEs, new dynamical variables were chosen. In this new picture, the excitation is a combination of valence and conduction states, situated in their respective branches of the dispersion. Subsequently, the occupation number for each band is simply the square \(n_{c/v,{\textbf{k}}} \equiv \eta ^{2}_{c/v,{\textbf{k}}}\), naturally a real quantity. The system is conservative, as seen by the normalisation of the density matrix—\(\text {Tr}(\rho _{{\textbf{k}}}) = 1\):
which in turn implies quasiparticle number conservation and rendering the electron and hole occupations dependent.
The microscopic polarisation was introduced as the product in the off-diagonal entries and is a measure of the mixing of two states in the basis: only when the excitation is in a combination of valence and conduction states will the product \(\eta _{v, {\textbf{k}}} \eta ^{*}_{c, {\textbf{k}}}\) be nonzero.
Employing the dipole approximation, the coupling to light is introduced as usual, leading to purely off-diagonal electric dipole momentum operator, as shown in Eq. (102):
where the dot product is performed over the Cartesian components of the field and the dipole moment. The full Hamiltonian of the two-level system at wavevector \({\textbf{k}}\) under consideration is then:
Given the properties of the density matrix, it follows that for a general operator \({\hat{Q}}\), its expectation value may be calculated as \({\langle {{\hat{Q}}}\rangle } = \text {Tr} \left( \rho _{{\textbf{k}}} {\hat{Q}} \right) \). This fact allows the energy of the Hamiltonian of Eq. (114) to be calculated as:
With all necessary elements in place, the evolution of this mixed state, is determined by the Liouville-von Neumann Equation:
The last term was added to account for decoherence mechanisms, naturally present in any open system. There are many ways to achieve such a term that preserves the properties of the density matrix, the most notable being given by the Lindblad master equation [84]. Alternatively, phenomenological decay rates \(\gamma _{1}\) and \(\gamma _{2}\), respectively for the inversion and microscopic polarisation and whose physical relevance will be examined in Sect. 5.6.2, may adequately be added, given that incoherent effects are not central in this work.
In this way, the free-carrier Semiconductor Bloch equations are obtained:
Here, the detuning is different for each state i.e. \(\omega _{{\textbf{k}}} = (\epsilon _{c, {\textbf{k}}} - \epsilon _{v, {\textbf{k}}}) / \hbar \) and therefore dependent on the shape of the dispersion. \(w_{{\textbf{k}}}^{0}\) is the equilibrium value of the populations for each momentum and a broader discussion of it may be found in Sect. 5.6.2 whereas \(\mu _{{\textbf{k}}}\) is the interband dipole moment matrix element that was introduced in Sect. 4.3.1.
In the absence of dephasing i.e. for \(\gamma _{1} = \gamma _{2} = 0\), the conservation of probability, given by the normalisation of Eq. (112) is re-expressed in the new dynamical variables as:
As performed previously, these equations can be adapted to model the slowly-varying part of the oscillations. In this case, the microscopic polarisation is split as \(p_{{\textbf{k}}} = q_{{\textbf{k}}}e^{- i \omega _{0}t}\) and, using the decomposition of Eq. (68) for a space-independent electric field E(t), the SVEA-approximated becomes:
The polarisation oscillates now with the detuning \(\delta _{{\textbf{k}}} \equiv \omega _{{\textbf{k}}} - \omega _{0}\). Importantly, only terms oscillating with \(e^{-i \omega _{0}t}\) were kept. It will be seen in the next section that this assumption is equivalent to applying the Rotating Wave Approximation.
5.5 Macroscopic polarisation
Following the discussion in Sect. 4.2, the polarisation of the medium, through its susceptibility, which acts as a response to the interaction with an electromagnetic field, encompasses a breadth of information about the light–matter interactions present.
The SBEs allow for the identification between the microscopic dynamics of the two-level systems to the polarisation described by Eq. (55) to be obtained.
To obtain the time dynamics of the polarisation, the carrier-field contribution \(\hat{{\mathcal {H}}}_{F-C}\) from the Hamiltonian in Eq. (34) allows for a sensible definition of it, namely from the condition:
where the volume of the sample \(V = Ad\) is comprised of its area and the atomic thickness \(d \approx 0.33\) nm and \(\epsilon _{0}\) the electric permittivity of free space. The polarisation operator is thus:
with the aid of the density matrix of Eq. (111), its expectation value, describing the time dynamics of the polarisation is:
Furthermore, since the polarisation is real-valued, and all dipole moments rotate with the frequency of the incident field, the following decomposition is possible:
Equating (124) to (123) and again decomposing the microscopic polarisation via \(p_{{\textbf{k}}} = q_{{\textbf{k}}}e^{- i \omega _{0}t}\), give:
The polarisation can thus be obtained by adequately calculating the \({\textbf{k}}\)-dependent polarisation, weighting it by the dipole moment and average this quantity over momentum space:
This scheme is rather useful. If the SBEs can be numerically retrieved, it is, in principle, possible to produce the macroscopic polarisation of the sample due to the optical excitation. This is exactly what shall be done in the Sect. 5.10.
5.6 Additional effects and mechanisms
5.6.1 Coulomb interactions
A major question not discussed up to this stage concerns the addition of Coulomb interactions. After all, electron–electron interactions are the fundamental mechanism driving an overwhelming number of phenomena in compounds and structures. To introduce such effects, and in view of what has been developed so far, two-level systems at different momenta must be able to exchange energy.
Rather surprisingly, their effect can be beautifully understood in terms of the picture so far developed. Equations(117)–(118) are coupled in two variables at the same \({\textbf{k}}\). Once a Coulomb potential is introduced in the dynamics of the carriers, the corresponding optical variables depend on any other across momentum space, meaning all two-level systems are now coupled.
The effective consequence is that the two-level systems suffer a renormalisation of all the parameters so far discussed. To see this, a second quantisation of the Hamiltonian is more suitable. The interested reader can find an extensive discussion on the renormalisation of Coulomb interactions in semiconductors in the book by Koch [60]. In the remaining of this Section, we are going to sketch out this procedure, using the language of second quantisation, i.e., using fermionic creation and annihilation operators. The unfamiliar reader, however, can skip the rest of the section entirely and just look at the final result, represented by Eqs. (132) and (133), and compare in particular Eq. (132) with the standard semiconductor Bloch equations derived above in Eqs. (117) and (118). A careful comparison will reveal that the renormalisation procedure gives rise to the same set of semiconductor Bloch equations, but with different coefficients, namely the quasiparticles energy and Rabi frequency, which have been renormalised, i.e., their new expression contains the effect of the Coulomb potential, thus allowing the Coulomb interaction to be conveniently absorbed in the new definition of these quantities.
Let us now briefly sketch the renormalisation procedure. In this setting, and for this particular problem, the operators of interest will be the usual creation and annihilation operators for each band. Using the band index c(v) for conduction (valence), the creation (annihilation) of an electron of momentum \({\textbf{k}}\) is denoted by \({\hat{a}}^{\dagger }_{c/v, {\textbf{k}}} ({\hat{a}}_{c/v, {\textbf{k}}})\).
In the electron–hole picture, one speaks strictly of creation and annihilation of these quasiparticles, rendering the band index unnecessary. For this purpose, one defines the electron creation and annihilation operators respectively by \({\hat{\alpha }}^{\dagger }_{{\textbf{k}}} \equiv {\hat{a}}^{\dagger }_{c,{\textbf{k}}}\). Likewise, the hole creation and annihilation operators are respectively defined as \({\hat{\beta }}^{\dagger }_{\mathbf {-k}} \equiv {\hat{a}}_{v,{\textbf{k}}}\), leading to a Hamiltonian:
Where the free Hamiltonian \(\hat{{\mathcal {H}}}_{K}\) denotes the kinetic contributions of the carriers, \(\hat{{\mathcal {H}}}_{C-C}\) denotes the carrier-carrier Coulomb interactions (electron–electron, hole-hole and electron–hole) and \(\hat{{\mathcal {H}}}_{F-C}\) contains the dipole coupling to the optical field E(t).
Through this formalism, the occupation probability \(n_{e/h, {\textbf{k}}}(t)\) and the transition probability \(p_{{\textbf{k}}}\) are expressed as the expectation value of suitable creation and annihilation operators:
Unfortunately, this procedure is recursive, demonstrating the richness of many-body correlations among the carriers. A closed-form of a dynamical equation describing the evolution of some interaction operator is in general not possible to be found. This can be seen through the Heisenberg equation of motion. For an operator \({\hat{Q}}\):
If the Hamiltonian of Eq. (127) is introduced in it, the evaluation of the commutator will indefinitely create new higher-order expectations: in the first step, four-operator expectation values coming from \({\mathcal {H}}_{C-C}\) would have to be determined. In principle, they can be evaluated again using Eq. (129), yielding new, longer products of operators. Even though this procedure clearly does not terminate, an exact decomposition of its left-hand side is possible.Footnote 1 In particular, the expectation value of the operator in question may be split in a Hartree-Fock term and a scattering term:
The Hartree–Fock term contains the exactly-solvable contributions whereas the second term contains scattering events which are responsible for the higher-order correlations. Any model therefore requires a truncation so an approximation to the solution may be obtained.
If one truncates the expansion at the level of four-operators, the Hartree–Fock (or mean-field approximation) decomposes its expectation value in terms of the two-operator expectation values in Eq. (128). For instance:
This decomposition allows the equations of motion of the variables to be obtained as:
Equations in (132) resemble the carrier-free Semiconductor Bloch Equations in Eqs. (117)–(118). Apart from the scattering contributions, the Hartree-Fock part is formally the same. The difference is, of course, that the quasiparticles’ energy and the Rabi frequency have been renormalised, respectively as:
In practice, due to the the conservation expressed in Eq. (112) and the fact that the Coulomb scattering terms in \({\mathcal {H}}_{C-C}\) conserve quasiparticle number, the quasiparticles’ occupations are not independent of each other and can thus be lumped into a single variable \(w_{{\textbf{k}}} \equiv 2n_{e, {\textbf{k}}} - 1\), i.e. the inversion at \({\textbf{k}}\).
This renormalisation is manifested in optical and electronic properties of semiconductors. Graphene again defies the expectable: it seems that the Rabi frequency renormalisation may be ignored in some energy scales. Firstly, Quantum Field Theories of graphene are not easy to obtain due to its non-perturbative nature. This is to be contrasted with perturbative renormalisation group methods, which are known to converge reliably. The fine-structure constant of (suspended) graphene is
This expression is obtained through the replacement \(c \mapsto v_{\textrm{F}}\) in the QED fine structure \(\alpha _{\textrm{QED}} \approx 1/137\), a number well below unity. Consequently, since \(v_{\textrm{F}} \approx c/300\), this means that \(\alpha _{\textrm{G}} \approx 300 \alpha _{\textrm{QED}}\), a figure above unity and thus troublesome to apply perturbative methods.
Most metals are described as Landau fermi liquids and their Coulomb interactions appropriately accounted for in such framework. A QED analysis of graphene reveals some differences, due to its quasirelativistic nature [49]. The vanishing of the density of states at the Fermi level leads to short-range interactions being irrelevant [85]. Similar conclusions were obtained by Hofmann et al [86] by applying non-perturbative Random Phase Approximation methods to conclude that long-ranged interactions are screened in the layer and the many-body system shows features of a weekly-interacting Landau Fermi Liquid. The screening effect no longer applies at very low electronic densities, at which stage a renormalisation of the Fermi velocity is both predicted [87] and measured [88]. For these reasons, the conceptualisation of graphene as a non-interacting ensemble of two-level systems should not lead to any major disagreement about its physics. This is what is assumed from now and no Coulomb interactions shall be considered in the graphene SBEs and, later in Sect. 6, in the DBEs.
5.6.2 Temperature and doping
Up until this point, the decay rates which render the two-level system decoherent have not been explained or introduced conceptually. This section is devoted to shed some light on the physics behind it and how to incorporate these mechanisms in the SBEs.Footnote 2
Since the band occupations \(n_{\lambda , {\textbf{k}}}\) arise from electron and hole distributions in momentum space and changes thereof, it is not surprising that the inversion is given by them. In particular:
If the sample is in a quasi-equilibrium regime described by a temperature T, and the system is doped by \(\mu \) so that the Fermi level no longer sits at the Dirac points, an approximation of the carrier distribution in momentum space may be obtained with the aid of the Fermi-Dirac distribution of the each type of carrier.
For \(\mu _{e} = \mu _{h} \equiv \mu \), the quasi-equilibrium populations follow:
Scattering mechanisms, such as carrier-carrier or carrier-phonon, radiative recombination, or defects in the sample drive the occupation distribution to change towards a quasi-equilibrium distribution, as alluded in the previous section.
In general, this re-equilibration takes time in a certain scale and is not easy to quantify. Moreover, many different processes take place. For a sample initially in thermal equilibrium, the carriers show a very narrow, isotropic occupation distribution in momentum space. After the application of an optical field, over a time in the order of approximately 5–15 fs, the system is no longer thermally distributed and a highly anisotropic, broad distribution is found to promote high-momentum states. Within a certain thermalisation time, this distribution is again equilibrated. This process is achieved mainly due to electron–electron scattering, especially of high momentum and, in graphene, takes roughly 50 fs. This results in a narrow, quasi-equilibrium distribution at a different temperature than the initial one. Subsequently, phonon-electron scattering, optical-to-phonon decay fully thermalise the distribution within a much slower time interval, of approximately 1 ps.
Modelling this situation presents many theoretical and experimental challenges. In particular, an estimate of such decay rates for suspended graphene seems unlikely to be accurately taken. To further complicate the matter, experimental measurements of samples on a substrates vary significantly given their composition and chemical preparation. Time and Angle-Resolved Photoemission Spectroscopy (ARPES) techniques estimate these relaxation times as \(T_1 \approx 150\) fs and \(T_2 \approx 0.8\) ps [89]. These figures are heavily affected by a combination of initial temperature, doping, pump fluence, excitation energy and substrate type. On the theoretical side, the SBEs themselves have been used in order to model such mechanisms [90].
With these figures, an estimate of the decay rates can be taken simply as the inverse of these lifetimes i.e. \(\gamma _{i} \equiv T_{i}^{-1}\). In the context of this work, the optical excitation considered is an ultrafast regime, allowing to safely disregard the decoherence rates altogether. This is approximately true for ultrashort pulses in the coherent regime, i.e. for pulse durations much shorter than the dephasing times, \(t_{0}\ll T_{1,2}\), where \(t_{0}\) is the input pulse duration. For more information on how to model the effect of finite temperature on the nonlinear optical response of graphene, we address the interested reader to a recent work by Sipe et al., where the finite temperature nonlinear conductivity is constructed starting from an analytical expression of the linear conductivity at zero temperature and investigating perturbative corrections at finite temperature to the Bloch equations around the Dirac point [91]. Many other details that are not mentioned in this Review for space reasons can be found in the classic book by Haug and Koch [60].
5.7 Low-field regime
As a starting point to understand nonlinear interactions, it is instructive to analyse the predictions of the SBEs when the external electric field intensity is small. The results that are obtained should be in conformity with the principles of Linear Optics, outlined in Sect. 4. The SBEs are explicitly dependent on the field and thus exceedingly complicated to solve analytically.
However, the \({\textbf{k}}\)-dependent microscopic polarisation \(p_{{\textbf{k}}}\) in the regime of low field intensity can be obtained analytically by solving the SBEs with suitable conditions. If one further assumes that the system is initially found in its ground state i.e. \(w_{{\textbf{k}}}[t=0] \approx -1\), this situation reflects a picture where all carriers are in a suitable \({\textbf{k}}\)-state in the valence band and only a negligible subset of carriers undergoes optical excitation or de-excitation. If the field dynamics is assumed to maintain this situation, the inversion becomes a simple constant dictated by this initial condition. Mathematically, this instance presents an advantage since the SBEs may be solved analytically. Although the SBEs are composed of two coupled equations, this prescription allows the dynamical equation governing the population inversion in the regime of low field intensity to be dismissed, leading to
for all momenta.
The solutions vary given the electric field profile and will be explored shortly. Before engaging in the derivation, the SVEA-approximated SBEs of Eq. (120) may be computed numerically.
The pulse central frequency is now described by the dimensionless parameter \(\Omega _{0}\), quantifying the number of optical cycles per pulse. The dimensionless field intensity parameter \({\mathcal {E}}_0\) runs between 0 and roughly 10 in order to capture linear to extreme nonlinear intensities, as will be shortly seen. In order not to confuse other usages of the symbol \(\tau \), the dimensionless time parameter will still be denoted by t.
To have a taste of what the SBEs predict, the complex-valued microscopic polarisation \(q_{{\textbf{k}}}\) and the real-valued inversion \(w_{{\textbf{k}}}\) are now shown for a field of dimensionless amplitude \({\mathcal {E}}_0 = 10^{-2}\) and frequency \(\Omega _{0} = 30\), ensuring the field envelope describes the field fairly well. A momentum state will be denoted by \({|{\tilde{{\textbf{k}}}, \phi _{\tilde{{\textbf{k}}}}}\rangle }\)—the dimensionless momentum magnitude and angle, respectively. \(\tilde{{\textbf{k}}}\) is scaled so that electronic states for which the band separation exactly matches the photon energy have dimensionless momentum \(\tilde{{\textbf{k}}}= 1\). The dimensionless detuning is then simply \(\delta _{\tilde{{\textbf{k}}}} = \tilde{{\textbf{k}}}- 1\).
Figure 5 shows the dynamics of the real and imaginary part of the microscopic polarisation \(q_{\tilde{{\textbf{k}}}}\) when probed with a sech plotted for various values of the detuning, for a fixed angle \(\phi _{\tilde{{\textbf{k}}}} = \pi /3\). The dimensionless electromagnetic field and respective vector potential may be found in Eq. (205). Figure 6a shows the same situation as before, but now showing how the detuning affects the inversion. In both figures, it is clear that the dynamics of the two-level system is heavily affected by the detuning \(\delta _{\tilde{{\textbf{k}}}}\): resonant or near-resonant states attain higher values of the inversion and have greater coherence amplitudes. Conversely, very detuned states are barely affected by the field.
The role of the detuning on the slowly-varying microscopic polarisation—a \(\text {Im}(q_{\tilde{{\textbf{k}}}})\) and b \(\text {Re}(q_{\tilde{{\textbf{k}}}})\)—for sech pulse of field intensity \({\mathcal {E}}_0 = 10^{-2}\) and frequency \(\Omega _{0} = 30\). An angle \(\phi _{\tilde{{\textbf{k}}}} = \pi /3\) is fixed
5.8 Analytical solutions of the SBEs
Setting \(w_{{\textbf{k}}} = -1\), and making use of the field decomposition in Eq. (68), the SVEA-approximated equation governing the microscopic polarisation (the first equation in Eq. (120)) reads:
The solution is obtained using the integrating factor \(e^{\int i(\omega _{{\textbf{k}}}-\omega _{0} -i\gamma _{2}) {\text {d}}t} = e^{i(\omega _{{\textbf{k}}} - \omega _{0} -i \gamma _{2}) t}\), leading to:
Noting that the dipole moment is not time-dependent and introducing a new variable \(\tau = t-t'\), it becomes:
This form is useful as long as such integral may be expressed analytically. Its formal simplicity stems from something more fundamental. The SVEA that was applied to the electric field implies the Rotating Wave Approximation (RWA). To see this, the full field is now kept in Eq. (120), leading to:
For the sake of simplicity, a continuous wave of amplitude \({\mathscr {E}}_{0}\) is assumed so the field may be taken out of the integral, which can be evaluated as:
It is clear that the resonant term, for which \(\omega _{{\textbf{k}}}-\omega _{0} \approx 0\), dominate over the non-resonant term for which \(\omega _{{\textbf{k}}} + \omega _{0} \approx 2 \omega _{0}\), meaning:
and therefore neglecting the terms rotating with \(e^{i \omega _{0}t}\) in the SBEs is congruent with the RWA.
The condition \(w_{{\textbf{k}}} = -1\) can be somewhat relaxed in an approximation known as the quasi-equilibrium approximation [92], in which the inversion is simply assumed to vary little in the dephasing time \(1/\gamma _{2}\) i.e. \(w_{{\textbf{k}}}(t') \approx w_{{\textbf{k}}}(t)\) for \(t' < 1/\gamma _{2}\), conveniently allowing this term to be taken out of the integral.
The form just found in Eq. (140) is very suggesting. If causality is imposed through the imposition of the Heaviside \(\Theta \)-step function, the integration range may be extended to the reals:
thus allowing a response function \(R(\tau ) = e^{-i(\omega _{{\textbf{k}}} - \omega _{0} - i \gamma _{2}) \tau } \Theta (\tau )\) to be identified. This looks remarkably similar to the linear response expressed in Eq. (56). The time-dependent polarisation is then expressed as a convolution of the field and the response function. A frequency-dependent polarisation may be obtained as:
where the tilded variables represent the Fourier transform of their time-dependent counterparts and \(\circledast \) denotes the convolution operation. This is nothing more than re-expressing Eq. (58) in its microscopic version. Given the SVEA treatment taken, the frequency argument refers to the detuning frequency i.e. \(\delta _{\omega } = \omega - \omega _{0}\). The response function can be easily Fourier-transformed to:
yielding a Fourier-transformed microscopic polarisation:
Even after applying a generous number of assumptions to simplify the problem, time-dependent solutions to Eq. (144) are challenging to obtain given the generality of the field profile. A continuous wave presented no difficulty, resulting in the solution in Eq. (142).
Analytical solutions for two pulse-like excitations are now shown—a Gaussian and sech profiles. The effect of dephasing is also ignored by setting \(\gamma _{2} = 0\). The dipole moment, approximated by SVEA and calculated in Eq. (86), rescales simply to \(\mu _{\tilde{{\textbf{k}}}} = \sin \phi _{\tilde{{\textbf{k}}}}\).
5.8.1 Gaussian pulse
If the electric field is taken as a Gaussian pulse, whose electric field envelope is \({\mathcal {E}}(t)\) of the form:
where \({\mathcal {E}}_0\) is the field peak amplitude, attained when \(t = t_{f}\), the polarisation is found to be:
Here, \(\delta _{\tilde{{\textbf{k}}}}\) is the dimensionless detuning and \(\text {Erfc}\) the complex complementary error function. The analytical form of the microscopic polarisation just derived may be compared with the its numerical output, computed from Eq. (120). For this comparison to be meaningful, a field intensity must be chosen so that the approximation in Eq. (137) holds. Note that, on resonance, the polarisation is purely imaginary. As for a general off-resonant state, real and imaginary part of the microscopic polarisation show general features: its real part is roughly similar in shape as the electric field, whereas its imaginary part is roughly similar to the derivative of the field.
5.8.2 Hyperbolic secant pulse
If the excitation is now chosen to be a sech pulse given by \({\mathcal {E}}(t) = {\mathcal {E}}_0 \text {sech} \left( t \right) \) and with the aid of new variables \(s = \frac{1}{2}(1+i \delta _{\tilde{{\textbf{k}}}})\) and \(y = e^{t}\), the polarisation of Eq. (140) takes the form:
where \(\,_2F_1(a;b;c;x)\) is the Gauss hypergeometric function [93]. Hypergeometric functions are known to be incredibly general. In fact, most elementary functions may be expressed as a limiting case of them, for particular functional relations in its four defining parameters. One such instance is provided by the resonant two-level systems with dimensionless wavevector \(\tilde{{\textbf{k}}}= 1\), i.e. \(\delta _{\tilde{{\textbf{k}}}} = 0\) and consequently \(s = \frac{1}{2}\). In the original variables, the resonant polarisation becomes:
a purely imaginary function. A detailed derivation of this result is reported in Appendix A. Equation (150) also admits a simpler analytical form, based on another special function, i.e., the incomplete Beta function, for the case of off-resonant states in the presence of a general detuning. To get this result, we need to manipulate the hypergeometric function, keeping a general expression for the parameter s, since we are now considering detuning. For the sake of clarity, here we only give the final result of this calculations. For the interested reader, the details are provided in Appendix B. The final result is given as follows
where \(\text {B}(x,a,b)\) is the incomplete Beta function [93].
As expected, all the machinery developed so far must break down when the condition \(w_{{\textbf{k}}}(t) \approx -1\) is violated. From this expectation, a reasonable critical field intensity \({\mathcal {E}}_0\) may be inferred, separating the linear from the nonlinear regime.
To verify this condition, the inversion \(w_{{\textbf{k}}}\) is plotted alongside the comparison of the polarisation obtained from analytical and numerical methods.
Comparison of \(\text {Im}(q_{{\textbf{k}}})\) between SBEs simulations (blue, full) and analytical forms (red, dashed) for the resonant momentum state \({|{\tilde{{\textbf{k}}}, \phi _{\tilde{{\textbf{k}}}}}\rangle } = {|{1, \pi /3}\rangle }\), and various input pulse amplitudes, for a Gaussian pulse. Insets show the corresponding inversion. One notices a drastic departure from the approximation \(w_{{\textbf{k}}}=-1\) (linear low-field case) and thus the failure of the analytical formulas in the prediction of the polarisation field
Figure 7 shows, as before, the comparison between the low-field-approximated microscopic polarisation, alongside its corresponding inversion obtained numerically from Eq. (120), for varying electric field amplitudes \({\mathcal {E}}_0\) for a state on resonance i.e. for \(\delta _{\tilde{{\textbf{k}}}} = 0\). The imaginary part of the coherence in increasing field intensity are shown with their respective inversions.
These allow to capture three different situations after the low-field assumption is broken. The first regime is described by a slight dephasing from the numerical microscopic polarisation, retaining the main shape. This happens for instances that change the inversion in time, but never enough to reach a positive value. For fields with intensity \({\mathcal {E}}_0 \approx 0.5\) it can be seen that the difference in the saturation value of the polarisation is very considerable. Its inversion is still always negative.
The assumption is then severely broken for field intensities that allow the inversion to attain positive values, happening for around \({\mathcal {E}}_0 = 1\). In that instance, the theoretical prediction fails to account for the inflection point occurring when the inversion switches sign. Subsequently, higher fields further modulate the inversion, as seen for a field intensity of \({\mathcal {E}}_0 = 5\).
The low-field breaking can be made more transparent mathematically if the conservation law of Eq. (119) is analysed: if the inversion is solved from it, it follows:
In the low excitation regime, the negative root is used, since the initial condition \(w^{0}_{{\textbf{k}}} = -1\). However, if the field is strong enough to excite the system so \(|q_{{\textbf{k}}}| \approx 1/2\), the inversion will take either branches throughout the time dynamics.
With this analysis, one may take an educated guess that a departure from the linear optical regime is attained for field intensity parameters of around \({\mathcal {E}}_0 = 0.2\). By \({\mathcal {E}}_0 = 1\) the complete divergence between the predictions from linear response is notable and linear theory no longer applies at all.
In the next section, these notions will become clearer as the macroscopic polarisation will be obtained. Most importantly, it will be seen that, particularly for high field intensities, and most importantly ultrashort pulses, the slowly-varying amplitude of the field and its effect on the slowly-varying polarisation fails to capture the exact light–matter dynamics.
5.9 Law of universal absorption
The framework of the SBEs allow for a rather important result of linear optics to be obtained. It was derived in Sect. 4.3.2 that, for low field amplitudes, the absorbance of a graphene monolayer, a quantity which measures the efficiency of light absorbed from a source, is a constant across the frequency spectrum i.e. independent of the input pulse frequency. This constant is known as the fine structure constant of graphene \(\alpha _{\textrm{G}} = \pi \alpha _{\textrm{QED}} \approx 2.3 \%\).
For this result to be retrieved from the SBEs, a low-field regime must naturally be assumed, by neglecting the inversion dynamics. In this regime, the microscopic polarisation, which in frequency domain takes the form given in Eq. (147) may be inserted into the definition of the macroscopic polarisation envelope Q, given in Eq. (125):
In this fashion, the linear optical susceptibility \(\chi ^{(1)}(\delta _{\omega })\), as introduced in Eq. (58) can easily be read off as the function multiplying the Fourier-transformed field envelope. The absorption is related to its imaginary part \(\chi ^{''}(\delta _{\omega })\), as was derived in Eq. (78). In the limit of vanishing dephasing i.e. \(\gamma _{2} \rightarrow 0\), and applying the continuum approximation, it is:
where the the integral was split in its angular and radial variables. With the interband-driven SVEA-approximated dipole moment \(\mu _{{\textbf{k}}} = (e v_{\textrm{F}}/\omega _{0}) \sin (\phi _{{\textbf{k}}})\) from Eq. (86).
As for the radial integration, the integrand is expressed in terms of the linear variable k with the aid of Eq. (45) which, with the sifting property of the(Eq. (47)) gives:
where the momentum detuning is \(\delta _{{\textbf{k}}} = \omega _{{\textbf{k}}} - \omega _{0} = 2 v_{\textrm{F}}k - \omega _{0}\). Therefore, at the optical frequency i.e. \(\delta _{\omega } = 0\), the linear optical absorption coefficient is, as dictated by the calculation obtained in Eq. (78):
i.e., a constant and, more importantly, independent of optical frequencies, as expected. Note that the \(\alpha _{\textrm{G}}\) is the absorption i.e. the absorption per unit length times (absorbance) multiplied by the distance \(d_{\textrm{G}}\).
The response function that dictated the introduction of the \(\delta \) distribution is, strictly speaking, an abuse of notation as it is meaningless without being integrated. The same result could be obtained by starting from the microscopic polarisation of Eq. (142) and integrating it to obtain Q, leading to:
The radial complex integral can be evaluated with the aid of the Sokhotski-Plemelj theorem stating that for a function \(f: {\mathbb {C}} \rightarrow {\mathbb {C}}\) continuous on \({\mathbb {R}}\):
\({\mathcal {P}}[f]\) denotes the Cauchy principal value of f, which expresses the improper integral without its singularity at \(\zeta = \zeta _{0}\):
The real part is irrelevant for this purpose. By inspection, if the variable \(\zeta \) is chosen as \(\zeta = \omega _{{\textbf{k}}} - \omega _{0} = 2 v_{\textrm{F}} k - \omega _{0}\), one has \(f(\zeta ) = (\zeta + \omega _{0})/(2 v_{\textrm{F}})\) and hence Eq. (159) can be used, yielding the same imaginary part as obtained in Eq. (157).
This result will be verified in the next section, where a method will be devised to verify this law numerically. To do this, the reflected and transmitted fields have to be constructed from the macroscopic polarisation. For these objects to constructed, the SBEs have to be obtained numerically.
5.10 Simulations of optical properties
So far, the variables under consideration refer to microscopic quantities, bearing no significance to the observables of the sample. In the framework so far developed, the system is comprised of all allowed momentum states, each one a two-level system. In this section, the connection between the microscopic quantities pertaining to all two-levels and described by the SBEs to macroscopic responses of the system will be made.
The regime that was used in obtaining the dynamics of the two-level system determines which momentum states are necessary to account for the macroscopic dynamics. If the full electric field and the polarisation are considered, any macroscopic quantity will be defined once all contributions are considered i.e. all momentum states considered. Naturally, the numerical realisation of this integral must contain a finite, momentum cutoff \(k_{\textrm{c}}\).
Conversely, if SVEA is applied to the SBEs, the resonant momentum states i.e. \(\tilde{{\textbf{k}}}\approx 1\) will contribute the most. It is thus natural to introduce a cutoff in the magnitude of \({\textbf{k}}\) to ensure only states within a width x from resonance are considered i.e. the region \((k_{0}-x, k_{0}+x)\), where \(k_{0}\) is the photon momentum.
Hence for a general \({\textbf{k}}\) dependent function \(f_{{\textbf{k}}}\), its macroscopic counterpart is:
where \(\sigma = k-k_{0}\) is the detuning from the photon momentum \(k_{0}\).
5.10.1 Macroscopic polarisation
In Sect. 5.8, a straightforward comparison against the predictions from low-field theory allowed a quick estimate for when nonlinear effects should be relevant in the dynamics of a two-level system coupled to light. This resulted in a critical value \({\mathcal {E}}_0 \approx 0.2\).
The same methodology can now be applied to the averaged, macroscopic polarisation Q(t), as given by Eq. (126), and reported here for the sake of simplicity
Typically Q is normalised by the quantity \(Q_{0} = e \omega _{0}/(2 v_{\textrm{F}} \pi ^2 \epsilon _{0} d_{\textrm{G}})\), where \( d_{\textrm{G}}\) is the graphene thickness. The linear regime can be roughly estimated when the sample is probed with a field intensity approximately within the range satisfying \({\mathcal {E}}_0\ll \Omega _{0}v_{F}/c\).
As one would expect, the dynamics of the polarisation in the nonlinear regime is non-trivial and depends hugely on the incident field profile, leading to very different time dynamics of the polarisation for the same field amplitude.
5.11 Dynamics of the reflected and transmitted fields
With the knowledge of the macroscopic polarisation, which accounts for the field generated by the time variation of the electric dipoles in the sample as a result of the optical excitation, it is possible to construct the reflected and transmitted fields that are set up as a consequence of the optical interaction.
If an incident wave of electric field \({\mathcal {E}}_{\textrm{0}}\) propagates in a medium of refractive index \(n_{1}\), the Maxwell equations can be used to model the light propagation in the graphene sample and construct the reflected field \({\mathcal {E}}_{\textrm{R}}\), which propagates in the outgoing direction, and transmitted field \({\mathcal {E}}_{\textrm{T}}\), which propagates in the incoming direction in a medium of refractive index \(n_{2}\). These naturally depend on the incoming field but also on the generated polarisation of the medium:
These fields are dimensionless, with \(Q_{0} = \frac{e \omega _0}{2v_{\textrm{F}} \epsilon _0 d_G \pi ^2}\) and \(A_{0} = \frac{2\hbar \omega _0}{e v_{\textrm{F}} t_0}\).
5.12 Law of universal absorption: numerical proof
With the time dynamics of the reflected and transmitted fields set up, the reflectance R, transmittance T and absorbance A are the coefficients satisfying:
Absorbance of the sample as a function of the log of the incident field intensity, as defined in Eq. (165). In the linear regime, a plateau at \(A = 2.3 \%\) confirms the law of universal absorption
After the SBEs are solved numerically and averaged, the reflected and transmitted fields are constructed respectively through Eqs. (163) and (164) and consequently the optical coefficients of Eq. (165) are retrieved through their numerical integration in time. If the variation of two independent coefficients, in this case the absorbance A and transmittance T, in terms of the field amplitude is shown, the same analysis regarding the linear-to-nonlinear regime transition holds.
Figure 8 displays this exact setup, where the horizontal axis shows the logarithm of the incident field intensity for easier visualisation. Firstly, the low-field intensity regime shows a plateau in the absorbance, shown in window (a), at exactly the value of the absorption \(\pi \alpha _{\textrm{QED}}\simeq 2.3 \%\), confirming the law of universal absorption. Subsequent higher values of the field lead to a decrease of the absorbance and an increase of the transmittance. Field intensities for which this behaviour is no longer constant again set a critical transition value. This is seen for \(\log _{10} {\mathcal {E}}_0 \approx -1\), agreeing with the previous estimate.
5.13 Third-harmonic generation
The construction of the reflected and transmitted fields is also useful since their harmonic composition allows to infer the existence of harmonic generation in the sample, through the nonlinear polarisation. A validation of the claim of strong \(\chi ^{(3)}\) nonlinearities in graphene can also be found using the SBEs.
For a clearly nonlinear incident field intensity \({\mathcal {E}}_0=1\), the full-field SBEs (Eqs. (117)–(118)) may be employed and appropriately averaged according to the prescription given in Eq. (161). The time-dependent profiles of all fields in the sample may consequently be reconstructed with the help of the above formulas. The Fourier-transform of the transmitted field are plotted in terms of the harmonic order \(\omega /\omega _{0}\) in Fig. 9. The pump frequency is thus found at \(\omega /\omega _{0}=1\).
As it is expected from centrosymmetric media, no even harmonics are generated, meaning sample-produced optical fields should not have intensity peaks centered at odd positions on the harmonic order axis. This is indeed observed. Interestingly, the the third-harmonic components of the transmitted field is higher than its counterpart in the reflected field. This behaviour is characteristic of materials with a high \(\chi ^{(3)}\). In this setting, one may see that graphene indeed shows nonlinear features, starting at the first allowed nonlinear contribution, the third.
The reason why the full-field polarisation was considered is related to the fact that the third-harmonic enhancement of the transmitted field cannot be captured by SVEA conditions i.e. the peaks would overlap with the peak of the reflected field. It is therefore reasonable to assume that the full-field dynamics, containing the full oscillations of the optical fields, is necessary to capture signatures of ultrashort, intense pulses. In the next section, this treatment will be employed to graphene but using a different, yet related, set of equations to model the carrier dynamics—the Dirac–Bloch Equations.
Fourier-transform of the transmitted fields generated from a graphene sample, simulated by the SBEs, plotted against the harmonic order \(\omega /\omega _{0}\). The pump frequency is found at \(\omega /\omega _{0}=1\). Pulse duration is \(t_{0}=10\) fs, central wavelength is \(\lambda _{0}=800\) nm, and \(\Omega _{0}\equiv \omega _{0}t_{0}\simeq 25\). \({\mathcal {E}}_{0}=0.5\) corresponds to an intensity \(I=3.2\) GW/cm\(^2\); \({\mathcal {E}}_{0}=1\) corresponds to an intensity \(I=13\) GW/cm\(^2\); \({\mathcal {E}}_{0}=5\) corresponds to an intensity \(I=320\) GW/cm\(^2\)
6 The Dirac–Bloch equations
6.1 Overview
In the previous section, the SBEs were used to model the optical behaviour of graphene. Although the linear regime was well described by them, it was seen that the slowly-varying polarisation used in the derivation of the SBEs fails to predict third harmonic generation in graphene, a well-established result in the literature [51].
That in itself does not prove the unsuitability of the SBEs—it merely shows that full field should be considered. This is particularly true for ultrashort pulses, whose envelope does not resemble the full field, leading to a wrong estimation of the dynamics of the two-level system and hence of any optical quantity which depends on it.
In Sect. 2, the reduction of the Schrödinger Equation to the Dirac Equation was established. If next-nearest-neighbour effects are neglected and the dispersion is expanded around two special, Dirac points, located at the corners of the first Brillouin zone, the bands become degenerate there, changing linearly with the momentum of the electron—leading to the famous Dirac cones. For that reason, graphene is rather peculiar, what is known as a zero-gap semiconductor.
Given this realisation, an appropriate question to ask is “why should graphene be modelled by the Semiconductor Bloch Equations?” One can wonder if the two-level systems modelling the carriers in graphene, obeying a completely different equation, given their pseudo-relativistic nature, are suitably described by the SBEs. This section tries to answer that question, by applying the machinery so far developed to a two-level system described by the Dirac Equation, leading to the Dirac–Bloch Equations (DBEs).
6.2 Derivation
The Dirac–Bloch Equations are now derived. The starting point must obviously be the Dirac equation for a massless electron in graphene. To couple light, the minimal substitution of Eq. (60), explained in Sect. 4.2, is applied to the corresponding Hamiltonian of the Dirac Equation, given in Eq. (34), leading to:
The operator on the right-hand side may be identified with the time-dependent Hamiltonian \(H^{\xi }_{{\textbf{k}}}(t)\). In this formalism, both valleys—\({\textbf{K}}\) (\(\xi = +1\)) and \({\textbf{K}}'\) (\(\xi = -1\))—are simultaneously considered through the inclusion of the valley degree of freedom \(\xi \). As usual, \(v_{\textrm{F}} \approx c/300\) is the Fermi velocity in a graphene monolayer, c the speed of light in vacuum, \(-e\) is electron charge, \(\varvec{\sigma }(\xi ) \equiv (\xi \sigma _{x},\sigma _{y})\) a valley-dependent 2D Pauli-matrix vector. In this way, and ignoring the field dependence for now i.e. by setting \({\textbf{A}}(t) = 0\), one can see that the Hamiltonian of a valley is related to the other simply by making the transformation \(p_{x} \mapsto -p_{x}\). The time-dependent 2-spinor \({|{\Psi ^{\xi }_{{\textbf{k}}}(t)}\rangle }\) is the solution to the equation and represents electrons in the conduction and valence bands for a specific electronic momentum \({\textbf{p}}\equiv \hbar {\textbf{k}}\).
This Hamiltonian has been minimally-coupled to light. The composition on the momentum that originates from it leads to the promotion of the time-dependent momentum to the field-dependent canonical momentum, with the following polar representation:
The phase \(\theta _{{\textbf{k}}}(t)\) is termed the dynamical angle. The electric field \({\textbf{E}}\equiv -(1/c) {\dot{{\textbf{A}}}}\) is assumed linearly polarised. Without loss of generality, since the dispersion is radial, such polarisation may be assumed to be along the arbitrary \({\hat{x}}\) axis i.e. \({\textbf{A}}(t) = (A(t),0,0)\). As before, normal incidence conditions are assumed, as well as the Coulomb gauge given by the condition \(\nabla \cdot {\textbf{A}}= 0\) and explained in Sect. 4.2.
A very subtle difference, which will only be lightly touched for now and expanded in Sect. 7.1, is that, unlike the treatment applied to the OBEs, and consequently the SBEs, the treatment in the DBEs is non-perturbative. Mathematically, this means that the solution to Eq. (166) must be obtained with the presence of the field. The concept of eigenstates in a time-dependent setting is a tricky one, as by definition these are stationary states. This fact presents a challenge.
To see this, the field-free Hamiltonian is considered, i.e. with \({\textbf{A}}= 0\). Then, since the Hamiltonian is time-independent, the solution to Eq. (166) is simply given by the evolution operator \(U_{{\textbf{k}}}(t) = e^{-\frac{it}{\hbar } H^{\xi }_{{\textbf{k}}}}\), meaning \({|{\Psi ^{\xi }_{{\textbf{k}}}(t)}\rangle } = U_{{\textbf{k}}}(t) {|{\psi ^{\xi }_{{\textbf{k}}}}\rangle }\), for an initial spinor \({|{\psi ^{\xi }_{{\textbf{k}}}}\rangle }\).
The reason is rather simple: if the evolution operator is Taylor-expanded:
it can be conveniently expressed as a matrix using an orthonormal basis comprised of the Hamiltonian eigenstates \({|{u^{\xi }_{\lambda , {\textbf{k}}}}\rangle }\), i.e. two states (\(\lambda = -1,1\)) for which \(H^{\xi }_{{\textbf{k}}} {|{u^{\xi }_{\lambda , {\textbf{k}}}}\rangle } = \epsilon ^{\xi }_{\lambda ,{\textbf{k}}} {|{u^{\xi }_{\lambda , {\textbf{k}}}}\rangle }\) and \( {\langle {u^{\xi }_{\lambda ', {\textbf{k}}}|u^{\xi }_{\lambda , {\textbf{k}}}}\rangle } = \delta _{\lambda ,\lambda '}\).
Given the Hamiltonian representation derived in Eq. (100), naturally diagonal, the computation of \(U_{{\textbf{k}}}(t)\) follows directly:
This representation clearly satisfies the required time evolution dictated by the solution: for a general, time-independent \({|{\psi ^{\xi }_{{\textbf{k}}}}\rangle } = \sum _{\lambda '} c^{\xi }_{\lambda '}{|{u^{\xi }_{\lambda ', {\textbf{k}}}}\rangle }\):
The reason why this solution may be obtained is of course due to the time-independence of the eigenstates. The addition of the electromagnetic potential \({\textbf{A}}(t)\) makes the Hamiltonian time-dependent and the reasoning just exposed breaks down. Naively, one could guess that the solution would be given by the integrating factor \(I(t) = \mathcal {{\hat{T}}}e^{\int _{-\infty }^{t'} H^{\xi }_{{\textbf{k}}}(t') {\text {d}}t'}\), where \(\mathcal {{\hat{T}}}\) is the time-ordering operator. However, the Hamiltonian is now a matrix, which does not commute at different times and such quantity seems hard, if not impossible, to retrieve.
Unlike what one could suppose, this issue is not solved by considering another dynamical picture (or representation) of the system. It is often the case that such a representation change does not allow the problem to be solved. For these reasons, general analytical solutions of Eq. (166) are not known.
However, a procedure, originally outlined in two seminal papers by Ishikawa [95, 96], may be applied to yield an Ansatz i.e. a formal guess which is solves Eq. (166). Conceptually, it is not terribly different to what was developed so far: the eigenstates will be generalised to their instantaneous counterparts and the evolution phase factor will now depend on time in such a way that the Dirac Equation is satisfied.
The instantaneous eigenstates are spinors which satisfy
where the instantaneous energy \(\epsilon ^{\xi }_{\lambda ,{\textbf{k}}}(t)\) is now time-dependent too. In order to obtain both, the Hamiltonian is first written in matrix form:
where the canonical momentum polar coordinates were introduced through the identity \(\xi \pi _x(t) - i \pi _y(t) = \xi |\varvec{\pi }_{{\textbf{k}}}(t)|e^{-i \xi \theta _{{\textbf{k}}}(t)}\).
Two symmetric dispersion branches arising from it take the form:
For this reason, the positive branch of the dispersion, equal for both valleys, will be denoted as \(\epsilon _{{\textbf{k}}}\) i.e. \(\epsilon ^{\xi }_{\lambda , {\textbf{k}}} = \lambda \epsilon _{{\textbf{k}}}\).
Unsurprisingly, the instantaneous eigenstates are not formally different to the eigenstates found for the free Dirac fermions in Eq. (37), albeit generalised to any valley \(\xi \). The instantaneous eigenstate is now decomposed into its upper and lower components:
in turn yielding the following system of equations to solve:
Both amplitudes must therefore satisfy \(\varphi ^{\xi }_{\lambda } = \xi e^{-i \xi \theta _{{\textbf{k}}}} \phi ^{\xi }_{\lambda }\). It is convenient to explicitly include the dynamical angle in the spinor. To do that, the lower component may be fixed to \(\phi ^{\xi }_{\lambda } \equiv \lambda e^{-i \xi \theta _{{\textbf{k}}}/2}\). Noting that \(\lambda ^2 = \xi ^2 = 1\), this choice leads to normalised states satisfying \({\langle {u^{\xi }_{\lambda , {\textbf{k}}}(t)|u^{\xi }_{\lambda ', {\textbf{k}}}(t)}\rangle } = \delta _{\lambda \lambda '}\):
Attending to the considerations that lead to the construction of the spinor when applying the tight-binding model for graphene in Sect. 2.4, it can be seen that the amplitude of the upper and lower components, which correspond to each sublattice A and B, are the same. This is a statement of sublattice equivalence and leads to the invariance of physics under each sublattice. The next section will address a way to break such symmetry.
Having obtained, in a sense, a time-dependent basis, the natural question to ask is: how can a solution \({|{\Psi ^{\xi }_{{\textbf{k}}}(t)}\rangle }\) be obtained? A sensible Ansatz is provided upon constructing the superposition:
where an additional yet-to-be-determined phase \(\Omega _{{\textbf{k}}}(t)\) was added. In this fashion, the field interaction is accounted for by generalising the field-free eigenstates to a time-dependent Ansatz. After inserting this Ansatz in Eq. (166), its left-hand side becomes:
As for the right-hand side:
it is clear that the third term in Eq. (178) cancels with the term from Eq. (179) if \(\hbar {\dot{\Omega }}_{{\textbf{k}}} = \epsilon _{{\textbf{k}}}\). This phase, termed dynamical phase, is then:
Now, noting that \({|{{\dot{u}}^{\xi }_{{\lambda }_{{\textbf{k}}}}}\rangle } = (-i \xi {\dot{\theta }}_{{\textbf{k}}}/2) {|{u^{\xi }_{-\lambda , {\textbf{k}}}}\rangle }\), the first two terms in Eq. (178) can be pre-multiplied by \({\langle {u^{\xi }_{{\bar{\lambda }}, {\textbf{k}}}}|}\). Then, using the state orthonormality, the sum over \(\lambda \in \{{\bar{\lambda }}, -{\bar{\lambda }}\}\) leads to the condition:
As per usual, the coefficients dynamical variables are converted the optically-relevant variables:
In the framework of the DBEs, the variable \(\rho ^{\xi }_{{\textbf{k}}} \equiv c^{\xi }_{+, {\textbf{k}}} \left( c^{\xi }_{-,{\textbf{k}}}\right) ^{*} \), previously used in the OBEs and SBEs, is termed coherence. The additional phase just introduced allows the DBEs to be conveniently written in same form as the OBEs. As usual, \(\omega _{0}\) denotes the central frequency of the input pulse. The derivatives of Eqs. (182)–(183) are straightforwardly obtained as:
Using the condition in Eq. (181), the Dirac–Bloch Equations for monolayer graphene are finally obtained as:
The dephasing effects are, as usual, included phenomenologically through the coefficients \(\gamma _{1,2} \equiv 1/T_{1,2}\) whereas the effect of intrinsic, field-independent parameters such as temperature and chemical potential can be incorporated in a momentum-dependent equilibrium value of the populations \(w^{0}_{{\textbf{k}}}\), following a methodology outlined in Sect. 5.6.2.
Following the discussion in the same section, these equations do not take into account any kind of effective Coulomb interactions amongst the carriers. Despite that, no further approximations other than modelling graphene as non-interacting electrons in a pair of Dirac cones, coming from the approximation of the tight-binding band structure of graphene around the two inequivalent Dirac points, were applied in obtaining the dynamics of the coefficients. In particular, no approximations on the shape of the impinging electric field, whether, for example, its amplitude is slowly varying or not, is necessary to derive the DBEs. This fact presents a remarkable possibility: to express the electric current generated in the sample as a consequence of the optical excitation in an exact way. It is expected that the dynamics of two-level system, described by the evolution of \(w^{\xi }_{{\textbf{k}}}\) and \(q^{\xi }_{{\textbf{k}}}\), determines such a current. This is indeed verified in the next section, where the link between the evolution of the dynamical variables and the photo-generated current is established. The price to pay for this exact form is, of course, that no analytical solutions of the DBEs may be found as was the case for the SBEs in the linear regime. One must therefore apply reliable numerical routines to solve the DBEs.
6.3 The relationship between the SBEs and DBEs
At this stage, the difference between the Semiconductor Bloch equations derived in Sect. 5.4, a mere cosmetic conceptual adjustment to the Optical Bloch equations given in Sect. 5.3 has not been justified beyond the introduction of the instantaneous eigenstates that resulted from the minimal substitution in the Hamiltonian of Eq. (166). It may even feel like such a distinction is based on theoretical pedantry alone. However, this feature is crucial in understanding the discrepancies in the current that is predicted by both models.
What exactly makes the SBEs and DBEs different? The answer boils down to the way the wavefunction is obtained and how it, in turn, relates to observables. The philosophy underlying the DBEs must be contrasted with the one employed in the SBEs. The Hamiltonian used in Eq. (166), unlike the OBEs and SBEs, is not understood as a “free” plus “perturbed” one, of the form \(H_{{\textbf{k}}}(t) = H^{0}_{{\textbf{k}}} + H^{\textrm{int}}_{{\textbf{k}}}(t)\) but rather as a non-separable time-dependent system, where the dependence comes from the composition \( {\textbf{k}}\mapsto {\textbf{k}}+ e/(\hbar c){\textbf{A}}(t)\). Mathematically, this situation is reflected in the structure of the wavefunction itself, which is accounted for by all contributions in the Hamiltonian, as opposed to using the field-free wavefunction.
An observable \({\mathcal {O}}(t)\) is thus obtained as \({\langle {\Psi ^{\xi }_{{\textbf{k}}}(t)|\hat{{\mathcal {O}}}(t)|\Psi ^{\xi }_{{\textbf{k}}}(t)}\rangle }\), where the spinor solves the full Hamiltonian, as opposed to the perturbative form \({\langle {\Psi ^{\xi }_{{\textbf{k}}}|\hat{{\mathcal {O}}}(t)|\Psi ^{\xi }_{{\textbf{k}}}}\rangle }\), where the latter spinor is a solution to the field-free Hamiltonian.
The SBEs are exactly a limiting case of the DBEs. In order to reduce the DBEs in Eqs. (185–186) to the SBEs in Eqs.(117)–(118), one must neglect the contribution of the photon momentum (e/c)A(t) in the quantities \({\dot{\Omega }}_{{\textbf{k}}}\) and \({\dot{\theta }}_{{\textbf{k}}}\), obtaining exactly the SBEs used, for instance, in Ref. [97]. This reduction is never acceptable in gapless media as will be shown shortly.
This difference leads, of course, to some differentiating features of the DBEs. These may be appreciated by comparing the full-field SBEs in to the DBEs. After an explicit computation from the definition of the dynamical angle given in Eq. (167) is performed:
the function that multiplies the electric field may be interpreted as the dipole moment:
Consequently, if \(A(t) = 0\) is set, the time-independent dipole moment of the SBEs is obtained. Additionally, it is clear that the SVEA-approximated dipole moment calculated in Eq. (86) is obtained by evaluating the SBE dipole moment when the electronic momentum is resonant with the photon’s i.e. whenever \(|{\textbf{k}}| = \omega _{0}/(2 v_{\textrm{F}}) \equiv |{\textbf{k}}^{0}|\):

The dipole moment in the DBEs is a time-dependent quantity—meaning that the dipole moment is temporally oscillating with the pulse. Given the lack of applications in any other realistic physical situations in the literature, this is very unusual in the theory of two-level systems. Furthermore, the light–matter coupling is not attained simply by incorporating the electric field in the equations, as was done in the OBEs and SBEs; the driving term now exhibits a complex coupling that includes both the electric field \({\textbf{E}}\) and the vector potential \({\textbf{A}}\).
Additionally, the frequency detuning between a specific two-level system with wavevector \({\textbf{k}}\) and the pulse frequency \(\omega _{0}\) is also oscillating in time as:
as seen in the second term in Eq. (185). In other words, the pulse itself modulates the band structure continuously, leading to global dynamical oscillations of the Dirac cone. This feature stems from the use of the dynamical phase of Eq. (180). It is expected that this rather non-trivial phase affects the generation of currents. The confirmation will be given when the significance of such a modulation in the generation of new harmonics will be given in Sect. 7.1, where both models are compared.
6.3.1 Shortcomings of SBEs
More relevantly, the SBEs are often inadequate when studying gapless Dirac media like graphene and, for pulses that are short or intense enough, they will also fail even in the case of gapped Dirac media [98].
To show precise conditions for the failure of SBEs, the model of Eqs. (185)–(186) is extended to a gapped layer solely for the purpose of obtaining its dispersion. For simplicity, only the \({\textbf{K}}\) valley is considered. To do this, a mass term in Eq. (166), proportional to the energy gap \(\Delta \) is inserted and only the \({\textbf{K}}\) valley is considered i.e. \(\xi = 1\):
where \(\sigma _{z}\) is the diagonal Pauli matrix.
From Eq. (191), one can write straightforwardly the instantaneous energy eigenstates as
In the vicinity of the band gap centre (\(p_{x} = p_{y} = 0\)), the contribution of the photon momentum can be neglected only for those pulse amplitudes satisfying \(|eA/c|\ll \Delta /2v_{\textrm{F}}\). In this case, the DBEs are identical to the SBEs, since in this way the time dependence of the frequency detuning and the dipole moment \(\mu _{{\textbf{k}}}\) are eliminated. Therefore, the SBEs are a valid description of light–matter interaction in gapped 2D Dirac media only when the pulse spectrum does not overlap substantially with the Dirac point, or when the intensity of the pulse is not too large with respect to the gap energy.
The above condition for the SBEs to be approximately valid can be translated into a condition for the input pulse intensity: \(I\ll I_{\textrm{cr}}\), where
If the intensity of the pulse is such that \(I\ge I_{\textrm{cr}}\), the SBE description loses its validity. To make things worse, even for low-intensity light, short pulses satisfying the condition \(\omega _{0}t_{0}<\Delta /(4\hbar \omega _{0})\) will overlap too much with the Dirac point, also leading to the breaking of the validity of the SBEs.
Therefore the SBEs description of gapped Dirac layers is approximately valid only if pulses are neither too short nor too intense. It is crucial to observe that for gapless media such as graphene, for which \(\Delta = 0\), it is in principle never possible to accurately describe light–matter interactions via the SBE, since the condition \(I\ll I_{\textrm{cr}}\) can never be satisfied.
7 Currents
Given the considerations that established that the treatment employed in the DBEs is nonperturbative in nature, since the full field is accounted for (as opposed to the usual field expansion and order truncation methods shown in Sect. 4.2), as well as the full pulse properties (as opposed to slowly-varying envelope/rotating wave approximation conditions), a desirable quantity to study is the two-dimensional current generated across the sample. Although the macroscopic polarisation produced in the sample provides many crucial insights, the photo-generated current allows for far more detailed information.
In the same spirit as the one used for obtaining the macroscopic polarisation in terms of the microscopic polarisation, the physical, macroscopic current generated in the sample may be obtained by adequately averaging over all microscopic current contributions generated by each momentum state.
This method ultimately allows an analysis of the system response to be obtained when probed in extreme nonlinear optical conditions, without any field expansion. The procedure to attain this goal is shown in this section.
To obtain the time dynamics of the photo-generated current, one proceeds by first determining the \(\mu \)-component (\(\mu = x,y\)) of the current contribution of a particular momentum state \({\textbf{p}}\) in a valley \(\xi \), in time domain. For consistency purposes, such contribution to the current is termed a microscopic current \(j^{\xi }_{\mu , {\textbf{k}}}\) and can be obtained by applying a suitable current density operator \({\hat{j}}^{\xi }_{\mu }\) to the Ansatz \({|{\Psi ^{\xi }_{{\textbf{k}}}}\rangle }\) given in Eq. (177), which reads:
Naively, one may expect this element to give the current observable as it is the expectation value of the current density operator for the wavefunction employed in this framework. However, since the system admits time reversibility, it is known that energy bands approximated within a tight-binding formalism must satisfy a sum rule that prevents dissipative currents in the valence bands to be produced [99].
The dispersion of the infinitely-extended bands given in Eq. (173) and instantaneous eigenstates of Eq. (176) are a result of an approximation in momentum space, namely for electronic states in the vicinity of the Dirac points, where they possess relativistic properties.
Therefore, the physical current cannot be simply accounted for by Eq. (191), as it contains unphysical divergences. The current can nonetheless be regularised through the introduction of a term which acts as an ad-hoc subtraction of the current generated in the valence band thus:
The Hamiltonian of Eq. (191) is a low-momentum representation of the carriers, since it was obtained as a first-order \({\textbf{k}}\cdot {\textbf{p}}\) approximation. A local form of the current density operator may be found which renders the current density operator valley-dependent. The full current, which takes in both valley contributions is of course independent of \(\xi \). For a Cartesian coordinate \(\mu \), it is given as:
resulting in momentum-independent quantities:
In this fashion, the construction of the current in Eq. (195) allows for the separation of current terms which originate within the same band (intraband) and across different bands (interband).
where, by parity, \(\cos (\xi \theta _{{\textbf{k}}}) = \cos (\theta _{{\textbf{k}}})\) and \(\sin (\xi \theta _{{\textbf{k}}}) = \xi \sin (\theta _{{\textbf{k}}})\).
As for the y component:
Importantly, the current elements satisfy the conditions:
Inserting the current elements calculated in Eqs. (198)–(199) in Eq. (195) leads to the microscopic current:
Similarly for the y component:
The valence band current term that has been subtracted is incorporated as a regularisation for the intraband current leading, in a sense, to a reassignment \(w_{{\textbf{k}}} \mapsto w_{{\textbf{k}}} + 1\) in Eqs. (202)–(203), which has been used in [95]. With the knowledge of the contribution from a particular momentum state and valley to the \(\mu \) component of the current, the physical photo-generated current is obtained through:
where \(g_{\textrm{s}}=2\) denotes the spin degeneracy (given that the quasirelativistic equations do not account for spin), \({\text {d}}^{2} {\textbf{k}}~ \equiv |{\textbf{k}}|~ d |{\textbf{k}}| {\text {d}} \phi _{{\textbf{k}}}\) is the 2D differential in momentum space and \( d_{\textrm{G}} = 0.33\) nm is the thickness of the monolayer. The macroscopic contributions from intraband and interband currents may of course be accessed given the explicit separation in \(j^{\xi }_{\mu , {\textbf{k}}}\).
Rather importantly, it must be emphasized that the integration over momentum must cover the whole space, as opposed to the usual first Brillouin zone, since the dispersion is not periodic, given the low-momentum approximation.
7.1 A comparison of the DBEs and SBEs
In the same spirit of Sect. 5.10, and to establish the different predictions from both the DBEs—Eqs. (185)–(186)—and the full-field SBEs—Eqs.(117)–(118)—in the nonlinear regime, both sets of equations were numerically simulated with the same parameters. As before, a highly accurate Runge–Kutta algorithm was used and, to this end, the equations were rescaled so all variables are dimensionless.
With a numerical output of the inversion and microscopic polarisation, the microscopic currents may be composed as given by Eqs. (202)–(203). The final, macroscopic current, whose definition is found in Eq. (204), is obtained by discretising momentum space in a reasonably fine mesh. The integration in momentum space is performed using the trapezoidal rule and, given the formalism that was developed, the space is parametrised by the polars of each dimensionless momentum state, as before denoted as \( \tilde{{\textbf{k}}}= {|{|\tilde{{\textbf{k}}}|, \phi _{\tilde{{\textbf{k}}}}}\rangle }\).
To ensure that all appropriate contributions are taken, the radial integration is performed up to a cutoff value. A sensible value for such cutoff was found to be \(|\tilde{{\textbf{k}}}| = 2c/(v_{F}\Omega _{0})\), which is the point where the electronic momentum starts to dominate the photonic momentum in Eq. (173). For instance, for \(\Omega _{0}=50\), the formula would give \(\tilde{{\textbf{k}}}\simeq 12\), so we have to make sure that we integrate the momenta at least up to this value to correctly capture the full dynamics of the pulse-graphene interactions.
Finally, the current in time domain is Fourier-transformed so a harmonic analysis may be performed. The same methodologies apply to the SBEs, where the current contributions are obtained by setting \(A(t)=0\) in their DBEs counterparts.
To solidify the claim that the nonlinear regime induces different time dynamics in the photo-generated current, the SBEs and DBEs were solved in the linear regime, for a field amplitude \({\mathcal {E}}_0 = 10^{-9}\) and nonlinear regime, for a field amplitude \({\mathcal {E}}_0 = 1\). The current predicted by both methods is shown in Fig. 10. Firstly, the current only shows a nonzero component \(J_{y}\), namely the one in the light polarisation direction, which was taken to be in \({\hat{x}}\). Consequently, the integrated current component \(J_{y}\) vanishes identically.
Figure 10a shows a perfect match between both models in the linear regime. However, a an intense field leads to additional time dependences in the DBEs, which ultimately make the current output slightly different to the SBEs.
Comparison of the macroscopic current \(J_{x}\) between the DBEs and the SBEs, in the full-field treatment, for a sech pulse of central frequency \(\Omega _{0} = 5\). a Shows an extreme similarity between the models since it is obtained in the linear regime. For intense fields, b shows slightly different outputs. These are crucial in understanding harmonic generation in the sample
The current formulae dictating its dynamics are dependent on which valley the excitations take place. It is thus in principle possible to obtain different outputs for each valley, leading to an asymmetrical contribution of the valleys to the overall current. However, the valley-dependent currents are the same. Consequently, a degeneracy factor of 2 may be introduced in the first line of Eq. (204). This degeneracy factor has also been found in works by Ishikawa [95, 96].
Total emission spectra excited by a \(t_{0}=10\) fs pulse, normally incident and linearly polarized, with an input energy \(I=114\) GW/cm\(^{2}\), at zero temperature. Results are obtained by solving numerically the DBEs (185–186) (red solid line), and the SBEs (blue dotted line). It is evident that the SBEs predict much higher amplitudes for the \(n>3\) harmonics
For the simulations that produced Fig. 11, the graphene sheet is pumped with a normally incident pulse, of duration \(t_{0} = 10\) fs, central wavelength \(\lambda _{0} = 800\) nm, intensity \(I=114\) GW/cm\(^{2}\), and at temperature \(T = 0\) \(^{\circ }\)K.
Realistic, zero-averaged localised electric and vector potential fields, in order not to introduce unphysical static electric fields. Their respective dimensionless definitions are given as:
The output spectra \(S(\omega ) = |\omega {\textbf{J}}(\omega )|^{2}\) in dB are shown in Fig. 11. The factor \(\omega \), proportional to the density of states in Eq. (48) is added so that the spectrum does not show decaying harmonic peaks. The solid red line is the result of the DBEs simulation, while the dotted blue line is obtained using the SBEs. The SBEs predict a much higher value of the harmonics \(n>3\), and the amplitudes of those harmonics tend to decrease quickly to zero when increasing the harmonic order n. The DBEs, on the contrary, show lower amplitudes for the harmonics, but they tend to reach a plateau even for large values of n. In conclusion, we have shown that the SBEs are overestimating the importance of the high-harmonic generation in gapless graphene, and they also give an incorrect prediction of the general behaviour of such harmonics, stressing the fact that the dynamical phase induced by the vector potential is crucial for a quantitative description of gapless graphene.
All the simulations in this Review were carried out by solving the DBEs with a standard 4th-order Runge–Kutta method [125]. There are two critical parts in the implementation of our code. The first one is the integration of the polarization and inversion fields over the momentum (which provide the macroscopic observables such as the current \(J_{x}\), polarization Q, etc), which must be performed with high accuracy. For this we use a Simpson “1/3 rule”, which we find to be excellently suited for the purpose. Using a lower accuracy rule, like the trapezoidal rule, does not achieve a good result due to the appearance of unphysical harmonics in the output spectra. The second critical part is that different value of the momenta have to satisfy the quantum probability conservation law \(w^2_{{\textbf{k}}} + 4|q_{{\textbf{k}}}|^2 = 1\) for each value of k, but the accuracy of this condition strongly depends on how close one is to the Dirac point. Far from the Dirac point, the error tolerance is easily satisfied even for a relatively low temporal sampling of the electric field, while getting closer to the Dirac point one needs to increase the temporal sampling using a large number of points. For this reason, to ensure exactly the same error tolerance for all k-points, we use an adaptive iterative algorithm. The programming language of our choice is Julia, which allows a very efficient implementation of the parallel computation (using 12 cores) of the momentum integration, since in the absence of Coulomb interactions all the momenta are independent. Our code can be downloaded freely, and the link is provided at the end of this Review.
8 The nonlinear response of graphene in the presence of artificial gauge fields
The nonlinear susceptibility of graphene in the presence of a strong magnetic field has been estimated theoretically to be inversely proportional to the applied magnetic field (a trend corroborated by the results above), and to be of the form \(\chi _{3D}^{(3)}\simeq 5\times 10^{-9}/B(\text {T})\) [100]. In the same work, the intensity of the nonlinear signal has also been estimated to be directly proportional to the magnitude of the magnetic field, i.e., \(I^{(3)}\simeq B\). This hints at how controlling the magnetic field applied to a flake of graphene would result in an overall control of the intensity of the emitted nonlinear signal. This feature, combined with the versatility artificial gauge fields offer in generating and controlling artificial magnetic fields, hints at the possibility to use real, or artificial, magnetic fields to boost the nonlinear properties of graphene, reducing the necessary pump intensity to trigger its nonlinear phenomena and might lead, in the future, to a new generation of integrated nonlinear devices. Recently, several works on the nonlinear response of graphene and 2D materials under the action of a magnetic field have appeared, including the model we are going to present in this Sect. [101], the effect of spin-orbit coupling [102,103,104,105,106], and tilted cones [107]. Other works, moreover, have put their attention on investigating the effect of constant, external electric fields on the structure of Landau levels induced by magnetic fields [108], inducing modulations on the angular momentum transfer between light and graphene [109], or induce coherent population transfer [110]. This research field is still new and very active, and, although the overall effect of magnetic fields is seemingly clear, there is still ample room to engineer and control the interplay between artificial gauge fields and the various degrees of freedom of the impinging electromagnetic field, to create a comprehensive framework, that would allow a complete control of this phenomenon, and the possibility of utilising it for integrated photonic or spintronic devices.
In this section, we then briefly review how the nonlinear response of graphene is influenced, and can be therefore controlled, by the presence of artificial gauge fields, arising from smooth elastic deformations of the crystalline structure of graphene. In general, these deformations can naturally occur both in-plane and out-f-plane due to thermal fluctuations, which cause, for example, corrugations in freely suspended graphene [111] or the existence of intrinsic ripples [112]. Here, however, we are not interested in the intrinsic unflattened structure of graphene, but rather on the artificially induced strain and bending fields, coming from suitable engineering of monolayers graphene flakes. The application of strain, stress, or bending, in fact, can give rise to both Abelian artificial gauge fields, such as effective electric and magnetic fields [113,114,115] and non Abelian gauge fields [116]. Moreover, here we will only focus on one particular case of artificial gauge fields, namely those arising from bending of the graphene flake, which results in an equivalent constant, out-of-plane magnetic field, and we concentrate on a model first presented by Guinea and co-workers in Ref. [117]. For a deeper insight on the physics of artificial gauge fields in graphene, we then invite the interested reader to consult the excellent review by Vozmediano et al. [113].
8.1 The connection between strain and gauge fields
To start with, let us consider a modified tight-binding Hamiltonian for the electronic structure of graphene, where all nearest-neighbour bonds are all different, i.e., the hopping constants \(t_j\) are all different. In particular, we can make the so-called weakly deformed lattice approximation, where we assume that the atomic displacement \(\varvec{\xi }\) of the carbon atoms from the undeformed position \(\varvec{\xi }_0\) is small, compared to the lattice constant a. Under this approximation, one can write the change in the hopping parameter as a function of this deformation as
where \({\textbf {r}}_j\) are the nearest-neighbours vectors, and \(\beta =-\partial \ln \,t/\partial \ln a\,\simeq 2\) is the electron Grüneisen parameter [44]. If we repeat the calculations to derive the Dirac Hamiltonian in the low-energy approximation as done in Sect. 2.4, but with the inequivalent (deformed) hopping constants given by the relation above, we arrive at the following result
where the vector field \({\textbf {A}}^{(g)}\) is a U(1) gauge field, whose components are directly related to the deformation by [114, 118, 119]
where the second equality is derived from the continuum limit of Eq. (206), i.e.,
where \(\varvec{\xi }({\textbf {r}})\) is the elastic displacement field [120], and \(\xi _{\mu \nu }=\partial _{\mu }\xi _{\nu }+\partial _{\nu }\xi _{\mu }\). Notice that the artificial gauge potential \({\textbf {A}}^{(g)}\) described above, has the correct form to preserve time reversal symmetry for the whole graphene flake, even if this symmetry can be locally broken, i.e., in a single valley. Moreover, \({\textbf {A}}^{(g)}\) generates an effective magnetic field according to the standard Maxwell vector potential relation \({\textbf {B}}^{(g)}=\nabla \times {\textbf {A}}^{(g)}\). Since the artificial gauge field is time independent, no effective electric field is generated. However, in the case the displacement field \(\varvec{\xi }({\textbf {r}})\) obeys \(\xi _{xx}+\xi _{yy}\ne 0\), an extra scalar potential \(V({\textbf {r}})\propto (\xi _{xx}+\xi _{yy})\) emerges from the deformation. This contributions, however, can be easily gauged away by choosing a suitable gauge, where the scalar potential is set to zero, and only the vector potential appears [121].
Choosing different profiles for the components of the displacement field \(\varvec{\xi }({\textbf {r}})\) can therefore lead to different forms of magnetic fields, with different orientations. Moreover, if the components of the displacement fields depend nonlinearly on the components of the position vector \({\textbf {r}}\), they will generate a spatially dependent, rather than uniform, magnetic field. In this work, we limit ourselves to consider a particular kind of deformation, shown in Fig. 12, which consists in bending a rectangular flake of monolayer graphene. The bending is characterised by a radius of curvature R, and the correspondent components of the displacement field are given by
a Geometry of a bent flake of graphene of length \(L=192\) nm, and width \(W=200\) nm. The radii of curvature of the lower and upper edges are, respectively R and \(R'\), and are connected to the length L and width W of the flake by the relations \(R=5L=960\) nm, \(R'=R+W=1.16\) \(\upmu \)m. With these parameter values, taken from Ref. [117], the maximum achievable magnetic field in the central region of the flake is \(B=10\) T. b Flattened equivalent geometry of the bent graphene flake in a. The curvature induced by the bending is replaced with an artificial gauge field, which gives rise to an artificial, constant magnetic field directed out of plane, i.e., \({\textbf {B}}=B\hat{{\textbf {z}}}\). Notice that the width w and length \(\ell \) of the flattened flake might extend to infinity, without compromising the role of the artificial magnetic field in the interaction dynamics
so that the total artificial gauge field generated by such displacement field is given by
which, in turn, induces a constant out-of-plane magnetic field \({\textbf {B}}=\nabla \times {\textbf {A}}^{(g)}=B\hat{{\textbf {z}}}\). Notice that for the parameter set displayed in Fig. 12, a magnetic field amplitude of \(B=10\) T can be easily reached. In general, however, from the relation above we can immediately see how the magnetic field amplitude is inversely proportional to the bending radius R of the flake, i.e., the bigger R is, the smaller the correspondent artificial magnetic field will be in amplitude. Moreover, one should also take into account that introducing strain and bending in a flake of graphene also has the effect of shifting the position of the Dirac points (by an amount proportional to the magnitude of the artificial gauge field generated by the deformation), and also induces a global anisotropy of the Fermi velocity since, in general, \({\textbf {v}}_F=v_{F0}\left( {\textbf {I}}-\beta {\textbf {u}}+{\textbf {u}}\right) \), where \({\textbf {u}}\) is the strain tensor, connected to the displacement field \(\varvec{\xi }\) [122]. For the purpose of this review, however, we neglect both of these issues, as we assume that at the leading order in the bending radius R of the flake, their contribution to the nonlinear response of the graphene flake is negligible.
8.2 Electron dynamics in the presence of a magnetic field
Electron dynamics in graphene flakes in presence of artificial gauge fields can be studied either in k-space using the Hamiltonian described in Eq. (207), or, alternatively, in position space, by minimally coupling Dirac equation with the artificial gauge field, i.e., by replacing the spatial derivative \(\partial _{\mu }\) with the (artificial ) covariant derivative \(\partial _{\mu }+eA_{\mu }^{(g)}\), which gives the following evolution equation for electrons in bent graphene flakes
For the case of the bending profile of Fig. 12, for which \({\textbf {A}}^{(g)}=By\hat{{\textbf {x}}}\), the above equation reduces to a Landau problem in 1D [123], and its solution can be found analytically in terms of plane waves in the x direction and Landau oscillator states in the y direction, i.e.,
where \({\mathcal {N}}\) is a suitable normalisation constant, \(\eta =(y+L_m^2k)/L_m\) is the y coordinate scaled with respect to the magnetic length \(L_m=\sqrt{\hbar /eB}\), \({\mathcal {E}}_n=\text {Sign}(n)\hbar \omega _c\sqrt{|n|}\) are the Landau eigenvalues (with \(\omega _c=v_F/L_m\) being the cyclotron frequency of graphene), corresponding to the 1D harmonic oscillator eigenstates \(\phi _{|n|}(\eta )\). In the above equation, moreover, ± indicates the Landau states in the valence (−) and conduction (\(+\)) bands, respectively, and the condition \(\phi _{-1}(\eta )=0\) is implicitly assumed [44]. One important feature of the Landau problem in graphene is, that the spacing of the oscillator spectrum is not constant, but grows as \(\sqrt{|n|}\). This is in contrast to the relativistic case, where the spacing remains constant [123]. Moreover, in the case of graphene we get a set of oscillator states for each of the conduction and valence band, as shown pictorially in Fig. 13a. However, since in the absence of magnetic field the two bands possess a conical intersection (i.e., Dirac points), the two set of Landau oscillator states are not independent from each other, but share their ground state, which sits at zero energy, i.e., at the crossing point.
a Schematic depiction of the band structure of graphene in the vicinity of a Dirac point (red dot) in the presence of a magnetic field. Landau levels are generated both in the valence (green lines) and conduction (blue lines) bands, as well as at the Dirac point itself (red line). The energies of these Landau levels are the same in modulus in the two bands, but have opposite sign, namely positive energy states are located in the conduction band, while negative energy states in the valence band. The dashed lines represent the unperturbed structure of the Dirac cones, in absence of magnetic field. b Schematic representation of the selection rules induced by an incoming linearly polarised electromagnetic pulse
8.3 Interaction of electromagnetic pulses with bent graphene
We describe the interaction of an electromagnetic pulse impinging on bent graphene in the framework of the electric dipole interaction, as usual [44]. This allows us to add an extra term in Eq. (212) as follows
We can, without loss of generality, assume that the impinging electromagnetic pulse is linearly polarised along, say, the x-direction. The main consequence of this assumption is, that the polarisation of the impinging pulse will activate a subset of the allowed transitions between the Landau states in the vicinity of the Dirac points, as depicted in Fig. 13b. If we choose to work in the Landau gauge, i.e., we se the scalar potential to zero, we can write the vector potential for the impinging electromagnetic pulse as
where \(\omega _L\) is the carrier frequency of the pulse, and A(t) accounts for its temporal shape, which we assume Gaussian, i.e.,
where \(\tau \) is the time duration of the pulse, \(E_0\) the amplitude of the electric field of the impinging pulse, ant \(t_0\) is an arbitrary temporal reference. Hence, we can collect both the electromagnetic and the artificial gauge vector potential in a single expression, i.e., \({\textbf {A}}(t)=\left[ A(t)+By\right] \hat{{\textbf {x}}}\), and we can recast Eq. (214) in a more compact form using the scaled system of coordinates \(\{v_ft,x,y\}\), and introduce the 2D representation of the gamma matrices as \(\gamma ^0=\sigma ^z\), \(\gamma ^1=i\sigma ^y\), and \(\gamma ^2=-i\sigma ^x\), so that Eq. (214) becomes
which represents a Lorentz covariant, 2D Dirac equation. In this form, the Dirac equation for electrons in bent graphene can be solved by means of the method of the instantaneous eigenstates, as described in detail in Ref. [95]. To do that, however, we can first further simplify the expression above, with the aim of highlighting the Landau equation, and therefore its eigenstates and eigenvalues. To this aim, let us first apply the following phase transformation to the spinor wave function \(\psi (x,y,t)\), i.e.,
where
and the integration over k is reminiscent of a Fourier transform along the x-direction, for which the corresponding momentum still constitutes a good quantum number, since it is not affected by the presence of the artificial magnetic field (i.e., the artificial gauge field potential depends only upon the coordinate y and not upon x). Substituting the expression above into Eq. (217), after some simple algebra we obtain
which is the Landau eigenvalue problem, whose solution have been presented in the previous section in Eq. (213).
Notice, that to go from Eq. (217) to Eq. (220) the following matrix representation for the exponential operator \(\exp \left[ iF(t)\sigma _x\right] \) and its derivative might be useful:
and then use the fact that
to be able to collect the terms proportional to the vector potential.
If we then call \(\phi ^{\pm }_n(y,t;k)\) the Landau eigenstates solutions of Eq. (220), we can use this set of complete orthonormal states to represent the general time dependent solution of Eq. (217), namely
If we substitute this Ansatz into Eq. (217), we get a set of coupled mode equations for the time dependent coefficients \(a_n^{\pm }(t)\), that reads, up to an inessential normalisation constant, as follows
where
is the Rabi frequency, \(\Delta \omega _n^{\pm }=\omega _m\pm \omega _n\), with \(\hbar \omega _m=\hbar \omega _C\sqrt{|m|}\) being the eigenvalue associated to the Landau eigenstate \(\phi _m^{\pm }(y,t)\), and
is the dipole transition matrix element of graphene for the case of impinging linear (i.e., x-oriented) polarisation.
Equation (224) describe the interaction of an arbitrarily shaped, linearly polarised electromagnetic pulse with graphene, in the presence of a magnetic field. Notice, that to derive Eq. (224), no prior knowledge on the nature of the applied magnetic field is necessary. This means, that these equations are valid both in the case of an actual externally applied, or artificially generated (through bending or strain, or any other lattice deformation) magnetic field.
8.4 Magnetic field induced nonlinear dynamics in bent graphene
Now that we have developed a comprehensive framework to account for the action of a magnetic field on graphene electrons in the vicinity of Dirac points, we can investigate the consequences that a magnetic field has on the nonlinear response of graphene. To do so, we first consider a simplified version of the model derived above, where the impinging electromagnetic pulse is resonant with one specific transition between Landau levels. Without loss of generality, we choose this to be the transition between the levels \(n=0\) and \(n=\pm 1\) in Fig. 13, i.e., we choose \(\omega _L=\omega _1-\omega _0=\omega _0-\omega _{-1}=\omega _C\). Under this assumption, the model above simplifies considerably, since the interaction now only interests three levels, namely the common ground state at the Dirac point, and the first Landau level in both valence and conduction band (see Fig. 13b). Equation (224) then reduce to a simple 3-level system scheme, namely
where \({\textbf {a}}(t)=\left[ a_1^-(t)\,\,a_0(t)\,\,a_1^+(t)\right] ^T\) is a vector containing the expansion coefficients for the three level involved in the dynamics, and \(\Pi (t)=\Omega _R(t)\exp \left( -i\omega _Ct\right) \). To solve the above set of differential equations, we use the initial condition \(a_1^-(0)=1\), i.e., we assume a populated valence band and an unpopulated conduction band at the beginning of the interaction. Moreover, we model the impinging electromagnetic pulse as possessing a vector potential with Gaussian profile in time, with duration \(\tau \) and amplitude \(E_0\) and central frequency \(\omega _l=\omega _C\), so that the Rabi frequency can be written explicitly as
where \(t_0\) is an arbitrary time reference, that can be chosen conveniently. Notice, that the above expression of the Rabi frequency contains both the resonant, as well as the off-resonant terms, and therefore the correspondent solution to Eq. (224) is not sought within the rotating wave approximation framework. Equation (224) can be either solved analytically (once the explicit expression of the functions \(\Pi (t)\), i.e., of the impinging electromagnetic pulse, has been determined) or numerically with the help of standard solvers, such as Crank-Nicolson schemes [124]. Once Eq. (224) have been solved, we can reconstruct the time-dependent spinor wave function \(\psi (x,y,t)\) using Eqs. (223) and (218), and calculate the electron current induced by the impinging electromagnetic field, using the standard definition [123]
where \(\varvec{\sigma }=\left( \sigma ^x\,\,\sigma ^y\right) \) is a vector containing the Pauli matrices \(\sigma ^{x,y}\), for the \(\{x,y\}\)-component of the current, respectively.
Nonlinear signal \(I(\omega )\), as defined in Eq. (231), as a function of the normalised frequency \(\omega /\omega _C\), for the case of a bent flake of graphene, whose bending profile corresponds to an artificial magnetic field of amplitude \(B=10\) T. For this plot, we have assumed an impinging electromagnetic pulse with carrier frequency \(\omega _L=\omega _C=174\) THz, a duration of \(\tau =60\) fs, and an amplitude of \(E_0=10^7\) V/m. For the carrier velocity, we have used the standard value of the Fermi velocity of graphene, i.e., \(v_F=c/300\)
Notice, that formally the integration runs over the physical dimensions of the flake of bent graphene. However, we can exploit the bending-gauge field correspondence to transform the bent sheet of graphene into an unbent one immersed into a constant magnetic field, and can then extend the integration limits to infinity, since we are considering only the effect of magnetic field on bulk, rather than edge, states (see Fig. 12b). By doing so, the spatial integration implicitly accounts for orthogonality relationships between the various Landau eigenstates appearing in the definition of the time-dependent spinor wave function \(\psi (x,y,t)\), so that, at the end of the calculation, the current only depends on the time-dependent expansion coefficients \(a_n^{\pm }(t)\). For the case of the 3-level system described by Eq. (227), the explicit expression of the components of the current as a function of the expansion coefficients reads
Nonlinear signal corresponding to an impinging electromagnetic pulse of amplitude \(e_0=10^7\) V/m, and duration \(\tau =60\) fs, as a function of the magnitude of the artificial magnetic field deriving from a change in the flake bending, namely a \(B=2\) T, b \(B=10\) T, and c \(B=18\) T. For low values of the magnetic field, we observe a very high intensity around the 15th harmonic, which indicates efficient transfer of energy between the impinging field and its 15th harmonic. As the magnitude of the magnetic field grows, the extend of the harmonic spectrum shrinks, and more peaks acquire high-intensity, signifying the possibility to efficiently transfer energy from different harmonics of the impinging field. For these plots, \(\omega _L=\omega _C\) has been always assumed for each value of the magnetic field, and \(v_F=c/300\) has also be assumed, as in Fig. 14
Once we have the time-dependent current, the nonlinear response of the system can be calculated in terms of the nonlinear intensity [95]
where \({\textbf {J}}(\omega )\) is the (vector) Fourier transform of the time-dependent current \({\textbf {J}}(t)\) defined above. An example of nonlinear signal, resulting from the interaction of an ultrashort laser pulse with graphene, is given in Fig. 14, for the case of a 60 fs pulse impinging on the graphene flake. As it has been pointed out in Ref. [101], long pulses show a richer and complicated spectrum. From Fig. 14, in fact, we can see how the spectrum is quite broad, stretching to the 20th harmonic, and, most interestingly, it contains both even and odd harmonics. A detailed discussion about the effect of the pulse duration on the nonlinear response of grpahene in the presence of an artificial magnetic field can be found in Ref. [101].
If we now modify the bending profile of the flake, i.e., we change the radius of curvature of the bent flake, we can control the amplitude of the magnetic field, and, ultimately, the resonance frequency of the Landau system. If we assume to always work on resonance, i.e., we adapt the central frequency of the impinging pulse to the new cyclotron frequency every time we change the applied magnetic field, and we fix all the other parameters, i.e., pulse duration and amplitude, we can study how a change in the amplitude of the magnetic field affects the nonlinear signal generated by the bent flake of graphene. The results of this analysis are displayed in Fig. 15. As is can be seen, for low magnetic fields, i.e., \(B=2\) T [panel (a)], we observe a high conversion efficiency (high peak intensity) between the impinging frequency \(\omega _L=\omega _C\) and its 15th harmonic, corresponding to a wavelength of \(\lambda _{15}\simeq 720\) nm. For high magnetic fields, i.e. \(B=18T\) [panel (c)], instead, we observe the emergence of different high-harmonic peaks, corresponding, for the parameters chosen in Fig. 15 to the 5th, 7th, 10th, and 12th harmonic of the impinging field. This suggests the possibility to use the artificial magnetic field amplitude, i.e., the degree of bending of the flake, as a control knob, to tune the frequency conversion action of the flake itself, from high conversion to a single wavelength [panel(a)], to versatile source of visible-to-THz conversion of light [panel(c)].
9 Conclusions and outlook
In this Review, we provided a detailed treatment and comprehensive framework for studying the linear and nonlinear light–matter interactions in gapless graphene. To do so, we have introduced several different, and complementary, tools to describe, from a theoretical point of view, and with a numerical and computer simulation approach in mind, the physics of graphene and its interaction with light. First, in Sect. 2, we have discussed in detail the general machinery commonly used to derive the tight-binding graphene Hamiltonian from its lattice structure. This served as basis for the continuum model of electrons in the vicinity of Dirac cones, that, as shown in Sect. 3, reduces to a massless Dirac equation. With this at hand, we then presented a comprehensive model for the optical response of graphene, based on the dipole approximation, for both the linear and nonlinear case, as discussed in Sect. 4. For the latter case, in particular, we have constructed the so-called Dirac–Bloch equations (DBEs, see Sect. 6), an adaptation of the traditional Semiconductor Bloch equations (SBEs, see Sect. 5) applied to pseudo-relativistic, gapless electrons.
The real advantage of using the DBEs, in fact, is when the optical nonlinearity is considered. The source of the optical nonlinearity is already naturally present in the DBEs, in the time-dependent dynamical phase, that heavily affects the electron dynamics in graphene. The comparison between the prediction of the DBEs and the SBEs for the same parameters, given in Sect. 7, demonstrates how the traditional SBEs are mostly inapplicable for gapless 2D materials, where the absence of an energy gap does not fix a scale of energy for the system. In that situation, one must use the DBEs, since they are able to treat the dynamics of electrons in graphene non-perturbatively, a feature necessary when dealing with systems that do not possess a reference energy scale, such as gapless materials.
To complete the picture, we have also explored he novel nonlinear effects arising from deformed graphene sheets. The deformation is equivalent to applying a pseudo-magnetic field on the system, which in turn can be described by an artificial gauge field. This gauge field introduces Landau levels in the dispersion, leading to a plethora of new powerful nonlinearities that is able to dramatically modify the spectrum of the input pulse. This, together with a direct, time-domain method to describe electron dynamics in the presence of artificial gauge fields, based on instantaneous eigenstate decomposition of the electron wave function, has been presented in Sect. 8.
We hope that this Review will help researchers to approach the numerical simulation of graphene with a more structured mindset, and will also spark in the curiosity and interest of those readers, that are not actively working on this research topic.
To conclude, we would like to point out, that the methods presented here can be easily generalised to explore, for instance, relativistic 2D media with an energy gap. Moreover, in the spirit of open science and the creation of a collaborative environment for its advance, we have decided to open the essential DBEs code used in this Review. We, in fact, believe, that this will constitute an excellent starting point for anyone interested in setting up their own simulation code on 2D materials. Our code can be found at the following web address: https://www.dropbox.com/sh/gmio8x8wk0vu1r4/AABfnz7goh2lp_3dA9lofP5ra?dl=0.
Data Availability
The original data presented in this manuscript are available from the authors upon reasonable request. The data reproduced from other sources can be enquired from the authors of the original publication. The code used to simulate the nonlinear optical response of graphene is openly available online (see the manuscript).
References
K.S. Novoselov, A.K. Geim, S.V. Morozov, D. Jiang, Y. Zhang, S.V. Dubonos, I.V. Grigorieva, A.A. Firsov, Electric field effect in atomically test thin carbon films. Science 306(5696), 666–669 (2004). https://doi.org/10.1126/science.1102896
P.R. Wallace, The band theory of graphite. Phys. Rev. 71(9), 622 (1947)
L.D. Landau, Zur theorie der phasenumwandlungen ii. Phys. Z. Sowjetunion 11(545), 26–35 (1937)
R.E. Peierls, Quelques proprietes typiques des corpses solides. Ann. IH Poincare 5, 177–222 (1935)
N. David Mermin, Crystalline order in two dimensions. Phys. Rev. 176(1), 250 (1968)
A. Autere, H. Jussila, Y. Dai, Y. Wang, H. Lipsanen, Z. Sun, Nonlinear optics with 2D layered materials. Adv. Mat. 30, 1705963 (2018)
A.K. Geim, K.S. Novoselov, The rise of graphene. Nat. Mater. 6, 183 (2007)
A.H.C. Neto, F. Guinea, N.M.R. Peres, K.S. Novoselov, A.K. Geim, The electronic properties of graphene. Rev. Mod. Phys. 81(1), 109 (2009)
K.S. Novoselov, A.K. Geim, Two-dimensional gas of massless Dirac fermions in graphene. Nature 438, 197–200 (2005). https://doi.org/10.1038/nature04233
L. Wu, H.S. Chu, W.S. Koh, E.P. Li, Highly sensitive graphene biosensors based on surface plasmon resonance. Opt. Express 18(14), 14395–14400 (2010)
A. Avsar, T.-Y. Yang, S. Bae, J. Balakrishnan, F. Volmer, M. Jaiswal, Z. Yi, S.R. Ali, G. Guntherodt, B.H. Hong et al., Toward wafer scale fabrication of graphene based spin valve devices. Nano Lett. 11(6), 2363–2368 (2011)
C. Lee, X. Wei, J.W. Kysar, J. Hone, Measurement of the elastic properties and intrinsic strength of monolayer graphene. Science 321(5887), 385–388 (2008)
C.W.J. Beenakker, Colloquium: Andreev reflection and Klein tunneling in graphene. Rev. Mod. Phys. 80(4), 1337 (2008)
M.I. Katsnelson, Zitterbewegung, chirality, and minimal conductivity in graphene. Eur. Phys. J. B Condens. Matter Complex Syst. 51(2), 157–160 (2006)
S. Zhang, Topological states of quantum matter. Physics 1, 6 (2008)
C.L. Kane, E.J. Mele, Z 2 topological order and the quantum spin hall effect. Phys. Rev. Lett. 95(14), 146802 (2005)
Y. Zhang, Y.-W. Tan, H.L. Stormer, P. Kim, Experimental observation of the quantum hall effect and berry’s phase in graphene. Nature 438(7065), 201 (2005)
Y. Cao, V. Fatemi, S. Fang, K. Watanabe, T. Taniguchi, E. Kaxiras, P. Jarillo-Herrero, Unconventional superconductivity in magic-angle graphene superlattices. Nature 556(7699), 43 (2018)
S. Gupta, A. Saxena, Importance of topology in materials science, in The Role of Topology in Materials. (Springer, Berlin, 2018), pp.3–33
Z. Wang, Y. Sun, X.-Q. Chen, C. Franchini, X. Gang, H. Weng, X. Dai, Z. Fang, Dirac semimetal and topological phase transitions in a 3 bi (a= na, k, rb). Phys. Rev. B 85(19), 195320 (2012)
S. Borisenko, Q. Gibson, D. Evtushinsky, V. Zabolotnyy, B. Büchner, R.J. Cava, Experimental realization of a three-dimensional Dirac semimetal. Phys. Rev. Lett. 113(2), 027603 (2014)
A.A. Burkov, L. Balents, Weyl semimetal in a topological insulator multilayer. Phys. Rev. Lett. 107(12), 127205 (2011)
A.A. Soluyanov, D. Gresch, Z. Wang, W. Quan Sheng, M. Troyer, X. Dai, B. Andrei Bernevig, Type-ii Weyl semimetals. Nature 527(7579), 495 (2015)
H. Huang, S. Zhou, W. Duan, Type-ii Dirac fermions in the PTSE 2 class of transition metal dichalcogenides. Phys. Rev. B 94(12), 121117 (2016)
G.E. Volovik, K. Zhang, Lifshitz transitions, type-ii Dirac and Weyl fermions, event horizon and all that. J. Low Temp. Phys. 189(5–6), 276–299 (2017)
Y. Tamashevich, L. Di Mauro Villari, M. Ornigotti, Nonlinear optical response of type-II Weyl fermions in two dimensions. Phys. Rev. B 105, 195102 (2022)
F. Bonaccorso, Z. Sun, T. Hasan, A.C. Ferrari, Graphene photonics and optoelectronics. Nat. Photon. 4, 611–622 (2005). https://doi.org/10.1038/nphoton.2010.186
T. Mueller, F. Xia, P. Avouris, Graphene photodetectors for high-speed optical communications. Nat. Photon. 4, 297–301 (2010). https://doi.org/10.1038/nphoton.2010.40
M. Liu, X. Yin, E. Ulin-Avila, B. Geng, T. Zentgraf, L. Ju, F. Wang, X. Zhang, A graphene-based broadband optical modulator. Nature 474, 64–67 (2011). https://doi.org/10.1038/nature10067
A. Marini, I. Silveiro, F.J. Garcia de Abajo, Molecular sensing with tunable graphene plasmons. ACS Photon. 2, 876–882 (2015). https://doi.org/10.1021/acsphotonics.5b00067
M. Gullans, D.E. Chang, F.H.L. Koppens, F.J. Garcia de Abajo, M.D. Lukin, Single-photon nonlinear optics with graphene plasmons. Phys. Rev. Lett. 111, 247401 (2013). https://doi.org/10.1103/PhysRevLett.111.247401
D.A. Smirnova, I.V. Shadrivov, A.I. Smirnov, Y.S. Kivshar, Dissipative plasmon-solitons in multilayer graphene. Laser Photon. Rev. 8, 291–296 (2014). https://doi.org/10.1002/lpor.201300173
S.A. Mikhailov, Non-linear electromagnetic response of graphene. EPL (Europhys. Lett.) 79(2), 27002 (2007)
Q. Bao, H. Zhang, Y. Wang, Z. Ni, Y. Yan, Z.X. Shen, K.P. Loh, D.Y. Tang, Atomic-layer graphene as a saturable absorber for ultrafast pulsed lasers. Adv. Funct. Mater. 19, 3077–3083 (2009). https://doi.org/10.1002/adfm.200901007
Z. Sun, T. Hasan, F. Torrisi, D. Popa, G. Privitera, F. Wang, F. Bonaccorso, D.M. Basko, A.C. Ferrari, Graphene mode-locked ultrafast laser. ACS Nano 4, 803–810 (2010). https://doi.org/10.1021/nn901703e
N.M. Peres, Y.V. Bludov, J.E. Santos, A. Jauho, M.I. Vasilevskiy, Optical bistability of graphene in the terahertz range. Phys. Rev. B 90, 125425 (2014). https://doi.org/10.1103/PhysRevB.90.125425
S.A. Mikhailov, Quantum theory of third-harmonic generation in graphene. Phys. Rev. B 90, 241301 (2014). https://doi.org/10.1103/PhysRevB.90.241301
A. Manjavacas, F. Marchesin, S. Thongrattanasiri, P. Koval, P. Nordlander, D. Sanchez-Portal, F.J.G. de Abajo, Tunable molecular plasmons in polycyclic aromatic hydrocarbons. ACS Nano 7, 363 (2013)
J.D. Cox, F.J. Garcia de Abajo, Nonlinear graphene nanoplasmonics. Acc. Chem. Res. 59, 2536 (2019)
S.A. Mikhailov, Quantum theory of the third-order nonlinear electrodynamic effects of graphene. Phys. Rev. B 93, 085403 (2016)
J.-N. Fuchs, M.O. Goerbig, Introduction to the physical properties of graphene. Lect. Notes 10, 11–12 (2008)
P.A.M. Dirac, The Principles of Quantum Mechanics (Oxford University Press, Oxford, 1988)
P.A.M. Dirac, The quantum theory of the electron. Proc. R. Soc. Lond. A 117(778), 610–624 (1928)
M.I. Katsnelson, Graphene: Carbon in Two Dimensions (Cambridge University Press, Cambridge, 2013)
C. Kittel, Introduction to Solid State Physics (Wiley, New York, 1953)
J.P. Hobson, W.A. Nierenberg, The statistics of a two-dimensional, hexagonal net. Phys. Rev. 89(3), 662 (1953)
A. Wright, The electronic and optical properties of graphene
A. Zhou, W. Sheng, Van hove singularities in graphene nanoflakes. J. Appl. Phys. 112(9), 094313 (2012)
M.A.H. Vozmediano, Renormalization group aspects of graphene. Philos. Trans. R. Soc. Lond. A Math. Phys. Eng. Sci. 369(1946), 2625–2642 (2011)
S.L. McCall, E.L. Hahn, Self-induced transparency by pulsed coherent light. Phys. Rev. Lett. 18(21), 908 (1967)
R.W. Boyd, Nonlinear Optics (Academic Press, New York, 2003)
M. Lax, Symmetry Principles in Solid State and Molecular Physics (Dover, Mineola, 2001)
J.D. Jackson, Classical Electrodynamics (Wiley, New York, 1998)
J.A. Stratton, Electromagnetic Theory (Wiley, New York, 2007)
R. Loudon, The Quantum Theory of Light (Oxford University Press, Oxford, 2000)
C. Cohen-Tannoudji, J. Dupont-Roc, G. Grynberg, Photons and Atoms: An Introduction to Quantum Electrodynamics (Wiley, New York, 1997)
M. Born, E. Wolf, Principles of Optics: Electromagnetic Theory of Propagation, Interference and Diffraction of Light (Pergamon Press, Oxford, 1964)
Y.-R. Shen, The Principles of Nonlinear Optics (Wiley, New York, 1984), p.575
M.O. Scully, M. Suhail Zubairy, Quantum Optics (Cambridge University Press, Cambridge, 1997)
H. Haug, S.W. Koch, Quantum Theory of the Optical and Electronic Properties of Semiconductors, 5th edn. (World Scientific Publishing Company, Singapore, 2009)
W. Schäfer, M. Wegener, Semiconductor Optics and Transport Phenomena (Springer, Berlin, 2013)
I.F. Herbut, V. Mastropietro, Universal conductivity of graphene in the ultrarelativistic regime. Phys. Rev. B 87(20), 205445 (2013)
L.A. Falkovsky, Optical properties of graphene, in Journal of Physics: Conference Series, vol. 129, (IOP Publishing, Bristol, 2008), p.012004
K.F. Mak, M.Y. Sfeir, Y. Wu, C.H. Lui, J.A. Misewich, T.F. Heinz, Measurement of the optical conductivity of graphene. Phys. Rev. Lett. 101(19), 196405 (2008)
P.D. Drummond, M. Hillery, The Quantum Theory of Nonlinear Optics (Cambridge University Press, Cambridge, 2014)
R.R. Nair, P. Blake, A.N. Grigorenko, K.S. Novoselov, T.J. Booth, T. Stauber, N.M.R. Peres, A.K. Geim, Fine structure constant defines visual transparency of graphene. Science 320(5881), 1308–1308 (2008). https://doi.org/10.1126/science.1156965
L. Allen, J.H. Eberly, Optical Resonance and Two-Level Atoms, vol. 28 (Courier Corporation, North Chelmsford, 1975)
M.A. Nielsen, I.L. Chuang, Quantum Computation and Quantum Information (Cambridge University Press, Cambridge, 2010)
M. Lindberg, S.W. Koch, Effective Bloch equations for semiconductors. Phys. Rev. B 38, 3342–3350 (1988). https://doi.org/10.1103/PhysRevB.38.3342
A. Knorr, R. Binder, M. Lindberg, S.W. Koch, Theoretical study of resonant ultrashort-pulse propagation in semiconductors. Phys. Rev. A 46(11), 7179 (1992)
A. Girndt, A. Knorr, M. Hofmann, S.W. Koch, Theory of coherent phenomena in pump-probe excitation of semiconductor amplifiers. J. Appl. Phys. 78(5), 2946–2954 (1995)
C.M. Bowden, J.P. Dowling, Near-dipole-dipole effects in dense media: generalized Maxwell–Bloch equations. Phys. Rev. A 47(2), 1247 (1993)
C.M. Bowden, G.P. Agrawal, Maxwell–Bloch formulation for semiconductors: effects of coherent Coulomb exchange. Phys. Rev. A 51(5), 4132 (1995)
T. Östreich, A. Knorr, Various appearances of Rabi oscillations for 2\(\pi \)-pulse excitation in a semiconductor. Phys. Rev. B 48(24), 17811 (1993)
T. Östreich, A. Knorr, Nonperturbative scaling behavior of the coherent semiconductor Bloch equations in the low-density regime. Phys. Rev. B 50(8), 5717 (1994)
M.E. Crenshaw, M. Scalora, C.M. Bowden, Ultrafast intrinsic optical switching in a dense medium of two-level atoms. Phys. Rev. Lett. 68(7), 911 (1992)
B. Meziane, Instability hierarchies in self-pulsing lasers. Phys. Rev. A 48(3), 2346 (1993)
S. Hughes, A. Knorr, S.W. Koch, Interplay of optical dephasing and pulse propagation in semiconductors. JOSA B 14(4), 754–760 (1997)
E. Malic, A. Knorr, Graphene and Carbon Nanotubes (Wiley-VCH, New York, 2013)
J. Gruska, Quantum Computing, vol. 2005 (McGraw-Hill, London, 1999)
D. Leibfried, B. DeMarco, V. Meyer, D. Lucas, M. Barrett, J. Britton, W.M. Itano, B. Jelenković, C. Langer, T. Rosenband et al., Experimental demonstration of a robust, high-fidelity geometric two ion-qubit phase gate. Nature 422(6930), 412 (2003)
I.I. Rabi, Space quantization in a gyrating magnetic field. Phys. Rev. 51(8), 652 (1937)
F. Arecchi, R. Bonifacio, Theory of optical maser amplifiers. IEEE J. Quant. Electron. 1(4), 169–178 (1965)
H.-P. Breuer, F. Petruccione, The Theory of Open Quantum Systems (Oxford University Press on Demand, Oxford, 2002)
J. González, F. Guinea, M.A.H. Vozmediano, Electron-electron interactions in graphene sheets. Phys. Rev. B 63(13), 134421 (2001)
J. Hofmann, E. Barnes, S. das Sarma, Why does graphene behave as a weakly interacting system? Phys. Rev. Lett. 113, 105502 (2014). https://doi.org/10.1103/PhysRevLett.113.105502
V.N. Kotov, B. Uchoa, V.M. Pereira, F. Guinea, A.H. Castro Neto, Electron-electron interactions in graphene: current status and perspectives. Rev. Mod. Phys. 84(3), 1067 (2012)
D.C. Elias, R.V. Gorbachev, A.S. Mayorov, S.V. Morozov, A.A. Zhukov, P. Blake, L.A. Ponomarenko IV., K.S.N. Grigorieva, F. Guinea et al., Dirac cones reshaped by interaction effects in suspended graphene. Nat. Phys. 7(9), 701 (2011)
I. Gierz, M. Mitrano, J.C. Petersen, C. Cacho, I.C.E. Turcu, E. Springate, A. Stöhr, A. Köhler, U. Starke, A. Cavalleri, Population inversion in monolayer and bilayer graphene. J. Phys. Condens. Matter 27(16), 164204 (2015)
T. Winzer, E. Malic, The impact of pump fluence on carrier relaxation dynamics in optically excited graphene. J. Phys. Condens. Matter 25(5), 054201 (2013)
J.L. Cheng, N. Vermeulen, J.E. Sipe, Third-order nonlinearity of graphene: effects of phenomenological relaxation and finite temperature. Phys. Rev. B 91, 235320 (2015)
W.W. Chow, S.W. Koch, Semiconductor-Laser Fundamentals: Physics of the Gain Materials (Springer, Berlin, 2013)
F.W.J. Olver, D.W. Lozier, R.F. Boisvert, C.W. Clark, NIST Handbook of Mathematical Functions (Cambridge University Press, Cambridge, 2010)
I.S. Gradshteyn, I.M. Ryzhik, Table of Integrals, Series, and Products (Academic Press, New York, 2007)
K.L. Ishikawa, Nonlinear optical response of graphene in time domain. Phys. Rev. B 82, 201402 (2010). https://doi.org/10.1103/PhysRevB.82.201402
K.L. Ishikawa, Electronic response of graphene to an ultrashort intense terahertz radiation pulse. New J. Phys. 15(5), 055021 (2013)
E. Malic, T. Winzer, E. Bobkin, A. Knorr, Microscopic theory of absorption and ultrafast many-particle kinetics in graphene. Phys. Rev. B 84, 205406 (2011). https://doi.org/10.1103/PhysRevB.84.205406
T.O. Wehling, A.M. Black-Schaffer, A.V. Balatsky, Dirac materials. Adv. Phys. 63(1), 1–76 (2014). https://doi.org/10.1080/00018732.2014.927109
J.E. Sipe, E. Ghahramani, Nonlinear optical response of semiconductors in the independent-particle approximation. Phys. Rev. B 48(16), 11705 (1993)
X. Yao, A. Belyanin, Nonlinear optics of graphene in a strong magnetic field. J. Phys. Condens. Matter 25, 054203 (2013)
M. Ornigotti, L. Ornigotti, F. Biancalana, Generation of half-integer harmonics and efficient THz-to-visible frequency conversion in strained graphene. APL Photon. 6, 060801 (2021)
A. Nieminen, M. Ornigotti, Harmonic generation in bent graphene with artificially enhanced spin-orbit coupling. Phys. Rev. A 106, 043517 (2022)
A.H. Castro Neto, F. Guinea, Imputiry-induced spin-orbit coupling in graphene. Phys. Rev. Lett. 103, 026804 (2009)
D. Huertas-Hernando, F. Guinea, A. Brataas, Spin-orbit mediated spin relaxation in graphene. Phys. Rev. Lett. 103, 146801 (2009)
E.I. Rashba, Graphene with structure-induced spin-orbit coupling. Phys. Rev. B 79, 161409(R) (2009)
A. De Martino, A. Hütten, R. Egger, Landau levels, edge states, and strained magnetic waveguides in graphene monolayers with enhanced spin-orbit interaction. Phys. Rev. B 84, 155420 (2011)
Y. Tamashevich, L. Di Mauro Villari, M. Ornigotti, 2D Weyl materials in the presence of constant magnetic fields (2022). arXiv:2209.04295
V. Lukose, R. Shankar, G. Baskaran, Novel electric field effects on landau levels in graphene. Phys. Rev. Lett. 98, 116802 (2007)
A. Lòpez, A. Di Teodoro, J. Schliemann, B. Berche, B. Santos, Laser-induced modulation of the Landau level structure in single-layer graphene. Phys. Rev. B 92, 235411 (2015)
C. Ding, R. Yu, X. Hao, D. Zhang, Controllable population dynamics in Landau-quantized graphene. Sci. Rep. 8, 1530 (2018)
J.C. Meyer, A.K. Geim, M.I. Katsnelson, K.S. Novoselov, T.J. Booth, S. Roth, The structure of suspended graphene sheets. Nature 446, 60 (2007)
A. Fasolino, J.H. Los, M.I. Katsnelson, Intrinsic ripples in graphene. Nat. Mater. 6, 858 (2007)
M.A.H. Vozmediano, M.I. Katsnelson, F. Guinea, Gauge fields in graphene. Phys. Rep. 496, 109 (2010)
H. Suzuura, T. Ando, Phonons and electron-phonon scattering in carbon nanotubes. Phys. Rev. B 65, 235412 (2002)
J.L. Mañes, Symmetry-based approach to electron–phonon interactions in graphene. Phys. Rev. B 76, 045430 (2007)
S. Gopalakrishnan, P. Ghaemi, S. Ryu, Non-Abelian \(SU(2)\) gauge fields through density wave order and strain in graphene. Phys. Rev. B 86, 081403(R) (2012)
F. Guinea, A.K. Geim, M.I. Katsnelson, K.S. Novoselov, Generating quantizing pseudomagnetic fields by bending graphene ribbons. Phys. Rev. B 81, 035408 (2010)
M.I. Katsnelson, K. Novoselov, Graphene: new bridge between condensed matter physics and quantum electrodynamics. Solid State Commun. 143, 3 (2007)
K. Sasaki, Y. Kawazoe, R. Saito, Local energy gap in deformed carbon nanotubes. Progr. Theoret. Phys. 113, 463 (2005)
L.D. Landau, E.M. Lifshitz, Theory of Elasticity, 3rd edn. (Butterworth-Heinemann, Oxford, 1984)
J.A. Stratton, Electromagnetic Theory (Dover, Mineola, 2013)
M. Oliva-Leyva, G.G. Naumis, Anisotropic AC conductivity of strained graphene. J. Phys. Condens. Matter 26, 125302 (2014)
L.D. Landau, E.M. Lifshitz, Quantum Mechanics: Relativistic Theory, 3rd edn. (Butterworth-Heinemann, Oxford, 1984)
J. Crank, P. Nicolson, A practical method for numerical evaluation of solutions of partial differential equations of the heat-conduction type. Proc. Camb. Philos. Soc. 43, 50 (1947)
A. Iserles, A First Course in the Numerical Analysis of Differential Equations, (Cambridge Texts in Applied Mathematics, Series Number 44, 2009)
Acknowledgements
M. O. acknowledges support from the Academy of Finland Flagship Programme, Photonics Research and Innovation (PREIN), decision 320165. F. B. and D. N. C. acknowledge funding from the German Max Planck Society for the Advancement of Science (MPG), under the auspices of the International Max-Planck Partnership (IMPP) between MPG and the Scottish SUPA Universities.
Funding
M. O. acknowledges support from the Academy of Finland Flagship programme, Photonics Research and Innovation (decision 320165). F.B. was supported by the International Max-Planck Partnership between the Max Planck Society (Germany) and SUPA Scottish Universities.
Author information
Authors and Affiliations
Contributions
MO and FB discussed and implemented the structure of the review, wrote the manuscript and derived the extensive theoretical framework. DNC made some of the original figures, and performed many of the theoretical and numerical calculations. MO and FB supervised and assisted at every step of the manuscript. MO and FB contributed to proofreading the manuscript.
Corresponding author
Ethics declarations
Conflict of interest
The authors declare that they have no conflicts of interest
Appendices
Appendix A: Derivation of Eq. (151)
Let us start by recalling the definition of the Gauss hypergeometric function [93]
where \((\alpha )_{k}\) is the Pochhammer symbol, defined by [93]
For the case of resonant two-level systems, \(\delta _{\tilde{{\textbf{k}}}}=0\) (which means \(s=1/2\)) and Eq. (150) reduces to
By recalling that \((1)_{k} = k!\), the computation of the remaining Pochhammer symbols yields:
and the series converges to
where \(\text {Erf}(x)\) is the error function [93]. Substituting this result into Eq. (A3) gives Eq. (151).
Appendix B: Derivation of Eq. (152)
Let us start by reqriting the expression of the Gauss hypergeometric function appearing in Eq. (150) in terms of the definition of the Gauss hypergeometric function given by Eq. (A1), i.e.,
The Pochhammer symbols in the equation above can be computed exactly as:
With this result, the series in Eq. (B1) sums to the Hurwitz–Lerch \(\Phi \) Transcendental [93], i.e.,
where the Hurwitz–Lerch \(\Phi \) Transcendental is defined as:
The next step is to use the following integral identity [94], to express the Hurwitz–Lerch \(\Phi \) Transcendental in terms of less esoteric functions
valid as long as \(t < 0\), \(\text {Re}(s)>0\), \(\text {Re}(a)>0\) and \(z \in {\mathbb {C}} {\backslash } [1, \infty )\). In our case, this integral identity allows us to rewrite Eq. (B3) in terms of the incomplete Beta function as follows
where the incomplete Beta function is:
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Ornigotti, M., Carvalho, D.N. & Biancalana, F. Nonlinear optics in graphene: theoretical background and recent advances. Riv. Nuovo Cim. 46, 295–380 (2023). https://doi.org/10.1007/s40766-023-00043-8
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s40766-023-00043-8