Introduction

In recent decades, multi-robot system (MRS) has received significant attention due to the accuracy and repeatability of robots [1]. The system with many robots to complete a common task in the same environment by communicating with each other is called MRS. Compared with single-robot system, MRS has many advantages. For example, MRS performs the task in a distributed manner, and enhances the robustness and fault tolerance of the system. Therefore, MRS has been applied to many engineering problems, such as formation control [2, 3], cooperative transportation [4, 5] and cooperative manufacture [6, 7].

In particular, the cooperative transportation is an important research topic in MRS. The control schemes of the cooperative transportation can be divided into centralized control [8,9,10,11,12,13,14,15,16,17,18] and distributed control [19, 20]. For the former, some results have been reported. In three-dimensional space, the cooperative transportation of large objects by multiple mobile robots was investigated, and a motion planning method was designed [8]. In [9], the shared manipulation of loads between human and robotic agents was considered by devising an adaptive controller. The minimum energy problem was studied in [10] and extended to systems with perturbation constraints. An optimization-based controller was proposed in [12], which solved the cooperative transportation problem by using the hierarchical quadratic programming method. An efficient iterative learning control method based on continuous projection was proposed in [13] for repetitive systems with randomly varying trial lengths. In [14], a control algorithm without utilizing force/torque sensors was applied to multiple mobile manipulators dealing with the coordinated motion of a single object. For the problem of sparse fault samples and cross-domain between data sets in real industrial environment, [16] developed a fault diagnosis method with few samples based on parameter optimization and feature metric. A symmetry position/force hybrid control framework was designed in [17], which realized the cooperative transportation of multiple humanoid robots. Although centralized architecture can control MRS, it requires a powerful master center to control all robots. Meanwhile, the whole system will collapse if the control center fails. In addition, in contrast to [10, 13, 18], which used the control approach, this paper considers the cooperative transport problem from the optimization perspective.

Distributed optimization algorithm (DOA) only require local communication and computation to solve optimization problems compared to centralized optimization algorithm. In addition, DOA has the advantages of privacy protection, faster computational speed and stronger robustness [21,22,23,24,25,26,27]. Accordingly, DOA based on mathematical programming, network communication and multi-agent control has a broad development prospecting real applications, such as deep learning [27, 28], economic dispatch [23, 29], and MRS [22, 30]. For instance, [31] discussed the distributional estimation of inertial parameters of unknown loads manipulated, and developed a distributed method for solving the kinematics and inertial parameters of unknown rigid bodies. The issue of network control for loosely connected cooperative robots was studied in [32], and a distributed architecture was proposed to allow robots to complete complex operational tasks with locally available information. In [33], the distributed control problem of multiple redundant mobile manipulators was studied by designing a distributed proximal gradient algorithm. Wu et al. [34] investigated distributed cooperative control problem for redundant mobile robots, and designed a new formation control scheme based on constraint optimization. In [35], the distributed coordination for mobile network robots with joint delay was considered by using the dynamical decoupling method. A fully distributed cooperative scheme for mobile network robots was studied in [36], in which an adaptive estimator was used for each robot to observe the desired local trajectory of the cooperative transportation. However, few scholars have considered cooperative transportation from the perspective of optimization. Besides, the virtual leader, the DOA with a fixed step size, and the rotation variable of the object are three important factors that affect the realization of the cooperative transportation. This is the main motivation of this paper.

In this paper, a discrete-time DOA with a fixed step size is utilized to optimize the total energy consumption of the MRS and manipulability of redundant manipulators. The main contributions are summarized in the following points:

  1. 1.

    A discrete-time DOA with a fixed step size is developed in the cooperative transportation, which is accessible to implement and has higher accuracy compared with the continuous-time algorithms [4, 14, 33, 35];

  2. 2.

    Compared with [33], a rotation variable is considered, resulting in the mobile manipulator’s joint angular and linear velocities changing more smoothly;

  3. 3.

    The actual leader transport strategy was used in [14, 15, 33], which required high communication bandwidth for the leader. At the same time, once the leader fails, the cooperative transportation fails too. This paper uses a virtual leader strategy, which does not lead failure for the leader and has strong applicability.

The remainder of the paper is organized as follows. “Preliminaries” includes some preliminaries. The model is introduced in “Problem statement”. In “Algorithm design and analysis”, a discrete-time DOA is put forward to tackle the cooperative transportation problem, and the algorithm is analyzed. The simulation and experiment are presented in “Simulation and experiment”. Finally, “Conclusions” concludes the paper.

Notations: We use \(\textrm{vec}\) to mean matrix vec operator. \(\otimes \) represents Kronecker product. \(I_{n}\) denotes the n-dimensional real identity matrix. \(\textbf{1}_{n}\), \(\textbf{0}_{n}\), and \(\textbf{O}_{n\times n}\) represent the n-dimensional column vector with entries 1, the n-dimensional column vector with entries 1, and the \(n\times n\)-dimensional zero matrix, respectively. \(\textrm{rank}(A)\) represents the rank of matrix A. \(\Vert \cdot \Vert \) represents the vector 2-norm and the induced matrix 2-norm. \(\textrm{diag}\{m_{1},m_{2},\ldots ,m_{N}\}\) denotes a diagonal matrix with diagonal elements \(m_{1},m_{2},\ldots ,m_{N}\). \(\textrm{blkdiag}\{M_{1},M_{2},\ldots ,M_{N}\}\) denotes a block diagonal matrix with matrices \(M_{1},M_{2},\ldots ,M_{N}\).

Preliminaries

In this section, some necessary descriptions about redundant mobile manipulators and projection operators are introduced.

Kinematics and manipulability of redundant mobile manipulators

A single mobile manipulator consists of a four-link manipulator and a wheeled mobile platform being shown schematically in Fig. 1. Assuming that there is no slip between the two wheels and that the end-effector can hold the object securely.

Fig. 1
figure 1

Model for one mobile manipulator

Full size image

The variables in Fig. 1 are explained as follows:

\((x_{r},y_{r},z_{r})\): position of the mobile platform,

\((x_{j},y_{j},z_{j})\): position of jth joint,

\(\vartheta _{j}\): angle of jth joint,

\(l_{j}\): length of jth joint,

\(b_{w}\): length between two wheels,

r: radius of the wheel.

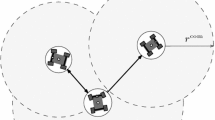
We consider the multiple redundant mobile manipulators in Fig. 2. Each manipulator arm consists of m joints, and the positions of the joints in joint space are denoted by \(\vartheta =(\vartheta _{1},\vartheta _{2},\ldots ,\vartheta _{m})^\mathrm{{T}}\in \mathbb {R}^{m}\). Combining the positions of mobile platform \(r\in \mathbb {R}^{k}\) (\(m>k\)) and \(\vartheta (t)\), the coordinate of the end-effector can be derived as

$$\begin{aligned} x(t)=r(t)+h(\vartheta (t)), \end{aligned}$$
(1)

in which \(h(\cdot )\) denotes the continuous nonlinear map from joint space to working space. Taking the time derivative on both sides of (1) results in \(v(t)=\dot{r}(t)+\mathcal {J}(\vartheta (t))\omega (t)\), where \(v(t)=\dot{x}(t)\in \mathbb {R}^{k}\) means the velocity of the end-effector, \(\omega (t)=\dot{\vartheta }(t)\in \mathbb {R}^{m}\) signifies the joint angular velocity, and \(\mathcal {J}(\vartheta (t))=\partial h/\partial \vartheta \in \mathbb {R}^{k\times m}\) represents the Jacobian matrix of \(h(\cdot )\), which is denoted as \(\mathcal {J}\) for simplicity.

Fig. 2
figure 2

The cooperative transportation of three mobile manipulators

Full size image

From [37], the manipulability of robot arm is represented by \(\mu (\vartheta )=\sqrt{\det (\mathcal {J}(\vartheta )\mathcal {J}(\vartheta )^\mathrm{{T}})}\), and \(\mu (\vartheta )\leqslant 1\). Moreover, \(\textrm{rank}(\mathcal {J})<m\) and \(\mu (\vartheta )=0\) if the manipulator is singular.

Rotation of transported object

Let \(\theta \) and \(\dot{\theta }\) denote the rotation angle and rotation angular velocity of transportation object respectively. Then, the rotation matrix is

$$\begin{aligned} R(\theta )=\left( \begin{array}{ccc} \cos \theta \quad &{} ~-\!\sin \theta \quad &{} ~~0\\ \sin \theta \quad &{} ~~~\cos \theta \quad &{} ~~0\\ 0 \quad &{} ~~~ 0 \quad &{} ~~1\\ \end{array} \right) . \end{aligned}$$

We define \(d_{i}=(d_{i1},d_{i2},0)^\mathrm{{T}}\) as the vector from the object centroid to the contact point of the ith manipulator. \(\phi _{i}(\theta )\) represents the coordinate of \(d_{i}\) after the object rotated with angle \(\theta \),

$$\begin{aligned} \phi _{i}(\theta )&=R(\theta )d_{i},~ \dot{\phi }_{i}(\theta )=\dot{\theta }\left( \begin{array}{ccc} -\!\sin \theta \quad &{} ~-\!\cos \theta \quad &{} ~~0\\ ~\cos \theta \quad &{} ~-\!\sin \theta \quad &{} ~~0\\ ~0 \quad &{} ~~0 \quad &{}~~0\\ \end{array} \right) d_{i}. \end{aligned}$$

Linearizing the items of the rotation matrix at the origin, we get

$$\begin{aligned} \phi _{i}(\theta )&=\frac{1}{1+\theta ^{2}}\left( \begin{array}{ccc} 1 \quad &{} ~-\!\theta \quad &{} ~~0\\ \theta \quad &{}~~1 \quad &{} ~~0\\ 0 \quad &{} ~~0 \quad &{}~~1\\ \end{array} \right) d_{i} \\&=\frac{1}{1+\theta ^{2}}\left( \begin{array}{ccc} d_{i1}-\theta d_{i2}\\ d_{i2}+\theta d_{i1}\\ 0\\ \end{array} \right) \triangleq \frac{1}{1+\theta ^{2}}(d_{i}+\theta \tilde{d}_{i}), \end{aligned}$$
$$\begin{aligned} \dot{\phi }_{i}(\theta )&=-\dot{\theta } \left( \begin{array}{ccc} -\!\theta \quad &{} ~-\!1 \quad &{} ~~0\\ ~1 \quad &{}~-\!\theta \quad &{} ~~0\\ ~0 \quad &{} ~~~0 \quad &{}~~0\\ \end{array} \right) d_{i} =\dot{\theta }\left( \begin{array}{ccc} -\theta d_{i1}-d_{i2}\\ -\theta d_{i2}+d_{i1}\\ 0\\ \end{array} \right) \\&\triangleq \dot{\theta }(\tilde{d}_{i}-\theta d_{i}), \end{aligned}$$

where \(\tilde{d}_{i}=(-d_{i2},d_{i1},0)^\mathrm{{T}}\) indicates the coordinates after \(d_{i}\) contrarotated \(\pi /2\) \((i\in \{1,2,\ldots ,n\})\).

Projection operator

Define the projection operator g: \(\mathbb {R}^{n}\rightarrow \varOmega \) as follows

$$\begin{aligned} g(a)=\mathrm {arg~min}_{b\in \varOmega }\Vert a-b\Vert , \end{aligned}$$

where \(\varOmega \subseteq \mathbb {R}^{n}\) is closed and convex, and \(a,b\in \mathbb {R}^{n}\).

Problem statement

In this paper, the center of the transported object is defined as the virtual leader. Denote \(v_{0}\) and \(x_{0}\) as the velocity and position of the virtual leader respectively, and assign the rotation angular velocity \(\dot{\theta }\) as \(\gamma _{1}, \gamma _{2},\dots ,\gamma _{n}\). We consider the following optimization problem regarding the cooperative transportation

$$\begin{aligned} \min _{\omega _{i},\beta _{i},\gamma _{i}}&\sum _{i=1}^{n}\left( \frac{1}{2}c_{i1}\Vert \omega _{i}\Vert ^{2}+\frac{1}{2}c_{i2} \Vert \beta _{i}\Vert ^{2}+\frac{1}{2}c_{i3}\gamma _{i}^{2}-c_{i4}\omega _{i}^\mathrm{{T}}\varXi _{i}\right) , \end{aligned}$$
(2a)
$$\begin{aligned} s.t. \quad&v_{i}=\frac{1}{\sum \limits _{j\in N_{i}}a_{ij}}\sum _{j\in N_{i}}a_{ij}\nonumber \\&\quad \quad \bigg [v_{j}-\bigg (\bigg (x_{i}-\frac{1}{1+\theta ^{2}}(d_{i}+\theta \tilde{d}_{i}) +(-\tilde{d}_{i}+\theta d_{i})\gamma _{i}\bigg )\nonumber \\&\quad \quad -\bigg (x_{j}-\frac{1}{1+\theta ^{2}}(d_{j}+\theta \tilde{d}_{j})+(-\tilde{d}_{j} +\theta d_{j})\gamma _{j}\bigg )\bigg )\bigg ], \end{aligned}$$
(2b)
$$\begin{aligned}&\beta _{i}=v_{i}-\mathcal {J}_{i}\omega _{i}, \end{aligned}$$
(2c)
$$\begin{aligned}&\gamma _{1}=\gamma _{2}=\cdots =\gamma _{n}, \end{aligned}$$
(2d)
$$\begin{aligned}&\omega _{i}\in \varOmega _{i}^{1},~\beta _{i}\in \varOmega _{i}^{2},~\gamma _{i}\in \varOmega ^{3}, \quad i=1,2,...,n, \end{aligned}$$
(2e)

where \(c_{i1},c_{i2},c_{i3}\) and \(c_{i4}\) are weighting factors, \(\theta \in \mathbb {R}\) is the rotation angle of moving object, \(v_{i}\in \mathbb {R}^{k}\) denotes the velocity of end-effector, \(\beta _{i}\in \mathbb {R}^{k}\) signifies the velocity of mobile platform, \(\omega _{i}\in \mathbb {R}^{m}\) represents the joint angular velocity, \(\gamma _{i}\in \mathbb {R}\) means the rotation angular velocity of moving object, and n denotes the number of robots. In addition, \(N_{i}\) is a set of subscripts of robots that communicate with robot \(r_{i}\). \(\varXi _{i}=\nabla _{\vartheta _{i}}\mu _{i}/|\nabla _{\vartheta _{i}}\mu _{i}|\) means the unit gradient of manipulability with \(K_{im}=\partial \mathcal {J}_{i}/\partial \vartheta _{i}^{m}\),

$$\begin{aligned} {\varXi _{i}=\frac{\sqrt{\det (\mathcal {J}_{i}\mathcal {J}_{i}^\mathrm{{T}})}(\mathcal {J}_{i}\diamond \{K_{i1},K_{i2},\ldots ,K_{im}\})\textrm{vec}((\mathcal {J}_{i}\mathcal {J}_{i}^\mathrm{{T}})^{-1})}{|\sqrt{ \det (\mathcal {J}_{i}\mathcal {J}_{i}^\mathrm{{T}})}(\mathcal {J}_{i}\diamond \{K_{i1},K_{i2},\ldots ,K_{im}\}) \textrm{vec}((\mathcal {J}_{i}\mathcal {J}_{i}^\mathrm{{T}})^{-1})|}}, \end{aligned}$$

and \(\mathcal {J}_{i}\diamond \{K_{i1},K_{i2},\ldots ,K_{im}\}=[\textrm{vec}(\mathcal {J}_{i}K_{i1}), \textrm{vec}(\mathcal {J}_{i}K_{i2}), \ldots ,\textrm{vec}(\mathcal {J}_{i}K_{im})]\) (refer to [38] for more details). Define \(\varOmega _{i}^{1}\), \(\varOmega _{i}^{2}\) and \(\varOmega ^{3}\) as the range of the allowed joint angular velocity, velocity of mobile platform and rotation angular velocity of moving object, respectively. The adjacency matrix \(\mathcal {A}_{n}\in \mathbb {R}^{n\times n}\) with nonnegative entry \(a_{ij}>0\) when \(j\in N_{i}\), and \(a_{ij}=0\) otherwise.

According to the inverse kinematics of manipulators, the redundancy of manipulators allows unbounded solutions for the joint angular velocity \(\omega _{i}\). Therefore, the redundant degrees of freedom can optimize the energy of MRS and the manipulability of manipulators, reducing energy dissipation and avoiding configuration singularity.

Remark 1

During cooperative transport, the energy dissipation of the mobile manipulators may be much large and the mobile manipulators may have configuration singularity. Therefore, we optimize the system energy and manipulability of redundant manipulators during the modeling process to reduce the energy cost and avoid the configuration singularity. In addition, the constraint (2b) in the optimization problem (2) makes the robot system achieve trajectory tracking and cooperative consistency.

Remark 2

In [33], the optimization problem is constructed by optimizing the system energy and manipulability. Then, a continuous-time distributed optimization algorithm is proposed based on the leader-follower strategy. However, compared to [33], this paper has some advantages. First, by introducing rotation variable into the optimization problem, the joint angular velocity of manipulator and the velocity of moving platform change more smoothly. Second, the stability of MRS is improved by using the virtual leader strategy. Third, the proposed discrete-time distributed optimization algorithm is easier to implement and has higher accuracy.

Next, we introduce a lemma derived from (2b).

Lemma 1

If the undirected graph \(\mathcal {G}_{n}\) is connected, it follows from (2b) that \(v_{i}+(-\tilde{d}_{i}+\theta d_{i})\gamma _{i}+x_{i}-(1/(1+\theta ^{2}))(d_{i}+\theta \tilde{d}_{i}) =v_{0}+x_{0}\) for \(i\in \{1,2,\ldots ,n\}\).

Proof

Denote \(L_{n}=[l_{ij}]_{n\times n}\) as the Laplacian matrix of \(\mathcal {G}_{n}\) with \(l_{ij}\) being given by

$$\begin{aligned} l_{ij}=\left\{ \begin{array}{l} \sum \limits _{t\in N_{i}}a_{it},\quad \textrm{if}~i=j,\\ -a_{ij},~\quad \quad \, \textrm{if}~i\ne j. \end{array}\right. \end{aligned}$$

Define

$$\begin{aligned}{} & {} v= \left( \begin{array}{ccc} v_{1}\\ v_{2}\\ \vdots \\ v_{n}\\ \end{array} \right) ,~ x= \left( \begin{array}{ccc} x_{1}\\ x_{2}\\ \vdots \\ x_{n}\\ \end{array} \right) ,~ \gamma = \left( \begin{array}{ccc} \gamma _{1}\\ \gamma _{2}\\ \vdots \\ \gamma _{n}\\ \end{array} \right) ,\\{} & {} \phi (\theta )=\left( \begin{array}{ccc} \frac{1}{1+\theta ^{2}}(d_{1}+\theta \tilde{d}_{1})\\ \frac{1}{1+\theta ^{2}}(d_{2}+\theta \tilde{d}_{2})\\ \vdots \\ \frac{1}{1+\theta ^{2}}(d_{n}+\theta \tilde{d}_{n})\\ \end{array}\right) , \end{aligned}$$

\(D=\textrm{diag}\{-\tilde{d}_{1}+\theta d_{1},-\tilde{d}_{2}+\theta d_{2},...,-\tilde{d}_{n}+\theta d_{n}\}\in \mathbb {R}^{kn\times n}\), \(\bar{L}_{n}=L_{n}+\textrm{diag}\{b\}\in \mathbb {R}^{n\times n}\), where \(b=(b_{1},b_{2},...,b_{n})^\mathrm{{T}}\), \(b_{i}>0\) if virtual leader \(r_{0}\) connected with robot \(r_{i}\), and \(b_{i}=0\) otherwise. Then, (2b) is compactly expressed as:

$$\begin{aligned} (\bar{L}_{n}\otimes I_{k})(v+x-\phi (\theta )+D\gamma )=(b\otimes I_{k})(x_{0}+v_{0}), \nonumber \\ \end{aligned}$$
(3)

which can be converted into

$$\begin{aligned} \left( (-b,\bar{L}_{n})\otimes I_{k}\right) \left( \begin{array}{ccc} x_{0}+v_{0}\\ v+x-\phi (\theta )+D\gamma \end{array} \right) =0. \end{aligned}$$

Since \(\mathcal {G}_{n}\) is connected, one has \(\textrm{rank}((-b,\bar{L}_{n}))=n\), which means that 0 is an eigenvalue of \((-b,\bar{L}_{n})\) and the corresponding eigenvector is \(\textbf{1}_{n+1}\). Therefore, from (2b) it implies that \(v_{i}+(-\tilde{d}_{i}+\theta d_{i})\gamma _{i}+x_{i}-(1/(1+\theta ^{2}))(d_{i}+\theta \tilde{d}_{i}) =v_{0}+x_{0}\) for \(i=1,2,\ldots ,n\). \(\square \)

Inspired by the work in [33], we have the following proposition.

Proposition 1

If \(\mathcal {G}_{n}\) is connected, the solution of problem (2) can track the desired trajectory.

Proof

The tracking error of i-th mobile manipulator can be defined as

$$\begin{aligned} e_{i}=\left( x_{i}-\frac{1}{1+\theta ^{2}}(d_{i}+\theta \tilde{d}_{i})\right) -x_{0},~ i\in \{1,2,\ldots ,n\}.\nonumber \\ \end{aligned}$$
(4)

Taking derivative to both sides of (4), we have

$$\begin{aligned} \dot{e}_{i}=v_{i}+(-\tilde{d}_{i}+\theta d_{i})\gamma _{i}-v_{0}. \end{aligned}$$
(5)

Based on Karush−Kuhn−Tucker (KKT) condition [39] and Lemma 1, it holds from (2b) that

$$\begin{aligned}&\,v_{i}+(-\tilde{d}_{i}+\theta d_{i})\gamma _{i}-v_{0}\nonumber \\&\quad -\left( x_{i}-\left( 1/\left( 1+\theta ^{2}\right) \right) \left( d_{i}+\theta \tilde{d}_{i}\right) -x_{0}\right) . \end{aligned}$$
(6)

Combining (4)–(6), it can be acquired that

$$\begin{aligned} \dot{e}_{i}(t)=-e_{i}(t). \end{aligned}$$
(7)

By direct calculation from (7), one has

$$\begin{aligned} e_{i}(t)=e_{i}(0)e^{-t}. \end{aligned}$$

Obviously, \(\lim _{t\rightarrow \infty }e_{i}(t)\rightarrow \textbf{0}_{k}\) and the solution of problem (2) can track the desired trajectory. \(\square \)

Algorithm design and analysis

Based on Proposition 1, we know that the cooperative transportation problem (2) is reasonable. Next, a discrete-time DOA is given to solve problem (2), and the convergence of the proposed algorithm is analyzed.

Algorithm design

In this subsection, a DOA is designed to solve the optimization problem (2). Next, the compact form of problem (2) is given by

$$\begin{aligned} \begin{aligned} \min _{q}\quad&\sum _{i=1}^{n}f_{i}(q_{i}),\\ s.t. \quad&L(v+D\gamma +x-\phi (\theta ))=\varsigma , Aq=v,L_{n}\gamma =0,q\in \varOmega , \end{aligned}\nonumber \\ \end{aligned}$$
(8)

where \(q=(q_{1}^\mathrm{{T}},q_{2}^\mathrm{{T}},\ldots ,q_{n}^\mathrm{{T}})^\mathrm{{T}}\in \mathbb {R}^{n(k+m+1)}\) with \(q_{i}=(\omega _{i},\beta _{i},\gamma _{i})\), \(A=\textrm{blkdiag}\{A_{1},A_{2},\ldots ,A_{n}\}\in \mathbb {R}^{kn\times n(k+m+1)}\) with \(A_{i}=(\mathcal {J}_{i},I_{k},\textbf{0}_{k})\), \(\varOmega =\prod _{i=1}^{n}\varOmega _{i}\) with \(\varOmega _{i}=\varOmega _{i}^{1}\times \varOmega _{i}^{2}\times \varOmega ^{3}\), \(\varsigma =(b\otimes I_{k})(x_{0}+v_{0})\in \mathbb {R}^{kn}\), \(L=\bar{L}\otimes I_{k}\in \mathbb {R}^{kn\times kn}\), and \(f_{i}(q_{i})=(c_{i1}\Vert \omega _{i}\Vert ^{2}+c_{i2}\Vert \beta _{i}\Vert ^{2}+c_{i3}\gamma _{i}^{2})/2 -c_{i4}\omega _{i}^\mathrm{{T}}\varXi _{i}\) is convex.

Furthermore, problem (8) is written as

$$\begin{aligned} \begin{aligned} \min _{q}\quad&\sum _{i=1}^{n}f_{i}(q_{i}),\\ s.t. \quad&Aq=v,~LBq=\xi ,~L_{n}Cq=\textbf{0}_{n},~q\in \varOmega , \end{aligned} \end{aligned}$$
(9)

where \(B=\textrm{blkdiag}\{B_{1},B_{2},\ldots ,B_{n}\}\) with \(B_{i}=(\textbf{O}_{k\times m}, \textbf{O}_{k\times k},-\tilde{d}_{i}+\theta d_{i})\), \(C=\textrm{blkdiag}\{C_{1},C_{2},\ldots , C_{n}\}\) with \(C_{i}=(\textbf{0}^\mathrm{{T}}_{m},\textbf{0}^\mathrm{{T}}_{k},1)\), and \(\xi =\varsigma -L(v+x-\phi (\theta ))\).

Lemma 2

[40] \(q^{*}\in \mathbb {R}^{n(k+m+1)}\) is an optimal solution of (9) if and only if there exist \(\rho \in \mathbb {R}^{kn\times n(k+m+1)}\), \(\mu \in \mathbb {R}^{kn}\) and \(\eta \in \mathbb {R}^{n}\) such that

$$\begin{aligned} \left\{ \begin{aligned} q^{*}=&\,(q^{*}-\delta (\nabla F(q^{*})+A^\mathrm{{T}}\rho ^{*}+(LB)^\mathrm{{T}}\mu ^{*}\\&+(L_{n}C)^\mathrm{{T}}\eta ^{*})),\\ Aq^{*}=&\,v,~LBq^{*}=\xi ,~L_{n}Cq^{*}=\textbf{0}_{n}, \end{aligned}\right. \end{aligned}$$
(10)

where \(F=\sum _{i=1}^{n}f_{i}\), \(g:\mathbb {R}^{n(k+m+1)}\rightarrow \varOmega \) is the projection operator, and \(\delta >0\) is a constant.

To solve problem (9), we develop the following DOA on the basis of (10)

$$\begin{aligned} \left\{ \begin{aligned} q(s+1)=&\,g(q(s)-\delta (\nabla F(q(s))+A^\mathrm{{T}}(\rho (s)\\&+Aq(s)-v)+B^\mathrm{{T}}(\mu (s)\\&+LBq(s)-\xi )+C^\mathrm{{T}}(\eta (s)+L_{n}Cq(s)))),\\ \rho (s+1)=&\,\rho (s)+Aq(s+1)-v,\\ \mu (s+1)=&\,\mu (s)+LBq(s+1)-\xi ,\\ \eta (s+1)=&\,\eta (s)+L_{n}Cq(s+1). \end{aligned}\right. \nonumber \\ \end{aligned}$$
(11)

Furthermore, the equivalent component form of the algorithm in (11) can be written as

$$\begin{aligned} \left\{ \begin{aligned} q_{i}(s+1)=&\,g_{i}\bigg (q_{i}(s)-\delta \Big (\nabla f_{i}(q_{i}(s))+A_{i}^\mathrm{{T}}(\rho _{i}(s)\\&+A_{i}q_{i}(s)-v_{i})+B_{i}^\mathrm{{T}}\big (\mu _{i}(s)\\&+\sum \limits _{j\in N_{i}}a_{ij}(B_{i}q_{i}(s)-B_{j}q_{j}(s))-\xi _{i}\big )\\&+C_{i}^\mathrm{{T}}\big (\eta _{i}(s) +\sum \limits _{j\in N_{i}}a_{ij}(\gamma _{i}-\gamma _{j})\big )\Big )\bigg ),\\ \rho _{i}(s+1)=&\,\rho _{i}(s)+A_{i}q_{i}(s+1)-v_{i},\\ \mu _{i}(s+1)=&\,\mu _{i}(s)+\sum \limits _{j\in N_{i}} a_{ij}(B_{i}q_{i}(s)-B_{j}q_{j}(s))-\xi _{i},\\ \eta _{i}(s+1)=&\,\eta _{i}(s)+\sum \limits _{j\in N_{i}}a_{ij}(\gamma _{i}-\gamma _{j}), \end{aligned}\right. \end{aligned}$$

where \(a_{ij}\) represents the weight of the connection between robots \(r_{i}\) and \(r_{t}\) in the MRS, \(g_{i}:\mathbb {R}^{k+m+1}\rightarrow \varOmega \) is the projection operator, and \(\delta >0\) is the fixed step size.

Next, we give an equivalent form of the algorithm (11)

$$\begin{aligned} \left\{ \begin{aligned} q(s+1)=&\,g(q(s)-\delta (\nabla F(q(s))+A^\mathrm{{T}}(\rho (s)\\&+Aq(s)-v)+B^\mathrm{{T}}L(\tilde{\mu }(s)\\&+Bq(s)-\tilde{\xi })+C^\mathrm{{T}}L_{n}(\tilde{\eta }(s)+Cq(s)))),\\ \rho (s+1)=&\,\rho (s)+Aq(s+1)-v,\\ \tilde{\mu }(s+1)=&\,\tilde{\mu }(s)+Bq(s+1)-\tilde{\xi },\\ \tilde{\eta }(s+1)=&\,\tilde{\eta }(s)+Cq(s+1), \end{aligned}\right. \nonumber \\ \end{aligned}$$
(12)

where \(L\tilde{\mu }(s)=\mu (s)\), \(L\tilde{\xi }=\xi \) and \(L_{n}\tilde{\eta }(s)=\eta (s)\).

Remark 3

According to Theorem 1 of [24], the algorithms (11) and (12) are equivalent if \(\mu (0)=L\tilde{\mu }(0)\) and \(\eta (0)=L_{n}\tilde{\eta }(0)\). It is noticed that \(\xi =L\tilde{\xi }\) has solution based on Lemma 2. Assuming \(\mu (s)=L\tilde{\mu }(s)\) based on mathematical induction due to \(\mu (0)=L\tilde{\mu }(0)\) in (11). Let \(\tilde{\mu }(s+1)=\tilde{\mu }(s)+Bq(s+1)-\tilde{\xi }\). From (11), one has \(\mu (s+1)=\mu (s)+LBq(s+1)-\xi =L\tilde{\mu }(s)+LBq(s+1)-L\tilde{\xi }=L\tilde{\mu }(s+1)\). Then, \(\mu (s)=L\tilde{\mu }(s)\) always holds by mathematical induction. Similarly, \(\eta (s)=L_{n}\tilde{\eta }(s)\) for \(\forall s\in \{0,1,...\}\).

Remark 4

The algorithm (12) is a discrete-time algorithm. Compared to continuous-time algorithms in [4, 14, 33, 35], the proposed algorithm does not require discretization of time. Therefore, (12) has higher accuracy and is easier to implement.

Fig. 3
figure 3

Simulation results of the cooperative transportation: a the trajectories of mobile manipulators and object; b the trajectories of object centroid and virtual leader; c the end-effector speed of the X-axis; d the end-effector speed of the Y-axis; e the end-effector speed of the Z-axis

Full size image

Algorithm analysis

Suppose that \(q^{*}\in \mathbb {R}^{n(k+m+1)}\) is a solution to the optimization problem (9). From Lemma 2, there exist \(\rho ^{*}\in \mathbb {R}^{kn}\), \(\tilde{\mu }^{*}\in \mathbb {R}^{kn}\) and \(\tilde{\eta }^{*}\in \mathbb {R}^{n}\) such that \((q^{*},\rho ^{*},\tilde{\mu }^{*},\tilde{\eta }^{*})\) satisfies (10). For the sake of proving the convergence of the algorithm (11), some functions are presented as follows:

$$\begin{aligned}{} & {} V_{1}(q(s))=\Vert q(s)-q^{*}\Vert ^{2},~V_{2}(\rho (s))=\Vert \rho (s)-\rho ^{*}\Vert ^{2}, \\{} & {} V_{3}(\tilde{\mu }(s))=(\tilde{\mu }(s) -\tilde{\mu }^{*})^\mathrm{{T}}L(\tilde{\mu }(s)-\tilde{\mu }^{*}),\\{} & {} V_{4}(\tilde{\eta }(s))=(\tilde{\eta }(s) -\tilde{\eta }^{*})^\mathrm{{T}}L_{n}(\tilde{\eta }(s)-\tilde{\eta }^{*}). \end{aligned}$$

Lemma 3

In algorithm (12), \(V_{1}(q(s))\), \(V_{2}(\rho (s))\), \(V_{3}(\tilde{\eta }(s))\) and \(V_{4}(\tilde{\mu }(s))\) have the following properties : 

$$\begin{aligned} (1)~&\,V_{1}(q(s+1))-V_{1}(q(s))\\ \leqslant&-\Vert q(s+1)-q(s)\Vert ^{2}+2\delta (q(s+1)-q(s))^\mathrm{{T}}\\&(\nabla F(q(s+1))-\nabla F(q(s))) -2\delta (Aq(s+1)\\&-v)^\mathrm{{T}}(\rho (s)-\rho ^{*}+Aq(s)-v)-2\delta (Bq(s+1)-\tilde{\xi })^\mathrm{{T}}\\&L(\tilde{\mu }(s)-\tilde{\mu }^{*} +Bq(s)-\tilde{\xi })\\&-2\delta (Cq(s+1))^\mathrm{{T}}L_{n}(\tilde{\eta }(s)-\tilde{\eta }^{*}+Cq(s)),\\ (2)~&\,V_{2}(\rho (s+1))-V_{2}(\rho (s))\\ \leqslant&\,2(Aq(s+1)-v)^\mathrm{{T}}(\rho (s)-\rho ^{*}+Aq(s)-v)\\&+\Vert A(q(s+1)-q(s))\Vert ^{2}-\Vert Aq(s)-v\Vert ^{2},\\ (3)~&\,V_{3}(\tilde{\mu }(s+1))-V_{3}(\tilde{\mu }(s))\\ =&\,2(Bq(s+1)-\tilde{\xi })^\mathrm{{T}}L(\tilde{\mu }(s)-\tilde{\mu }^{*}+Bq(s)-\tilde{\xi })\\&+(Bq(s+1)-Bq(s))^\mathrm{{T}}L(Bq(s+1)\\&-Bq(s))-(Bq(s)-\tilde{\xi })^\mathrm{{T}}L(Bq(s)-\tilde{\xi }),\\ (4)~&\,V_{4}(\tilde{\eta }(s+1)-V_{4}(\tilde{\eta }(s)))\\ =&\,2(Cq(s+1))^\mathrm{{T}}L_{n}(\tilde{\eta }(s)-\tilde{\eta }^{*}+Cq(s))\\&+(Cq(s+1)-Cq(s))^\mathrm{{T}}L_{n}(Cq(s+1)\\&-Cq(s))-(Cq(s))^\mathrm{{T}}L_{n}Cq(s). \end{aligned}$$

Proof

The proof is similar to the Lemma 4 in [24], and we omit it here. \(\square \)

Theorem 1

Assume that the graph \(\mathcal {G}_{n}\) is connected and undirected. q(s) in (12) is convergent globally to an optimal solution of problem (9), if   \(\delta <1/(2\sigma +\lambda _{\max }(A^\mathrm{{T}}A+B^\mathrm{{T}}LB+C^\mathrm{{T}}L_{n}C))\), where \(\lambda _{\max }(A^\mathrm{{T}}A+B^\mathrm{{T}}LB+C^\mathrm{{T}}L_{n}C)\) denotes the maximum eigenvalue of matrix and \(\sigma \) represents the Lipschitz constant of \(\nabla F\).

Proof

According to Lemma 2, let \(q^{*}\in \mathbb {R}^{n(k+m+1)}\) be a solution of problem (9), there exist \(\rho ^{*}\in \mathbb {R}^{kn}\), \(\tilde{\mu }^{*}\in \mathbb {R}^{kn}\) and \(\tilde{\eta }^{*}\in \mathbb {R}^{n}\) such that \((q^{*},\rho ^{*},\tilde{\mu }^{*},\tilde{\eta }^{*})\) satisfies (10). Then, the Lyapunov function is designed as

$$\begin{aligned}&V(s)\triangleq \,V(q(s),\rho (s),\tilde{\mu }(s),\tilde{\eta }(s))\\&\quad =V_{1}(q(s))+\delta (V_{2}(\rho (s))+V_{3}(\tilde{\mu }(s))+V_{4}(\tilde{\eta }(s))). \end{aligned}$$

Using the inequalities in Lemma 3, it can be obtained that

$$\begin{aligned}&\,V(s+1)-V(s)\\&\quad =V_{1}(q(s+1))-V_{1}(q(s))+\delta (V_{2}(\rho (s+1))-V_{2}(\rho (s)))\\&\qquad +\delta (V_{3}(\tilde{\mu }(s+1))-V_{3}(\tilde{\mu }(s)))\\&\qquad +\delta (V_{4}(\tilde{\eta }(s+1))-V_{4}(\tilde{\eta }(s)))\\&\quad \leqslant -\Vert q(s+1)\!-\!q(s)\Vert ^{2}+2\delta (q(s+1)\!-\!q(s))^\mathrm{{T}}\\&\qquad (\nabla F(q(s+1))\!-\!\nabla F(q(s))) +\delta \Vert A(q(s+1)\!-\!q(s))\Vert ^{2}\\&\qquad -\delta \Vert Aq(s)-v\Vert ^{2}+\delta (Bq(s+1)-Bq(s))^\mathrm{{T}}\\&\quad L(Bq(s+1)-Bq(s))-\delta (Bq(s)-\tilde{\xi })^\mathrm{{T}}L(Bq(s) \\&\qquad -\tilde{\xi })+\delta (Cq(s+1)-Cq(s))^\mathrm{{T}}\\&\quad L_{n}(Cq(s+1)-Cq(s))-\delta (Cq(s))^\mathrm{{T}}L_{n}Cq(s). \end{aligned}$$

Since \(\nabla F\) is Lipschitz continuous on \(\varOmega \) and Lipschitz constant is \(\sigma \), then

$$\begin{aligned}&(q(s+1)-q(s))^\mathrm{{T}}[\nabla F(q(s+1))-\nabla F(q(s))]\\&\quad \leqslant \sigma \Vert q(s+1)-q(s)\Vert ^{2}. \end{aligned}$$

Hence, one has

$$\begin{aligned}&\,V(s+1)-V(s)\nonumber \\&\leqslant -(q(s+1)-q(s))^\mathrm{{T}}\nonumber \\&\quad (I-\delta (2\sigma I+A^\mathrm{{T}}A+B^\mathrm{{T}}LB+C^\mathrm{{T}}L_{n}C))(q(s+1)-q(s))\nonumber \\&\quad -\delta \Vert Aq(s)-v\Vert ^{2}-\delta (Bq(s)-\tilde{\xi })^\mathrm{{T}}\nonumber \\&\quad L(Bq(s)-\tilde{\xi })-(Cq(s))^\mathrm{{T}}L_{n}Cq(s). \end{aligned}$$
(13)

When \(\delta <1/(2\sigma +\lambda _{\max }(A^\mathrm{{T}}A+B^\mathrm{{T}}LB+C^\mathrm{{T}}L_{n}C))\), the matrix \(I-\delta (2\sigma I +A^\mathrm{{T}}A+B^\mathrm{{T}}LB+C^\mathrm{{T}}L_{n}C)\) is positive definite. Thus, \(V(s+1)-V(s)\leqslant 0\).

Fig. 4
figure 4

Simulation results of the cooperative transportation with object rotation: a the joint angular velocity; b the platform velocity; c the rotation velocity; d the manipulability measure

Full size image
Fig. 5
figure 5

Simulation results of the cooperative transportation without object rotation: a the sum of projection and constraint errors of algorithm (12); b the joint angular velocity; c the platform velocity; d the manipulability measure

Full size image
Fig. 6
figure 6

A physical picture of the cooperative transportation

Full size image
Fig. 7
figure 7

Experimental results of the cooperative transportation: a the trajectories of end-effector of the mobile manipulators; b the trajectories of the object centroid and virtual leader

Full size image
Fig. 8
figure 8

Experimental results of the cooperative transportation: a the sum of projection and constraint errors of algorithm (12); b the joint angular velocity; c the platform velocity; d manipulability measure

Full size image

From LaSalle invariance principle [41], q(s) converges to the largest invariant subset of the set \(\varTheta =\{q(s)\in \mathbb {R}^{n(k+m+1)}:V(s+1)-V(s)=0\}.\) Using (13), if \(V(s+1)-V(s)=0\), we have \(q(s+1)-q(s)=0\), \(Aq-v=0\), \((Bq(s)-\tilde{\xi })^\mathrm{{T}}L(Bq(s)-\tilde{\xi })=0\), and \((Cq(s))^\mathrm{{T}}L_{n}Cq(s)=0\), which implies \(q(s)=q(s+1)=g(q(s)-\delta (\nabla F(q(s)) +A^\mathrm{{T}}(\rho (s)+Aq(s)-v)+B^\mathrm{{T}}L(\tilde{\mu }(s)+LBq(s)-\tilde{\xi })+C^\mathrm{{T}}L_{n}(\tilde{\eta }(s)+Cq(s))))\), \(Aq(s)-v=0\), \(L(Bq(s)-\tilde{\xi })=0\), and \(L_{n}Cq(s)=0\). Therefore, \(\rho (s)\), \(L\tilde{\mu }(s)\) and \(L_{n}Cq(s)\) are all constant vectors depending on (12). By (13) and the definition of V(s), it can be obtained that \(\Vert q(s)-q^{*}\Vert ^{2}+\delta \Vert \rho (s)-\rho ^{*}\Vert ^{2} +\delta (\tilde{\mu }(s)-\tilde{\mu }^{*})^\mathrm{{T}}L(\tilde{\mu }(s)-\tilde{\mu }^{*})+\delta (\tilde{\eta }(s)-\tilde{\eta }^{*})^\mathrm{{T}}L_{n}(\tilde{\eta }(s)-\tilde{\eta }^{*})= V(s)\leqslant V(0)\). It follows that q(s), \(\rho (s)\), \(L\tilde{\mu }(s)\) and \(L_{n}\tilde{\eta }(s)\) are bounded. Next, there exist limit points \(q^{0}\), \(\rho ^{0}\), \(\tilde{\mu }^{0}_{L}\), \(\tilde{\eta }^{0}_{L_{n}}\) and a strictly increasing subsequence \(\{s_{m}\}_{m=1}^{\infty }\) such that \(\lim _{m\rightarrow \infty }p_{s_{m}}=q^{0}\), \(\lim _{m\rightarrow \infty }\rho _{s_{m}}=\rho ^{0}\), \(\lim _{m\rightarrow \infty }L\tilde{\mu }_{s_{m}}=\tilde{\mu }^{0}_{L}\) and \(\lim _{m\rightarrow \infty }L_{n}\tilde{\eta }_{s_{m}}=\tilde{\eta }^{0}_{L_{n}}\), in which \(q^{0}\) be a solution of problem (9). From \(\lim _{m\rightarrow \infty }L\tilde{\mu }_{s_{m}}=\tilde{\mu }^{0}_{L}\) and the completeness of linear space \(L\tilde{\mu }\), there exists a vector \(\tilde{\mu }^{0}\in \mathbb {R}^{kn}\) such that \(L\tilde{\mu }^{0}=\tilde{\mu }^{0}_{L}\). Similarly, there also exists a vector \(\tilde{\eta }^{0}\in \mathbb {R}^{n}\) such that \(L_{n}\tilde{\eta }^{0}=\tilde{\eta }^{0}_{L_{n}}\). Hence, \(q^{0}\), \(\rho ^{0}\), \(\tilde{\mu }^{0}\), and \(\tilde{\eta }^{0}\) satisfy (10).

Next, we construct the function as follows

$$\begin{aligned} V^{0}\triangleq&\,V^{0}(q(s),\rho (s),\tilde{\mu }(s),\tilde{\eta }(s))\\ =&\,\Vert q(s)-q^{0}\Vert ^{2}+\Vert \rho (s)-\rho ^{0}\Vert ^{2}\\&+\delta (\tilde{\mu }(s)-\tilde{\mu }^{0})^\mathrm{{T}}L (\tilde{\mu }(s)-\tilde{\mu }^{0})\\&+\delta (\tilde{\eta }(s)-\tilde{\eta }^{0})^\mathrm{{T}}L_{n}(\tilde{\eta }(s)-\tilde{\eta }^{0}). \end{aligned}$$

From the above proof, \(V^{0}(s)\leqslant V^{0}(s-1)\). There exists \(s_{m}\) such that \(V^{0}(s)\leqslant V^{0}(s_{m})\) for any s. It holds that \(\lim _{s\rightarrow \infty }V^{0}(s)=\lim _{s\rightarrow \infty }V^{0}(s_{m})=0\). Based on \(V^{0}(s)\geqslant \Vert q(s)-q^{0}\Vert \), we have \(\lim _{s\rightarrow \infty }q(s)=q^{0}\). \(V^{0}(q(s),\rho (s), s\tilde{\mu }(s),\tilde{\eta }(s))\) is radially unbounded with respect to q(s), so q(s) in (12) is globally convergent to an optimal solution to minimax problem (9) for any initial point \(q(0)\in \mathbb {R}^{mn}\). Therefore, it can be achieved that q(s) globally converges to an optimal solution of problem (2). \(\square \)

Simulation and experiment

The simulation and experiment are presented in this section to demonstrate the effectiveness of the distributed projection algorithm (12).

Transporting an object to track smooth path

This subsection verifies the validity of the distributed projection algorithm (12) for a three-robot system to cooperatively transport an objective while tracking a target trajectory, e.g., a piecewise function. This simulation uses a computer with Intel(R) Core(TM) i5-10210U CPU@ 1.60GHz.

We set the initial joint angles of the manipulators \(\vartheta _{1}=(\pi /6,-1.05,0.35,0.70)\) rad, \(\vartheta _{2}=(5\pi /6, -1.05, 0.35, 0.70)\) rad, \(\vartheta _{3}=(3\pi /2, -1.05, 0.35, 0.70)\) rad. The arm lengths of manipulators are set as \(l_{1}=0.077\) m, \(l_{2}=0.130\) m, \(l_{3}=0.124\) m, \(l_{4}=0.126\) m, \(c_{ij}=1\) for \(i,j=1,2,3\) and \(c_{i4}=0.01\) for \(i=1,2,3\). The sampling interval is \(\pi /40\). The transported object is an isosceles triangle with vertex coordinates (0.1054, 0.0609, 0.2414) m, (0.2946, 0.0609, 0.2414) m, (0.200, 0.2247, 0.2414) m. The coordinate of virtual leader is (0.2000, 0.1155, 0.2414) m. When \(0\leqslant t\leqslant 5\pi /6\), the velocity of virtual leader is \((6t/(5\pi ),\textrm{sin}t,0)\) m/s, the transport trajectory is a cosine path. When \(5\pi /6<t\leqslant 7\pi /6\), the velocity of virtual leader is (1, 0.5, 0)m/s, the transport trajectory is a straight path. When \(7\pi /6<t\leqslant 2\pi \), the velocity of virtual leader is \((1-6(t-7\pi /6)/(5\pi ),-\textrm{sin}t,0)\) m/s, the transport trajectory is a cosine path.

In Fig. 3a, the triangle represents transported object, short lines represent mobile manipulators, and three piecewise curves represent the trajectories of end-effectors. From Fig. 3b, the red line indicates the trajectory of the object centroid, while the green line indicates the trajectory of the virtual leader, and we see that the object centroid could track the virtual leader. From Fig. 3c–e, the end-effector speed of the manipulator is gradually increased from (0, 0, 0) m/s to (1, 0.5, 0) m/s, the end-effector keep this speed running for a period of time, and finally gradually decreases to (0, 0, 0) m/s.

Based on the above given parameters, the case of the object without rotation is introduced. Figure 5a shows the errors of the algorithm (12) in each loop. By comparing Figs. 4a and 5b, we know that in the process of the cooperative transportation, the introduction of rotation variables can make the change of joint angular velocity of the manipulator smoother. Similarly, it can be seen from Figs. 4b and 5c that the rotation variable also makes the change of velocity of the platform smoother. Moreover, from Figs. 4d and 5d, the manipulability of the manipulators keep increasing in the process of the cooperative transportation.

Experiment

In the experiment, three real robots are used to carry the object along the sinusoidal curve to demonstrate the effectiveness of the designed distributed algorithm. The initial positions of three mobile platforms are (0, 0, 0) m, \((0, -0.45,0)\) m, (0.45, 0, 0) m. The initial joint angles of the manipulators \(\vartheta _{1}=(\pi /2, -1.05, 0.35, 0.70)\) rad, \(\vartheta _{2}=(\pi /2, -1.05, 0.35, 0.70)\) rad, \(\vartheta _{3}=(3\pi /2, -1.05, 0.35, 0.70)\) rad. The velocity of virtual leader is \(2.2(1,\textrm{cos}(t/10),0)\) cm/s. The transported object is an right angled isosceles triangle with vertex coordinates (0.274, 0, 0.346) m, (0.274, \(-\)0.45, 0.346) m, (0.724, 0, 0.346) m. The arm lengths of manipulators are \(l_{1}=0.077\) m, \(l_{2}=0.130\) m, \(l_{3}=0.124\) m, \(l_{4}=0.126\) m. The sampling interval is 0.1s. Moreover, as shown in Fig. 6, the Turtlebot 3 with Raspberry Pi 3B+ is the platform and the Open-manipulator-X is utilized to carry the object.

In Fig. 7, the trajectory of each end-effector is a sinusoidal curve, and the trajectories of the object center and virtual leader coincide almost. Since communication delays exist among the robots, each robot may be unable to update speed and position information of its neighbor in time, which leads to a specific error in the computation of velocities. In addition, there may be insufficient friction between the tire and the ground of the Turtlebot 3 robots, causing the robots to slip slightly in a small area. In Fig. 8, the actual experimental data is consistent with the simulation data in the above subsection. As can be seen from Fig. 8a, every robot converges to the preset error within \(t=1.5\times 10^{-3}\)s. And the convergence speed is less than the sampling time, which proves the real-time performance of the algorithm proposed in this paper. The joint angular velocities and platform velocities for each robot are displayed in Fig. 8b and c. During the cooperative transport task, the robots maintain a good speed continuity. The manipulability of robot is shown and the maneuverability of robot keeps increasing from the beginning to the end of the task. In summary, the algorithm proposed in this paper can better complete the collaborative transport task.

Conclusions

In this paper, the cooperative transportation of MRS has been studied by optimizing the total energy consumption of MRS and manipulability of redundant manipulators. A discrete-time DOA for cooperative transportation has been designed to realize cooperative transportation and move along an expected trajectory. The virtual leader has been introduced into the the cooperative transportation to make the proposed algorithm more robust. Smoother changes in the angular velocity of the manipulator joints and the speed of the moving platform are achieved by introducing rotational variables into the optimization problem. In addition, simulation and physical examples have shown the validity of developed algorithm. In the future, we will consider the time-varying optimization based cooperative transportation problem with obstacle avoidance.