Bi-indicator driven surrogate-assisted multi-objective evolutionary algorithms for computationally expensive problems

Abstract

This paper presents a bi-indicator-based surrogate-assisted evolutionary algorithm (BISAEA) for multi-objective optimization problems (MOPs) with computationally expensive objectives. In BISAEA, a Pareto-based bi-indictor strategy is proposed based on convergence and diversity indicators, where a nondominated sorting approach is adopted to carry out two-objective optimization (convergence and diversity indicators) problems. The radius-based function (RBF) models are used to approximate the objective values. In addition, the proposed algorithm adopts a one-by-one selection strategy to obtain promising samples from new samples for evaluating the true objectives by their angles and Pareto dominance relationship with real non-dominated solutions to improve the diversity. After the comparison with four state-of-the-art surrogate-assisted evolutionary algorithms and three evolutionary algorithms on 76 widely used benchmark problems, BISAEA shows high efficiency and a good balance between convergence and diversity. Finally, BISAEA is applied to the multidisciplinary optimization of blend-wing-body underwater gliders with 30 decision variables and three objectives, and the results demonstrate that BISAEA has superior performance on computationally expensive engineering problems.

Introduction

Real-life engineering problems often need to simultaneously optimize multiple conflicting objectives [1], which are named multi-objective optimization problems (MOPs). A minimization MOP can be defined as follows [2]:

$$ \begin{gathered} {\text{min }}F({\mathbf{X}}) = (f_{1} ({\mathbf{x}}),f_{2} ({\mathbf{x}}), \ldots f_{M} ({\mathbf{x}}))^{{\text{T}}} \hfill \\ {\text{s.t.}} \quad L_{i} \le x_{i} \le U_{i} \, i \in \{ 1,2, \ldots ,d\} \hfill \\ \end{gathered} $$

(1)

where $f_{1} ,f_{2} ,...f_{M}$ are M objective functions to be optimized, $\, L_{i}$ and $U_{i}$ are the lower and upper boundaries of $x_{i}$.${\mathbf{x}} = \{ x_{1} ,x_{2} ,...,x_{d} \}$, and d is the number of decision variables of the optimization problem.

As an important method to solve MOPs, multi-objective optimization evolutionary algorithms (MOEAs) have been developed rapidly in recent 20 years. MOEAs search for a set of solutions to represent the whole Pareto front (PF). Commonly used MOEAs can be roughly divided into three categories: indicator-based methods [3], dominance-based methods [4], and decomposition-based methods [5, 6].

It is worth mentioning that MOEAs require a large number of function evaluations (NFEs) to obtain the true PF. However, in some engineering optimization problems, the fitness functions are quite time-consuming simulations, such as Computational fluid dynamics (CFD) and Finite element analysis (FEA). To reduce the overall NFEs, the mainstream is to adopt surrogate models for approximation of expensive physical models of expensive optimization [7]. Various surrogates have been used to solve real engineering optimization problems [8,9,10], such as polynomial response surface (PRS) [11], Kriging [12], neural network (NN) [13], radius-based function (RBF) [14] and so on. Surrogate-assisted evolutionary algorithms (SAEAs) are proposed to handle single-objective optimization using classification or regression-based fitness approximation, which have been adopted successfully in engineering optimization e.g., a novel evolutionary sampling optimization method (ESAO) [15], surrogate-assisted grey wolf optimization (SAGWO) [16] and surrogate-assisted teaching and learning optimization (SATLBO) [17].

Inspired by these studies, numerous SAEAs for expensive multi-objective optimization are proposed in the past decades. Many surrogate models are used to approximate the function values in SAEAs, which can be roughly divided into two categories. In the first category, the surrogate models are used to approximate the objective functions, scalarized functions, and so on. The Kriging-assisted reference vector guided evolutionary algorithm (K-RVEA) [18] and expected improvement (EI) matrix-based infill criteria MOEA [19] for expensive multi-objective optimization are representative methods. Liu et al. [20] suggested a reference vector-assisted adaptive Kriging model management strategy (RVMM) and Song et al. [21] developed a Kriging-assisted two-archive evolutionary algorithm (KTA2) for surrogate-assisted many-objective optimization. The Kriging models are also used in MOEA-based decomposition (MOEA/D-EGO) [22], MOEA/D-EGO applies a fuzzy clustering-based modeling method in the decision space to build many local surrogate models for each objective. In addition, an efficient dropout neural network-assisted indicator-based MOEA with reference point adaptation (EDN-ARMOEA) [23] and a surrogate-assisted particle swarm optimization algorithm with an adaptive dropout mechanism (ADSAPSO) [24] was developed using the neural network. Meanwhile, the bagging technology of the surrogate models is also adopted to approximate function values, such as a heterogeneous ensemble-based infill criterion for MOEA (HeE-MOEA) [25].

In the second category, the classifiers are adopted as surrogate models. A classification-based SAEA (CSEA) [26] uses feedforward neural networks (FNNs) to predict the dominant relationship between candidate solutions and reference solutions. Zhang et al. [27] suggest a classification-based preselection for the multi-objective evolutionary algorithm (CPS-MOEA).

Significantly, some of the above-mentioned surrogate-assisted MOEAs use the indicator to improve their performance, such as RVMM [20], KTA2 [21], EDN-ARMOEA [23], and so on. To take full advantage of indicators, we propose a bi-indicator-based surrogate-assisted MOEA (BISAEA), where the RBF models are adopted to approximate the expensive function evaluation, a Pareto-based bi-indicator (convergence indicator, CI and diversity indicator, DI) strategy is proposed to transform the MOPs into a bi-objective (CI and DI) optimization problem, and a one-by-one selection strategy is adopted to get expected samples for re-evaluation. To verify the effectiveness of BISAEA, it is compared with four state-of-the-art SAEAs and three MOEAs on 76 widely used benchmark problems and applied to the multidisciplinary optimization design of Blend-Wing-Body Underwater Gliders (BWBUGs). The contributions of this work are summarized as follows:

• 1. A Pareto-based bi-indicator strategy is designed to obtain new samples by using approximate objective values. A convergence indicator and diversity indicator are calculated by approximating objective values, and which are taken as the bi-objective optimization to select new samples based on Pareto sorting.

• 2. The one-by-one selection strategy is adopted to select several promising samples for re-evaluation. The candidate samples are selected by evaluating the angle of their approximate function values and exiting advantage samples successively.

• 3. The performance of BISAEA is evaluated on 76 benchmark functions and multidisciplinary design optimization of BWBUGs with three objectives, the results show that BISAEA outperforms the comparison algorithms.

The remainder of this article is organized as follows. In “Related work”, we review the related work on indicator and RBF models. The details of the proposed BISAEA are presented in “The proposed algorithm”, and the results of experiments on mathematical cases are shown in “Empirical studies”. The engineering applications are reported in “Application to engineering problem”, and “Conclusions” concludes the article and draws the future work.

Related work

Indicator-based MOEAs

As an important component of MOEAs, indicator-based MOEAs adopt the evaluation indicator to measure the performance of the solutions to obtain the final optimal solutions. Several indicators have been proposed, such as hypervolume [3, 28], IGD-NS [29], R² [31, 32], $I_{{\varepsilon^{ + } }}$ [32,33,34,35] and others [36]. In this article, $I_{{\varepsilon^{ + } }}$ is adopted as a convergence indicator, and $I_{{\varepsilon^{ + } }}$ reflects the smallest adjustment that may be made to allow one solution set to marginally outperform another for each objective. It might be characterized as follows:

$$ \begin{gathered} {I}_{{\varepsilon^{ + } }} (X_{1} ,X_{2} ) = {\text{min }}\{ \varepsilon |\forall x_{2} \in X_{2} ,\exists x_{1} \in X_{1} : \hfill \\ f_{i} (x_{1} ) - \varepsilon \le f_{i} (x_{2} ),{\text{for }}i = 1,2,...,M\} \hfill \\ \end{gathered} $$

(2)

where $X_{1}$ and $X_{2}$ are two solutions sets and $M$ is the number of objectives. $I_{{\varepsilon^{ + } }}$ could be defined as follows:

$$ {\mathbf{I}}({\mathbf{x}}_{1} ,{\mathbf{x}}_{2} ) = \max ({\mathbf{F}}({\mathbf{x}}_{1} ) - {\mathbf{F}}({\mathbf{x}}_{2} )) $$

(3)

where ${\mathbf{F}}({\mathbf{x}}_{1} )$ and ${\mathbf{F}}({\mathbf{x}}_{2} )$ are objective values of ${\mathbf{x}}_{1}$ and ${\mathbf{x}}_{2}$. The maximum indicator value for all ${\mathbf{x}}_{i} \in X$ will be evaluated as a scalar indicator by Eq. (4).

$$ c({\mathbf{x}}_{j} ) = \mathop {\max }\limits_{{{\mathbf{x}}_{i} \in X}} \left| {{\mathbf{I}}({\mathbf{x}}_{i} ,{\mathbf{x}}_{j} )} \right| $$

(4)

Finally, the fitness values can be computed for all ${\mathbf{x}}_{i} \in X$ in the following equation:

$$ Fit({\mathbf{x}}_{i} ) = \sum\limits_{{{\mathbf{x}}_{j} \in X\backslash \{ {\mathbf{x}}_{i} \} }} { - e^{{ - {\mathbf{I}}({\mathbf{x}}_{i} ,{\mathbf{x}}_{j} )/(c({\mathbf{x}}_{j} ) \cdot K)}} } $$

(5)

where $K$ is the scaling factor.

Meanwhile, the minimum angle is used as a diversity indicator, which was used in relevant research [9]. As shown in Fig. 1, it is obvious that the new samples 3 and 4 have two angles ($\gamma ,\gamma_{1}$ and $\lambda ,\lambda_{1}$) with the reference points, the angle indicator between each new sample and the reference point is shown in Fig. 1b) based on the minimum angle.

Fig. 1

The minimum angle with reference points

Different from the above indicator-based MOEAs, BISAEA adopts two indicators (CI and DI) as bi-objective to select the promising samples. Especially, the above MOEAs [28,29,30,31,32,33,34,35,36] use the indicators to select the expected samples to promote the convergence or diversity independently, the two indicators (bi-indicator, minimum angle and $I_{{\varepsilon^{ + } }}$) are used as bi-objective optimization to enhance the convergence and diversity simultaneously in BISAEA.

Radial basis function

In this article, the RBF model [14] is used as the surrogate model. Studies [37] reveal that RBF can obtain more accurate approximations for high dimensional problems, and its modeling speed is fast compared with the Kriging model. Given the data points $\left\{ {({\mathbf{x}}_{i} ,y_{i} )|{\mathbf{x}}_{i} \in \Re^{d} ,i = 1,2,..,N} \right\}$, the RBF surrogate is defined as follows:

$$ \hat{f}({\mathbf{x}}) = \sum\limits_{i = 1}^{n} {\lambda_{i} } \phi (\left\| {{\mathbf{x}} - {\mathbf{x}}_{i} } \right\|) + p({\mathbf{x}}),{\mathbf{x}} \in \Re^{d} $$

(6)

where $\left\| {{\mathbf{x}} - {\mathbf{x}}_{i} } \right\|$ is the Euclidean distance between the points x and ${\mathbf{x}}_{i}$, $\phi ( \cdot )$ is the basic function. Many forms of the basis function can be used here. In this article, the cubic form ($\phi (r) = r^{3}$) is adopted because it was successfully employed in several surrogate-based algorithms [17, 38]. In addition, the weight vector ${{\varvec{\uplambda}}} = (\lambda_{1} ,\lambda_{2} ,...,\lambda_{N} )^{T}$ can be computed as follows:

$$ {{\varvec{\uplambda}}} = (\Phi^{T} \Phi )^{ - 1} \Phi^{T} {\mathbf{y}} $$

(7)

where ${\mathbf{y}} = (y_{1} ,y_{2} ,...,y_{N} )^{T}$ is the output vector and ${{\varvec{\Phi}}}$ is the following matrix:

$${\varvec{\varPhi}}= \left[ \begin{gathered} \phi ({\mathbf{x}}_{1} - {\mathbf{x}}_{1} ),{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \phi ({\mathbf{x}}_{1} - {\mathbf{x}}_{2} ),{\kern 1pt} {\kern 1pt} {\kern 1pt} \ldots ,{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \phi ({\mathbf{x}}_{1} - {\mathbf{x}}_{N} ) \hfill \\ \phi ({\mathbf{x}}_{2} - {\mathbf{x}}_{1} ),{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \phi ({\mathbf{x}}_{2} - {\mathbf{x}}_{2} ),{\kern 1pt} {\kern 1pt} {\kern 1pt} \ldots ,{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \phi ({\mathbf{x}}_{2} - {\mathbf{x}}_{N} ) \hfill \\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \vdots {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \vdots {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \ddots {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \vdots \hfill \\ \phi ({\mathbf{x}}_{N} - {\mathbf{x}}_{1} ),{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \phi ({\mathbf{x}}_{N} - {\mathbf{x}}_{2} ),{\kern 1pt} {\kern 1pt} {\kern 1pt} \ldots ,\phi ({\mathbf{x}}_{N} - {\mathbf{x}}_{N} ) \hfill \\ \end{gathered} \right] $$

(8)

$p(x)$ is a linear polynomial in d variables with d + 1 coefficients as in the formula:

$$ p(x) = c_{0} + c_{1} x_{1} + c_{2} x_{2} + \cdot \cdot \cdot + c_{d} x_{d} = c^{T} \cdot x $$

(9)

The proposed algorithm

The framework of BISAEA

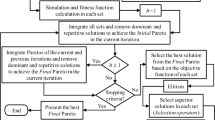
The framework of BISAEA is shown in Fig. 2, which can be divided into three parts, initialization, Pareto-based bi-indicator selection strategy, and one-by-one selection strategy. In the first part, the initial population and reference vector are obtained and the relevant parameters are set. In the second part, a Pareto-based bi-indicator selection strategy is used to obtain better candidate samples. Variation operation is applied to produce offspring using the parent populations, and the RBF model is used to approximate the function values for each objective of offspring. The bi-indicator is calculated by the approximate function values and selecting better samples for the next operation. Finally, the best samples are selected by the one-by-one selection strategy to evaluate the real function.

Fig. 2

The framework of BISAEA

The pseudocode of BISAEA is given in Algorithm 1, which can be divided into the following steps:

• (1) Initialization (Lines 1–4): The initial population $P$ is generated using the Latin hypercube sampling (LHS) [39, 40]. The initial reference vector $V_{0}$ and the Pareto non-dominated samples $P_{nd}$ are obtained. Besides, the parent population is determined.

• (2) Pareto-based bi-indicator selection strategy (Lines 5–14): Generating offspring from parent populations by crossover and mutation and approximating the objective values of the offspring by RBF model. The bi-indicator is evaluated using the approximate objective values of offspring and the non-dominated method is adopted to select better samples based on the bi-indicator.

• (3) The one-by-one selection strategy (Lines 15–27): The better samples are combined with $P_{nd}$, and a non-dominated sorting method is employed to obtain the new PFs of them, and the better samples are selected from new PFs. If the size of the better sample is larger than $N_{\max }$, select the $N_{\max }$ best samples by Algorithm 4 and re-evaluate it to add into the database, otherwise re-evaluate $X_{better}$ to add into the database.

• (4) Repeat (2)–(3) until the termination condition is met.

  

Pareto-based bi-indicator selection strategy

In BISAEA, a Pareto-based bi-indicator strategy is proposed to select better samples from offspring. This strategy includes two parts, i.e., bi-indicator calculation and selection based on the Pareto relationship.

In the first part (Lines 1–8), we adopt the non-dominated method to select the new PFs of offspring and their parent populations. The new PFs ($X_{better}$ and $Y_{better}$) are selected using the $I_{{\varepsilon^{ + } }}$ and the minimum angle. It should be noted that the objective values ($Y_{new}$ and $Obj$) are the approximate values of the RBF model.

In the second part (Lines 9–10), the convergence indicator ($I_{{\varepsilon^{ + } }}$) and the diversity indicator (The opposite of the minimum angle) is adopted as the bi-objective, and the non-dominated method is used to obtain the PFs of them. In this way, the selected samples will have a good convergence and diversity at the same time.

The details of the Pareto-based bi-indicator selection strategy can be found in Figs. 3 and 4. The offspring samples and their parent samples are taken as a combination, and the non-dominated sorting method is employed to obtain the new PFs and the candidate samples are selected from new PFs.

Fig. 3

The non-domination selection of the combination of parent and offspring

Fig. 4

Selecting samples by bi-indicator

To select the samples with better diversity and convergence, the Pareto-based bi-indicator strategy is proposed. The main idea of the Pareto-based bi-indicator strategy is to formulate the selected samples as the MOP, where convergence and diversity indicators are two objectives to be optimized. It is worth noting that the convergence and diversity indicators are evaluated by the approximate objective values of the RBF model in BISAEA.

After obtaining two indicators, the Pareto-based bi-indicator strategy can be written as:

$$ \begin{gathered} {\mathbf{min}} \, G(x) = (g_{1} (x),g_{2} (x)) \hfill \\ \, g_{1} (x) = DI \hfill \\ \, g_{2} (x) = CI \hfill \\ \end{gathered} $$

(10)

The Pareto-based bi-indicator selection process is shown in Fig. 4. The convergence and diversity indicators (Fig. 4b and c) are evaluated by the candidate samples (Fig. 4a) based on $I_{{\varepsilon^{ + } }}$ and minimum angle. It is clear that the convergence indicator and diversity indicator have a big difference for candidate samples. Sample 6 has the advantage of both convergence and diversity indicators, but sample 7 has the opposite performance. To give consideration to both convergence and diversity, the bi-indicator is adopted as the bi-objective as shown in Fig. 4d. The non-dominated sorting method is used to carry out the bi-objective (CI and DI) optimization problem, the new PFs of them are represented in Fig. 4e and the corresponding function values are shown in Fig. 4f. It is obvious that the better samples have better performance compared to the candidate samples.

The one-by-one selection strategy

The one-by-one selection is a selection strategy in MOEAs, which has been proven to be effective in improving the performance of corresponding algorithms [21, 23]. Inspired by the relevant work [21, 23, 41,42,43], a one-by-one selection strategy is adopted in BISAEA to improve its performance. Especially, the one-by-one selection strategy has two parts, Pareto-based selection and one-by-one selection. To obtain better convergence, the Pareto-based method is used to select the samples from better samples. The one-by-one selection is proposed to select the best samples based on the angle. The details of the Pareto-based selection strategy are shown in Fig. 5. The better samples and the existing non-dominated samples (PFs samples) are taken as a combination. Then Pareto-based method is employed to obtain the new PFs of them and better samples are selected from new PFs.

Fig. 5

The non-domination selection of the combination of PFs samples and better samples

The details of the one-by-one strategy are presented in Algorithms 4. To obtain better diversity, the non-dominated solutions of the current population are chosen as the reference points (PFs samples), and the minimum angle between the better samples and the PFs samples is calculated. As shown in Fig. 6, taking the example of selecting the three best samples. The minimum angles between the better samples and PFs samples are represented as colored sectors. Sample 1 corresponding to the maximum angle is first selected as the best sample and merged with the PFs samples (Fig. 6b). Then, samples 5 and 3 are selected with the maximum angle in turn (Fig. 6c and d). The final selection result is shown in Fig. 6e.

Fig. 6

The process of the one-by-one strategy

Empirical studies

In this section, to validate the effectiveness of BISAEA, we empirically compare it with several state-of-the-art multi-objective optimization algorithms, including several SAEAs (K-RVEA [18], HeEMOEA [25], EDN-ARMOEA [23], KTA2 [21] and several MOEAs (NSGA-III [4], RVEA [6] and IBEA [33]). All the test instances are implemented in PlatEMO [44]. The seven compared algorithms are summarized as follows.

• 1. K-RVEA [18] is a Kriging-assisted reference vector-guided evolutionary algorithm, which uses Kriging to approximate each objective and uncertainty information is provided to balance convergence and diversity.

• 2. HeE-MOEA [25] is a heterogeneous ensemble-assisted MOEA, in which a support vector machine and two RBF networks are constructed to enhance the reliability of ensembles for uncertainty estimation.

• 3. EDN-ARMOEA [23] is an efficient dropout neural network (EDN) assisted indicator-based MOEA [29], in which the EDN replaces the Gaussian process to achieve a good balance between convergence and diversity.

• 4. KTA2 [21] is a Kriging-assisted two-archive evolutionary algorithm and uses one influential point-insensitive model to approximate each function value. Moreover, an adaptive infill criterion for convergence, diversity and uncertainty is adopted to determine the promising samples for real function evaluation.

• 5. NSGA-III [4] is an evolutionary multi-objective optimization algorithm using a reference-point-based nondominated sorting approach.

• 6. IBEA [33] uses a binary additive $\varepsilon { - }$indicator (${I}_{{\varepsilon^{ + } }}$) as its selection criterion install of the Pareto dominance criterion.

• 7. RVEA [6] is a reference vector-guided evolutionary algorithm for multi-objective optimization, and the reference vectors are used to decompose the original multi-objective optimization problem into a number of single-objective subproblems.

The experiments are conducted on 76 test instances from test suite DTLZ [45] and ZDT [46] with 2 and 3 objectives. For each test instance, the MFEs is set to 500, and the numbers of decision variables are set as 10, 15, 30 and 50.

We used the inverted generational distance (IGD) [47] as the performance indicator to assess the performance of the compared SAEAs. In general, the lower the IGD value is, the better the solutions approximate the true PF. All experiments are conducted using MATLAB with an Intel (R) Core (TM) i7, 3.4 GHz CPU. The Wilcoxon rank-sum (WRS) is used to conduct statistical tests at a significance level of 5%. Symbols “+” and “−” indicate that BISAEA is significantly superior and inferior to the compared algorithm, “≈” means that there is no significant difference between BISAEA and the compared algorithm.

Parameter setting

The common parameter settings of all the compared algorithms are listed as follows:

• 1. The population size is set to 100.

• 2. The scaling factor ($K$) is set as 0.05 consistent with the original literature [33].

• 3. The maximum number of expensive function evaluations is set to 500.

• 4. The maximum number of iterations ($w_{\max }$) is set as 20, which is the same as K-RVEA[18].

• 5. The parameters for reproduction (crossover and mutation) are set to $P_{c} = 1.0$, $P_{m} = 1/d$,$\eta_{c} = 20$,$\eta_{m} = 20$.

• 6. The dimension of the design variable is set as 10, 15, 30 and 50.

In addition, for a fair comparison, we adopt the recommended setting in the original literature for specific parameters of compared algorithms.

Behavior study of the BISAEA

Sensitivity analysis of parameters in BISAEA

The maximum number of new samples for real function evaluation each time ($N_{\max }$) is a key parameter in BISAEA. $N_{\max }$ is set as 1, 3, 5 and 7 to explore the influence of this parameter on the BISAEA, which are name BISAEA_1, BISAEA_3, BISAEA_5 and BISAEA_7. The average IGD results of each algorithm based on 30 independent runs on DTLZ1, 2, 7 and ZDT 1, 2 problems are shown in Table 1, where the WRS test is also listed and the best results are highlighted.

Table 1 Statistic results for IGD values obtained by BISAEA_1, 3, 5 and 7

As shown in Table 1, BISAEA_1 has the best performance, followed by BISAEA_3. It is obvious that the performance of algorithms deteriorates with the increase of $N_{\max }$. However, the smaller values of $N_{\max }$ will lead to a longer calculation time, which can be found in Fig. 7. In Fig. 7, the mean runtime of different problems on BISAEA_1 and BISAEA_3 is displayed based on 30 independent runs. It is clear that the mean runtime of BISAEA_3 is shorter than BISAEA_3, and the performance of the two algorithms is similar as shown in Table 1. Based on computational efficiency and overall performance, $N_{\max }$ is set as 3 in this article.

Fig. 7

The mean runtime with different problems on BISAEA_1 and BISAEA_3

Effect of the Pareto-based bi-indicator strategy

In this part, we first investigate the effects of the Pareto-based bi-indicator strategy of BISAEA. A variant of BISAEA named BISAEA(one), which does not adopts the Pareto-based bi-indicator strategy and only uses the one-by-one selection strategy. The average IGD results of BISAEA(one) and BISAEA based on 30 independent runs on DTLZ1, 2, 7 and ZDT 1, 2 problems are shown in Table 2, where the WRS test is also listed and the best results are highlighted.

Table 2 Statistic results for IGD value obtained by BISAEA and BISAEA(one)

In the benchmark problems of the above test, DTLZ1 has multi-model landscapes that is difficult to converge and DTLZ2 is easy to converge but maintains diversity with difficulty. DTLZ7 has irregular and discontinuous PF, ZDT1 and ZDT2 have convex PF. As shown in Table 2, it is easy to that BISAEA has better performance than BISAEA(one).

To better investigate the effects of the Pareto-based bi-indicator strategy, the final non-dominated solutions achieved by BISAEA(one) and BISAEA on 10D and 30D are shown in Figs. 8 and 9. Moreover, the true PF of DTLZ1 and DTLZ7 is shown in the last of Figs. 8 and 9. It is obvious that the results of BISAEA in DTLZ1 and DTLZ7 on 10D and 30D have better convergence that BISAEA(one), which also could be found in ZDT1 and ZDT2. The main reason is that the Pareto-based bi-indicator strategy adopts a convergence indicator, which could improve the convergence speed. From the results of DTLZ2 of two algorithms in Figs. 8 and 9, both BISAEA(one) and BISAEA could converge in 10D, BISAEA has the better performance based on diversity. For the DTLZ2 on 30D, BISAEA has advantages in convergence and diversity. From the above results, it can be concluded that the Pareto-based bi-indicator strategy of BISAEA not only accelerates convergence but also play an important role in maintaining diversity.

Fig. 8

The PF of DTLZ1,2,7 and ZDT 1,2 associated with the median IGD value on 10D

Fig. 9

The PF of DTLZ1,2,7 and ZDT 1,2 associated with the median IGD value on 30D

Effect of the one-by-one selection strategy

To further study the role of the one-by-one selection strategy in BISAEA, we compare BISAEA with the BISAEA(pb) and BISAEA(only_one), where BISAEA(pb) only adopts the Pareto-based bi-indicator strategy, and BISAEA(only_one) uses the Pareto-based bi-indicator strategy and only one-time selection strategy to choose the same number new samples.

The experiments are conducted on DTLZ1, 2, 7 and ZDT 1, 2 problems with two and three objectives. The average IGD results of three algorithms based on 30 independent runs are is listed in Table 3, where the WRS test is also listed and the best results are highlighted.

Table 3 Statistic results for IGD values obtained by BISAEA, BISAEA(pb) and BISAEA(only_one)

It can be observed that the BISAEA and BISAEA(only_one) have better performance than BISAEA(pb). The reason is that BISAEA(pb) only selects the new samples through the Pareto-based bi-indicator strategy, the selected sample size cannot be effectively controlled, which will cause a waste of real function evaluation times.

To better explain the effects of the one-by-one selection strategy, the true PF and final non-dominated solutions achieved by BISAEA(pb), BISAEA(only_one) and BISAEA on 10D and 30D are shown in Fig. 10. It is obvious that the results of BISAEA(only_one) and BISAEA on 10D and 30D have the better convergence than BISAEA(pb), which shows that reselection after Pareto-based bi-indicator strategy could improve the convergence of the algorithm. From the results of DTLZ2 of BISAEA(only_one) and BISAEA on two and three objectives in Fig. 10, both BISAEA(only_one) and BISAEA could converge in true PFs, and the results of BISAEA has the better diversity. This can indicate that the one-by-one selection strategy is of great significance for the improvement of diversity.

Fig. 10

The PF of DTLZ1,2 associated with the median IGD value on 10D

Comparison with other algorithms

Results on DTLZ problems

The results of IGD values achieved by seven algorithms over 30 independent runs on DTLZ problems are summarized in Tables 4 and 5, where the best results are highlighted. Tables 4 and 5 show the statistical results of SAEAs and EAs in DTLZ1-7 with two and three objectives on 10D, 15D, 30D and 50D, respectively.

Table 4 Statistic results of the four SAEAs and BISAEA on DTLZ1-7

Table 5 Statistic results of the three EAs and BISAEA on DTLZ1-7

Both DTLZ1 and DTLZ3 have multi-model landscapes that are difficult to converge. BISAEA and KTA2 have superior performance on DTLZ1 and DTLZ3, followed by IBEA and K-RVEA. The true PF and final non-dominated solutions achieved by the compared algorithms on DTLZ1 associated with the median IGD values are shown in Fig. 11. The IGD values and the final solutions are illustrative of the convergence of BISAEA and KTA2. For DTLZ2, BISAEA achieves a satisfactory result. As shown in Fig. 12, both K-RVEA, KTA2 and BISAEA converge to the true PF, and the final non-dominated solutions achieved by BISAEA are more evenly distributed on the true PF. The reason is that the diversity indicator and one-by-one selection strategy could improve diversity.

Fig. 11

The PF of DTLZ1 associated with the median IGD value on 30D

Fig. 12

The PF of DTLZ2 associated with the median IGD value on 30D

DTLZ4 is modified from DTLZ2 and mainly used for measuring the diversity of algorithms. As shown in Tables 4 and 5, BISAEA and KTA2 are the top two algorithms for DTLZ4, BISAEA obtains the best average IGD values on 50D, and KTA2 gets the best results for other dimensions. The main reason is that one influential point-insensitive Kriging model is used in KTA2, which plays an important role in low-dimensional problems. However, the accuracy of Kriging models decreases with the increase of dimensions. The PFs of DTLZ5-7 are irregular, which brings a challenge to obtaining a set of diverse and well-converged solutions. Among them, the PFs of DTLZ5 and DTLZ6 have degenerated curves, DTLZ6 is modified from DTLZ5, and DTLZ7 is discontinuous. It can be seen from Tables 4 and 5, BISAEA achieve better results on these problems.

To better describe the performance of BISAEA in DTLZ series problems, the IGD values iteration process of BISAEA, K-RVEA, HeE-MOEA, EDNARMOEA and KTA2 of DTLZ2 is shown in Fig. 13. It is clear that BISAEA has the satisfactory convergence speed and performance. Especially, BISAEA and KTA2 have similar iteration curves and performance, and the convergence speed of BISAEA wins over KTA2. In addition, the runtime of the above SAEAs is represented in Fig. 14. With the increase of design dimensions, the runtime of K-RVEA, EDNARMOEA and KTA2 increase dramatically, and HeE-MOEA and BISAEA has small changes. The main reason is that Kriging and EDN models are adopted in K-RVEA and KTA2, and EDNARMOEA, the training time of the Kriging model increases with the design dimension. Moreover, the GD values of the above SAEAs, EAs and BISAEA are shown in Tables 1 and 2 of the supplementary materials, and the runtime of four SAEAs and BISAEA are shown in Table 5 of the supplementary materials. It can indicate that KTA2 and BISAEA have similar performance in DTLZ series problems, and BISAEA has advantages in runtime.

Fig. 13

The IGD values iteration process of five algorithms in DTLZ2

Fig. 14

The runtime of five algorithms of DTLZ2-2M with different dimension

We can draw a conclusion from the above analysis, BISAEA and KTA2 can obtain competitive results in DTLZ series problems with two and three objectives. From the perspective of runtime, BISAEA has great advantages over KTA2. Therefore, it is obvious that BISAEA has better performance than the above comparison algorithms.

Results on ZDT problems

To further analyze the performance of BISAEA in two objectives problems, we use the ZDT problems as test problems. ZDT problems include six two-objective test problems, which introduce different difficulties for evolutionary optimization[46]. We choose five unconstrained problems, referred to as ZDT1-ZDT4 and ZDT6. The statistical results of compared algorithms on ZDT problems are summarized in Tables 6 and 7.

Table 6 Statistic results of the four SAEAs and BISAEA on ZDT1-4 and ZDT6

Table 7 Statistic results of the three EAs and BISAEA on ZDT1-4 and ZDT6

From Tables 6 and 7, it is obvious that BISAEA has the best performance for ZDT1,2, 4 and 6. Both ZDT1 and ZDT4 have convex PF, while ZDT4 is harder to converge. As shown in Fig. 15, only BISAEA and KTA2 can obtain the true PF completely both on ZDT1 and 2 in 30D, and K-RVEA can converge to the PF. Meanwhile, as shown in Table 6, with the dimensions increasing, KTA2 and K-RVEA deteriorate greatly both on convergence and diversity. The reason may be the dimension limitation of the Kriging model.

Fig. 15

The PF of ZDT1 in the run associated with the median IGD value on 30D

Then we focus on ZDT2 and ZDT6, which have concave PF, For ZDT2, only BISAEA and KTA2 can obtain the true PF completely on 30D in Fig. 16. The last discussions occur on ZDT3, whose disconnected PF brings a challenge for diversity. From the average IGD values, we find that BISAEA still has a competitive lead.

Fig. 16

The PF of ZDT2 in the run associated with the median IGD value on 30D

The IGD values iteration process is shown in Fig. 17, it is clear that BISAEA and KTA2 can obtain the desired IGD values quickly (less than 150 NFEs). Moreover, the GD values of four SAEAs, three EAs and BISAEA are shown in Tables 3 and 4 of the supplementary materials, and the runtime of four SAEAs and BISAEA are represented in Table 6 of the supplementary materials, which also indicates the superior performance of BISAEA.

Fig. 17

The IGD values iteration process of five algorithms in ZDT1 and 2

Application to engineering problem

Engineering problem description

As a new type of marine equipment, blend-wing-body underwater gliders (BWBUGs) have been used for ocean observation [48, 49]. BWBUGs adopt a smooth connection between their bodies and wings [50,51,52,53,54]. BWBUGs is a complex multidisciplinary system involving shape, skeleton, pressure cabins, and other disciplines. The shape and skeleton design are important parts of the BWBUGs system design. For the multidisciplinary design for shape and skeleton, a larger lift-drag ratio (L/D), smaller skeleton volume ratio ($V_{s} /V$) and better skeleton strength ($\sigma_{s}$) are expected. The L/D is affected by the shape, angle of attack (AOA) and velocity. The AOA and velocity are set as $2^{^\circ }$ and 1.028 m/s in this article. The larger L/D means the glider has a larger glide angle, which is of great significance to improve the glide range. The smaller the skeleton volume ratio, means the smaller the ratio of skeleton volume to glider volume, the more energy and other equipment it can carry when the glider's gravity and buoyancy are balanced. Moreover, the strength of the skeleton shall be as large as possible to ensure that the glider has higher safety.

The multidisciplinary design of the shape and skeleton for BWBUGs is shown in Fig. 18. The geometry models of the shape and skeleton are obtained by using the parametric methods. The CFD technology is adopted to evaluate the performance of shape by pretreatment and CFD, the FEA technology is used to evaluate the strength of the skeleton. In addition, the shape design is the basis of the skeleton, which means that shape affects the strength of the skeleton in the same thickness of the skeleton. The shape of BWBUGs can be divided into plane shape and wing shape. Both the fuselage profile and the transition mode of the fuselage and wing reflect the wing-body fusion arrangement. The plane shape of the fuselage is created in this part using the Bezier curve.

Fig. 18

The multidisciplinary design of BWBUGs

For the design of the shape, the layouts of 4 sections are adopted as shown in Fig. 18, where L and D₁ are set as 1500 mm and 1000 mm respectively, and the other nine parameters are design variables. Among them, the locations of section 1 and section 4 are fixed. And the locations of the other sections are related to the variable $Z_{2} ,Z_{3}$ and L. Selecting NACA0022, NACA0019, NACA0016 and NACA0012 as the reference airfoil for sections 1, 2, 3, and 4, respectively. The Class-Shape function Transformation (CST) method is used for wing parameterization [55], and the airfoil is controlled by five design variables. There are 29 design variables for the shape design, and the range is shown in Eq. (11)–(16).

$$ {\text{Sec}} tion{1}\left\{ {\begin{array}{*{20}c} {A_{Low} = {[ - 0}{\text{.0860, - 0}}{.0741, - 0}{\text{.0835, - 0}}{.0574, - 0}{\text{.0861]}}} \\ {A_{Up} = {[0}{\text{.0860,0}}{.0741,0}{\text{.0835,0}}{.0574,0}{\text{.0861]}}} \\ \end{array} } \right. $$

(11)

$$ {\text{Sec}} tion2\left\{ {\begin{array}{*{20}c} {A_{Low} = {[ - 0}{\text{.0717, - 0}}{.0618, - 0}{\text{.0696, - 0}}{.0478, - 0}{\text{.0718]}}} \\ {A_{Up} = {[0}{\text{.0717,0}}{.0618,0}{\text{.0696,0}}{.0478,0}{\text{.0718]}}} \\ \end{array} } \right. $$

(12)

$$ {\text{Sec}} tion{3}\left\{ {\begin{array}{*{20}c} {A_{Low} = {[ - 0}{\text{.0573, - 0}}{.0494, - 0}{\text{.0557, - 0}}{.0383, - 0}{\text{.0574]}}} \\ {A_{Up} = {[0}{\text{.0573,0}}{.0494,0}{\text{.0557,0}}{.0383,0}{\text{.0574]}}} \\ \end{array} } \right. $$

(13)

$$ {\text{Sec}} tion{4}\left\{ {\begin{array}{*{20}c} {A_{Low} = {[ - 0}{\text{.0287, - 0}}{.0247, - 0}{\text{.0278, - 0}}{.0191, - 0}{\text{.0287]}}} \\ {A_{Up} = {[0}{\text{.0287,0}}{.0247,0}{\text{.0278,0}}{.0191,0}{\text{.0287]}}} \\ \end{array} } \right. $$

(14)

$$ \begin{gathered} Plane\left\{ \begin{gathered} P_{low} = \left[ {350,\;150,\;350,1000,150,300,500,300,150} \right]mm \hfill \\ P_{up} = \left[ {450,300,400,1200,250,450,600,450,250} \right]mm \hfill \\ \end{gathered} \right. \hfill \\ \, \qquad \qquad (D_{2} ,D_{3} ,D_{4} ,D_{5} ,Z_{1} ,Z_{2} ,Z_{3} ,Z_{4} ,Z_{5} ) \hfill \\ \end{gathered} $$

(15)

$$ A_{shape} = [{\text{section}}1, {\text{section}}2, {\text{section}}3, {\text{section}}4, {\text{Plane}}] $$

(16)

The skeleton is generated based on the shape. Subsequently, the skeleton is defined by 7 geometric parameters in Fig. 18. To be specific, t denotes the thickness of the skeleton, and others related to the geometrical parameters of the shape are given by using Eqs. (17)–(19).

$$ \begin{aligned} rh_{1} &= Z_{1} \\ rh_{2} &= Z_{3} - Z_{1} \\ rh_{3} &= \frac{{Z_{4} - Z_{3} }}{4} \end{aligned} $$

(17)

$$ \begin{gathered} rv_{1} = \frac{{D_{4} }}{2} \hfill \\ rv_{2} = \frac{{D_{4} }}{2} + \frac{{D_{2} }}{4} \hfill \\ rv_{3} = \frac{{D_{2} }}{4} \hfill \\ \end{gathered} $$

(18)

$$ t \in [{5},1{0}]mm $$

(19)

BWBUGs pump water in/out of the reservoir when moving, and the pressure on its outer surface is very small. This article mainly considers the stress in the process of dipping into the water, the distributed force is set as 1000 N in all skeleton.

To obtain better performance of the multidisciplinary design for shape and skeleton, L/D), $V_{s} /V$ and $\sigma_{s}$ are set as the objective. Hence, a 30-dimensional multi-objective optimization problem is summarized below:

$$ \begin{gathered} {\text{min F}}({\mathbf{x}}) = \{ - L/D,V_{s} /V,\sigma_{s} \}^{T} \hfill \\ s.t.{\text{ x}}_{i} \in [A_{{{\text{shape}}}} ,A_{skeleton} ],i = 1,2,...,30 \hfill \\ {\text{ A}}_{{{\text{shape}}}} \in [A_{shapeLow} ,A_{shapeUp} ],A_{skeleton} \in t \hfill \\ \end{gathered} $$

(20)

Optimization results

BISAEA, K-RVEA, and HeE-MOEA are all operated with 500 NFEs, with a population size of 100, for the multidisciplinary design of the shape and skeleton of BWBUGs. The same 200 initial sample points from BISAEA, K-RVEA, and HeE-MOEA are shared for fair comparison and are displayed in Fig. 19. Following the run, the obtained solutions are shown in Fig. 20.

Fig. 19

The initial sample points

Fig. 20

The obtained solutions of K-RVEA, HeE-MOEA and BISAEA

To further compare the performance mathematically, hypervolume is adopted because the actual PF is unknown. The hypervolume values of K-RVEA, HeE-MOEA and BISAEA are 0.6098, 0.5876 and 0.5986, respectively. It is obvious that K-RVEA and BISAEA are at the same level. In addition, the influence of calculation time on optimization efficiency is considered. The computation time of three algorithms under the different number of samples in the optimization process is shown in Fig. 21. The computation times only include the modeling and evolution of the optimization process, leaving out the evaluation of true functions. It is obvious that the time of K-RVEA utilized in different numbers of samples differs greatly, and the time grows as the number of samples rises. HeE-MOEA also has a rule that is somewhat similar to that of K-RVEA. In comparison to K-RVEA and HeE-MOEA, BISAEA shows negligible time variation over a range of sample sizes. The superiority of BISAEA in the multidisciplinary design optimization of BWBUGs can be demonstrated by combining hypervolume values and computation time.

Fig. 21

The computation time of three algorithms under 200, 300 and 400 samples

Besides, the three non-domination solutions of common PF from the three algorithms are selected in Fig. 20, and the pressure nephogram of shape, stress nephogram of the skeleton, and multidisciplinary system model are shown in Figs. 22 and 23.

Fig. 22

Three typical pressure nephogram of shape

Fig. 23

Three typical schemes and their nephogram

Conclusions

In this paper, a bi-indicator-based surrogate-assisted multi-objective evolutionary algorithm named BISAEA is proposed based on two strategies. Pareto-based bi-indicator strategy employs the convergence and diversity indicator as the bi-objective to enhance the convergence and diversity, and the bi-indicator is calculated by the approximate objective values of the RBF model. To further improve the performance of the selected samples, a one-by-one selection strategy is adopted to filter samples. Besides, BISAEA is compared with the four state-of-art SAEAs and three EAs in DTLZ and ZDT benchmark problems on the dimensions of 10, 15, 30 and 50, BISAEA shows high efficiency and a good balance between convergence and diversity. Finally, BISAEA is applied to the multidisciplinary optimization of blend-wing-body underwater gliders with 30 decision variables and three objectives, and the results show its effectiveness on the engineering problem. The overall experiment results and application show that BISAEA has significant competitiveness for some state-of-art algorithms.

For future research, BISAEA may get a further study on the many-objectives optimization and this algorithm will be applied to more engineering problems. Moreover, we will attempt to use the surrogate models to approximate the indicator values directly and adopt some latest technologies in artificial intelligence and machine learning to improve the accuracy of the approximation of surrogate models.