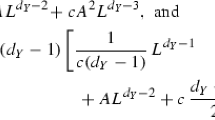Abstract
Let X be a K3 surface. We prove that Addington’s \(\mathbb {P}^n\)-functor between the derived categories of X and the Hilbert scheme of points \(X^{[k]}\) maps stable vector bundles on X to stable vector bundles on \(X^{[k]}\), given some numerical conditions are satisfied.
Similar content being viewed by others
1 Introduction
Moduli spaces of stable sheaves on K3 surfaces are examples of hyperkähler manifolds, also known as compact irreducible holomorphic symplectic manifolds. These arise in the classification of compact Kähler manifolds with trivial first Chern class and are therefore interesting objects to study. It is natural to wonder if moduli spaces of stable sheaves on hyperkähler manifolds of higher dimension also have interesting properties.
Unfortunately moduli spaces of stable sheaves on higher dimensional varieties behave badly in general. Furthermore there are not many explicit examples of stable sheaves on higher dimensional hyperkähler manifolds. There are the tautological bundles on Hilbert schemes of points on a K3 surface and on generalized Kummer varieties, see [1,2,3] and [4]. A second class is given by the “wrong-way” fibers of a universal family of stable vector bundles on a moduli space of stable vector bundles, see [5, 6] and [7].
In this article we want to give a new class of stable sheaves on Hilbert schemes of points. For this we use a result by Addington in [8], saying that the integral functor
with kernel the universal ideal sheaf \({{\,\mathrm{\mathcal {I}_{\mathcal {Z}}}\,}}\) on \(X\times X^{[k]}\) is a \({{\,\mathrm{\mathbb {P}}\,}}^{k-1}\)-functor.
Our main results can be summarized as follows:
Theorem
Let X be a K3 surface with \({{\,\textrm{NS}\,}}(X)=\mathbb {Z}h\) and assume E is a \(\mu _h\)-stable locally free sheaf with Mukai vector \(v=(r,h,s)\) such that
Then the image of E under the integral functor \(\Phi : {{\,\mathrm{D^b}\,}}(X)\rightarrow {{\,\mathrm{D^b}\,}}(X^{[k]})\) is a \(\mu _H\)-stable locally free sheaf on \(X^{[k]}\) (for some ample class \(H\in {{\,\textrm{NS}\,}}(X^{[k]})\)).
Choosing \(v=(r,h,s)\) such that \(v^2+2<2r\) implies that all sheaves classified by the moduli space \({{\,\textrm{M}\,}}_{X,h}(v)\) are locally free. If furthermore \({{\,\textrm{M}\,}}_{X,h}(v)\) is a fine moduli space, then the integral functor \(\Phi \) restricts to a morphism
which identifies \({{\,\textrm{M}\,}}_{X,h}(v)\) with a smooth connected component of a certain moduli space \(\mathcal {M}\) of stable sheaves on \(X^{[k]}\).
The main theorem is not void, that is there are Mukai vectors on certain K3 surfaces that satisfy all conditions stated in the theorem. We will give two examples in Example 4.5.
This result is in the same vein as Yoshioka’s results in [9]. There he starts with an arbitrary K3 surface together with an isotropic Mukai vector v such that \({{\,\textrm{M}\,}}_{X,h}(v)\) is also a fine moduli space with universal family \(\mathcal {E}\). It is well known that \(Y={{\,\textrm{M}\,}}_{X,h}(v)\) is again a K3 surface. He then proves that the Fourier–Mukai transform \(\Phi _{\mathcal {E}}: {{\,\mathrm{D^b}\,}}(X)\rightarrow {{\,\mathrm{D^b}\,}}(Y)\), an equivalence in this case, preserves stability (even S-equivalence classes), given that some numerical conditions are satisfied.
All objects in this text are defined over the field of complex numbers \(\mathbb {C}\).
2 Background on \(\mathbb {P}^{n}\)-functors
We start by recalling some basic facts about the \(\mathbb {P}^n\)-functors we are interested in. For the general definition of \(\mathbb {P}^n\)-functors we refer to Addington’s paper, see [8, Section 4]. For similar results see also [10, Theorem 1.1] and [11].
Definition 1.1
Let X be a K3 surface. Define the integral functor \(\Phi \) by
Thus \(\Phi \) has the universal ideal sheaf \({{\,\mathrm{\mathcal {I}_{\mathcal {Z}}}\,}}\) on \(X \times X^{[k]}\) as kernel. Here \(p: X\times X^{[k]}\rightarrow X^{[k]}\) and \(q: X\times X^{[k]}\rightarrow X\) are the projections. We note that \(\Phi \) is a \({{\,\mathrm{\mathbb {P}}\,}}^{k-1}\)-functor with associated autoequivalence \(H=[-2]\), see [8, Theorem 3.1, Example 4.2(2)].
Remark 2.2
The fact that the integral functor \({\Phi }\) is a \(\mathbb {P}^{k-1}\)-functor with associated autoequivalence \(H=[-2]\) has the following helpful consequence: for any two elements \(E, F\in {{\,\mathrm{D^b}\,}}(X)\) there is an isomorphism of graded vector spaces
see for example [12, Section 2.1].
Remark 2.3
Remark 2.2 shows that if \({{\,\textrm{Ext}\,}}^i_X(E,F)=0\) for \(i<0\), then the natural maps
are isomorphisms for \(i=0\) and 1. This especially applies to the case that E and F are in fact sheaves (interpreted as complexes concentrated in degree zero in \({{\,\mathrm{D^b}\,}}(X)\)).
3 Preservation of slope-stability for vector bundles
Throughout this article we assume that X is a K3 surface with \({{\,\textrm{NS}\,}}(X) = \mathbb {Z}h\), where h is a primitive ample class.
Lemma 1.4
Let E be a \(\mu _h\)-stable vector bundle on X with Mukai vector \(v=(r,h,s)\) such that
then \(\textrm{H}^i(X,E\otimes I_Z)=0\) for \(i=1,2\) and all \([Z]\in X^{[k]}\).
Proof
Note that \(I_Z\) is \(\mu _h\)-stable with \(\mu _h(I_Z)=0\) so
by [13, Proposition 1.2.7] as \(\mu _h(E^{*})<0\).
Next we prove that \(\textrm{H}^1(E\otimes I_Z)=0\) for all \([Z]\in X^{[k]}\), following the proof of [14, Proposition 2.2.].
Assume \(\textrm{H}^1(X,E\otimes I_Z)\ne 0\). By Serre duality we find
Thus there is a non-trivial extension

Using [15, Lemma 2.1] shows that G is also \(\mu _h\)-stable with Mukai vector
The Euler characteristic of a pair \((F_1,F_2)\) of coherent sheaves can be expressed as
We can now compute
Using the inequality (1) shows that we have \(\chi (G,G)\geqslant 4\). But this implies
One more application of Serre duality thus gives \(\textrm{hom}_X(G,G)\geqslant 2\). But this impossible, since G is simple, as it is \(\mu _h\)-stable. So we do have \(\textrm{H}^1(X,E\otimes I_Z)=0\). \(\square \)
Corollary 1.5
Let E be a locally free \(\mu _h\)-stable sheaf with Mukai vector \(v=(r,h,s)\) satisfying the inequality (1), then
We are now ready to study the image of a \(\mu _h\)-stable locally free sheaf with Mukai vector \(v=(r,h,s)\) under the \(\mathbb {P}^{k-1}\)-functor \(\Phi \). A priori this object is just a complex in \({{\,\mathrm{D^b}\,}}(X^{[k]})\) but in our situation we have:
Lemma 1.6
Let E be a locally free \(\mu _h\)-stable sheaf with Mukai vector \(v=(r,h,s)\) satisfying the inequality (1), then \(\Phi (E)\) is a locally free sheaf of rank \(r+s-rk\) on \(X^{[k]}\).
Proof
Using cohomology and base change results, the vanishing in Lemma 3.1 implies
Consequently \(\Phi (E)=p_{*}(q^{*}E\otimes {{\,\mathrm{\mathcal {I}_{\mathcal {Z}}}\,}})\) is a sheaf. Furthermore the map
is constant. Therefore \(p_{*}(q^{*}E\otimes {{\,\mathrm{\mathcal {I}_{\mathcal {Z}}}\,}})\), that is \(\Phi (E)\), is indeed a locally free sheaf on \(X^{[k]}\). As the fiber at a point [Z] is just \(\textrm{H}^0(X,E\otimes I_Z)\) the rank follows from Corollary 3.2. \(\square \)
Next we want to study the slope-stability of \(\Phi (E)\). For this we recall that in our situation we have
where \(h_k\) is the divisor on \(X^{[k]}\) induced by the divisor h on X and \(2\delta \) is the exceptional divisor of the Hilbert–Chow morphism \(X^{[k]}\rightarrow X^{(k)}\). For any coherent sheaf F on X we denote the associated coherent tautological sheaf by
Lemma 1.7
Let E be a locally free \(\mu _h\)-stable sheaf with Mukai vector \(v=(r,h,s)\) satisfying the inequality (1), then \(c_1(\Phi (E))=-h_k+r\delta \).
Proof
By Lemma 3.3 we have \(R^1p_{*}(q^{*}E\otimes \mathcal {I}_{\mathcal {Z}})=0\), thus there is an exact sequence:

We have
and the sheaf \(p_{*}(q^{*}E\otimes {{\,\mathrm{\mathcal {O}}\,}}_{\mathcal {Z}})\) is by definition the tautological bundle \(E^{[k]}\). The exact sequence (2) can be rewritten as

Using [4, Lemma 1.5] we get
\(\square \)
We also recall the notations introduced by Stapleton in [3, Section 1]. The ample divisor h on X induces the ample divisor
on \(X^k\), where \(q_i\) is the i-th projection from \(X^k\), as well as a semi-ample divisor \(h_k\) on \(X^{[k]}\).
We denote by \(X^k_\circ \), \(S^kX_\circ \) and \(X^{[k]}_\circ \) the loci of the relevant spaces parametrizing distinct points. The natural map
is an étale cover and \(j: X^k_\circ \rightarrow X^k\) is an open embedding. Given a coherent sheaf F on \(X^{[k]}\), we denote by \(F_\circ \) the restriction of F to \(X^{[k]}_\circ \), and define
which is a torsion free coherent sheaf on \(X^k\) if F is on \(X^{[k]}\). Coherence follows since the complement of \(X^k_{\circ }\) has codimension two, see, e.g. [16, Théorème 1, Théorème 2]. It is torsion free since \(j: X^k_{\circ }\hookrightarrow X^k\) is dominant, see [17, Proposition 7.4.5].
Lemma 1.8
Let E be a locally free \(\mu _h\)-stable sheaf with Mukai vector \(v=(r,h,s)\) satisfying the inequality (1), then
Proof
Note that \((-)_\circ \) and \({\overline{\sigma }}_\circ ^*(-)\) are exact, and \(j_*(-)\) is left exact. Applying these functors to (3) we obtain an exact sequence of \({\mathfrak {S}}_k\)-invariant reflexive sheaves on \(X^k\):

where \(\varphi \) may not be surjective. Certainly we have
and also by [3, Lemma 1.1]
The above sequence can be written as

More accurately, \(\varphi \) is the evaluation map on \(X^k_\circ \): for any k-tuple \((x_1,\ldots , x_k) \in X^k\) of closed points with \(x_i \ne x_j\), the morphism of fibers can be written as
Since for a non-trivial section \(s \in \textrm{H}^0(E)\), one can always choose a k-tuple of distinct points \((x_1,\ldots x_k) \in X^k\) with \((s(x_1),\ldots , s(x_k)) \ne (0,\ldots , 0)\), we see that the induced map
is injective. It follows by exact sequence (5) that \(\left( \Phi (E) \right) _{X^k}\) has no global sections. \(\square \)
Proposition 1.9
Let E be a locally free \(\mu _h\)-stable sheaf with Mukai vector \(v=(r,h,s)\) satisfying the inequality (1), then the locally free sheaf \(\Phi (E)\) defined in Lemma 3.3 is slope stable with respect to \(h_k\).
Proof
We follow the proof of [3, Theorem 1.4] and start with the exact sequence

and note that \(\varphi \) is surjective on \(X^k_\circ \), hence its cokernel \({{\,\textrm{coker}\,}}(\varphi )\) is supported on the big diagonal of \(X^k\), which is of codimension 2. We get
Now assume G is a reflexive subsheaf of \(\Phi (E)\). Then \((G)_{X^k}\) is an \({\mathfrak {S}}_k\)-invariant reflexive subsheaf of \(\left( \Phi (E) \right) _{X^k}\). By [3, Lemma 1.2] we have
It is therefore enough to prove that \(\left( \Phi (E) \right) _{X^k}\) has no \({\mathfrak {S}}_k\)-invariant destabilizing subsheaf (with respect to \(h_{X^k}\)). Assume F is an \({\mathfrak {S}}_k\)-invariant subsheaf, then we find:
If \(a \leqslant -1\), then
Since \(1 \leqslant {{\,\textrm{rk}\,}}(F) < {{\,\textrm{rk}\,}}(\left( \Phi (E) \right) _{X^k})\), we see that \(\mu _{h_{X^k}}(F) < \mu _{h_{X^k}}(\left( \Phi (E) \right) _{X^k})\). Hence F is not destabilizing.
If \(a=0\), we pick a (not necessarily \({\mathfrak {S}}_k\)-invariant) nonzero stable subsheaf \(F' \subseteq F\) that has maximal slope with respect to \(h_{X^k}\) (for example one could take a stable factor in the first Harder–Narasimhan factor of F). Without loss of generality, we may assume F and \(F'\) are both reflexive. Since \(F'\) is also a subsheaf of \(\textrm{H}^0(E)\otimes {{\,\mathrm{\mathcal {O}}\,}}_{X^k}\), there is a projection from \(\textrm{H}^0(E)\otimes {{\,\mathrm{\mathcal {O}}\,}}_{X^k}\) to a certain direct summand of it, such that the composition of the embedding and projection
is nonzero. Since
and \({{\,\mathrm{\mathcal {O}}\,}}_{X^k}\) is also stable with respect to \(h_{X^k}\), the map \(F' \rightarrow {{\,\mathrm{\mathcal {O}}\,}}_{X^k}\) must be injective, and its cokernel is supported in codimension at least 2. Since both sheaves are reflexive, we must have \(F' = {{\,\mathrm{\mathcal {O}}\,}}_{X^k}\). As a result F, and consequently \(\left( \Phi (E)\right) _{X^k}\), have non-trivial global sections, a contradiction to Lemma 3.5.
If \(a \geqslant 1\), F would be a subsheaf of the trivial bundle \(\textrm{H}^0(E) \otimes {{\,\mathrm{\mathcal {O}}\,}}_{X^k}\) of positive slope which is not possible since a trivial bundle is semistable of slope zero.
\(\square \)
Theorem 1.10
Let E be a locally free \(\mu _h\)-stable sheaf with Mukai vector \(v=(r,h,s)\) satisfying the inequality (1), then \(\Phi (E)\) is a locally free \(\mu _H\)-stable sheaf for some ample class \(H \in {{\,\textrm{NS}\,}}(X^{[k]})\) near \(h_k\).
Proof
Proposition 3.6 and [18, Theorem 2.3.1] guarantee that the assumptions in [3, Proposition 4.8] are satisfied for \(\Phi (E)\), hence \(\Phi (E)\) is slope stable with respect to some ample class H near \(h_k\) by [3, Proposition 4.8]. \(\square \)
Remark 3.8
-
1.
Here we understand slope stability with respect to the non-ample divisor \(h_k\) as slope stability with respect to a movable curve class. This stability was studied in detail by Greb, Kebekus and Peternell in [19, Section 2.2]. They show that all elementary properties satisfied by sheaves that are stable with respect to an ample polarization also hold for this notion of stability.
-
2.
We restrict to locally free sheaves in this paper for two reasons: The first is to pass freely between \(\textrm{H}^{*}(E\otimes I_Z)\) and \({{\,\textrm{Ext}\,}}_X^{2-*}(I_Z,E^{*})\) in Lemma 3.1. The second reason is that we use Stapleton’s description of \((E^{[k]})_{X^k}\), see [3, Lemma 1.1]. This result uses the fact that \((E^{[k]})_{X^k}\) and \(E^{\boxplus k}\) are reflexive (since they are locally free). But this fails if we start with a torsion free but not locally free sheaf E.
4 A morphism of moduli spaces
In the last section we saw that given a locally free \(\mu _h\)-stable sheaf E with Mukai vector v satisfying the inequality (1), then there is an ample class \(H\in {{\,\textrm{NS}\,}}(X^{[k]})\) such that \(\Phi (E)\) is a locally free \(\mu _H\)-stable sheaf on \(X^{[k]}\).
In this section we want to see that in certain cases we get a morphism
for some moduli space \(\mathcal {M}\) of stable sheaves on \(X^{[k]}\).
Let \(v=(r,h,s)\) be a Mukai vector satisfying the following conditions:
-
1.
v satisfies the inequality (1),
-
2.
all sheaves classified by \({{\,\textrm{M}\,}}_{X,h}(v)\) are locally free and
-
3.
the moduli space \({{\,\textrm{M}\,}}_{X,h}(v)\) is fine.
Let \(v=(r,h,s)\) be a Mukai vector that satisfies the conditions (1) and (2). Then for every \([E]\in {{\,\textrm{M}\,}}_{X,h}(v)\) we know that there is an ample class H such that \(\Phi (E)\) is \(\mu _H\)-stable. One may ask how H depends on [E]. This question is answered in the following theorem.
Theorem 1.12
Let v be a Mukai vector that satisfies conditions (1) and (2), then there is an ample class \(H\in {{\,\textrm{NS}\,}}(X^{[k]})\) such that \(\Phi (E)\) is \(\mu _H\)-stable for all \([E]\in {{\,\textrm{M}\,}}_{X,h}(v)\) simultaneously.
Proof
The proof is same as for [6, Theorem 2.8]. We just have to replace the sheaf \(E_x\) by \(\Phi (E)\) and the surface X by the moduli space \({{\,\textrm{M}\,}}_{X,h}(v)\). Then we note that the value of
is independent of the choice of \([E] \in {{\,\textrm{M}\,}}_{X,h}(v)\) by Lemma 3.4.
The finiteness of the set
can be seen as follows: using Corollary 3.2 and exact sequence (3) we see that every \(\Phi (E)\) is a subsheaf of \({{\,\mathrm{\mathcal {O}}\,}}_{X^{[k]}}^{r+s}\). Hence S is a subset of
But \(S'\) is finite due to [19, Theorem 2.29], so S is also finite. The rest of the proof works unaltered. \(\square \)
From now on we fix a Mukai vector v that satisfies conditions \((1)-(3)\) and an ample class \(H\in {{\,\textrm{NS}\,}}(X^{[k]})\) that satisfies Theorem 4.1. We denote by \({{\,\textrm{M}\,}}_{X^{[k]},H}(\Phi ^C(v))\) the moduli space of \(\mu _H\)-stable sheaves on \(X^{[k]}\) with Mukai vector \(\Phi ^C(v)\). Here
is the induced cohomological Fourier–Mukai transform, see [20, 5.28, 5.29].
In the following we want to give an explicit construction of the morphism
We start by constructing a classifying family for the \(\Phi (E)\).
Lemma 1.13
There is a family \(\mathcal {F}\) of sheaves on \(X^{[k]}\times {{\,\textrm{M}\,}}_{X,h}(v)\), flat over \({{\,\textrm{M}\,}}_{X,h}(v)\), such that for every \([E]\in {{\,\textrm{M}\,}}_{X,h}(v)\) the restriction to the fiber over [E] is given by
Proof
As \({{\,\textrm{M}\,}}_{X,h}(v)\) is fine, there is a universal family \(\mathcal {U}\) on \(X\times {{\,\textrm{M}\,}}_{X,h}(v)\), flat over \({{\,\textrm{M}\,}}_{X,h}(v)\). Lemma 3.3 shows that the complex \(\Phi (\mathcal {U}_{[E]})=\Phi (E)\) is in fact a sheaf on \(X^{[k]}\) for every \([E]\in {{\,\textrm{M}\,}}_{X,h}(v)\). The existence of the family \(\mathcal {F}\) now follows from [21, Proposition 4.2]. \(\square \)
The family \(\mathcal {F}\) induces a classifying morphism
The morphism f has the following property:
Theorem 1.14
The family \(\mathcal {F}\) identifies \({{\,\textrm{M}\,}}_{X,h}(v)\) with a smooth connected component of \({{\,\textrm{M}\,}}_{X^{[k]},H}(\Phi ^C(v))\).
Proof
Using the family \(\mathcal {F}\) as the kernel of an integral functor, we get an induced morphism
which is the Kodaira–Spencer map of the family \(\mathcal {F}\) at the point \([E]\in {{\,\textrm{M}\,}}_{X,h}(v)\) by [21, Proposition 4.4]. Using the canonical identifications
one can rewrite the induced morphism as
which is an isomorphism by Remark 2.3.
This implies that the classifying map \(f: {{\,\textrm{M}\,}}_{X,h}(v) \longrightarrow {{\,\textrm{M}\,}}_{X^{[k]},H}(\Phi ^C(v))\) is étale and surjective onto a smooth connected component. But using again Remark 2.3 shows that f has to be of degree one since for \([E]\ne [F]\in {{\,\textrm{M}\,}}_{X,h}(v)\) we have
So f must be an isomorphism to a smooth connected component. \(\square \)
Remark 4.4
This argument uses essentially the same arguments as the proof in [22, Section 1] where a component in a moduli space of stables bundles on a moduli space of bundles on a curve is constructed.
Theorem 4.1 and Theorem 4.3 are not void, that is there are Mukai vectors on certain K3 surfaces that satisfy conditions \((1)-(3)\). Here we give two examples:
Example 4.5
-
1.
Let X be a K3 surface with \({{\,\textrm{NS}\,}}(X)=\mathbb {Z}h\) such that \(h^2=50\). For \(k=2\) the Mukai vector \(v=(3,h,8)\) satisfies the conditions \((1)-(3)\): we have \(\chi =11\). On the other hand \(v^2=h^2-48=2\) and \((r+1)k=8\) so that \(\chi =11 \geqslant 10=\frac{v^2}{2}+(r+1)k+1\). A further computation shows \(v^2+2 = 4 < 6 =2r\) so that all sheaves in \({{\,\textrm{M}\,}}_{X,h}(v)\) are locally free by [7, Lemma 4.4.2]. As \(\textrm{gcd}(3,8)=1\) we see that \({{\,\textrm{M}\,}}_{X,h}(v)\) is a fine moduli space by [13, Corollary 4.6.7]. In this case we have \(\dim ({{\,\textrm{M}\,}}_{X,h}(v))=4\) which gives a four-dimensional component in \({{\,\textrm{M}\,}}_{X^{[2]},H}(\Phi ^C(v))\).
-
2.
Let X be a K3 surface with \({{\,\textrm{NS}\,}}(X)=\mathbb {Z}h\) such that \(h^2=186\). Then a similar computation shows that for \(k=3\) then the Mukai vector \(v=(5,h,18)\) satisfies the conditions \((1)-(3)\). In this example \(\dim ({{\,\textrm{M}\,}}_{X,h}(v))=8\) which gives an eight-dimensional component in \({{\,\textrm{M}\,}}_{X^{[3]},H}(\Phi ^C(v))\).
Data Availability
Data sharing not applicable to this article as no datasets were generated or analysed during the current study.
References
Reede, F., Zhang, Z.: Stable vector bundles on generalized Kummer varieties. Forum Math. 34(4), 1015–1031 (2022). https://doi.org/10.1515/forum-2021-0249
Schlickewei, U.: Stability of tautological vector bundles on Hilbert squares of surfaces. Rend. Semin. Mat. Univ. Padova 124, 127–138 (2010). https://doi.org/10.4171/RSMUP/124-7
Stapleton, D.: Geometry and stability of tautological bundles on Hilbert schemes of points. Algebra Number Theory 10(6), 1173–1190 (2016). https://doi.org/10.2140/ant.2016.10.1173
Wandel, M.: Tautological sheaves: stability, moduli spaces and restrictions to generalised Kummer varieties. Osaka J. Math. 53(4), 889–910 (2016)
Reede, F., Zhang, Z.: Examples of smooth components of moduli spaces of stable sheaves. Manuscripta Math. 165(3–4), 605–621 (2021). https://doi.org/10.1007/s00229-020-01223-0
Reede, F., Zhang, Z.: Stability of some vector bundles on Hilbert schemes of points on K3 surfaces. Math. Z. 301(1), 315–341 (2022). https://doi.org/10.1007/s00209-021-02920-6
Wray, A.: Moduli Spaces of Hermite-Einstein Connections over K3 Surfaces. PhD thesis, University of Oregon (2020)
Addington, N.: New derived symmetries of some hyperkähler varieties. Algebr. Geom. 3(2), 223–260 (2016). https://doi.org/10.14231/AG-2016-011
Yoshioka, K.: Stability and the Fourier-Mukai transform. II. Compos. Math. 145(1), 112–142 (2009). https://doi.org/10.1112/S0010437X08003758
Markman, E., Mehrotra, S.: Integral transforms and deformations of K3 surfaces. Preprint arXiv:1507.03108 (2015)
Anno, R., Logvinenko, T.: \({\mathbb{P}}^n\)-functors. Preprint arXiv:1905.05740 (2019)
Addington, N., Donovan, W., Meachan, C.: Moduli spaces of torsion sheaves on K3 surfaces and derived equivalences. J. Lond. Math. Soc. (2) 93(3), 846–865 (2016). https://doi.org/10.1112/jlms/jdw022
Huybrechts, D., Lehn, M.: The Geometry of Moduli Spaces of Sheaves, 2nd edn. Cambridge Mathematical Library. Cambridge University Press, Cambridge. https://doi.org/10.1017/CBO9780511711985
Marian, A., Oprea, D., Pandharipande, R.: Higher rank Segre integrals over the Hilbert scheme of points. J. Eur. Math. Soc. (JEMS) (2021). https://doi.org/10.4171/JEMS/1149
Yoshioka, K.: Some examples of Mukai’s reflections on \(K3\) surfaces. J. Reine Angew. Math. 515, 97–123 (1999). https://doi.org/10.1515/crll.1999.080
Serre, J.-P.: Prolongement de faisceaux analytiques cohérents. Ann. Inst. Fourier (Grenoble) 16(fasc. 1), 363–374 (1966)
Grothendieck, A.: Éléments de géométrie algébrique. I. Le langage des schémas. Inst. Hautes Études Sci. Publ. Math. (4), 228 (1960)
de Cataldo, M.A.A., Migliorini, L.: The hard Lefschetz theorem and the topology of semismall maps. Ann. Sci. École Norm. Sup. (4) 35(5), 759–772 (2002). https://doi.org/10.1016/S0012-9593(02)01108-4
Greb, D., Kebekus, S., Peternell, T.: Movable curves and semistable sheaves. Int. Math. Res. Not. IMRN 2, 536–570 (2016). https://doi.org/10.1093/imrn/rnv126
Huybrechts, D.: Fourier-Mukai Transforms in Algebraic Geometry. Oxford Mathematical Monographs. The Clarendon Press, Oxford University Press, Oxford. https://doi.org/10.1093/acprof:oso/9780199296866.001.0001
Bridgeland, T.: Equivalences of triangulated categories and Fourier-Mukai transforms. Bull. London Math. Soc. 31(1), 25–34 (1999). https://doi.org/10.1112/S0024609398004998
Lange, H., Newstead, P.E.: On Poincaré bundles of vector bundles on curves. Manuscripta Math. 117(2), 173–181 (2005). https://doi.org/10.1007/s00229-005-0553-6
Acknowledgements
I thank Ziyu Zhang for many useful discussions. I am also grateful to the anonymous referees who helped to improve the presentation of the manuscript greatly.
Funding
Open Access funding enabled and organized by Projekt DEAL.
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Reede, F. Stability and certain \(\mathbb {P}^n\)-functors. Res Math Sci 10, 42 (2023). https://doi.org/10.1007/s40687-023-00405-y
Received:
Accepted:
Published:
DOI: https://doi.org/10.1007/s40687-023-00405-y