General equilibrium analysis of trade and environment under alternative market structure: a computable general equilibrium study for India

Abstract

The purpose of the present paper is to understand general equilibrium implications of international trade and globalization on social welfare and environmental emission caused on account of energy consumption by production sectors and domestic households. We applied computable general equilibrium (CGE) modelling as our relevant methodology following Shoven and Whalley (J Econ Lit XXII:1007–1051, 1984). Constructing an energy/environmental social accounting matrix (SAM), paper attempts to purport the effects of liberalized trade over different macroeconomic aspects, energy consumption and green house gas emission through an environmental CGE model logically based on SAM. Attempts have been made to simulate various trade related policies like import liberalization, foreign capital inflow and use of energy saving technologies for examining the impact over macroeconomic variables and domestic physical environment under both perfect and monopolistic competition market structure assumption.

Introduction

Environmental emission now a day has received great deal of attentions so far as global sustainable development is concerned. Advocates of free trade sometimes point out that developing economies emerge as the ‘pollution haven’ for dirty manufacturing industries migrated from developed nations owing to their lax environmental standard (see Copeland and Taylor 1994). It is doubtful whether freer trade policy, has expanded global production structure by employing resources in efficient lines of production since production takes place under imperfect competition; it is strongly likely that it has damaged the economy by changing pollution levels adversely through scale, technique and composition effects (see Grossman and Krueger 1993). Serious question thus arise while formulating appropriate energy/environmental policies whether less developed country like India has been ‘Pollution Haven’ due to the migration of dirty manufacturing industries during the period of economic liberalization.

With the expanding globalization Indian economy embraces rapid industrialization which led to greater consumption of energy inputs as well as deterioration of environmental standard by generating air pollution. A very serious cognizance now a day has been developed among the policy makers to search for low carbon emission strategies for India that could reduce carbon-di-oxide emission intensity by 25–30 % by 2020 starting from India’s 12th 5-year-plan period in April 2012.¹ It is thus a very pertinent question how international trade in the phase of liberalized regime has affected the pattern of India’s energy consumption and greenhouse gas (GHG) emission generated through fossil fuel burning.

Considering various kinds of energy sectors like (a) electricity (b) petroleum and its products, (c) coal and (d) natural gas and (e) bio-fuel attempts have been made to study different trade policy effects on energy consumption pattern, environmental emission and different economic factors. In particular, we studied the impact of trade liberalization and foreign capital inflow on different macro-economic factors, energy consumption and domestic physical environment by formulating country specific environmental computable general equilibrium model following Conrad and Schroder (1993).To measure ‘Pollution Haven’ effect, an indicator has been considered known as pollution terms of trade (PTOT) proposed by Antweiler (1996). Trade policy effects have also been studied on PTOT.

Since pure theory of international trade is not much akin to perfectly competitive set up, monopolistically competitive market structure is assumed with the presence of scale economy in production structures and consumer’s love for variety by introducing (Spence 1976; Dixit and Stiglitz 1977) type social welfare function in the demand side of the model. To address our research problems we applied Computable General Equilibrium (CGE) approach as it seems to be most appropriate methodology for policy simulations. For calibration of our model we used Social Accounting Matrix (SAM) of India for the year 2003–2004 constructed by Shaluja and Yadav (2006) and aggregated it into Energy/Environmental SAM according to our requirement.

CGE modelling originates its foundation with the works of Adelman and Robinson (1978), Shoven and Whaley (1984), Dixon et al. (1982) and others. They have studied impacts of socially relevant policy changes over different macroeconomic aspects in an open economy applied general equilibrium framework. Among them, Shoven and Whaley (1984) examined trade and tax policies for the Canadian economy while Dixon et al. (1982) studied trade policies for the Australian economy using empirical General equilibrium models. In Indian context CGE models are constructed by Parikh et al. (1997), Panda and Quizon (2001) and many others. However, none of the studies has included environmental externality exclusively in Indian context using CGE models. This research gap has been traced in this paper by way of addressing Energy consumption and Environmental problems exclusively in an open economy Computable General Equilibrium framework.

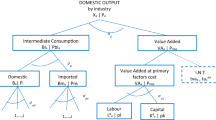
Social accounting matrix

CGE models are traditionally based on SAM which is matrix representation of all transactions and transfers that takes place between different production activities, various factors of production and different institutions like households, corporate and government within the country and with respect to rest of the world in a particular financial year. SAM therefore defines a comprehensive framework that can depict full circular flow of income from production activities to factor service providers like households. Each row of a SAM represents total receipts of any account and column represents expenditure of that account. Therefore, row total is supposed to be equal with corresponding column total. An entry in the ith row and jth column represents receipts of ith account from the jth account.²

A SAM is a database and extension over input/output matrix (I/O). Use of I/O matrix is widely accepted with the pioneering work of Wassily Leontief. I/O matrix, however, does not represent interrelationship between factor value added and agent’s final expenditure. Extension of an I/O table with the introduction agent’s behaviour and institutional characteristics one can get essential features of a SAM. This can depict entire circular flow of income much more effectively. Our environmental CGE model is based on schematic structure of SAM and for calibration of the model we constructed Energy/Environmental SAM for India for the year 2003–2004 following Saluja and Yadav (2006) (Table 1).³

Structure of energy/environmental CGE

Sectors and agents: Following SAM for India of the year 2004 produced by Saluja and Yadav (2006) and Ojha et al. (2009) we grouped all sectors of the economy into seven aggregated sectors, i.e. (1) primary sector consists of all agricultural products, minerals, primary products such as iron ores, crude petroleum and agro process activities, (2) secondary sector is comprised mainly of all manufacturing activities like, cotton and textile, plastic, rubber and lather products, cement, different chemical products etc., (3) tertiary sector consists infrastructural services and other service sectors like education, health care services, public administration, bank and insurance, postal services etc. and four separate energy sectors, (4) electricity, (5) coal, (6) natural gas and petroleum products and (7) bio-mass. ⁴ We considered four types of agents in the economy, i.e. (a) household, (b) firm, (c) government and (d) rest of the world (ROW). There are four types of households, i.e. (i) RHH-1 (rural agricultural and other labourers), (ii) RHH-2 (agricultural self employed and other households), (iii) UHH-1(urban salaried class) and (iv) UHH-2(urban casual labour and others). All other countries and regions are clubbed together into ROW.

Production and factor inputs: We have considered two basic factors of production i.e. labour and capital that take part in the production process within which substitution is possible through Cobb–Dauglus production technology. Each production unit requires intermediate inputs following fixed coefficient type Liontief technology. Apart from intermediate inputs and basic factors, production sectors require energy inputs as fuels. We assumed four types of energy inputs (a) coal, (b) natural gas and oil, (c) electricity and (d) biomass.

Prices: Product prices are determined from the equality of price and average cost. Average cost is comprised of basic factor cost, cost of intermediate inputs that includes cost of energy inputs. Increasing returns to scale is assumed through the presence of fixed cost in the production units.

Household income and expenditure: Households are rendering factor services in terms of labour and capital while in return they are receiving factor payments in the form of wages and rentals. We have considered four types of household, two of them are rural type and other two are urban type. Household spends his income for consumption purposes. We have assumed linier expenditure system type demand function for household.

Government income and expenditure: Source of income of the Government is (a) direct, indirect and corporate taxes, (b) import tariff⁵, (c) income from entrepreneurial activity. In the expenditure front we assumed government’s expenditure in any sector is exogenously determined, i.e. determined in the government’s budget and adjusted to benchmark SAM. Difference between government’s income and expenditure is government’s savings.⁶

Investment and savings: We considered neo-classical type closure rule where investment is guided by saving. Total saving is comprised of (i) household saving, (ii) government saving, (iii) corporate saving, (iv) foreign savings. Total saving is converted to total investment.

Armington function and trade: International trade in our model is guided by Armington function. Total availability of composite commodity in the domestic economy is composed of domestically produced variety of the good demanded by the domestic people and foreign variety of the same good. Both types of variety is combined together following a constant elasticity of substitution type preference function.

Production of output and transformation: Total supply of each domestic good produced using labour, capital and intermediate input is used up by export of that good and to meet up domestic demand of domestic variety. Both export and domestic demand of the produced good is combined together following CES type transformation function.

Factor prices and equilibrium: We consider two basic factors of production i.e. labour and capital. The quantity supplied of each factor is fixed at the observed level, i.e. factor value added observed in SAM database. Economy wide factor prices are free to vary to assure that sum of demands from all production activities equals to the quantity supplied.⁷ An increase in factor price raises factor payment per unit of the factor in each production activity, which is inversely related to the quantities of factor demand. All factors are mobile between the demanding production activities.

Equilibrium in commodity market: In the commodity market total supply of the composite commodity is constituted by domestic variety as well as imported foreign variety corresponds to each good. Demand for the composite commodity is generated from household consumption, government consumption expenditure, total investment demand and demand for intermediate input. Composite commodity prices are determined from the demand and supply of composite commodities.

GDP and Welfare: Under perfect competition GDP has been computed adding all sectoral outputs. Social welfare has been of Cobb–Dauglus type and depends on private household consumption.

Inclusion of market imperfection in CGE model

Standard trade theory models based on perfect competition assumption is not very much akin to the reality. In order to explain actual patterns of trade commonly visible among the industrial countries or prevalent trade arising out of two—way exchanges of differentiated products among the similar countries, a new trade theory framework is essential which could comprehensively include—economies of scale, the possibility of product differentiation and imperfect competition (Krugman 1980).

In our analysis, we assumed presence of fixed cost in the production sector which gives rise to economics of scale at the firm level enabling the firms to have sufficient market power in respect of price setting. Firms may act cooperatively or non-cooperatively. In this point, we have been restricted to non-cooperative behaviour of firms only as we followed Helpman and Krugman (1985)⁸ essentially.

The outcome of non-cooperative behaviour of firms in an industry depends on two factors: (a) strategic aspects of non-cooperation, (b) condition of entry and exit in the industry. Most of the theoretical works on trade models incorporating oligopoly⁹ considered either output decision or price decision as strategic variables. In our analysis, we followed Monopolistic competition approach based on the assumption of Bertrand-type competition where each firm takes rival’s price as given while taking decision over his own price. We also assume, firms are able to differentiate their products such that products are not perfect substitute for those products of existing competitors as well as potential entrants. Here each firm is acting as monopolist facing downward sloping demand curve. Regarding entry we assumed no barriers to entry or free entry that drives profit to zero. This is known as Chemberlin’s ‘large group’ case which is quite consistent with Bertrand model.

Inclusion of fixed cost

We modelled fixed cost as the part of total cost which is invariant to output. In actual practice it is not the ‘sunk’ cost but a recurrent expenditure must be incurred by the firms in each year to carry on production process. For example: maintenance cost of building and construction, machinery, various equipments¹⁰ etc. We further assume certain part of the total capital cost is fixed cost which is independent of output. Presence of fixed cost implies, higher output production reduces per unit capital cost. This gives sufficient market power to the existing farms. According to our assumption scale economy is external to the firms but internal to the industry.¹¹

$$ {\text{pz(j)}} = \underbrace{{{\text{ay(j)}} \times {\text{py(j)}}}}_{{\text{Basic}}\,{\text{factor}}\,{\text{cost}}} + \underbrace{{\sum\limits_{\text{i}} {{\text{ax(i,j)}} \times {\text{pq(i)}}}}}_{{\text{Intermediate}}\,{\text{input}}\,{\text{cost}}} + \underbrace{{\text{FC(j)/Z(j)}}}_{{\text{Average}}\,{\text{fixed}}\,{\text{cost}}} ; $$

(1)

Above equation shows that average total cost is the sum of (a) unit basic factor cost, (b) unit intermediate input cost and (c) average fixed cost. Unit basic factor cost includes both labour and capital cost while capital cost excludes fixed cost.

Inclusion of consumer’s preference for varieties

Preferences for differentiated products can be introduced by assuming commodities are being consumed by the individuals with different varieties. Following the works of Spence (1976), Dixit and Stiglitz (1977) individual preference for varieties can be modelled by specifying concave shaped and symmetrical sub-utility functions for each commodities in the form of $u_{i} = u\left( {D_{i1} ,D_{i2} , \ldots } \right)$ where $D{}_{i\omega }$ is the quantity of ith good being consumed with $\omega$ variety. There can be an infinite number of potential varieties which can be produced. But assuming certain amount of fixed costs present in the industry, only finite numbers of varieties are supplied to the consumers in equilibrium.¹²

The CES sub utility function

A workable form of sub utility function can be specified as symmetrical constant elasticity of substitution function which can be represented as follows:

$$ U_{i} = \left( {D_{i1} ,D_{i2} , \ldots } \right) \equiv \left( {\sum\limits_{\omega } {D_{i\omega }^{\beta i} } } \right)^{{{1 \mathord{\left/ {\vphantom {1 {\beta_{i} }}} \right. \kern-0pt} {\beta_{i} }}}} ,\quad \beta_{i} \equiv \left( {1 - \frac{1}{{\sigma_{i} }}} \right),\quad \,\sigma_{i} \ge 1, $$

(2)

Equation 2 is a Dixit–Stiglitz type utility functions, where $\sigma_{i}$ is the elasticity of substitution between two varieties of the same product i. The need of elasticity of substitution greater than one stems from the requirement that elasticity of demand is larger than one. If we have $n_{i}$ number of variety for the good i, then all varieties will be priced almost equally at $p_{i}$.

Demand function can be obtained following Dixit and Stiglitz (1977)¹³ as follows:

$$ D_{i\omega } = \frac{{p_{i\omega }^{{ - \sigma_{i} }} }}{{\sum\nolimits_{{\varpi \in \Upomega_{i} }} {p_{i\varpi }^{{1 - \sigma_{i} }} } }}E_{i} \,\omega \in \Upomega_{i} $$

(3)

Here $p_{i\omega }$ is the price of variety $\omega$ and $\Upomega_{i}$ is the set of all available varieties and $E_{i}$ is the expenditure on ith product. Price elasticity of demand faced by the firm that produces variety $\omega$ can be represented by the following expression¹⁴:

$$ E_{p} = \sigma_{i} + \frac{{p_{i\omega }^{{1 - \sigma_{i} }} }}{{\sum\nolimits_{\omega \in \Upomega } {p_{i\varpi }^{{1 - \sigma_{i} }} } }}\left( {1 - \sigma_{i} } \right) $$

(4)

When all varieties of the ith product are equally priced second term of the expression becomes ${{\left( {1 - \sigma_{i} } \right)} \mathord{\left/ {\vphantom {{\left( {1 - \sigma_{i} } \right)} {n_{i} }}} \right. \kern-0pt} {n_{i} }}$. This simplifies the expression for price elasticity as follows:

$$ {E_{P} = \sigma_{i} + \left( {\frac{{ 1- \sigma_{i} }}{{n_{i} }}} \right)} $$

(5)

Above expression shows that if we assume n is very large, almost close to infinity, the second term becomes zero and price elasticity of demand for the ith product becomes $\sigma_{i}$.

Welfare function for S-D-S¹⁵ preference

Assuming all individuals are identical with same preferences and endowments, the utility function serves as the social welfare function.¹⁶ Society will try to optimize the following welfare function which is constructed by the transformation of variables, i.e. consumption demand and prices in each sector are adjusted by number of variety and elasticity of substitution between varieties.¹⁷ Reformulated problem can be represented as follows:

$$ \mathop {\text{Max}}\limits_{{\tilde{D}1,\tilde{D}2, \ldots ,\,\tilde{D}I}} U\left( {\tilde{D}_{1} ,\tilde{D}_{2} , \ldots ,{\kern 1pt} \,\tilde{D}_{I} } \right) $$

(6)

Subject to $\sum\nolimits_{i \in i} {\tilde{p}_{i} \tilde{D}_{i} \le E}$, where $\tilde{D}_{i} = n_{i}^{{{{\sigma i} \mathord{\left/ {\vphantom {{\sigma i} {\left( {\sigma i - 1} \right)}}} \right. \kern-0pt} {\left( {\sigma i - 1} \right)}}}} D_{i}$ is an index of consumption services derived from sector i. $\tilde{p}_{i} = p_{i} n_{i}^{{{{ - 1} \mathord{\left/ {\vphantom {{ - 1} {\left( {\sigma i - 1} \right)}}} \right. \kern-0pt} {\left( {\sigma i - 1} \right)}}}}$ is the effective price of the product of sector i.

Particular form of social welfare functions for two industry model can be represented by following Krugman (1981)¹⁸ as follows:

$$ \begin{aligned} W & = \ln \left( {\sum\limits_{\omega = 1}^{N1} {D_{1,\omega }^{\beta } } } \right)^{{{1 \mathord{\left/ {\vphantom {1 \beta }} \right. \kern-0pt} \beta }}} + \ln \left( {\sum\limits_{\omega = 1}^{N2} {D_{2,\omega }^{\beta } } } \right)^{{{1 \mathord{\left/ {\vphantom {1 \beta }} \right. \kern-0pt} \beta }}} \quad 0 < \beta < 1, \\ \beta_{i} & \equiv \left( {1 - \frac{1}{{\sigma_{i} }}} \right)\,\quad {\text{and}}\quad \,\sigma_{i} > 1 \\ \end{aligned} $$

(7)

Here $D_{i,\omega }$ is the consumption level of the $\omega$th product of industry i (i = 1, 2). N₁, N₂ are the numbers of potential products in each industry. Not all products will necessarily be produced, actually n ₁, n ₂ numbers of products will be produced domestically. The numbers which will fall short will be imported from rest of the world.

To introduce above theoretical framework into our CGE model we extended social welfare function for the seven sector economy. Here ${E_{P} = \sigma_{i} + \left( {\frac{{ 1- \sigma_{i} }}{{N_{i} }}} \right)}$.¹⁹ Now E _p value can be computed from our model and setting N = 10,²⁰ we can compute $\sigma_{i}$ which determines elasticity of substitution parameter in each sector.²¹ From our model, we calculated price elasticity of demand for (a) primary sector, (b) secondary sector, (c) tertiary service sector as −0.35215, −0.2642, −0.3107, respectively.²²

Evaluation of green house gases

Green house gases are generated due to the consumption of fossil fuels on their function of output of the industries. Following Mukhopadhyay and Forssell (2005) we can calculate emission as follows:

$$ F_{\text{GHG}} = C * L1 * Z $$

(8)

Here $F_{\text{GHG}}$ is a scalar representing total quantity of emission from fossil fuel combustion. We have considered three types of emission (a) CO₂, (b) SO₂, (c) NO _x defined as GHG. C is a vector of dimension (1 × m), representing emission coefficients for a particular type of GHG from m²³ different types of primary fuels. L1 represents a matrix (m × n) of energy consumption coefficients for different sectors. Z is a vector of dimension (n × 1) representing output of n different sectors.

Different Emission coefficients correspond to various fossil fuels are computed following IPCC (Inter Governmental Panel on Climate Change) guideline.

$$ \begin{aligned} {\text{Carbon/sulphur/nitrogen - di - oxide}}\;{\text{emission}}\;{\text{coefficient}}\, = & \,\left( {{\text{Carbon/sulphur/nitrogen}}\;{\text{content}}\;{\text{in}}\;{\text{the}}\;{\text{fuel}}} \right)\, \\ & * \,\left( {\% \;{\text{of}}\;{\text{fuel}}\;{\text{oxidized}}} \right)\, * \,\left( {{\text{Specific}}\;{\text{gravity}}} \right) \\ & * \,\left( {{\text{Molecular}}\;{\text{weight}}\;{\text{ratio}}} \right) \\ \end{aligned} $$

Energy/environmental welfare function

To take into account benefits of improved environmental quality, we assume that each consumer has a constant elasticity of substitution (CES) utility function defined over the standard utility aggregate plus environmental quality, which is inversely related to the amount of environmental damage done by the emission. The welfare function is having following form:

$$ \tilde{W} = F\left( {W,Q} \right) $$

(9)

$$ \tilde{W} = \left[ {W^{ - \sigma } + Q^{ - \sigma } } \right]^{{ - \frac{1}{\sigma }}} $$

(10)

Here F has a CES functional form, W is the measure of welfare obtained from benchmark. CGE model as well as imperfectly competitive CGE model. Here Q is the environmental quality which can be defined by the following relation.

$$ Q = \bar{Q} - D $$

(11)

$$ D = s \cdot {\text{Emis,}} $$

(12)

where $\bar{Q}$ refers to the ‘endowment’ of environmental quality and $D$ is the damages from Emissions. Rupee value of damage is computed from the total value of emission generated through the production process. Here we assumed that marginal value of damage from emission is constant. Here we assume that share of initial (benchmark) damages to the endowment of environmental quality $\left( {{D \mathord{\left/ {\vphantom {D {\bar{Q}}}} \right. \kern-0pt} {\bar{Q}}}} \right)$ is .25. s stands for social marginal value of damage and its value is assumed to be Rs 0.50 per Kg of CO₂ emission.²⁴

Modelling ‘pollution heaven’ in CGE

To make an exact link between trade and environment we modelled ‘Pollution Haven’ by computing PTOT proposed by Antweiler (1996). PTOT is computed taking the ratio of pollution content of export and pollution content of import. Pollution content of export and import can be given by:

$$ F_{{{\text{GHG}}\left( {\text{EXPORT}} \right)}} = C * L1 * \left( {I - A_{d} } \right)^{ - 1} \,*\, E $$

(13)

$$ F_{\text{GHG(IMPORT)}} = C * L1 * \left( {I - A_{\text{d}} } \right)^{ - 1} \,*\, M $$

(14)

Here E and M are (n × 1) vectors representing export and import of the domestic economy in different sectors. Here A _d is the matrix domestic input/output coefficient. Hence (I − A _d)⁻¹ is the Lieontief domestic inverse matrix. Here we assume identical technology as of domestic production²⁵ for the import from ROW. Here $C * L1 * \left( {I - A_{\text{d}} } \right)^{ - 1}$ represents both direct and indirect requirements of pollution intensities within export and import. Pollution terms of trade for India with rest of the World can be given by:

$$ \begin{aligned} PTOT = & F_{{{\text{GHG}}\left( {\text{EXPORT}} \right)}} /F_{\text{GHG(IMPORT)}} \\ =&\;C\,*\,L1\,*\,\left( {I - A_{\text{d}} } \right)^{ - 1}\,*\,E/C\,*\,L1\,*\,\left( {I - A_{\text{d}} } \right)^{ - 1}\,*\,M \\ \end{aligned} $$

(15)

A country gains environmentally from trade in relative terms whenever pollution content of its imported good is higher than that of its exported good. Whenever PTOT value is greater than unity, it indicates country’s export contains higher pollution than it is receiving through import. PTOT is an indicator to reflect pollution haven effect.

Database and calibration of model parameters

After specifying Energy/Environmental CGE model, model parameters will have to be estimated from benchmark dataset. We have used energy/environmental SAM (ESAM) constructed by segregating separate energy sectors (Table 2). In our ESAM we have total seven sectors. Three of them are conventional production sectors excepting energy sectors namely (1) primary sector, (2) secondary manufacturing sector, (3) tertiary sector and four of them are energy sectors, namely (4) electricity, (5) coal, (6) petroleum and natural gas and (7) biomass. Excepting electricity, others are primary energy sector and emit green house gases on their burning. Our constructed SAM is for the year 2003–2004 and we aggregated the SAM produced by Saluja and Yadav (2006) for the same year according to our requirement. Emission coefficients for various GHG from different fuels are computed following IPCC guideline. Fixed cost is assumed to be 10 % of the total capital expenditure in any sector (Table 3).

Table 1 Schematic structure of SAM source: Shaluja and Yadav (2006)

Table 2 Energy/environmental SAM of India C1 = primary sector, C2 = secondary sector, C3 = tertiary sector (in Rs lakhs)

Simulation experiments

We performed different simulation experiments to find the impacts of international trade and globalization on domestic energy consumption, greenhouse gas emission and social welfare under both perfect and imperfect competition. Two different types of trade liberalization policies have been experimented to find general macroeconomic impacts and to test whether there is any evidence of ‘Pollution Haven’ and ‘Dirty industry migration’ in the context of Indian economy. Simulation experiment results have been described below.

Experiment-1: Trade liberalization by 50 % tariff reduction under perfect and imperfect competition

We first examined the effect of import liberalization through the reduction of import duty 50 % under perfect and imperfect competition (Fig. 1). Immediate impact is the reduction of domestic import price which led to an increase of domestic import leaving a depreciation of exchange rate owing to higher foreign currency demand. Profitable export market with higher domestic price of foreign currency increases export. However, government’s income reduces with lower tariff revenue earnings and consequently transfer of the government to different types of household also declines. In spite of that, household’s real income is also affected by the reduction of composite commodity price. We find excepting urban salaried class, trade liberalization benefits domestic households. Trade-6 shows that liberalization expands domestic market and competition which led to an increase of domestic output to exploit the benefit of increasing returns to scale.²⁶ Higher output in industrial manufacturing and in service sector increases energy consumption which are used as intermediate inputs in various production units. We find electricity consumption has been increased by 1.005 % in case of imperfect completion while it increases by 0.587 % in case of perfect competition. Since more than 55 % of electricity production depends on coal, its consumption also increases along with liquid petroleum products and natural gas. Only biomass consumption has been diminished, probably because of shifting towards much cleaner fuels for cooking purposes among rural households, like Kerosene, LPG, coal etc. instead of using biomass. Hence under both perfect and imperfect competition all types of energy fuel consumption increases excepting biomass consumption. Table 4 shows trade liberalization effects on energy consumption.

Fig. 1

Major interactions due to import liberalization

Table 3 Energy/environmental SAM of India (continued) (in Rs lakhs)

On environmental front, trade liberalization increases total CO₂ emission owing to higher consumption of energy fuels under both perfect competition and under market imperfection. Pollution embodied in India’s import is greater than pollution embodied in its export leading to a measure of PTOT less than unity under benchmark scenario. With trade liberalization through 50 % tariff reduction, PTOT increases by 18.428 and 16.4 %, respectively, under perfect and imperfect competition. Our simulation results indicate that Pollution Haven Hypothesis is no longer relevant for India in the benchmark scenario and Indian economy has not been pollution haven in 2003–04. In the benchmark scenario Indian economy exports comparatively lesser pollution than it imports from ROW. However, with trade liberalization manifestation of ‘Pollution Haven’ in India is predicted as PTOT increases by 18.438 % over the benchmark to take a value greater than unity. Simulation study reveals that, Indian export in 2003–2004 is 10 % less pollution intensive than its imports and with gradual trade liberalization pollution intensiveness of both export and import decrease over the corresponding base period values. Nevertheless, on account of tariff reduction, pollution intensiveness of export has been reduced by lower percentage as compared to reduction of pollution content in imports leaving PTOT to be raised by 18.428 and 16.4 %, respectively, under perfect and imperfect competition over the base period value. Comprehensively, Indian economy has not been ‘Pollution Haven’ in 2003–2004 and with trade liberalization PTOT value crosses the critical value unity predicting Pollution Haven effect to be persistent in India under alternative market structures.

Our results also corroborates with the results obtained by Mukhopadhyay et al. (2005), Mukhopadhya and Chakraborty (2005) and Mukhopadhyay (2007). Mukhopadhyay (2007) obtained PTOT value for India in 1991–1992 to be 0.75 and that for 1996–1997 as 0.72, i.e. PTOT value is less than unity in 90’s, and thus they concluded that Pollution Haven Hypothesis should be rejected for India.²⁷ Mukhopadhyay (2007) computed PTOT for 90’s and simulated corresponding value for the year 2006–2007 as 0.97 i.e. very close to the border line of unity. In our analysis, we also obtained value of PTOT as 0.902 and it increases by 18.43 and 16.4 % owing to 50 % tariff reduction under perfect and imperfect competition. This indicates that, there may be the manifestation of Pollution Haven in the coming decades as PTOT value exceeds unity on tariff simulation. In addition, trade liberalization increases overall domestic consumption and aggregate social welfare under alternative market scenarios. Since environmental damage is caused by increasing air pollution and greenhouse gas emission owing to greater uses of energy fuels, environmental social welfare that takes into account both consumption gain as well as environmental damage is reduced. Thus, increasing consumption gain is completely outweighed by environmental damage caused by GHG emission under both perfect and imperfect competition. Table 4 depicts environmental impacts of trade liberalization.

Experiment-2: Greater inflow of foreign capital

We simulated higher foreign capital inflow to get the impact over domestic energy consumption and GHG emission. We increased foreign capital inflow up to the extent such that net capital A/C deficit is zero. Greater foreign capital inflow appreciates exchange rate making import cheaper and so import increases in all sectors under alternative market structures. Export becomes less profitable leading to a reduction of sectoral domestic export. Domestic saving is augmented with higher inflow of capital. Sectoral GDP increases in manufacturing sector, while overall GDP increases under both perfect and imperfectly competitive market structure.

Energy consumption for almost all types of fuels like, electricity, Coal, Petroleum and Natural gas and even biomass consumption increases with the expansion of secondary manufacturing sector which is intensive in energy usage. Table 4 shows that increased energy consumption is higher in case of imperfect competition than under perfect competition. This can be explained by the fact that under imperfect competition with return to scale benefit and diverse consumer preference, there has been a greater expansion of secondary sector production as compared to perfect competition.

In the environmental front pollution content of both import and export has been reduced under perfect competition by −4.32 and −5.45 %, respectively, may be due to the greater use of energy saving and environment friendly technologies accompanied by higher foreign capital inflow. In contrast, under imperfect competition assumption, results have been slightly different as pollution content of import has been increased by around 5.2 % with a usual decline of −2.6 % in pollution content of export. This could be explained by the increased import owing to the appreciation of exchange rate that leads to higher pollution embodied in import while lower export reduces pollution content of export. In effect, PTOT has been reduced by −9.271 and −7.424 %²⁸, respectively, over the benchmark under perfect and imperfect competition. Environmental social welfare although increases by little percentage, its rate is lower as compared to consumption based welfare as there is environmental damage caused by greenhouse gas emission.

Summary and conclusion

In this paper, we examined the impact of different trade related policy changes on India’s macroeconomic variables and on domestic physical environment, while the impacts are coming particularly through energy consumption and consequent air pollution. We find that trade liberalization expands trade, increases GDP, social welfare, private consumption, gross investment and reduces composite commodity prices, while it deteriorates environment through higher greenhouse gas emission. Greater foreign capital inflow appreciates exchange rate, increases import and reduces export. GDP, gross investment, welfare and private consumption expand with the negative effect of emission. Thus, in general we find that liberalized trade policies although expand economic activities; they generate deteriorating impact over domestic physical environment.

‘Pollution Haven effect’ has been evaluated constructing an index known as PTOT which exhibits a value less than unity for India in the benchmark scenario. This indicates India’s export contains lower pollution than pollution embodied in its import, and thus India has not been a pollution Haven in the benchmark period of 2003–2004. Thus, Pollution Haven Hypothesis should be rejected for India in the early phase of trade liberalization, i.e. in the decade of 90’s and few initial years of the next decade. This phase of liberalization has been termed by Mukhopadhyay (2007) as the manifestation of Green Lieontief Paradox where a country endowed with higher comparative cost advantage with respect to the Energy/Environmental factor,²⁹ is exporting products which are less energy/emission intensive than its import. However, import liberalization increases the value of PTOT indicating that Indian economy might manifest Pollution Haven in the coming decades. Contrary to this, greater inflow of foreign capital seems to be environment friendly as it promotes the usage of green technologies.

It follows that, greater uses of energy saving technologies, scaling up and expansion of investment in research and development of green technologies and increased implementation of green technology transfer from developed countries are the possible options to reduce greenhouse gas emission in the globalized scenario and also to make India energy sustainable. In order to finance energy saving technologies, policymakers should provide adequate emphasis on Private Public Partnership basis. Banking sectors may be instrumental in this regard by promoting Green Financing among the domestic households.³⁰

Appendices

Appendices

Appendix-1: Mathematical structure of the benchmark CGE model

Production block:

$$ Y_{j} = b_{j} \cdot \left[ {\prod\limits_{h} {F_{h,j}^{{\beta_{j,h} }} } } \right] $$

(16)

$$ X_{i,j} = ax_{i,j} \cdot Z_{j} $$

(17)

$$ Y_{j} = ay_{j} \cdot Z_{j} $$

(18)

$$ F_{h,j} = {{\beta_{h,j} \cdot py_{j} \cdot Y_{j} } \mathord{\left/ {\vphantom {{\beta_{h,j} \cdot py_{j} \cdot Y_{j} } {pf_{h} }}} \right. \kern-0pt} {pf_{h} }} $$

(19)

$$ pz_{j} = ay_{j} \cdot py_{j} + \sum\limits_{i} {ax_{i,j} \cdot pq_{i} + \frac{{FC_{j} }}{{Z_{j} }}} $$

(20)

Government behaviour:

$$ GINC = Td + Tdc + TInd + NCAT + ENT + TARR - Ts $$

(21)

$$ Td = \sum\limits_{b} {taud_{b} \cdot \left[ {\sum\limits_{h} {pf_{h} \cdot FF_{h} \cdot r_{h,b} } + GT_{b} + NCUT_{b} } \right]} $$

(22)

$$ Tdc = tcorp \cdot \left( {OPR + IND} \right) $$

(23)

$$ OPR = sop \cdot \left[ {\sum\limits_{h} {pf_{h} \cdot FF_{h} } + NF_{1} + NF_{2} } \right] $$

(24)

$$ TInd = \sum\limits_{b} {tauz_{j} } \cdot pz_{j} \cdot Z_{j} $$

(25)

$$ TARR = \sum\limits_{i} {taum_{i} \cdot pm_{i} \cdot M_{i} } $$

(26)

$$ Ts = taus \cdot \sum\limits_{i} {pe_{i} \cdot E_{i} } $$

(27)

$$ Xg_{i} = {{mu \times GDP} \mathord{\left/ {\vphantom {{mu \times GDP} {pq_{i} }}} \right. \kern-0pt} {pq_{i} }} $$

(28)

$$ GT_{b} = gt_{b} \cdot GINC $$

(29)

$$ GEXP = \sum\limits_{i} {Xg_{i} + \sum\limits_{b} {GT_{b} + Ts} } $$

(30)

$$ S_{G} = GINC - GEXP $$

(31)

Investment behaviors:

$$ Xv_{i} = lamda_{i} \cdot {{\left[ {Dep + \sum\limits_{b} {Sp_{b} } + Sg + Sc + Sf \cdot epsilon} \right]} \mathord{\left/ {\vphantom {{\left[ {Dep + \sum\limits_{b} {Sp_{b} } + Sg + Sc + Sf \cdot epsilon} \right]} {pq_{i} }}} \right. \kern-0pt} {pq_{i} }} $$

(32)

Savings:

$$ HHIN_{b} = \sum\limits_{h} {\left[ {\sum\limits_{h} {FF_{h} \cdot pf_{h} + NF_{1} + NF_{2} } } \right] \cdot r_{hb} } + NCUT_{b} + GT_{b} $$

(33)

$$ HHIN_{b} = \left[ {\sum\limits_{h} {FF_{h} \cdot pf_{h} + NF_{1} + NF_{2} } } \right] \cdot r_{b} + NCUT_{b} + GT_{b} $$

(33a)

where $r_{b} = \sum\limits_{h} {r_{h,b} }$

$$ Sp_{b} = ssp_{b} \cdot HHIN_{b} $$

(34)

$$ Sc = ssc \cdot \left( {OPR + IND} \right) $$

(35)

Household consumption:

$$ Xp_{i,b} = alpha_{i,b} \cdot {{\left[ {HHIN_{b} - Td_{b} - Sp_{b} } \right]} \mathord{\left/ {\vphantom {{\left[ {HHIN_{b} - Td_{b} - Sp_{b} } \right]} {pq_{i} }}} \right. \kern-0pt} {pq_{i} }} $$

(36)

International trade:

$$ pm_{i} = epsilon * pWm_{i} * \left( {1 + taum_{i} } \right) $$

(37)

$$ pe_{i} = epsilon * pWe_{i} * \left( {1 + taus_{{}} } \right) $$

(38)

$$ \begin{gathered} \sum\limits_{i} {pWe_{i} * E_{i} } + Sf + \sum\limits_{b} {NCUT_{b} + NF_{1} + NF_{2} + NCAT + Ts} = \sum\limits_{i} {pWm_{i} * M_{i} } \hfill \\ \hfill \\ \end{gathered} $$

(39)

Armington function:

$$ Q_{i} = gamma_{i} \left[ {deltam_{i} \cdot M_{i}^{{eta_{I} }} + deltad_{i} \cdot D_{i}^{{eta_{i} }} } \right]^{\frac{1}{eta}}_{i} $$

(40)

$$ \frac{{M_{i} }}{{Q_{i} }} = \left[ {gamma_{i}^{{eta_{i} }} \cdot deltam_{i \cdot } \cdot \frac{{pq_{i} }}{{pm_{i} }}} \right]^{{\frac{1}{{1 - eta_{i} }}}} $$

(41)

$$ \frac{{D_{i} }}{{Q_{i} }} = \left[ {gamma_{i}^{{eta_{i} }} \cdot deltad_{i \cdot } \cdot \frac{{pq_{i} }}{{pd_{i} }}} \right]^{{\frac{1}{{1 - eta_{i} }}}} $$

(42)

Transformation function:

$$ Z_{i} = theta_{i} \cdot \left[ {xie_{i} \cdot E_{i}^{{phi_{i} }} + xid_{i} \cdot D_{i}^{{phi_{i} }} } \right]^{{\frac{1}{{phi_{i} }}}} $$

(43)

$$ \frac{{E_{i} }}{{Z_{i} }} = \left[ {theta_{i}^{{phi_{i} }} \cdot xie_{i} \cdot \left( {1 + tind} \right)\frac{{pz_{i} }}{{ \cdot pe_{i} }}} \right]^{{\frac{1}{{1 - phi_{i} }}}} $$

(44)

$$ \frac{{D_{i} }}{{Z_{i} }} = \left[ {theta_{i}^{{phi_{i} }} \cdot xid_{i} \cdot \left( {1 + tind} \right) \cdot \frac{{pz_{i} }}{{pd_{i} }}} \right]^{{\frac{1}{{1 - phi_{i} }}}} $$

(45)

Market clearing condition:

$$ Q_{i} = \sum\limits_{b} {Xp_{i,b} + Xg_{i} + Xv_{i} + \sum\limits_{j} {X_{i,j} } } $$

(46)

$$ FF_{h} = \sum\limits_{j} {F_{h,j} } $$

(47)

Fictitious objective function:

$$ UU = \sum\limits_{b} {\prod\limits_{i} {Xp_{i,b}^{{\alpha_{i,b} }} } } $$

(48)

List of endogenous variables

• $Y_{j}$ = Combined input used in jth activity.

• $F_{h,j}$ = Demand for basic input h in jth activity.

• $Z_{j}$ = Output of jth activity

• $py_{j}$ = Price of combined input in jth activity.

• $pf_{h}$ = Price of basic input h.

• $pq_{i}$ = Price of the ith commodity.

• $GINC$ = Total government income.

• $Td$ = Household income tax.

• $Tdc$ = Corporate tax.

• $TInd$ = Indirect tax.

• $pf_{h}$ = Factor price of the hth factor.

• $FF_{h}$ = Factor demand of the hth factor

• $GT_{b}$ = Government transfer to the bth household.

• $gt_{b}$ = Government income share transferred to bth household.

• $Xp_{i,b}$ = bth household consumption of the ith good.

• $Xg_{i}$ = Government consumption of the ith good.

• $X_{i,j}$ = ith sector’s output goes to jth sector as intermediate input.

• $Xv_{i}$ = ith commodity used as investment good.

• $pq_{i}$ = Price of the ith commodity.

• $pe_{i}$ = Price of export.

• $Sg$ = Government savings.

• $Sp_{b}$ = Private savings of the bth household.

• $Sg$ = Government savings.

• $Sc$ = Corporate savings.

• $epsilon$ = Exchange rate.

• $HHIN_{b}$ = Income of the bth household.

• $pe_{i}$ = Export price of good i in domestic currency.

• $pm_{i}$ = Imports price of good i in domestic currency.

• $pd_{i}$ = Price of domestic good.

• $pz_{i}$ = Supply price of the ith good.

• $pWe_{i}$ = World export price.

• $pWm_{i}$ = World import price.

• $E_{i}$ = Export of good i.

• $M_{i}$ = Import of good i.

• $epsilon$ = Exchange rate.

• $Q_{i}$ = Output composite good.

• $D_{i}$ = Output domestic good.

• $UU$ = Social welfare function.

List of exogenous variables

• $b_{j}$ = Production function shift parameter.

• $\beta^{j,h}$ = Share of hth input within combined input in jth activity.

• $ax_{i,j}$ = Per unit requirement of ith commodity in jth activity as intermediate input.

• $ay_{j}$ = Per unit requirement of combined input in jth activity.

• $r_{h,b}$ = hth factor income share of bth household.

• $ENT$ = Income of the government from entrepreneurial activity.

• $taud_{b}$ = Share of total household income paid as income tax by bth household.

• $mu_{i}$ = Share of government expenditure on ith commodity.

• $NCAT$ = Net transfer to government.

• $Sf$ = Foreign savings at world prices.

• $lamda_{i}$ = Proportion of savings converted into investment.

• $Dep$ = Depreciation of capital.

• $FF_{h}$ = Total factor demand of the hth factor.

• $gamma_{i}$ = Scale parameter in Armington function.

• $deltad_{i}$ = Share coefficient of domestic good in Armington function.

• $deltam_{i}$ = Share coefficient of import good in Armington function.

• $eta_{i}$ = Constant determining elasticity of substitution in Armington function.

• $theta_{i}$ = Scale parameter transformation function.

• $xie_{i}$ = Share parameter of export in Transformation function.

• $xid_{i}$ = Share parameter of domestic good in transformation function.

• $phi_{i}$ = Constant determining elasticity of substitution in Transformation function.

• $tind$ = Indirect tax rate.

• $taum_{i}$ = Import tariff rate.

• $taus$ = Export subsidy rate.

• $NCUT_{b}$ = Net current transfer to bth household.

• $tcorp$ = Share of corporate income to tax.

• $OPR$ = Operating profit.

• $IND$ = Interest on debt.

• $sop$ = Share of operating profit to total factor income.

• $NF_{1}$ = Net labour income earned abroad.

• $NF_{2}$ = Net capital income earned abroad.

• $Tpurhh$ = bth household purchase tax.

• $Tpurg$ = Government purchase tax.

• $Ting$ = Taxes on intermediate.

• $Tinv$ = Taxes on investment good.

• $Ts$ = Taxes on export.

• $tpurhh_{b}$ = Share of household purchase paid as purchase tax by bth household.

• $tpurg$ = Share of government purchase paid as purchase tax.

• $ting$ = Share of intermediate good purchase to tax.

• $tinv$ = Share of investment to tax.

• $taus$ = Share of export paid as tax.

• $FC_{j}$ = Fixed cost in the jth sector.

Appendix-2

See Table 5

Table 4 Effects of tariff reduction and foreign capital inflow on Environment

Table 5 Simulation experiment results