Abstract
The aim of this paper is to study Iséki spaces of distinguished classes of ideals of a semiring endowed with a topology. We show that every Iséki space is quasi-compact whenever the semiring is Noetherian. We characterize Iséki spaces for which every non-empty irreducible closed subset has a unique generic point. Furthermore, we provide a sufficient condition for the connectedness of Iséki spaces and show that the strongly connectedness of an Iséki space implies the existence of non-trivial idempotent elements of semirings.
Similar content being viewed by others
1 Introduction
Since the introduction of semirings by Vandiver [31], it is natural to compare and extend results from rings to semirings. One may think that semirings can always to be extended to rings, but Vandiver [32] gave examples of semirings which can not be embedded in rings. Moreover, semirings arise naturally when we consider the set of endomorphisms of a commutative additive semigroup.
As for rings, various classes of ideals have been topologized with hull-kernel topology (also known as Stone topology or Jacobson topology, or Zariski topology) and the corresponding spaces have been studied intensively. It all started with Stone [29], imposing hull-kernel topology on maximal ideals of a Boolean ring. The same have been done on rings of continuous functions and commutative normed rings by Gelfand and Kolmogoroff [12] (see also [9, 28]) and by Gelfand and Šilov [13] respectively, whereas for the algebra of all continuous complex-valued functions, Loomis [25] considered the same topology on maximal ideals. Jacobson [23] (see also [24]) considered that topology on the set of primitive ideals of an arbitrary ring and Grothendieck [11] used it on prime ideals of a commutative ring to construct affine schemes. The hull-kernel topology on minimal prime ideals of a commutative ring have been studied by Henriksen and Jerison [16] (see also Hochster [18]). In a more recent paper, Azizi [1] endowed it on strongly irreducible ideals of a commutative ring.
As far as semirings are concerned, Iséki [22] considered various algebraic properties of distinguished classes of ideals and studied hull-kernel topology on strongly irreducible ideals. In [20], Iséki and Miyanaga studied the same on maximal ideals of a semiring, whereas Iséki [21] studied that topology on prime ideals and have called them structure spaces. In the context of (m, n)-semirings, Hila, Kar, Kuka and Naka [17] studied structure spaces of n-ary prime k-ideals, n-ary prime full k-ideals, n-ary prime ideals, maximal ideals, and strongly irreducible ideals.
Note that we can not endow a hull-kernel topology on an arbitrary class of ideals of a ring or of a semiring. McKnight [26, Section 2.2, p. 11] characterized such classes of ideals for rings and the same characterization holds good for semirings. The closest topology which is of the hull-kernel-type is coarse lower topology and it can be imposed on any class of ideals. Moreover, this topology coincide with hull-kernel topology whenever the class of ideals is ‘good’ enough. An attempt has been made in Dube and Goswami [7] to study this spaces (called ideal spaces) of all topologized classes of ideals of a commutative ring.
Although the book [14] by GŁazek covers references on semirings at the encyclopedic level, but to best of author’s knowledge, a study of all classes of topologized ideals of a semiring has never been considered before. Our purpose of this paper is to generalize the notion of ideal spaces of commutative rings to Iséki spaces (in honour of Kiyoshi Iséki) of semirings. We shall use definitions and results, whenever applicable for semirings, from Dube and Goswami [7] (and also from Finocchiaro, Goswami, and Spirito [8]) without explicitly referring to them.
2 Preliminaries
Recall from Golan [10] that a semiring is a system \((\mathfrak S,+,0,\cdot , 1)\) such that \((\mathfrak S,+,0)\) is a commutative monoid, \((\mathfrak S, \cdot ,1)\) is a monoid, \(0r=0=r0\) for all \(r\in \mathfrak S,\) and \(\cdot \) distributes over \(+\) both from the left and from the right sides. A semiring \(\mathfrak S\) is called commutative if \(rr'=r'r\) for all \(r,r'\in \mathfrak S.\) All our semirings are assumed to be commutative. A semiring homomorphism \(\phi :\mathfrak S\rightarrow \mathfrak S'\) is a map such that (i) \(\phi (a+b)=\phi (a)+\phi (b),\) (ii) \(\phi (ab)=\phi (a)\phi (b),\) and \(\phi (1)=1\) for all \(a, b\in \mathfrak S.\) A semiring homomorphism \(\phi \) is called an isomorphism if \(\phi \) is also a bijection on the underlying sets.
An ideal \(\mathfrak {S}\) of a semiring \(\mathfrak {S}\) is a nonempty proper subset of \(\mathfrak S\) satisfying the conditions: (i) \(a+b\in \mathfrak {a}\) and (ii) \(ra\in \mathfrak {a}\) for all \(a, b\in \mathfrak {a}\) and \(r\in \mathfrak S.\) If \(\{\mathfrak {a}_{\lambda }\}_{\lambda \in \Lambda }\) is a family of ideals of a semiring \(\mathfrak S\), then \(\bigcap _{\lambda \in \Lambda } \mathfrak {a}_{\lambda }\) is also an ideal of \(\mathfrak S\). The sum of a family \(\{\mathfrak {a}_{\lambda }\}_{\lambda \in \Lambda }\) of ideals of a semiring \(\mathfrak S\) is defined by
which is also an ideal of \(\mathfrak S\). If \(\mathfrak {a}\) and \(\mathfrak {b}\) are two ideals of \(\mathfrak S\), then their product \(\mathfrak {a}\mathfrak {b}\) is the ideal generated by the set \(\{a\cdot b\mid a\in \mathfrak {a}, b\in \mathfrak {b}\}.\) As it has been pointed out by Brown and McCoy [5] that it does not matter whether the product \(\mathfrak {a}\mathfrak {b}\) of ideals \(\mathfrak {a}\) and \(\mathfrak {b}\) is defined to be the set of all finite sums \(\sum a_{\lambda } b_{\lambda }\) (\(a_{\lambda }\in \mathfrak {a}\), \(b_{\lambda }\in \mathfrak {b}\)), or the smallest ideal of \(\mathfrak S\) containing all products \(a_{\lambda } b_{\lambda }\), or merely the set of all these products. For rings, Behrens [3] has used the second of these definitions, whereas Amitsur [2] has applied the third.
The radical \(\sqrt{\mathfrak {a}}\) of an ideal \(\mathfrak {a}\) of a semiring \(\mathfrak S\) is defined by
It is easy to verify that \(\mathfrak {a}\subseteq \sqrt{\mathfrak {a}}\) and \(\sqrt{\mathfrak {a}}\) is also an ideal of \(\mathfrak S\). An ideal \(\mathfrak {a}\) is called a radical ideal if \(\mathfrak {a}=\sqrt{\mathfrak {a}}.\) An ideal \(\mathfrak {p}\) of a semiring \(\mathfrak S\) is called prime if \(ab\in \mathfrak {p}\) implies \(a\in \mathfrak {p}\) or \(b\in \mathfrak {p}\) for all \(a, b \in \mathfrak S.\) Likewise in rings, radicals of semirings also have the following important representation.
Proposition 2.1
[27] If \(\mathfrak {a}\) is an ideal of a semiring \(\mathfrak S\), then
An ideal \(\mathfrak {m}\) of a semiring \(\mathfrak S\) is said to be maximal if \(\mathfrak {m}\) is not properly contained in any other ideals of \(\mathfrak S\). Slowikowski and Zawadowski [30, Theorem 2] proved the following
Proposition 2.2
Every ideal of a semiring \(\mathfrak S\) is a subset of at least one maximal ideal of \(\mathfrak S\).
Furthermore, by Nasehpour [27], we have the following
Proposition 2.3
Every maximal ideal of a semiring is a prime ideal.
A proper ideal \(\mathfrak {a}\) of a semiring \(\mathfrak S\) is called primary (see Golan [10]) if \(xy\in \mathfrak {a}\) implies either \(x\in \mathfrak {a}\) or \(y^n\in \mathfrak {a}\) for some \(n\in \mathbb {N}.\) By Iséki [22], an ideal \(\mathfrak {s}\) is called strongly irreducible (irreducible), if \(\mathfrak {a}\cap \mathfrak {b}\subseteq \mathfrak {s}\) (\(\mathfrak {a}\cap \mathfrak {b}= \mathfrak {s}\)) for any two ideals \(\mathfrak {a},\) \(\mathfrak {b}\) implies \(\mathfrak {a}\subseteq \mathfrak {s}\) (\(\mathfrak {a}=\mathfrak {s}\)) or \( \mathfrak {b}\subseteq \mathfrak {s}\) (\(\mathfrak {b}= \mathfrak {s}\)). Any one of the classes of ideals of a semiring \(\mathfrak S\) considered above will be called a spectrum of \(\mathfrak S\) and we shall denote it by \(\sigma _{\mathfrak S}\). We shall assume that \(\mathfrak S\notin \sigma _{\mathfrak S}\) for all spectra of \(\mathfrak S\).
3 Iséki spaces
Suppose \(\mathfrak {S}\) is a semiring. The ideal topology (also known as coarse lower topology Dickmann, Schwartz, and Tressal [6, A.8, p. 589] or lower topology Gierz et al. [15, Definition O\(-\)5.4, p. 43]) on a spectrum \(\sigma _{\mathfrak S}\) of \(\mathfrak S\) will be the topology for which the sets of the type
(where \(\mathfrak a\) runs among the ideals of \(\mathfrak S\)) form a subbasis of closed sets. A spectrum \(\sigma _{\mathfrak S}\) of a semiring \(\mathfrak S\) endowed with an ideal topology is called an Iséki space, and we denote the Iséki space also by \(\sigma _{\mathfrak S}\). The following results are easy to prove.
Proposition 3.1
The subbasic closed subsets of an Iséki space have the following properties.
-
(i)
The map \(^{\uparrow }:\textrm{Ideal}(\mathfrak {S})\rightarrow \mathcal {P}(\sigma _{\mathfrak {S}})\) defined in (4) is order-reversing, where \(\textrm{Ideal}(\mathfrak {S})\) denotes the set of all ideals of the semiring \(\mathfrak {S}\) and \(\mathcal {P}(\sigma _{\mathfrak {S}})\) is the power set of the spectrum \(\sigma _{\mathfrak {S}}\). Furthermore, \(\mathfrak {o}^{\uparrow }=\mathfrak {S}\) and \(\mathfrak {S}^{\uparrow }=\emptyset \), where \(\mathfrak {o}\) is the zero ideal of \(\mathfrak {S}.\)
-
(ii)
For any two ideals \(\mathfrak {a},\) \(\mathfrak {b}\) of \(\mathfrak {S}\), \(\mathfrak {a}^{\uparrow }\cup \mathfrak {b}^{\uparrow } \subseteq (\mathfrak {a}\cap \mathfrak {b})^{\uparrow }\subseteq (\mathfrak {ab})^{\uparrow }.\)
-
(iii)
For a family \(\{\mathfrak {a}_{\alpha }^{\uparrow } \}_{\alpha \in \Lambda }\) of subbasic closed sets, \(\bigcap _{\alpha \in \Lambda }\mathfrak {a}_{\alpha }^{\uparrow }=\left( \sum _{\alpha \in \Lambda }\mathfrak {a}_{\alpha } \right) ^{\uparrow }\).
-
(iv)
For every ideal \(\mathfrak {a}\) of \(\mathfrak {S},\mathfrak {a}^{\uparrow }\supseteq (\sqrt{\mathfrak {a}})^{\uparrow },\) where \(\sqrt{\mathfrak {a}}\) is as defined in (2).
-
(v)
A spectrum \(\sigma _{\mathfrak {S}}\) is a radical ideal if and only if \(\mathfrak {a}^{\uparrow }=(\sqrt{\mathfrak {a}})^{\uparrow }\) for every ideal \(\mathfrak {a}\) in \(\mathfrak {S}.\)
It is evident from (4) that if \(\mathfrak {x}\ne \mathfrak {x}'\) for any two \(\mathfrak {x}, \mathfrak {x}'\in \sigma _{\mathfrak S}\), then \(\mathfrak {x}^{\uparrow }\ne \mathfrak {x}'^{\uparrow }.\) Therefore, we have
Proposition 3.2
Every Iséki space \(\sigma _{\mathfrak S}\) is a \(T_0\)-space.
Recall that a topological space is called quasi-compact if every open cover of it has a finite subcover, or equivalently, the space satisfies the finite intersection property. In this definition of quasi-compactness, we do not assume the space is \(T_2.\) Quasi-compactness of prime, maximal, and strongly irreducible ideals endowed with hull-kernel topology (= coarse lower topology) have respectively been shown in Iséki [21], Iséki and Miyanaga [20], and Iséki [22]. The following result gives a sufficient condition for quasi-compactness of all Iséki spaces. The proof relies on the application of Alexander subbase theorem.
Theorem 3.3
If a semiring \(\mathfrak S\) has an identity and if a spectrum \(\sigma _{\mathfrak S}\) of \(\mathfrak S\) contains all maximal ideals of \(\mathfrak S\), then \(\sigma _{\mathfrak S}\) is a quasi-compact space.
Proof
Suppose \(\{\mathcal K_{ \lambda }\}_{\lambda \in \Lambda }\) is a family of subbasic closed sets of \(\sigma _{\mathfrak S}\) with \(\bigcap _{\lambda \in \Lambda }\mathcal K_{ \lambda }=\emptyset .\) This implies \(\mathcal K_{ \lambda }=\mathfrak {x}_{\lambda }^{\uparrow }\) for some ideals \(\mathfrak {x}_{\lambda }\) of \(\mathfrak S\), and
where the sum is defined in (1), and the first equality follows from Proposition 3.1 (iii). If \(\sum _{\lambda \in \Lambda } \mathfrak {x}_{\lambda } \ne \mathfrak S,\) then we must have a maximal ideal \(\mathfrak {m}\) of \(\mathfrak S\) (see Proposition 2.2) such that \(\sum _{\lambda \in \Lambda } \mathfrak {x}_{\lambda } \subseteq \mathfrak {m}.\) Moreover,
for all \(\lambda \in \Lambda .\) Therefore \(\mathfrak {m}\in \mathfrak {x}_{\lambda }^{\uparrow }=\mathcal K_{\lambda }\) for all \(\lambda \in \Lambda \), a contradiction of our assumption. Hence \(\sum _{\lambda \in \Lambda } \mathfrak {x}_{\lambda }=\mathfrak S,\) and the identity \(1\in \sum _{\lambda \in \Lambda } \mathfrak {x}_{\lambda }.\) This implies the existence of a finite subset \(\{\lambda _{\scriptscriptstyle 1}, \ldots , \lambda _{\scriptscriptstyle n}\}\) of \(\Lambda \) such that \(1= \sum _{i=1}^n x_{\lambda _i}\) (where \(x_{\lambda _i}\in \mathfrak {x}_{\lambda _i}\)), and hence \(R= \sum _{i=1}^n \mathfrak {x}_{\lambda _i},\) which establishes the finite intersection property. Therefore, \(\sigma _{\mathfrak S}\) is quasi-compact by Alexander’s subbase theorem. \(\square \)
Corollary 3.4
The Iséki spaces of maximal, prime, strongly irreducible, primary, irreducible, radical ideals are all quasi-compact.
Remark 3.5
In a (m, n)-semiring, our coarse lower topology coincide with the hull-kernel topology on n-ary prime full k-ideals, n-ary prime ideals, and strongly irreducible ideals, and hence, we obtain quasi-compactness (see respectively [17, Theorem 3.1, Theorem 5.4, and Theorem 6.2]).
Notice that in Theorem 3.3 the containment of all maximal ideals to an arbitrary spectrum \(\sigma _{\mathfrak S}\) is a sufficient condition for quasi-compactness of the Iséki space \(\sigma _{\mathfrak S}\). For the spectrum of finitely generated ideals of a semiring, for instants, it is also a necessary condition.
Proposition 3.6
If the Iséki space \(\sigma _{\mathfrak S}\) of finitely generated proper ideals is quasi-compact then \(\sigma _{\mathfrak S}\) contains all maximal ideals of \(\mathfrak S.\)
Proof
Suppose \(\mathfrak m\) is a maximal ideal of the semiring \(\mathfrak S\) such that \(\mathfrak m\) is not finitely generated. Let us consider the collection of closed subspaces:
We claim that \(\bigcap \mathcal C=\emptyset \). If not, let \(\mathfrak y\in \bigcap \mathcal C\). Then \(\mathfrak b\) is finitely generated and \(\mathfrak m\subseteq \mathfrak y\). Since \(\mathfrak m\) is not a finitely generated ideal, we must have \(\mathfrak y\supsetneq \mathfrak m,\) and that implies \(\mathfrak y=\mathfrak S\), which contradicts the fact that \(\sigma _{\mathfrak S}\) consists of proper ideals. But clearly \(\mathcal C\) has the finite intersection property and hence \(\sigma _{\mathfrak S}\) is not quasi-compact. \(\square \)
If \(\mathfrak {S}\) is a Noetherian semiring, then we have the following result which may considered as a semiring-theoretic version of the corresponding result proved in Finocchiaro, Goswami, and Spirito, [8] for rings.
Theorem 3.7
If \(\mathfrak S\) is a Noetherian semiring then every Iséki space \(\sigma _{\mathfrak {S}}\) is quasi-compact.
Proof
Consider a collection \(\{\sigma _{\mathfrak {S}}\cap \mathfrak x_{\lambda }^{\uparrow } \}_{\lambda \in \Omega }\) of subbasic closed sets of \(\sigma _{\mathfrak {S}}\) with the finite intersection property. By assumption, the ideal \(\mathfrak y=\sum _{\lambda \in \Omega }\mathfrak x_{\lambda }\) is finitely generated, say \(\mathfrak y=(\alpha _1,\ldots ,\alpha _n)\). For every \(1 \le j\le n\), there exists a finite subset \(\Lambda _j\) of \(\Omega \) such that \(\alpha _j\in \sum _{\lambda \in \Lambda _j}\mathfrak x_{\lambda }\). Thus, if \(\Lambda :=\bigcup _{j=1}^n\Lambda _j\), it immediately follows that \(\mathfrak y=\sum _{\lambda \in \Lambda }\mathfrak x_{\lambda }\). Hence we have
since \(\Lambda \) is finite and \(\{\sigma _{\mathfrak {S}}\cap \mathfrak x_{\lambda }^{\uparrow } \}_{\lambda \in \Omega }\) has the finite intersection property. Then the conclusion follows by the Alexander Subbasis Theorem. \(\square \)
Corollary 3.8
If \(\mathfrak S\) is a Noetherian semiring then every Iséki space \(\sigma _{\mathfrak {S}}\) is Noetherian.
Next we consider the separation axiom of sobriety. Recall that a topological space X is called sober if every non-empty irreducible closed subset \(\mathcal K\) of X is of the form: \(\mathcal K=\textrm{Cl}(\{x\})\), the closure of an unique singleton set \(\{x\}\). The following result characterizes sober Iséki spaces of a semiring.
Theorem 3.9
An Iséki space \(\sigma _{\mathfrak S}\) is sober if and only if
for every non-empty irreducible subbasic closed subset of \(\mathfrak {a}^{\uparrow }\) of \(\sigma _{\mathfrak S}\).
Proof
If \(\sigma _{\mathfrak S}\) is a sober space and \(\mathfrak {a}^{\uparrow }\) is a non-empty irreducible subbasic closed subset of \(\sigma _{\mathfrak S}\), then \(\mathfrak {a}^{\uparrow }=\textrm{Cl}(\{\mathfrak {b}\})=\mathfrak {b}^{\uparrow }\) for some \(\mathfrak {b}\in \sigma _{\mathfrak S}\), and we have
Conversely, suppose the condition (5) holds for every non-empty irreducible subset of \(\sigma _{\mathfrak S}\). Let \(\mathcal K\) be an irreducible closed subset of \(\sigma _{\mathfrak S}\). Then
for some ideals \(\mathfrak x_{ji}\) of \(\mathfrak S\). Since \(\mathcal K\) is irreducible, for every \(i\in \Omega \) there exists an ideal \(\mathfrak x_{ji}\) of \(\mathfrak S\) such that \(\displaystyle \mathcal K\subseteq \mathfrak {x}_{ji}^{\uparrow }\subseteq \bigcup _{j=1}^m\mathfrak {x}_{ji}^{\uparrow }\) and thus, if \(\mathfrak y= \sum _{i\in \Omega }\mathfrak x_{ji}\), then we have
By assumption, \(\displaystyle \bigcap _{\begin{array}{c} \mathfrak {y}\subseteq \mathfrak {s} \\ \mathfrak {s}\in \sigma _{\mathfrak S} \end{array}} \mathfrak {s}\in \sigma _{\mathfrak S},\) and thus \(\displaystyle \mathcal K=\textrm{Cl}\left( {\bigcap _{\begin{array}{c} \mathfrak {y}\subseteq \mathfrak {s} \\ \mathfrak {s}\in \sigma _{\mathfrak S} \end{array}} \mathfrak {s}}\right) .\) The uniqueness part follows from Proposition 3.2. \(\square \)
Corollary 3.10
The Iséki spaces of proper ideals, prime ideals, and strongly irreducible ideals are sober.
Like Alexander subbase theorem, there is no characterization of connectedness in terms of subbasic closed sets. Nevertheless, we wish to present a disconnectivity result of Iséki spaces of a semiring that bears resemblance to the fact that if spectrum of prime ideals (of a commutative ring with identity) endowed with Zariski topology is disconnected, then the ring has a proper idempotent element (see Bourbaki [4], Section 4.3, Corollary 2).
We say a closed subbase \(\mathcal {S}\) of a topological space X strongly disconnects X if there exist two non-empty subsets A, B of \(\mathcal {S}\) such that \(X=A\cup B\) and \(A\cap B=\emptyset \). It is clear that if some closed subbase strongly disconnects a topological space, then the space is disconnected. Also, if a space is disconnected, then some closed subbase (for instance the collection of all its closed subspaces) strongly disconnects it.
Proposition 3.11
Suppose \(\mathfrak S\) is a semiring with multiplicative identity 1 and \(\mathfrak S\) has zero Jacobson radical. Let \(\sigma _{\mathfrak S}\) be a spectrum of \(\mathfrak S\) containing all maximal ideals of \(\mathfrak S.\) If the subbase \(\mathcal {S}\) of the Iséki space \(\sigma _{\mathfrak S}\) strongly disconnects \(\sigma _{\mathfrak S}\), then \(\mathfrak S\) has a non-trivial idempotent element.
Proof
Let \(\mathfrak {x}\) and \(\mathfrak {y}\) be ideals of \(\mathfrak S\) such that
-
(i)
\( \mathfrak {x}^{\uparrow }\cap \mathfrak {y}^{\uparrow } =\emptyset ,\)
-
(ii)
\(\mathfrak {x}^{\uparrow }\cup \mathfrak {y}^{\uparrow } =\sigma _{\mathfrak S},\) and
-
(iii)
\(\mathfrak {x}^{\uparrow }\ne \emptyset , \mathfrak {y}^{\uparrow } \ne \emptyset . \)
Since \(\mathfrak {x}^{\uparrow }\cap \mathfrak {b}^{\uparrow }=(\mathfrak {x} +\mathfrak {y})^{\uparrow }\), we therefore have \((\mathfrak {x}+\mathfrak {y})^{\uparrow }=\emptyset \) and hence \(\mathfrak {x}+\mathfrak {y} =\mathfrak S\) because \(\sigma _{\mathfrak S}\) contains all maximal ideals of \(\mathfrak S\). On the other hand,
which then implies that \(\mathfrak {x}\mathfrak {y}\) is contained in every maximal ideal of \(\mathfrak S\), and is therefore the zero ideal since \(\mathfrak {S}\) has zero Jacobson radical. Note that the condition (iii) implies that neither \(\mathfrak {x}\) nor \(\mathfrak {y}\) is the entire semiring \(\mathfrak S\). So the equality \(\mathfrak {x}+\mathfrak {y}=\mathfrak S\) furnishes non-zero elements \(x\in \mathfrak {x}\) and \(y\in \mathfrak {y}\) such that \(x+y=1\). Since \(xy=0\) as \(xy\in \mathfrak {x}\mathfrak {y}=\mathfrak {o}\), we therefore have \( x= x(x+y)=x^{ 2}+xy =x^{ 2}, \) showing that x is a non-zero idempotent element in \(\mathfrak S\). Since \(\mathfrak {x}\ne \mathfrak S\), \(x\ne 1\), and hence x is a non-trivial idempotent element of \(\mathfrak S\). \(\square \)
Theorem 3.13 below gives a sufficient condition for an Iséki space to be connected and to prove that result we first need the following
Lemma 3.12
In every Iséki space \(\sigma _{\mathfrak S}\), the subbasic closed sets of the form: \(\{\mathfrak {y}^{\uparrow }\mid \mathfrak {y}\in \mathfrak {y}^{\uparrow }\}\) are irreducible.
Proof
It is sufficient to show that \(\mathfrak {y}^{\uparrow }=\textrm{Cl}(\mathfrak {y})\) whenever \(\mathfrak {y}\in \mathfrak {y}^{\uparrow }\). Since \(\textrm{Cl}(\mathfrak {y})\) is the smallest closed set containing \(\mathfrak {x}\), and since \(\mathfrak {y}^{\uparrow }\) is a closed set containing \(\mathfrak {y}\), obviously then \(\textrm{Cl}(\mathfrak {y})\subseteq \mathfrak {y}^{\uparrow }\). For the reverse inclusion, if \(\textrm{Cl}(\mathfrak {y})= \sigma _{\mathfrak S}\), then
This proves that \(\mathfrak {y}^{\uparrow }=\textrm{Cl}(\mathfrak {y})\). Suppose that \(\textrm{Cl}(\mathfrak {y})\ne \sigma _{\mathfrak S}\). Since \(\textrm{Cl}(\mathfrak {y})\) is a closed set, there exists an index set, \(\Omega \), such that, for each \(\lambda \in \Omega \), there is a positive integer \(x_{\lambda }\) and ideals \(\mathfrak {x}_{\lambda 1},\dots , \mathfrak {x}_{\lambda n_\lambda }\) of \(\mathfrak S\) such that
Since \(\textrm{Cl}(\mathfrak {y})\ne \sigma _{\mathfrak S},\) we can assume that \({\bigcup _{ i\,=1}^{ x_\lambda }}\mathfrak {x}_{\lambda i}^{\uparrow }\) is non-empty for each \(\lambda \). Therefore, \(\mathfrak {y}\in {\bigcup _{ i\,=1}^{ x_\lambda }}\mathfrak {x}_{\lambda i}^{\uparrow }\) for each \(\lambda \), and hence \(\mathfrak {y}^{\uparrow }\subseteq {\bigcup _{ i=1}^{ x_\lambda }}\mathfrak {x}_{\lambda i}^{\uparrow }\), that is, \(\mathfrak {y}^{\uparrow }\subseteq \textrm{Cl}(\mathfrak {y})\) as desired. \(\square \)
Theorem 3.13
If a spectrum \(\sigma _{\mathfrak S}\) of a semiring \(\mathfrak S\) contains the zero ideal, then the Iséki space \(\sigma _{\mathfrak S}\) is connected.
Proof
Since \(\sigma _{\mathfrak S}=\mathfrak {o}^{\uparrow }\) and irreducibility implies connectedness, the claim now follows from Lemma 3.12. \(\square \)
Corollary 3.14
Iséki spaces of proper, finitely generated, principal ideals of a semiring are connected.
Iséki and Miyanaga [20, Theorem 2] has shown that the spectrum of maximal ideals with the Stone topology (= coarse lower topology) is a \(T_1\)-space. Furthermore, Iséki [21, Theorem 3] proved that every prime ideal is maximal, if and only if the topological space is a \(T_1\)-space. Surprisingly, Iséki space of maximal ideals of a semiring also characterizes \(T_1\)-space as we shall see in the following
Theorem 3.15
An Iséki space \(\sigma _{\mathfrak {S}}\) is \(T_1\) if and only if the spectrum \(\sigma _{\mathfrak {S}}\) is the set of all maximal ideals of \(\mathfrak {S}.\)
Proof
Suppose \(\sigma _{\mathfrak {S}}\) is a \(T_1\)-space and let \(\mathfrak {a}\in \sigma _{\mathfrak {S}}\). Then \(\mathfrak {a}\in \mathfrak {a}^{\uparrow }\), and so, by Theorem 3.12, \(\textrm{Cl}({\{\mathfrak {a}\}})=\mathfrak {a}^{\uparrow }\). Let \(\mathfrak {m}\) be a maximal ideal of \(\mathfrak {S}\) with \(\mathfrak {a}\subseteq \mathfrak {m}\). Then
where the last equality follows from the hypothesis. Therefore \(\mathfrak {m}=\mathfrak {a}\), showing that \(\sigma _{\mathfrak {S}}\) is contained in the set of all maximal ideals of \(\mathfrak {S}\). Conversely, \(\mathfrak {m}^{\uparrow }=\{\mathfrak {m}\}\) for every maximal ideal \(\mathfrak {m}\) of \(\mathfrak {S},\) so that \(\mathfrak {m}\in \mathfrak {m}^{\uparrow }\), and hence, by Theorem 3.12, \(\textrm{Cl}({\{\mathfrak {m}\}})=\{\mathfrak {m}\}\), showing that the Iséki space \(\sigma _{\mathfrak {S}}\) is a \(T_{ 1}\)-space. \(\square \)
Corollary 3.16
Let \(\mathfrak {S}\) be a Noetherian ring. If \(\sigma _{\mathfrak {S}}\) is a discrete space then \(\mathfrak {S}\) is Artinian.
Remark 3.17
Note that in an (m, n)-semiring, maximal ideals endowed with two special topologies generated respectively by \(\Delta _x\) and \(\Omega _x\) (see [17, Theorem 4.2 and Theorem 4.3]) satisfy \(T_2\) and \(T_1\) separation axioms.
We now discuss about continuous maps between Iséki spaces of semirings. Observe that although inverse image of an ideal under a semiring homomorphism is an ideal, but the same may not hold for an arbitrary spectra \(\sigma _{\mathfrak S}\). To resolve this problem, we need to impose that property on a spectrum. We say a spectrum \(\sigma _{\mathfrak S}\) satisfies the contraction property if for any semiring homomorphism \(\phi :\mathfrak S\rightarrow \mathfrak S',\) the inverse image  is in \(\sigma _{\mathfrak S}\), whenever \(\mathfrak {x}'\) is in \(\sigma _{\mathfrak S'}.\) Since the sets \(\{\mathfrak {x}^{\uparrow }\mid \mathfrak {x}\;\text {is an ideal of}\; \mathfrak {S}\}\) only form a (closed) subbasis, all our arguments need to be at this level rather than just closed sets.
is in \(\sigma _{\mathfrak S}\), whenever \(\mathfrak {x}'\) is in \(\sigma _{\mathfrak S'}.\) Since the sets \(\{\mathfrak {x}^{\uparrow }\mid \mathfrak {x}\;\text {is an ideal of}\; \mathfrak {S}\}\) only form a (closed) subbasis, all our arguments need to be at this level rather than just closed sets.
Proposition 3.18
Let \(\sigma _{\mathfrak S}\) be a spectrum satisfying the contraction property. Let \(\phi :\mathfrak S\rightarrow \mathfrak S'\) be a semiring homomorphism and \(\mathfrak {x}'\in \sigma _{\mathfrak S'}.\)
-
(i)
The induced map \(\phi _*:\sigma _{\mathfrak S'}\rightarrow \sigma _{\mathfrak S}\) defined by
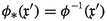 is continuous.
is continuous. -
(ii)
If \(\phi \) is surjective, then the Iséki space \(\sigma _{\mathfrak S'}\) is homeomorphic to the closed subspace \(\textrm{Ker}(\phi )^{\uparrow }\) of the Iséki space \(\sigma _{\mathfrak S}.\)
-
(iii)
The subset \(\phi _*(\sigma _{\mathfrak S'})\) is dense in \(\sigma _{\mathfrak S}\) if and only if \(\textrm{Ker}(\phi )\subseteq \bigcap _{\mathfrak {s}\in \sigma _{\mathfrak S}}\mathfrak {s}.\)
Proof
To show (i), let \(\mathfrak {x}\) be an ideal of \(\mathfrak {S}\) and \(\mathfrak {x}^{\uparrow }\) be a subbasic closed set of the ideal space \(\sigma _{\mathfrak S}.\) Then

and hence the map \(\phi _*\) continuous. For (ii), observe that  follows from the fact that \(\mathfrak {o}\subseteq \mathfrak {x}'\) for all \(\mathfrak {x}'\in \sigma _{\mathfrak S'}.\) It can thus been seen that \(\phi _*(\mathfrak {x}')\in \textrm{Ker}(\phi )^{\uparrow },\) and hence \(\textrm{Im}(\phi _*)=\textrm{Ker}(\phi )^{\uparrow }.\) If \(\mathfrak {x}'\in \sigma _{\mathfrak S'},\) then
follows from the fact that \(\mathfrak {o}\subseteq \mathfrak {x}'\) for all \(\mathfrak {x}'\in \sigma _{\mathfrak S'}.\) It can thus been seen that \(\phi _*(\mathfrak {x}')\in \textrm{Ker}(\phi )^{\uparrow },\) and hence \(\textrm{Im}(\phi _*)=\textrm{Ker}(\phi )^{\uparrow }.\) If \(\mathfrak {x}'\in \sigma _{\mathfrak S'},\) then  Thus \(\phi _*\) is injective. To show that \(\phi _*\) is closed, first we observe that for any subbasic closed subset \(\mathfrak {a}^{\uparrow }\) of \(\sigma _{\mathfrak S'}\), we have
Thus \(\phi _*\) is injective. To show that \(\phi _*\) is closed, first we observe that for any subbasic closed subset \(\mathfrak {a}^{\uparrow }\) of \(\sigma _{\mathfrak S'}\), we have

Now if \(\mathcal K\) is a closed subset of \(\sigma _{\mathfrak S'}\) and \(\mathcal K=\bigcap _{ \lambda \in \Omega } (\bigcup _{ i \,= 1}^{ n_{\lambda }} \mathfrak {x}_{ i\lambda }^{\uparrow }),\) then

a closed subset of \(\sigma _{\mathfrak S}.\) Since by (i), \(\phi _*\) is continuous, we have the desired claim. Finally to prove (iii), first we wish to show:  for all ideals \(\mathfrak {x}'\) of \(\mathfrak S'\). For that, let \(\mathfrak {s}\in \phi _*(\mathfrak {x}'^{\uparrow }).\) This implies \(\phi (\mathfrak {s})\in \mathfrak {x}'^{\uparrow },\) and that means \(\mathfrak {x}'\subseteq \phi (\mathfrak {s}).\) Therefore,
for all ideals \(\mathfrak {x}'\) of \(\mathfrak S'\). For that, let \(\mathfrak {s}\in \phi _*(\mathfrak {x}'^{\uparrow }).\) This implies \(\phi (\mathfrak {s})\in \mathfrak {x}'^{\uparrow },\) and that means \(\mathfrak {x}'\subseteq \phi (\mathfrak {s}).\) Therefore,  Since
Since  , the other inclusion follows. If we take \(\mathfrak {x}'\) as the trivial ideal \(\mathfrak {o}'\) of \(\mathfrak S'\), the above identity reduces to \(\textrm{Cl}(\phi _*(\sigma _{\mathfrak S'}))=\textrm{Ker}(\phi )^{\uparrow },\) and hence \(\textrm{Ker}(\phi )^{\uparrow }\) to be equal to \(\sigma _{\mathfrak S}\) if and only if \(\textrm{Ker}(\phi )\subseteq \bigcap _{\mathfrak {s}\in \sigma _{\mathfrak S}}\mathfrak {s}.\) \(\square \)
, the other inclusion follows. If we take \(\mathfrak {x}'\) as the trivial ideal \(\mathfrak {o}'\) of \(\mathfrak S'\), the above identity reduces to \(\textrm{Cl}(\phi _*(\sigma _{\mathfrak S'}))=\textrm{Ker}(\phi )^{\uparrow },\) and hence \(\textrm{Ker}(\phi )^{\uparrow }\) to be equal to \(\sigma _{\mathfrak S}\) if and only if \(\textrm{Ker}(\phi )\subseteq \bigcap _{\mathfrak {s}\in \sigma _{\mathfrak S}}\mathfrak {s}.\) \(\square \)
Note that for the spectrum of prime ideals, the inclusion condition in (iii) is replaced by an equality. If \(\phi \) is the quotient map \(\mathfrak S\rightarrow \mathfrak {S}/\mathfrak {x}\), then we have the following
Corollary 3.19
If \(\sigma _{\mathfrak S}\) is a spectrum of \(\mathfrak {S}\) satisfying the contraction property, then the Iséki space \(\sigma _{{\mathfrak {S}/\mathfrak {x}}}\) is homeomorphic to the closed subspace \(\mathfrak {x}^{\uparrow }\) of \(\sigma _{\mathfrak S}\) for every \(\mathfrak {x}\) of \(\mathfrak {S}\).
References
Azizi, A.: Strongly irreducible ideals. J. Aust. Math. Soc. 84, 145–154 (2008)
Amitsur, S.A.: A general theory of radicals III. Am. J. Math. 76, 126–136 (1954)
Behrens, E.A.: Zur additiven idealtheorie in nichtassozialiven ringen. Math. Z. 64, 169–182 (1956)
Bourbaki, N.: Elements of Mathematics: Commutative Algebra. Addison-Wesley, Reading, MA (1972)
Brown, B., McCoy, N.H.: Prime ideals in nonassociative rings. Trans. Am. Math. Soc. 89, 245–255 (1958)
Dickmann, M., Schwartz, N., Tressal, M.: Spectral Spaces. Cambridge University Press, Cambridge (2019)
Dube, T., Goswami, A.: Ideal spaces: an extension of structure spaces of rings. J. Algebra. Appl. (online ready) (2022)
Finocchiaro, C.A., Goswami, A., Spirito, D.: Distinguished classes of ideal spaces and their topological properties. Commun. Algebra (2022) (online ready)
Gillman, L., Jerison, M.: Rings of Continuous Functions. D. Van Nostrand Company, Inc. (1960)
Golan, J. S.: Semirings and Their Applications. Springer, New York (1999)
Grothendieck, A.: Éléments de géométrie algébrique I, Le langage des schémas. Inst. Hautes Études Sci. Publ. Math. 4 (1960)
Gelfand, I., Kolmogoroff, A.: On rings of continuous functions on topological spaces. C. R. (Dokl.) Acad. Sci. URSS, n. Ser. 22, 11–15 (1939)
Gelfand, I., Šilov, G.: Über verschiedene Methoden der Einführung der topologie in die menge der maximalen ideale eines normierten ringes. Math. Sbornik 9(51), 25–39 (1941)
Głazek, K.: A guide to the literature on semirings and their applications in mathematics and information sciences. Kluwer Academic Publishers, With complete bibliography (2002)
Gierz, G., Hofmann, K.H., Keimel, K., Lawson, J.D., Mislove, M., Scott, D.S.: Continuous Lattices and Domains. Cambridge University Press, Cambridge (2003)
Henriksen, M., Jerison, M.: The space of minimal prime ideals of a commutative ring. Trans. Am. Math. Soc. 115, 110–130 (1965)
Hila, K., Kar, S., Kuka, S., Naka, K.: Some structure spaces of generalized semirings. Filomat 32(13), 4461–4472 (2018)
Hochster, M.: The minimal prime spectrum of a commutative ring. Can. J. Math. XXIII(5), 749–758 (1971)
Ilzuka, K.: On the Jacobson radical of a semiring. Tohuku Math. J. 11, 409–421 (1959)
Iséki, K., Miyanaga, Y.: Notes on topological spaces. III. On space of maximal ideals of semiring. Proc. Jpn. Acad. 32, 325–328 (1956)
Iséki, K.: Notes on topological spaces. V. On structure spaces of semiring. Proc. Jpn. Acad. 32, 426–429 (1956)
Iséki, K.: Ideal theory of semiring. Proc. Jpn. Acad. 32, 554–559 (1956)
Jacobson, N.: A topology for the set of primitive ideals in an arbitrary ring. Proc. Natl. Acad. Ser. USA 31, 333–338 (1945)
Jacobson, N.: Structure of rings, Amer. Math. Soc. Colloquium Publications, vol. 37, Providence (1956)
Loomis, L.H.: An Introduction to Abstract Harmonic Analysis. D. Van Nostrand Company, Inc (1953)
McKnight, J.D. Jr.: On the Characterisation of Rings of Functions. Purdu Doctoral Thesis (1953)
Nasehpour, P.: Some remarks on ideals of commutative semirings. Quasigroup Relat. Syst. 26, 281–298 (2018)
Šilov, G.: Ideals and subrings of the rings of continuous functions. C. R. (Dokl.) Acad. Sci. URSS n. Ser. 22, 7–10 (1939)
Stone, M.H.: Applications of the theory of Boolean rings to general topology. Trans. Am. Math. Soc. 41, 375–481 (1937)
Slowikowski, W., Zawadowski, W.: A generalisation of maximal ideals method of Stone and Gelfand. Fund. Math. 42, 216–231 (1955)
Vandiver, H.S.: Note on a simple type of algebra in which the cancellation law of addition does not hold. Bull. Am. Math. Soc. 40(12), 914–920 (1934)
Vandiver, H.S.: On some simple types of semi-rings. Am. Math. Monthly 46(1), 22–26 (1939)
Funding
Open access funding provided by University of Johannesburg.
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Conflict of interest
Not applicable.
Research involving human participants and/or animals
Not applicable.
Informed consent
Not applicable.
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Goswami, A. Iséki spaces of semirings. Boll Unione Mat Ital 16, 677–686 (2023). https://doi.org/10.1007/s40574-023-00355-x
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s40574-023-00355-x



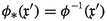 is continuous.
is continuous.