Resolved CFD-DEM simulation of blood flow with a reduced-order RBC model

Abstract

Mathematical modeling of the blood flow with a resolved description of biological cells mechanics such as red blood cell (RBC) has been a challenge in the past decades as it involves physical complexities and demands high computational costs. In the present study, we propose an approach for efficient simulation of blood flow with several suspended RBCs. In this approach, we employ our previously proposed reduced-order model for deformable particles (Nair et al. in Comput Part Mech 7:593–601, 2020) to mimic the mechanical behavior of an individual RBC as a cluster of overlapping spheres interconnected by flexible mathematical bonds. This discrete element method-based model is then coupled with a fluid flow solver using the immersed boundary method with continuous forcing in the context of computational fluid dynamics-discrete element method (CFD-DEM) coupling. The present computational method is tested with a couple of validation cases in which the single RBC dynamics, as well as the blood flow with several RBCs, were tested in comparison with existing literature date. First, the RBC deformation index in shear flow at different shear rates is studied with a good accuracy. Then, the blood flow in micro-tubes of different diameters and hematocrits was simulated. The key characteristics of blood flow such as cell-free layer (CFL) thickness, Fahraeus effect and the relative apparent viscosity are used as the validation metrics. The proposed approach can predict the formation of the migration of RBC toward the tube center-line and the CFL thickness in good agreement with previous measurement and simulations. Furthermore, the model is employed to study the CFL enhancement for plasma separation based on channel constriction. The simulation results compute the CFL thickness downstream of the channel constriction in good agreement with the experiments in a wide range of flow rates and constriction lengths. The original contribution of this study lies in proposing an efficient resolved CFD-DEM simulation method for blood flows with many RBCs which can be employed for numerical investigation of bio-microfluidic applications.

1 Introduction

Blood is an important physiological fluid which is vital for the transportation of oxygen and nutrients to various parts of the body. It consists of red blood cells (erythrocytes), white blood cells (leukocytes) and platelets (thrombocytes) that are suspended in the blood plasma. Under ideal conditions, the volume concentration of RBCs in the blood (hematocrit) is around $45\%$ [1]. A healthy human RBC has a biconcave disc shape with an approximate diameter of $8 \; \upmu$m and a thickness of around $2 \; \upmu$m. They are highly deformable due to which they can pass through channels having smaller diameters [2]. Since RBCs are the largest component in blood, they play a major role in determining the rheological behavior of blood. From in vitro experiments conducted by [3], it was observed that the flow behavior was influenced by the collective dynamics of RBCs. In fact, the cross-stream migration of the RBCs towards the core of the flow forms a cell-free depletion layer (CFL) near the surrounding walls. Since the flow core is populated with RBCs, it has a higher viscosity compared to the CFL near the tube walls, which in turn produces a lubricating effect. This effect increases with the CFL thickness and reduces the apparent viscosity, which is known as the Fahraeus–Lindqvist effect [4, 5]. Therefore, the blood flow characteristics are majorly governed by the RBC dynamics. This justifies the significant amount of investigations from different perspectives on red blood cells ranging from the mechanobiological behavior of an individual RBC towards the features of RBC-populated flows (e.g., aggregates and coagulation).

Numerical simulation of blood flow is challenging because of the strongly-coupled interactions between the biological cells including the erythrocytes, leukocytes and thrombocytes and the surrounding blood plasma. Several mathematical models have been developed in recent years, such as the continuum-based membrane models [6,7,8] and the finite element models [9,10,11], which simulate deformable vesicles and RBCs in a coupled fluid environment. Besides, particle-based spring network models [12,13,14,15,16,17,18] assume an RBC membrane as a network of springs connecting massless points. While some of these methodologies treat both the RBCs and the fluid system as a particle system, others couple the RBC membrane model with a fluid flow solver to simulate the flow. All these methods can result in accurate modeling of RBCs; however, they prove to be computationally expensive when simulating complex flow scenarios.

To overcome the computational costs, reduced-order approaches are commonly employed to reduce the complexity of the physical problem to a simpler description, which is less expensive to model. In the context of RBC in blood flow, such reduced-order models usually simplify the RBC shape and deformation dynamics to a resembling discrete entity which is then coupled with a computational fluid dynamics (CFD) platform to enable modeling the RBCs in interaction with surrounding blood plasma. [19] proposed a torus of overlapping colloidal particles connected using worm-like chain (WLC) springs to represent an RBC. This model is then coupled to a Dissipative Particle Dynamics (DPD) method and revealed a good degree of accuracy with a reduction in computational cost, but also lacked some of the critical behaviors of RBC such as viscoelasticity and tank-treading behavior. This model is recently used by [20] in combination with the lattice Boltzmann method. From a mathematical modeling viewpoint, such a combination of different sub-models is also common in the simulation of dispersed multiphase systems, e.g., particle-laden flows. In this context, the coupling between computational fluid dynamics and discrete element method (CFD-DEM) is employed to model the interaction between suspended particles and the carrier fluids. Therefore, it can provide another proper modeling framework for suspended RBCs in blood plasma. However, the CFD-DEM techniques have been conventionally used for rigid particles, and the state-of-the-art CFD-DEM still lacks a robust model for deformable particles. Following the concept of model order reduction, we have recently introduced a reduced-order model for deformable particles in the frame of DEM [21]. In this model, a single RBC consists of several constituent spheres with their centroids interconnected by mathematical elastic bonds. This model has revealed a good level of accuracy for modeling the mechanical behavior of a single RBC in response to static and dynamic loads. When coupled with the fluid flow solver, this model has shown a reasonable performance by predicting the drag force on a single RBC in a channel flow compared with experimental measurements [21]. It has to be noted this coupling is established by adopting the resolved CFD-DEM methodology, which is technically an immersed boundary method with fictitious domain for the flow where the DEM describes the particle interactions.

In the present study, we employ this reduced-order model in a more complex situation where multiple RBCs are involved. The inter-cellular interactions are modeled using a Hertz–Mendelian model with the attractive forces enforced utilizing a cohesive force based on the Morse potential. We investigate the performance of this reduced-order approach in predicting the blood flow characteristics in a microchannel such as the blood velocity profile, the formation of the CFL, the non-Newtonian macroscopic viscosity (also referred to as apparent viscosity) and the Fahraeus effect.

The paper is structured as follows. In Sect. 2, the mathematical concept for developing the reduced-order model and the coupled solver is described including the details of resolved CFD-DEM and the immersed boundary method. Additionally, the interaction model for inter-cellular interactions and the cohesion model will be discussed. Section 3 presents the description of the simulation setup as well as a detailed discussion on the results. The paper ends with the conclusion in Sect. 4.

2 Mathematical model description

The classical Navier–Stokes equations describe the flow of an incompressible, viscous fluid as given by

$$\begin{aligned}&\nabla \cdot {\mathbf {u}} = 0 \end{aligned}$$

(1)

$$\begin{aligned}&\frac{\partial \left( \rho {\mathbf {u}}\right) }{\partial t} + \nabla \cdot \left( \rho {\mathbf {u}}{\mathbf {u}}\right) = - \nabla p + \mu \nabla ^2 {\mathbf {u}} + F_g + F_B \end{aligned}$$

(2)

where ${\mathbf {u}}$ is the fluid velocity field, $\rho$ is the fluid density, $\mu$ is the dynamic viscosity of the fluid, p is the pressure, $F_g$ is the body force due to gravity and $F_B$ is the momentum source term acting on the fluid. The motion of particles is governed by Newton’s laws of motion, which read

$$\begin{aligned} m_p \frac{\mathrm{d} \mathbf {u_p}}{\mathrm{d}t}= & {} m_p {\mathbf {g}} + F_p^f + \sum _{N_p} F_p^p + \sum _{N_w} F_p^w+ F_p^{\mathrm{ext}} \end{aligned}$$

(3)

$$\begin{aligned} I_p \frac{\mathrm{d} {\omega _{\mathbf{p}}}}{\mathrm{d}t}= & {} {\mathbf {r}} \times \left( F_p^f + \sum _{N_p} F_p^p + \sum _{N_w} F_p^w + F_p^{\mathrm{ext}}\right) \end{aligned}$$

(4)

In this system of equations, ${\mathbf {g}}$ is the gravitational acceleration, $m_p$ is the mass of the particle, $F_p^f$ is the hydrodynamic forces acting on the particle and $F_p^p$ and $F_p^w$ are the particle–particle and particle–wall interaction forces, respectively. $F_p^{\mathrm{ext}}$ is the external force acting on the particle which comes from cohesion, adhesion and other interaction forces. $I_p$ is the second moment of inertia of the particle, ${\omega _{\mathbf{p}}}$ is the angular velocity, and ${\mathbf {r}}$ is the distance between the particle centroid and a point on the surface of the particle. For a sphere, the moment of inertia can be calculated as $I = \frac{2 mr^2}{5}$.

Coupling between the fluid phase and the discrete particle phase is performed in the context of CFD-DEM methodology [22]. There exist two primary classes of CFD-DEM based on their scale of resolution. In the unresolved CFD-DEM, the particle size is much smaller than the finite volume cell. The fluid–particle interactions are not fully resolved and the hydrodynamic forces are calculated from mathematical correlations, whereas in resolved CFD-DEM, the particle size is larger than the finite volume cell as schematically depicted in Fig. 1a. This allows to achieve a fully resolved description of the particle–fluid interactions. The present reduced-order model is also developed based on the resolved CFD-DEM approach to account for RBC deformation. Thus, this technique is briefly introduced in the following section.

2.1 Resolved CFD-DEM method

The resolved CFD-DEM is technically a combination of the immersed boundary (IB) method [23] with the DEM. In this technique, the particle is assumed as an immersed body in the fluid domain and its influence on the fluid is considered in a coupled manner. There are two common approaches to account for the interactions between fluid and immersed particle. A direct forcing method can be used to correct the fluid flow with the particle velocity which enforces a no-slip boundary condition [24, 25]. This methodology is severely dependent on the spatial discretization since an additional immersed boundary flux has to be calculated to keep the velocity field divergence-free. The continuous forcing approach is to introduce a momentum source in the continuous momentum equation before discretization [24]. This method requires no body-conforming moving mesh and this, in turn, reduces the computational cost and complexity significantly. Following the latter, we have incorporated a porous media approximation, wherein the source term in the momentum equation is calculated by considering the particle region as a low permeability porous medium (also known as the penalization method [26,27,28]).

Fig. 1

a Schematics of an immersed body in a fluid domain. $\varOmega _f$ and $\varOmega _s$ are the fluid and solid domain, and $\varGamma _f$ and $\varGamma _s$ are the boundary surfaces of the fluid and solid domains, respectively. b Illustration of the solid volume fraction $\alpha$ within a finite volume grid cell

Thus, the source term is added directly to the momentum equation before discretization, and hence, the approach is independent of the spatial discretization. Therefore, the momentum source term in Eq. 2 reads

$$\begin{aligned} F_B = \frac{\rho \alpha \left( \mathbf {u_p} - {\mathbf {u}} \right) }{\kappa \varDelta t} \end{aligned}$$

(5)

where ${\mathbf {u}}$ and $\mathbf {u_p}$ are the fluid and particle velocity vectors, respectively, and $\alpha$ is the solid volume fraction determining the cells that are fully occupied by the particle ($\alpha = 1$), by the surrounding fluid ($\alpha = 0$) and at the interface ($0< \alpha < 1$) as shown in Fig. 1b. The dependency to $\alpha$ ensures that the momentum forcing term is only imposed at the particle regions. $\kappa$ is the permeability of the solid region which enforces the rigid body constraint. In this method, the fluid is allowed to penetrate the particle and the degree of penetration is controlled by $\kappa$. For solid regions $0 < \kappa \ll 1$, and in this study $\kappa = 10^{-7}$ is employed [27, 28]. It is worth mentioning that this permeability concept is the essence of our current continuous forcing implementation, which was not adopted in our previous work [21].

It has to be noted that the IB method itself has been widely used for modeling cell-loaded blood flow [10, 18, 29,30,31], but the original contribution of the present study is to employ this concept in combination with our DEM-based for deformable particles as briefly presented in the following section.

2.2 Description of the reduced-order RBC model

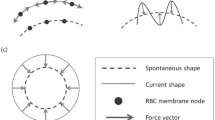
A reduced-order model for the deformable particles has been proposed in our previous work [21] based on the dynamics of RBC. The model consists of overlapping constituent spheres which represent the contour of an RBC as schematically depicted in Fig. 2a. The deformability is introduced using flexible bonds between the centroids of the constituent sphere (Fig. 2b).

Fig. 2

a A reduced-order RBC model with 10 constituent spheres. The black lines are the bonds between the spheres, and the dotted white circle shows the constituent sphere. b The flexible bond between two adjacent constituent sphere with the imposed forces and moments

The bonds can translate and rotate based on the forces and torques acting on the constituent spheres. The bond forces and moments are calculated incrementally [32]

$$\begin{aligned}&dF^b = K^b v^r \delta t \end{aligned}$$

(6)

$$\begin{aligned}&dM^b = S^b \omega ^r \delta t \end{aligned}$$

(7)

$$\begin{aligned}&K^b = \frac{E_b A_b}{l_b} \end{aligned}$$

(8)

$$\begin{aligned}&S^b = \frac{G_b A_b}{l_b} \end{aligned}$$

(9)

where $F^b$ and $M^b$ are the bond forces and moments, $v^r$ and $\omega ^r$ are the relative translational and angular velocities, and $K^b$ and $S^b$ are the normal and bending stiffness of the bonds, respectively. $E_b$ and $G_b$ are the Young’s and Shear modulus of the bond that can be related to the material properties of the body. $A_b$ and $l_b$ are the cross-sectional area and the length of the bond. The flexible bonds behave similar to cantilever beams; thus, under no damping, they undergo free oscillation under external loads. Thus, it is required to counter this oscillation through damping forces. Furthermore, the damping forces must account for dissipation of energy due to the elastic force propagation within the bonds. Velocity-dependent damping forces and moments are considered as

$$\begin{aligned} F_d^b= & {} 2 \beta \sqrt{m K^b} v^r \end{aligned}$$

(10)

$$\begin{aligned} M_d^b= & {} 2 \beta \sqrt{I S^b} \omega ^r \end{aligned}$$

(11)

where $v^r$ and $\omega ^r$ are the relative translational and angular velocities, respectively, and $\beta$ is the damping coefficient. These forces and moments are added to equations 3 and 4 as the external particle force to preserve the viscoelastic behavior of RBC. It has to be noted that a calibration study based on the viscoelastic behavior was conducted in our previous work [21].

2.3 Inter-cellular interaction model

The hydrodynamic interactions of RBC with the plasma as well as the inter-cellular interactions, such as aggregation of RBCs, affect the blood viscosity significantly. Adjacent RBCs interact with each other and form coin-like stacked configurations known as rouleaux, which is a reversible process [33]. Due to the formation of rouleaux, the viscosity of blood increases at low shear rate flows and hence can cause problems like a blockage in microfluidic channels at low shear rates.

In numerous studies, the interaction between RBCs is modeled using the Morse potential force [34, 35]. Accordingly, the RBCs have two interaction regimes—a weak far-field attractive force and a repulsive force in the collision regime. This provides a model by which the aggregation and disaggregation of RBCs can be simulated at low and high shear rates. In the low-dimensional model by [19], this interaction between RBCs was modeled by computing the forces between the center-of-masses of RBCs and considering their orientation with respect to each other [35].

In the framework of DEM, the interaction between two spherical particles is based on the soft-sphere approach [36, 37], where small overlaps between spheres are allowed to calculate the interaction forces. The elastic forces are dependent on the material properties of the spheres such as the Youngs modulus (E), Poissons ratio ($\nu$) and the degree of overlap that is permitted. The contact between two soft spheres is modeled mainly according to the linear Hooke’s law or based on the nonlinear Hertz theory given as [36, 37]

$$\begin{aligned} F_{n,\mathrm{contact}} = \frac{4}{3} \frac{E_i E_j}{E_i \left( 1 - \nu _j \right) + E_j \left( 1 - \nu _i \right) } R_{ij}^{\left( 2 - a\right) } h_{ij}^a {\mathbf {n}}_{ij} \end{aligned}$$

(12)

where subscripts i and j are the two adjacent spheres, and a is the parameter to switch between a linear relation ($a = 1$) and a nonlinear one ($a = 3/2$). In this study, a non-linear Hertzian model is used for modeling the interaction between the constituent spheres. E and $\nu$ are the Young’s modulus and the Poisson’s ratio, respectively. $R_{ij}$ is the reduced radius ($R_{ij} = \frac{R_i R_j}{R_i + R_j}$) and $h_{ij}$ denotes the overlap between the spheres. $F_{n,\mathrm{contact}}$ is one of the major particle–particle interaction forces that contributes to the summation of particle–particle interaction forces (term $F_p^p$ in Eq. (3)). In this study, $F_{n,\mathrm{contact}}$ is only computed for the constituent spheres interacting from two different RBCs and is switched-off between constituent spheres that belong to the same RBC.

Besides, RBC aggregation is an important phenomenon that has been observed in hemorheology. Attractive potentials exist between RBCs and this leads to the formation of rouleaux at low shear rates which breaks down as the shear rate increases. The Morse potential has been implemented to model RBC aggregation and reads [38,39,40,41,42]

$$\begin{aligned} V_M \left( r \right) = D_e \left[ e^{2 \beta \left( r_0 -r \right) } - 2e^{\beta \left( r_0 -r \right) } \right] \end{aligned}$$

(13)

where r is the distance between the centroids of the spheres, $r_0$ is the zero force distance, $D_e$ is the interaction energy, and $\beta$ is the scaling factor. To provide an accurate depiction of the inter-cellular interactions, we incorporate the non-linear Hertzian contact model to determine the contact forces between the constituent spheres of the RBCs and the Morse potential that computes the weak attractive forces (at far distances) and strong repulsive forces (at short distances) between the RBCs. The combination of these two force models is essential for determining the formation of coin-like stack formation of RBC (rouleaux), which becomes critical at low shear flows. In the present study, the zero force distance was taken to be 20 nm and the scaling factor as $2.0\; \upmu \mathrm{m}^{-1}$. [43] conducted double-beam optical tweezers experiments on RBC aggregates and measured the interaction force to be $8.4 \pm 1.1 \;$pN. The interaction force is obtained by $F_M = -\partial V_M / \partial r$. Thus, the interaction energy was found to be in the range of $10 - 35 \; \upmu \mathrm{J} / \mathrm{m}^2$.

3 Results and discussions

In order to perform numerical simulation, the herein proposed reduced-order RBC model is implemented in the open-source DEM software LIGGGHTS$^\circledR$ [22] based on the flexible bond model [32]. Then, this RBC model is coupled with a modified version of the resolved CFD-DEM solver cfdemSolverIB from the libraries of the open-source software package CFDEMcoupling$^\circledR$ [22, 44]. In the remainder of the paper, we present the simulation results using the resolved CFD-DEM approach. First, two validation cases for single-RBC and multiple-RBC scenarios are carried out. Then, the method is employed for an industrial application of CFL enhancement for plasma separation. We also analyze the computational efficiency of the method.

3.1 Single RBC dynamics in shear flow

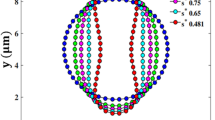
To investigate the performance of proposed method in predicting the deformability of RBC a Wheeler test is carried out. According to the experimental study by Yao et al. [45], a single RBC is positioned in a shear flow and its deformation is tracked under different shear rates. A square channel with a length of 90 $\; \upmu$m and height and depth of 45$\; \upmu$m is chosen as the simulation domain. A constant velocity at different directions is applied to the top and bottom of the channel to produce the shear flow with intended shear rates. Periodic conditions are applied in other directions. The domain was discretized with a grid resolution of $d/ \varDelta = 6$. The RBC is placed at the center of the domain such that its axis of symmetry lies in the shear plane of the flow. Simulations were performed for shear rates ranging from 17 to $200 \; \mathrm{s}^{-1}$ and the initial RBC diameter $D_0 = 7.82 \; \upmu$m. The initial setup and the deformed shapes of the RBC at shear rates ${\dot{\gamma }} = 17 \; \mathrm{s}^{-1}$ and $200 \; \mathrm{s}^{-1}$ are shown in Fig. 3.

Fig. 3

a Initial condition of RBC in the shear flow, and the deformed shapes of the RBC at shear rates, b ${\dot{\gamma }} = 17 \; \mathrm{s}^{-1}$ and (c) $200 \; \mathrm{s}^{-1}$

It has to be noted that the deformation of a single RBC in shear flow is important since it is closely related to the accuracy of the fluid-particle coupling [18]. For a quantitative validation, we use the deformation index (DI) which reads

$$\begin{aligned} {DI = \frac{\left( \left( \frac{D_{\mathrm{max}}}{D_0} \right) ^2 - 1 \right) }{\left( \left( \frac{D_{\mathrm{max}}}{D_0} \right) ^2 + 1 \right) }} \end{aligned}$$

(14)

where $D_0$ is the equilibrium RBC diameter and $D_{\mathrm{max}}$ is the maximum diameter of the deformed RBC under the shear flow. The deformation index obtained from the present simulations is compared with those obtained from experiments [45] and simulations [18, 46] in Fig. 4. For low shear rates, the simulations predict the DIs that match tightly with the results from the literature. As the shear rate increases, the deformation index also increases, showing the largely deformed configuration of RBCs at high shear rates.

Fig. 4

RBC deformation index for different shear rates

3.2 Blood flow in micro-tubes

To verify the method performance for modeling many RBCs, blood flow in micro-tubes of diameters $20 \; \upmu$m, $30 \; \upmu$m and $40 \; \upmu$m are simulated. Blood is modeled as a suspension of biological cells (mostly RBCs) in a Newtonian carrier fluid (blood plasma). The density and kinematic viscosity of the plasma are $1025 \; \mathrm{kg/m}^3$ and $0.0012 \; \mathrm{Pa.s}$, respectively. A cylindrical computational domain (as illustrated in Fig. 5a) is considered with periodic boundary conditions in the flow direction and no-slip conditions at the walls. The Poiseulle flow is driven by a momentum source accounting for the average bulk velocity of the fluid (${{\bar{\mathbf{u}}}}$). The mean bulk velocity is calculated based on the pressure gradient for the flow. The ratio between the constituent spheres and the finite volume cell size is 4 ($d/\varDelta = 4$). The near-wall cell size is refined to resolve the flow between the particles and the wall accurately. As an example, the initial distribution of RBCs in a tube of $D = 40 \; \upmu$m for $H_t = 0.3$ is shown in Fig. 5b. The number of RBCs for each tube hematocrit value is obtained by

$$\begin{aligned} N_{\mathrm{RBC}} = \frac{H_t V}{V_r} \end{aligned}$$

(15)

where $H_t$ is the tube hematocrit, V is the volume of the tube and $V_r$ is the volume of a single RBC. The details of the computational domain and the simulation setup are provided in Table 1. Figure 6 demonstrates two instantaneous snapshots of the RBCs for the largest tube at different hematocrits after the steady-state condition is reached. At this stage, the formation of RBC core is evident, and the RBCs are mostly in the slipper-shape. Now, we present more quantitative analysis of the simulations.

Table 1 Simulation parameters of the blood flow in micro-tubes. $N_{\mathrm{FVM}}$ denotes the number of finite volume cells

Fig. 5

a Schematics of the computational domain, and b initial distribution of RBCs in a tube of $D = 40 \; \upmu$m for $H_t = 0.3$

Fig. 6

Instantaneous snapshots of the RBCs in the tube of $D = 40 \; \upmu$m for a $H_t = 0.15$, and b $H_t = 0.45$, after the steady state has been achieved

3.2.1 Red blood cell core characteristics

The migration of RBCs toward the center of the channel plays a vital role in the formation of the CFL near the tube walls. Figure 7 shows the radial distribution profiles of RBCs for various tube hematocrits in the smallest and largest tubes. The profile has been temporally-averaged after the steady-state has been achieved. The steady-state condition is observed after 0.9 s of physical time. For $H_t = 0.15$, the RBC profile is mostly concentrated at the center of the tube. This is mainly due to the lower number of RBCs at this low hematocrit. As the tube hematocrit increases, the distribution profile widens further reflecting the formation of a larger RBC core at the center of the flow.

Fig. 7

Radial distribution profile of RBCs for different hematocrits in the tube of a $D = 20 \; \upmu$m, and b $D = 40 \; \upmu$m

For a better understanding, the temporally averaged contours plots at the outlet and the mid-plane sections of $D = 20$ and $40 \; \upmu$m for various tube hematocrits are depicted in Figs. 8 and 9. The concentration profile shows a larger accumulation of RBCs near the center-line of the tube. Two factors affect the migration of RBCs to a large extent: (i) the hydrodynamic interaction between the blood plasma and the RBCs and (ii) the attractive–repulsive interaction between the RBCs. At lower hematocrits, the hydrodynamic interactions play a major role, and with increasing hematocrits, the concentration of RBCs increases, increasing the inter-cellular interactions. Thus, the width of the RBC core increases with increasing hematocrit and the region near the tube wall with lower RBC concentration becomes narrower.

Fig. 8

Temporally averaged contour of RBC concentration at the outlet and mid-plane for blood flow in a tube of $D = 20 \; \upmu$m for a $H_t = 0.15$, and b $H_t = 0.45$

Fig. 9

Temporally averaged contour of RBC concentration at the outlet and mid-plane for blood flow in a tube of $D = 40 \; \upmu$m for a $H_t = 0.15$, and b $H_t = 0.45$

3.2.2 Cell-free depletion layer

The red blood cells migrate towards the center of the tube and form two specific regions within the blood flow: a RBC-populated core, and a region of lower concentration of RBCs near the walls, known as the CFL. The CFL has a lower viscosity compared to the RBC core thus producing a lubricating effect on the RBC core. This, in turn, has an important role in the rheological behavior of RBCs and its shear thinning property. The effect of the CFL is more significant in tubes of lower diameter compared to larger tubes, where the CFL thickness becomes negligible.

In the present study, the CFL thickness is measured after the steady-state flow condition has been achieved. It is calculated after the flow has achieved a migration-free, steady state. In our study, the thickness of the CFL is calculated as

$$\begin{aligned} \delta _{\mathrm{CFL}} = \frac{\Vert D - \delta _{\mathrm{RBC}} \Vert }{2} \end{aligned}$$

(16)

where $\delta _{\mathrm{CFL}}$ is the CFL thickness, $\delta _{\mathrm{RBC}}$ is the thickness of the RBC core and D is the diameter of the micro-tube. The RBC core edge and the computed CFL thickness are shown in Fig. 10.

For better comparison with the literature data, the instantaneous CFL thickness values are averaged over time as

$$\begin{aligned} {\bar{\delta }}_{\mathrm{CFL}} = \frac{1}{t_f - t_i} \; \int _{t_i}^{t_f} \delta _{\mathrm{CFL}} \; \mathrm{d}t \end{aligned}$$

(17)

Accordingly, Fig. 11 presents the temporally averaged CFL thickness from the simulations compared with existing measurement and simulation literature data. For the same tube hematocrit, the CFL thickness increases with increasing tube diameter. A wider CFL is observed at lower hematocrits indicating a higher migration of RBCs. With increasing hematocrit, the migration is restricted by the inter-cellular interactions, hence a smaller CFL thickness. A good agreement is evident for $D = 20 \; \upmu$m and $40 \; \upmu$m between the present simulation and the results reported by [34].

Furthermore, the simulation results reveal a qualitative agreement with experiments by [47, 48], showing an increasing trend as the tube diameter increases. The current methodology can capture the trends observed with varying hematocrits and tube diameters, both qualitatively and quantitatively.

Fig. 10

RBC core edge for calculating the instantaneous CFL thickness in a tube with $D = 20 \upmu$m and $H_t = 0.3$

Fig. 11

Cell-free depletion layer for different tube diameters and hematocrits from present simulations compared against a experimental and b simulation literature data

3.2.3 Fahraeus effect

From in vitro experiments [3], it has been observed that for blood flow in a glass tube, the discharge hematocrit at the outlet of the tube ($H_d$) was higher compared to the tube hematocrit. It can be attributed to the formation of the cell-free layer near the tube walls and the cross-migration of RBCs to the center of the tube forming an RBC-populated flow core. The RBC core has a higher viscosity compared to the CFL due to the larger concentration of RBCs, which in turn produces a lubricating effect. Thus, the RBC core yields a higher velocity compared to the blood flow which results in a higher throughput of RBCs at the outlet.

Fig. 12

Discharge hematocrit ($H_d$) as a function of tube diameter and tube hematocrit ($H_t$) compared with empirical relation from experiment [3]

The discharge hematocrit is the volume fraction of RBCs at the exit of the tube. In the present study, it is defined as

$$\begin{aligned} H_d = \frac{Q_{\mathrm{RBC}}}{Q_f} \end{aligned}$$

(18)

where $Q_{RBC}$ is the volumetric flow rate of RBCs, and $Q_f$ is the volumetric flow rate of blood at the outlet. Both quantities have been calculated after the cross-migration of the RBCs as well as the flow has achieved steady-state. The surface integral of the flow over the outlet provides the volumetric flow rate of RBCs and reads

$$\begin{aligned} Q_{\mathrm{RBC}} = \mathop {\oiint }\limits _A \alpha u_p(r) \cdot \mathrm{d}A \end{aligned}$$

(19)

where A is the cross-sectional area of the outlet face, and $\alpha$ is the volume-fraction of RBC in the finite-volume cell. [3] proposed an empirical relation for the discharge hematocrit as a function of the tube diameter and the tube hematocrit,

$$\begin{aligned} \frac{H_t}{H_d} = H_d + \left( 1 - H_d \right) \left( 1 + 1.7 \exp ^{-0.35D} - 0.6\exp ^{-0.01D} \right) \end{aligned}$$

(20)

Figure 12 compares the discharge hematocrit obtained from simulations with the values obtained from the empirical relation in Eq. 20. For each tube hematocrit, it was observed that the discharge hematocrit decreased as the tube diameter increases, and it follows the trend observed from the empirical relation [3] and literature [19, 34]. The decreasing trend in the discharge hematocrit with increasing tube diameter can be attributed to the formation of larger CFL in larger tubes. This, in turn, leads to an increase in the lubricating effect of the CFL due to which the RBC core has higher throughput. Small discrepancies can be observed for $H_t \; = \; 0.15$ which can be attributed to the shape transition of the RBCs. As the flow progresses and achieves steady-state, the RBCs attain a slipper configuration aligned to the flow direction. This reduces the fluid resistance on the RBCs leading to a higher flow rate of the RBCs. This in turn increases the discharge hematocrit of the flow.

3.2.4 Relative apparent viscosity

Another key characteristic of the blood flow in microchannels is that the apparent viscosity of blood increased with increasing tube diameter and tube hematocrit [3]. This characteristic of blood flow is known as the Fahraeus–Lindqvist effect [4]. As the hematocrit increases, the density of RBCs increases leading to higher flow resistance. Additionally, the CFL thickness decreases with increasing hematocrit, which results in a decrease in the lubricating effect on the flow. The relative apparent viscosity is the quantitative parameter used to measure the effect of tube diameter and tube hematocrit on blood viscosity. It is defined as

$$\begin{aligned} \mu _{\mathrm{rel}} = \frac{Q_p}{Q_f} \end{aligned}$$

(21)

where $Q_p$ is the volumetric flow rate of pure plasma, and $Q_f$ is the volumetric flow rate of blood from the simulations. It has to be noted that to achieve a buoyancy-free configuration for the RBCs in the present simulations, the blood flow is driven by a mean flow velocity based on an equivalent pressure gradient. Therefore, it is important to consider the volume fraction of the RBC in the finite volume cells to accurately calculate the flow rate of the carrier fluid. In Fig. 13, we compare the relative apparent viscosity from the simulations with the corresponding experimental values from literature [3]. The model reveals reasonable agreement with the experiment for the $D = 20$ and $30 \; \upmu$m. It can capture the increasing trend in the relative apparent viscosity with increasing tube diameter. However, we observed a large discrepancies between the simulation and experiment for $D = 40 \; \upmu$m. This is mainly attributed to the model limitation in capturing the RBC shape transition, which reduces the flow resistance of RBC-populated core at larger channel diameters, leading to lower apparent viscosity. This shortcoming could be partially overcome by using higher RBC resolution that is planned for future work.

Fig. 13

Relative apparent viscosity for different tube diameters and hematocrits from simulations as well as literature data [3]

Table 2 Computational load statistics for each case based on the number of RBCs ($N_{\mathrm{RBC}}$), number of constituent particles ($N_p$), number of finite volume cells ($N_{\mathrm{FVM}}$) and number of cores for 11,000,000 time steps computation

In fact, the RBCs transition from a discoid shape to a parachute form but does not maintain the shape stability and transform into a slipper-shape (as shown in Fig. 7). This, in turn, reduces the flow resistance due to the RBC shape. Thus, the lubricating effect of the CFL is more influential, as opposed to the flow resistance due to the RBC crowding. As a result, the flow throughput increases producing a lower apparent viscosity. For $D = 40 \; \upmu$m, the relative apparent viscosity follows the trend from experiment [3]; however, the values obtained are lower compared to those obtained from the correlation. The thickness of the CFL increases with increasing tube diameter (see Fig. 11). The CFL has a lubricating effect on the RBC core due to which the apparent viscosity of blood decreases. With the slipper-like shape attained by the RBCs as well as the lubricating effect of the CFL on the RBC core, reduction in the apparent viscosity is higher than those obtained from experimental correlation.

3.2.5 Computational efficiency

To evaluate the efficiency of the proposed approach, the computational load for each blood flow simulation has been measured. Table 2 presents the computational details for different micro-tubes. With increasing domain size, the number of CPUs required for running the simulation increased due to an increase in the finite volume mesh size. Thus, the major factor that determines the number of CPUs is the size of the finite volume mesh.

The contributions from various components of the solver to the computational time are shown in Fig. 14. It consists of DEM loop time to update the particle position and velocity, the communication time for various sub-domains, the Lagrangian-to-Eulerian field conversion time and the solver time for the finite volume method. Majority of the computational time is consumed in converting or mapping the Lagrangian DEM data to a Eulerian field. This step is crucial in the immersed boundary method, where the solid velocity is required to perform the continuous forcing.

Fig. 14

Computational load distribution for different components of the solver

For many industrial applications, a mathematical model with reasonable computational demands is of great interest. Therefore, the model performance in the absence of large computational clusters should be evaluated. The proposed approach for blood flow simulation with the highest number of RBCs reveals a reasonable accuracy with an acceptable computational cost (maximum 32 CPUs for 480 number of RBCs in the domain). Furthermore, improving the Lagrangian-to-Eulerian mapping algorithm will reduce the overall computational time, increasing computational efficiency. This will enable to simulate a larger population of RBCs in larger domains, and pave the path to large-scale simulations for microfluidic chips.

Finally, for the state-of-the-art solvers for cellular flows, scalability has been demonstrated very well. According to Zavodszky et al. [49], who employ a lattice Boltzmann method-based approach, the simulation of a cellular flow in a tube of $D = 128$ $\upmu$m and $H_t = 0.46$ has been performed in 51 h (2.1 days) for 2 million simulation time-steps executed on 1024 cores. For the identical simulation setup, the present model is expected to perform the computation in 20 h for 11 million time-steps using 250 cores. The expected computational advantage of the present model is estimated to be one order of magnitude, which can be even further increased after improving the Lagrangian-to-Eulerian mapping algorithm. However, a detailed analysis of the accuracy and computational efficiency using a larger number of RBCs is planned for future work.

3.3 Application to a CFL enhancement technique

One important application of microfluidics is blood separation into its components. If hydrodynamic characteristics of blood are properly exploited, the blood plasma can be separated from the cellular structures in a passive manner. One essential characteristic is the CFL formation which could facilitate plasma extraction close to the confining walls. Faivre et al. [50, 51] have shown in a set of experiments that the presence of geometrical constrictions in blood micro-channels can increase the CFL thickness and enhance the potentials for plasma extraction. We perform numerical simulations using the proposed method to investigate this effect. To this end, a similar numerical setup to their experimental setup is considered as shown in Fig. 15.

Fig. 15

Schematics of the simulation domain. $L_U$ and $L_D$ are the length upstream and downstream of the constriction, and W is the width of the channel. $L_C$ and $W_C$ are the constriction length and width, respectively

Fig. 16

a Velocity contour, and b RBC distribution along with a constriction with $L_C = 200 \; \upmu$m for $Q = 250 \; \upmu \mathrm{L /h}$

The upstream and downstream channel lengths are $L_U = 225 \; \upmu$m and $L_D = 200 \; \upmu$m. The channel width and height are $W = 100 \; \upmu$m and $H = 75 \; \upmu$m [50]. The tube hematocrit is equivalent to a discharge hematocrit of $2.6 \%$. The density and the dynamic viscosity of the suspending fluid are $1025 \; \mathrm{kg/m}^3$ and $0.02 \; \mathrm{Pa . s}$, respectively. A fixed flow-rate inlet velocity and zero-gradient velocity boundary conditions are applied at the inlet and outlet, respectively. The no-slip velocity boundary condition is imposed on the channel walls. Local mesh refinement is employed to remove the requirement of a significantly fine mesh in large domains. The assumption of periodic boundary condition fails in this simulation, as this can lead to a double-focusing effect on the red blood cells. Thus, for each simulation, a separate simulation was performed with periodic BC only for the upstream flow until the steady-state conditions were reached. Then, the spatial distribution of RBCs is used as the initial condition for each simulation. It has to be noted that in the experiments [50], the solution was prepared such that no aggregation of red blood cells can occur. Hence, in the present simulations, the Morse potential interaction is not considered.

The volume flow rate Q and constriction length $L_C$ are varied to explore their effects on CFL thickness enhancement. First, simulations for four flow rates of $Q = 100, 250, 500$ and $1000 \; \upmu \mathrm{L/h}$ were carried out. Figure 16 shows the velocity and spatial distribution of the RBC along with the constriction. As expected, the geometrical change results in a high-velocity region inside the constriction. Also, a thinner RBC-populated core is evident downstream the constriction. For a quantitative analysis, we compared the ratio of CFL thickness at upstream ($W_1$) and downstream ($W_2$) the constraint with the measurement data in Fig. 17.

Then, with a fixed flow rate of $Q = 250 \; \upmu \mathrm{L/h}$, the $L_C$ was varied from 50 to $300 \; \upmu$m. Similarly, the CFL thickness ratio is compared with experimental data in Fig. 18. The $W_2/W_1$ yields a decreasing trend as the constriction length increases. When $L_C$ increases, the focusing effect on the red blood cells is enhanced, resulting in a thicker cell-free layer, because the red blood cells follow a high-velocity region in the constriction for a longer duration with increasing constriction length. Furthermore, it is observed that the maximum velocity in the constriction is inversely related to the constriction length (not presented here). Thus, as the red blood cells exit a shorter constriction, it has higher inertia. This, in turn, leads to higher collision energy between the RBCs causing the RBCs to disperse more. Having lower inertia upon exiting a longer constrict, the RBCs can follow the streamlines more strictly, and a better CFL enhancement is achieved. Based on these simulation results, it can be concluded that the present numerical method is able to simulate microfluidic applications where the key characteristics of blood flow are the central mechanism for blood flow manipulation.

Fig. 17

Variation of $W_2 / W_1$ with the flow rate. The simulation results are compared with experimental data from [50]

Fig. 18

Variation of $W_2 / W_1$ with the constriction length for flow rate of $250 \; \upmu \mathrm{L/h}$. The simulation results are compared with experimental data from [50]

4 Conclusion

An approach for modeling blood flow with several suspended red blood cells is presented in the context of resolved CFD-DEM. In this approach, the mechanical behavior of the deformable RBCs in interaction with each other as well as with the carrier plasma liquid is accounted by a DEM-based reduced-order model for deformable particles [21]. This RBC model is coupled with a fluid flow solver based on the immersed boundary method with continuous forcing. This model for deformable red blood cells considers an individual RBC as a cluster of constituent spheres interconnected by flexible mathematical bonds. The bonds can translate and rotate with the spheres and this helps in reproducing the RBC deformability in a low-cost manner. Additionally, a potential-based force model has been implemented to compute the inter-cellular interactions.

The coupled solver has been used to simulate micro-scale flows with single and multiple RBCs for validation purposes. The dynamics of a single RBC in shear flow is tested against literature data. Then, the flow of blood plasma with suspended RBCs in a micro-tube at various hematocrits and diameters is similar to the benchmarks in the literature. The blood flow characteristics such as the formation of the RBC core and the cell-free layer near the tube wall as well as the increase in the relative apparent viscosity and the Fahraeus effect were investigated. This approach is capable of picturing the overall hydrodynamics of blood flow and the CFL formation in a good agreement with other benchmark simulations. Also, it shows consistency with the experimental results for discharge hematocrit and the relative apparent viscosity. The computational requirements for the present model have been shown to be rather low and do not require large clusters of CPUs to simulate the flow of significant populations of RBCs within a reasonable time. However, it should be noted that the present approach reveals limitations in capturing more complex behavior of the RBC membrane such as tank-treading rotational motions. This can be explained by the reduced-order nature of our RBC model. Finally, we simulated an industrial application of blood separation based on the CFL thickness enhancement. The model shows excellent performance in reproducing experimental data indicating its capability to simulate microfluidic applications for blood flow manipulation.

In future, we will focus on improvements on both physical and computational aspects. An extension to the mathematical bond model to include RBC rupture is planned for future work. In order to further improve the computational performance, we plan to optimize the solver implementation and will explore a combination between resolved and unresolved CFD-DEM. We expect that such a hybridization would boost the computational performance by a least one order of magnitude, enabling the simulation of very large populations of RBCs (in the order of ten-thousands) in bio-microfluidic devices.