A local adaptive discretization algorithm for Smoothed Particle Hydrodynamics

Abstract

In this paper, an extension to the Smoothed Particle Hydrodynamics (SPH) method is proposed that allows for an adaptation of the discretization level of a simulated continuum at runtime. By combining a local adaptive refinement technique with a newly developed coarsening algorithm, one is able to improve the accuracy of the simulation results while reducing the required computational cost at the same time. For this purpose, the number of particles is, on the one hand, adaptively increased in critical areas of a simulation model. Typically, these are areas that show a relatively low particle density and high gradients in stress or temperature. On the other hand, the number of SPH particles is decreased for domains with a high particle density and low gradients. Besides a brief introduction to the basic principle of the SPH discretization method, the extensions to the original formulation providing such a local adaptive refinement and coarsening of the modeled structure are presented in this paper. After having introduced its theoretical background, the applicability of the enhanced formulation, as well as the benefit gained from the adaptive model discretization, is demonstrated in the context of four different simulation scenarios focusing on solid continua. While presenting the results found for these examples, several properties of the proposed adaptive technique are discussed, e.g. the conservation of momentum as well as the existing correlation between the chosen refinement and coarsening patterns and the observed quality of the results.

1 Introduction

Due to its meshless nature, typical fields of application of the Lagrangian particle method Smoothed Particle Hydrodynamics (SPH) are simulation scenarios that are characterized by large deformations of the modeled domain of material, disintegrating structures, and/or highly dynamic impacts. But although there are no issues coming up that are a result of a distorted mesh when employing a meshless discretization method, the model quality is still highly dependent on the number of interpolation points that are used for the discretization of the investigated spatial domain. For this reason, an important field of research concerning SPH is the development of discretization strategies that allow for an adaptation of the number of SPH particles being placed in certain areas of a simulation model at runtime. Recent research activities dealt with fundamental issues of such adaptive extensions and provided the basis for some first combined refinement and coarsening techniques. The approach proposed in [1] gives a good starting point, but relies on an exclusively random-based particle selection strategy for the coarsening process, which is restricted to pairs of adaptive particles. Therefore, we have been working on a more advanced adaptive discretization extension to the SPH method over the last few years.

After having developed an enhanced version of the refinement procedure presented in [2] and [3], as well as an appropriate coarsening algorithm, we implemented the combined adaptive discretization strategy into the SPH plugin for the particle simulation package Pasimodo [4]. By testing the approach for a broad range of different simulation setups, we have been able to verify its validity. In this paper, the theoretical basis of this newly developed discretization approach, along with some of the validation examples, is presented.

First, a brief introduction to the SPH spatial discretization method in general as well as to its most important extensions necessary to be able to reproduce the behavior found for real solid matter is provided.

Second, the modifications made to allow for a local adaptive refinement and coarsening of the modeled structure are presented. In this context, suitable criteria to decide whether the discretization level of an existing particle is to be adapted or not are discussed. In case of refinement, different patterns specifying the positions of the additional particles are introduced and, in case of coarsening, different strategies to identify the particles to be merged are presented. Furthermore, the way how to determine the state variables of the new particles are discussed in detail. All of these modifications can also be applied to SPH fluid simulations without further adjustments.

Third and finally, four of the various simulation scenarios used for the validation of the implemented routine are presented. That way, it is shown that the introduced approach provides correct results when being applied to simulations focusing on solid continua. In a first step, the focus is laid on the basic properties of the presented adaptive technique, e.g. the conservation of kinetic energy. To that end, the results found for the simulations of an ordinary and a notched tensile test are discussed. For these two rather simple setups, analytical solutions as well as numerical results obtained with the Finite Element Method (FEM) [5] will be compared with the ones provided by the adaptive SPH method. In a second step, the applicability of the proposed approach to more typical and demanding scenarios is demonstrated for two examples; a rigid torus falling onto an elastic membrane and an orthogonal cutting process.

2 Smoothed Particle Hydrodynamics

Originally developed for the purpose of investigating astrophysical phenomena [6, 7], the meshfree Smoothed Particle Hydrodynamics (SPH) method experienced the necessary modifications to be also applicable to fluid simulations, i.e., to allow for a discretization of the well-known Navier-Stokes Eq. [8]. In this context, SPH, as a spatial discretization method, is used to replace the considered continuum domain with a set of particles, which can be interpreted as interpolation points. At these points, the underlying differential equations of continuum mechanics are evaluated. In doing so, the initial system of partial differential equations (PDEs) in time and space is transformed into one that consists only of ordinary differential equations (ODEs) in time [9], which can be numerically integrated with common integration schemes. In addition to fluid simulations, SPH has proven its ability to correctly reproduce the physical effects that are observed for real solid material over the last two decades [10, 11].

Next, the basic principle of the SPH discretization method is presented. After having described its basic idea, the SPH simulation technique is applied to the Euler equations, which can be used to reproduce the behavior of solid matter in simulations. Then, the focus is laid on some of the extensions to the basic SPH solid formulation introduced in [12] that improve the significance of the obtained results. Namely, these are the Johnson-Cook (JC) plasticity model, the JC damage model, as well as a modified version of the Lennard-Jones potential.

2.1 Basic principle of Smoothed Particle Hydrodynamics

The SPH discretization process to transform a PDE into an ODE consists of the following three steps. First, an ensemble of abstract, not discrete particles is introduced into the considered simulation domain. Each of these SPH particles represents a specific part of the original spatial domain and, according to that, combines all of its properties, such as position, mass, density, etc. That way, it is possible to eliminate the dependency on the spatial position and its derivatives in case of any PDE while using the SPH particles, i.e. the introduced interpolation points, in conjunction with the Dirac delta function.

Second, the Dirac delta function used for the discretization of a PDE is approximated by a kernel function of finite extent, e.g. a truncated Gaussian distribution. The contribution of each neighboring particle to a property of the particle of interest is weighted according to the distance between these two SPH particles as well as the actual shape of the chosen kernel function. For this reason, the kernel function is also referred to as weight function. That way, the level of smoothing of the properties of an SPH particle is determined. Commonly, the functions that are used as kernel functions are cut off at a user-defined distance from the interpolation center, i.e. the so-called smoothing length, to save computational effort by not taking into account the relatively minor contributions from distant particles.

Third, when using a finite number of SPH particles for the discretization of a spatial domain, the integral over the entire support area, which has been introduced in combination with the Dirac delta function in the first step, has to be replaced with a sum over all neighboring particles.

2.2 Discretized Euler equations

The basic equations which are used to describe the behavior of a solid continuum domain are the Euler equations, i.e. the acceleration equation

$$\begin{aligned} \frac{\hbox {d} \varvec{v}}{\hbox {d} t} = \frac{1}{\rho } \nabla \cdot \varvec{\sigma } + \varvec{g} \end{aligned}$$

(1)

and the continuity equation

$$\begin{aligned} \frac{\hbox {d} \rho }{\hbox {d} t} = -\rho \nabla \cdot \varvec{v}\,, \end{aligned}$$

(2)

where $\varvec{v}$ represents the velocity vector, $\rho$ the density, $\varvec{\sigma }$ the Cauchy stress tensor, and $\varvec{g}$ the vector of volume forces per unit mass.

When applying the SPH discretization method to the Euler equations, as it is shown in [12], the acceleration Eq. (1) can be written as

$$\begin{aligned} \frac{\hbox {d} \varvec{v}_\mathrm {i}}{\hbox {d} t} = \sum _\mathrm {j} m_\mathrm {j} \left( \frac{\varvec{\sigma }_\mathrm {i}}{\rho _\mathrm {i}^2} + \frac{\varvec{\sigma }_\mathrm {j}}{\rho _\mathrm {j}^2} \right) \cdot \nabla _\mathrm {i} W( \varvec{r}_\mathrm {i} - \varvec{r}_\mathrm {j}, h) + \varvec{g} \end{aligned}$$

(3)

and the continuity Eq. (2), in a similar manner, as

$$\begin{aligned} \frac{\hbox {d} \rho _\mathrm {i}}{\hbox {d} t} = \sum _\mathrm {j} m_\mathrm {j} \left( \varvec{v}_\mathrm {i} - \varvec{v}_\mathrm {j} \right) \cdot \nabla _\mathrm {i} W( \varvec{r}_\mathrm {i} - \varvec{r}_\mathrm {j}, h), \end{aligned}$$

(4)

where $m$ represents the mass, $\varvec{r}_\mathrm {i}$ and $\varvec{r}_\mathrm {j}$ denote the position vectors of the particles $i$ and $j$, and $W( \varvec{r}_\mathrm {i} - \varvec{r}_\mathrm {j}, h)$ is the kernel function. The expanse of the support domain and, therefore, the number of neighboring particles involved in the smoothing process of particle $i$ is determined by the choice of the smoothing length $h$. In many cases, a Gaussian distribution is chosen as kernel function, cutting off the support radius at a distance of $2h$, which means that only the particles that are located within this section of the kernel function of particle $i$ are taken into account when evaluating (3) and (4).

In addition to the aforementioned Euler equations, another equation specifying the relation between stress tensor $\varvec{\sigma }$ and the remaining state variables, often referred to as material state equation, is required when simulating solid matter. It consists of a hydrostatic and a deviatoric part and can be written as

$$\begin{aligned} \varvec{\sigma } \quad = \underbrace{- p \varvec{E}}_{\text {\normalsize hydrostatic part}} + \underbrace{ \varvec{S}}_{\text {\normalsize deviatoric part}}. \end{aligned}$$

(5)

In this equation, $p$ denotes the hydrodynamic pressure, $\varvec{E}$ the identity matrix, and $\varvec{S}$ the deviatoric stress tensor. The hydrodynamic pressure can be calculated using the Mie-Grüneisen state equation [13]

$$\begin{aligned} p = c_\mathrm {s}^2 \left( \rho - \rho _\mathrm {0} \right) , \end{aligned}$$

(6)

where pressure $p$ is a function of sound velocity $c_\mathrm {s}$ and initial material density $\rho _\mathrm {0}$. When assuming, at first, an ideally elastic response of the solid material, the Jaumann rate of change of the deviatoric stress tensor $\varvec{S}$ can be expressed as

$$\begin{aligned} \frac{\hbox {d} \varvec{S}}{\hbox {d} t} = 2 \, G \left( \dot{\varvec{\varepsilon }} - \frac{1}{3} \hbox {tr} \left( \dot{\varvec{\varepsilon }} \right) \varvec{E} \right) + \varvec{S} \cdot \varvec{\varOmega }^\mathrm {T} + \varvec{\varOmega } \cdot \varvec{S}. \end{aligned}$$

(7)

In (7), $G$ represents the shear modulus of the considered material, $\dot{\varvec{\varepsilon }}$ the strain rate tensor given by

$$\begin{aligned} \dot{\varvec{\varepsilon }} = \frac{1}{2} \left( \nabla \varvec{v} + \left( \nabla \varvec{v} \right) ^\mathrm {T} \right) , \end{aligned}$$

(8)

and $\varvec{\varOmega }$ is the rotation rate tensor defined through

$$\begin{aligned} \varvec{\varOmega } = \frac{1}{2} \left( \nabla \varvec{v} - \left( \nabla \varvec{v} \right) ^\mathrm {T} \right) . \end{aligned}$$

(9)

The SPH material model described above can be extended to plastic behavior based on the von Mises equivalent stress $\sigma _\mathrm {vM}$. With the von Mises stress and the yield strength $\sigma _\mathrm {y}$, a plastic character of the material is identified in the case that the von Mises yield criterion

$$\begin{aligned} f_\mathrm {pl} = \frac{\sigma _\mathrm {y}}{\sigma _\mathrm {vM}} < 1 \end{aligned}$$

(10)

is met. If $f_\mathrm {pl}$ shows a value lower than $1$, the stress state found for the elastically calculated deviatoric stress tensor $\varvec{S}_\mathrm {el}$ is located outside the von Mises yield surface around the hydrostatic axis and, as a consequence, that part of the stress tensor $\varvec{\sigma }$ being responsible for the plastification of the material, i.e. the deviatoric part $\varvec{S}$, is reduced according to the relation

$$\begin{aligned} \varvec{S}_\mathrm {pl} = f_\mathrm {pl} \, \varvec{S}_\mathrm {el} \end{aligned}$$

(11)

in order to bring it back onto the given yield surface.

2.3 Plasticity model

Plasticity models are used to specify the relationship between stress and strain within the plastic region for the simulated material. To achieve a more realistic representation of the plastic behavior of real matter in the simulations presented in Sect. 4, the perfectly plastic formulation (yield strength $\sigma _\mathrm {y}$ remains constant) is extended to the purely empirical JC flow stress model. In contrast to the perfectly plastic relationship between von Mises equivalent stress and corresponding strain, the JC model also takes the interdependencies between the stress-strain behavior and the material temperature as well as the strain rate into account [14]. The JC plasticity model follows the equation

$$\begin{aligned} \sigma _\mathrm {y} = \left[ A + B \varepsilon _\mathrm {pl}^n \right] \left[ 1 + C \, \mathrm {ln} \left( \dot{\varepsilon }_\mathrm {pl}^* \right) \right] \left[ 1 - T^{* m} \right] ~\text {,} \end{aligned}$$

(12)

where $\varepsilon _\mathrm {pl}$ represents the equivalent plastic strain, $\dot{\varepsilon }_\mathrm {pl}$ is the equivalent plastic strain rate, and $A$, $B$, $C$, $n$, and $m$ are material dependent constants. Furthermore, the normalized equivalent plastic strain rate and temperature used in (12) are defined as

$$\begin{aligned} \dot{\varepsilon }_\mathrm {pl}^* = \frac{\dot{\varepsilon }_\mathrm {pl}}{\dot{\varepsilon }_\mathrm {pl \text {,} 0}}\quad \text {and}\quad T^* = \frac{T - T_\mathrm {ambient}}{T_\mathrm {melt} - T_\mathrm {ambient}}, \end{aligned}$$

(13)

where $\dot{\varepsilon }_\mathrm {pl \text {,} 0}$ is the reference equivalent plastic strain rate, $T_\mathrm {ambient}$ is the ambient temperature, and $T_\mathrm {melt}$ is the melting temperature. For all implemented constitutive models, the so-called Bauschinger effect [15], which describes the phenomenon of a direction-dependent modification of the yield strength after previous plastic deformation, is taken into consideration and the unloading behavior of the modeled material is assumed to be elastic.

2.4 Damage model

As an extension to the plasticity model presented in (12), Johnson and Cook introduced a cumulative-damage fracture model [16], which is, just as the already mentioned flow model, not only primarily dependent on the actual plastic strain, but also on the strain rate and the temperature of the simulated material. To quantify the local damage state, a scalar parameter $D$ is defined for each particle, using an initial value of $0$, which means that the represented domain of material is – still – completely intact. The parameter $D$ is allowed to grow during both tensile and compressive loading until a maximum value of $1$ is reached. A value of $1$ indicates that an SPH particle suffers from total damage and, thus, that material fracture occurs. The relationship used to describe the loading-dependent evolution of the damage parameter $D$ reads

$$\begin{aligned} D = \sum \frac{\Delta \varepsilon _\mathrm {pl}}{\varepsilon _\mathrm {f}}, \end{aligned}$$

(14)

where $\Delta \varepsilon _\mathrm {pl}$ represents the increment of equivalent plastic strain occurring during one integration cycle and $\varepsilon _\mathrm {f}$ denotes the equivalent strain to fracture relation given by

$$\begin{aligned} \varepsilon _\mathrm {f}&= \left[ D_\mathrm {1} + D_\mathrm {2} \, \mathrm {exp} \left( D_\mathrm {3} \sigma ^* \right) \right] \left[ 1 + D_\mathrm {4} \, \mathrm {ln} \left( \dot{\varepsilon }_\mathrm {pl}^* \right) \right] \nonumber \\&\quad \times \left[ 1 + D_\mathrm {5} \, T^* \right] ~\text {,} \end{aligned}$$

(15)

where the pressure-stress ratio $\sigma ^*$ is defined as the ratio of the average of the three normal stresses $\sigma _\mathrm {m}$ to the von Mises equivalent stress and $D_{1}$ to $D_{5}$ are material constants. In a last step, the original stress tensor $\varvec{\sigma }$, i.e. the one found in case that the process of material damage is absent, is replaced by the damaged stress tensor $\varvec{\sigma }_\mathrm {D}$ [17], which is defined through

$$\begin{aligned} \varvec{\sigma }_\mathrm {D} = \left( 1 - D \right) \varvec{\sigma }, \end{aligned}$$

(16)

in order to take into consideration the reduction of the stress level resulting from the actual incurred material damage.

2.5 Force model for boundary interaction

Boundaries and nonspherical objects in Pasimodo are represented by triangular surface meshes. To prevent particles from passing through a mesh geometry, a penalty approach is used. According to this, a penalty force is evaluated and applied for each pair of particle and triangle. The number of possible penalty functions is large and diversified, but we settle on one introduced in [18], which is similar to a Lennard-Jones potential, but does not tend to infinity as the distance between the particle and the triangle goes to zero. It is defined through

$$\begin{aligned} F(d) =\left\{ \begin{array}{l@{\quad }l} \psi \frac{(R - d)^4 - (R - s)^2 (R - d)^2}{R^2 s (2 R - s)} &{}\text { if } d \le R\\ 0 &{}\text { otherwise} \end{array}\right. , \end{aligned}$$

(17)

where $d$ marks the distance between the particle and the triangle and $R$ denotes the maximum distance up to which a contact occurs. The resulting force $F$ points in the direction of the triangle’s normal and changes from repulsion to attraction at distance $s$, while the scalar $\psi$ determines the strength of the force in such a way that $\psi$ is its maximum absolute value and, therefore, $F(0) = \psi$. Furthermore, the contact model can include damping and viscosity based on the difference in velocity.

3 Refinement and coarsening algorithm for Smoothed Particle Hydrodynamics

Many different technical processes of high industrial importance are characterized by a major increase in the level of plastic deformation, equivalent stress, or temperature that are restricted to small areas of the processed solid material. This leads to fairly inhomogeneous distributions of the mentioned state variables over the workpiece structure. Therefore, a finer discretization for these particular parts of the workpiece model is needed in order to achieve the same accuracy of the numerical results as found for the areas that are influenced only to a certain extent by the actual technical process. But instead of increasing the discretization level of the whole structure and with it the overall computational cost, the adaptation shall be restricted to the parts that really have need for it. By developing a combined local adaptive refinement and coarsening algorithm, we found an SPH formulation that allows for such an adaptive increase in the discretization level for specific areas of the model that satisfy given refinement criteria. At the same time, the number of SPH particles is decreased in domains where the criteria chosen for coarsening are fulfilled.

The adaptive refinement and coarsening approach presented in this section consists of three steps. First, it is decided if a particle needs to be adapted by checking whether a user-defined criterion is met or not. In the implementation, this can be a check of an absolute value, a gradient, and/or a relative geometric position. Second, if the criterion is met, the particle is split into several smaller ones or merged with some of its neighbors into a bigger one according to a chosen refinement or coarsening pattern. Third, the state variables of the new, adapted particles are calculated either directly from the corresponding values of the original particles or by interpolating them from the values provided by their neighboring particles. In the following two subsections, the refinement and coarsening approaches are presented separately, starting with the refinement algorithm.

3.1 Local adaptive refinement extension

The adaptive refinement approach presented in this section follows the procedure introduced in [2] and [3]. When using it, the first question to be answered is when to refine an SPH particle at all. One or several suitable criteria need to be chosen for each simulation setup, e.g. single particle values, field gradients over the neighborhood, or numerical data. While developing and testing the refinement algorithm, it turned out that for lots of different simulation scenarios, already quite simple refinement criteria that compare a single particle value, e.g. one of the particle’s spatial coordinates or its von Mises stress, to a given threshold work very well. Especially when applying the introduced refinement approach to avoid a numerical fracture, a criterion that is based on a particle’s coordination number, i.e. the overall number of neighbors that are located within its smoothing area, proved to be quite useful in this context. As we allow for multiple refinement, it is necessary to restrict the particle size or the number of times a particle is split up in addition to the user-defined refinement criteria. Otherwise, the number of particles could increase uncontrolled, leading to an enormous computational effort, or the refinement process could create particles with almost zero masses and smoothing lengths. This results in various numerical problems, such as very small time steps.

Having specified the refinement criteria to be considered, the next step is to define how an SPH particle is actually refined. There are many ways to place the newly created particles. For a two-dimensional simulation, a triangular and a hexagonal pattern as shown in Figs. 1 and 2 are proposed in [2]. At this point, we want to emphasize that, in contrast to [2], we chose the distance with which the new particles are placed around the original one to be $0.5\,\varepsilon$ instead of $\varepsilon$. Therefore, in this work, $\varepsilon$ denotes the total dispersion of the pattern, not only its radius. As a cubical grid is often used as an initial setup for arranging the particles in SPH simulations, we implemented an additional refinement pattern retaining the initial configuration. For this purpose, it splits the original particle, in case of a two-dimensional simulation, into four smaller ones, which are placed on the corners of a cube with a length of the edge of $\varepsilon$ as can be seen in Fig. 3. Note that the original particle located at the center is removed for this pattern. Correspondingly, the triangular and the hexagonal pattern are enhanced by the possibility to remove the center particle as well. For three-dimensional simulations, the cubical pattern is extended accordingly.

Fig. 1

Two-dimensional triangular refinement pattern and relative particle positions in terms of $\varepsilon$ (red: original particle; blue: additional particle). (Color figure online)

Fig. 2

Two-dimensional hexagonal refinement pattern and relative particle positions in terms of $\varepsilon$ (red: original particle; blue: additional particle). (Color figure online)

Fig. 3

Two-dimensional cubical refinement pattern and relative particle positions in terms of $\varepsilon$ (red: original particle; blue: additional particle). (Color figure online)

After having determined the positions of the additional particles, their masses have to be specified. It is the simplest way to distribute the mass of the original particle equally among the new ones. However, this choice pays no regard to the original density field of the simulated domain of material. Therefore, the use of a mass distribution that introduces the least disturbance in the smoothed density field is suggested in [2]. It is defined as

$$\begin{aligned} \mathcal {E} := \int \left( m_\mathrm {i} W(\varvec{x}_\mathrm {i} - \varvec{x}, h_\mathrm {i}) - \sum \limits _{\mathrm {j}} m_\mathrm {j} W(\varvec{x}_\mathrm {j} - \varvec{x}, h_\mathrm {j}) \right) ^2 \mathrm {d} \varvec{x}, \end{aligned}$$

(18)

where $i$ denotes the original particle and $j$ the new ones, with the corresponding positions $\varvec{x}_\mathrm {i}$ and $\varvec{x}_\mathrm {j}$ and smoothing lengths $h_\mathrm {i}$ and $h_\mathrm {j}$, respectively. If the new particle masses are rewritten as $m_\mathrm {j} = \lambda _\mathrm {j} m_\mathrm {i}$, with $\sum _\mathrm {j} \lambda _\mathrm {j} = 1$ to give conservation of mass, (18) yields

$$\begin{aligned} \mathcal {E}&= m_\mathrm {i}^2 \left( \int W^2(\varvec{x}_\mathrm {i} - \varvec{x}, h_\mathrm {i}) \, \mathrm {d} \varvec{x}\right. \nonumber \\&\quad \left. -\, 2 \sum \limits _\mathrm {j} \lambda _\mathrm {j} \int W(\varvec{x}_\mathrm {i} - \varvec{x}, h_\mathrm {i}) W(\varvec{x}_\mathrm {j} - \varvec{x}, h_\mathrm {j}) \, \mathrm {d} \varvec{x} \right. \nonumber \\&\quad \left. + \sum \limits _\mathrm {j,k} \lambda _\mathrm {j} \lambda _\mathrm {k} \int W(\varvec{x}_\mathrm {j} - \varvec{x}, h_\mathrm {j}) W(\varvec{x}_\mathrm {k} - \varvec{x}, h_\mathrm {k}) \mathrm {d} \varvec{x} \right) . \end{aligned}$$

(19)

Equation (18) can also be expressed vectorially, i.e.

$$\begin{aligned} \mathcal {E} = m_\mathrm {i}^2 \left( C - 2 \varvec{\lambda }^\mathrm {T} \varvec{b} + \varvec{\lambda }^\mathrm {T} \varvec{A} \varvec{\lambda } \right) , \end{aligned}$$

(20)

with

$$\begin{aligned}&C = \int W^2(\varvec{x}_\mathrm {i} - \varvec{x}, h_\mathrm {i}) \, \mathrm {d} \varvec{x},\end{aligned}$$

(21)

$$\begin{aligned}&b_\mathrm {s} = \int W(\varvec{x}_\mathrm {i} - \varvec{x}, h_\mathrm {i}) W(\varvec{x}_\mathrm {s} - \varvec{x}, h_\mathrm {s}) \, \mathrm {d} \varvec{x},\, \text {and} \end{aligned}$$

(22)

$$\begin{aligned}&A_\mathrm {rs} = \int W(\varvec{x}_\mathrm {r} - \varvec{x}, h_\mathrm {r}) W(\varvec{x}_\mathrm {s} - \varvec{x}, h_\mathrm {s}) \, \mathrm {d} \varvec{x}. \end{aligned}$$

(23)

With the choice $h_\mathrm {j} = \alpha h_\mathrm {i}$ for all particles $j$, (20) can be rewritten as

$$\begin{aligned} \mathcal {E} = \frac{m_\mathrm {i}^2}{h_\mathrm {i}^q} \left( \bar{C} - 2 \varvec{\lambda }^\mathrm {T} \bar{\varvec{b}} + \varvec{\lambda }^\mathrm {T} \bar{\varvec{A}} \varvec{\lambda } \right) , \end{aligned}$$

(24)

with the dimension $q$ and

$$\begin{aligned}&\bar{C} = \int W^2(\varvec{x}_\mathrm {i} - \varvec{x}, 1) \, \hbox {d} \varvec{x},\end{aligned}$$

(25)

$$\begin{aligned}&\bar{b}_\mathrm {s} = \int W(\varvec{x}_\mathrm {i} - \varvec{x}, 1) W(\varvec{x}_\mathrm {s} - \varvec{x}, \alpha ) \, \mathrm {d} \varvec{x},\quad \text {and} \end{aligned}$$

(26)

$$\begin{aligned}&\bar{A}_\mathrm {rs} = \frac{1}{\alpha ^q} \int W(\varvec{x}_\mathrm {r} - \varvec{x}, \alpha ) W(\varvec{x}_\mathrm {s} - \varvec{x}, \alpha ) \, \hbox {d} \varvec{x}. \end{aligned}$$

(27)

For further details, see [2]. With $\sum _\mathrm {j} \lambda _\mathrm {j} = 1$, the optimization problem reads

$$\begin{aligned} \min \limits _{\varvec{\lambda }} \left( \bar{C} - 2 \varvec{\lambda }^\mathrm {T} \bar{\varvec{b}} + \varvec{\lambda }^\mathrm {T} \bar{\varvec{A}} \varvec{\lambda } \right) . \end{aligned}$$

(28)

In general, a solution exists as $\bar{\varvec{A}}$ is symmetric and positive definite, but this solution may also result in unwanted and unphysical negative particle masses. The solution depends on the choices for the dispersion $\varepsilon$, the smoothing length scale $\alpha$, as well as the kernel function. This approach makes the solution independent from the initial particle distance, mass, and smoothing length. Therefore, it has to be evaluated only once while using the unit mass and length at the beginning of the simulation, which takes little additional computation time. During the simulation, the pattern can be adapted by scaling it with the actual values of the state variables of the original particle.

Up to now, the positions, masses, and smoothing lengths of the new particles have been specified. The other properties, such as the densities and the velocities, need to be set, too. While most state variables, as for example the densities, can be calculated via SPH interpolation from the ones of the original particles without experiencing any issues concerning a further inaccuracy of the simulation results, this is not the case for the velocities of the additional particles. When they are set to the ones of the original particles, a conservation of linear and angular momentum as well as kinetic energy is achieved. Choosing $\varvec{v}_\mathrm {j} = \varvec{v}_\mathrm {i}$ for all particles $j$ is the only way to ensure an exact conservation, which is a must when looking for reliable numerical results. Conversely, due to the fact that the smaller particles are positioned somewhere around the location of the original one without modifying their velocity values accordingly when following this approach, this choice may modify the existing velocity field and, thus, also lead to additional, unwanted inaccuracies in the simulation results. This dilemma needs to be further investigated in the future.

3.2 Local adaptive coarsening extension

The coarsening approach presented in this paper basically follows the same procedure as the adaptive refinement algorithm described above. First, those areas that are of little interest are to be identified. For this purpose, coarsening criteria need to be defined. These criteria can be chosen similar to the refinement routine, e.g. based on a particle’s velocity or its von Mises stress.

Having marked the particles to be coarsened, the next step is to find a proper selection of adjacent particles for the coarsening process. To that end, we added two different selection strategies to our SPH code; a simple neighborhood search and an area-based procedure. In case of the neighborhood search strategy, it is sufficient to loop over all chosen particles and merge them with their nearest neighbors. This is an extension to the algorithm introduced in [1], which merges the two nearest neighbors, i.e., only pairs of particles are merged each time step. The second approach is a more sophisticated one. For this, a rectangular box is placed around each particle that has been marked for coarsening. Then, all the boxes overlapping each other are collected, resulting in a finite number of linked regions. For each of these regions, an enclosing cuboid is formed and, subsequently, divided into

$$\begin{aligned}&\text {number of subregions}\nonumber \\&\quad \approx \frac{\text {number of particles in the cuboid}}{N} \end{aligned}$$

(29)

smaller ones, where $N$ denotes the desired number of particles to be merged. For the process of dividing the cuboid into subregions, two different approaches can be employed. On the one hand, there is the possibility for a dynamic division, which splits each region into several subregions containing the same number of SPH particles. On the other hand, a static division, which divides a region into equally sized subregions, can be used. Finally, the particles that belong to the same subregion are merged.

Originally, the aforementioned procedures were developed for the simulation of fluids. When considering SPH simulations that have their focus on solid material, the particles often experience a lot less relative motion and reordering than in case of fluid simulations. Inspired by the approach presented in [19], which keeps the original particles instead of removing them, we implemented a family-based coarsening strategy, which aims on merging particles that originate from the same particle if possible. For this purpose, each refined particle is initialized with a variable providing the ID of its origin particle. By adding an additional merging condition that ensures that SPH particles with the same origin are preferred for merging, one gets a suitable extension to the neighbor-based strategy that takes into account the refinement history of an adaptive particle.

After a set of particles to be merged has been found by any of the approaches described above, the properties of the new, coarsened particles have to be calculated. In order to fulfill the conservation of mass, the mass $m_\mathrm {j}$ of the coarsened particle $j$ needs to be the sum of the merged particles’ masses $m_\mathrm {i}$, i.e.

$$\begin{aligned} m_{\mathrm {j}} = \underset{\hbox {i}}{\sum } m_\mathrm {i}. \end{aligned}$$

(30)

Furthermore, we ensure a conservation of momentum by positioning the new particle at the merged particles’ center of mass and setting its velocity $\varvec{v}_\mathrm {j}$ to the weighted average of the particle velocities $\varvec{v}_\mathrm {i}$. This yields the two convex combinations

$$\begin{aligned} \varvec{r}_{\mathrm {j}} = \frac{1}{m_{\mathrm {j}}} \underset{\mathrm {i}}{\sum } m_\mathrm {i} \varvec{r}_\mathrm {i}\quad \text {and}\quad \varvec{v}_{\mathrm {j}} = \frac{1}{m_{\mathrm {j}}} \underset{\mathrm {i}}{\sum } m_\mathrm {i} \varvec{v}_\mathrm {i}. \end{aligned}$$

(31)

Except for the smoothing length $h_\mathrm {j}$, all other particle properties that still have to be determined are calculated via SPH interpolation. The new smoothing length is calculated by reducing the density error in the coarsened particle’s position, i.e. by searching the root of

$$\begin{aligned} m_\mathrm {j} W(\varvec{r}_\mathrm {j}-\varvec{r}_\mathrm {j},h_\mathrm {j}) - \underset{\mathrm {i}}{\sum } m_\mathrm {i} W(\varvec{r}_\mathrm {j}-\varvec{r}_\mathrm {i}, h_\mathrm {i}). \end{aligned}$$

(32)

In order to prevent particles from being coarsened shortly after having been refined, for each adaptive SPH particle a counter variable is added. It provides the number of time steps since the particle’s last refinement. With this counter, it is possible to avoid an alternating coarsening and refinement process for an adaptive particle. Besides this counter-based restriction to the coarsening algorithm, a second control mechanism is employed. In order to avoid introducing too much inaccuracy when merging particles, we check the error in the angular momentum against a predefined tolerance limit for each coarsening process, i.e.

$$\begin{aligned} \parallel \underset{\mathrm {i}}{\sum } m_\mathrm {i}(\varvec{r}_\mathrm {i} \times \varvec{v}_\mathrm {i}) - m_\mathrm {j}(\varvec{r}_\mathrm {j} \times \varvec{v}_\mathrm {j}) \parallel ^2 < \text {tolerance limit}. \end{aligned}$$

(33)

If the condition is unmet, the particles $i$ are not merged in this step.

4 Examples

Having discussed the theoretical basis of the developed combined local adaptive refinement and coarsening algorithm in the previous section, the focus is laid on its applicability to different types of simulation scenarios focusing on solid matter as well as on the benefit taken from the adaptive formulation in the following. First, the SPH simulation of an ordinary tensile test setup is presented. In the context of this quite simple simulation setup, the capability of the introduced adaptive discretization technique to avoid a numerical fracture and to ensure a conservation of linear and angular momentum as well as kinetic energy is illustrated. Second, emphasis is placed on the deviations in the simulation results found for an SPH notched tensile specimen when employing the different refinement patterns introduced in Sect. 3.1. Next, a fully three-dimensional simulation of a rigid torus falling onto an elastic membrane demonstrates that the adaptive routine presented in this paper is also suitable to SPH simulations showing a highly dynamic behavior of the modeled structures. As a final simulation setup, which is more related to real technical applications than the aforementioned scenarios, the simulation of an orthogonal cutting process is presented. Unless otherwise stated, the set of parameter values for the combined refinement and coarsening algorithm given in Table 1 is used for the SPH solid simulation scenarios discussed hereinafter.

Table 1 Parameter values for the combined refinement and coarsening algorithm

4.1 Ordinary tensile test

The uniaxial tensile test is one of the most basic experimental setups that are employed to investigate the elastic, the plastic, and the fracture behavior of real solid material and is, for this reason, also suitable for a comparison with simulation data. It is the first step in our working process of transferring an ordinary flat tensile specimen used in experiments into a simulation model to build up a regular lattice of SPH particles that has the same shape and dimensions as the gauge section of the real specimen. For building up this lattice, the particles are positioned according to a structure consisting of quadratic cells. In addition to that, to both ends of the simulated specimen whose normal vector is parallel to the loading direction additional rows of SPH particles, which represent the grips applied to the real one, are attached. The particles belonging to one of these grip areas are fixed in space, while a constant velocity is applied to the particles of the other one. Thus, one finds an invariable elongation rate level throughout the entire simulation. The SPH particles that are located within the measuring area are not at rest at the beginning of the simulation, but to them an initial velocity according to their relative distance from the grip sections is assigned. That way, a linear velocity field is established in order to avoid having shock waves running from one end of the specimen to the other resulting in a noisy stress-strain-curve.

When applying the SPH simulation technique in its original formulation, i.e. without any adaptive extension, to the tensile test simulation or, speaking more generally, to problems showing large deformations of the modeled structure, a possible increase in the distance between adjacent particles can lead to a decrease in the number of neighbors that are located within the smoothing areas. Sooner or later, this results in a numerically induced fracture. To ensure that the damage behavior of the simulated material is controlled exclusively by the fracture model introduced in Sect. 2.4, even in case of large strain values, the presented refinement algorithm can be used to avoid a numerical fracture by adapting the model discretization in accordance to its deformation.

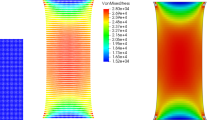
The relationships between stress and strain found when employing both the original and the adaptive SPH formulation on the simulation of a flat tensile specimen made of C45E while using approximately $2\,500$ particles for the discretization of its gauge section with an initial length of $l_0 = 5 \cdot 10^{-2} \, \hbox {m}$ and an initial width of $b = 1.25 \cdot 10^{-2} \, \hbox {m}$ are shown in Fig. 4a. As can be clearly seen, both the stress-strain curve found for the SPH simulation with a constant number of particles and the one obtained with the adaptive model take the same elastic and plastic path up to the point when the tensile specimen simulated with the unmodified SPH method shows a loss of influence between neighboring particles and, thus, a numerical fracture can be observed. At this point, the SPH particles that are located within the area showing the largest value of strain have too few neighbors in the stretching direction and, as a consequence of this, become decoupled from each other. Running the identical simulation setup as done in case of the standard SPH method with the extended one leads to a fairly different, but expected behavior. With an increase in the elongation of the tensile specimen, the distance between neighboring particles is increased, too. In the case that the coordination number of a particle decreases, the discretization level of this particular part of the specimen is adapted accordingly to stop the formation of a numerical fracture already in its early state. As a result, the number of neighboring particles that are located within the smoothing areas of the refined ones stays above the critical value until the end of the simulation and the stress-strain curve of the adaptive SPH simulation follows the perfectly plastic path up to a strain value of $\varepsilon = 0.15$. As expected from a theoretical point of view, a decrease in the coordination number is observed first for the SPH particles that form the neck of the tensile specimen. According to that, these are also the particles that first experience an adaptation as shown in Fig. 4b.

Fig. 4

Simulation results obtained for the ordinary tensile specimen. a Stress-strain curves obtained when employing the original and the adaptive SPH formulation for solids, b Refined SPH model of the tensile specimen showing the particle’s masses (red: high mass; blue: low mass). (Color figure online)

When using the introduced refinement algorithm to eliminate the effects leading to a numerical fracture, one has to ensure that the linear and angular momentum as well as the kinetic energy is conserved in order to keep the reliability of the obtained numerical results. For this purpose, a second adaptive scenario is set up. It is quite similar to the one of the ordinary tensile specimen presented above and shown in Fig. 5a. But instead of employing a refinement criterion that depends on a particle’s coordination number, two position-based criteria are introduced this time; one used for the refinement and the other one used for the coarsening algorithm. Now, the entire tensile specimen is moved in such a way that it first passes the position of the refinement criterion, represented by the left of the two gray planes depicted in Fig. 5a, and, after a while, runs through the one of the coarsening criterion. Thus, the SPH particles of the adaptive model are first refined based on the chosen cubical refinement pattern and, afterwards, coarsened according to the introduced family-based pattern. To make it easier to distinguish between the particles of different size, the initial overall number of SPH particles is decreased to approximately 500, of which 100 belong to the two grip areas and are not to be refined or coarsened, and the graphical radius of the coarsened particles is decreased, too. In Fig. 5b, the amount of kinetic energy that is stored in three of the original SPH particles at different longitudinal positions of the adaptive tensile specimen, the values of accumulated energy for the refined particles into which the original ones have been split up, and the kinetic energy values for the merged particles is shown. As can be seen, both the refinement and the coarsening process do not lead to a change in the kinetic energy level when cloning the velocities of the new SPH particles from the one of the previous particles. Therefore, also the overall amount of kinetic energy being stored in the adaptive tensile model is conserved throughout the entire simulation.

Fig. 5

Modified tensile test simulation setup used to assess the conservation properties of the presented local adaptive discretization algorithm. a Modified SPH tensile specimen showing the particle’s longitudinal velocities (red: high longitudinal velocity; blue: low longitudinal velocity), b Kinetic energy of the original SPH particles, the refined ones, and the coarsened particles for three different relative longitudinal positions. (Color figure online)

In Sect. 3.2, both the neighbor-based coarsening pattern and its extension to a family-based one have been introduced. Unlike the basic version, the latter one takes into account the hierarchic structure as well as the refinement and coarsening history of an SPH particle for a possible further process of adapting its discretization level. This modified coarsening pattern is especially useful when simulating solids with the presented adaptive SPH formulation. While the basic neighbor-based coarsening strategy includes a unification of randomly picked neighboring particles, the family-based one tries to merge SPH particles that originate from the same particle. In the case that the simulated solid bodies experience no or only small changes in their topologies while being refined and, afterwards, coarsened again, the neighbor-based pattern does not ensure that the original particle distribution over the discretized structure is restored. This can lead to a significant degradation in the result quality due to a nonoptimal particle distribution as shown in Fig. 6a, especially in the areas of the model that are located close to its outer surface. In contrast to this, the family-based strategy helps to reconstruct the original discretization of the simulation model, see Fig. 6b, and, therefore, to achieve a quality of the obtained results that is as good as the one of the original distribution.

Fig. 6

Simulation results obtained for the modified tensile test setup when using different coarsening patterns (red: high mass; blue: low mass). a Neighbor-based coarsening pattern, b Family-based coarsening pattern. (Color figure online)

4.2 Notched tensile test

A more challenging evaluation setup for the introduced adaptive SPH formulation than the ordinary tensile specimen considered above is the simulation of a notched specimen due to the fairly inhomogeneous stress distribution found in this case. In analogy to the tensile specimen regarded in the previous section, a regular lattice with quadratic cells of SPH particles serves as a basis for the two-dimensional model of a flat double-edge notched tensile specimen with an initial width of $1 \cdot 10^{-2} \, \hbox {m}$ and an initial length of $1.34 \cdot 10^{-2} \, \hbox {m}$. Halfway up the length of the created geometry round notches with a radius $r = 1.5 \cdot 10^{-3} \, \hbox {m}$ and an offset of $2 \cdot 10^{-4} \, \hbox {m}$ from the outer edge are introduced on both long sides of the specimen. To achieve a satisfactory level of reproduction of the high gradients in stress that can be observed next to the roots of the notches, an initial particle spacing of $2.3 \cdot 10^{-3} \, \hbox {m}$ is used for the discretization of the adaptive SPH simulation, leading to an overall number of particles of about $2\,700$ at the beginning of the simulation. The cubical refinement pattern as depicted in Fig. 3 with $\varepsilon = 0.5$ and $\alpha = 0.85$ is employed and the chosen refinement criterion is stress-based. For comparison, an unrefined SPH simulation with an initial particle spacing of $1.15 \cdot 10^{-3} \, \hbox {m}$ is performed, leading to an overall number of particles of about 10 000. As it is hardly possible to determine the stress distribution that can be found for a notched tensile specimen in an analytical way, two simulation-based references are used for comparing the results computed by the SPH method; a simulation of a notched tensile test performed by the Finite Element program ADINA and one employing the Discrete Element Method (DEM) [20].

As can be clearly seen when analyzing the distribution of the von Mises equivalent stress given in Fig. 7, the results obtained when employing the four different simulation techniques on the notched tensile scenario are in good agreement. Thus, the adaptive SPH method is able to reproduce the stress distribution observed for a real notched specimen. According to that, the maximum value of the von Mises stress can be found right at the roots of the two notches, whereas the level of equivalent stress decreases when following the paths from the roots to the centerline of the tensile specimen. Furthermore, the von Mises stress attains lower and lower values along the notch radii, starting with a high stress level at the roots and showing stress-free areas next to the outer surface of the specimen. When examining the three reference solutions, an elliptic section of the model that is characterized by a high magnitude of equivalent stress and is aligned with its minor axis along the ligament line is also obvious in case of the adaptive SPH notched tensile test.

Fig. 7

Distribution of the von Mises stress found for the model of a double-edge notched tensile specimen when using different simulation methods (red: high stress; blue: low stress). a Adaptive SPH, b SPH, c FEM, d DEM [21]. (Color figure online)

To give an impression how the adaptively refined area evolves with increasing simulation time, Fig. 8 shows three different stages of the refinement process found for the SPH double-edge notched tensile specimen. As one can see, the areas of highest stress are also the areas where the simulation model first experiences an increase in the discretization level. Accordingly, the refinement process is initiated right at the roots of the two notches and, subsequently, spreads into deeper particle layers along the elliptic section of the specimen that is characterized by a high magnitude of von Mises equivalent stress. In contrast to this, small parts of the notched tensile specimen, which are located close to the outer surface of the particle model, remain unchanged due to the fact that the stress level stays below the specified refinement threshold value for these regions. Following this procedure, the adaptive SPH method provides the same simulation results as found for the original, unmodified formulation, although the overall number of SPH particles and, thus, the necessary computational effort is much lower for the adaptive simulation.

Fig. 8

Different stages of the refinement of the adaptive SPH notched tensile specimen (red: high stress; blue: low stress). (Color figure online)

For a further validation of the adaptive algorithm, the results found for the three different refinement patterns introduced in Sect. 3.1, i.e. the cubical one with $\varepsilon = 0.5$, the hexagonal one with $\varepsilon = 2/3$, and the triangular one with $\varepsilon = 2/3$, are compared. For each of these refinement patterns, the value of the dispersion parameter $\varepsilon$ is chosen to give an equidistant particle spacing in the refined area between the roots of the two notches. In case of the hexagonal and the triangular pattern with an additional center particle and an unequal distribution of mass along the particles of the same refinement cell, the smoothing length multiplication factor $\alpha$ has to be increased. Otherwise, negative mass values would be used in the optimization process. This is illustrated in Fig. 9, which provides the pairs of values of the parameters $\varepsilon$ and $\alpha$ for which positive particle masses are found. Since the critical value of the smoothing length multiplication factor $\alpha$ is roughly $0.945$ for both patterns when setting $\varepsilon = 2/3$, we choose $\alpha = 0.95$ to ensure that the masses are positive.

Fig. 9

Combinations of the parameters $\varepsilon$ and $\alpha$ leading to positive and negative mass values when using different refinement patterns (white: negative mass value; blue: positive mass value). a Hexagonal pattern with center particle and unequal masses, b Triangular pattern with center particle and unequal masses. (Color figure online)

Results from the simulations with the two-dimensional cubical and hexagonal pattern at an early stage are shown in Fig. 10. As can be clearly seen, the hexagonal pattern leads in general to a similar behavior of the notched tensile model as seen before, with the highest stress located next to the roots of the notches and the formation of an elliptic section of high equivalent stress. There are only small differences between the cubical pattern, which is shown in Fig. 10a, and the hexagonal one without a centrally located particle, which is shown in Fig. 10b. For instance, the edge areas of the refined part of the adaptive model found for the cubical pattern seems to be a bit more inhomogeneous, i.e., there are some more unrefined particles that are located between the already refined ones in this case. In contrast to these minor deviations in the simulation results, the hexagonal pattern with a center particle and an unequally distributed mass leads to a stress distribution that is even more concentrated in the notch-near areas as well as the elliptic section of the specimen that is characterized by a high magnitude of von Mises equivalent stress as shown in Fig. 10c. Thus, the simulation employing the hexagonal pattern with center particles and an unequal distribution of mass shows for the same point in the simulation time a refined area that is smaller and fits more tightly around the elliptic section of high stress than the ones found for the other adaptive models. According to that, the expansion process of the refined area of the hexagonal pattern placing an additional particle in the center of a refinement cell lags behind the one of the cubical and the one of the hexagonal pattern without a central particle.

Fig. 10

Comparison of the two-dimensional cubical and hexagonal refinement pattern at early stage (red: high stress; blue: low stress). a Cubical pattern, b Hexagonal pattern without center particle, c Hexagonal pattern with center particle and unequal masses. (Color figure online)

All the differences between the hexagonal pattern with and without a centrally located particle described above can also be found for the triangular refinement pattern. In addition to that, also the orientation of the introduced triangular particle cells has an influence on the obtained solution. As can be seen in Fig. 11, the triangular pattern gives a better approximation of the borderline between the refined and the unrefined area, but, at the same time, the refined model no longer shows a perfect symmetry as can be seen when comparing the discretization of the two notch radii depicted in Fig. 11c. For this reason and due to the fact that the cubical refinement pattern provides the same result quality as found for the hexagonal one while introducing a much lower number of SPH particles during the refinement process, this pattern retaining the initial particle configuration is also used for the simulations presented below.

Fig. 11

Comparison of the two-dimensional cubical and triangular refinement pattern at late stage (red: high stress; blue: low stress). a Cubical pattern, b Triangular pattern without center particle, c Triangular pattern with center particle and unequal masses. (Color figure online)

4.3 Torus falling onto a membrane

The adaptive SPH formulation proposed in this paper is also applicable to fully three-dimensional simulations that are characterized by a highly dynamic behavior of the modeled solid structures. This is demonstrated in the following by presenting the results found for the simulation of a rigid torus falling onto an elastic membrane. While for the representation of the torus a triangular surface mesh along with the force model for boundary interactions introduced in Sect. 2.5 is deployed, the membrane is discretized using the SPH method. As shown in Fig. 12a, the elastic body consists of three layers of adaptive particles. The overall number of particles at the beginning of the simulation is about 5 300, of which the ones that are located close to the sides of the model are fixed in space.

Fig. 12

Simulation results obtained for the rigid torus falling onto an elastic membrane. a Side view of the simulation setup showing the torus and the membrane (red: fixed particles; blue: free particles), b Top view of the refined membrane model showing the particle’s masses (red: high mass; blue: low mass), c Top view of the coarsened membrane model showing the particle’s masses (red: high mass; blue: low mass). (Color figure online)

In the initial configuration of the simulation setup, the torus is placed at some distance above the membrane. After having released the torus from its starting position, the gravitational force acting on it leads to a free fall motion of the rigid body until it hits the elastic membrane. With this contact, the process of transferring kinetic energy from the torus to the membrane begins. Subsequently, the rigid body is gradually decelerated until its vertical velocity completely vanishes. Due to the interparticle bonds, the amount of kinetic energy absorbed by the adaptive SPH particles is step-by-step transformed into elastic deformation energy. For this reason, the stress level of the particles is increased and they are refined once the employed stress-based refinement criterion is met. As can be seen in Fig. 12b, this first happens for the particles being directly in contact with the meshed body and, as a consequence, the adaptive discretization algorithm projects the geometry of the torus (dashed lines) onto the uppermost layer of SPH particles, i.e. the surface of the elastic membrane.

In the second part of the simulation, some of the energy being stored in the elastic membrane is retransferred to the torus as part of the rebound effect. Therefore, the torus does not stay at rest, but is accelerated in vertical direction and begins an upward motion. When the torus and the surface layer of the membrane are no longer in contact, the stress level of the uppermost membrane particles falls below the specified coarsening threshold value and, as shown in Fig. 12c, the previously refined particles are coarsened again.

4.4 Orthogonal cutting process

A simulation scenario that is more related to real technical applications than the previous examples is the orthogonal cutting process. The orthogonal cutting setup represents an elementary cutting process where the motion of the tool is perpendicular to the cutting edge. When assuming a sufficiently large width of cut compared to the chosen depth of cut, a two-dimensional state of stress can be assumed in the workpiece and the machining process becomes a planar problem [22].

As part of the evaluation process of the introduced combined local adaptive refinement and coarsening algorithm, a model of an orthogonal cutting specimen is created while using, as already done in case of the previously discussed validation scenarios, a regular lattice with quadratic cells for the arrangement of the SPH particles and an initial smoothing length of the particles of $h = 5 \cdot 10^{-4} \, \hbox {m}$. To prevent the workpiece model from following an unconstrained translational motion, five additional rows of particles, which are fixed in space, are attached to the bottom of the specimen. The material used for the cutting simulation is, again, steel C45E, which is chosen because of its wide application in mechanical engineering. The corresponding material parameters found for this type of steel at room temperature are given in Table 2.

Table 2 Material properties for steel C45E at room temperature

Besides the workpiece material, the geometry of the cutting tool can have significant influence on the behavior of the cutting system and, therefore, the obtained results. Due to manufacturing reasons, the cutting edge of a real tool reveals deviations in its geometry from an ideal wedge shape [23]. As a consequence, not a tool with an ideal geometry, i.e. a wedge shape, but a more sophisticated one taking into account the imperfections resulting from limitations of the manufacturing process is employed for the presented machining simulation. One model that promises a sufficient imitation of a real tool is introduced in [24]. For the calculation of the particle forces resulting from the interaction with the cutting tool, once more the penalty approach presented in Sect. 2.5 is deployed. Further information on the presented orthogonal cutting setup can be found in [25]. The behavior of the cutting model that can be observed when using both the original as well as the adaptive SPH formulation is discussed hereinafter.

When the cutting of material takes place, the distribution of the von Mises stress that is shown in Fig. 13a, with red meaning high stress and blue indicating a low level of von Mises equivalent stress, can be found for the original SPH model. The highest level of stress appears next to the tip of the tool where the separation of material happens. This zone showing a high magnitude of equivalent stress is surrounded by a zone of mid-level stress, which is color coded in yellow and green. Both the particle layers that are located at some distance from the tool tip as well as the parts of the material that form the chip show low values of von Mises stress, as indicated by the blue color of these SPH particles. In similarity to experimental results, a continuous chip is separated from the remaining workpiece material in the cutting simulation. In this context, it is important to remember that the particles that are shown in Fig. 13a only illustrate the interpolation points where the equations of the underlying continuum model are evaluated, not domains of material.

Fig. 13

Simulation results obtained for the orthogonal cutting specimen when using both the original and the adaptive SPH formulation. a Distribution of the von Mises stress found for the original SPH model (red: high stress; blue: low stress), b Adaptive SPH model showing the particle’s masses (red: high mass; blue: low mass). (Color figure online)

If the introduced adaptive discretization technique is applied to the orthogonal cutting simulation, one observes a refinement of the load-carrying particles in the different shear zones of the cutting specimen as it is shown in Fig. 13b. While the blue-colored particles still have the initial size, the red-colored ones have been refined in order to be able to resolve the high gradients in stress found for these regions. Again, a stress-based refinement criterion together with the cubical refinement pattern introduced in Sect. 3.1 is used. For the areas of the workpiece model that have already been passed by the tool geometry, the previously refined SPH particles are adaptively coarsened, as indicated by their red color, when showing a stress level that is at least ten times lower than the specified refinement threshold value.

5 Conclusion

In this paper, a local adaptive discretization algorithm for the SPH method has been proposed. With the presented approach, it is possible to improve the accuracy of the simulation results while reducing the required computational cost at the same time. To that end, the number of SPH particles is adaptively increased in certain areas of a simulation model if necessary, whereas it is decreased for domains of low interest. In a first step towards such a combined refinement and coarsening strategy, an enhanced version of the refinement procedure has been integrated into the SPH solid formulation that had been extended to the JC plasticity model, the JC damage model, as well as an appropriate boundary force model. In a second step, we developed a coarsening algorithm that is compatible with the refinement routine implemented before. Both adaptive components follow the same basic procedure, which consists of the following three steps. First, it is decided if the discretization level of an already existing SPH particle is to be adapted by checking whether a user-defined criterion is met or not. Second, if the criterion is met, the particle is split into several smaller ones or, respectively, merged with some of its neighbors into a bigger one according to a chosen refinement or coarsening pattern. Third, the state variables of the additional particles are calculated either by interpolation or by cloning and subsequent scaling the ones of the original particle. In a last step, the validity of the coupled approach, as well as its applicability, was shown by applying it to a broad range of different simulation setups.

Four of the various simulation scenarios used for the validation of the implemented adaptive discretization routine were then presented. In the context of an ordinary tensile test setup, the capability of the introduced adaptive discretization technique to avoid a numerical fracture as well as to ensure a conservation of linear and angular momentum as well as kinetic energy was demonstrated. Next, it was shown for a notched tensile test setup that the combined refinement and coarsening strategy provides the same results as found with the FEM or a lot more computational expensive SPH simulations with a fixed number of particles. The fact that the results quality of the adaptive SPH formulation depends on the choice which of the introduced refinement and coarsening patterns are employed was discussed. Besides these two simulation scenarios used to illustrate the basic qualities of the introduced local adaptive discretization algorithm, it is also applicable to SPH simulations showing a highly dynamic behavior of the modeled structures and is suitable to solve problems related to real technical applications. This has been shown in the context of a simulation of a rigid torus falling onto an elastic membrane and one of an orthogonal cutting process.