1 Introduction

Wind energy has been the fastest growing renewable energy resource throughout the world. It is indicated that by the end of 2014, the global total installed wind power capacity has reached to 369.6 GW, and 24 countries equipped the installed wind power capacity of more than 1 GW [1]. In most cases, the clean wind power is dispatched prior to other types of generation sources. However, due to the uncertainty of wind [2], the generation of wind power in a wind farm usually varies over a wide range, making it difficult to set up a dispatch plan accurately. As a result, wind power forecasting performance is of crucial importance for the secure operation and economic dispatch of power systems.

Wind power forecasting is a challenging task in power system research, and some effective methods have been promptly introduced to address wind power forecasting. Generally, there are physical models [3], auto-regressive moving average (ARMA) models [4, 5], Artificial Neural Network (ANN) methods [6], spatial models [7], Kalman filter techniques [8], Grey model [9], and volatility model represented by GARCH model [10] and hybrid approaches [11]. Reference [10] reported that wind power time series exhibited time varying volatility and obtained satisfying results with the GARCH-M forecasting model. Nevertheless, the volatility characteristics of the wind power time series are complicated and meaningful. The latent news in these characteristics which can improve forecasting performance remains to be further explored. Based on the analysis of large amounts of real-world historical wind power data, it can be frequently found that a number of recurrent extra-large magnitude shocks exist in wind power time series. These shocks may lead particular impacts on the future volatility of wind power time series, which can be regarded as an outlier. In this work, this impact on the volatility is called outlier effect. This paper reflects efforts in analyzing outlier effect caused by the idiosyncratic shocks while outlier smooth transition autoregressive (OSTAR) structure is highlighted and the OSTAR-GARCH model is proposed to improve the performance of wind power forecasting.

This paper is organized as follows. Section 2 proposes the OSTAR-GARCH wind power forecasting model to illustrate the outlier effect. Meanwhile, fat-tail distribution is further employed to generalize the OSTAR-GARCH model. The outlier effect is investigated by the news impact curve (NIC) and the proposed regime switching index (RSI) in Section 3. Section 4 provides a case study based on practical examples to validate the proposed models. Moreover, the outlier effect is depicted graphically by NIC and the extent of regime switching is measured by RSI quantitatively. Section 5 concludes the discussions.

2 OSTAR-GARCH model

In this section, the OSTAR model is proposed on the basis of the STAR model. Furthermore, combined with the volatility model, the OSTAR-GARCH wind power forecasting model is prospectively proposed to capture the outlier effect of wind power time series. The proposed OSTAR-GARCH model is further generalized by taking into account the fat-tail effect.

2.1 STAR model

One of leading nonlinear forecasting models is smooth transition autoregressive (STAR) model proposed by Teräsvirta, which can achieve smooth transition between different regimes in time series [12].

If the time series {y t } satisfies

$$\begin{aligned} y_{t} = \left( {1 - F(y_{t - d} )} \right)\left( {c_{0} + \sum\limits_{i = 1}^{p} {\phi_{0,i} y_{t - i} } } \right) \hfill \\ \quad +\, F(y_{t - d} )\left( {c_{1} +\, \sum\limits_{i = 1}^{p} {\phi_{1,i} y_{t - i} } } \right) + \varepsilon_{t} \hfill \\ \end{aligned}$$
(1)

where d is lagged order parameter; p is the order of STAR model; \(F( \cdot )\) is smooth transition function satisfying \(0 \le F( \cdot ) \le 1\); {y t } follows the STAR(p) process of two regimes.

2.2 OSTAR model

In practice, the expression of \(F( \cdot )\) in (1) is set to be one of many classical forms. When the logistic functions or exponential functions are employed, the model is known as the LSTAR (logistic STAR) model or ESTAR (exponential STAR) model, respectively.

The exponential function in the ESTAR model is represented as

$$F(x;\gamma ) = 1{\text{ - exp(}} - \gamma x_{{}}^{2} )$$
(2)

ESTAR models incorporating (2) can depict the different impacts at different magnitudes of x. However, the smooth transition structure of ESTAR is unable to give useful information on providing clear cutting lines for differentiating large shocks from others [13].

As a result, it is necessary to activate the threshold parameter Δ into smooth transition function in order to separate the idiosyncratic shocks from others. Meanwhile, to avoid the “step change” at the threshold point, the slope parameter \(\gamma\) should be refined to achieve gradual switching and control the transition speed between different regimes. Therefore, a novel smooth transition function, which is named tumbler function, is proposed in this work as follows,

$$F(x;\varDelta ,\gamma ) = {1 \mathord{\left/ {\vphantom {1 {\left( {1 + \exp ( - \gamma (\left| x \right| - \varDelta ))} \right)}}} \right. \kern-0pt} {\left( {1 + \exp ( - \gamma (\left| x \right| - \varDelta ))} \right)}}$$
(3)

where Δ is the threshold parameter; the slope parameter γ is a positive parameter with \(\gamma \gg {1 \mathord{\left/ {\vphantom {1 \varDelta }} \right. \kern-0pt} \varDelta }\) satisfied.

Equation (3) is effective to depict the outlier effect. As a result, the STAR model with the tumbler function in (3) is proposed as the OSTAR model in this work.

The dynamic behavior of F(x,y) with the varying γ is illustrated in Fig. 1. The threshold parameter Δ is designated to differentiate the isolated outlier shocks from other normal shocks.

Fig. 1
figure 1

OSTAR function with different γ

Full size image

2.3 Combination of OSTAR model and GARCH model

GARCH models can provide a systematic framework for modelling volatility of time series [14, 15]. On the second order moment level, the OSTAR structure and the GARCH model can be combined to capture the regime switching between the outlier shocks and others in the volatility of the wind power time series.

The specification of OSTAR-GARCH model can be expressed as conditional mean (4) and variance equation (5).

$$y_{t} = E(y_{t} \left| {\psi_{t - 1} )} \right. + \varepsilon_{t}$$
(4)
$$h_{t} = \alpha_{0} + \sum\limits_{j = 1}^{p} {\beta_{j} } h_{t - j} + \sum\limits_{i = 1}^{q} {\alpha_{i} } \varepsilon_{t - i}^{2} { + }\sum\limits_{k = 1}^{r} {\lambda_{k} \varepsilon_{t - k}^{2} F(\varepsilon_{t - k} )}$$
(5)

where \(\varepsilon_{t} = \sqrt {h_{t} } \nu_{t} ,\;\nu_{t} \sim i.i.d.\), with \(E(\nu_{t} ) = 0\), \(E(\nu_{t}^{2} ) = 1\) satisfied. Also, \(E(y_{t} \left| {\psi_{t - 1} )} \right.\) is the conditional mean considering the information set at t − 1. \(F(\varepsilon_{t - k} ) = {1 \mathord{\left/ {\vphantom {1 {\left( {1 + \exp ( - \gamma_{k} (\left| {\varepsilon_{t - k} } \right| - \Delta ))} \right)}}} \right. \kern-0pt} {\left( {1 + \exp ( - \gamma_{k} (\left| {\varepsilon_{t - k} } \right| - \varDelta ))} \right)}}\) follows the OSTAR function structure, and \(\lambda_{k}^{{}}\) is called outlier effect parameter. The parameters p, q, r are the order parameters of OSTAR-GARCH, respectively. To apply the new model to practice conveniently, all order parameters are set to 1 in the following discussion.

The following analysis can be provided from the specification of OSTAR-GARCH.

  1. 1)

    In the conditional variance equation in (5), If λ is negative, the outlier shocks will have weaker impact on the conditional variance than others, and vice versa.

  2. 2)

    Δ in the OSTAR structure is used to quantitatively differentiate the outlier shocks and analyze the outlier effect, theoretically, \(\varDelta \in (0,\infty )\). To effectively examine the outlier effect in the case study, Δ is assigned to be twice the estimate of the residuals’ standard deviation \(\hat{\sigma }\). As a result, the outlier shocks are defined as outside the interval \(\left[ { - 2\hat{\sigma },\;2\hat{\sigma }} \right]\).

  3. 3)

    γ in tumbler function represent the transition smoothness between different regimes. Considering \(\gamma \gg {1 \mathord{\left/ {\vphantom {1 \varDelta }} \right. \kern-0pt} \varDelta }\), when \(\left| {\varepsilon_{t - 1} } \right| \to \infty\), then \(F(\varepsilon_{t - 1} ) \to 1\); on the contrast, when \(\left| {\varepsilon_{t - 1} } \right| = 0\), then \(F(\varepsilon_{t - 1} ) \to 0\). Specially, if \(\left| {\varepsilon_{t - 1} } \right| = \varDelta\), then \(F(\varepsilon_{t - 1} ) = 0.5\). As a result, no non-continuous point exists even near threshold point.

According to the analysis above, the OSTAR-GARCH model can depict the outlier effect in the volatility and achieve a smooth transition between isolated outlier shocks and others in wind power time series.

2.4 Fat-tail OSTAR-GARCH model

To effectively capture the fat-tail effect in the wind power time series, \(\nu_{t}\), in the OSTAR-GARCH wind power forecasting model, is generalized from normal distribution to non-Gaussian distributions. As the most popular non-Gaussian distributions, t distribution [16], Laplace distribution [17], and generalized error distribution (GED) [18] are employed, respectively.

  1. 1)

    t distribution

    The probability density function (PDF) of t distribution is given by

    $$f(x,n) = \frac{{\Gamma \left( {{{\left( {n + 1} \right)} \mathord{/ {\vphantom {{\left( {n + 1} \right)} 2}} \kern-0pt} 2}} \right)}}{{(n\pi )^{1/2} \Gamma \left( {{n \mathord{/ {\vphantom {n 2}} \kern-0pt} 2}} \right)}}\left( {1 + \left( {{x \mathord{/ {\vphantom {x n}} \kern-0pt} n}} \right)^{2} } \right)^{{ - {{\left( {n + 1} \right)} \mathord{/ {\vphantom {{\left( {n + 1} \right)} 2}} \kern-0pt} 2}}}$$
    (6)

    where \(\Gamma \left( \cdot \right)\) is the Gamma function and n is the degree of freedom. In this work, the OSTAR-GARCH model that follows the t distribution is called OSTAR-t model for short.

  2. 2)

    Generalized error distribution

    The PDF of generalized error distribution (GED) is

    $$f(x,v) = \frac{{v \cdot \exp \left( { - 0.5 \cdot \left| {x/\lambda } \right|^{v} } \right)}}{{\lambda \cdot 2^{{\left( {1 + 1/v} \right)}} \Gamma \left( {{1 \mathord{/ {\vphantom {1 v}}\kern-0pt} v}} \right)}}$$
    (7)

    where \(\lambda = \left( {2^{{ - {2 \mathord{/ {\vphantom {2 v}} \kern-0pt} v}}} {{\Gamma \left( {1/v} \right)} \mathord{/ {\vphantom {{\Gamma \left( {1/v} \right)} {\Gamma \left( {3/v} \right)}}} \kern-0pt} {\Gamma \left( {3/v} \right)}}} \right)^{{{1 \mathord{/ {\vphantom {1 2}} \kern-0pt} 2}}}\) is a function of the distribution shape parameter v; when \(v < 2\), GED will have a fatter tail than normal distribution. In this work, the OSTAR-GED model is derived when OSTAR-GARCH model follows GED.

  3. 3)

    Laplace distribution

    Laplace distribution is with the following probability density function,

    $$f(x) = \frac{{\exp \left( {{{ - \left| x \right|} \mathord{/ {\vphantom {{ - \left| x \right|} b}} \kern-0pt} b}} \right)}}{2b}$$
    (8)

    If the parameter b is set to be\({{\sqrt 2 } \mathord{/ {\vphantom {{\sqrt 2 } 2}}\kern-0pt} 2}\), the Laplace distribution can be standardized, satisfying mean = 0 and variance = 1. The standardized Laplace distribution possesses fatter tail than normal distribution spontaneously. In this paper, the OSTAR-GARCH model that follows the standardized Laplace distribution is named OSTAR-Laplace model for short.

2.5 Parameter estimation

Nonlinear least squares (NLS) or conditional maximum likelihood estimation (CMLE) [13, 19], can be used to estimate the OSTAR-GARCH model. Considering that the log-likelihood function of the OSTAR model can be obtained conveniently, CMLE is employed to estimate the OSTAR-GARCH model in the case study. At the same time, BHHH algorithm [20] is used to control the iteration process.

Furthermore, the parameters of the fat-tailed OSTAR-GARCH models are estimated by CMLE as well, with the assumption that \(\varepsilon_{t}\) follows t distribution, GED, or Laplace distribution (for OSTAR-t, OSTAR-GED, or OSTAR-Laplace model), respectively.

3 Regime switching index

OSTAR-GARCH wind power forecasting model is effective to capture the outlier effect in wind power time series. To analyze how outlier shocks affects the next period variance in time series, NIC based on OSTAR-GARCH model is used to analyze outlier effect graphically. Moreover, to provide a quantitative evaluation to measure the extent of regime switching, the regime switching index (RSI) is proposed.

NIC was proposed [21] as a standard measure to analyze how new information affects the next period variance in time series.

Holding constant the information dated t − 2 and earlier, the implied relation between \(\varepsilon_{t - 1}\) and \(h_{t}\) can be illustrated. With all lagged conditional variances evaluated at the level of the unconditional variance of the wind power time series, the curve relates past wind power shocks (news) to current volatility, so it is named the news impact curve.

In classical GARCH model, the NIC based on GARCH is a quadratic curve centered on \(\varepsilon_{t - 1} = 0\). Originally, the standard version of NIC in [21] was used to analyze the asymmetry effect in the volatility, and the attention was paid to the comparison of the symmetric relationship between the left and right branches of the NIC. Nevertheless, in this paper, the application of NIC is generalized. NIC is employed to analyze the different impacts of the amplitude of shocks, that is, the focus here is to investigate the distortion of the NIC shape caused by the outlier effect. Further discussion about NIC based on OSTAR-GARCH model is in the case study.

Though NIC can graphically judge the extent of regime switching by the shape of NIC, the quantitative evaluation method is still necessary. In this paper, the regime switching index (RSI) is proposed to give a quantitative index to judge the extent of regime switching as follows.

An OSTAR-GARCH model can be decomposed as

$$g(h_{t} ) = c + f\left( {\varepsilon_{t - 1} ,\varepsilon_{t - 2} , \cdots } \right) + \sum\limits_{i = 1}^{n} {\lambda_{i} F_{i} ( \cdot )\eta_{i} \left( {\varepsilon_{t - 1} ,\varepsilon_{t - 2} , \cdots } \right)}$$
(9)

where \(\lambda_{i} F_{i} \left( \cdot \right)\eta_{i} \left( {\varepsilon_{t} } \right)\) is a function decided by \(F\left( \cdot \right) \in \left[ {0,1} \right]\); \(f(\varepsilon_{t - i} )\) has no relevance with \(F( \cdot )\); c includes the term which has no relevance with \(\varepsilon_{t}\).

The RSI is defined by

$$K_{RSI} = \frac{{f\left( {\varepsilon_{t - 1} ,\varepsilon_{t - 2} , \cdots } \right) + \sum\limits_{k = 1}^{n} {\lambda_{k}^{ + } \eta \left( {\varepsilon_{t - 1} ,\varepsilon_{t - 2} , \cdots } \right)} }}{{f\left( {\varepsilon_{t - 1} ,\varepsilon_{t - 2} , \cdots } \right) + \sum\limits_{k = 1}^{n} {\lambda_{k}^{ - } \eta \left( {\varepsilon_{t - 1} ,\varepsilon_{t - 2} , \cdots } \right)} }}$$
(10)

where \(\lambda_{i}^{ + } = \hbox{max} (\lambda_{i} ,0);\;\lambda_{i}^{ - } = \hbox{min} (\lambda_{i} ,0)\).

As is readily apparent, if GARCH model has no regime switching structure, the K RSI is fixed at 1, consequentially,

$$K_{RSI}^{GARCH} = \frac{{f\left( {\varepsilon_{t - 1} ,\varepsilon_{t - 2} , \cdots } \right) + 0}}{{f\left( {\varepsilon_{t - 1} ,\varepsilon_{t - 2} , \cdots } \right) + 0}} = 1$$
(11)

Then, with the assumption of \(\lambda \le 0\), K RSI is applied to OSTAR-GARCH (1, 1) models as follows.

$$K_{RSI}^{OSTAR} = \frac{{\alpha_{1} \varepsilon_{t - 1}^{2} }}{{\alpha_{1} \varepsilon_{t - 1}^{2} + \lambda \varepsilon_{t - 1}^{2} }} = \frac{{\alpha_{1} }}{{\alpha_{1} + \lambda }} > 1$$
(12)

It is apparent that the index K RSI is related to the parameter α 1 and λ. By means of the K RSI , the extent of regime switching of different OSTAR-GARCH models can be compared quantitatively. For example, if the \(K_{RSI}^{OSTAR}\) is further beyond 1, the outlier effect is more significant.

4 Case study

4.1 Data

The historical wind power data from a coastal wind farm group in Jiangsu Province is used to examine the proposed forecasting models. The sample is the 5-minute wind power data set from April 1, 2013 to April 7, 2013.

The 5-minute ahead forecasting of wind power on April 8, 2013 is studied using the proposed OSTAR-GARCH wind power forecasting models. NIC and RSI are employed to investigate on the outlier effect in the wind power time series. Forecasting performance of the proposed models is validated by a comparison using 3 statistical indices.

4.2 Stationary test result

Stationary tests are first carried out by augmented dickey fuller (ADF) test and Phillips-Perron (PP) test to examine the stationarity of the wind power time series. The results of the two tests consistently report that the wind power series Y t is not stationary at the 5% significance level. Then, differencing is used to obtain the first differenced series, I t .

$$I_{t} = Y_{t} - Y_{t - 1}$$
(13)

At this time, ADF and PP tests are both statistically significant at the 5% significance level, indicating that it is stationary, and the stationary precondition of modelling is met. Consequently, the following study is based on the series of I t .

4.3 Modelling with OSTAR-GARCH models

Considering serial dependence in wind power series, ARMA structure is employed in the mean equation of the OSTAR-GARCH model. The mean equation of the OSTAR-GARCH model is shown below.

$$I_{t} = \omega + \sum\limits_{j = 1}^{p} {\phi_{j} I_{t - j} } + \varepsilon_{t} + \sum\limits_{i = 1}^{q} {\psi_{i} \varepsilon_{t - i} }$$
(14)

Based on the routine from [11], the orders of ARMA are determined as ARMA (4, 5)- OSTAR-GARCH (1, 1) with the specification of (5) (OSTAR, for short). Consequently, the parameter set \(\varTheta_{OSTAR} = \left( {\omega ,\phi ,\psi ,\varOmega ,\alpha_{1} ,\beta_{1} ,\lambda } \right)\) is obtained by CMLE. Parameter estimates of OSTAR models are shown in Table 1.

Table 1 Parameter estimate
Full size table

With the CMLE, parameter estimate is calculated for the OSTAR model.

Taking into account the fat-tail effect in wind power time series, the OSTAR-t, OSTAR-Laplace, OSTAR-GED models are presented. Furthermore, the parameters of all the fat-tail version of OSTAR models are estimated as shown in Table 1.

According to Table 1, some discussions are reported as follows:

  1. 1)

    Firstly, the conditional variance is examined. The outlier effect parameters in the four OSTAR-GARCH models are −0.148684, −0.15329, −0.16414, −0.21517, respectively. The realistic meanings implicated by the signs of parameter λ are consistent; moreover, all the λ are negative, so it is indicated that the impact on the conditional variance of outlier shocks is suppressed. Ulteriorly, the volatility of wind power time series might be over-rated, on condition that the outlier shocks are treated the same as ordinary shocks, and this error evaluation of volatility may harm the performance of wind power forecasting. Therefore, the OSTAR-GARCH models are formulated to incorporate outlier effect in the volatility of wind power time series.

  2. 2)

    Secondly, the shape parameter v of OSTAR-GED is 1.429912, which is significantly less than 2.0. Similarly, the freedom degree n of the OSTAR-t models is in a low level, 7.981401 and the corresponding z statistics is 7.467363, indicating that parameter n is significant. Consequently, the estimated values v and n from the non-Gaussian distributions explicitly reflect the fat-tail effect in wind power time series. Moreover, the Laplace distribution of the OSTAR-Laplace model also performs fat-tail effect naturally. The estimate results validate that the employment of three types of non-Gaussian distribution is appropriate and essential for modelling wind power time series.

  3. 3)

    The conditional mean equation is concerned. It is noted that the estimate values of the corresponding mean equation parameters of these models are close to each other, respectively, though the conditional variance specifications of these models are rather different. Hence, it is indicated that some inherent characteristics on the mean level is depicted by these models.

  4. 4)

    Finally, according to the iteration times on Table 1, OSTAR-GARCH models with non-Gaussian distribution require less iterations of estimate than the original version of OSTAR-GARCH model, even if the conditional log likelihood function structures of fat-tail OSTAR-GARCH models are more complicated. Moreover, owing to the decrease of iterations, the total calculation time of parameter estimate are not prolonged considerably.

4.4 NIC analysis

As it can show the response in the volatility to the different characteristic of shocks, NIC is employed to witness the outlier effect in wind power time series in this work.

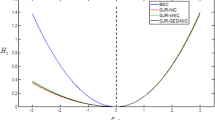
The NIC of the OSTAR-GARCH model determined by the conditional variance function in (4) and the tumbler transition function in (3) is represented as the black line in Fig. 2. After all, to simplify the comparison and highlight the outlier effect of \(\varepsilon_{t - 1}\) on \(h_{t}\), all the lowest points of NICs are moved to the origin point, respectively.

Fig. 2
figure 2

NIC of OSTAR-GARCH

Full size image

Consequently, two extreme cases should be considered:

  1. 1)

    Let F(\(\varepsilon_{t - 1}\)) in (5) equals to 0. The OSTAR structure is smoothed out and the OSTAR-GARCH model is degenerated into a special GARCH model with \(h_{t} = \alpha_{0} + \beta_{1} h_{t - 1} + \alpha_{1} \varepsilon_{t - 1}^{2}\). In this case, the corresponding GARCH NIC is abbreviated to NIC-A.

  2. 2)

    Let F(\(\varepsilon_{t - 1}\)) equals to 1. the OSTAR-GARCH model degenerated into another special GARCH model with \(h_{t} = \alpha_{0} + \beta_{1} h_{t - 1} + \left( {\alpha_{1} { + }\lambda } \right)\varepsilon_{t - 1}^{2}\). In this case, NIC-B is correspondingly obtained.

In our case study, NIC-A is represented in the blue dash curve and NIC-B is expressed as the red dash curve. Furthermore, owing to λ < 0, \(\varepsilon_{t - 1}^{2}\) expressed in NIC-A has more significant impact on the \(h_{t}\) of wind power time series than that in NIC-B, as shown in Fig. 2.

From Fig. 2, the following conclusions can be drawn: When \(\varepsilon_{t - 1} \to 0\), the NIC of OSTAR-GARCH model is verging to NIC-A, while \(\left| {\varepsilon_{t - 1} } \right| \gg \varDelta\), it is verging to NIC-B. In other words, the larger the \(\left| {\varepsilon_{t - 1} } \right|\) is, the weaker the impacts from the large shocks to conditional variance become gradually, and the outlier shocks receive less weight than others when \(\left| {\varepsilon_{t - 1} } \right|\) increases over a threshold value. Hence, the outlier effect in wind power time series is clearly witnessed.

Note that the NIC of OSTAR-GARCH is continuous and differentiable at every point, and the curve is still smooth even at the threshold, on account of the structure of tumbler transition function. As a result, the specification without non-differentiable point is qualified at satisfying the physical circumstances of the wind power.

4.5 Calculation of RSI

With the help of the results in Table 1, the RSI value of each model is calculated in Table 2.

Table 2 RSI of OSTAR-GARCH models
Full size table

As shown in Table 2, the extent of regime switching is measured quantitatively. It is obvious that the four conditional distribution specifications of the OSTAR-GARCH model induce the RSI values, respectively. The model with fat-tail distributions obtained larger RSI.

4.6 Wind power forecasting performance

According to the estimate result of Table 1, the 5-minute wind power forecasting for April 8, 2013 (containing 288 points) is implemented with the OSTAR-GARCH models.

Wind power forecasting using the selected models is performed based on the following formation

$$\hat{Y}_{t} \,{ = }\,Y_{t - 1} { + }\hat{I}_{t}$$
(15)

where \(\hat{I}_{t}\) is modelled by the proposed OSTAR-GARCH wind power forecasting models: OSTAR, OSTAR-t, OSTAR-GED, OSTAR-Laplace models, respectively. At the same time, the t-1 hour time persistence (TP) model (which is widely used in the electric power industry) and the classical GARCH model are employed in the case study as reference models.

To verify the forecasting performance of the proposed models, the forecasting results based on the proposed models are compared by means of 3 statistical indices: root mean squared error (RMSE), mean absolute error (MAE), and mean absolute percentage error (MAPE). The specifications of these 3 indices are shown in (16)–(18). The comparison of forecasting performance is summarized in Table 3.

Table 3 Comparison of forecasting performance
Full size table
$$E_{RMSE}^{{}} = \sqrt {\sum\limits_{t = T + 1}^{T + h} {\left( {\hat{y}_{t} - y_{t} } \right)_{{}}^{2} /h} }$$
(16)
$$E_{MAE} = \sum\limits_{t = T + 1}^{T + h} {\left| {\hat{y}_{t} - y_{t} } \right|/h}$$
(17)
$$ E_{MAPE} = \sum\limits_{t = T + 1}^{T + h} {\left| {{{\left( {\hat{y}_{t} - y_{t} } \right)} \mathord{\left/ {\vphantom {{\left( {\hat{y}_{t} - y_{t} } \right)} {y_{t} }}} \right. \kern-0pt} {y_{t} }}} \right|/h} \times 100{\text{\% }} $$
(18)

From Table 3, it can be witnessed that the forecasting performance of all the proposed OSTAR-GARCH models is significantly better than TP mode and even better than the classical GARCH model. Moreover, based on the criteria of RMSE and MAE, it can be consistently concluded that the OSTAR-t wind power forecasting model excels other models. Based on the criterion of MAPE, the OSTAR-Laplace outperforms the others. Overall, the OSTAR-GARCH models following non-Gaussian distributions outperform the original OSTAR-GARCH model and GARCH model.

In brief, considering the existence of outlier effect and the fat-tail effect in the wind power time series, it is a reasonably good practice to combine STAR structure and GARCH models with non-Gaussian distributions.

5 Conclusion

The OSTAR-GARCH models are proposed in this study for wind power forecasting, and the impact of outlier shocks in wind power time series is analyzed quantitatively by the proposed RSI. Forecasting performance comparison is achieved based on different criteria.

The OSTAR-GARCH model can depict the outlier effect in wind power time series. Case studies demonstrate that outlier shocks show more restrained impacts on the conditional variances. By employing the classical NIC, the outlier effect is clearly demonstrated graphically. With the proposed RSI, the extent of regime switching is quantitatively measured. When a high RSI reports the existence of regime switching, the implementation of OSTAR-GARCH models can provide prospective wind power forecasting precision.

Taking into account the existence of fat-tail effect of wind power time series, the innovation of the proposed OSTAR-GARCH model is refined from classical Gaussian distribution to fat-tail distribution. Case studies demonstrate that the OSTAR-GARCH models with fat-tail distribution can give more efficient forecasting performance.

In conclusion, with new challenges of wind power analysis, it is necessary to highlight novel wind power forecasting models to analyze and explore the inherent volatility characteristics of wind power time series, such as to contribute to the improvement of wind power forecasting performance.