A simple epidemic model for semi-closed community reveals the hidden outbreak risk in nursing homes, prisons, and residential universities

Abstract

We develop a general SIS model to study the epidemic transmission in such semi-closed communities. The community population is divided into susceptible and infected in terms of the infection state, and concerning the physical structure of the crowd, they are classified into mobile and fixed individuals. The mobile individuals can be inside or outside the community, while the fixed individuals can be only inside the community. There are fixed infection sources outside the community, measuring the epidemic severity in society. We attribute the spreading to two reasons: (i) clustered infection among the community population and (ii) the epidemic in society spreading to the community population. We discuss the model in two cases. In the first case, the epidemic spreads in society, such that reasons (i) and (ii) work together. The results show that concerning fixed individuals (e.g. the elderly in nursing homes), a more closed community always promotes the infection. In the second case, there is no epidemic spreading in society, such that only reason (i) works. The results show that restricting all individuals to the community produces equivalent consequences as allowing them going outside the community. We should evenly distribute individuals inside and outside to form isolation. A counterexample is residential universities implementing closed management, where only students are restricted to campus. The model shows such management may lead to severe epidemics, and to prevent the epidemic outbreaks, students should have free access to being on or off campus.

1 Introduction

Since Kermack and McKendrick [1] proposed the compartment model of epidemic transmission, this simple mathematical paradigm has been obtained for studying propagation dynamics. In recent years, the compartment model, used not only to describe the spread of epidemics [2,3,4] but also to describe the fermentation of rumours [5], radicalization [6,7,8,9], and public opinions [10, 11], has become a popular research tool of sociophysics. One of the classic epidemic compartment models is the SIS model. In the classic SIS epidemic model, the population is divided into susceptible individuals (S), not infected by the disease, and infected individuals (I), infected by the disease. The epidemic spreads at a rate of $\alpha$ through human-to-human transmission, and the infected individuals heal at a rate of $\mu$. In a unit time, on the one hand, susceptible individuals whose number depends on the different incidence rates, such as the bilinear incidence rate $\alpha SI$ [12, 13], the fractional or standard incidence rate $\alpha SI/(S+I)$ [14, 15], the saturated incidence rate $\alpha SI/(1+\sigma I)$ [16,17,18], the non-monotone incidence rate $\alpha SI/(1+\sigma I^2)$ [19, 20], become infected individuals. On the other hand, $\mu I$ infected individuals recover and become susceptible individuals. The above process happens in a well-mixed population, but the SIS model has also been investigated on graphs [21, 22] and hypergraphs [23, 24]. Studies on introducing new factors into the SIS epidemic model continued to appear, including the study on vaccination [25], heterogeneous contacts [26], competing mechanism on complex networks [27, 28], immigrants arriving with the same infection [29], and the external source of infection [30,31,32]. In particular, the external source of infection, measured by a constant, is an additional infection source to the infected individuals, to which we refer for the description of epidemic severity in society in this paper.

The inspiration for this work begins as follows. Ref. [33] proposed an epidemic model in a semi-closed community to study closed management in residential universities for epidemic prevention. The semi-closed community divides the environment into internal and external environments, with individuals in the internal environment by default, and only a fraction of individuals able to go to the external environment. Ref. [33] supposed that individuals with a proportion of $\theta$ per unit time could freely choose to stay in or out of the community (we label these individuals as the mobile individuals), and the remaining individuals with a proportion of $(1-\theta )$ can only stay in the community (we label these individuals as the fixed individuals). They considered susceptible individuals S and infected individuals I in the population N, $S+I=N$; therefore, on average, $\theta S$ susceptible individuals and $\theta I$ infected individuals are mobile individuals, while the remaining $(1-\theta )S$ susceptible individuals and $(1-\theta )I$ infected individuals are fixed individuals, in a unit time. Ref. [33] studied the evolution of the system when there is no diagnosed case and also explained why nursing homes and prisons worldwide are prone to become severe epidemic communities by the mathematical model.

However, Ref. [33] did not take into account the fact that, in the above scenarios, mobile individuals (e.g. faculty and staff, nursing workers, corrections officers) and fixed individuals (e.g. students, the elderly, prisoners) are the same people, rather than a result of average selection from the population in each unit time. We could ask: is infected proportion in mobile and fixed individuals in the two cases equivalent? Let us denote the number of susceptible fixed individuals $S_0$ and infected fixed individuals $I_0$ in fixed individuals $N_0{:}{=}(1-\theta )N$, and susceptible mobile individuals $S_1$ and infected mobile individuals $I_1$ in mobile individuals $N_1{:}{=}\theta N$, yielding $S_0+I_0=N_0$, $S_1+I_1=N_1$, $S_0+S_1=S$, $I_0+I_1=I$; that is,

$$\begin{aligned} {{\textbf {A}}}\varvec{\Psi }={{\textbf {b}}}. \end{aligned}$$

(1)

where

$$\begin{aligned} {{\textbf {A}}}= \begin{pmatrix} 1 &{} 0 &{} 1 &{} 0 \\ 0 &{} 1 &{} 0 &{} 1 \\ 0 &{} 0 &{} 1 &{} 1 \\ 1 &{} 1 &{} 0 &{} 0 \end{pmatrix}, \varvec{\Psi }= \begin{pmatrix} I_0 \\ I_1 \\ S_0 \\ S_1 \end{pmatrix}, {{\textbf {b}}}= \begin{pmatrix} N_0 \\ N_1 \\ S \\ I \end{pmatrix}. \end{aligned}$$

(2)

An obvious solution of the system of Eq. (1) is $I_0=(1-\theta )I$, $I_1=\theta I$, $S_0=(1-\theta )S$, $S_1=\theta S$ (the average selection in each unit time proposed by Ref. [33]). However, by calculating the rank $r([{{\textbf {A}}},{{\textbf {b}}}])=r({{\textbf {A}}})=3\ne n$ (the order of matrix ${{\textbf {A}}}$ is $n=4$), we can know that the solution of non-homogeneous linear equations (1) is not unique. Therefore, if mobile and fixed individuals are classified into two fixed sub-populations instead of the average selection per unit time, the evolution results will be different from those in Ref. [33], worthy of further study.

This paper intends to qualitatively investigate the risk of transmission of epidemics in several typical semi-closed communities (including but not limited to nursing homes, prisons, residential universities, etc.). Instead of the SIR model [34, 35] or the SEIR model [36], this paper develops on the classic SIS model, because the SIS system has the simplest irreducible complexity for the questions we would like to study. This paper aims to address the following questions: In the presence of different intensities of infectious sources outside the community, how does the closeness of a community and the propensity of people to enter and leave the community affect the transmission of epidemics? How can we adjust variables such as community closeness, to minimize the risk of transmission of epidemics in such communities?

2 Model

Consider a semi-closed community of N individuals. Among them, some individuals, called mobile individuals, can be within and outside the community freely. As stated in Introduction, we assume them a fixed group, the proportion of whom is $\theta$, and the number of whom is $N_1=\theta N$. Other individuals, called fixed individuals, are restricted to the community, the proportion of whom is $(1-\theta )$, and the number of whom is $N_0=(1-\theta )N$.

An infectious disease spreads through the population. Based on whether an individual is infected with the disease, the population is further divided into infected individuals (I) and susceptible individuals (S). The susceptible individuals are not infected, while the infected individuals are infected and are infectious. In summary, we have the following classification. Among the mobile individuals, there are $I_1$ infected individuals and $S_1$ susceptible individuals, $S_1+I_1=N_1$, and, among the fixed individuals, there are $I_0$ infected individuals and $S_0$ susceptible individuals, $S_0+I_0=N_0$. The infected (or susceptible) individuals among the mobile and fixed individuals must be regarded as independent variables, because $I_1\not \equiv \theta I$, $I_0\not \equiv (1-\theta )I$ (or $S_1\not \equiv \theta S$, $S_0\not \equiv (1-\theta )S$) as a result of groups fixed.

Consider the personal will of mobile individuals. Unlike fixed individuals who can only stay in the community, the mobile individuals can freely stay in and out of the community. The isolation of the internal and external environment of the community (the meaning of a closed community) leads to the following assumption. In a unit time, if a mobile individual chooses to stay in the community, she is isolated from the crowd outside the community. If she goes outside the community, she is isolated from the crowd inside the community. We suppose that mobile individuals stay outside and inside the community with the respective tendency of $\varepsilon$ and $(1-\varepsilon )$. The tendency $\varepsilon$ can be understood as the average proportion of mobile individuals outside the community each time, or the probability of a mobile individual being out of the community.

Suppose additional infected individuals (not included in the community population) in the external environment of the community, measuring the epidemic severity in society. To keep the model concise, the number of these individuals is regarded as a constant, denoted by $I_c$. The size of $I_c$ depends on the epidemic severity in given countries or regions. The mobile individuals outside the community are exposed to these fixed infected individuals. Below, we discuss the exposure of each part of the population.

(i) The susceptible fixed individuals, whose number is $S_0$, can only be inside the community, and contact the following infected individuals. (i-1) The infected fixed individuals, who can only be inside the community, numbered $I_0$. (i-2) The infected mobile individuals, who stay inside the community with a tendency $(1-\varepsilon )$, numbered $I_1$. Therefore, the average size of the infection sources that the susceptible fixed individuals are exposed to is $I_0+(1-\varepsilon ) I_1$.

(ii) The susceptible mobile individuals, whose number is $S_1$, have the following possibility. (ii-1) They are inside the community with a tendency $(1-\varepsilon )$, and contact: (ii-1-1) the infected fixed individuals, who can only be inside the community, numbered $I_0$; (ii-1-2) the infected mobile individuals, who stay inside the community with a tendency $(1-\varepsilon )$, numbered $I_1$. (ii-2) They are outside the community with a tendency $\varepsilon$, and contact: (ii-2-1) the infected mobile individuals, who stay outside the community with a tendency $\varepsilon$, numbered $I_1$; (ii-2-2) the fixed infected individuals in the external environment of the community, numbered $I_c$. Therefore, the average size of the infection sources that the susceptible mobile individuals are exposed to is $(1-\varepsilon )[I_0+(1-\varepsilon ) I_1]+\varepsilon (\varepsilon I_1+I_c)$.

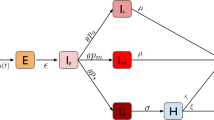
The schematic diagram of population classification and epidemic transmission direction is shown in Fig. 1.

Fig. 1

The schematic diagram of population classification and epidemic transmission direction. The arrows indicate the direction of transmission of the epidemic. $I_0$, $I_1$, $S_0$, $S_1$ are independent variables. $N_0$, $N_1$ are auxiliary variables, calculated by $\theta$, N. $I_0+S_0$ is constrained by $N_0$; $I_1+S_1$ is constrained by $N_1$. I, S are dependent variables, calculated by $I_0$, $I_1$ or $S_0$, $S_1$. $I_c$ is an input parameter

We only study the evolution before any individual is diagnosed (i.e. all the infected individuals are infected, so people are unaware and do not take action); therefore, it is reasonable to assume a well-mixed population. The epidemic spreads at a constant rate of $\alpha$ through human-to-human contact. In order to reflect the aggregation of infection, we use bilinear incidence rate $\alpha SI$ [12, 13]. In addition, we assume the infected individuals spontaneously heal at a rate of $\mu$ (i.e. in a unit time, respectively, $\mu I_0$ and $\mu I_1$ individuals flow from compartment $I_0$ and $I_1$ to compartment $S_0$ and $S_1$).

In summary, the following nonlinear system is proposed.

$$\begin{aligned} \dot{\varvec{\Psi }}= \begin{pmatrix} {\dot{I}}_0 \\ {\dot{I}}_1 \\ {\dot{S}}_0 \\ {\dot{S}}_1 \end{pmatrix}, \end{aligned}$$

(3)

where

$$\begin{aligned} \left\{ \begin{aligned} {\dot{I}}_0=&~\alpha S_0 [I_0+(1-\varepsilon ) I_1 ]-\mu I_0, \\ {\dot{I}}_1=&~\alpha S_1 \{(1-\varepsilon )[I_0+(1-\varepsilon ) I_1 ]+\varepsilon (\varepsilon I_1+I_c )\} \\&-\mu I_1, \\ {\dot{S}}_0=&-{\dot{I}}_0, \\ {\dot{S}}_1=&-{\dot{I}}_1. \end{aligned}\right. \end{aligned}$$

In system (3), we stipulate $\theta ,\varepsilon \in (0,1)$, $\alpha ,\mu ,N\in (0,+\infty )$, $I_c\in [0,+\infty )$. According to the sociological feasible region, we have the variables’ domain $I_0,S_0\in [0,N_0 ]$, $I_1,S_1\in [0,N_1 ]$.

Note that ${\dot{I}}_0=-\mu N_0<0$, when $I_0=N_0$; ${\dot{I}}_1=-\mu N_1<0$, when $I_1=N_1$; ${\dot{I}}_0=\alpha N_0 (1-\varepsilon ) I_1\ge 0$, when $I_0=0$; ${\dot{I}}_1=\alpha N_1 [(1-\varepsilon ) I_0+\varepsilon I_c ]\ge 0$, when $I_1=0$; therefore, if the initial state of variables is in the domain, then they will not leave the domain during the evolution of system (3).

3 Discussion and results

Substituting the constraints $S_1+I_1\equiv N_1$, $S_0+I_0\equiv N_0$ into system (3), we can eliminate $S_1$ and $S_0$. We denote $\varvec{\Phi }=(I_1,I_0)^\mathrm {T}$, satisfying system (4) where $S_1$ and $S_0$ have been eliminated.

$$\begin{aligned} \dot{\varvec{\Phi }}= \left\{ \begin{aligned} {\dot{I}}_0=&-\alpha {I_0}^2+(\alpha N_0-\mu ) I_0-\alpha (1-\varepsilon ) I_0 I_1 \\&+\alpha N_0 (1-\varepsilon ) I_1, \\ {\dot{I}}_1=&-\alpha (2\varepsilon ^2-2\varepsilon +1) {I_1}^2 \\&+[\alpha N_1 (2\varepsilon ^2-2\varepsilon +1)-\alpha \varepsilon I_c-\mu ] I_1\\&-\alpha (1-\varepsilon ) I_0 I_1+\alpha N_1 (1-\varepsilon ) I_0 \\&+\alpha N_1 \varepsilon I_c. \end{aligned}\right. \end{aligned}$$

(4)

Then, the study of the state $\varvec{\Psi }=(I_0,I_1,S_0,S_1)^\mathrm {T}$ of system (3) can be converted into the study of the state $\varvec{\Phi }=(I_0,I_1 )^\mathrm {T}$ of system (4).

We denote system (4) achieving equilibrium at $\varvec{\Phi }^*=(I_1^*,I_0^* )^\mathrm {T}$. Obviously, when system (4) achieves equilibrium, we have $\dot{\varvec{\Phi }}=0$; that is,

$$\begin{aligned} \left\{ \begin{aligned} 0=&-\alpha {I_0^*}^2+(\alpha N_0-\mu ) I_0^*-\alpha (1-\varepsilon ) I_0^* I_1^* \\&+\alpha N_0 (1-\varepsilon ) I_1^*, \\ 0=&-\alpha (2\varepsilon ^2-2\varepsilon +1) {I_1^*}^2 \\&+[\alpha N_1 (2\varepsilon ^2-2\varepsilon +1)-\alpha \varepsilon I_c-\mu ] I_1^*\\&-\alpha (1-\varepsilon ) I_0^* I_1^*+\alpha N_1 (1-\varepsilon ) I_0^* \\&+\alpha N_1 \varepsilon I_c. \end{aligned}\right. \end{aligned}$$

(5)

Directly solving Eq. (5) involves complex quartic equations. However, we can use some mathematical techniques to understand the properties of the analytical solution indirectly. The applicable mathematical techniques vary in different cases ($I_c>0$ and $I_c=0$). We discuss them separately below.

3.1 The case of $I_c>0$

In this case, the epidemic spreads in society (outside the community). For semi-closed communities in these societies, the fixed infected individuals outside the community meet $I_c>0$.

In order to avoid solving complicated quartic equations (after attempts, it is almost impossible to solve it), we use the first equation in Eq. (5) to write $I_1^*$ as a function of $I_0^*$, denoted by $g_1 (I_0^* )$,

$$\begin{aligned} I_1^*=\frac{I_0^*}{1-\varepsilon } \left[ \frac{\mu }{\alpha (N_0-I_0^*)} -1\right] {=}{:}g_1 (I_0^* ), \end{aligned}$$

(6)

and use the second equation in Eq. (5) to write $I_0^*$ as a function of $I_1^*$, denoted by $g_0 (I_1^* )$,

$$\begin{aligned} I_0^*=&~\frac{I_1^*}{1-\varepsilon } \left[ \frac{\mu }{\alpha (N_1-I_1^* )} -(2\varepsilon ^2-2\varepsilon +1)\right] \nonumber \\&-\frac{\varepsilon }{1-\varepsilon } I_c\nonumber \\ {=}{:}&~g_0 (I_1^* ). \end{aligned}$$

(7)

At first glance, as $I_c$ increases, $I_0^*$ in Eq. (7) decreases; then, from Eq. (6), $I_1^*$ further decreases with a decrease in $I_0^*$. This is an illusion, in fact. Figure 2a presents $I_1^*$ as a function $g_1 (I_0^* )$ of $I_0^*$ and $I_0^*$ as a function $g_0 (I_1^* )$ of $I_1^*$, where the parameters take $\alpha =0.1$, $\mu =0.05$, $N=1$, $\theta =0.5$, $\varepsilon =0.5$. The equilibrium of system (4) satisfies both equations in Eq. (5); that is, the equilibrium point is the intersection point of the function curves of $g_1 (I_0^* )$ and $g_0 (I_1^* )$. We denote such an intersection point by $\varvec{\Phi }^{*(1)}=(I_1^{*(1)},I_0^{*(1)})^\mathrm {T}$, labelling it as the endemic equilibrium. The function curves when $I_c=0.1$ and $I_c=0.9$ are plotted, respectively, in Fig. 2a; $g_1 (I_0^* )$ is independent of $I_c$, hence the curve of $g_1 (I_0^* )$ keeping the same with different $I_c$. It is seen that, when $I_c=0.9$, $I_0^*=g_0 (I_1^* )$ is indeed smaller than when $I_c=0.1$. However, the intersection coordinates $I_1^{*(1)}$ and $I_0^{*(1)}$ of the curves $g_1 (I_0^* )$ and $g_0 (I_1^* )$ both increases in effect. In other words, an increase in $I_c$ (epidemic severity in society) aggravates the epidemic in the community population, which is in line with common sense. Meanwhile, it is robust—it is easy to verify $\partial g_1 (I_0^* )/\partial I_0^*>0$, $\partial ^2 g_1 (I_0^* )/\partial {I_0^*}^2 >0$, and $\partial g_0 (I_1^* )/\partial I_1^*>0$, $\partial ^2 g_0 (I_1^* )/\partial {I_1^*}^2 >0$; therefore, a decrease in $I_1^*$ or $I_0^*$ always leads to the increase in the intersection coordinates $I_1^{*(1)}$ and $I_0^{*(1)}$. In addition, from the above four inequalities and the concavity and convexity of the function, it is known that curves $g_1 (I_0^* )$ and $g_0 (I_1^* )$ have at most two intersections. Considering $g_1 (I_0^* )=0$ in Eq. (6) when $I_0^*=0$, and $g_0 (I_1^* )<0$ in Eq. (7) when $I_1^*=0$, we can know that the other possible intersection is not within the sociological feasible region, and $(I_1^{*(1)},I_0^{*(1)})^\mathrm {T}$ is the unique intersection of curves $g_1 (I_0^* )$ and $g_0 (I_1^* )$. Therefore, $\varvec{\Phi }^{*(1)}$ is the unique equilibrium of system (4) when $I_c>0$. Considering that system (4) is continuous, $\varvec{\Phi }^{*(1)}$ is stable.

Fig. 2

When $\alpha =0.1$, $\mu =0.05$, $N=1$, $\theta =0.5$, $\varepsilon =0.5$, a the analytic curves of functions $I_1^*=g_1 (I_0^* )$ and $I_0^*=g_0 (I_1^* )$ with $I_c=0.1$ and $I_c=0.9$; b1 time evolution of indexes $pI_0 (t)$, $pI_1 (t)$ and pI(t) when $I_c=0.1$; b2 time evolution of indexes $pI_0 (t)$, $pI_1 (t)$ and pI(t) when $I_c=0.9$. The intersection coordinate of $g_1 (I_0^* )$ and $g_0 (I_1^* )$ is the equilibrium point. The theoretical prediction is consistent with numerical simulations under different $I_c$

In numerical simulation, we set the following three indexes to measure the epidemic severity in the community population: $pI_0=I_0/N_0$, the infected proportion in fixed individuals; $pI_1=I_1/N_1$, the infected proportion in mobile individuals; $pI=I/N=(I_1+I_0)/(N_1+N_0)$, the infected proportion in community population. The numerical method follows the forward-Euler difference method in Ref. [33], with time-step $10^{-2}$, letting system (4) evolves from $t=10^{-2}$ to $t=10^4$.

Figure 2b1 and b2, respectively, demonstrates the time evolution of indexes $pI_0 (t)$, $pI_1 (t)$ and pI(t) when $I_c=0.1$ and $I_c=0.9$, with other parameters unchanged from Fig. 2a. It is seen that, at the approximate equilibrium at $t=10^4$, $pI_0 (t)$ and $pI_1 (t)$ achieves the intersection coordinates of $g_1 (I_0^* )$ and $g_0 (I_1^* )$ presented in Fig. 2a: $\varvec{\Phi }^{*(1)}=(0.2852,0.3130)^\mathrm {T}$ when $I_c=0.1$, and $\varvec{\Phi }^{*(1)}=(0.5830,0.4134)^\mathrm {T}$ when $I_c=0.9$. The theoretical results in Fig. 2a and numerical results in Fig. 2b1, b2 are verified by each other.

Figures 3, 4, and 5 take the numerical equilibrium state at $t=10^4$, and study the index $pI_0^{*(1)}$, $pI_1^{*(1)}$ and $pI^{*(1)}$ as functions of the proportion of mobile individuals and their personal will (i.e. parameter $\theta$ and $\varepsilon$) under different $I_c$, where $\theta$ and $\varepsilon$ vary from 0.01 to 0.99 with step 0.01. For each index, we denote two functions: (i) $\theta ^* (\varepsilon )$, the value of $\theta$ that minimizes the index (of the epidemic severity) for a given $\varepsilon$; (ii) $\varepsilon ^* (\theta )$, the value of $\varepsilon$ that minimizes the index for a given $\theta$. The numerical methods of solving $\theta ^* (\varepsilon )$ is to go through $\varepsilon =0.01,0.02,\dots ,0.99$ in the numerical results; for each $\varepsilon$, go through $\theta =0.01,0.02,\dots ,0.99$ and mark the $\theta$ that minimizes the index. The same method applies to the numerical solution of $\varepsilon ^* (\theta )$. Figures 3, 4, and 5, respectively, demonstrate the situations when $I_c=1.2$, $I_c=0.5$ and $I_c=0.1$, with parameters $\alpha =0.1$, $\mu =0.05$, $N=1$ unchanged. The subfigures (a), (b1), (b2), respectively, show the index $pI_0^{*(1)}$, $pI_1^{*(1)}$ and $pI^{*(1)}$.

Fig. 3

When $I_c=1.2$, $\alpha =0.1$, $\mu =0.05$, $N=1$, the heat maps depicting different indexes as binary functions of $\theta$ and $\varepsilon$. The numerical solution of $\theta ^* (\varepsilon )$ and $\varepsilon ^* (\theta )$ are directly marked in the heat maps. a $pI^{*(1)}$. b1 $pI_0^{*(1)}$. b2 $pI_1^{*(1)}$. In this case, the epidemic in society is relatively severe

In Fig. 3, $I_c=1.2$, which means the epidemic in society is relatively severe. As seen in Fig. 3a, for the community population, when the mobile individuals’ tendency of being out of the community $\varepsilon \le 0.30$, we have $\theta ^* (\varepsilon )=0.01$, and the proportion of mobile individuals should be as small as possible; when $\varepsilon \ge 0.31$, $\theta ^* (\varepsilon )$ increases with $\varepsilon$. The more mobile individuals tend to go out of the community, the larger their proportion should be to best control the epidemic in the community population. When the mobile individuals’ proportion $\theta \le 0.63$, we have $\varepsilon ^* (\theta )=0.99$, and they should stay out of the community as much as possible; when $\theta \ge 0.64$, we have $\varepsilon ^* (\theta )=0.01$, and they should stay in the community as much as possible. As seen in Fig. 3b1, for fixed individuals, we have $\theta ^* (\varepsilon )=0.99$, $\varepsilon ^* (\theta )=0.99$. To reduce the infected proportion in fixed individuals, there should be as many mobile individuals as possible, and mobile individuals should tend to go out of the community as much as possible. As seen in Fig. 3b2, for mobile individuals, we have $\theta ^* (\varepsilon )=0.99$ when $\varepsilon \le 0.20$, and $\theta ^* (\varepsilon )$ increases from 0.01 to 0.99 with $\varepsilon$ when $0.21\le \varepsilon \le 0.54$, and $\theta ^* (\varepsilon )=0.01$ when $\varepsilon \ge 0.55$. The more mobile individuals tend to go out of the community, the more their proportion should be reduced. In addition, $\varepsilon ^* (\theta )=0.01$, which means that mobile individuals should stay in the community as much as possible to best control the epidemic transmission in mobile individuals.

Fig. 4

When $I_c=0.5$, $\alpha =0.1$, $\mu =0.05$, $N=1$, the heat maps depicting different indexes as binary functions of $\theta$ and $\varepsilon$. The numerical solution of $\theta ^* (\varepsilon )$ and $\varepsilon ^* (\theta )$ are directly marked in the heat maps. a $pI^{*(1)}$. b1 $pI_0^{*(1)}$. b2 $pI_1^{*(1)}$. In this case, the epidemic in society is mild

In Fig. 4, $I_c=0.5$, and the epidemic severity in society is milder than in Fig. 3. For the community population (Fig. 4a), the mobile individuals’ optimum proportion $\theta ^* (\varepsilon )$ initially decreases and ultimately increases as $\varepsilon$ increases, and their optimum tendency towards being out of the community $\varepsilon ^* (\theta )$ decreases with an increase in $\theta$. For fixed individuals (Fig. 4b1), we have $\theta ^* (\varepsilon )=0.99$, $\varepsilon ^* (\theta )=0.99$. For mobile individuals (Fig. 4b2), the mobile individuals’ optimum proportion $\theta ^* (\varepsilon )$ decreases with an increase in $\varepsilon$, and their optimum tendency towards being out of the community $\varepsilon ^* (\theta )$ decreases with an increase in $\theta$.

Fig. 5

When $I_c=0.1$, $\alpha =0.1$, $\mu =0.05$, $N=1$, the heat maps depicting different indexes as binary functions of $\theta$ and $\varepsilon$. The numerical solution of $\theta ^* (\varepsilon )$ and $\varepsilon ^* (\theta )$ are directly marked in the heat maps. a $pI^{*(1)}$. b1 $pI_0^{*(1)}$. b2 $pI_1^{*(1)}$. In this case, the epidemic in society is not severe

In Fig. 5, $I_c=0.1$, which means the epidemic in society is not severe. To benefit the community population (Fig. 5a), the mobile individuals’ proportion $\theta ^* (\varepsilon )$ should decrease with an increase in $\varepsilon$, and their tendency towards going out of the community $\varepsilon ^* (\theta )$ should decrease with an increase in $\theta$. To benefit fixed individuals (Fig. 5b1), the mobile individuals’ proportion and their tendency towards being outside the community should be as large as possible. To benefit mobile individuals (Fig. 5b2), the mobile individuals’ proportion $\theta ^* (\varepsilon )$ should decrease with an increase in $\varepsilon$, and their tendency towards going out of the community $\varepsilon ^* (\theta )$ should decrease with an increase in $\theta$.

In a word, a simple model like system (3) creates complex results. Under different epidemic severity in society, the epidemic transmission in the community is different, which leads to different strategies for epidemic prevention and control. An open community is defined to have a large proportion of mobile individuals, whose tendency towards going outside the community is significant; that is, $\theta \rightarrow 1^-$, $\varepsilon \rightarrow 1^-$. On the contrary, a closed community is defined to have a tiny proportion of mobile individuals, whose tendency towards being outside the community is slight; that is, $\theta \rightarrow 0^+$, $\varepsilon \rightarrow 0^+$. In this model, a semi-closed community is between a completely open community and a completely closed community. According to the size of $\theta$ and $\varepsilon$, we can describe a semi-closed community as relatively open or relatively closed. It is known from Figs. 3a, 4a, and 5a that, with the same epidemic severity in society, a more open community always leads to a more severe epidemic in the community. Nevertheless, with a relatively mild epidemic in society, we find that a more closed community also leads to a severe epidemic (Fig. 5a). This is because, when the community is more closed, the contact density of the individuals increases; that is, what we call “clustered infection”. When the community is more open, more mobile individuals go out of the community, which produces the effect of isolation between mobile and fixed individuals, reducing the contact density of the crowd; however, this inevitably increases the contact between the community population and the fixed infected individuals in society, such that the impact of the epidemic severity in society becomes more significant. With a more severe epidemic in society, the epidemic severity in society plays the key role, and, when the epidemic in society is less severe, the clustered infection within the community becomes the leading role.

An explanation for clustered infection in typical semi-closed communities in daily life such as nursing homes and prisons is provided by Figs. 3b1, 4b1, and 5b1. The numerical results reveal that, for fixed individuals (the elderly and prisoners), a more closed community ($\theta \rightarrow 0^+$, $\varepsilon \rightarrow 0^+$) always leads to a more severe epidemic. On the contrary, with a more open community ($\theta \rightarrow 1^-$, $\varepsilon \rightarrow 1^-$), the epidemic is less severe. This result is robust under different values of $I_c$; therefore, for fixed individuals in these communities, the clustered infection rather than the epidemic severity in society plays the leading role. In other words, a closed community always leads to a more severe epidemic in fixed individuals than a completely open community does.

3.2 The case of $I_c=0$

In the second case, the epidemic does not spread in society. For the semi-closed communities in such society, the fixed infected individuals outside the community meet $I_c\rightarrow 0^+$. Ignoring the sporadic cases and making idealized assumptions, let us say, $I_c=0$.

In this case, Eqs. (6) and (7), respectively, satisfy $g_1 (0)=0$, $g_0 (0)=0$; therefore, $I_1^*=I_0^*=0$ is an intersection of curves $g_1 (I_0^* )$ and $g_0 (I_1^* )$ (i.e. a solution of Eq. (5). Figure 6a presents the analytical curves of functions $I_1^*=g_1 (I_0^* )$ and $I_0^*=g_0 (I_1^* )$ when $I_c=0$, $\mu =0.05$, $N=1$, $\theta =0.5$, $\varepsilon =0.5$, $\alpha =0.1$. As seen in Fig. 6a, such an intersection is different from endemic equilibrium $\varvec{\Phi }^{*(1)}$; therefore, we label such an intersection as “epidemic-free equilibrium”, denoted by

$$\begin{aligned} \varvec{\Phi }^{*(0)}=(I_1^{*(0)},I_0^{*(0)})^\mathrm {T}=(0,0)^\mathrm {T} \end{aligned}$$

(8)

or

$$\begin{aligned} \varvec{\Psi }^{*(0)}&=(I_0^{*(0)},I_1^{*(0)},S_0^{*(0)},S_1^{*(0)})^\mathrm {T}\nonumber \\&=(0,0,N_0,N_1)^\mathrm {T}. \end{aligned}$$

(9)

As discussed in Sect. 3.1, the concavity and convexity of the functions $g_1 (I_0^* )$ and $g_0 (I_1^* )$ make them have at most two intersections. Now, given $I_c=0$, the two intersections both exist and are nonnegative; that is, system (4) has two equilibrium points.

To analyse the stability of the two equilibrium points (i.e. which equilibrium does the system achieve), we use the mathematical techniques proposed by van den Driessche and Watmough [37] to solve the basic reproduction number of the epidemic and then judge the system’s stability. Using this method, investigating system (3) is more convenient. We separate system (3) into $\dot{\varvec{\Psi }}={\mathcal {F}}-{\mathcal {V}}$, where

$$\begin{aligned} {\mathcal {F}}= & {} \begin{pmatrix} {\mathcal {F}}_{I_0} \\ {\mathcal {F}}_{I_1} \\ {\mathcal {F}}_{S_0} \\ {\mathcal {F}}_{S_1} \end{pmatrix}\nonumber \\= & {} \begin{pmatrix} \alpha S_0 [I_0+(1-\varepsilon ) I_1 ] \\ \alpha S_1 [(1-\varepsilon ) I_0+(2\varepsilon ^2-2\varepsilon +1) I_1 ] \\ -{\mathcal {F}}_{I_0} \\ -{\mathcal {F}}_{I_1} \end{pmatrix}, \end{aligned}$$

(10)

$$\begin{aligned} {\mathcal {V}}= & {} \begin{pmatrix} {\mathcal {V}}_{I_0} \\ {\mathcal {V}}_{I_1} \\ {\mathcal {V}}_{S_0} \\ {\mathcal {V}}_{S_1} \end{pmatrix} = \begin{pmatrix} \mu I_0 \\ \mu I_1 \\ -{\mathcal {V}}_{I_0} \\ -{\mathcal {V}}_{I_1} \end{pmatrix}. \end{aligned}$$

(11)

Let alone the uninfected compartments, and calculate the Jacobian matrix of the remaining compartments at the epidemic-free equilibrium $\varvec{\Psi }^{*(0)}$:

$$\begin{aligned} {\mathbf {F}}= & {} \begin{pmatrix} \displaystyle \frac{\partial {\mathcal {F}}_{I_0}}{\partial I_0} &{} \displaystyle \frac{\partial {\mathcal {F}}_{I_0}}{\partial I_1} \\ \displaystyle \frac{\partial {\mathcal {F}}_{I_1}}{\partial I_0} &{} \displaystyle \frac{\partial {\mathcal {F}}_{I_1}}{\partial I_1} \end{pmatrix} (\varvec{\Psi }^{*(0)})\nonumber \\= & {} \alpha \begin{pmatrix} \displaystyle N_0 &{} (1-\varepsilon )N_0 \\ (1-\varepsilon )N_1 &{} (2\varepsilon ^2-2\varepsilon +1)N_1 \end{pmatrix}, \end{aligned}$$

(12)

$$\begin{aligned} {\mathbf {V}}= & {} \begin{pmatrix} \displaystyle \frac{\partial {\mathcal {V}}_{I_0}}{\partial I_0} &{} \displaystyle \frac{\partial {\mathcal {V}}_{I_0}}{\partial I_1} \\ \displaystyle \frac{\partial {\mathcal {V}}_{I_1}}{\partial I_0} &{} \displaystyle \frac{\partial {\mathcal {V}}_{I_1}}{\partial I_1} \end{pmatrix} (\varvec{\Psi }^{*(0)})=\mu \begin{pmatrix} 1 &{} 0 \\ 0 &{} 1 \end{pmatrix}. \end{aligned}$$

(13)

Then, calculate the following spectral radius of ${\mathbf {F}}\cdot {\mathbf {V}}^{-1}$.

$$\begin{aligned} {\mathcal {R}}_0 =&~\frac{\alpha }{2\mu }\left[ N_0+(2\varepsilon ^2-2\varepsilon +1) N_1\right. \nonumber \\&\left. +\sqrt{[N_0+(2\varepsilon ^2-2\varepsilon +1) N_1 ]^2-4\varepsilon ^2 N_0 N_1}\right] \nonumber \\ =&~\frac{\alpha N}{2\mu }\left[ 1-2(1-\varepsilon ) (\theta \varepsilon )\right. \nonumber \\&\left. +\sqrt{4(\varepsilon ^2-2\varepsilon +2) (\theta \varepsilon )^2-4(\theta \varepsilon )+1}\right] . \end{aligned}$$

(14)

${\mathcal {R}}_0$ is called the basic reproduction number. Therefore, in terms of $I_c=0$, we are able to judge the stability of system (3) or (4) with the help of Ref. [37] - the epidemic-free equilibrium $\varvec{\Psi }^{*(0)}$ ($\varvec{\Phi }^{*(0)}$) is locally asymptotically stable, if ${\mathcal {R}}_0<1$; and, the epidemic-free equilibrium $\varvec{\Psi }^{*(0)}$ ($\varvec{\Phi }^{*(0)}$) is not stable, if ${\mathcal {R}}_0>1$. In the latter case, considering that the system is continuous, $\varvec{\Psi }^{*(1)}$ ($\varvec{\Phi }^{*(1)}$) is stable.

Figure 6b1 demonstrates the time evolution of indexes $pI_0 (t)$, $pI_1 (t)$ and pI(t) when $\mu =0.05$, $N=1$, $\theta =0.5$, $\varepsilon =0.5$, $\alpha =0.1$. According to Eq. (14), we have ${\mathcal {R}}_0=1.3090>1$; therefore, $\varvec{\Phi }^{*(0)}$ is not stable. It is seen from Fig. 6b1 that system (4) is stable at $\varvec{\Phi }^{*(1)}$, consistent with our analytical judgement. Secondly, Fig. 6b2 demonstrates the time evolution of indexes $pI_0 (t)$, $pI_1 (t)$ and pI(t) when $\mu =0.05$, $N=1$, $\theta =0.5$, $\varepsilon =0.5$, $\alpha =0.05$. According to Eq. (14), we have ${\mathcal {R}}_0=0.6545<1$; therefore, $\varvec{\Phi }^{*(0)}$ is locally asymptotically stable. It is seen from Fig. 6b2 that system (4) is stable at $\varvec{\Phi }^{*(0)}$, consistent with our theoretical prediction as well.

Fig. 6

When $I_c=0$, $\mu =0.05$, $N=1$, $\theta =0.5$, $\varepsilon =0.5$, a the analytic curves of functions $I_1^*=g_1 (I_0^* )$ and $I_0^*=g_0 (I_1^* )$ with $\alpha =0.1$; b1 time evolution of indexes $pI_0 (t)$, $pI_1 (t)$ and pI(t) when $\alpha =0.1$ (${\mathcal {R}}_0=1.3090>1$); b2 time evolution of indexes $pI_0 (t)$, $pI_1 (t)$ and pI(t) when $\alpha =0.05$ (${\mathcal {R}}_0=0.6545<1$). The intersection coordinates of $g_1 (I_0^* )$ and $g_0 (I_1^* )$ are the equilibrium points. The theoretical prediction is consistent with numerical simulations under different ${\mathcal {R}}_0$

Similar to Figs. 3, 4, and 5, the stable indexes as functions of $\theta$ and $\varepsilon$ when $I_c=0$ and $\alpha =0.1$, $\mu =0.05$, $N=1$ are presented in Fig. 7. As shown in the numerical heat maps, to benefit the total community population (Fig. 7a), fixed individuals (Fig. 7b1), or mobile individuals (Fig. 7b2), the strategies for controlling the proportion of infected individuals are similar. When $\varepsilon$ is smaller than half, we have $\theta ^* (\varepsilon )=0.99$, and when $\varepsilon$ is greater than half, $\theta ^* (\varepsilon )$ decreases to half as $\varepsilon$ increases. When $\theta$ is smaller than half, we have $\varepsilon ^* (\theta )=0.99$, and when $\theta$ is greater than half, $\varepsilon ^* (\theta )$ decreases to half as $\theta$ increases. It is noticed that in the region of $\theta >1/2$ and $\varepsilon >1/2$, the numerical solutions of $\theta ^* (\varepsilon )$ and $\varepsilon ^* (\theta )$ are coincident. We find such a phenomenon can be derived from Eq. (14), the expression of the basic reproduction number ${\mathcal {R}}_0$.

Fig. 7

When $I_c=0$, $\alpha =0.1$, $\mu =0.05$, $N=1$, the heat maps depicting different indexes as binary functions of $\theta$ and $\varepsilon$. The numerical solution of $\theta ^* (\varepsilon )$ and $\varepsilon ^* (\theta )$ are directly marked in the heat maps. a $pI^{*(1)}$ or $pI^{*(0)}$. b1 $pI_0^{*(1)}$ or $pI_0^{*(0)}$. b2 $pI_1^{*(1)}$ or $pI_1^{*(0)}$. In this case, there is no epidemic in society

According to the reduction result in the second line of Eq. (14), we assume that $(\theta \varepsilon )$ is a whole as an independent variable, and the remaining $\varepsilon$ in the equation and other parameters are regarded as constants. Performing elementary mathematical knowledge (prompt: solving the equation with the first derivative of $(\theta \varepsilon )$ equal to zero), the minimum point of ${\mathcal {R}}_0$ can be found. In the solution of the equation, the remaining $\varepsilon$ in the equation are fortunately eliminated. Two extreme points are found: (i) ${\mathcal {R}}_0=\alpha N/(2\mu )$, when $(\theta \varepsilon )=1/2$; (ii) ${\mathcal {R}}_0\rightarrow \alpha N/\mu$, when $(\theta \varepsilon )\rightarrow 0^+$. Through comparison, it is obvious that ${\mathcal {R}}_0$ achieves the minimum value $\alpha N/(2\mu )$ when $(\theta \varepsilon )=1/2$. Since the basic reproduction number ${\mathcal {R}}_0$ is a measure of the reproductive capacity of the epidemic, the minimum ${\mathcal {R}}_0$ leads to the infection in the community population being the mildest. Therefore, we can declare that the analytic solution of $\theta ^* (\varepsilon )$ and $\varepsilon ^* (\theta )$ in Fig. 7a is $\theta ^* \varepsilon ^*=1/2$; that is, a hyperbola curve with inverse proportional coefficient 1/2.

As seen in Fig. 7, when there is no epidemic in society, the clustered infection plays a leading role in epidemic outbreaks in the community. Gathering all individuals outside the community ($\theta \rightarrow 1^-$, $\varepsilon \rightarrow 1^-$) and gathering all individuals inside the community ($\theta \rightarrow 0^+$, $\varepsilon \rightarrow 0^+$) produce the same consequences. As Ref. [33] has studied before, when $I_c=0$, we have a scenario of semi-closed community: residential universities with closed management. With regard to such a scenario, the mobile individuals include the faculty and staff, the children of the faculty and staff, the resident express personnel, and construction personnel, while the fixed individuals include merely the students. The original intention of the closed management includes preventing and controlling epidemics; meanwhile, for universities, the number of fixed individuals is far greater than that of mobile individuals (i.e. $\theta \rightarrow 0^+$). Therefore, our model predicts that such closed management will put the population in the university at risk (Fig. 7a). Of course, in the absence of patient zero, the risk does not appear—As we analysed before, when $I_c=0$, the epidemic-free equilibrium $\varvec{\Psi }^{*(0)}$ always exists; however, it is not always stable. Once exposed to a patient zero, the universities implementing such closed management will suffer severe epidemics. Below, we discuss the optimal management policy. As a rough estimate, a person’s rest and bedtime take up about half of the day. In general, a student not only goes to bed in the dormitory at night, but also needs to have classes on campus when they are wake up; therefore, we have an estimation $\varepsilon <1/2$. According to Fig. 7, there is always $\theta ^* (\varepsilon )\rightarrow 1^-$ when $\varepsilon <1/2$. Therefore, the model suggests that the universities should make all students mobile individuals (allowed free access to being inside and outside the campus) to reduce the risk of clustered infection, thus achieving the effect of epidemic prevention and control.

4 Conclusion

The frequent epidemic outbreaks in semi-closed communities such as nursing homes and prisons are of great concern to the public. In this work, we developed a general SIS model in semi-closed community, where an epidemic repeatedly transmits. The system’s evolution is studied before any individual is diagnosed. In one dimension, the population is divided into susceptible (S) and infected (I). In the other dimension, the population is classified into mobile ($S_1$, $I_1$) and fixed individuals ($S_0$, $I_0$). Based on human-to-human contact propagation, a nonlinear system (3) was proposed. We, respectively, studied theoretical properties and numerical results of system (3) against the background of the epidemic spreading or not in society.

First, we studied the case where the epidemic spreads in society ($I_c>0$). In this case, the endemic equilibrium is the unique solution of system (3). We attribute the infection to two reasons: (i) a number of individuals gather in the community, resulting in increased contact between them (i.e. clustered infection); (ii) the epidemic in society (fixed infected individuals outside the community) spreads to the community population. Reasons (i) and (ii) cannot be logically dealt with simultaneously. With the community’s openness varying, they shift and produce complex numerical results. The results show that, with a severe epidemic in society, the epidemic in society spreading to the community population plays a leading role. We should adjust the proportion of mobile individuals and their tendency, and reduce the community’s openness. Secondly, when the epidemic in society is mild, the clustered infection within the community plays a key role for infection. We should adjust the proportion of mobile individuals and their tendency, and increase the openness of the community. In addition, we notice that, having nothing to do with the epidemic severity in society, the clustered infection within the community always plays the key role for fixed individuals. The more closed the community is, the more severe the infection is among fixed individuals, which provides a new qualitative explanation for frequent pandemics in communities such as nursing homes and prisons: compared with a completely open community, a semi-closed community is always more closed, thus causing more infections in fixed individuals (the elderly and prisoners).

Secondly, we studied the case where the epidemic does not spread in society ($I_c=0$). In this case, system (3) has both epidemic-free equilibrium and endemic equilibrium. We solve the basic reproduction number ${\mathcal {R}}_0$ of the epidemic, and judge that the system is stable at epidemic-free equilibrium when ${\mathcal {R}}_0<1$, and is stable at endemic equilibrium when ${\mathcal {R}}_0>1$ [37]. Without the threat of epidemics outside the community, the clustered infection among the community population plays the leading role of infection. The results show that gathering all individuals inside the community produces the same consequences as gathering all individuals outside the community. To prevent and control the epidemic, individuals should be evenly distributed inside and outside the community, thus forming isolation and reducing aggregation. More specifically, the optimal proportion of mobile individuals $\theta ^*$ and their tendency towards being outside the community $\varepsilon ^*$ lie on a hyperbola with 1/2 as the inverse proportion coefficient. A counterexample is residential universities implementing closed management. The closed management is effectively semi-closed, among which only students are fixed individuals, and other people are mobile individuals. We estimated the parameter range on a qualitative level. The results under the parameters show that the closed management results in excessive aggregation of the crowd, leading to severe epidemic outbreaks once there is a patient zero. The results also indicate that to prevent and control the epidemic, we should allow all students free access to being on or off campus, forming isolation.

In this paper, we were unable to find a simple mathematical tool like the basic reproduction number ${\mathcal {R}}_0$ to analyse the optimal control strategy at an analytic level when $I_c>0$. Also, the global stability of the two equilibria can be further studied strictly. In some real situations, the fixed individuals can manage to go out of the community. Future research can further consider the description of fixed individuals being outside the community in some ways.