Composite feedback control of linear singularly perturbed systems: a bond graph approach

Abstract

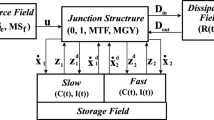
A procedure to obtain a composite control of linear systems with singular perturbations modelled by bond graphs is presented. The state feedback gains of the composite control based on the slow and fast bond graph models are separately designed. The composite control system is formed by: (1) The original Bond Graph in an Integral causality assignment (BGI) with a state feedback of the fast and slow dynamics. (2) An additional bond graph denoted by Singular Perturbed Bond Graph (SPBG) with a state feedback whose storage elements have integral and derivative causality for the slow and fast dynamics, respectively. The advantages of this approach are: (1) From the BGI, the reduced fast models for open and closed loop systems in a direct way are obtained. (2) From the SPBG, the reduced slow models are determined where the change of the causality of the storage elements for the fast dynamics produces inverse matrices required in the traditional approach. (3) The mathematical models are not required. A junction structure of the bond graph with a composite control to determine the mathematical model of the closed loop system is proposed. Finally, the modelling and control of two illustrative examples applying the proposed methodology are described.

Appendices

Fast models procedures

The bond graph model of a fast reduced model can be obtained by using one of the next two procedures proposed by [23] for the case when a bond graph model has C or I elements of different order of magnitude and R elements of the same order of magnitude (Procedure 1) and when a bond graph model has R elements of different order of magnitude and C or I elements of the same order of magnitude (Procedure 2).

Procedure 1

The fast reduced bond graph is deduced from the global one by suppressing:

• All the C or I elements with large modulus. The state variables of the slow dynamics.

• All the R elements causally connected with these C or I elements directly or indirectly through other R elements.

• All the input sources having no causal connection with the remaining C, I and R elements.

Procedure 2

The fast reduced bond graph is deduced from the global one by suppressing:

• All the C or I elements causally connected with large valued R elements or large valued R elements in the case of an algebraic loop.

• All the R elements without causal connection with the remaining C, I or R directly or indirectly through other R elements.

• All the input sources having no causal connection with the remaining C or I directly or indirectly through other R elements.

Proof of Lemma

From the fourth and fifth lines of (61) with (16) to (19) and their derivatives with respect to time

$$\begin{aligned} \overset{\bullet }{x}_{1}^{d}\left( t\right)= & {} \left( F_{1}^{d}\right) ^{-1}R_{31}^{11}F_{1}\overset{\bullet }{x}_{1}\left( t\right) \end{aligned}$$

(119)

$$\begin{aligned} \overset{\bullet }{x}_{2}^{d}\left( t\right)= & {} \left( F_{2}^{d}\right) ^{-1}R_{31}^{22}F_{2}\overset{\bullet }{x}_{2}\left( t\right) \end{aligned}$$

(120)

from ninth and tenth lines of (61) with (16) to (19) and different respect to the time

$$\begin{aligned} \overset{\bullet }{x}_{1s}^{d}\left( t\right)= & {} \left( F_{1}^{d}\right) ^{-1}R_{64}^{11}F_{1}\overset{\bullet }{x}_{1s}^{c}\left( t\right) \end{aligned}$$

(121)

$$\begin{aligned} \overset{\bullet }{x}_{2s}^{d}\left( t\right)= & {} \left( F_{2}^{d}\right) ^{-1}R_{64}^{22}F_{2}\overset{\bullet }{x}_{2s}^{c}\left( t\right) \end{aligned}$$

(122)

from the eighth line of (61) with (20)

$$\begin{aligned} D_{in}^{s}=\left( I-R_{55}L_{s}\right) ^{-1}\left( R_{54}^{11}z_{1s}^{c}+R_{54}^{12}\overset{\bullet }{x}_{1s}^{c}\right) \end{aligned}$$

(123)

from the third line of (61) with (20)

$$\begin{aligned} D_{in}= & {} \left( I-R_{22}L\right) ^{-1}\left[ R_{11}^{21}z_{1}+R_{21}^{12}z_{2}+R_{24}^{11}z_{1s}^{c}\right. \nonumber \\&\left. +\,R_{25}L_{s}D_{in}^{s}+R_{24}^{12} \overset{\bullet }{x}_{2s}^{c}+R_{27}v\right] \end{aligned}$$

(124)

and substituting (123) into (124)

$$\begin{aligned} D_{in}^{s}= & {} \left( I-R_{22}L\right) ^{-1}\left[ R_{11}^{21}z_{1}+R_{21}^{12}z_{2}+R_{24}^{11}z_{1s}^{c}+R_{24}^{12}\overset{ \bullet }{x}_{2s}^{c}\right. \nonumber \\&\left. R_{25}Q_{s}\left( R_{54}^{11}z_{1s}^{c}+R_{54}^{12}\overset{\bullet }{x}_{1s}^{c}\right) +R_{27}v\right] \end{aligned}$$

(125)

where $Q_{s}=L_{s}\left( I-R_{55}L_{s}\right) ^{-1}$.

From the first line of (61) with (119)

$$\begin{aligned} E_{1}^{c}\overset{\bullet }{x} _{1}= & {} R_{11}^{11}z_{1}+R_{11}^{12}z_{2}+R_{12}^{11}D_{out}+R_{14}^{11}z_{1s}^{c}+R_{14}^{12} \overset{\bullet }{x}_{2s}^{c}\nonumber \\&+\,R_{15}^{11}D_{out}^{s}+R_{17}^{12}v \end{aligned}$$

(126)

where $E_{1}^{c}=I-R_{13}^{11}\left( F_{1}^{d}\right) ^{-1}R_{31}^{11}F_{1}$.

Substituting (125) and (124) into (126) with (20)

Fig. 29

Bond graphs with a class 1 and b class 2 zero-order causal paths

Fig. 30

Bond graphs with a class 3, b class 4 and c class 5 zero-order causal paths

$$\begin{aligned} E_{1}^{c}\overset{\bullet }{x}_{1}= & {} \left( R_{11}^{11}+R_{12}^{11}M_{c}R_{21}^{11}\right) z_{1}+\left( R_{11}^{12}+R_{12}^{11}M_{c}R_{21}^{12}\right) z_{2} \nonumber \\&+\,\left( R_{14}^{11}+R_{12}^{11}M_{c}R_{24}^{11}+R_{12}^{11}M_{c}R_{25}Q_{s}R_{54}^{11}+R_{15}^{11}M_{s}R_{54}^{11}\right) z_{1s}^{c} \nonumber \\&+\,\left( R_{14}^{12}+R_{12}^{11}M_{c}R_{24}^{12}+R_{12}^{11}M_{c}R_{25}Q_{s}R_{54}^{12}+R_{15}^{11}M_{s}R_{54}^{12}\right) \overset{\bullet }{x}_{2s}^{c} \nonumber \\&+\,\left( R_{17}^{12}+R_{12}^{11}M_{c}R_{27}\right) v \end{aligned}$$

(127)

where $M_{c}=L\left( I-R_{22}L\right) ^{-1}$. From (127) with (64), (65), (66) and (70), the state equation for the slow dynamics (62) is proved.

From the second line of (61) with (120)

$$\begin{aligned} E_{2}^{c}\overset{\bullet }{x} _{2}= & {} R_{11}^{21}z_{1}+R_{11}^{22}z_{2}+R_{12}^{21}D_{out}+R_{14}^{21}z_{1s}^{c}+R_{14}^{22} \overset{\bullet }{x}_{2s}^{c}\nonumber \\&+\,R_{15}^{21}D_{out}^{s}+R_{17}^{22}v \end{aligned}$$

(128)

substituting (125) and (124) into (128) with (20)

$$\begin{aligned} E_{2}^{c}\overset{\bullet }{x}_{2}= & {} \left( R_{11}^{21}+R_{12}^{21}M_{c}R_{21}^{11}\right) z_{1}+\left( R_{11}^{22}+R_{12}^{21}M_{c}R_{21}^{12}\right) z_{2} \nonumber \\&+\,\left[ R_{14}^{21}+R_{12}^{21}M_{c}\left( R_{24}^{11}+R_{25}Q_{s}R_{54}^{11}\right) +R_{15}^{21}Q_{s}R_{54}^{12}\right] z_{1s}^{c} \nonumber \\&+\,\left[ R_{14}^{22}+R_{12}^{21}M_{c}\left( R_{24}^{12}+R_{25}Q_{s}R_{54}^{12}\right) +R_{15}^{21}Q_{s}R_{54}^{12}\right] \overset{\bullet }{x}_{2s}^{c} \nonumber \\&\left( R_{17}^{22}+R_{12}^{21}M_{c}R_{27}\right) v \end{aligned}$$

(129)

from (129) with (67), (68), (69) and (71), the state equation for the fast dynamics (63) is proved.

From the eleventh line of (61) with (124), (125) and removing the terms of $\overset{\bullet }{x}_{2s}^{c}$

$$\begin{aligned} u= & {} \left( R_{71}^{11}+R_{72}M_{c}R_{21}^{11}\right) z_{1}+\left( R_{71}^{12}+R_{72}M_{c}R_{21}^{12}\right) z_{2} \nonumber \\&+\,\left[ R_{74}^{11}+R_{72}M_{c}\left( R_{24}^{11}+R_{25}Q_{s}R_{54}^{11}\right) \right. \nonumber \\&\left. +\,R_{75}Q_{s}R_{54}^{11}\right] z_{1s}^{c}+R_{77}v \end{aligned}$$

(130)

from (77), (78), (79), (80) and (130), (76) is proved.

From (56) with $u_{s}=G_{0}x_{1}^{s},$ we have

$$\begin{aligned} x_{2}^{s}=\left( \widetilde{A_{21}}+\widetilde{B_{2}}G_{0}\right) x_{1}^{s} \end{aligned}$$

(131)

applying the relationships between BGI and SPBG (42) and (45) to (131)

$$\begin{aligned} x_{2}^{s}=\left( -A_{22}^{-1}A_{21}-A_{22}^{-1}B_{2}G_{0}\right) x_{1}^{s} \end{aligned}$$

(132)

from Fig. 4 and (132)

$$\begin{aligned} u= & {} G_{2}x_{2}+G_{0}x_{1}-G_{2}\left( -A_{22}^{-1}A_{21}-A_{22}^{-1}B_{2}G_{0}\right) x_{1}^{s}+v \nonumber \\ \end{aligned}$$

(133)

considering that the slow dynamics $x_{1}^{s}$ is approximated to $x_{1}$ then it is proved that (133) represents the control signal in a bond graph approach given by (76) of the composite control defined by (10) with (11).

Causal paths

In this section the definition and classification of the zero-causal paths [31] are described.

The classification of zero-order causal paths follows from the research work carried out by Van Dijk and Breedveld [31].

Definitions

Causal path is a sequence of causal bonds between two vertices of the bond graph. The causal strokes must be attached to each bond at “same relative position”.

Causal cycle is a closed causal path.

Topological loop is a signal (flow or effort) loop associated with a causal cycle.

Causal mesh is a closed causal path, usually ends in a port of an element and it has to contain an odd number of gyrators.

A causal cycle is an essential causal cycle if:

• 1. There is a closed path along a simple junction structure. If more conservation principles than just power conservation are applicable, then the bond graph must represent them explicitly.

• 2. There is a closed causal path along a weighted junction structure and the loop gain associated with this causal cycle is not equal 1.

In all other cases the causal cycle is not essential.

Zero-order causal path is a causal path with topological loops whose variables are related themselves by means of algebraic assignments [31].

The following classification of zero-order causal can be described [31],

Class 1 zero-order causal path Causal path is between a storage element (or port) with derivative and a storage element (port) with integral causality (Fig. 29a).

Class 2 zero-order causal path Causal path is between elements (ports) whose the constitutive relations are algebraic (algebraic loop) (Fig. 29b).

Class 3 zero-order causal path The closed causal path is an essential causal cycle (Fig. 30a).

Class 4 zero-order causal path Causal cycle is not essential. The loop gain of the topological loops is always $+\,1$ (Fig. 30b).

Class 5 zero-order causal path The closed causal path is a causal mesh (Fig. 30c).