Skip to main content
SpringerLink
Log in

Dynamic stability of porous functionally graded nanotubes via nonlocal strain and velocity gradient theory

  • Technical Paper
  • Published:
Journal of the Brazilian Society of Mechanical Sciences and Engineering Aims and scope Submit manuscript

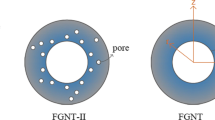
Abstract

Dynamic stability of simply supported porous functionally graded (PFG) nanotubes under parametric axial excitation is investigated. The material properties which vary radially are described according to a power law function including the volume fraction of porosity. The nonlocal strain and velocity gradient theory together with Euler–Bernoulli hypothesis is employed to incorporate the size effects into the governing partial differential equation of motion. To discretize the considered continuum, the Galerkin approach is used. To investigate the effects of length scale parameters (i.e., nonlocal nanoscale parameter, gradient length scale, and inertia parameter) as well as power low index and porosity volume fraction on the instability region, Bolotine's method is utilized. Free vibration and buckling characteristics of PFG nanotubes are discussed as well. Findings show the opposite effects of the gradient length scale parameter and inertia parameter on natural frequencies and instability region of PFG nanotubes. It is seen that with an increase in the length scale parameter or decrease in the nonlocal nanoscale parameter or velocity gradient length scale parameter, the instability region will be wider and the corresponding excitation frequency grows.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8
Fig. 9
Fig. 10
Fig. 11
Fig. 12
Fig. 13
Fig. 14
Fig. 15
Fig. 16
Fig. 17
Fig. 18

Similar content being viewed by others

Data availability

The raw/processed data required to reproduce these findings cannot be shared at this time due to technical or time limitations.

References

  1. Mota AF, Loja MAR (2019) Mechanical behavior of porous functionally graded nanocomposite materials. C J Carbon Res. https://doi.org/10.3390/c5020034

    Article  Google Scholar 

  2. El-Galy IM, Saleh BI, Ahmed MH (2019) Functionally graded materials classifcations and development trends from industrial point of view. SN Appl Sci 1:1378. https://doi.org/10.1007/s42452-019-1413-4

    Article  Google Scholar 

  3. Thang PT, Nguyen-Thoi T, Lee D, Kang J, Lee J (2018) Elastic buckling and free vibration analyses of porous-cellular plates with uniform and non-uniform porosity distributions. Aerosp Sci Technol 79:278–287

    Google Scholar 

  4. Hung DX, Tu TM, Long NV, Anh PH (2020) Nonlinear buckling and postbuckling of FG porous variable thickness toroidal shell segments surrounded by elastic foundation subjected to compressive loads. Aerosp Sci Technol 107:106253

    Google Scholar 

  5. Rao R, Sahmani S, Safaei B (2021) Isogeometric nonlinear bending analysis of porous FG composite microplates with a central cutout modeled by the couple stress continuum quasi-3D plate theory. Arch Civ Mech Eng 21:98

    Google Scholar 

  6. Li Q, Wu D, Chen X, Liu L, Yu Y, Gao W (2018) Nonlinear vibration and dynamic buckling analyses of sandwich functionally graded porous plate with graphene platelet reinforcement resting on winkler-pasternak elastic foundation. Int J Mech Sci 148:596–610

    Google Scholar 

  7. She G-L, Ren Y-R, Yuana F-G, Xiao W-S (2018) On vibrations of porous nanotubes. Int J Eng Sci 125:23–35

    MathSciNet  MATH  Google Scholar 

  8. Radić N (2018) On buckling of porous double-layered FG nanoplates in the Pasternak elastic foundation based on nonlocal strain gradient elasticity. Compos Part B Eng 153:465–479

    Google Scholar 

  9. Saffari Sh, Hashemian M, Toghraie D (2017) Dynamic stability of functionally graded nanobeam based on nonlocal Timoshenko theory considering surface effects. Physica B Phys Condens Matter. https://doi.org/10.1016/j.physb.2017.06.029

    Article  Google Scholar 

  10. Ke L-L, Wang Y-S, Yang J, Kitipornchai S (2012) Nonlinear free vibration of size-dependent functionally graded microbeams. Int J Eng Sci 50:256–267

    MathSciNet  MATH  Google Scholar 

  11. Askes H, Aifantis EC (2011) Gradient elasticity in statics and dynamics: an overview of formulations, length scale identification procedures, finite element implementations and new results. Int J Solids Struct 48:1962–1990

    Google Scholar 

  12. Thai H-T, Vo TP, Nguyen T-K, Kim S-E (2017) A review of continuum mechanics models for size-dependent analysis of beams and plates. Compos Struct 177:196–219

    Google Scholar 

  13. Lim CW, Zhang G, Reddy JN (2015) A higher-order nonlocal elasticity and strain gradient theory and its applications in wave propagation. J Mech Phys Solids 78:298–313

    MathSciNet  MATH  Google Scholar 

  14. Aifantis EC (2011) On the gradient approach-relation to Eringen’s nonlocal theory. Int J Eng Sci 49:1367–1377

    MathSciNet  Google Scholar 

  15. Li L, Hu Y, Ling L (2015) Flexural wave propagation in small-scaled functionally graded beams via a nonlocal strain gradient theory. Compos Struct 133:1079–1092

    Google Scholar 

  16. Li L, Hu Y (2016) Wave propagation in fluid-conveying viscoelastic carbon nanotubes based on nonlocal strain gradient theory. Comp Mater Sci 112:282–288

    Google Scholar 

  17. Tang Y, Liu Y, Zhao D (2016) Viscoelastic wave propagation in the viscoelastic single walled carbon nanotubes based on nonlocal strain gradient theory. Physica E 84:202–208

    Google Scholar 

  18. Ebrahimi F, Barati MR, Dabbagh A (2016) A nonlocal strain gradient theory for wave propagation analysis in temperature-dependent inhomogeneous nanoplates. Int J Eng Sci 107:169–182

    Google Scholar 

  19. Ebrahimi F, Dabbagh A (2017) On flexural wave propagation responses of smart FG magneto-electro-elastic nanoplates vibrational strain gradient theory. Compos Struct 162:281–293

    Google Scholar 

  20. Li X, Li L, Hu Y, Ding Z, Deng W (2017) Bending, buckling and vibration of axially functionally graded beams based on nonlocal strain gradient theory. Compos Struct 165:250–265

    Google Scholar 

  21. Li L, Hu Y (2019) Buckling analysis of size-dependent nonlinear beams based on a nonlocal strain gradient theory. Int J Eng Sci 97:84–94

    MathSciNet  MATH  Google Scholar 

  22. Li L, Hu Y (2017) Post-buckling analysis of functionally graded nanobeams incorporating nonlocal stress and microstructure-dependent strain gradient effects. Int J Mech Sci 120:159–170

    Google Scholar 

  23. Li L, Hu Y, Li X (2016) Longitudinal vibration of size-dependent rods via nonlocal strain gradient theory. Int J Mech Sci 115–116:135–144

    Google Scholar 

  24. Lu L, Guo X, Zhao J (2017) Size-dependent vibration analysis of nanobeams based on the nonlocal strain gradient theory. Int J Eng Sci 116:12–24

    MathSciNet  MATH  Google Scholar 

  25. Li L, Li X, Hu Y (2016) Free vibration analysis of nonlocal strain gradient beams made of functionally graded material. Int J Eng Sci 102:77–92

    MATH  Google Scholar 

  26. Nematollahi MS, Mohammadi H, Nematollahi MA (2017) Thermal vibration analysis of nanoplates based on the higher-order nonlocal strain gradient theory by an analytical approach. Microstructures 111:944–959

    Google Scholar 

  27. Li L, Hu Y (2017) Torsional vibration of bi-directional functionally graded nanotubes based on nonlocal elasticity theory. Compos Struct 172:242–250

    Google Scholar 

  28. Sahmani S, Aghdam MM (2017) Nonlinear vibrations of pre- and post-buckled lipid supramolecular micro/nano-tubules via nonlocal strain gradient elasticity theory. J Biomech 65:49–60

    Google Scholar 

  29. Şimşek M (2016) Nonlinear free vibration of a functionally graded nanobeam using nonlocal strain gradient theory and a novel hamiltonian approach. Int J Eng Sci 105:12–27

    MathSciNet  MATH  Google Scholar 

  30. Liua H, Lvb Z, Wu H (2019) Nonlinear free vibration of geometrically imperfect functionally graded sandwich nanobeams based on nonlocal strain gradient theory. Compos Struct 214:47–61

    Google Scholar 

  31. Chu L, Dui G, Zheng Y (2020) Thermally induced nonlinear dynamic analysis of temperature-dependent functionally graded flexoelectric nanobeams based on nonlocal simplified strain gradient elasticity theory. Eur J Mech A Solid 82:103999

    MathSciNet  MATH  Google Scholar 

  32. Li L, Hu Y (2016) Nonlinear bending and free vibration analyses of nonlocal strain gradient beams made of functionally graded material. Int J Eng Sci 107:77–97

    MathSciNet  MATH  Google Scholar 

  33. Şimşek M (2019) Some closed-form solutions for static, buckling, free and forced vibration of functionally graded (FG) nanobeams using nonlocal strain gradient theory. Compos Struct 224:111041

    Google Scholar 

  34. Askes H, Aifantis EC (2006) Gradient elasticity theories in statics and dynamics-A unification of approaches. Int J Fracture 139:297–304

    MATH  Google Scholar 

  35. Polizzotto C (2012) A gradient elasticity theory for second-grade materials and higher order inertia. Int J Solids Struct 49(15–16):2121–2137. https://doi.org/10.1016/j.ijsolstr.2012.04.019

    Article  Google Scholar 

  36. Mousavi SM, Paavola J, Reddy JN (2015) Variational approach to dynamic analysis of third-order shear deformable plates within gradient elasticity. Meccanica 50(6):1537–1550. https://doi.org/10.1007/s11012-015-0105-4

    Article  MathSciNet  MATH  Google Scholar 

  37. Yaghoubi ST, Mousavi SM, Paavola J (2015) Strain and velocity gradient theory for higher-order shear deformable beams. Arch Appl Mech 85(7):877–892. https://doi.org/10.1007/s00419-015-0997-4

    Article  MATH  Google Scholar 

  38. Guo S, He Y, Liu D, Lei J, Shen L, Li Z (2016) Torsional vibration of carbon nanotube with axial velocity and velocity gradient effect. Int J Mech Sci 119:88–96

    Google Scholar 

  39. Fernandes R, Mousavi M, El-Borgi S (2016) Free and forced vibration nonlinear analysis of a microbeam using finite strain and velocity gradients theory. Acta Mech 227:2657–2670

    MathSciNet  MATH  Google Scholar 

  40. Fernandes R, El-Borgi S, Mousavi SM, Reddy JN (2017) A. mechmoum, nonlinear size-dependent longitudinal vibration of carbon nanotubes embedded in an elastic medium. Phys E Low Dimens Syst Nanostruct 88:18–25

    Google Scholar 

  41. El-Borgi S, Rajendran P, Friswell MI, Trabelssi M, Reddy JN (2018) Torsional vibration of size-dependent viscoelastic rods using nonlocal strain and velocity gradient theory. Compos Struct 186:274–292

    Google Scholar 

  42. Ouakad HM, El-Borgi S, Mousavi SM, Friswell MI (2018) Static and dynamic response of CNT nanobeam using nonlocal strain and velocity gradient theory. Appl Math Model 62:207–222

    MathSciNet  MATH  Google Scholar 

  43. Liang L, Wang Y (2011) Size effect on dynamic stability of functionally graded microbeams based on a modified couple stress theory. Compos Struct 93:342–350

    Google Scholar 

  44. Saffari S, Hashemian M, Toghraie D (2017) Dynamic stability of functionally graded nanobeam based on nonlocal Timoshenko theory considering surface effects. Physica B 520:97–105

    Google Scholar 

  45. Al-shujairi M, Mollamahmutoğlu Ç (2018) Dynamic stability of sandwich functionally graded micro-beam based on the nonlocal strain gradient theory with thermal effect. Compos Struct 201:1018–1030

    Google Scholar 

  46. Chen X, Lud Y, Li Y (2019) Free vibration, buckling and dynamic stability of bi-directional FG microbeam with a variable length scale parameter embedded in elastic medium. Appl Math Model 67:430–448

    MathSciNet  MATH  Google Scholar 

  47. Jalaei MH, Civalek Ӧ (2019) On dynamic instability of magnetically embedded viscoelastic porous FG nanobeam. Int J Eng Sci 143:14–32

    MathSciNet  MATH  Google Scholar 

  48. Pham Q-H, Tran VK, Tran TT, Nguyen P-C, Malekzadeh P (2022) Dynamic instability of magnetically embedded functionally graded porous nanobeams using the strain gradient theory. Alexandria Eng J 61:10025–10044

    Google Scholar 

  49. Mollamahmutoğlu Ç, Mercan A, Levent A (2022) A comprehensive mechanical response and dynamic stability analysis of elastically restrained bi-directional functionally graded porous microbeams in the thermal environment via mixed finite elements. J Braz Soc Mech Sci 44:333

    Google Scholar 

  50. Ma T, Mu A (2022) Study on the stability of functionally graded simply supported fluid-conveying microtube under multi-physical fields. Micromachines 13:895. https://doi.org/10.3390/mi13060895

    Article  Google Scholar 

  51. Hoffman WP, Upadhya K (1994) The universal applications of microtubes and microtube composites. In: NASA, Washignton, technology 2003: the fourth national technology transfer conference and exposition. V1

  52. Babaei H (2021) On frequency response of FG-CNT reinforced composite pipes in thermally pre/post buckled configurations. Compos Struct 276:114467

    Google Scholar 

  53. Babaei H, Eslami MR (2021) Thermally induced nonlinear stability and imperfection sensitivity of temperature- and size-dependent FG porous micro-tubes. Int J Mech Mater Des 17:381–401. https://doi.org/10.1007/s10999-021-09531-3

    Article  Google Scholar 

  54. Babaei H, Eslami MR (2020) Limit load analysis and imperfection sensitivity of porous FG micro-tubes surrounded by a nonlinear softening elastic medium. Acta Mech 231:4563–4583. https://doi.org/10.1007/s00707-020-02781-w

    Article  MathSciNet  MATH  Google Scholar 

  55. Lu L, Wang S, Li M, Guo X (2021) Free vibration and dynamic stability of functionally graded composite microtubes reinforced with graphene platelets. Compos Struct 272:114231

    Google Scholar 

  56. Beni YT (2022) Size dependent coupled electromechanical torsional analysis of porous FG flexoelectric micro/nanotubes. Mech Syst Signal Process 178:109281

    Google Scholar 

  57. Nayfeh AH, Pai PF (2004) Linear and nonlinear structural mechanics. Wiley, New Jersey

    MATH  Google Scholar 

  58. Bolotin VV (1964) The dynamic stability of elastic systems. Translated from the Russian. Weingarten VI, Greszcuzuk LB, Trirogoff KN, Gallegos KD (eds) Holden-Day, San Francisco, Calif

Download references

Funding

This research received no specific grant from any funding agency in the public, commercial, or not-for-profit sectors.

Author information

Authors and Affiliations

  1. Department of Mechanical Engineering, Yasouj University, Yasouj, 75914-353, Iran

    S. Ziaee

Authors
  1. S. Ziaee
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to S. Ziaee.

Ethics declarations

Conflict of interest

The author declares that she has no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.

Additional information

Technical Editor: Marcela Rodrigues Machado.

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Rights and permissions

Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Ziaee, S. Dynamic stability of porous functionally graded nanotubes via nonlocal strain and velocity gradient theory. J Braz. Soc. Mech. Sci. Eng. 45, 643 (2023). https://doi.org/10.1007/s40430-023-04548-5

Download citation

  • Received:

  • Accepted:

  • Published:

  • DOI: https://doi.org/10.1007/s40430-023-04548-5

Keywords

Search

Navigation