1 Introduction

Many fluids dealt by engineers and scientist, such as air, water and oil can be regarded as Newtonian fluids. However, in many cases, the premise of Newtonian behavior is not rational and rather more complex so non-Newtonian response must be molded. Many fluid materials such as glue, custard, paint, blood and ketchup present non-Newtonian fluid behavior. Due to its wide range of applications in industry, chemical engineering, petroleum engineering, etc., it has gained a lot of importance by many researchers [1,2,3,4,5,6,7,8]. Ellahi et al. [9] studied non-Newtonian micropolar fluid in arterial blood flow through composite stenosis. Among these non-Newtonian fluids, one is Eyring–Powell fluid, it was firstly introduced by Eyring and Powell in 1944. Researchers [10,11,12,13,14] have discussed various aspects of Eyring–Powell fluid.

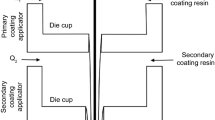
Wire coating process is very necessary to prevent injuries and reduce the reduction that can be created by machine vibration. In industries, different melt polymers are in use to coat the wire. For wire coating, generally two processes are used. In first, melt polymer is deposited continuously on moving wire, and in second, wire is pulled through the die suffused with viscoelastic material. For wire coating, three different processes are used known as coaxial process, dripping process and electrostatistical deposition process. The dipping process in wire coating process gives much stronger association among the continuums but is slow when compared to other two processes. A typical process of wire coating is demonstrated below in Fig. 1.

Fig. 1
figure 1

A typical wire coating process

Full size image

It consists of a payoff device, straightener, preheater, extruder device and die, cooling device, capstan, tester and a take-up reel. In this process, the uncoated wire is rolled on the payoff device which passes through straighter, then, temperature is given to the wire through preheater, and a crosshead die contains a canonical die where it assembles the melt polymer and gets coated. After it, this coated wire is cooled by cooling device and then passes along a capstan and a tester, and at the end, coated wire is winded at take-up reel. Many researchers [15,16,17,18,19,20,21,22,23] investigated wire coating phenomena using different non-Newtonian fluids.

In magnetohydrodynamic, the applied magnetic field produces current due to its Lorentz force, which affects fluid motion impressively. These days, magnetohydrodynamic has become an important topic for research due to its usage at high rate in numerous industrial processes like magnetic field material processing and glass manufacturing. Magnetohydrodynamic treats the electrically conducting fluid flows in the existence of magnetic field. Many researchers [24,25,26,27,28,29,30] remit appreciable regard to the study of magnetohydrodynamic flow problems.

Fluid flow in porous media has great importance for researchers due to its wide range of applications in engineering field. Carbonated rocks, wood, metal foams, etc. are various well-known forms of porous media. These days, a very thin porous layer has been used in many industrial and domestic applications such as filters, printing papers, fuel cells and batteries. Many researchers [31,32,33,34] also paid a lot of attention to porous media.

The interest in heat transfer of non-Newtonian fluid flows is increasing with the passage of time due to its usage in various industries. Rehman and Nadeem [35] carried out heat transfer analysis for three-dimensional stagnation point flow. Ahmed and many other researchers [36,37,38,39,40] discussed the impact of heat transfer analysis and magnetohydrodynamic fluid.

To the best of authors’ knowledge, no one has still studied wire coating process using magnetohydrodynamic flow of viscoelastic Eyring–Powell fluid as coating material. The objective of the present work is to discuss the process of wire coating with the effects of heat generation and porous media with temperature-dependent variable viscosity using Reynolds and Vogel’s model.

2 Modeling of wire coating

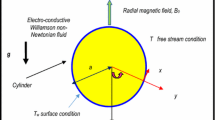
The geometry of the problem under examination is viewed in Fig. 2. Here L is the length of pressure-type die, Rd is the radius and θd is the temperature which is saturated by an incompressible elastic-viscous Eyring–Powell fluid. The wire is dragged through center line of die in a stationary pressure-type die when the temperature of wire is indicated with θw, radius Rw and velocity Uw in porous medium. Emerging fluid is worked simultaneous by a constant pressure gradient \(\frac{{{\text{d}}p}}{{{\text{d}}z}}\) parallel to axis of body and a transverse magnetic field with power Bo. The magnetic field is making right angle with incompressible Eyring–Powell fluid flow’s direction. The magnetic Reynolds number is used as minor to ignore the urge magnetic field in our present problem. The die and wire are coaxial. Coordinate system is taken along the axis of the wire.

Fig. 2
figure 2

Geometry of the problem

Full size image

The suitable expressions for velocity of fluid \((\overleftrightarrow q)\), extra stress tensor (S) and temperature field (θ) for above-mentioned problem may be considered as

$$\overleftrightarrow {\mathbf{q}} = 0\underline{i} + 0\underline{j} + w(r)\underline{k} ,$$
(1)
$$S = S(r),$$
(2)
$$\theta = \theta (r).$$
(3)

The Cauchy stress tensor of viscoelastic Eyring–Powell fluid is expressed as

$$S = \mu \nabla {\mathbf{v}} + \frac{1}{\beta }\sinh^{ - 1} \left( {\frac{1}{C}\nabla {\mathbf{v}}} \right),\,$$
(4)

where μ is the shear viscosity, S is the Cauchy stress tensor, C is the material constant, V is the velocity and C is the material constant. Equation (4) is simplified as

$$\sinh^{ - 1} \left( {\frac{1}{C}\nabla {\mathbf{v}}} \right) \approx \frac{1}{C}\nabla {\mathbf{v}} - \frac{1}{6}\left( {\frac{1}{C}\nabla {\mathbf{v}}} \right)^{3} ,\quad \left| {\frac{1}{C}\nabla {\mathbf{v}}} \right| \ll 1.$$
(5)

The suitable boundary conditions for the present consideration can be defined as

$$\begin{aligned} & w(R_{\text{w}} ) = U_{\text{w}} ,\quad \, \theta (R_{\text{w}} ) = \theta_{\text{w}} , \\ & w(R_{d} ) = 0,\quad \, \theta (R_{d} ) = \theta_{d} . \\ \end{aligned}$$
(6)

The governing equations are

$$\overleftrightarrow \nabla \cdot \overleftrightarrow q = 0,$$
(7)
$$\rho \left( {\frac{D\overleftrightarrow q}{Dt}} \right) = \overleftrightarrow F - \overleftrightarrow \nabla p + \overleftrightarrow J \times \overleftrightarrow B + \frac{\mu \overleftrightarrow q}{{K_{\text{p}}^{ * } }},$$
(8)
$$\rho C_{p} \frac{D\theta }{Dt} = k\nabla^{2} + \varphi + Q_{0} (\theta - \theta_{\text{w}} ) + J_{\text{d}} ,$$
(9)

where \(\overleftrightarrow q\) is velocity vector, ρ represent density, \(\frac{D}{Dt}\) is temporal derivative, \(\overleftrightarrow J \times \overleftrightarrow B\) indicates electromagnetic origin per unit volume appears due to the correspondence of magnetic arena, current Q0 represents the rate of volumetric heat generation and Jd is the Joule dissipation term. The magnetic body force produced along the z-direction can be defined as

$$\overleftrightarrow J \times \overleftrightarrow B = \left( {0,\,0,\,\sigma \beta_{0}^{2} w} \right).$$
(10)

Applying (1–3), the continuity of Eq. (7) is identically satisfied and we get nonvanishing components of extra stress tensor S as

$$S_{zr} = \left( {\mu + \frac{1}{\beta C}} \right)\frac{{{\text{d}}w}}{{{\text{d}}r}} - \frac{1}{{6\beta C^{3} }}\left( {\frac{{{\text{d}}w}}{{{\text{d}}r}}} \right)^{3} .$$
(11)

Putting the velocity field and Eqs. (10–11) in Eq. (8), we get

$$\frac{\partial P}{\partial r} = 0,$$
(12)
$$\frac{\partial P}{\partial \theta } = 0,$$
(13)
$$\frac{\partial P}{\partial z} = \frac{1}{r}\frac{\text{d}}{{{\text{d}}r}}\left[ {r\left\{ {\left( {\mu + \frac{1}{\beta C}} \right)\frac{{{\text{d}}w}}{{{\text{d}}r}} - \frac{1}{6\beta C}\left( {\frac{{{\text{d}}w}}{{{\text{d}}r}}} \right)^{3} } \right\}} \right] - \sigma \beta_{0}^{2} w - \frac{\mu w}{{K_{\text{p}}^{ * } }}.$$
(14)

However, Eq. (14) shows the flow owing the pressure gradient. When we leave the die then, only drag of wire happened. That’s why pressure gradient is contributing nothing in the axial direction. So Eq. (14) takes the form as

$$\frac{1}{r}\frac{\text{d}}{{{\text{d}}r}}\left[ {r\left\{ {\left( {\mu + \frac{1}{\beta C}} \right)\frac{{{\text{d}}w}}{{{\text{d}}r}} - \frac{1}{6\beta C}\left( {\frac{{{\text{d}}w}}{{{\text{d}}r}}} \right)^{3} } \right\}} \right] - \sigma \beta_{0}^{2} w - \frac{\mu w}{{K_{\text{p}}^{ * } }} = 0,$$
(15)

and energy Eq. (9) becomes

$$K\left( {\frac{{{\text{d}}^{2} \theta }}{{{\text{d}}r^{2} }} + \frac{1}{r}\frac{{{\text{d}}\theta }}{{{\text{d}}r}}} \right) + \left( {\left( {\mu + \frac{1}{\beta C}} \right)\frac{{{\text{d}}w}}{{{\text{d}}r}} - \frac{1}{{6\beta C^{3} }}\left( {\frac{{{\text{d}}w}}{{{\text{d}}r}}} \right)^{3} } \right).\frac{{{\text{d}}w}}{{{\text{d}}r}} + Q_{0} (\theta - \theta_{\text{w}} ) + \sigma \beta_{0}^{2} w^{2} = 0.$$
(16)

3 Constant viscosity

Defining dimensionless parameters as

$$\begin{aligned} & r^{ * } = \frac{r}{{R_{\text{w}} }}, \, \quad \, w^{ * } = \frac{w}{{U_{\text{w}} }},\quad \, M^{2} = \frac{{\sigma \beta_{0}^{2} R_{\text{w}}^{2} }}{\mu },\, \, \quad \, K_{\text{p}} = \frac{{R_{\text{w}}^{2} }}{{K_{\text{p}}^{ * } }},\, \, \quad w = \frac{{v_{0} }}{{U_{\text{w}} }},\, \, \quad N = \frac{1}{\mu \beta C},\, \, \\ & \theta^{ * } = \frac{{(\theta - \theta_{\text{w}} )}}{{(\theta_{d} - \theta_{\text{w}} )}},\quad \, Q = \frac{{Q_{0} R_{\text{w}}^{2} }}{K},\quad \, B_{r} = \frac{{\mu U_{\text{w}}^{2} }}{{K(\theta_{d} - \theta_{\text{w}} )}},\, \, \quad R_{\text{w}} = \frac{{\beta v_{0} }}{\mu },\, \, \quad \varepsilon = \frac{\mu }{{6w^{2} (\beta C)^{3} }}. \\ \end{aligned}$$
(17)

Using these new variables in Eqs. (15) and (16) with Eq. (6) and after removing asterisks, we get the following form

$$(1 + N)\left[ {r\frac{{{\text{d}}^{2} w}}{{{\text{d}}r^{2} }} + \frac{{{\text{d}}w}}{{{\text{d}}r}}} \right] - \varepsilon \left[ {\left( {\frac{{{\text{d}}w}}{{{\text{d}}r}}} \right)^{3} + 3r\left( {\frac{{{\text{d}}w}}{{{\text{d}}r}}} \right)^{2} \frac{{{\text{d}}^{2} w}}{{{\text{d}}r^{2} }}} \right] - M^{2} wr - K_{\text{p}} wr = 0,$$
(18)
$$w(1) = 1 \, \quad {\text{ and}}\quad \, w(\delta ) = 0.$$
(19)
$$\frac{{{\text{d}}^{2} \theta }}{{{\text{d}}r^{2} }} + \frac{1}{r}\frac{{{\text{d}}\theta }}{{{\text{d}}r}} + B_{r} (1 + N)\left( {\frac{{{\text{d}}w}}{{{\text{d}}r}}} \right)^{2} + \varepsilon B_{r} \left( {\frac{{{\text{d}}w}}{{{\text{d}}r}}} \right)^{4} + Q\theta + B_{r} M^{2} w^{2} = 0,$$
(20)
$$\theta (1) = 0 \, \quad {\text{and}}\quad \, \theta (\delta ) = 1.$$
(21)

4 Reynolds model

Here, we used Reynolds model to explain temperature-dependent viscosity. The dimensionless viscosity can be expressed for Reynolds model as

$$\mu \approx 1 - \beta_{0} m\theta .$$
(22)

It will be applied for variation of temperature-dependent viscosity, while m is used for viscosity parameter. Using nondimensional parameters,

$$\begin{aligned} & r^{ * } = \frac{r}{{R_{\text{w}} }},\, \, \quad w^{ * } = \frac{w}{{U_{\text{w}} }},\, \, \quad M^{2} = \frac{{\sigma \beta_{0}^{2} R_{\text{w}}^{2} }}{{\mu_{0} }},\,\quad \, K_{\text{p}} = \frac{{R_{\text{w}}^{2} }}{{K_{\text{p}}^{ * } }},\, \, \quad w = \frac{{v_{0} }}{{U_{\text{w}} }},\, \, \quad N = \frac{1}{{\mu_{0} \beta C}},\quad \, \, \mu^{ * } = \frac{\mu }{{\mu_{0} }},\, \\ & \theta^{ * } = \frac{{(\theta - \theta_{\text{w}} )}}{{(\theta_{d} - \theta_{\text{w}} )}},\, \, \quad \, Q = \frac{{Q_{0} R_{\text{w}}^{2} }}{K},\, \, \quad \, B_{r} = \frac{{\mu_{0} U_{\text{w}}^{2} }}{{K(\theta_{d} - \theta_{\text{w}} )}},\, \, \quad \, R_{\text{w}} = \frac{{\beta v_{0} }}{{\mu_{0} }},\,\quad \, \varepsilon = \frac{{\mu_{0} }}{{6w^{2} (\beta C)^{3} }}. \\ \end{aligned}$$
(23)

After removing asterisks, we obtain nondimensional form of momentum and energy equation along boundary conditions

$$\frac{{{\text{d}}^{2} w}}{{{\text{d}}r^{2} }}\left[ {r(1 - \beta_{0} m\theta ) + rN - 3r\varepsilon \left( {\frac{{{\text{d}}w}}{{{\text{d}}r}}} \right)^{2} } \right] + \frac{{{\text{d}}w}}{{{\text{d}}r}}\left[ {1 - \beta_{0} m\theta + N - \beta_{0} mr\frac{{{\text{d}}\theta }}{{{\text{d}}r}}} \right] - \varepsilon \left( {\frac{{{\text{d}}w}}{{{\text{d}}r}}} \right)^{3} - K_{\text{p}} wr - M^{2} wr = 0,$$
(24)
$$w(1) = 1 \, \quad {\text{ and}}\quad \, w(\delta ) = 0,\,$$
(25)

and

$$\frac{{{\text{d}}^{2} \theta }}{{{\text{d}}r^{2} }} + \frac{1}{r}\frac{{{\text{d}}\theta }}{{{\text{d}}r}} + (1 - \beta_{0} m\theta )B_{r} \left( {\frac{{{\text{d}}w}}{{{\text{d}}r}}} \right)^{2} + B_{r} \left( {\frac{{{\text{d}}w}}{{{\text{d}}r}}} \right)^{2} (N + \varepsilon ) + Q\theta + B_{r} M^{2} w^{2} = 0,$$
(26)
$$\theta (1) = 0 \, \quad {\text{and}}\quad \, \theta (\delta ) = 1.$$
(27)

5 Vogel’s model

In this case, we take temperature-dependent viscosity as

$$\mu = \mu_{{_{{_{0} }} }} \exp \left( {\frac{D}{B' + \theta } - \theta_{\text{w}} } \right).$$
(28)

Applying expansions, we get

$$\mu = \varOmega \left( {1 - \frac{D}{{B^{\prime 2} }}\theta } \right),\,$$
(29)

where D, B are parameters of viscosity and \(\varOmega = \mu_{{_{{_{0} }} }} \exp (\tfrac{D}{{B^{\prime 2} }} - \theta_{\text{w}} )\).

We obtain nondimensional equations of momentum and energy along boundary conditions after removing asterisks

$$\frac{{{\text{d}}^{2} w}}{{{\text{d}}r^{2} }}\left[ {r\varOmega \left( {1 - \frac{D}{{B^{\prime 2} }}\theta } \right) + rN - 3r\varepsilon \left( {\frac{{{\text{d}}w}}{{{\text{d}}r}}} \right)^{2} } \right] + \frac{{{\text{d}}w}}{{{\text{d}}r}}\left[ {\varOmega \left( {1 - \frac{D}{{B^{\prime 2} }}\theta } \right) + N - \varOmega \frac{D}{{B^{\prime 2} }}r\frac{{{\text{d}}\theta }}{{{\text{d}}r}}} \right] - \varepsilon \left( {\frac{{{\text{d}}w}}{{{\text{d}}r}}} \right)^{3} - K_{p} wr - M^{2} wr = 0,\,$$
(30)
$$w(1) = 1 \, \quad {\text{and}}\quad \, w(\delta ) = 0,\,$$
(31)

and

$$\frac{{{\text{d}}^{2} \theta }}{{{\text{d}}r^{2} }} + \frac{1}{r}\frac{{{\text{d}}\theta }}{{{\text{d}}r}} + \varOmega \left( {1 - \frac{D}{{B^{\prime 2} }}\theta } \right)B_{r} \left( {\frac{{{\text{d}}w}}{{{\text{d}}r}}} \right)^{2} + B_{r} \left( {\frac{{{\text{d}}w}}{{{\text{d}}r}}} \right)^{2} (N + \varepsilon ) + Q\theta + B_{r} M^{2} w^{2} = 0,\,$$
(32)
$$\theta (1) = 0 \, \quad {\text{and}}\quad \, \theta (\delta ) = 1.$$
(33)

6 Numerical solution

6.1 Constant viscosity

The governing higher-order differential equations are firstly converted into first-order ordinary differential equations. They are solved numerically utilizing Runge–Kutta method with shooting technique. First of all, we convert momentum and energy equation into first-order form. Equations (18) and (20) become

$$\frac{{{\text{d}}^{2} w}}{{{\text{d}}r^{2} }} = \frac{{\varepsilon \left( {\frac{{{\text{d}}w}}{{{\text{d}}r}}} \right)^{3} - (1 + N)\frac{{{\text{d}}w}}{{{\text{d}}r}} + M^{2} wr + K_{p} wr}}{{(1 + N)r + 3r\varepsilon \left( {\frac{{{\text{d}}w}}{{{\text{d}}r}}} \right)^{2} }},\,$$
(34)
$$\frac{{{\text{d}}^{2} \theta }}{{{\text{d}}r^{2} }} = - \left[ {\frac{1}{r}\frac{{{\text{d}}\theta }}{{{\text{d}}r}} + B_{r} (1 + N)\left( {\frac{{{\text{d}}w}}{{{\text{d}}r}}} \right)^{2} + \varepsilon B_{r} \left( {\frac{{{\text{d}}w}}{{{\text{d}}r}}} \right)^{4} + Q\theta + B_{r} M^{2} w^{2} } \right].$$
(35)

Defining new variables to convert higher-order ordinary differential equation into first order as

$$w = y_{1} ,\, \, \quad w^{\prime} = y_{2} ,\, \, \quad w^{\prime\prime} = y_{2}^{\prime } ,\, \, \quad \theta = y_{3} ,\, \, \quad \theta^{\prime} = y_{4} ,\, \, \quad \theta^{\prime\prime} = y_{4}^{\prime } ,\,$$
(36)
$$y_{2}^{\prime } = \frac{{\varepsilon (y_{2} )^{3} - (1 + N)y_{2} + M^{2} y_{1} r + K_{p} y_{1} r}}{{(1 + N)r + 3r\varepsilon (y_{2} )^{2} }},\,$$
(37)
$$y_{4}^{\prime } = - \left[ {\frac{1}{r}y_{4} + B_{r} (1 + N)(y_{2} )^{2} + \varepsilon B_{r} (y_{2} )^{4} + Qy_{3} + B_{r} M^{2} y_{1}^{2} } \right].$$
(38)

The boundary conditions convert into initial conditions as

$$y_{1} (1) = 1 \, \quad {\text{ and}}\quad \, y_{1} (\delta ) = 0,\,$$
(39)
$$y_{3} (1) = 0\quad {\text{and}}\quad y_{3} (\delta ) = 1.$$
(40)

6.2 Reynolds model

Equations (24) and (26) may be written as

$$\frac{{{\text{d}}^{2} w}}{{{\text{d}}r^{2} }} = \frac{{\varepsilon \left( {\frac{{{\text{d}}w}}{{{\text{d}}r}}} \right)^{3} + K_{p} wr + M^{2} wr - \frac{{{\text{d}}w}}{{{\text{d}}r}}\left[ {1 - \beta_{0} m\theta + N - \beta_{0} mr\frac{{{\text{d}}\theta }}{{{\text{d}}r}}} \right]}}{{\left[ {r(1 - \beta_{0} m\theta ) + rN - 3r\varepsilon \left( {\frac{{{\text{d}}w}}{{{\text{d}}r}}} \right)^{2} } \right]}},\,$$
(41)
$$\frac{{{\text{d}}^{2} \theta }}{{{\text{d}}r^{2} }} = - \left[ {\frac{1}{r}\frac{{{\text{d}}\theta }}{{{\text{d}}r}} + (1 - \beta_{0} m\theta )B_{r} \left( {\frac{{{\text{d}}w}}{{{\text{d}}r}}} \right)^{2} + B_{r} \left( {\frac{{{\text{d}}w}}{{{\text{d}}r}}} \right)^{2} (N + \varepsilon ) + Q\theta + B_{r} M^{2} w^{2} } \right].$$
(42)

Using variables from Eq. (36) to reduce higher-order differential equation into first order as

$$y_{2}^{\prime } = \frac{{\varepsilon (y_{2} )^{3} + K_{p} y_{1} r + M^{2} y_{1} r - y_{2} [1 - \beta_{0} my_{3} + N - \beta_{0} mry_{4} ]}}{{[r(1 - \beta_{0} my_{3} ) + rN - 3r\varepsilon (y_{2} )^{2} ]}},\,$$
(43)
$$y_{4}^{\prime } = - \left[ {\frac{1}{r}y_{4} + (1 - \beta_{0} my_{3} )B_{r} (y_{2} )^{2} + B_{r} (y_{2} )^{2} (N + \varepsilon ) + Qy_{3} + B_{r} M^{2} y_{1}^{2} } \right].$$
(44)

The boundary conditions converted into initial conditions as

$$y_{1} (1) = 1 \, \quad {\text{and}}\quad \, y_{1} (\delta ) = 0,\,$$
(45)
$$y_{3} (1) = 0 \, \quad {\text{and}}\quad \, y_{3} (\delta ) = 1.$$
(46)

6.3 Vogel’s model

Equations (30) and (32) can be written as

$$\frac{{{\text{d}}^{2} w}}{{{\text{d}}r^{2} }} = \frac{{\varepsilon \left( {\frac{{{\text{d}}w}}{{{\text{d}}r}}} \right)^{3} + K_{p} wr + M^{2} wr - \frac{{{\text{d}}w}}{{{\text{d}}r}}\left[ {\varOmega \left( {1 - \frac{D}{{B^{\prime 2} }}\theta } \right) + N - \varOmega \tfrac{D}{{B^{\prime 2} }}r\frac{{{\text{d}}\theta }}{{{\text{d}}r}}} \right]}}{{r\varOmega \left( {1 - \frac{D}{{B^{\prime 2} }}\theta } \right) + rN - 3r\varepsilon \left( {\frac{{{\text{d}}w}}{{{\text{d}}r}}} \right)^{2} }},\,$$
(47)
$$\frac{{{\text{d}}^{2} \theta }}{{{\text{d}}r^{2} }} = - \left[ {\frac{1}{r}\frac{{{\text{d}}\theta }}{{{\text{d}}r}} + \varOmega \left( {1 - \frac{D}{{B^{\prime 2} }}\theta } \right)B_{r} \left( {\frac{{{\text{d}}w}}{{{\text{d}}r}}} \right)^{2} + B_{r} \left( {\frac{{{\text{d}}w}}{{{\text{d}}r}}} \right)^{2} (N + \varepsilon ) + Q\theta + B_{r} M^{2} w^{2} } \right].$$
(48)

Using Eq. (36) in Eqs. (47) and (48), we get

$$y_{2}^{\prime } = \frac{{\varepsilon (y_{2} )^{3} + K_{p} y_{1} r + M^{2} y_{1} r - y_{2} \left[ {\varOmega \left( {1 - \tfrac{D}{{B^{\prime 2} }}y_{3} } \right) + N - \varOmega \tfrac{D}{{B^{\prime 2} }}ry_{4} } \right]}}{{r\varOmega \left( {1 - \tfrac{D}{{B^{\prime 2} }}y_{3} } \right) + rN - 3r\varepsilon (y_{2} )^{2} }},\,$$
(49)
$$y_{4}^{\prime } = - \left[ {\frac{1}{r}y_{4} + \varOmega \left( {1 - \frac{D}{{B^{\prime 2} }}y_{3} } \right)B_{r} (y_{2} )^{2} + B_{r} (y_{2} )^{2} (N + \varepsilon ) + Qy_{3} + B_{r} M^{2} y_{1}^{2} } \right].$$
(50)

Along boundary conditions

$$y_{1} (1) = 1 \, \quad {\text{and}}\quad \, y_{1} (\delta ) = 0,\,$$
(51)
$$y_{3} (1) = 0 \, \quad {\text{and}}\quad \, y_{3} (\delta ) = 1.$$
(52)

7 Graphical results and discussions

In this work, we examine Eyring–Powell fluid as coating material for wire. The process of wire coating is occurring in a die with uniform magnetic and heat generation effects in porous medium. The effects of different emerging physical parameters known as non-Newtonian parameter \(\beta_{{_{0} }} ,\) heat generation parameter Q, viscosity parameters m and Ω for Reynolds and Vogel’s models, respectively, porous parameter Kp, Brinkman number Br and other parameters D and M on velocity and temperature profile are expressed by graphs. Figure 2 displays geometry of given problem. Figure 3 presents the result of Kp over velocity profile for constant viscosity when Br, Kp and Q remain constant. The velocity profile decreased by enlargement in the worth of Kp. Figure 4 proposes the ascendancy of ɛ on velocity profile when viscosity is constant and having other parameters as constant. The velocity profile presents increasing behavior because of escalating ɛ. Figure 5 shows the effect of M on velocity profile. Figure 6 points out the Br on velocity profile for Reynolds model. Velocity profile shows increasing actions owing to escalating Br. Figure 7 interprets the outcomes of permeability parameter on velocity profile for Reynolds model when \(\beta_{{_{0} }} = 0.1,\) M = 0.6,  Br = 0.1,  Q = 0.1 and m = 0.3. Figure 8 illuminates the influence of N on velocity profile for Reynolds model. Velocity curve eliminates the increasing action due to increase in N. Figure 9 expounds that velocity profile shows increasing response by accelerating Br for Vogel’s model, while M = 0.11,  Kp = 0.1 and Q = 0.2. Figure 10 comes out that the velocity distribution illustrates increasing actions by accelerating D for Vogel’s model. The curve of the graph shows increasing behavior. Figure 11 represents the inclination in velocity profile due to increasing Q for Vogel’s model keeping D = 0.2,  M = 0.11 and Br = 0.2. Figure 12 explains the variations in temperature profile resulting due to ɛ for constant viscosity when M = 0.6,  Kp = 0.6 and N = 0.01. Velocity profile is downward due to rise in ɛ. Figure 13 explicates the result of Br coefficient on temperature profile for constant viscosity. Velocity profile is decreasing by accelerating Br. Figure 14 presents the effects of Q on temperature profile when viscosity is constant and having other parameters as constant. The velocity profile presents increasing behavior because of escalating Q. Figure 15 displays the increasing response of temperature profile due to the boosting in value of ɛ for Reynolds model. Figure 16 illustrates that temperature distribution goes upward due to increase in M for Reynolds model. The temperature distribution illustrates increasing actions by accelerating M for Reynolds model. Figure 17 comes out that the enlargement in the value of Q curve shows decreasing behavior. Figure 18 expresses that temperature distribution accelerates due to amplification in the value of M for Vogel’s model with D = 0.2,  Kp = 0.1 and Q = 0.6. Figure 19 indicates the decreasing temperature curve is caused by increasing Ω for Vogel’s model with N = 0.2,  \(B^{{{\prime } }} = 1.3,\) Kp = 0.1 and D = 0.3. Figure 20 clarifies the S.T lines impact for different worth of Br for constant viscosity. Figure 21 illustrates the effects of stream lines (S.T lines) for distinct values of Br for Reynolds model. Figure 22 clarifies the influence of stream lines on disparate worth of Br for Vogel’s model. 3D result for distinct value of Br for constant viscosity is shown in Fig. 23 properly. Figure 24 shows the 3D impact for distinct value for Reynolds model. Figure 25 expounds the 3D effects for distinct value of Q for Vogel’s model.

Fig. 3
figure 3

Effects of Kp on velocity distribution

Full size image
Fig. 4
figure 4

Influence of ϵ on velocity profile

Full size image
Fig. 5
figure 5

Influence of M on velocity distribution

Full size image
Fig. 6
figure 6

Effects of Br on velocity distribution in case of Reynolds model

Full size image
Fig. 7
figure 7

Impact of Kp on velocity distribution in Reynolds model

Full size image
Fig. 8
figure 8

Effects of N on velocity distribution in Reynolds model

Full size image
Fig. 9
figure 9

Effects of Br on velocity distribution in case of Vogel’s model

Full size image
Fig. 10
figure 10

Impact of D on velocity distribution in case of Vogel’s model

Full size image
Fig. 11
figure 11

Impact of Q on velocity distribution for Vogel’s model

Full size image
Fig. 12
figure 12

Influence of ϵ on temperature distribution

Full size image
Fig. 13
figure 13

Impact of Br on temperature distribution

Full size image
Fig. 14
figure 14

Influence of Q on temperature profile

Full size image
Fig. 15
figure 15

Influence of ϵ on temperature distribution for Reynolds model

Full size image
Fig. 16
figure 16

Influence of M on temperature distribution for Reynolds model

Full size image
Fig. 17
figure 17

Impact of Q on temperature distribution in case of Reynolds model

Full size image
Fig. 18
figure 18

Effects of M on temperature distribution in case of Vogel’s model

Full size image
Fig. 19
figure 19

Impact of Q on temperature distribution for Vogel’s model

Full size image
Fig. 20
figure 20

Stream lines for Br = 0.3

Full size image
Fig. 21
figure 21

Stream lines for Br = 0.5 in case of Reynolds model

Full size image
Fig. 22
figure 22

Stream lines for Br = 0.1 in case of Vogel’s model

Full size image
Fig. 23
figure 23

3-D graph of w(r) for Br = 0.3

Full size image
Fig. 24
figure 24

3-D graph of w(r) for Br = 0.5 in case of Reynolds model

Full size image
Fig. 25
figure 25

3-D graph of w(r) for Br = 0.1 in case of Vogel’s model

Full size image

8 Concluding remarks

In the present work, we have computed impact of magnetohydrodynamic flow and heat transfer in wire coating process using melt polymer in a porous medium along Joule heating and variable viscosity. Wire is coated in a pressure-type die where it meets Eyring–Powell fluid. Porous matrix is used as insulator due to which the flow and heat mobility process saves loss of heat and increases the cooling/heating process. The solution of given problem is obtained using shooting method. The result of engaged parameter is presented on velocity profile and temperature distribution. Important points of the current study that are procured are presented below as:

  1. 1.

    The velocity of fluid shows upward behavior by increase in the value of ɛ,  M,  Br, N and D and presents decreasing behavior due to increase in value of Kp,  Q and ɛ.

  2. 2.

    The temperature profile shows flourishing behavior for blowing up in the value of ɛ and M and decreasing behavior for the value Br,  Q and ɛ.