Numerical investigation on the dynamic behavior of an onboard rotor system by using the FEM approach

Abstract

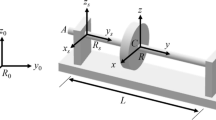
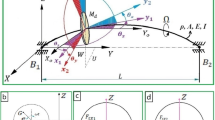
In this paper, an investigation regarding the dynamic behavior of a rotating machine subjected to a base excitation is presented numerically. Regarding aeronautical applications, the aircraft engine is considered a typical onboard rotor that has its dynamic behavior influenced by base excitations. The mathematical model of the machine is derived from the finite element method, which is obtained by considering the strain and kinetic energies of the rotor subsystems (shaft, discs, bearings, mass unbalance, etc.). The resulting differential equations are used to provide information about the vibration responses of the rotor under base and unbalance excitations, simultaneously. The rotating machine used in this work is represented by a horizontal flexible shaft containing two rigid discs and supported by two ball bearings. In this case, the base of the rotor system is considered as being rigid. Therefore, the proposed analysis is performed both in the time and frequency domains, as generated by the orbits, unbalance response, and Campbell diagram of the rotor. This study illustrates the differences between fixed and onboard rotors, focusing on the dynamic behavior of the system.

Appendix

Equations (17) and (18) present the damping and stiffness matrices of the discs, respectively, obtained by considering the motion of the rotor base.

$${\mathbf{D}}_{d}^{*} = \left[ {\begin{array}{*{20}c} 0 & {2M_{D} \dot{\beta }_{s} } & 0 & 0 \\ { - 2M_{D} \dot{\beta }_{s} } & 0 & 0 & 0 \\ 0 & 0 & 0 & {2\dot{\beta }_{s} I_{Dm} - \dot{\beta }_{s} I_{Dy} } \\ 0 & 0 & { - 2\dot{\beta }_{s} I_{Dm} + \dot{\beta }_{s} I_{Dy} } & 0 \\ \end{array} } \right]$$

(17)

$${\mathbf{K}}_{d}^{*} = \left[ {\begin{array}{*{20}c} { - M_{D} (\dot{\gamma }_{s}^{2} + \dot{\beta }_{s}^{2} )} & {M_{D} (\dot{\alpha }_{s} \dot{\gamma }_{s} + \ddot{\beta }_{s} )} & 0 & 0 \\ {M_{D} (\dot{\alpha }_{s} \dot{\gamma }_{s} - \ddot{\beta }_{s} )} & { - M_{D} (\dot{\alpha }_{s}^{2} + \dot{\beta }_{s}^{2} )} & 0 & 0 \\ 0 & 0 & {(I_{Dm} - I_{Dy} )(\dot{\gamma }_{s}^{2} - \dot{\beta }_{s}^{2} ) + I_{Dy} \dot{\beta }_{s} \varOmega } & {I_{Dy} \dot{\alpha }_{s} \dot{\gamma }_{s} + ( - \dot{\alpha }_{s} \dot{\gamma }_{s} + \ddot{\beta }_{s} )I_{Dm} } \\ 0 & 0 & {(\dot{\alpha }_{s} \dot{\gamma }_{s} + \ddot{\beta }_{s} )(I_{Dy} - I_{Dm} )} & {(I_{Dm} - I_{Dy} )(\dot{\alpha }_{s}^{2} - \dot{\beta }_{s}^{2} ) + I_{Dy} \dot{\beta }_{s} \varOmega } \\ \end{array} } \right]$$

(18)

in which I _Dm  = (I _Dx  + I _Dz )/2.

Equations (19) and (20) present the damping and stiffness matrices of the shaft, respectively, obtained by considering the motion of the rotor base.

$${\mathbf{D}}_{s}^{*} = 2\rho (\dot{\beta }_{s} S{\mathbf{D}}_{1} + I_{m} \varOmega {\mathbf{D}}_{2} )$$

(19)

$${\mathbf{K}}_{s}^{*} = \rho S({\mathbf{K}}_{1} + \ddot{\beta }_{s} {\mathbf{D}}_{1} + \dot{\gamma }_{s} \dot{\alpha }_{s} {\mathbf{K}}_{2} ) + \rho I_{m} \left[ {{\mathbf{K}}_{3} - (\ddot{\beta }_{s} + \dot{\gamma }_{s} \dot{\alpha }_{s} ){\mathbf{M}}_{4} + 2\dot{\beta }_{s} (\dot{\beta }_{s} + \varOmega ){\mathbf{M}}_{2} } \right],$$

(20)

where M ₂ and M ₄, K ₂, and D ₁ are mass, stiffness and damping matrices, respectively, which depend only of the length L (see Fig. 4). The stiffness matrices K ₁ and K ₃ are also dependent on $\dot{\alpha }_{s}$, $\dot{\beta }_{s}$, and $\dot{\gamma }_{s}$.

All these matrices and the ones common to the fixed base rotor can be seen in Duchemin [6].