Asymptotic action and asymptotic winding number for area-preserving diffeomorphisms of the disk

Abstract

Given a compactly supported area-preserving diffeomorphism of the disk, we prove an integral formula relating the asymptotic action to the asymptotic winding number. As a corollary, we obtain a new proof of Fathi’s integral formula for the Calabi homomorphism on the disk.

Résumé

Étant donné un difféomorphisme du disque à support compact qui préserve l’aire, nous prouvons une formule intégrale reliant l’action asymptotique au nombre d’enlacement asymptotique moyen. Comme corollaire, nous obtenons une nouvelle preuve de la formule intégrale de Fathi pour l’homomorphisme de Calabi sur le disque.

1 Introduction

Let $\phi : {\mathbb {D}}\rightarrow {\mathbb {D}}$ be a diffeomorphism of the disk ${\mathbb {D}}\subset {\mathbb {R}}^2$ compactly supported on the interior and preserving the standard area form $\omega _0 = dx\wedge dy$. If $\lambda$ is any primitive of $\omega _0$, we can define the action $a_{\phi ,\lambda }(z)$ of a point $z\in {\mathbb {D}}$ with respect to $\lambda$ as the value at z of the unique primitive of the exact form $\phi ^* \lambda - \lambda$ that vanishes near the boundary of ${\mathbb {D}}$. Equivalently, if one sees $\phi$ as the time-one map of the isotopy $\phi ^t$ that is obtained by integrating the vector field coming from a compactly supported time-dependent Hamiltonian $(z,t) \mapsto H_t(z)$, the action has the expression

$$\begin{aligned} a_{\phi ,\lambda }(z) = \int _{\{t\mapsto \phi ^t(z)\}} \lambda + \int _0^1 H_t(\phi ^t(z))\, dt. \end{aligned}$$

See Sect. 2 below for precise definitions and sign conventions. In general, the value $a_{\phi ,\lambda }(z)$ depends on the choice of the primitive $\lambda$, but it is independent of $\lambda$ at the fixed points of $\phi$. The integral of $a_{\phi ,\lambda }$ over the disk, which we denote by

$$\begin{aligned} {\mathcal {C}}(\phi ) := \int _{\mathbb {D}}a_{\phi ,\lambda } \,\omega _0, \end{aligned}$$

is also independent of the choice of $\lambda$. The real valued function $\phi \mapsto {\mathcal {C}}(\phi )$ is a homomorphism on $\text {Diff}_c({\mathbb {D}}, \omega _0)$, the group of area-preserving diffeomorphisms of ${\mathbb {D}}$ compactly supported in the interior and is named the Calabi homomorphism after [4].

In this note, we define the asymptotic action of $\phi$ as the limit

$$\begin{aligned} a_{\phi }^{\infty }(z) := \lim _{n\rightarrow \infty } \frac{a_{\phi ^n,\lambda }(z)}{n}. \end{aligned}$$

Indeed, a simple application of Birkhoff’s ergodic theorem implies that the above limit exists for almost every $z\in {\mathbb {D}}$ and defines a $\phi$-invariant integrable function $a_{\phi }^{\infty }$, whose integral over ${\mathbb {D}}$ coincides with the integral of $a_{\phi ,\lambda }$. In particular, if z is a k-periodic point of $\phi$, then the above limit exists and coincides with the average action of the orbit of z:

$$\begin{aligned} a_{\phi }^{\infty }(z) = \frac{1}{k} \sum _{j=0}^{k-1} a_{\phi ,\lambda }(\phi ^j(z)). \end{aligned}$$

As the notation suggests, the asymptotic action $a_{\phi }^{\infty }$ is independent of the primitive $\lambda$ and hence can be expected to capture dynamical properties of $\phi$. In [9], P. Py uses the Ergodic theorem in a similar context.

If x and y are distinct points of ${\mathbb {D}}$, the winding number $W_{\phi }(x,y)$ is defined as the winding number¹ of the curve

$$\begin{aligned}{}[0,1] \rightarrow {\mathbb {S}}^1, \qquad t\mapsto \frac{\phi ^t(y)-\phi ^t(x)}{\Vert \phi ^t(y)-\phi ^t(x)\Vert } = e^{i\theta (t)}, \end{aligned}$$

i.e.

$$\begin{aligned} W_{\phi }(x,y):= \frac{\theta (1)-\theta (0)}{2\pi }. \end{aligned}$$

In the definition, we have used a Hamiltonian isotopy $\phi ^t$ joining the identity to $\phi$, but the fact that the space $\text {Diff}_c({\mathbb {D}}, \omega _0)$ is contractible implies that the value of $W_{\phi }(x,y)$ does not depend on the choice of the isotopy. The asymptotic winding number of the pair (x, y) can now be defined as the ergodic limit

$$\begin{aligned} W_{\phi }^{\infty }(x,y) := \lim _{n\rightarrow \infty } \frac{W_{\phi ^n}(x,y)}{n}, \end{aligned}$$

which again exists for almost every pair (x, y) in ${\mathbb {D}}\times {\mathbb {D}}$ and defines an integrable function $W_\phi ^{\infty }$ on ${\mathbb {D}}\times {\mathbb {D}}$ that is invariant under the action of $\phi \times \phi$ and whose integral over ${\mathbb {D}}\times {\mathbb {D}}$ agrees with the integral of $W_{\phi }$. Moreover, if x is a k-periodic point of $\phi$ then the limit defining $W_{\phi }^{\infty }(x,y)$ exists for almost every $y\in {\mathbb {D}}$.

The main result of this note is the following formula relating the asymptotic action and the asymptotic winding number.

Theorem 1.1

If $\phi : {\mathbb {D}}\rightarrow {\mathbb {D}}$ is a compactly supported diffeomorphism of the disk ${\mathbb {D}}$ preserving the standard area form $\omega _0=dx\wedge dy$, then the identity

$$\begin{aligned} a_{\phi }^{\infty }(x) = \int _{{\mathbb {D}}} W_\phi ^{\infty } (x,y) \,\omega _0(y) \end{aligned}$$

holds for every x in a subset $\Omega$ of ${\mathbb {D}}$ that has full measure and contains all periodic points of $\phi$.

By integrating this identity over $\Omega$, and by using the fact that the integrals of the ergodic limits $a_{\phi }^{\infty }$ and $W_{\phi }^{\infty }$ agree with those of the functions $a_{\phi ,\lambda }$ and $W_{\phi }$, we obtain as an immediate corollary the following result, which is originally due to Fathi [5].

Corollary 1.2

The Calabi homomorphism on $\text {Diff}_c({\mathbb {D}}, \omega _0)$ can be expressed by the double integral

$$\begin{aligned} {\mathcal {C}}(\phi )=\int _{{\mathbb {D}}\times {\mathbb {D}}\setminus \Delta }W_\phi (x, y) \, \omega _0(x) \wedge \omega _0(y). \end{aligned}$$

Other proofs of this corollary are known. In [6], Gambaudo and Ghys give two algebraic proofs of it, one of which uses the fact that every homomorphism from $\text {Diff}_c({\mathbb {D}}, \omega _0)$ into ${\mathbb {R}}$ is a multiple of the Calabi homomorphism. The latter fact is a deep result of Banyaga, see [2]. An elementary proof of Corollary 1.2 using complex analysis is presented by Shelukhin in [10]. Our proof of Theorem 1.1 uses elementary results about intersection numbers between curves and surfaces in dimension three.

2 Action, winding and the Calabi homomorphism

Denote by $\omega _0:= dx\wedge dy$ the standard area form on ${\mathbb {R}}^2$ and by ${\mathbb {D}}\subset {\mathbb {R}}^2$ the unit disk. The symbol $\text {Diff}_c({\mathbb {D}}, \omega _0)$ denotes the group of smooth diffeomorphisms of ${\mathbb {D}}$ compactly supported on the interior which preserve $\omega _0$. The group $\text {Diff}_c({\mathbb {D}}, \omega _0)$ is contractible, see e.g. [3, 11].

2.1 Action of disk diffeomorphisms

Take $\phi \in \text {Diff}_c({\mathbb {D}}, \omega _0)$ and let $\lambda$ be a smooth primitive of $\omega _0$ on ${\mathbb {D}}$. Since $\phi$ preserves $\omega _0$, the 1-form $\phi ^* \lambda - \lambda$ is closed and hence exact on ${\mathbb {D}}$.

Definition 2.1

The action of $\phi$ with respect to $\lambda$ is the unique smooth function

$$\begin{aligned} a_{\phi , \lambda } : {\mathbb {D}}\rightarrow {\mathbb {R}}\end{aligned}$$

such that

$$\begin{aligned} da_{\phi ,\lambda } = \phi ^* \lambda - \lambda , \end{aligned}$$

(2.1)

and

$$\begin{aligned} a_{\phi ,\lambda } (z) = 0, \end{aligned}$$

(2.2)

for every $z\in \partial {\mathbb {D}}$.

The existence of the function $a_{\phi ,\lambda }$ satisfying (2.1) and (2.2) follows from the fact that any primitive of $\phi ^*\lambda -\lambda$ is constant on $\partial {\mathbb {D}}$ because $\phi _{|\partial {\mathbb {D}}}= \mathrm {id}.$

Lemma 2.2

Let ${ \phi }$ and ${\psi }$ be elements of $\mathrm {Diff}_c({\mathbb {D}}, \omega _0)$. Let $\lambda$ be a smooth primitive of $\omega _0$ and let u be a smooth real function on ${\mathbb {D}}$. Then:

• (i) $a_{ { \phi }, \lambda +du} = a_{ { \phi }, \lambda } + u\circ \phi - u$.

• (ii) $a_{ {\psi }\circ { \phi }, \lambda } = a_{ {\psi }, \lambda } \circ \phi + a_{ { \phi }, \lambda } = a_{ {\psi }, \lambda } + a_{ { \phi }, \psi ^* \lambda }$.

• (iii) $a_{ { \phi }^{-1}, \lambda } = - a_{ { \phi }, \lambda } \circ \phi ^{-1} = - a_{ { \phi }, ( \phi ^{-1})^*\lambda }$.

Proof

The first claim follow from the identities

$$\begin{aligned} \phi ^* (\lambda + du) - (\lambda + du) = d a_{ { \phi }, \lambda } + \phi ^* (du) - du = d(a_{ { \phi }, \lambda }+u\circ \phi - u), \end{aligned}$$

and

$$\begin{aligned} a_{ { \phi }, \lambda }(z) + u( \phi (z)) - u(z)=u( \phi (z)) - u(z)=0, \qquad \forall z\in \partial {\mathbb {D}}. \end{aligned}$$

The first identity in (ii) follows from

$$\begin{aligned} (\psi \circ \phi )^* \lambda - \lambda = \phi ^*(\psi ^* \lambda - \lambda ) + \phi ^* \lambda - \lambda = \phi ^*(da_{ {\psi }, \lambda }) + d a_{ { \phi }, \lambda } = d ( a_{ {\psi }, \lambda } \circ \phi + a_{ { \phi }, \lambda } ), \end{aligned}$$

and

$$\begin{aligned} a_{ { \phi }, \lambda } (z) + a_{ {\psi }, \lambda } ( \phi (z))=0, \qquad \forall z\in \partial {\mathbb {D}}. \end{aligned}$$

The second identity in (ii) follows from

$$\begin{aligned} (\psi \circ \phi )^* \lambda - \lambda = \phi ^*(\psi ^* \lambda ) - \psi ^* \lambda + \psi ^* \lambda - \lambda = d( a_{ { \phi }, \psi ^* \lambda } + a_{ {\psi }, \lambda }), \end{aligned}$$

and

$$\begin{aligned} \begin{aligned} a_{ {\psi }, \lambda }(z) + a_{ { \phi }, \psi ^* \lambda }(z)=0, \qquad \forall z\in \partial {\mathbb {D}}. \end{aligned} \end{aligned}$$

The two formulas in (iii) follow from those in (ii) applied to the case ${\psi }= { \phi }^{-1}$, because $a_{\mathrm {id}, \lambda }=0$ for every $\lambda$. $\square$

Remark 2.3

Statement (i) in the lemma above implies that the value of $a_{\phi ,\lambda }(z)$ is independent of the primitive $\lambda$ if $z\in {\mathbb {D}}$ is a fixed point of $\phi$.

It is convenient to view the action also in terms of the Hamiltonian formalism. Let $H:{\mathbb {D}}\times [0,1] \rightarrow {\mathbb {R}}$, $H_t(z)=H(z,t)$ be a smooth time-dependent Hamiltonian that vanishes near $\partial {\mathbb {D}}\times [0,1]$. Consider its time-dependent Hamiltonian vector field $X_t$, which is defined by the condition

$$\begin{aligned} \omega _0(X_{t}, \cdot ) = dH_t(\cdot ). \end{aligned}$$

(2.3)

We denote by $\phi ^t$ its non-autonomous flow, i.e. the isotopy that is defined by

$$\begin{aligned} \frac{d}{dt}\phi ^t=X_{t}\circ \phi ^t, \qquad \phi ^0 = \mathrm {id}. \end{aligned}$$

Any $\phi$ in $\text {Diff}_c({\mathbb {D}}, \omega _0)$ is the time-one map $\phi =\phi ^1$ of an isotopy $\phi ^t$ as above, which we shall call a Hamiltonian isotopy.

Proposition 2.4

If $\phi$, $\phi ^t$ and H are as above, then

$$\begin{aligned} a_{\phi , \lambda }(z)=\int _{ \{ t\rightarrow \phi ^t(z) \} }\lambda + \int _0^1 H_t(\phi ^t(z))dt. \end{aligned}$$

(2.4)

Proof

Let $\gamma :[0, 1]\rightarrow {\mathbb {D}}$ be a smooth path such that $\gamma (0)=z$ and $\gamma (1)\in \partial {\mathbb {D}}$. Define the smooth map

$$\begin{aligned} \psi : [0, 1]^2 \rightarrow {\mathbb {D}}, \qquad \psi (s, t) := \phi ^t(\gamma (s)). \end{aligned}$$

We compute the integral of $\psi ^*\omega _0$ on $[0, 1]^2$ in two different ways. The first computation gives us:

$$\begin{aligned} \begin{aligned} \int _{[0, 1]^2} \psi ^* \omega&= \int _{[0, 1]^2} \omega _0(\phi ^t(\gamma (s)))\left[ \frac{\partial }{\partial s} \phi ^t(\gamma (s)), X_{t} (\phi ^t(\gamma (s))) \right] \, ds \, dt \\&=- \int _{[0, 1]^2} dH_t(\phi ^t(\gamma (s)))\left[ \frac{\partial }{\partial s} \phi ^t(\gamma (s)) \right] \, ds\, dt \\&=- \int _0^1 \left( \int _0^1 \frac{\partial }{\partial s} H_t(\phi ^t(\gamma (s)))\, ds \right) \, dt \\&= - \int _0^1 \left( H_t(\phi ^t(\gamma (1))) - H_t(\phi ^t(z)) \right) \, dt = \int _0^1 H_t(\phi ^t(z))\, dt. \end{aligned} \end{aligned}$$

The second computation uses Stokes’ theorem and the fact that ${\phi ^t}|_{\partial {\mathbb {D}}}= \mathrm {id}$:

$$\begin{aligned} \begin{aligned} \int _{[0, 1]^2} \psi ^* \omega _0&= \int _{[0, 1]^2} \psi ^* d\lambda = \int _{[0, 1]^2} d\psi ^* \lambda = \int _{\partial [0, 1]^2} \psi ^* \lambda \\&= \int _{\gamma } \lambda + \int _{\{t\mapsto \phi ^t(\gamma (1))\}} \lambda - \int _{\phi \circ \gamma } \lambda - \int _{\{t\mapsto \phi ^t(z)\}}\lambda \\&= - \int _{\gamma } ( \phi ^* \lambda - \lambda ) - \int _{\{t\mapsto \phi ^t(z)\}} \lambda \\&= - \int _{\gamma } da_{\phi , \lambda } - \int _{\{t\mapsto \phi ^t(z)\}} \lambda \\&= a_{\phi , \lambda }(z) - \int _{\{t\mapsto \phi ^t(z)\}}\lambda . \end{aligned} \end{aligned}$$

The desired formula for $a_{\phi , \lambda }(z)$ follows by comparing the above two identities.

$\square$

2.2 The Calabi homomorphism

Introduced by Calabi in [4], the Calabi homomorphism is an important tool in the study of the structure of the group of Hamiltonian diffeomorphisms of a symplectic manifold. Next we give a definition in our context, see [8] for a further discussion.

Definition 2.5

The Calabi homomorphism is the map

$$\begin{aligned} {\mathcal {C}}:\text {Diff}_c({\mathbb {D}}, \omega _0) \rightarrow {\mathbb {R}}\end{aligned}$$

defined by

$$\begin{aligned} {\mathcal {C}}(\phi )=\int _{{\mathbb {D}}}a_{\phi , \lambda }\, \omega _0. \end{aligned}$$

The first thing we remark is that this map is well defined, meaning that it does not depend on the choice of the primitive of $\omega _0$. This follows from Lemma 2.2(i) and the fact that $\phi$ is an area preserving diffeomorphism.

Next we should prove that it is in fact a homomorphism. This is the following:

Proposition 2.6

If $\phi , \psi \in \text {Diff}_c({\mathbb {D}}, \omega _0)$ then ${\mathcal {C}}(\phi \circ \psi )={\mathcal {C}}(\phi )+{\mathcal {C}}(\psi )$.

Proof

From Lemma 2.2(ii) we have

$$\begin{aligned} a_{\phi \circ \psi , \lambda }=a_{\psi , \phi ^*\lambda }+a_{\phi , \lambda }, \end{aligned}$$

and integrating on both sides we get the desired result.

$\square$

Remark 2.7

We can express ${\mathcal {C}}(\phi )$ also in terms of a defining Hamiltonian. If $H: {\mathbb {D}}\times [0,1] \rightarrow {\mathbb {R}}$ is a time-dependent Hamiltonian vanishing near $\partial {\mathbb {D}}\times [0,1]$ such that the time-one map of the corresponding Hamiltonian isotopy is $\phi$, then ${\mathcal {C}}(\phi )$ is given by the formula

$$\begin{aligned} {\mathcal {C}}({\phi }) = 2 \int _{{\mathbb {D}}\times [0,1]} H(z,t)\, \omega _0 \wedge dt. \end{aligned}$$

The proof of this equality can be found in [8] [Lemma 10.27] or as a consequence of (2.4) and with the above notation as in [1] [Prop 2.7] in the more general setting of Hamiltonian diffeomorphisms of ${\mathbb {D}}$ that are not necessarily compactly supported. It can be used for instance, to show that the Calabi homomorphism is not continuous in the $\text {C}^0$-topology. This can be done by constructing radially defined Hamiltonians using bump functions with fixed non-zero integral and whose time one-maps converge to the identity, as shown in [6].

2.3 Winding and intersection numbers for disk diffeomorphisms

Let $\phi \in \text {Diff}_c({\mathbb {D}}, \omega _0)$ and let $\phi ^t$ be a compactly supported Hamiltonian isotopy such that $\phi ^0=\mathrm {id}$ and $\phi ^1=\phi$.

Definition 2.8

The winding number $W_\phi (x, y)$ of a pair of distinct points $x,y\in {\mathbb {D}}$ is the real number

$$\begin{aligned} W_\phi (x, y):=\frac{{\theta }(1)-{\theta }(0)}{2\pi }, \end{aligned}$$

where $\theta : [0,1] \rightarrow {\mathbb {R}}$ is a continuous function such that

$$\begin{aligned} \frac{\phi ^t(y)-\phi ^t(x)}{||\phi ^t(y)-\phi ^t(x)||}=e^{i\theta (t)}. \end{aligned}$$

(2.5)

The value of $W_\phi (x, y)$ does not depend on the isotopy joining $\phi$ to the identity. This holds because $\text {Diff}_c({\mathbb {D}},\omega _0)$ is contractible and in particular any two paths joining $\phi$ to the identity are homotopic, which implies that the winding number is the same. The map $W_\phi$ is smooth and bounded on $({\mathbb {D}}\times {\mathbb {D}})\setminus \Delta$, where $\Delta$ denotes the diagonal $\{(x, x)|x\in {\mathbb {D}}\}$ in ${\mathbb {D}}\times {\mathbb {D}}$ (see [6]).

We want to define another relevant quantity and for this we need to work with intersection numbers in dimension three.

To begin with, consider an embedded compact oriented curve $\Gamma \subset {\mathbb {D}}\times [0,1]$. If $S \subset {\mathbb {D}}\times [0,1]$ is a compact co-oriented surface, that is, the normal bundle ${\mathcal {N}}S$ is oriented, then an intersection point $p\in S\cap \Gamma$ is called transverse if

$$\begin{aligned} T_p \Gamma \oplus T_p S=T_p ({\mathbb {D}}\times [0,1]). \end{aligned}$$

A transverse intersection point p is called positive if the orientation of $T_p\Gamma$ coincides with the orientation of ${\mathcal {N}}_p S$ and otherwise is called negative. Assume that $\Gamma$ is everywhere transverse to S. Then the set $\Gamma \cap S$ is finite and we denote by $I_+(\Gamma ,S)$ the number of positive intersections and $I_-(\Gamma ,S)$ the number of negative intersections. The difference of these two numbers defines the intersection number of $\Gamma$ and S:

$$\begin{aligned} I(\Gamma ,S) := I_+(\Gamma ,S) - I_-(\Gamma ,S) \in {\mathbb {Z}}. \end{aligned}$$

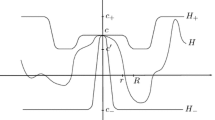
Let $\phi \in \text {Diff}_c({\mathbb {D}}, \omega _0)$ and $\{\phi ^t\}_{t\in [0, 1]}$ be a Hamiltonian isotopy that connects the identity to $\phi$. Given $x\in {\mathbb {D}}$, we denote by $\Gamma _{\phi }(x)$ the embedded curve

$$\begin{aligned} \Gamma _{\phi }(x) := \{ (\phi ^t(x),t) \mid t\in [0,1] \} \subset {\mathbb {D}}\times [0,1] \end{aligned}$$

with its natural orientation. Fix an element $e\in \partial {\mathbb {D}}$ and for every $x \text { in the interior of } {\mathbb {D}}$ consider the compact surface

$$\begin{aligned} S^e_\phi (x)\subset {\mathbb {D}}\times [0,1] \end{aligned}$$

that is obtained by connecting each point $(\phi ^t(x),t)$ of $\Gamma _{\phi }(x)$ to the boundary point (e, t) by a line segment. In other words, $S^e_\phi (x)$ is parametrized by the smooth embedding

$$\begin{aligned} {} \Psi :[0, 1] \times [0, 1]&\rightarrow {\mathbb {D}}\times [0, 1],&(t,r) \mapsto (\phi ^t(x) + r(e-\phi ^t(x)), t), \end{aligned}$$

(2.6)

which induces an orientation on S. We consider the disk and real line as having their canonical orientations and the ambient space ${\mathbb {D}}\times [0,1]$ the induced product orientation. The vector

$$\begin{aligned} (i(e-\phi ^t(x)),0 )\in T_{\Psi (t,r)}({\mathbb {D}}\times [0,1]), \end{aligned}$$

(2.7)

where i denotes the counterclockwise rotation by $\pi /2$ on ${\mathbb {R}}^2$, is everywhere transverse to $S_\phi ^e(x)$ and hence defines a co-orientation of this surface. We note that this co-orientation coincides with that induced by the above mentioned orientations on $S_\phi ^e(x)$ and ${\mathbb {D}}\times [0,1]$. Indeed, it suffices to check this at a single point, and we observe that at the point $(e,0)\in S_\phi ^e(x)\subset {\mathbb {D}}\times [0,1]$, the basis $\{\partial _t\Psi , \partial _r\Psi , \big (i(e-\phi ^t(x)),0\big )\}$ equals $\{(0,1),\big (e-\phi ^t(x),0\big ),\big (i(e-\phi ^t(x)),0\big ) \}$ which has the same orientation as $\{\big (e-\phi ^t(x),0\big ),\big (i(e-\phi ^t(x)),0\big ),(0,1)\}$ which is clearly positive.

If x is an interior point of ${\mathbb {D}}$ and $y\ne x$ is another point in ${\mathbb {D}}$, then we define the intersection number of $x \text { and } y$ as

$$\begin{aligned} I^e_\phi (x, y):= I(\Gamma _{\phi }(y), S^e_\phi (x)), \end{aligned}$$

whenever $\Gamma _{\phi }(y)$ meets $S^e_\phi (x)$ transversely.

Fig. 1

$I(\Gamma _{\phi }(y), S^e_\phi (x))=0$

Remark 2.9

Given $x\ne y$ as above, it follows from Sard’s theorem that the set of points $e\in \partial {\mathbb {D}}$ for which $\Gamma _{\phi }(y)$ is transverse to $S^e_{\phi }(x)$ has full Lebesgue measure. Furthermore, even though the definition above depends on the choice of the element $e\in \partial {\mathbb {D}}$, a different choice of e changes the value of $I_{\phi }^e(x,y)$ by at most one. This follows from Proposition 2.10 below.

Next we relate the winding number and the intersection number.

Proposition 2.10

Let $x\in \mathrm {int}({\mathbb {D}})$, $y\in {\mathbb {D}}\setminus \{x\}$ and $e\in \partial {\mathbb {D}}$ be such that $\Gamma _{\phi }(y)$ meets $S^e_{\phi }(x)$ transversally. Then

$$\begin{aligned} \Big |W_\phi (x, y)-I^e_\phi (x, y)\Big |\le \frac{3}{2}. \end{aligned}$$

(2.8)

Remark 2.11

Although we will not use this fact, the constant $\frac{3}{2}$ in (2.8) is optimal.

Proof

For every $t\in [0,1]$, we can push out the trajectory of y in ${\mathbb {D}}\times [0,1]$ to the boundary of the cylinder in the following way: consider the curve $\beta :[0,1]\rightarrow \partial {\mathbb {D}}\times [0,1]$ defined by $\beta (t)=(h_t(\phi ^t(y)),t)$ where $h_t:{\mathbb {D}}\rightarrow \partial {\mathbb {D}}$ maps each ray from $\phi ^t(x)$ to its intersection with $\partial {\mathbb {D}}$. More precisely, every $z\ne \phi ^t(x)$ in ${\mathbb {D}}\setminus \{\phi ^t(x)\}$ can be written as $z=\phi ^t(x)+r e^{i\alpha }$ where

$$\begin{aligned} r=|z-\phi ^t(x)| \text { and } e^{i\alpha }:=\frac{z-\phi ^t(x)}{|z-\phi ^t(x)|}, \end{aligned}$$

and we set

$$\begin{aligned} h_t(z):=\phi ^t(x)+R e^{i\alpha }, \end{aligned}$$

where

$$\begin{aligned} R =\max \{s>0|\, ||\phi ^t(x)+se^{i\alpha (z) }|| \le 1 \}. \end{aligned}$$

The winding of this new trajectory on $\partial {\mathbb {D}}$ is given by

$$\begin{aligned} w_\phi (x,y)=\frac{\sigma (1)-\sigma (0)}{2\pi } \end{aligned}$$

where

$$\begin{aligned} e^{i \sigma (t)}=h_t(\phi ^t(y)). \end{aligned}$$

Since the absolute value of the angle between the vectors $\phi ^t(y)-\phi ^t(x)$ and $h_t(\phi ^t(y))$ is not larger than $\frac{\pi }{2}$, the lifts $\sigma$ as above and $\theta$ as in (2.5) can be chosen so that $|\theta (t)-\sigma (t)|\le \frac{\pi }{2}$. It follows that

$$\begin{aligned} |w_\phi (x,y)-W_\phi (x,y)|\le \frac{1}{2}. \end{aligned}$$

(2.9)

Next, we consider the curve $\eta :[0, 1] \rightarrow \partial {\mathbb {D}}$,

$$\begin{aligned} t \rightarrow \eta (t):=h_t(\phi ^t(y)), \end{aligned}$$

and extend it to a closed curve ${\hat{\eta }}: [0,2] \rightarrow \partial {\mathbb {D}}$ in such a way that ${\hat{\eta }}((1,2))$ does not contain the chosen point $e\in \partial {\mathbb {D}}$ used in the definition of $I^e_\phi (x,y)$. The absolute value of the winding number of the curve ${\hat{\eta }}|_{[1,2]}$ does not exceed one. We now lift ${\hat{\eta }}$ to a self-map of $\partial {\mathbb {D}}$:

$$\begin{aligned} f:\partial {\mathbb {D}} \rightarrow \partial {\mathbb {D}}, \qquad e^{ 2 \pi i t} \mapsto {\hat{\eta }}(2t). \end{aligned}$$

The oriented degree of this map coincides with its winding number, which differs from the winding number $w_\phi (x,y)$ exactly by the winding number of ${\hat{\eta }}|_{[1,2]}$, and hence

$$\begin{aligned} |w_\phi (x,y)-\deg (f)|\le 1. \end{aligned}$$

On the other hand, our transversality assumption implies that e is a regular value for the map f, so the oriented degree of this map can be computed as

$$\begin{aligned} \deg (f)=\sum _{q\in f^{-1}(e)}\text {sgn}(f'(q)), \end{aligned}$$

but we claim that the latter sum gives us precisely $I_{\phi }^e(x,y)$. To see this, first notice that from the construction of f it follows that $q=e^{2\pi it}\in f^{-1}(e)$ if and only if $h_t(\phi ^t(y))=e$, or equivalently if $(\phi ^t(y),t)\in S^e_\phi (x)$. This shows that there is a one-to-one correspondence between the sets $f^{-1}(e)$ and $\Gamma _{\phi }(y)\cap S^e_\phi (x)$. Finally since the orientation on $\partial {\mathbb {D}}$ is induced by orientation of ${\mathbb {D}}$, which in turn defines the orientation on ${\mathbb {D}}\times [0,1]$, we see that $\text {sgn}(f'(e^{2\pi i t}))=+ 1\text {(respectively } -1)$ if and only if $(\phi _t(y),t)\in \Gamma _{\phi }(y)\cap S^e_\phi (x)$ is a positive (respectively negative) intersection point. These observations settle the claim. This fact, together with (2.9), yields (2.8). $\square$

In order to state the next result, we need to fix some notation and recall some basic facts about the oriented degree for smooth maps between surfaces. Let M and N be two oriented surfaces (possibly with boundary), with M compact, and let $f:M\rightarrow N$ be a smooth map. We set

$$\begin{aligned} N_{\text {reg}}(f) :=\{y\in N |\, y \text { is a regular value of } f\}. \end{aligned}$$

Then by Sard’s theorem $N\setminus {N_{\text {reg}}(f)}$ has measure zero. For every $y\in N_{\text {reg}}(f)\setminus f(\partial M)$ the set $f^{-1}(y)$ is finite and the degree of f relative to y is the integer

$$\begin{aligned} \deg (f,M,y)=\sum _{x\in f^{-1}(y)}\text {sgn}\det df(x) \in {\mathbb {Z}}. \end{aligned}$$

(2.10)

Furthermore, the function $y\mapsto \deg (f,M,y)$ extends to a locally constant function on $N\setminus {f(\partial M)}$, and for $\eta$ any 2-form on N we have the identity

$$\begin{aligned} \int _M f^*\eta =\int _N \deg (f,M,y)\, \eta (y). \end{aligned}$$

(2.11)

We shall now show that $I_\phi ^e(x,y)$ coincides with the degree of a suitable map between two oriented surfaces. Let $x\in {\mathbb {D}}$ and $e\in \partial {\mathbb {D}}$ be as above and consider the smooth map

$$\begin{aligned} \rho :S_\phi ^e(x) \rightarrow {\mathbb {D}}, \qquad \rho (z,t):=(\phi ^t)^{-1}(z). \end{aligned}$$

Note that the boundary of $S_\phi ^e(x)$ consists of the two curves $\Gamma _{\phi }(x)$ and $\Gamma _{\phi }(e)=\{e\}\times [0,1]$ and of the line segments $[x,e]\times \{0\}$ and $[\phi (x),e]\times \{1\}$. The curves $\Gamma _{\phi }(x)$ and $\Gamma _{\phi }(e)$ are mapped into x and e by $\rho$, whereas $[x,e]\times \{0\}$ and $[\phi (x),e]\times \{1\}$ are mapped into [x, e] and $\phi ^{-1}([\phi (x),e])$, respectively. We conclude that

$$\begin{aligned} \rho (\partial S_{\phi }^e(x)) = [x,e] \cup \phi ^{-1}([\phi (x),e]). \end{aligned}$$

In the following result, the disk ${\mathbb {D}}$ is given its standard orientation and the surface $S_\phi ^e(x)$ the orientation that is induced by the parametrization (2.6), meaning that

$$\begin{aligned} \partial _t \Psi (t,r) = \bigl ( (1-r) X_t(\phi ^t(x)),1\bigr ), \qquad \partial _r \Psi (t,r) = \bigl ( e-\phi ^t(x),0 \bigr ) \end{aligned}$$

(2.12)

is a positively oriented basis of $T_{\Psi (t,r)} S_\phi ^e(x)$, for every $(t,r)\in [0,1]\times [0,1]$. With respect to these orientations the degree of the map $\rho$ is well defined and at regular values is given by the formula (2.10). Recall that the intersection number $I_\phi ^e(x,y)$ of the curve $\Gamma _{\phi }(y)$ with the surface $S_\phi ^e(x)$ is defined with respect to the co-orientation in (2.7).

Lemma 2.12

The point $y\in {\mathbb {D}}$ is a regular value for $\rho$ if and only if the curve $\Gamma _\phi (y)$ meets $S_\phi ^e(x)$ transversally. Moreover, whenever y is a regular value for $\rho$, we have the identity

$$\begin{aligned} \deg (\rho ,S_\phi ^e(x),y)=I_\phi ^e(x,y). \end{aligned}$$

(2.13)

Proof

Set for simplicity $S:= S_\phi ^e(x)$. The map $\rho$ is the restriction to the surface S of the map

$$\begin{aligned} {\tilde{\rho }} : {\mathbb {D}}\times [0,1] \rightarrow {\mathbb {D}}, \qquad (z,t) \mapsto (\phi ^t)^{-1}(z). \end{aligned}$$

The restriction of ${\tilde{\rho }}$ to ${\mathbb {D}}\times \{t\}$ is a diffeomorphism for every $t\in [0,1]$ and hence ${\tilde{\rho }}$ is a submersion. The inverse image of each $y\in {\mathbb {D}}$ by ${\tilde{\rho }}$ is the curve

$$\begin{aligned} {\tilde{\rho }}^{-1}(y) = \Gamma _{\phi }(y), \end{aligned}$$

and hence if ${\tilde{\rho }}(z,t)=y$ we have

$$\begin{aligned} \ker d{\tilde{\rho }}(z,t) = T_{(z,t)} \Gamma _\phi (y) = {\mathbb {R}}{\tilde{X}}(z,t), \end{aligned}$$

(2.14)

where

$$\begin{aligned} {\tilde{X}}(z,t) := \bigl ( X_t(z),1 \bigr ). \end{aligned}$$

These considerations imply that $(z,t)\in S$ belongs to $\rho ^{-1}(y)$ if and only if $\Gamma _\phi (y)$ and S meet at (z, t). Fix such a point $(z,t)\in \Gamma _\phi (y)\cap S$. Then the range of $d\rho (z,t)$ equals the range of $d{\tilde{\rho }}(z,t)|_{T_{(z,t)}S}$ which is surjective if and only if it coincides with the range of $d{\tilde{\rho }}(z,t)$, which, since the latter is a submersion, is the case if and only if the kernel of $d{\tilde{\rho }}(z,t)$ is transverse to $T_{(z,t)}S$. From (2.14), this shows that $y\in {\mathbb {D}}$ is a regular value for $\rho$ if and only if the curve $\Gamma _\phi (y)$ meets S transversally.

To prove the second part of the Lemma, we fix a regular value $y\in {\mathbb {D}}$ for $\rho$ and we fix a point

$$\begin{aligned} (z,t)\in \rho ^{-1}(y) = \Gamma _\phi (y) \cap S. \end{aligned}$$

We wish to prove that this intersection point is positive if and only if $d\rho (z,t)$ is orientation preserving. Once this is proven, the last claim of the Lemma follows from the formula (2.10) for the degree with respect to a regular value.

Recall $\Psi$ the parametrization of S given by (2.6). This gives us the basis

$$\begin{aligned} (v,1):=\partial _t\Psi (t,r)=\Big ((1-r)X_t(\phi ^t(x)),1\Big )\qquad (u,0):=\partial _r\Psi (t,r)=\Big (e-\phi ^t(x),0\Big ) \end{aligned}$$

for the tangent space $T_{\Psi (t,r)}S$, while $T_{\Psi (t,r)}\Gamma _\phi (y)$ is generated by the non-zero vector

$$\begin{aligned} (w,1):=\Big (X\big (\phi ^t(x) + r(e-\phi ^t(x))\big ),1\Big ). \end{aligned}$$

The co-orientation of S at (z, t) is given as in (2.7) by the vector (iu, 0). The intersection at $\Psi (t,r)$ is by definition positive, precisely when the two co-orientations (iu, 0) and (w, 1) of $T_{\Psi (t,r)}S$ agree. In other words, precisely when the two bases $\big ((v,1),(u,0),(w,1)\big )$ and $\big ((v,1),(u,0),(iu,0)\big )$ determine the same orientation for $T_{(z,t)}{({\mathbb {D}}\times [0,1])}$. By the discussion following (2.7) the latter is the standard orientation on ${\mathbb {D}}\times [0,1]$. Hence it is enough to prove that $\big ((v,1),(u,0),(w,1)\big )$ is a positive basis if and only if $d\rho (z,t)$ is orientation preserving with respect to the basis $\big ((v,1),(u,0)\big )$ for $T_{\Psi (t,r)}S$. The basis $\bigl ((v,1),(u,0),(w,1)\bigr )$ is positive if and only if the following determinants are positive

$$\begin{aligned} \det \left( \begin{array}{c@{\quad }c} v &{} 1 \\ u &{} 0 \\ w &{} 1 \end{array} \right) = \det \left( \begin{array}{c@{\quad }c} v-w &{} 0 \\ u &{} 0 \\ w &{} 1 \end{array} \right) = \det \left( \begin{array}{c@{\quad }c} v-w \\ u \end{array} \right) . \end{aligned}$$

Since $\phi$ is isotopic to the identity, so $d(\phi ^t)^{-1}(z,t)$ must be symplectic and therefore

$$\begin{aligned} \det \left( \begin{array}{c@{\quad }c} v-w \\ u \end{array} \right) = \det \left( \begin{array}{c@{\quad }c} d(\phi ^t)^{-1}(z,t)[v-w] \\ d(\phi ^t)^{-1}(z,t)[u] \end{array} \right) = \det d{\hat{\rho }}(t,r) \end{aligned}$$

where $\det d{\hat{\rho }}(t,r)$ is taken with respect to the standard basis of ${\mathbb {R}}^2$ and the basis $\partial _t,\partial _r$ of $T_{(t,r)}[0,1]^2$. The last equality above follows from the computation of the tangent map $d{\hat{\rho }}(t,r):T_{(t,r)}[0,1]^2 \rightarrow T_y {\mathbb {D}}$ as

$$\begin{aligned} d{\hat{\rho }}(t,r)[\partial _{r}]&=d(\phi ^t)^{-1}\big (\phi ^t(x) + r(e-\phi ^t(x))\big )[e-\phi ^{t}(x)]\\&=d(\phi ^t)^{-1}(z,t)[u],\\ d{\hat{\rho }}(t,r)[\partial _t]&=-X\left( (\phi ^t)^{-1}\big (\phi ^t(x) + r(e-\phi ^t(x))\big )\right) \\&\quad +(1-r)d(\phi ^t)^{-1}\big (\phi ^t(x) + r(e-\phi ^t(x))\big )[X(\phi ^{t}(x))]\\&=d(\phi ^t)^{-1}\big (\phi ^t(x) + r(e-\phi ^t(x))\big )[-X(\phi ^t(x) + r(e-\phi ^t(x))\\&\quad +(1-r)X(\phi ^{t}(x))]\\&= d(\phi ^t)^{-1}(z,t)[v-w]. \end{aligned}$$

Since $d{\hat{\rho }}(t,r)$ is orientation preserving if and only if $d\rho (z,t)$ also is, we conclude ${\tilde{X}}(z,t)$ positively intersects S at (z, t) if and only if $d\rho (z,t)$ is orientation preserving. $\square$

Remark 2.13

The above lemma and Sard’s theorem imply that $\Gamma _\phi (y)$ meets $S_\phi ^e(x)$ transversally for almost every $y\in {\mathbb {D}}$. Together with the properties of the oriented degree mentioned above, this lemma implies also that the function $I_\phi ^e(x,\cdot )$ extends to a locally constant function on ${\mathbb {D}}\setminus ([x,e] \cup \phi ^{-1}([\phi (x),e]))$. Of course, this extension could also be obtained by defining the intersection number of an oriented curve and a co-oriented surface without assuming transversality, but just the condition that there are no intersections on either of the two boundaries, by the usual perturbation argument. Actually, we shall not need this extension of the function $y\mapsto I_{\phi }^e(x,y)$: It will be enough to know that it is well-defined for almost every $y\in {\mathbb {D}}$ and that the bound of Proposition 2.10 and the identity of Lemma 2.12 hold.

3 Asymptotic action & asymptotic winding number

In this section we define the asymptotic versions of the action and winding number introduced in the previous section. These definitions build on Birkhoff’s ergodic theorem, which we shall use in the following form.

Theorem

(Birkhoff’s Ergodic Theorem) If $\varphi$ is an endomorphism of a finite measure space $(\Omega , {\mathcal {A}}, \mu )$ and if $f\in L^1(\Omega ,{\mathcal {A}},\mu )$, then the averages

$$\begin{aligned} A_n f=\frac{1}{n}\sum _{i=0}^{n-1}f\circ \varphi ^i \end{aligned}$$

converge $\mu -$a.e. and in $L^1(\Omega ,{\mathcal {A}},\mu )$ to a $\varphi$-invariant function $\bar{f}$. Furthermore for each $\varphi$-invariant $A\in {\mathcal {A}}$

$$\begin{aligned} \int _{A}\bar{f}d\mu =\int _A fd\mu . \end{aligned}$$

(3.1)

3.1 Asymptotic action

In our setup we will work with the space $({\mathbb {D}}, {\mathcal {B}}, \mu )$ where ${\mathcal {B}}$ is the Borel $\sigma$-algebra on ${\mathbb {D}}$ and $\mu$ is the Lebesgue measure.

Definition 3.1

Let $\phi \in \text {Diff}_c({\mathbb {D}}, \omega _0)$ and let $\lambda$ be a smooth primitive of $\omega _0$ on ${\mathbb {D}}$. With $a_{\phi , \lambda }$ as presented before we define the asymptotic action of $\phi$ with respect to $\lambda$ as the limit

$$\begin{aligned} a^\infty _{\phi , \lambda }(z)=\lim _{n\rightarrow \infty }\frac{a_{\phi ^n, \lambda }(z)}{n}. \end{aligned}$$

By Lemma 2.2(ii) we can write

$$\begin{aligned} \frac{a_{\phi ^n, \lambda }(z)}{n}=\frac{1}{n}\sum _{j=0}^{n-1}a_{\phi , \lambda }(\phi ^j(z)) \end{aligned}$$

(3.2)

and then taking $n\rightarrow \infty$ and applying Birkhoff’s ergodic theorem we can ensure that the limit $a^\infty _{\phi , \lambda }(z)$ exists for almost every $z\in {\mathbb {D}}$. Furthermore, Birkhoff’s theorem guarantees that

$$\begin{aligned} \int _{{\mathbb {D}}}a^\infty _{\phi , \lambda }(z)\, \omega _0(z)=\int _{\mathbb {D}}a_{\phi , \lambda }(z)\, \omega _0(z). \end{aligned}$$

(3.3)

The first thing to remark is that the asymptotic action does not depend on the primitive $\lambda$ of $\omega _0$.

Proposition 3.2

The asymptotic action $a^\infty _{\phi , \lambda }$ is independent of the primitive $\lambda$ of $\omega _0$.

Proof

Let $\lambda +du$ be another primitive of $\omega$. Then by Lemma 2.2(i) the action with respect to this primitive is

$$\begin{aligned} a_{\phi , \lambda +du}=a_{\phi , \lambda }+u\circ \phi -u. \end{aligned}$$

We can now check the Birkhoff sum up to a finite order

$$\begin{aligned} \sum _{j=0}^{n-1} a_{\phi , \lambda +du}(\phi ^j(z))=\sum _{j=0}^{n-1} a_{\phi , \lambda }(\phi ^j(z)+\sum _{j=0}^{n-1} (u\circ \phi -u)(\phi ^j(z)). \end{aligned}$$

Note that the last term on the right hand side is a telescopic sum of the form

$$\begin{aligned} \sum _{j=0}^{n-1} \bigl ( u(\phi ^{j+1}(z))-u(\phi ^{j}(z)) \bigr ) =u(\phi ^{n}(z))-u(z), \end{aligned}$$

and this is uniformly bounded for all n. Therefore when taking the Birkhoff average, this last term goes to zero i.e.

$$\begin{aligned} \lim _{n\rightarrow \infty }\frac{1}{n}\sum _{j=0}^{n-1} a_{\phi , \lambda }(\phi ^j(z))=\lim _{n\rightarrow \infty }\frac{1}{n}\sum _{j=0}^{n-1} a_{\phi , \lambda +du}(\phi ^j(z)). \end{aligned}$$

This shows that $a_{\phi , \lambda }^\infty (z)$ does not depend on the primitive $\lambda$. More precisely, the existence and value of the limit of $a_{\phi ^n,\lambda }(z)/n$ do not depend on the primitive $\lambda$. $\square$

This lets us write from now on the asymptotic action as $a_\phi ^\infty$. It readily follows from (3.2) that if z is a k-periodic point of the map $\phi$, then the asymptotic action of $\phi$ coincides with the average action of the orbit of z:

$$\begin{aligned} a_{\phi }^{\infty }(z) = \frac{1}{k} \sum _{j=0}^{k-1} a_{\phi ,\lambda }(\phi ^j(z)). \end{aligned}$$

(3.4)

The average action of periodic points is the object of study of [7], in which Hutchings proves the existence of periodic points of $\phi$ whose action satisfies suitably bounds in terms of ${\mathcal {C}}(\phi )$.

3.2 Asymptotic winding number

In the same way as with the action we now consider the asymptotic winding number.

Definition 3.3

The asymptotic winding number of $\phi \in \text {Diff}_c({\mathbb {D}}, \omega _0)$ is the limit

$$\begin{aligned} W^\infty _\phi (x, y)=\lim _{n\rightarrow \infty } \frac{W_{\phi ^n}(x, y)}{n}. \end{aligned}$$

To guarantee its existence we can also use Birkhoff’s ergodic theorem. This time we take

$$\begin{aligned} (Q:={\mathbb {D}}\times {\mathbb {D}},\, {\mathcal {B}}({\mathbb {D}}\times {\mathbb {D}}),\, \mu _Q :=\mu \oplus \mu ) \end{aligned}$$

with the action of $\phi _Q:=(\phi , \phi )$. It is a fact that $W_\phi \in L^1(Q,{\mathcal {B}}({\mathbb {D}}\times {\mathbb {D}}),\mu _Q)$, see [6] for a proof. For $x\ne y$ in ${\mathbb {D}}$ the winding number satisfies

$$\begin{aligned} W_{\phi ^n}(x, y)=\sum _{j=0}^{n-1}W_\phi (\phi _Q^j(x, y)), \end{aligned}$$

and hence the time average

$$\begin{aligned} W_\phi ^\infty (x, y)=&\lim _{n\rightarrow \infty }\frac{W_{\phi ^n}(x, y)}{n}\\=&\lim _{n\rightarrow \infty }\frac{1}{n}\sum _{j=0}^{n-1}W_\phi (\phi _Q^j(x, y)) \end{aligned}$$

exists for $\mu _Q$-a.e $(x, y)\in {\mathbb {D}}\times {\mathbb {D}}$. Furthermore Birkhoff’s theorem ensures that the time and space averages coincide i.e.

$$\begin{aligned} \int _{{\mathbb {D}}\times {\mathbb {D}}}W^\infty _\phi (x, y)\, \omega _0(x) \wedge \omega _0(y)=\int _{{\mathbb {D}}\times {\mathbb {D}}}W_\phi (x, y) \, \omega _0(x) \wedge \omega _0(y). \end{aligned}$$

(3.5)

In particular $W_\phi ^\infty$ is an integrable function and hence by the theorem of Fubini-Tonelli we obtain that the integral

$$\begin{aligned} \int _{{\mathbb {D}}}W_\phi ^\infty (x, y) \, \omega _0(y) \end{aligned}$$

(3.6)

is well-defined for almost every $x\in {\mathbb {D}}$ and defines an integrable function of x.

Remark 3.4

If x is a k-periodic point of $\phi$, then the sequence of functions

$$\begin{aligned} y \mapsto \frac{W_{\phi }^n(x,y)}{n} \end{aligned}$$

converges to $W_{\phi }^{\infty }(x,y)$ for almost every $y\in {\mathbb {D}}$ and in $L^1({\mathbb {D}})$. Indeed, the identity

$$\begin{aligned} W_{\phi ^{kh}}(x,y) = \sum _{j=0}^{h-1} W_{\phi ^k}(\phi ^{kj}(x),\phi ^{kj}(y)) = \sum _{j=1}^{h-1} W_{\phi ^k}(x,\phi ^{kj}(y)) \end{aligned}$$

shows that this function of y is the Birkhoff sum of the function $y\mapsto W_{\phi ^k}(x,y)$ with respect to the map $\phi ^k$. By Birkhoff’s ergodic theorem, there is an integrable function $w:{\mathbb {D}}\rightarrow {\mathbb {R}}$ such that

$$\begin{aligned} \frac{W_{\phi ^{kh}}(x,y)}{h} \rightarrow w(y) \end{aligned}$$

for almost every $y\in {\mathbb {D}}$ and in $L^1({\mathbb {D}})$. Together with the uniform bound

$$\begin{aligned} \left| W_{\phi ^{k \lceil \frac{n}{k} \rceil }} (x,y) - W_{\phi ^n}(x,y) \right| = \left| \sum _{j=n}^{k \lceil \frac{n}{k} \rceil - 1} W_{\phi }(\phi ^j(x),\phi ^j(y)) \right| \le k \Vert W_{\phi }\Vert _{\infty }, \end{aligned}$$

this implies that the sequence of functions

$$\begin{aligned} y \mapsto \frac{W_{\phi }^n(x,y)}{n} \end{aligned}$$

converges to $W_{\phi }^{\infty }(x,y):= w(y)/k$ for almost every $y\in {\mathbb {D}}$ and in $L^1({\mathbb {D}})$.

4 Main results

Let $\phi \in \text {Diff}_c({\mathbb {D}}, \omega _0)$ and let $\phi ^t$ be a compactly supported Hamiltonian isotopy such that $\phi ^0=\mathrm {id}$ and $\phi ^1=\phi$. We fix x in the interior of ${\mathbb {D}}$, a point $e\in \partial {\mathbb {D}}$ and we define the surface $S^e_\phi (x)\subset {\mathbb {D}}\times [0,1]$ as in (2.6). Given $y\in {\mathbb {D}}\setminus \{x\}$ such that the curve $\Gamma _\phi (y) = \{(\phi ^t(y),t) \mid t\in [0,1]\}$ meets $S^e_\phi (x)$ transversally, we denote by $I_\phi ^e(x,y)$ the intersection number of $\Gamma _\phi (y)$ with $S^e_\phi (x)$, as in Sect. 2.3. As observed in Remark 2.13, $I_\phi ^e(x,\cdot )$ is defined on a full measure subset of ${\mathbb {D}}$.

Proposition 4.1

The action of x with respect to a primitive $\lambda$ of $\omega _0$ and the intersection numbers $I^e_\phi (x,\cdot )$ are related by the identity

$$\begin{aligned} a_{\phi ,\lambda }(x)=\int _{\mathbb {D}}I_\phi ^e(x,y)\, \omega _0(y)-\int _{[e,x]}\lambda +\int _{[e,\phi (x)]}\lambda , \end{aligned}$$

(4.1)

where [e, x] and $[e,\phi (x)]$ denote oriented line segments in ${\mathbb {D}}$.

Proof

Let $H_t$ be the time-dependent compactly supported Hamiltonian that defines the isotopy $\phi ^t$ and denote by $X_t$ its Hamiltonian vector field. We lift the differential forms $\lambda$ and $\omega _0$ and the vector field $X_t$ to corresponding objects on the three-manifold ${\mathbb {D}}\times [0,1]$:

$$\begin{aligned} \tilde{\lambda }&:=\lambda +H_t dt, \\ \tilde{\omega }_0&:=d{\tilde{\lambda }}=\omega _0+dH_t\wedge dt, \\ {\tilde{X}}&:=X_t+\partial _t. \end{aligned}$$

Note that ${\tilde{X}}$ is an autonomous vector field on ${\mathbb {D}}\times [0,1]$ and

$$\begin{aligned} \imath _{{\tilde{X}}}{\tilde{\omega }_{0}}&= \imath _{(X_t+\partial _t)}[ \omega _0+dH_t \wedge dt)]\nonumber \\&= \imath _{X_t}\omega _0+\imath _{X_t}(dH_t \wedge dt)+\imath _{\partial _t}\omega _0+\imath _{\partial _t}(dH_t \wedge dt)\nonumber \\&=dH_t+0 + 0 - dH_t = 0. \end{aligned}$$

(4.2)

In particular, using also the fact that $\tilde{\omega }_0$ is closed, we have

$$\begin{aligned} L_{{\tilde{X}}} \tilde{\omega }_0 = d \imath _{{\tilde{X}}} \tilde{\omega }_0 + \imath _{{\tilde{X}}} d \tilde{\omega }_0 = 0, \end{aligned}$$

and hence $\tilde{\omega }_0$ is invariant with respect to the local flow of ${\tilde{X}}$, which we denote by ${\tilde{\phi }}$. Note that

$$\begin{aligned} {\tilde{\phi }}^t(z,0) = (\phi ^t(z),t) \qquad \forall z\in {\mathbb {D}}, \; t\in [0,1]. \end{aligned}$$

Note that (4.2) together with the fact that ${\tilde{\omega }}_0$ is closed, also shows that ${\tilde{\omega }}_0$ is invariant with respect to any reparametrization of this local flow. The map

$$\begin{aligned} \rho : S^e_\phi (x) \rightarrow {\mathbb {D}}, \qquad (z,t) \mapsto (\phi ^t)^{-1}(z), \end{aligned}$$

from Sect. 2.3 maps each $(z,t)\in S^e_\phi (x)$ into the unique point $y\in {\mathbb {D}}$ such that (y, 0) is on the backward orbit of (z, t) by ${\tilde{\phi }}$. In other words, this map has the form

$$\begin{aligned} \rho (p)=\pi \circ {\tilde{\phi }}^{-\tau (p)}(p), \end{aligned}$$

where $\pi : {\mathbb {D}}\times [0,1]\rightarrow {\mathbb {D}}$ and $\tau : {\mathbb {D}}\times [0,1] \rightarrow [0,1]$ are the two projections. We set $\psi (p) := {\tilde{\phi }}^{-\tau (p)}(p)$ and we compute its differential

$$\begin{aligned} d\psi (p)[u]=d{\tilde{\phi }}^{-\tau (p)}(p)[u]- d\tau (p)[u]{\tilde{X}}({\tilde{\phi }}^{-\tau (p)}(p)), \qquad \forall u\in T_p S^e_\phi (x). \end{aligned}$$

Notice that $\rho =\pi \circ \psi$ and $\pi ^*\omega _0={\tilde{\omega }}_0-dH_t\wedge dt$. These two identities let us compute the pullback of the form $\omega _0$ by the map $\rho$ at some point $p\in S^e_{\phi }(x)$: for every $u,v\in T_p S^e_{\phi }(x)$ we have

$$\begin{aligned} \rho ^*\omega _0(p)[u,v]&=(\psi ^*\pi ^*\omega _0)(p)[u,v]\\&=\psi ^*({\tilde{\omega }}_0-dH_t\wedge dt)(p)[u,v]\\&=\psi ^*{\tilde{\omega }}_0(p)[u,v]-\psi ^*(dH_t\wedge dt)(p)[u,v]\\&={\tilde{\omega }}_0(\psi (p))\big [d\psi (p)[u],d\psi (p)[v]\big ]{-}dH_0(\psi (p))\\&\wedge dt \big [d\psi (p)[u],d\psi (p)[v]\big ]. \end{aligned}$$

The fact that the flow ${\tilde{\phi }}$ and reparametrizations of it preserve the form $\tilde{\omega _0}$ implies that $\psi ^*\tilde{\omega }_0 = \tilde{\omega }_0$, and hence the first term in the last expression equals ${\tilde{\omega }}_0(p)[u,v]$. On the other hand, the second term in the last expression vanishes, because the vectors $d\psi (p)[u]$ and $d\psi (p)[v]$ belong to the space $T_{\psi (p)}{\mathbb {D}}\times \{0\}$, on which dt vanishes. We conclude that

$$\begin{aligned} \rho ^*\omega _0={\tilde{\omega }}_{0} |_{S^e_\phi (x)}. \end{aligned}$$

By Stokes’ theorem and (2.4) we obtain the identity

$$\begin{aligned} {} \int _{S^e_\phi (x)}\rho ^*\omega _0= & {} \int _{S^e_\phi (x)}{\tilde{\omega }}_0 = \int _{\partial S^e_\phi (x)}{\tilde{\lambda }}\nonumber \\= & {} \int _{\partial S^e_\phi (x)} (\lambda + H_t \, dt) = a_{\phi ,\lambda }(x)+\int _{[e,x]}\lambda -\int _{[e,\phi (x)]}\lambda . \end{aligned}$$

(4.3)

On the other hand, equation (2.11) and Lemma 2.12 yield

$$\begin{aligned} {} \int _{S^e_\phi (x)}\rho ^*\omega _0=\int _{\mathbb {D}}\deg (\rho ,S^e_\phi (x),y)\, \omega _0(y)=\int _{\mathbb {D}}I_\phi ^e(x,y)\, \omega _0(y). \end{aligned}$$

(4.4)

The desired identity (4.1) follows from (4.3) and (4.4).

$\square$

Remark 4.2

In the particular case of a fixed point $x\in {\mathbb {D}}$ of $\phi$, the formula of Proposition 4.1 reduces to the identity

$$\begin{aligned} a_{\phi ,\lambda }(x)=\int _{\mathbb {D}}I_\phi ^e(x,y)\omega _0(y). \end{aligned}$$

We can finally prove Theorem 1.1 from the Introduction.

Proof of Theorem 1.1

By applying Proposition 4.1 to the map $\phi ^n$ we obtain the identity

$$\begin{aligned} \frac{a_{\phi ^n,\lambda }(x)}{n}=\frac{1}{n}\int _{\mathbb {D}}I_{\phi ^n}^{e}(x,y)\, \omega _0(y)-\frac{1}{n}\int _{[e,x]}\lambda +\frac{1}{n}\int _{[e,\phi ^n(x)]}\lambda . \end{aligned}$$

for every x in ${\mathbb {D}}$. The last two integrals are uniformly bounded in $x\in {\mathbb {D}}$ and $n\in {\mathbb {N}}$. Together with the bound from Proposition 2.10 applied to $\phi ^n$, we deduce the bound

$$\begin{aligned} \frac{a_{\phi ^n,\lambda }(x)}{n}-\frac{1}{n}\int _{\mathbb {D}}W_{\phi ^n}(x,y)\, \omega _0(y) = O \left( \frac{1}{n} \right) \end{aligned}$$

(4.5)

uniformly in $x\in {\mathbb {D}}$. The set $\Omega$ consisting of all points $x\in {\mathbb {D}}$ for which the sequence $a_{\phi ,\lambda }(x)/n$ converges to $a_\phi ^{\infty }(x)$ and the integrals of $W_{\phi ^n}(x,\cdot ) \omega _0/n$ converge to the integral of $W_\phi ^{\infty }(x,\cdot )$ has full measure in ${\mathbb {D}}$. Taking the limit in (4.5) we obtain the identity

$$\begin{aligned} a_\phi ^{\infty }(x) = \int _{\mathbb {D}}W_\phi ^{\infty }(x,y)\, \omega _0(y) \end{aligned}$$

(4.6)

for every $x\in \Omega$. The set $\Omega$ contains all periodic points of $\phi$ thanks to the identity (3.4) and Remark 3.4. $\square$

Fathi’s formula stated as Corollary 1.2 in the Introduction now follows by integrating (4.6) over the full measure set $\Omega$ and using the identities (3.3) and (3.5).