1 Introduction and basics

In the recent years, there has been a lot of interest in modeling and forecasting the temporal dependence and evolution of time series of low counts. Integer-valued time series arise in many applications, such as queueing systems, finance, reliability theory, medicine, and epidemiology, among others. The non-negative integer-valued autoregressive (INAR) model was developed by Al-Osh and Alzaid (1987) based on the binomial thinning operator introduced by Steutel and van Harn (1979) and McKenzie (1985). The INAR process has undergone numerous generalizations and modifications thanks to the efforts of many authors, including Alzaid and Al-Osh (1990), Al-Osh and Aly (1992), and Alzaid and Al-Osh (1993). Models based on the negative binomial thinning operator were also constructed and taken into consideration (Aly and Bouzar 1994; Ristić et al. 2009; Ristić and Nastić 2012). All of the models previously described have one common feature, which is considering on independent counting random variables to the thinning operation. The assumption of independence simplifies the computations and enables obtaining simple, not complex, models with nice characteristics. However, the fundamental drawback of such models is that they cannot be used in practice with data that do not support this assumption. For example, it is reasonable to expect some dependence between the survival or bankruptcy of some big companies in the economy, or it is logical to expect that the occurrence of some natural disasters affects the appearance or non-appearance of some other disasters in meteorology, etc. Therefore, a model with dependent counting sequences is needed to be established. Brännäs and Hellström (2001), Ristić et al. (2013), Ilić (2016), and Nastić et al. (2017) introduced thinning operators with dependent counting series. In this paper, the proposed model is based on the generalized thinning with dependent Bernoulli counting series and Pegram’s mixture operators that were introduced by Ilić (2016) and Biswas and Song (2009), respectively.

The generalized binomial thinning operator is defined as follows:

Definition 1.1

(Generalized binomial thinning operator with a dependent Bernoulli counting series, GBT) As in Ilić (2016), the GBT operator \(\alpha \ \star _{\vartheta }\) was defined as

$$\begin{aligned} \alpha \star _{\vartheta }\ X {\mathop {=}\limits ^{d}}\left\{ \begin{array}{ll} X, &{}\quad w.p.\ 1-(1-\alpha )/\vartheta , \\ Bin(X,1-\vartheta ), &{}\quad w.p.\ (1-\alpha )/\vartheta , \end{array}\right. \end{aligned}$$
(1.1)

where X is a non-negative integer-valued random variable (RV), \(0 \le 1-\alpha \le \vartheta \), and \(\vartheta \in (0,1] \).

Ilić (2016) defined the first-order dependent counting INAR model [NDCINAR(1)] based on the GBT operator \((\star _{\vartheta })\) as

$$\begin{aligned} X_{t}=\alpha \star _{\vartheta }X_{t-1}+\xi _{t},\ t\in \mathbb {Z}, \end{aligned}$$
(1.2)

where \(\{\xi _{t}\}\) is a sequence of i.i.d. RVs such that \(Cov(\xi _{t}, X_{s})=0\) for \(s < t\). For more details about this operator and its properties, see Ilić (2016).

Pegram (1980) introduced the discrete AR(p) that looks like ARMA models and permits some of the serial correlations to be negative. Biswas and Song (2009) used the Pegram operator to define the discrete ARMA model.

Khoo et al. (2017) introduced an INAR process with Poisson marginal via mixing the binomial thinning that consists of independent Bernoulli counting series, with the mixture Pegram operators (abbreviated MPT), and Khoo (2016) handled the MPT(1) process with some discrete marginal distributions, such as binomial, geometric, and negative binomial. Shirozhan and Mohammadpour (2018) and Shirozhan et al. (2019) presented the INAR(1) process with Poisson and geometric marginal distributions by combining the mixture Pegram with the generalized binomial thinning, which was based on the Bernoulli dependent counting series (Ristić et al. 2013).

The models based on combining the mixture Pegram and thinning operators are easy to interpret, have a simple form, and are more flexible in terms of the range of correlation. They are appropriate for any discrete marginal distributions, including infinite and finite divisible distributions, unlike the models based on the thinning operator, which are applied only for infinite range distributions, and also applied to the multimodal data.

The conditional variance of the INAR(1) based on the independent counting series is linear in \(X_{t}\), but for a Pegram model, it is a quadratic function like the INAR(1) with dependent counting series. Therefore, the quadratic property is not satisfied for INAR(1) with independent counting series. This property implies large values of variance, which may be appropriate to model over-dispersed data. The one-misrecorded Poisson distribution—also known as a simple modified Poisson distribution or a Cohen Poisson distribution—forms the basis of the proposed model and is introduced in the following definition.

Definition 1.2

(The one-misrecorded Poisson) The one-misrecorded Poisson distribution, abbreviated as (OMP), of a RV X with parameters \(\lambda >0, , \ 0\le \phi \le 1\), has the probability mass function (p.m.f.)

$$\begin{aligned} P(X=x)=\left\{ \begin{array}{ll} e^{-\lambda }(1+\lambda \phi ) &{}\quad {x}= 0, \\ e^{-\lambda }\lambda (1-\phi ) &{}\quad {x}= 1,\\ e^{-\lambda }\frac{\lambda ^{x}}{x!} &{}\quad {x}= 2,3, \ldots .\end{array}\right. \end{aligned}$$
(1.3)

The OMP was invented by Cohen (1960) to model the data (or misclassified data) that contain errors in reporting one as a zero, or it sometimes happens that a few of the observations taking value one are misclassified and reported as zero. \(\phi \) is the probability of misclassification, or the proportion of ones reported as zeros. The OMP distribution has its application in situations where the true values of ones are erroneously recorded as zeros with probability \(\phi \), while values of two and more are recorded correctly from a Poisson. For example, when determining the number of defects per unit or item examined, an inspector may make an error by reporting units that actually contain a single defect as being perfect or defect-free. The OMP is reduced to a Poisson distribution when \(\phi =0\), the equi-dispersion case. Also, all the observations falling into class one will be reported as zero when \(\phi =1\).

For the OMP distribution, the corresponding probability generating function (p.g.f.), mean, variance, second, third, and fourth moments are, respectively, given by

$$\begin{aligned} \textbf{G}_{X}(s)= & {} \lambda \phi e^{-\lambda }(1-s)+e^{\lambda (s-1)}, \end{aligned}$$
(1.4)
$$\begin{aligned} E(X)= & {} \mu _{X}=\lambda (1-\phi e^{-\lambda }),\end{aligned}$$
(1.5)
$$\begin{aligned} Var(X)= & {} C_{2}(0)=\sigma ^{2}_{X}=\lambda ^{2}+\lambda (1-\phi e^{-\lambda })(1-\lambda (1-\phi e^{-\lambda })),\end{aligned}$$
(1.6)
$$\begin{aligned} E(X^{2})= & {} \mu _{(0)}=\lambda ^{2}+\lambda (1-\phi e^{-\lambda }),\end{aligned}$$
(1.7)
$$\begin{aligned} E(X^{3})= & {} \mu _{(0,0)}=\lambda ^{3}+3\lambda ^{2}+\lambda (1-\phi e^{-\lambda }),\end{aligned}$$
(1.8)
$$\begin{aligned} E(X^{4})= & {} \mu _{(0,0,0)}=\lambda ^{4}+6\lambda ^{3} +7\lambda ^{2}+\lambda (1-\phi e^{-\lambda }). \end{aligned}$$
(1.9)

Therefore, the Fisher index of dispersion (variance to mean ratio) is obtained as follows:

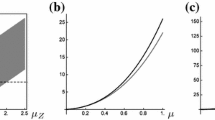
$$\begin{aligned} I_{X}=\frac{Var(X)}{E(X)}=1+\frac{\lambda \phi e^{-\lambda }(2-\phi e^{-\lambda })}{(1-\phi e^{-\lambda })}=1+D(\phi ,\lambda ), \end{aligned}$$

where \(D(\phi ,\lambda )=\frac{\lambda \phi e^{-\lambda }(2-\phi e^{-\lambda })}{(1-\phi e^{-\lambda })}.\) \(D(\phi ,\lambda )\) increases as \(\phi \) increases from 0 to 1 and the degree of over-dispersion increases. The value of function \(D(\phi ,\lambda )=0\) for large values of \(\lambda \) or for \(\phi =0\). The behavior of this function can be seen graphically in Fig. 1.

Fig. 1
figure 1

Behavior of the function \(D(\phi ,\lambda )\) on the index dispersion

Full size image

We can say that the OMP distribution is zero-inflated (there is an excess of zeros) and one-deflated (there are fewer ones than expected), according to the two definitions given by Ahmad (1968):

The first definition is that a class in a distribution will be said to be inflated if some of the observations falling in other classes are erroneously misclassified in this class.

The second definition is that a class in a distribution will be said to be deflated if some of the observations falling in the class are erroneously misclassified in another class.

Also, according to Johnson et al. (2005), pages (211 and 353), in describing the modified distribution’s zero probability, we can conclude that if \(\phi _{0}=\lambda \phi e^{-\lambda } > 0\), then the Poisson’s zero probability is increased (zero-inflation), while the Poisson’s one probability is decreased for \(\phi _{1}=-\lambda \phi e^{-\lambda } < 0\) (one-deflation).

Moreover, according to Puig and Valero (2006), a random variable X is zero-inflated when its proportion of zeros is greater than the proportion of zeros of a Poisson variate with the same expectation; zero inflation can be studied in a standard way using the zero-inflation index, \(I_{\textrm{Zero}}\), as

$$\begin{aligned} I_{\textrm{Zero}}=1+\frac{\ln (P_{0})}{\mu _{X}}=1+\frac{-\lambda +\ln (1+\lambda \phi )}{\lambda (1-\phi e^{-\lambda })}=1+Z(\lambda ,\phi ). \end{aligned}$$
(1.10)

The value of function \(Z(\lambda ,\phi )=-1\) for \(\phi =0\) and any value of \(\lambda \), and this implies that \(I_{\textrm{Zero}}=0\), consequently, X is a Poisson distribution. The value of \(Z(\lambda ,\phi )\) is greater than -1 since \(Z(\lambda ,\phi )\) increases as \(\phi \) increases from 0 to 1. In particular, the behavior of the function \(Z(\lambda , \phi )\) is shown graphically in Fig. 2. As a result, the values of \(I_{\textrm{Zero}} > 0\) and from the plot in Fig. 2, we conclude that \(I_{\textrm{Zero}}\in (0,1)\), which indicates zeroinflation (an excess of zero with respect to a Poisson distribution).

Fig. 2
figure 2

Behavior of the function \(Z(\phi ,\lambda )\) on the zero index

Full size image

Practical over-dispersed INAR(1) processes have been presented in the literature, such as the negative binomial INAR(1) process (McKenzie 1986) and the compound Poisson INAR(1) process (Schweer and Weiß 2014). These over-dispersed classes of INAR(1) models fail when the data set contains a large number of zeros. To analyze count data with excess zeros, Jazi et al. (2012) and Barreto-Souza (2015) introduced INAR(1) with zero-inflated Poisson (ZIP) innovations and zero-modified geometric INAR(1) models, respectively. The over-dispersed and zero-inflated INAR(1) models, however, fail when a data set contains both a large number of zeros and ones, which occurs frequently in practice, for example, in the number of patients with a rare disease in various areas, the monthly counts of Computer-Aided Dispatch (CAD) drug calls, etc. Furthermore, the illustrative examples in Sect. 4 show real-life data examples with excesses of zero-and-one. So that a change in the p.m.fs. for modeling zero-and-one observation is necessary. Qi et al. (2019), Mohammadi et al. (2022a, 2022b) introduced INAR(1) models with zero-and-one inflated Poisson (ZOIP), Poisson–Lindely (ZOIPL), and geometric (ZOIG) that are useful tools for capturing the characteristics of such count data. In these processes, the authors assume that the innovation term has a zero-and-one inflated distribution.

The main aim of this paper is to construct an INAR(1) process for modeling over-, equi-dispersed, and multimodality data by assuming that the main time series \(\{X_{t}\}\) follows the OMP distribution based on combining the GBT and mixture Pegram operators. Also, the proposed process can be used to model zero-inflated and one-deflated data, and the misclassification of ones as zeros (errors in recording at one or one-misrecorded data).

This paper is constructed as follows: In Sect. 2, an extension or generalization of the MPT(1) model based on a dependent Bernoulli counting series with OMP distribution (OMP-EMPT(1)) is defined, and some properties of the innovation process and its p.m.f. are derived. Also, several statistical and conditional properties of the model, including conditional and joint distributions and jumps, are shown, along with a study of the distribution of zeros and ones in the proposed process. In Sect. 3, the parameters of the process are estimated via the maximum-likelihood (ML), modified conditional least-squares (MCLS), and modified Yule–Walker (MYW) methods. Also, the performance of the estimates is checked via a simulation study. In Sect. 4, we provide two real-life data sets to model over-dispersed data, illustrating the performance of the process throughout the goodness-of-fit statistics. Also, the model’s adequacy is checked by the mean logarithmic score, benchmark chart, and non-randomized probability integral transform (PIT). The predictive capacity of the proposed model is checked through forecasting.

2 Construction of the model and its statistical properties

This section is implemented as follows: An extension of the MPT(1) with OMP marginal distribution is constructed using a generalized binomial thinning (abbreviated as OMP-EMPT(1)). The p.m.f. for the innovation term of the model is obtained. The bivariate p.g.f., conditional p.g.f., conditional mean and variance, \(k-\)step-ahead conditional mean and variance, transition probability, autocorrelation function, and the number of zeros and ones in the model are discussed.

The proposed model is defined as follows:

Definition 2.1

(Extended MPT(1) with OMP, OMP-EMPT(1)) The OMP-EMPT(1) \(\{X_{t}\}\) is defined as

$$\begin{aligned} X_{t} = \left\{ \begin{array}{ll} \alpha \star _{\vartheta }\ X_{t-1} &{}\quad \ \text {with probability}\ p,\\ \xi _{t}&{}\quad \text {with probability}\ 1- p, \end{array}\right. \end{aligned}$$

also, this model can be expressed as

$$\begin{aligned} X_{t} = \left\{ \begin{array}{ll} X_{t-1} &{}\quad \text {w.p}.\ p \left( 1-\frac{1-\alpha }{\vartheta }\right) ,\\ (1-\vartheta )\circ X_{t-1} &{}\quad \text {w.p}.\ p \frac{(1-\alpha )}{\vartheta },\\ \xi _{t}&{}\quad \text {w.p}.\ 1- p, \end{array}\right. \end{aligned}$$

where \("\alpha \star _{\vartheta }"\) refers to the GBT operator, and \(\{\xi _{t}\}\) is a sequence of i.i.d. RVs such that \(\vartheta \in (0,1]\), \(p\in (0,1)\), \(\ 0\le 1-\alpha \le \vartheta \), \(\lambda >0\), and \(\phi \in [0,1]\).

Remark 2.1

Note the following sub-models:

  • When \(\vartheta =1-\alpha \), the GBT is reduced to binomial thinning, and hence, the MPT(1) with OMP marginal, OMP-MPT(1), process is obtained, which has not been discussed before.

  • When \(\phi =0\) and \(\vartheta =1-\alpha \), the constructed process is reduced to the MPT(1) with Poisson distribution that is given by Khoo et al. (2017).

2.1 Probability distribution of the innovation term

The following proposition provides the distribution of the innovation process:

Proposition 2.1

The p.m.f. for \({\xi _{t}}\) has the following representations:

$$\begin{aligned} P(\xi _{t}=0)= & {} \frac{1}{1-p}\nonumber \\{} & {} \times \left[ \lambda \phi e^{-\lambda }(1-p\alpha )+e^{-\lambda } \left( 1-p\left( 1-\frac{1-\alpha }{\vartheta }\right) \right) -\left( \frac{p(1-\alpha )e^{-\lambda (1-\vartheta )}}{\vartheta }\right) \right] ,\nonumber \\ P(\xi _{t}=1)= & {} \frac{1}{1-p}\left[ -\lambda \phi e^{-\lambda }(1-p\alpha ) +e^{-\lambda }\lambda \left( 1-p \left( 1-\frac{1-\alpha }{\vartheta }\right) \right) \right. \nonumber \\{} & {} \left. -\left( \frac{p(1-\alpha )(\lambda (1-\vartheta )) e^{-\lambda (1-\vartheta )}}{\vartheta }\right) \right] \nonumber ,\\ P(\xi _{t}=j)= & {} \frac{1}{1-p}\left[ e^{-\lambda }\frac{\lambda ^{j}}{j!} \left( 1-p\left( 1-\frac{1-\alpha }{\vartheta }\right) \right) \right. \nonumber \\{} & {} \left. -\left( \frac{p(1-\alpha )(\lambda (1-\vartheta ))^{j} e^{-\lambda (1-\vartheta )}}{j! \vartheta }\right) \right] , \ j=2,\ 3,\ \ldots , \end{aligned}$$
(2.1)

for \(\lambda >0\), \(\vartheta \in (0,1]\), \(\alpha \in [0,1]\), and \(0\le 1-\alpha \le \vartheta \). The condition

$$\begin{aligned} {0\le p\le \min (C_{1},C_{2})}, \end{aligned}$$
(2.2)

where \(C_{1}\) and \(C_{2}\) are defined as

$$\begin{aligned} C_{1}= & {} \frac{1+\lambda \phi }{\lambda \phi \alpha +\left( 1-\frac{1-\alpha }{\vartheta }\right) +\left( \frac{1-\alpha }{\vartheta }\right) e^{\lambda \vartheta }}, \end{aligned}$$
(2.3)
$$\begin{aligned} C_{2}= & {} \frac{1-\phi }{\frac{1-\alpha }{\vartheta }(1-\vartheta ) e^{\lambda \vartheta }+\left( 1-\frac{1-\alpha }{\vartheta }\right) -\alpha \phi }, \end{aligned}$$
(2.4)

is necessary for the p.m.f. of the innovation process \(\xi _{t}\) in Eq. (2.1) to be well defined and non-negative for any j.

Proof

By using the definition of \((1-\vartheta )\circ X=\sum _{i=1}^{X}Z_{i}\), where \(Z_{i}\sim Ber((1-\vartheta ))\), as a result the p.g.f. of \((1-\vartheta )\circ X\) is given by \(G_{(1-\vartheta )\circ X}=G_{X}(\vartheta +(1-\vartheta )s)\). First, we get the p.g.f. of the innovation process \(\{\xi _{t}\}\) as a mixture representation of ones to the \(\{X_{t}\}\) as follows:

For this purpose, the p.g.f. of \(\{X_{t}\}\) given by Definition (2.1) has the expression

$$\begin{aligned} \textbf{G}_{X_{t}}(s)= & {} p \textbf{G}_{\alpha \star _{\vartheta } X_{t-1}}(s)+(1-p) \textbf{G}_{\xi _{t}}(s)\\= & {} p\left( 1-\frac{1-\alpha }{\vartheta }\right) \textbf{G}_{X_{t-1}}(s)+p\left( \frac{1-\alpha }{\vartheta }\right) \textbf{G}_{(1-\vartheta )\circ X_{t-1}}(s)+(1-p)\textbf{G}_{\xi _{t}}(s)\\= & {} p\left( 1-\frac{1-\alpha }{\vartheta }\right) \textbf{G}_{X_{t-1}}(s)+p\left( \frac{1-\alpha }{\vartheta }\right) \textbf{G}_{X_{t-1}}(\vartheta +(1-\vartheta )s)+(1-p) \textbf{G}_{\xi _{t}}(s). \end{aligned}$$

Hence, the p.g.f. of the innovation process \(\{\xi _{t}\}\) is

$$\begin{aligned} \textbf{G}_{\xi _{t}}(s)= & {} \frac{1}{1-p} \left[ \textbf{G}_{\textbf{X}_{\textbf{t}}}(s)-p \left( 1-\frac{1-\alpha }{\vartheta }\right) \textbf{G}_{X_{t-1}}(s) -p\left( \frac{1-\alpha }{\vartheta }\right) \textbf{G}_{X_{t-1}}(\vartheta +(1-\vartheta )s)\right] \nonumber \\= & {} \frac{1}{1-p}\left[ \lambda \phi e^{-\lambda }(1-s) +e^{\lambda (s-1)}-p\left( 1-\frac{1-\alpha }{\vartheta }\right) (\lambda \phi e^{-\lambda }(1-s)+e^{\lambda (s-1)})\right. \nonumber \\{} & {} \left. -p\left( \frac{1-\alpha }{\vartheta }\right) (\lambda \phi e^{-\lambda }(1-(\vartheta +(1-\vartheta )s)) +e^{\lambda ((\vartheta +(1-\vartheta )s)-1)})\right] \nonumber \\= & {} \frac{1}{1-p}\left[ \lambda \phi e^{-\lambda }(1-p\alpha )(1-s) +\left( 1-p\left( 1-\frac{1-\alpha }{\vartheta }\right) \right) e^{\lambda (s-1)}\right. \nonumber \\{} & {} \left. -p\left( \frac{1-\alpha }{\vartheta }\right) e^{\lambda (1-\vartheta )(s-1)}\right] . \end{aligned}$$
(2.5)

From Eq. (2.5), it can be noted that \(\textbf{G}_{\xi _{t}}(1)=1\) and \(\textbf{G}_{\xi _{t}}(0)=p(\xi _{t}=0)\) with (2.2).

Using Eq. (2.5), the innovation process \(\{\xi _{t}\}\) has a mixture distribution of degenerate distributions at 0 and 1, \(Poisson(\lambda )\) and \(Poisson((1-\vartheta )\lambda )\) with mixing weights \(\frac{\lambda \phi e^{-\lambda }(1-p\alpha )}{1-p}, -\frac{\lambda \phi e^{-\lambda }(1-p\alpha )}{1-p}, \frac{1-p(1-\frac{1-\alpha }{\vartheta })}{1-p}\), and \(\frac{-p(\frac{1-\alpha }{\vartheta })}{1-p}\), respectively. Hence, the p.m.f. of \(\xi _{t}\) is represented by equation’s system given in Eq. (2.1). Finally, we demonstrate as follows that this function is a p.m.f.

By the definition of generalized mixture of the distribution functions (Mohammadpour et al. 2018), the sum of preceding mixing weights equals 1, and hence, it follows that \(\sum _{j=0}^{\infty }P(\xi _{t}=j)=1.\)

The following step will demonstrate and confirm that the system of equations outlined in Eq. (2.1) yields non-negative probabilities under the condition specified in by Eq. (2.1). For each \(j=0, 1, 2, \ldots \), we aim to prove that \(P(\xi _{t}=j)\ge 0\) as outlined below.

When \(j=0\), ensuring \(P(\xi _{t}=0)\ge 0\) is achieved through solving the subsequent inequality

$$\begin{aligned} \frac{1}{1-p}\left[ \lambda \phi e^{-\lambda }(1-p\alpha ) +\left( 1-p\left( 1-\frac{1-\alpha }{\vartheta }\right) \right) e^{-\lambda }-p\left( \frac{1-\alpha }{\vartheta }\right) e^{-\lambda (1-\vartheta )}\right] \ge 0; \end{aligned}$$

consequently,

$$\begin{aligned} \lambda \phi e^{-\lambda }+e^{-\lambda }\ge p\left[ \alpha \lambda \phi e^{-\lambda }+\left( 1-\frac{1-\alpha }{\vartheta }\right) e^{-\lambda } +\left( \frac{1-\alpha }{\vartheta }\right) e^{-\lambda (1-\vartheta )}\right] . \end{aligned}$$

Upon solving the aforementioned inequality for p, the following result is obtained:

$$\begin{aligned} p\le \frac{\lambda \phi +1}{\alpha \phi \lambda +(1-\frac{1-\alpha }{\vartheta })+(\frac{1-\alpha }{\vartheta })e^{\lambda \vartheta }}. \end{aligned}$$
(2.6)

In the case of \(j=1\), the condition \(P(\xi _{t}=1)\ge 0\) is satisfied if

$$\begin{aligned}{} & {} \frac{1}{1-p}\left[ -\lambda \phi e^{-\lambda }(1-p\alpha ) +e^{-\lambda }\lambda (1-p(1-\frac{1-\alpha }{\vartheta })) -\left( \frac{p(1-\alpha )(\lambda (1-\vartheta )) e^{-\lambda (1-\vartheta )}}{\vartheta }\right) \right] \\{} & {} \qquad \ge 0; \end{aligned}$$

therefore, we have

$$\begin{aligned} -\lambda \phi e^{-\lambda }+\lambda e^{-\lambda } \ge p\left[ \frac{1-\alpha }{\vartheta }(\lambda (1-\vartheta )) e^{-\lambda (1-\vartheta )}+\left( 1-\frac{1-\alpha }{\vartheta }\right) \lambda e^{-\lambda }-\alpha \phi \lambda e^{-\lambda }\right] . \end{aligned}$$

Following the resolution for the preceding inequality, the condition for p is determined to be

$$\begin{aligned} p\le \frac{1-\phi }{-\alpha \phi +\left( 1-\frac{1-\alpha }{\vartheta }\right) +\frac{1-\alpha }{\vartheta }(1-\vartheta )e^{\lambda \vartheta }}. \end{aligned}$$
(2.7)

Finally, when \(j=2,\ 3,\ 4,\ \ldots \), the condition \(P(\xi _{t}=j)\ge 0\) is satisfied if

$$\begin{aligned} \frac{1}{1-p}\left[ e^{-\lambda }\frac{\lambda ^{j}}{j!} \left( 1-p\left( 1-\frac{1-\alpha }{\vartheta }\right) \right) -\left( \frac{p(1-\alpha )(\lambda (1-\vartheta ))^{j} e^{-\lambda (1-\vartheta )}}{j! \vartheta }\right) \right] \ge 0, \end{aligned}$$

or equivalently

$$\begin{aligned} 1-p\left( 1-\frac{1-\alpha }{\vartheta }\right) \ge p\frac{(1-\alpha )(1-\vartheta )^{j}e^{\lambda \vartheta }}{\vartheta }. \end{aligned}$$

Consequently, the condition for p will be

$$\begin{aligned} p\le \frac{1}{\left( 1-\frac{1-\alpha }{\vartheta }\right) +\frac{1-\alpha }{\vartheta }(1-\vartheta )^{j}e^{\lambda \vartheta }}. \end{aligned}$$
(2.8)

Let us assume that

$$\begin{aligned} C_{1}= & {} \frac{1+\lambda \phi }{\lambda \phi \alpha +\left( 1-\frac{1-\alpha }{\vartheta }\right) +\left( \frac{1-\alpha }{\vartheta }\right) e^{\lambda \vartheta }},\\ C_{2}= & {} \frac{1-\phi }{\frac{1-\alpha }{\vartheta }(1-\vartheta ) e^{\lambda \vartheta }+\left( 1-\frac{1-\alpha }{\vartheta }\right) -\alpha \phi },\\ C_{3}= & {} \frac{1}{1-\frac{1-\alpha }{\vartheta } +\frac{1-\alpha }{\vartheta }(1-\vartheta )^{j}e^{\lambda \vartheta }}. \end{aligned}$$

Hence, it is evident that \(C_{3}\) increases with an increase in j, reaching its minimum at \(j = 2\). This is depicted in Fig. 3 and supported by the numeric findings (conditions, confirmation numeric values, and folder of plots) available at https://drive.google.com/drive/folders/1oDmUr-vuSw98V9eYDmIsLbKA6Ha35J1t?usp=sharing. Hence, \(C_{3}\) is consistently greater than or equal to \(C_{2}\) or \(C_{1}\), leading to the conclusion that \(\min (C_{1},C_{2},C_{3})=\min (C_{1},C_{2})\). \(\square \)

Remark 2.2

Taking the minimum of \(C_{1}\) and \(C_{2}\) guarantees that the p.m.f. of \(\xi _{t}\) is non-negative for \(j=0,\ 1,\ 2,\ \ldots \).

From the numeric results and the graphs of the two conditions (\(C_{1}\) and \(C_{2}\)), the minimum is changed from \(C_{1}\) to \(C_{2}\), and this means that there is an inflection point or intersection point of the two conditions. By setting \(C_{1}=C_{2}\), the value of the intersection point, \(\phi \), can be obtained as follows:

$$\begin{aligned} \phi =\phi _{0}= \frac{\vartheta e^{\lambda \vartheta }}{\vartheta +(e^{\lambda \vartheta }-1) (1+\lambda -\lambda \vartheta )}. \end{aligned}$$

\(\phi _{0}\) is considered as an inflection point between the two conditions, and at \(\phi _{0}\), we have \( C_{1}=C_{2}\). Figure 4 illustrates the two conditions, \(C_{1}\) and \(C_{2}\), plotted under the specified intervals for \(\phi \), with \(0\le \phi \le \phi _{0}\) and \(\phi _{0}\le \phi \le 1,\) and for \(\lambda = 0.5,\ 1, \ 5,\ 10\), \(\alpha =0.83\), and \(\vartheta =0.21\). The illustrations in Fig. 4, coupled with the confirmation numeric values file (https://drive.google.com/file/d/1-hHVIoHLUMZUn2Z9o-AxghExHADjzHPY/view?usp=drive_link), demonstrate that:

  • When \(\phi <\phi _{0}\), \(C_{1}\) becomes the minimum. Therefore, p should be within the interval \(0\le p\le C_{1}\).

  • When \(\phi >\phi _{0}\), \(C_{2}\) becomes the minimum. Thus, p should be within the interval \(0 \le p\le C_{2}\).

  • If \(\phi =\phi _{0}\), then \(C_{2}=C_{1}=C\). Hence, p should be within the interval \(0 \le p\le C\).

Remark 2.3

  • If \(\phi =0\), then \(\min (C_{1},C_{2})=C_{1}\), which implies that p falls within the interval \(0\le p\le C_{1}\). The condition in Eq. (2.2) is reduced to that proposed by Khoo et al. (2017) for the case where \(\phi =0\) and \(\vartheta =1-\alpha \), in the context of the MPT(1) with Poisson distribution, which is a sub-model of the proposed model.

  • If \(\phi =1\), then \(\min (C_{1},C_{2})=C_{2}\) and consequently \(0\le p\le C_{2}\).

As a visual illustration of the p.m.f. under the mentioned conditions:

For \(\lambda =10;\alpha =0.83;\vartheta =0.21\), the p.m.f. of the innovation process, \(\xi _{t}\), is shown in:

  • Figure 5a with \(\phi =\phi _{0}=0.02679988802\) and \(C_{1}=C_{2}=0.1805334165\), so p must be in the range \(0\le p\le 0.1805334165\).

  • Figure 6a with \(\phi =0.5>\phi _{0}\) and taking \(p\le C2\), i.e., \(p\le 0.1000412914\). For \(\lambda =1;\alpha =0.6;\vartheta =0.5\), the p.m.f of \(\xi _{t}\) is represented in:

  • Figure 5a with \(\phi =\phi _{0}=0.5596162930\) and \(C_{1}=C_{2}=0.8408782799\), so \(0\le p\le 0.8408782799\).

  • Figure 6b with \(\phi =0.7>\phi _{0}\) and taking \(p\le C2\), i.e., \(p\le 0.6826117049\).

Fig. 3
figure 3

Conditions \(C_{1}, C_{2}\), and \(C_{3}\) at \(j=2,3,4\); \(\lambda =0.1 \ to \ 10;\ \alpha =0.83;\ \vartheta =0.21\)

Full size image
Fig. 4
figure 4

The conditions \(C_{1}\) and \(C_{2}\)

Full size image
Fig. 5
figure 5

PMF of the innovation process at \(\phi =\phi _{0}\), \(C_{1}=C_{2}=C\), and \(p\le C\)

Full size image
Fig. 6
figure 6

PMF of the innovation process at \(\phi >\phi _{0}\) and \(p\le C_{2}\)

Full size image

Consequently, based on the aforementioned proposition, the mean, variance, and the second and third moments of \(\{\xi _{t}\}\) are provided as follows, respectively:

$$\begin{aligned} E(\xi _{t})= & {} \frac{\lambda (1-p\alpha )(1-\phi e^{-\lambda })}{1-p}=\mu _{\xi _{t}}, \end{aligned}$$
(2.9)
$$\begin{aligned} Var(\xi _{t})= & {} \frac{1}{1-p}\left[ (\lambda ^{2} (1+p+p\alpha (-2+\vartheta )-p\vartheta ))\right. \nonumber \\{} & {} \left. +(\lambda (1-\phi e^{-\lambda }))(1-p\alpha ) \left( 1-\frac{(1-p\alpha )(1-\phi e^{-\lambda }) \lambda }{1-p}\right) \right] ,\end{aligned}$$
(2.10)
$$\begin{aligned} E(\xi _{t}^{2})= & {} \frac{(1-p\alpha )\lambda (1-\phi e^{-\lambda })+\lambda ^{2}(1+p+p\alpha (-2+\vartheta )-p\vartheta )}{1-p}, \end{aligned}$$
(2.11)

and

$$\begin{aligned} E(\xi _{t}^{3})= & {} \frac{(1-p\alpha )\lambda (1-\phi e^{-\lambda })+3(\lambda ^{2}(1+p+p\alpha (-2+\vartheta )-p\vartheta ))}{1-p}\nonumber \\{} & {} -\frac{\lambda ^{3}(-1+p(-2+3\vartheta -\vartheta ^{2}+\alpha (3-3\vartheta +\vartheta ^{2})))}{1-p}. \end{aligned}$$
(2.12)

2.2 Conditional properties of the process, joint distributions, and jumps

Regression properties are useful for estimating unknown parameters as well as forecasting future values. In particular, the conditional expectation is used for the conditional least-squares estimation method, k-step-ahead expectation for forecasting the future values of time series data, and a conditional probability function for the maximum-likelihood estimation method. The joint distributions are used to check the model’s time reversibility.

Let \(\{X_{t}\}\) be a stationary OMP-EMPT(1) process, then the conditional probability generating function (c.p.g.f.) and its corresponding conditional probability (one-step transition probability) function are as follows:

$$\begin{aligned} \textbf{G}_{X_{t}|X_{t-1}}(s)= & {} E(s^{X_{t}}|X_{t-1})\nonumber \\= & {} pE(s^{\alpha \star _{\vartheta }X_{t-1}}|X_{t-1})+(1-p) E(s^{\xi _{t}}|X_{t-1})\nonumber \\= & {} p\left[ \left( 1-\frac{1-\alpha }{\vartheta }\right) s^{X_{t-1}} +\frac{1-\alpha }{\vartheta }(\vartheta +(1-\vartheta )s)^{X_{t-1}}\right] +(1-p)\textbf{G}_{\xi _{\textbf{t}}}(s)\nonumber \\= & {} p\left( 1-\left( \frac{1-\alpha }{\vartheta }\right) \right) s^{X_{t-1}}\nonumber \\{} & {} +p\left( \frac{1-\alpha }{\vartheta }\right) (\vartheta +(1-\vartheta )s)^{X_{t-1}}+\lambda \phi e^{-\lambda }(1-p\alpha )(1-s)\nonumber \\{} & {} +\left( 1-p\left( 1-\frac{1-\alpha }{\vartheta }\right) \right) e^{\lambda (s-1)} -p\left( \frac{1-\alpha }{\vartheta }\right) e^{\lambda (1-\vartheta )(s-1)}, \end{aligned}$$
(2.13)
$$\begin{aligned} P(X_{t}=i|X_{t-1}=j)= & {} P(i|j)=p P(\alpha \star _{\vartheta } X_{t-1}=i|X_{t-1}=j)+(1-p) P(\xi _{t}=i)\nonumber \\= & {} p\left( 1-\frac{1-\alpha }{\vartheta }\right) \textbf{I}_{\{j\}}\nonumber \\{} & {} +p\textbf{I}_{\{i\le j\}}\frac{1-\alpha }{\vartheta } \left( {\begin{array}{c}j\\ i\end{array}}\right) (1-\vartheta )^{i}\vartheta ^{j-i}+(1-p) P(\xi _{t}=i), \end{aligned}$$
(2.14)

where \(P(\xi _{t}=i)\), the p.m.f. of \(\{\xi _{t}\}\) is given by Eq. (2.1), t=0, 1, 2, \(\ldots \), and \(|s|\le 1\), and \(I_{\{j\}}\) is the indicator function with a degenerate random variable defined as

$$\begin{aligned} I_{\{j\}}= \left\{ \begin{array}{ll} 1 &{}\quad X_{t-1}=j \\ 0 &{}\quad X_{t-1}\ne j.\end{array}\right. \end{aligned}$$
(2.15)

Proposition 2.2

Let \(\{X_{t}\}\) be a stationary OMP-EMPT(1) process, then

  1. 1.

    The one-step-ahead conditional expectation is

    $$\begin{aligned} E(X_{t+1}|X_{t})=p\alpha X_{t}+(1-p\alpha )\lambda (1-\phi e^{-\lambda }), \end{aligned}$$
    (2.16)
  2. 2.

    The k-step-ahead conditional expectation is formulated as

    $$\begin{aligned} E(X_{t+k}|X_{t})=(p\alpha )^{k} X_{t}+(1-(p\alpha )^{k})\lambda (1-\phi e^{-\lambda }). \end{aligned}$$
    (2.17)
  3. 3.

    The one-step-ahead conditional variance is

    $$\begin{aligned} Var(X_{t+1}|X_{t})= & {} p[(2\alpha -\alpha \vartheta +\vartheta -1) -p\alpha ^{2}]X^{2}_{t}\nonumber \\{} & {} +p[(1-\alpha )(1-\vartheta )-2\alpha \lambda (1-p\alpha )(1-\phi e^{-\lambda })]X_{t}\nonumber \\{} & {} +((1-p\alpha )\lambda (1-\phi e^{-\lambda })(1-\lambda (1-p\alpha )(1-\phi e^{-\lambda }))\nonumber \\{} & {} +\lambda ^{2}(1+p+p\alpha (-2+\vartheta )-p\vartheta ). \end{aligned}$$
    (2.18)
  4. 4.

    The k-step-ahead conditional variance is given as

    $$\begin{aligned} Var(X_{t+k}|X_{t})= & {} (p\textbf{A}_{\textbf{0}})^{k}X^{2}_{t} +p^{k}\textbf{B}_{\textbf{0}}\left( \frac{\textbf{A}_{\textbf{0}}^{k} -\alpha ^{k}}{\textbf{A}_{\textbf{0}}-\alpha }\right) X_{t}\nonumber \\{} & {} +((1-p\alpha )\lambda (1-\phi e^{-\lambda })+\lambda ^{2} (1-p\textbf{A}_{\textbf{0}}))\left( \frac{1-(p\textbf{A}_{\textbf{0}})^{k}}{1-p\textbf{A}_{\textbf{0}}}\right) \nonumber \\{} & {} +\left( \frac{(1-p\alpha )\lambda (1-\phi e^{-\lambda })}{\textbf{A}_{\textbf{0}}-\alpha }\right) \textbf{B}_{\textbf{0}}\left( \frac{(p\textbf{A}_{\textbf{0}})^{k}-1}{p\textbf{A}_{\textbf{0}}-1} -\frac{(p\alpha )^{k}-1}{p\alpha -1}\right) \nonumber \\{} & {} -((p\alpha )^{k} X_{t}+(1-(p\alpha )^{k})\lambda (1-\phi e^{-\lambda }))^{2}, \end{aligned}$$
    (2.19)

where \(\textbf{A}_{\textbf{0}}= (2\alpha -\alpha \vartheta +\vartheta -1)\), \(\textbf{B}_{\textbf{0}}=(1-\alpha )(1-\vartheta )\).

Proof

The proof of Proposition 2.2 is given in Appendix A.1. \(\square \)

The autocovariance, autocorrelation, and partial autocorrelation functions at lag k of \(\{X_{t}\}\) are, respectively, given as follows:

$$\begin{aligned} \gamma _{X}(k)= & {} (p\alpha )^{k}[\lambda ^{2}+\lambda (1-\phi e^{-\lambda })(1-\lambda (1-\phi e^{-\lambda }))],\end{aligned}$$
(2.20)
$$\begin{aligned} \rho _{X}(k)= & {} (p\alpha )^{k},\ k\in \mathbb {Z}, \end{aligned}$$
(2.21)
$$\begin{aligned} \beta _{X}(k)= & {} Corr(X_{k+1}-E(X_{k+1}|X_{2},\ldots ,X_{k}), X_{1})\nonumber \\= & {} Corr(X_{k+1}-(p\alpha )X_{k}-(1-p)\mu _{\xi },X_{1})=(p\alpha )^{k} -p\alpha (p\alpha )^{k-1}=0, \ k>1,\nonumber \\ \end{aligned}$$
(2.22)
$$\begin{aligned} \beta _{X}(1)= & {} Corr(X_{k+1},X_{k})=p\alpha . \end{aligned}$$
(2.23)

Remark 2.4

  • The unconditional mean and variance of the OMP-EMPT(1) process are obtained by taking the limit of Eqs. (2.17) and (2.19) at \(k\longrightarrow \infty \), that is

    $$\begin{aligned}{} & {} \lim _{k\rightarrow \infty }E(X_{t+k}|X_{t})=\lambda (1-\phi e^{-\lambda })=E(X_{t}), \end{aligned}$$
    (2.24)
    $$\begin{aligned}{} & {} \lim _{k\rightarrow \infty }Var(X_{t+k}|X_{t}) = [(1-p\alpha )\lambda (1-\phi e^{-\lambda }) +\lambda ^{2}(1-p\textbf{A}_{\textbf{0}})] \left( \frac{1}{1-p\textbf{A}_{\textbf{0}}}\right) \nonumber \\{} & {} \qquad +\left( \frac{(1-p\alpha )\lambda (1-\phi e^{-\lambda })}{\textbf{A}_{\textbf{0}}-\alpha }\right) \textbf{B}_{\textbf{0}}\left( \frac{-1}{p\textbf{A}_{\textbf{0}}-1} -\frac{-1}{p\alpha -1}\right) -(\lambda (1-\phi e^{-\lambda }))^{2}\nonumber \\{} & {} \quad =\frac{\lambda (1-\phi e^{-\lambda })(1-p\alpha )}{1-p \textbf{A}_{\textbf{0}}}+\lambda ^{2}-\frac{\lambda (1-\phi e^{-\lambda }) (1-p\alpha )\textbf{B}_{\textbf{0}}}{-\textbf{B}_{\textbf{0}}(p\textbf{A}_{\textbf{0}}-1)}\nonumber \\{} & {} \qquad + \frac{\lambda (1-\phi e^{-\lambda })(1-p\alpha )\textbf{B}_{\textbf{0}}}{-\textbf{B}_{\textbf{0}}(p\alpha -1)}-(\lambda (1-\phi e^{-\lambda }))^{2}\nonumber \\{} & {} \quad =\lambda ^{2}-(\lambda (1-\phi e^{-\lambda }))^{2} +\frac{(1-p\alpha )\lambda (1-\phi e^{-\lambda })}{1-p\textbf{A}_{\textbf{0}}}[1-1]+\lambda (1-\phi e^{-\lambda })\nonumber \\{} & {} \quad =\lambda ^{2}+\lambda (1-\phi e^{-\lambda })(1-\lambda (1-\phi e^{-\lambda }))=Var(X_{t}). \end{aligned}$$
    (2.25)

  • From Eq. (2.19), it is concluded that the \(k-\)step-ahead conditional variance, \(Var(X_{t+k}|X_{t})\), depends on \(X^{2}_{t}\), that is, quadratically depends on the past of the process, and the coefficient of this dependence is \((p\textbf{A}_{\textbf{0}})^{k}-(p\alpha )^{2k}\). Thus, if \(\vartheta \ne 0\) and \(\alpha \in (0,1)\), which is a general case, then large values of variance could be expected when the process reaches some significant realizations. This goes with the fact that \(Var(X_{t})\) is approximated by \(Var(X_{t + k}|X_{t})\) for large values of k. Therefore, OMP-EMPT(1) model provides a very convenient property in the application to over-dispersed data.

  • The process is stationary, since the mean, variance, and autocovariance are finite and independent of time.

  • The autocorrelation and partial autocorrelation functions can be thought as model specification tools. When \(k\longrightarrow \infty \) in Eq. (2.21), the autocorrelation function decays exponentially to zero. Also, we have from Eq. (2.22), and noting that \(\beta (1) = p\alpha \), the PACF of OMP-EMPT(1) cuts off after lag 1. As a result, it could be remarked that the OMP-EMPT(1) model is an autoregressive process of order one.

The joint p.g.f. of two consecutive observations of this process, \(X_{t}\) and \(X_{t-1}\), is

$$\begin{aligned} \textbf{G}_{\textbf{X}_{\textbf{t}-\textbf{1}}, \textbf{X}_{\textbf{t}}}(s_{1},s_{2})= & {} p\left( 1-\frac{1-\alpha }{\vartheta }\right) [\lambda \phi e^{-\lambda }(1-s_{1}s_{2}) +e^{\lambda (s_{1}s_{2}-1)}]\nonumber \\{} & {} +p\frac{1-\alpha }{\vartheta } (\lambda \phi e^{-\lambda }(1-s_{1}(\vartheta +(1-\vartheta )s_{2}))+e^{\lambda (s_{1} (\vartheta +(1-\vartheta )s_{2})-1)})\nonumber \\{} & {} + (\lambda \phi e^{-\lambda }(1-s_{1}) +e^{\lambda (s_{1}-1)})\left[ \lambda \phi e^{-\lambda } (1-p\alpha )(1-s_{2})\right. \nonumber \\{} & {} \left. +\left( 1-p\left( 1-\frac{1-\alpha }{\vartheta }\right) \right) e^{\lambda (s_{2}-1)}-p\left( \frac{1-\alpha }{\vartheta }\right) e^{\lambda (1-\vartheta )(s_{2}-1)}\right] . \nonumber \\ \end{aligned}$$
(2.26)

It is clear from Eq. (2.26) that \(\textbf{G}_{\textbf{X}_{\textbf{t}-\textbf{1}}, \textbf{X}_{\textbf{t}}}(s_{1},\ s_{2})\) is not symmetric in \(s_{1}\) and \(s_{2}\), implying that the process is not time-reversible, and thus, the joint distribution of \((X_{t-1},X_{t})\) is not equal to the joint distribution of \((X_{t},X_{t-1})\).

The joint probability function of \(X_{t-1},\ X_{t}\) is

$$\begin{aligned} P_{X_{t-1}, X_{t}}(i,j)=P(X_{t}=j|X_{t-1}=i)P(X_{t-1}=i), \end{aligned}$$
(2.27)

where \(P(X_{t}=j|X_{t-1}=i)\) is the one-step transition probability function given by Eq. (2.13) and \(P(X_{t-1}=i)\) is the marginal probability distribution defined by Eq.(1.2).

The adequacy or sufficiency of the fitted models can be checked by jumps (see Weiß (2009)). The jump process is also used to construct control charts that show changes in the serial dependence structure. The p.g.f. of the jump process, \(J_{t}\equiv X_{t}-X_{t-1}\), for \(t\ge 2\) is obtained by replacing \(s_{1}\) and \(s_{2}\) by \(u^{-1}\) and u, respectively, in Eq. (2.26), as

$$\begin{aligned} \textbf{G}_{X_{t-1},X_{t}}(u^{-1},u)= & {} p \left( 1-\frac{1-\alpha }{\vartheta }\right) \nonumber \\{} & {} +p\frac{1-\alpha }{\vartheta }\left( \lambda \phi e^{-\lambda } \left( 1-\left( \frac{\vartheta }{u}+(1-\vartheta )\right) \right) +e^{\lambda \left( \left( \frac{\vartheta }{u} +(1-\vartheta )\right) -1\right) }\right) \nonumber \\{} & {} + (\lambda \phi e^{-\lambda }(1-u^{-1})+e^{\lambda (u^{-1}-1)}) \left[ \lambda \phi e^{-\lambda }(1-p\alpha )(1-u)\right. \nonumber \\{} & {} \left. +\left( 1-p\left( 1-\frac{1-\alpha }{\vartheta }\right) \right) e^{\lambda (u-1)}-p\left( \frac{1-\alpha }{\vartheta }\right) e^{\lambda (1-\vartheta )(u-1)}\right] . \nonumber \\ \end{aligned}$$
(2.28)

Utilizing Eq. (2.28) and the definition of the jump process, it is determined that the mean, variance, autocovariance, and autocorrelation of \(J_{t}\) are, respectively, specified by

$$\begin{aligned} E(J_{t})= & {} E(X_{t}-X_{t-1})=0, \end{aligned}$$
(2.29)
$$\begin{aligned} Var(J_{t})= & {} Var(X_{t}-X_{t-1})=2Var(X_{t}) -2Cov(X_{t},X_{t-1})\nonumber \\= & {} 2(1-p\alpha )[\lambda ^{2}+\lambda (1-\phi e^{-\lambda })(1-\lambda (1-\phi e^{-\lambda }))],\end{aligned}$$
(2.30)
$$\begin{aligned} \gamma _{J}(k)= & {} Cov(J_{t},J_{t+k})\nonumber \\= & {} (p\alpha )^{k-1}(2p\alpha -1-(p\alpha )^{2})[\lambda ^{2}+\lambda (1-\phi e^{-\lambda })(1-\lambda (1-\phi e^{-\lambda }))], \nonumber \\ \end{aligned}$$
(2.31)
$$\begin{aligned} \rho _{J}(k)= & {} Corr(J_{t},J_{t+k})=(p\alpha )^{k-1} (2p\alpha -1-(p\alpha )^{2}). \end{aligned}$$
(2.32)

2.3 Distribution of zeros and ones

The run is defined by Mood (1940), as a succession of similar events that are preceded and succeeded by different events, and the length of the run is determined by its number. The distribution of runs has been extensively studied in the context of i.i.d. set-ups, and a well-known application of runs is the runs test in non-parametric hypothesis testing. Jacobs and Lewis (1978) introduced the distribution of the run length for a stationary discrete autoregressive process of first-order. The expected time of its stay in state i at a stress after entering the process at state i from another state j can be evaluated using the run length. The expected length of zeros and ones will be discussed in two different ways. Let \(\{X_{t}\}\) be the OMP-EMPT(1) process, for a fixed state \(i\in \{0,1,2,\ldots \}\), suppose \(\mathcal {N}_{i}=\inf \{n\ge 1: X_{n}\ne i\}-1\), \(\mathcal {N}_{i}\) is the run length of state i starting at time 1, where the length can be \(0, 1, 2, \cdots \). Then, the survival function, probability of \(\mathcal {N}_{i}\) greater than or equal to n, of \(\mathcal {N}_{i}\) is

$$\begin{aligned} P(\mathcal {N}_{i}\ge n)= & {} P(X_{1}=X_{2}=\ldots =X_{n}=i)\nonumber \\= & {} P(X_{1}=i)(P(X_{n}=i|X_{n-1}=i))^{n-1} \nonumber \\= & {} P(X_{1}=i)(P(i|i))^{n-1},\ n\ge 1 \end{aligned}$$
(2.33)

and \(P(\mathcal {N}_{i}=0)=P(X_{1}\ne i)=1-P(X_{1}=i)\), where \(P(X_{1}=i)\) and \(P(i|i)=P(X_{n}=i|X_{n-1}=i) =p(1-\frac{1-\alpha }{\vartheta })I_{\{i\}}+p\frac{1-\alpha }{\vartheta }(1-\vartheta )^{i}+(1-p)P(\xi _{n}=i)\) are, respectively, the stationary distribution and conditional distribution of the process given by Eqs. (1.3) and (2.13).

Using the stationary and Markov properties of the proposed process, and based on the expression of the survival function of \(\mathcal {N}_{i}\) given by Eq.(2.33), the p.m.f. of \(\mathcal {N}_{i}\) is obtained as

$$\begin{aligned} P(\mathcal {N}_{i}=n)= & {} P(\mathcal {N}_{i}\ge n)-P(\mathcal {N}_{i}\ge n+1)\nonumber \\= & {} P(X_{n+1}\ne i, X_{n}=i, X_{n-1}=i,\ldots ,X_{1}=i)\nonumber \\= & {} P(X_{n+1}\ne i|X_{n}=i)P(X_{n}=i|X_{n-1}=i)\ldots P(X_{2}=i|X_{1}=i)P(X_{1}=i)\nonumber \\= & {} P(X_{1}=i)[1-P(X_{n+1}=i|X_{n}=i)](P(X_{n}=i|X_{n-1}=i))^{n-1} \nonumber \\= & {} -P(X_{1}=i)(P(X_{n+1}=i|X_{n}=i))^{n}\nonumber \\= & {} (1-P(X_{n+1}=i|X_{n}=i))\nonumber \\= & {} P(X_{1}=i)[1-P(i|i)](P(i|i))^{n-1}, n\ge 1. \end{aligned}$$
(2.34)

Therefore, based on the previous expression for the p.m.f. of \(\mathcal {N}_{i}\) given by Eq. (2.34), the expected run length of state i is given by

$$\begin{aligned} E(\mathcal {N}_{i}=n)= & {} \sum _{n=0}^{\infty }nP(\mathcal {N}_{i}=n)\nonumber \\= & {} \sum _{n=1}^{\infty }nP(X_{1}=i)[1-P(i|i)](P(i|i))^{n-1}\nonumber \\= & {} P(X_{1}=i)[1-P(i|i)]\sum _{n=1}^{\infty }n(P(i|i))^{n-1}\nonumber \\= & {} P(X_{1}=i)[1-P(i|i)]\left( \frac{1}{[1-P(i|i)]^{2}}\right) \nonumber \\= & {} \frac{P(X_{1}=i)}{1-P(i|i)}. \end{aligned}$$
(2.35)

The p.g.f. of \(\mathcal {N}_{i}\) is

$$\begin{aligned} \textbf{G}_{\mathcal {N}_{i}}(s)= & {} \sum _{n=0}^{\infty }s^{n}P(\mathcal {N}_{i}=n)\nonumber \\= & {} P(\mathcal {N}_{i}=0)+\sum _{n=1}^{\infty }s^{n}p(\mathcal {N}_{i}=n)\nonumber \\= & {} (1-P(X_{1}=i))+P(X_{1}=i)\sum _{n=1}^{\infty }s^{n}\nonumber \\{} & {} \times [(1-P(X_{n}=i|X_{n-1}=i))(P(X_{n}=i|X_{n-1}=i))^{n-1}]\nonumber \\= & {} (1-P(X_{1}=i))+\frac{s(1-P(i|i))P(X_{1}=i)}{1-sP(i|i)}. \end{aligned}$$
(2.36)

For the OMP-EMPT(1) process, the transition probability functions from zero to zero and non-zero are, respectively, given by

$$\begin{aligned} P(X_{n}=0|X_{n-1}=0)= & {} p\left( 1-\frac{1-\alpha }{\vartheta }\right) I_{\{0\}}+p\frac{1-\alpha }{\vartheta }+\lambda \phi e^{-\lambda }(1-p\alpha )\nonumber \\{} & {} -p\frac{1-\alpha }{\vartheta }e^{-\lambda (1-\vartheta )} +e^{-\lambda }\left( 1-p\left( 1-\frac{1-\alpha }{\vartheta }\right) \right) , \end{aligned}$$
(2.37)

and

$$\begin{aligned} {\delta }_{0}= P(X_{n}\ne 0|X_{n-1}=0)=1-P(X_{n}=0|X_{n-1}=0). \end{aligned}$$
(2.38)

Also, the transition probability functions from one to one and non-one are, respectively, given by

$$\begin{aligned} P(X_{n}=1|X_{n-1}=1)= & {} p\left( 1-\frac{1-\alpha }{\vartheta }\right) I_{\{1\}} +p\frac{1-\alpha }{\vartheta }(1-\vartheta )-\lambda \phi e^{-\lambda }(1-p\alpha )\nonumber \\{} & {} -p\frac{1-\alpha }{\vartheta }e^{-\lambda (1-\vartheta )} \lambda (1-\vartheta )+\lambda e^{-\lambda }\left( 1-p\left( 1 -\frac{1-\alpha }{\vartheta }\right) \right) , \nonumber \\ \end{aligned}$$
(2.39)

and

$$\begin{aligned} {\eta }_{1}= P(X_{n}\ne 1|X_{n-1}=1)=1-P(X_{n}=1|X_{n-1}=1). \end{aligned}$$
(2.40)

Using Eq. (2.35), the expected length of the runs of zeros and ones, the number of zeros between two non-zero values, and the number of ones between two non-one values of the process can be, respectively, derived as

$$\begin{aligned} E(\mathcal {N}_{0})= & {} \frac{P(X_{1}=0)}{1-P(X_{n}=0|X_{n-1}=0)} =\frac{e^{-\lambda }(1+\lambda \phi )}{P(X_{n}\ne 0|X_{n-1}=0)},\nonumber \\ E(\mathcal {N}_{0})= & {} \frac{ e^{-\lambda }(1+\lambda \phi )}{\begin{array}{c}1-p\left( 1-\frac{1-\alpha }{\vartheta }\right) I_{\{0\}}-p\frac{1-\alpha }{\vartheta }-\lambda \phi e^{-\lambda }(1-p\alpha )+p\frac{1-\alpha }{\vartheta } e^{-\lambda (1-\vartheta )}\\ {[}-e^{-\lambda } \left( 1-p\left( 1-\frac{1-\alpha }{\vartheta }\right) \right) ]\end{array}}.\end{aligned}$$
(2.41)
$$\begin{aligned} E(\mathcal {N}_{1})= & {} \frac{P(X_{n}=1)}{1-P(X_{n}=1|X_{n-1}=1)} =\frac{\lambda e^{-\lambda }(1-\phi )}{ P(X_{n}\ne 1|X_{n-1}=1)}, \nonumber \\ E(\mathcal {N}_{1})= & {} \frac{\lambda e^{-\lambda }(1-\phi )}{\begin{array}{c}1-p \left( 1-\frac{1-\alpha }{\vartheta }\right) I_{\{1\}}-p\frac{1-\alpha }{\vartheta }(1-\vartheta )+\lambda \phi e^{-\lambda }(1-p\alpha )\\ {[}+p\frac{1-\alpha }{\vartheta } e^{-\lambda (1-\vartheta )}\lambda (1-\vartheta )-\lambda e^{-\lambda }\left( 1-p\left( 1-\frac{1-\alpha }{\vartheta }\right) \right) ]\end{array}}. \end{aligned}$$
(2.42)

Using Eq. (2.33), the survival functions of \(\mathcal {N}_{0}\) and \(\mathcal {N}_{1}\) are, respectively, given by

$$\begin{aligned} P(\mathcal {N}_{0}\ge n)= & {} P(X_{1}=0)(P(X_{n}=0|X_{n-1}=0))^{n-1},\ n\ge 1 \end{aligned}$$
(2.43)

and

$$\begin{aligned} P(\mathcal {N}_{1}\ge n)=P(X_{1}=1)(P(X_{n}=1|X_{n-1}=1))^{n-1},\ n\ge 1. \end{aligned}$$
(2.44)

Using the stationarity of the process, as in Barreto- Souza W (2015), and Eq. (2.34), the p.m.f. for the number of zeros and ones is given as follows, respectively:

$$\begin{aligned} P(\mathcal {N}_{0}=n)= & {} P(X_{n}\ne 0, X_{n-1}=0,\ldots ,X_{1}=0|X_{0}=0)\\= & {} P(X_{n}\ne 0| X_{n-1}=0)P(X_{n-1}=0|X_{n-2}=0)\ldots P(X_{1}=0|X_{0}=0) \\= & {} {\delta }_{0}(1-{\delta }_{0})^{n-1}, \\ \end{aligned}$$

for \(n\ge 2\) and \(P(\mathcal {N}_{0}=1)=P(X_{1}\ne 0| X_{0}=0)={\delta }_{0}\).

$$\begin{aligned} P(\mathcal {N}_{1}=n)= & {} P(X_{n}\ne 1, X_{n-1}=1,\ldots ,X_{1}=1|X_{0}=1)\\= & {} P(X_{n}\ne 1| X_{n-1}=1)P(X_{n-1}=1|X_{n-2}=1)\ldots P(X_{1}=1|X_{0}=1) \\= & {} {\eta }_{1}(1-{\eta }_{1})^{n-1}, \end{aligned}$$

for \(n\ge 2\) and \(P(\mathcal {N}_{1}=1)=P(X_{1}\ne 1| X_{0}=1)={\eta }_{1}\). Based on Eq. (2.36), the p.g.f. for \(\mathcal {N}_{0}\) and \(\mathcal {N}_{1}\) are, respectively, given by

$$\begin{aligned} \textbf{G}_{\mathcal {N}_{0}}(s)=(1-P(X_{1}=0)) +\frac{s(1-P(0|0))P(X_{1}=0)}{1-sP(0|0)}, \end{aligned}$$
(2.45)

and

$$\begin{aligned} \textbf{G}_{\mathcal {N}_{1}}(s)= (1-P(X_{1}=1)) +\frac{s(1-P(1|1))P(X_{1}=1)}{1-sP(1|1)}. \end{aligned}$$
(2.46)

Remark 2.5

  1. 1.

    The expected run length of zeros and ones in the process, as in Jazi et al. (2012) and Barreto-Souza (2015), can be determined in a different way, because the run length of zeros and ones has a geometric distribution with probabilities \({\delta }_{0}\) and \({\eta }_{1}\), that is, \(P(\mathcal {N}_{0}=n)={\delta }_{0}(1-{\delta }_{0})^{n-1}, n\ge 1\), where \({\delta }_{0}\) is given by Eq. (2.38) and \(P(\mathcal {N}_{1}=n)={\eta }_{1}(1-{\eta }_{1})^{n-1}, n\ge 1\), where \({\eta }_{1}\) is given by Eq. (2.40), respectively. The expected run length zeros and ones are calculated as

    $$\begin{aligned} E(\mathcal {N}_{0})=\frac{1}{\begin{array}{c}1-p\left( 1-\frac{1-\alpha }{\vartheta }\right) I_{\{0\}}-p\frac{1-\alpha }{\vartheta }-\lambda \phi e^{-\lambda }(1-p\alpha )\\ {[}+p\frac{1-\alpha }{\vartheta } e^{-\lambda (1-\vartheta )}- e^{-\lambda }\left( 1-p\left( 1-\frac{1-\alpha }{\vartheta }\right) \right) ]\end{array}}, \end{aligned}$$
    (2.47)

    and

    $$\begin{aligned} E(\mathcal {N}_{1})=\frac{1}{\begin{array}{c}1-p\left( 1-\frac{1-\alpha }{\vartheta }\right) I_{\{1\}}-p\frac{1-\alpha }{\vartheta }(1-\vartheta )+\lambda \phi e^{-\lambda }(1-p\alpha )\\ {[}+p\frac{1-\alpha }{\vartheta } e^{-\lambda (1-\vartheta )}\lambda (1-\vartheta )-\lambda e^{-\lambda }\left( 1-p\left( 1-\frac{1-\alpha }{\vartheta }\right) \right) ]\end{array}}. \end{aligned}$$
    (2.48)
  2. 2.

    The expected run length for the MPT(1) with Poisson marginal is obtained by setting \(\phi =0\) and \(1-\alpha =\vartheta \) in Eqs. (2.41 and 2.42) or Eqs. (2.47 and 2.48).

3 Estimation of parameters and a simulation study

In this section, the unknown parameters of the OMP-EMPT(1) model will be estimated based on the maximum-likelihood (ML), modified Yule–Walker (MYW), and modified conditional least-squares (MCLS) methods. Suppose that \(\Theta =(\alpha ,\vartheta ,\phi ,\lambda ,p)^{T}\) is the vector of parameters that will be estimated using a realization \({X_{1},X_{2},\ldots ,X_{n}}\) from the process, where n is the sample size.

3.1 Maximum-likelihood estimation

The considered maximum-likelihood (ML) estimators take into account the temporal dependence between time series ordered records. The ML function of the considered realization is given by

$$\begin{aligned} L(\Theta ;x) = P(X_{1}=x_{1},\ldots ,X_{n}=x_{n}) =P(X_{1}=x_{1})\prod _{j=2}^{n}P(X_{j}=x_{j}|X_{j-1}=x_{j-1}). \end{aligned}$$

The corresponding log-likelihood function can be written as

$$\begin{aligned} l(\Theta ;x) = \log L(\Theta ;x) =\log p_{x_{1}}+\sum _{j=2}^{n}\log P(X_{j}=x_{j}|X_{j-1}=x_{j-1}), \end{aligned}$$
(3.1)

where \(P(X_{j}=x_{j}|X_{j-1}=x_{j-1})\) is the one-step transition probability given by Eq. (2.13) and \(p_{x_{1}}\) is given by Eq. (1.3). The maximum-likelihood (ML) estimator of \(\Theta \) is the value \(\hat{\Theta }_{\textrm{ML}}=(\hat{\alpha }_{\textrm{ML}},\hat{\vartheta }_{\textrm{ML}}, \hat{\phi }_{\textrm{ML}},\hat{\lambda }_{\textrm{ML}},\hat{p}_{\textrm{ML}})^{T}\), which maximizes the log-likelihood function in Eq. (3.1). The ML estimators are computed using the numerical methods found in most statistical software to solve the nonlinear system obtained from \(\frac{\partial l(\Theta ;x)}{\partial \Theta }=0\). To maximize the log-likelihood function of the proposed process, the optim function in R software is used.

3.2 Modified Yule–Walker estimation

The Modified Yule–Walker (MYW) estimators are computed via a combination of Yule–Walker estimators and ML estimators that have been introduced by Miletić Ilić et al. (2018). The MYW estimators of the parameters \(\alpha , p, \lambda , \phi , \theta \) are based on the sample values of \(\rho _{X}(1), E(X^{2}_{t})-E(X_{t}),E(X_{t}),Cov(X^{2}_{t},X_{t-1})\). Recall that \(\rho _{X}(1)=Corr(X_{t},X_{t-1})=p\alpha \), \(E(X_{t})=\lambda (1-\phi e^{-\lambda })\) and \(E(X^{2}_{t})=\lambda ^{2}+\lambda (1-\phi e^{-\lambda })\). Using the earlier sample values, the estimators for \(\alpha , p, \lambda ,\) and \(\phi \) are obtained as

$$\begin{aligned} \widehat{\lambda }_{YW}= & {} \sqrt{\frac{\sum _{t=1}^{n}X^{2}_{t}-\sum _{t=1}^{n}X_{t}}{n}}, \\ \widehat{\phi }_{YW}= & {} e^{\widehat{\lambda }_{YW}} \left( 1-\frac{\overline{X}}{\widehat{\lambda }_{YW}}\right) ,\\ \widehat{\alpha }_{YW}= & {} \widehat{\rho }_{X}(1) =\frac{\sum _{t=2}^{n}(X_{t}-\overline{X})(X_{t-1} -\overline{X})}{\widehat{p}_{\textrm{ML}} \sum _{t=1}^{n}(X_{t}-\overline{X})^{2}}, \end{aligned}$$

where \(\widehat{p}_{\textrm{ML}}\) is the ML estimator of p and it is used as the initial estimator of the parameter. Then, the YW estimator of p is given by

$$\begin{aligned} \widehat{p}_{YW}=\frac{\sum _{t=2}^{n}(X_{t}-\overline{X}) (X_{t-1}-\overline{X})}{\widehat{\alpha }_{YW}\sum _{t=1}^{n} (X_{t}-\overline{X})^{2}}. \end{aligned}$$

To estimate the parameter \(\vartheta \), first, the \(Cov(X^{2}_{t},X_{t-1})\) is computed

$$\begin{aligned} Cov(X^{2}_{t},X_{t-1})= & {} pCov((\alpha \star _{\vartheta }X_{t-1})^{2}, X_{t-1})+(1-p)Cov(\xi ^{2}_{t},X_{t-1}) \\= & {} p(2\alpha -\alpha \vartheta +\vartheta -1)[E(X^{3}_{t-1}) -\mu _{X}E(X^{2}_{t-1})]\\{} & {} +p(1-\alpha )(1-\vartheta )Var(X_{t-1}), \end{aligned}$$

using Eqs. (1.8), (1.7), and (1.6) for \(E(x^{3}_{t-1}), E(X^{2}_{t-1})\) and \(Var(X_{t})\), then

$$\begin{aligned} Cov(X^{2}_{t},X_{t-1})= & {} p(2\alpha -1)(\lambda ^{3}+3\lambda ^{2}+\lambda (1-\phi e^{-\lambda })(1-\lambda ^{2}-\lambda (1-\phi e^{-\lambda }))) \\{} & {} +p(1-\alpha )[\lambda ^{2}+\lambda (1-\phi e^{-\lambda })(1-\lambda (1-\phi e^{-\lambda })) \\{} & {} +\lambda ^{2}(2+\lambda \phi e^{-\lambda })p\vartheta (1-\alpha ). \end{aligned}$$

By solving the previous equation to \(\vartheta \), then the YW estimator of the parameter \(\vartheta \) is obtained as

$$\begin{aligned} \widehat{\vartheta }_{YW} = \frac{\widehat{C} -\widehat{p}_{YW}[(2\widehat{\alpha }_{YW}-1)\widehat{M}_{1} +(1-\widehat{\alpha }_{YW})\widehat{V}_{1}]}{\widehat{p}_{YW} (1-\widehat{\alpha }_{YW})\widehat{\lambda }^{2}_{YW} (2+\widehat{\lambda }_{YW}\widehat{\phi }_{YW}e^{-\widehat{\lambda }_{YW}})}, \end{aligned}$$

where \(\widehat{M}_{1}\) and \(\widehat{V}_{1}\) are defined as

$$\begin{aligned} \widehat{M}_{1}= & {} \widehat{\lambda }^{3}_{YW}+3\widehat{\lambda }^{2}_{YW}+\widehat{\lambda }_{YW}(1-\widehat{\phi }_{YW}e^{-\widehat{\lambda }_{YW}})(1-\widehat{\lambda }^{2}_{YW}-\widehat{\lambda }_{YW}(1-\widehat{\phi }_{YW}e^{-\widehat{\lambda }_{YW}})),\\ \widehat{V}_{1}= & {} \widehat{\lambda }^{2}_{YW}+\widehat{\lambda }_{YW}(1-\widehat{\phi }_{YW}e^{-\widehat{\lambda }_{YW}})(1-\widehat{\lambda }_{YW}(1-\widehat{\phi }_{YW}e^{-\widehat{\lambda }_{YW}})), \end{aligned}$$

and \(\widehat{C}\) is the estimator of \(Cov(X^{2}_{t},X_{t-1})\) given by

$$\begin{aligned} \widehat{C} = \frac{1}{n-1}\sum _{t=2}^{n}X^{2}_{t}X_{t-1} -\left( \frac{1}{n-1}\sum _{t=2}^{n}X^{2}_{t}\right) \left( \frac{1}{n-1}\sum _{t=2}^{n}X_{t-1}\right) . \end{aligned}$$

3.3 Modified conditional least-squares estimation

In this section, the unknown parameters of the proposed model are estimated by modified conditional least-squares (MCLS). The MCLS is presented by Miletić Ilić et al. (2018) and Karlsen and TjøStheim (1988) to estimate the parameters, and it is based on a combination of CLS and ML estimators. The parameters \(\alpha ,\ \vartheta ,\ p,\ \phi , \ \text {and}\ \lambda \) are estimated by the two-step CLS method. The first step is estimating the parameters \(\alpha , p, \phi , \ \text {and,}\ \lambda \) by minimizing the function \(Q_{n}(\alpha ,\ p,\ \phi ,\ \lambda )\)

$$\begin{aligned} Q_{n}(\Theta )= & {} \sum _{t=2}^{n}(X_{t}-E(X_{t}|X_{t-1}))^{2}\\= & {} \sum _{t=2}^{n}(X_{t}-p\alpha X_{t-1}-(1-p\alpha )\lambda (1-\phi e^{-\lambda }))^{2}; \end{aligned}$$

the estimators are then obtained by solving the system of equations: \(\frac{\partial Q_{n}(\Theta )}{\partial (\alpha ,\ p,\ \phi ,\ \lambda )^{T} }=0\) and combining the CLS method with the ML approach. Because the parameters \(\alpha \) and p cannot be separable and because when the \(Q_{n}\) function is differentiated with respect to \(\phi \) and \(\lambda \), they lead to the same estimated equation, the method of moments is used to estimate one of these parameters. With this, we use the CLS to derive the estimators of \(\alpha \), \(\phi ,\) and p and suppose that \(\lambda \) will be estimated using the method of moments; also, we have that \(\frac{\partial Q_{n}(\Theta )}{\partial (\alpha ,\ p,\ \phi )^{T} }=0\), then the estimators of \(\alpha \), \(\lambda \), p and \(\phi \) are, respectively, given by

$$\begin{aligned} \widehat{\alpha }_{\textrm{cls}}= & {} \frac{\sum _{t=2}^{n}X_{t}X_{t-1} -\frac{1}{n-1}\sum _{t=2}^{n}X_{t}\sum _{t=2}^{n}X_{t-1}}{\widehat{p}_{\textrm{ML}} \left( \sum _{t=2}^{n}X^{2}_{t-1}-\frac{1}{n-1} \left( \sum _{t=2}^{n}X_{t-1}\right) ^{2}\right) }, \end{aligned}$$
(3.2)
$$\begin{aligned} \widehat{\lambda }_{\textrm{cls}}= & {} \widehat{\lambda }_{\textrm{mm}} =\sqrt{\frac{\sum _{t=1}^{n}X^{2}_{t}-\sum _{t=1}^{n}X_{t}}{n}}, \end{aligned}$$
(3.3)

where \(\widehat{p}_{\textrm{ML}}\) is the ML estimator of the parameter p used as the initial estimate of the parameter. Thus, the \(\widehat{p}_{\textrm{cls}}\) is given by

$$\begin{aligned} \widehat{p}_{\textrm{cls}}=\frac{\sum _{t=2}^{n}X_{t}X_{t-1} -\frac{1}{n-1}\sum _{t=2}^{n}X_{t}\sum _{t=2}^{n}X_{t-1}}{\widehat{\alpha }_{\textrm{cls}}\left( \sum _{t=2}^{n}X^{2}_{t-1} -\frac{1}{n-1}\left( \sum _{t=2}^{n}X_{t-1}\right) ^{2}\right) }. \end{aligned}$$

Consequently, we get

$$\begin{aligned} \widehat{\phi }_{\textrm{cls}} = e^{\widehat{\lambda }_{\textrm{cls}}} \left( 1-\left( \frac{\sum _{t=2}^{n}X_{t}-\widehat{\alpha }_{\textrm{cls}} \widehat{p}_{\textrm{cls}}\sum _{t=2}^{n}X_{t-1}}{(n-1) \widehat{\lambda }_{\textrm{cls}}(1-\widehat{p}_{\textrm{cls}} \widehat{\alpha }_{\textrm{cls}})}\right) \right) . \end{aligned}$$
(3.4)

The calculations for the expressions in Eqs. (3.2), (3.3), and (3.4) are provided in Appendix A.2.

In the second step, the CLS estimator of the parameter \(\vartheta \) is obtained using the method introduced by Karlsen and TjøStheim (1988) by minimizing the function

$$\begin{aligned} \mathcal {S}_{n}(\vartheta ) = \sum _{t=2}^{n}((X_{t}-E(X_{t}|X_{t-1}))^{2}-Var(X_{t}|X_{t-1}))^{2}, \end{aligned}$$

where \(E(X_{t}|X_{t-1})\) and \(Var(X_{t}|X_{t-1})\) are given by (2.16) and (2.18), respectively. Therefore, by solving the equation \(\frac{\partial \mathcal {S}_{n}(\vartheta )}{\partial \vartheta }=0\), the estimator of \(\vartheta \) is given by

$$\begin{aligned} \widehat{\vartheta }_{\textrm{cls}}= & {} \frac{\sum _{t=2}^{n}(X^{2}_{t-1} -X_{t-1}-\lambda ^{2}_{\textrm{cls}})(\widehat{\mathcal {V}}_{t} -\widehat{\mathcal {H}}_{t-1})}{(1-\widehat{\alpha }_{\textrm{cls}}) \widehat{p}_{\textrm{cls}}\sum _{t=2}^{n}(X^{2}_{t-1}-X_{t-1} -\lambda ^{2}_{\textrm{cls}})^{2}}, \end{aligned}$$

where

$$\begin{aligned} \widehat{\mathcal {V}}_{t}=(X_{t}- \widehat{p}_{\textrm{cls}} \widehat{\alpha }_{\textrm{cls}}X_{t-1}-(1- \widehat{p}_{\textrm{cls}} \widehat{\alpha }_{\textrm{cls}}) \widehat{\lambda }_{\textrm{cls}}(1- \widehat{\phi }_{\textrm{cls}}e^{- \widehat{\lambda }_{\textrm{cls}}}))^{2}, \end{aligned}$$

and

$$\begin{aligned} \widehat{\mathcal {H}}_{t-1}= & {} [(2 \widehat{\alpha }_{\textrm{cls}}-1) \widehat{p}_{\textrm{cls}}- \widehat{p}^{2}_{\textrm{cls}} \widehat{\alpha }^{2}_{\textrm{cls}}]X^{2}_{t-1}\\{} & {} +( \widehat{p}_{\textrm{cls}}(1- \widehat{\alpha }_{\textrm{cls}})-2 \widehat{\alpha }_{\textrm{cls}} \widehat{p}_{\textrm{cls}}(1- \widehat{p}_{\textrm{cls}} \widehat{\alpha }_{\textrm{cls}}) \widehat{\lambda }_{\textrm{cls}}(1- \widehat{\phi }_{\textrm{cls}}e^{-\widehat{\lambda }_{\textrm{cls}}}))X_{t-1}\\{} & {} +(1- \widehat{p}_{\textrm{cls}} \widehat{\alpha }_{\textrm{cls}}) \widehat{\lambda }_{\textrm{cls}}(1- \widehat{\phi }_{\textrm{cls}}e^{- \widehat{\lambda }_{\textrm{cls}}})(1-(1- \widehat{p}_{\textrm{cls}} \widehat{\alpha }_{\textrm{cls}}) \widehat{\lambda }_{\textrm{cls}}(1- \widehat{\phi }_{\textrm{cls}}e^{-\widehat{\lambda }_{\textrm{cls}}}))\\{} & {} +\widehat{\lambda }^{2}_{\textrm{cls}}(1+\widehat{p}_{\textrm{cls}}-2\widehat{p}_{\textrm{cls}}\widehat{\alpha }_{\textrm{cls}}). \end{aligned}$$

Remark 3.1

The OMP-EMPT(1) process is an irreducible Feller chain, stationary, strictly stationary, and ergodic. The proof of these properties is similar to the ones in Khoo et al. (2017), Shirozhan and Mohammadpour (2018), Nastić et al. (2012), and Schweer and Weiß (2014).

3.4 Simulation

Some simulated trajectories of the OMP-EMPT(1) process for sample size \(n=100\) and \(\lambda =0.5,\ 1.5,\ 5\) with \(\alpha =0.5; \vartheta =0.6; p=0.2; p=0.02; \phi =0.5\), and \(\alpha =0.7;\vartheta =0.3; p=0.1; \phi =0.7\) are presented in Fig. 7. From these simulated series, one can conclude that the proposed process is stationary, and for lower values of \(\lambda \), the number of ones and zeros increases. When \(\lambda \) is large, the number of zeros and ones decreases, resulting in larger values for the sample path. The details of the simulations and how the innovation process \(\xi _{t}\) has been simulated are shown by the R code for simulated series at \(n=100\); \(\alpha =0.5;\vartheta =0.6;p=0.2;\lambda =1.5;\phi =0.5\); see Appendix A.3.

Fig. 7
figure 7

Sample paths of OMP-EMPT(1) process

Full size image

A Monte Carlo simulation study is performed for different parameter values and different sample sizes to evaluate the performance of the ML, MYW, and MCLS estimators. The mean square errors (MSE) and empirical biases were calculated over 100 replications with the sample sizes \(n=100, 500, 1000, 5000\) to evaluate the performance of the estimates and check their properties. The true values of the parameters in the simulations are: \((\alpha ,\vartheta ,\phi ,\lambda ,p)= (0.7,0.3,0.01,1,0.1),\ (0.4,0.6,0.1,1,0.1)\), (0.5, 0.6, 0.2, 0.5, 0.5),  and (0.5, 0.6, 0.2, 1, 0.5). Using this simulation, Tables 1 and 2 show the bias and MSE (in brackets) of the estimates of different parameter values \((\alpha ,\vartheta ,\phi ,\lambda ,p)\) and through different sample sizes. From these tables, we conclude that the MSEs and biases are reduced by increasing the sample sizes for the three methods. The estimation using using the ML approach is better than MYW and MCLS. The ML-estimated parameters converged to their true values faster. Furthermore, we can conclude that the MLEs have the smallest MSE for all parameters and thus give the best performance, as expected.

Table 1 Simulated values of biases (MSEs within parentheses) of estimates of \(\hat{\alpha }\), \(\hat{\vartheta }\), \(\hat{\phi }\), \(\hat{\lambda }\), and p
Full size table
Table 2 Simulated values of biases (MSEs within parentheses) of estimates of \(\alpha \), \(\vartheta \), \(\phi \), \(\lambda \), and p based on MYW
Full size table

4 Real-life data analysis, model selection, diagnostic tools, and forecasting

In this section, the usefulness and applicability of the OMP-EMPT(1) process are shown using two real-life data sets. The assessment of the adequacy of the models proposed and fitted to the data under analysis is a critical step in any statistical investigation. In the literature, several methods for model validation and diagnostics in discrete-valued time series have been proposed. These methods are broadly classified as follows: model comparisons using information criteria and scores; residual-based methods; and predictive distribution-based methods.

4.1 Data and model selection based on information criteria

The application of the proposed process is investigated using economic and crime data sets:

  • The first data set represents \(n=242\) weekly sales of a particular soap product in a supermarket, obtained from a database provided by the Kilts Center for Marketing, Graduate School of Business of the University of Chicago (available at http://research.chicagobooth.edu/marketing/databases/dominicks/categories/soa.aspx; the product is ‘Zest White Water 15 oz’, with code 3700031165), or data can also be accessed from https://drive.google.com/drive/folders/165XirSF7gKiACX-Mg0Ho16QZ0J0KlqIe?usp=sharing.

  • The second data set represents \(n=142\) monthly counts of liquor law violations, reported in the 12th police car beat in Pittsburgh Plus, reported in a period from January 1990 to October 2001, and obtained from the Crime data section of the Forecasting Principles site http://www.forecastingprinciples.com or it can be obtained by https://drive.google.com/drive/folders/1b4a1Z2y9MPSFl1e3uMMmWc8zC-kjYVxU?usp=sharing. Table 3 displays some descriptive statistics for the two data sets. The time series, sample autocorrelation, partial autocorrelation functions (SACF and SPACF, respectively), and empirical p.m.f. for the weekly sales counts and monthly counts of liquor law violations are displayed in Figs. 8 and 9, respectively. From these plots, we conclude that a first-order autoregressive model may be appropriate for the two data sets, as the first autocorrelation is more significant than the other and the SPACF cuts off after lag one. Moreover, the behavior of the two data sets indicates that they may be stationary, and we confirm that result using the test of stationarity. The stationarity of the data is justified throughout the Augmented Dickey–Fuller (ADF) test based on the p-value of the ADF test; the stationarity of the data is supported, and the null hypothesis (non-stationary) is rejected.

The empirical p.m.f. displayed in black in Figs. 8d and 9d, while gray bars refer to the fitted OMP distribution below. From these figures, the empirical p.m.f. and the estimated OMP p.m.f. are close to each other.

As can seen in Table 3, the sample variance is greater than the sample mean for the data sets; therefore, they are over-dispersed. Schweer and Weiß (2014) proposed an over-dispersion test that is used to check this assumption, with a test statistic based on the empirical dispersion index \(\hat{I}_{x}=\frac{S^{2}}{\overline{X}}\), where \(S^{2}\) and \(\overline{X}\) are, respectively, the sample variance and mean. The null hypothesis \(H_{0}:x_{1},\ldots , x_{n}\) is derived from an equi-dispersed PINAR(1) process (Al-Osh and Alzaid 1987), while the alternative \(H_{1}:x_{1},\ldots , x_{n}\) stems from an over-dispersed INAR(1) process, with a level of significance of \(\beta _{0}=0.05\). If the observed value of \(\hat{I}_{x}\) exceeds the critical value \(1+z_{1-\beta _{0}}\sqrt{\frac{2(1+\alpha ^{2})}{n(1-\alpha ^{2})}}\), or if the p-value \(1-\Phi \left( \sqrt{\frac{n(1-\alpha ^{2})}{2(1+\alpha ^{2})}}\times (\hat{I}_{x}-1)\right) \) falls below \(\beta _{0}\), the null hypothesis is rejected, where \(z_{1-\beta _{0}}\) and \(\Phi (.)\) represents the \((1-\beta _{0})-\) quantile and the distribution function of the standard normal distribution, respectively, and \(\alpha =\hat{\rho }(1)\). The considered data sets are empirically over-dispersed, with dispersion indices, \(\hat{I}_{x}\) given in Table 3. By applying the over-dispersion test, the critical values and the p-values for the weekly sales and monthly liquor law violations counts are (1.165164, 1.232448) and (0.000,0.000), respectively. Therefore, the data sets stem from an over-dispersed INAR(1) process.

For comparison purposes, the two data sets are used to compare the proposed process, OMP-EMPT(1), with the following relevant INAR(1) models: PINAR(1) (Al-Osh and Alzaid 1987), Pegram AR(1) model with Poisson marginal (Biswas and Song 2009), Poisson MPT(1) (Khoo et al. 2017), MPDBPINAR(1) (Shirozhan and Mohammadpour 2018). We use the following goodness-of-fit statistics: the Akaike information criterion (AIC), the Hannan–Quinn information criterion (HQIC), and the corrected Akaike information criterion (AICc), where the best model has the ones with the lowest values. The results of these goodness-of-fit statistics and ML estimates with their standard error (S.E.) are displayed in Tables 4 and 5. These tables show that the values of the AIC, HQIC, and AICc are the smallest for the OMP-EMPT(1) process. Hence, we conclude that the proposed model works well for the two data sets. Also, we can conclude that the OMP-EMPT(1) model is significantly better than the Poisson-MPT(1) model for explaining both data sets, as we have \(\hat{\phi }=0.3185468,\ 0.6040971\), i.e., the proportion of ones that were misclassified as zeros in the process does not equal zero for the considered data sets. When \(\hat{\phi }=0.6040971\), this means that most ones are misclassified and reported as zeros, and this implies a zero inflation as seen in Fig. 9d. This means that when determining the number of weekly sales or liquor violations per unit, an inspector may make an error by reporting units that actually contain one item or one person as having no item or no one, respectively. The R script that was used to fit the data to the OMP-EMPT(1) model is included in the Appendix A.4.

Table 3 Descriptive statistics of weekly sales and monthly liquor law violations counts
Full size table
Fig. 8
figure 8

Sample path, SPACF, SACF, and PMF of the number of weekly sales

Full size image
Fig. 9
figure 9

Sample path, SACF, SPACF, and PMF of the number of monthly liquor law violations counts

Full size image
Table 4 ML estimates with their corresponding standard error (S.E.) in brackets and some goodness-of-fit statistics for weekly sales
Full size table
Table 5 ML estimates with their corresponding standard error (S.E.) and some goodness-of-fit statistics for monthly liquor law violations counts
Full size table

4.2 Diagnostic tools and model adequacy

In this subsection, we check the model’s adequacy throughout the logarithmic scoring rule, non-randomized probability integral transform (PIT), and benchmark chart.

Scoring rules can be used to assess a model’s relative performance within a given group of competing models. In decision analysis, scoring rules are frequently used to evaluate the accuracy of probabilistic predictions by assigning a numerical score based on the predictive distribution and observed data. To compare the observation \(x_{t}\) realized at time t with the conditional distribution \(p_{.|x_{t-1}}\) based on the previous observation, typical scoring rules are of the form \(s(p_{.|x_{t-1}},x_{t})\), with smaller score values indicating better agreement. The mean score \(\frac{1}{T-1}\sum _{t=2}^{T} s(p_{.|x_{t-1}},x_{t})\) is used to evaluate the model’s overall predictive performance with respect to the time series \(x_{1}, \cdots , x_{T}\). There are many scoring rules, such as quadratic, logarithmic, ranked probability, and spherical scores, to select the model with the smallest value of its mean. For the two data sets, we compute the logarithmic score defined as

$$\begin{aligned} s_{ls}(p_{(.|x_{t-1})},x_{t})=-\ln p_{x_{t}|x_{t-1}}, \end{aligned}$$
(4.1)

which corresponds to the conditional log-likelihood calculation defined by Eq. (2.13). Table 6 shows the mean logarithmic score (\(\overline{S_{ls}}\)) for the proposed fitted process and the competing models of the two data series. The mean score recommends the OMP-EMPT(1) model among the competitive INAR models.

The adequacy of the proposed fitted model is checked using the jumps \(J_{t}=X_{t}-X_{t-1},\) for \(t=2,\ 3,\ \cdots ,\ n\), \(E(J_{t})\), and \(Var(J_{t})\), which are given by Eq.(2.29) and Eq.(2.30), respectively. Figures 10 and 11a represent the jumps against time (Shewhart control chart) of the two data sets with \(\pm 3\sigma _{J}\) limits chosen as the benchmark chart as proposed by Weiß (2009), where \(\sigma _{J} =\sqrt{Var(J_{t})}=3.072668,\ \text {and}\ 1.288924\), respectively. The Shewhart control chart for the two considered data sets indicates that there is no particular point causing a huge impact in the model and implies that the proposed model fits the two data sets well. If a model is suitable for the data series, the non-randomized probability integral transform (PIT) histogram, Czado et al. (2009), should be uniform. Figures 10 and 11b show the PIT for the two data sets, indicating that the PIT histogram is close to uniform and that the proposed model fits the two data sets well, i.e., the model is adequate for these data series.

Fig. 10
figure 10

Jumps against time and PIT of fitted OMP-EMPT(1) for weekly sales

Full size image
Fig. 11
figure 11

Jumps against time and PIT of fitted OMP-EMPT(1) for monthly liquor law violations counts

Full size image
Table 6 The mean logarithmic score for the considered data sets
Full size table
Fig. 12
figure 12

Actual and predicted values of weekly sales

Full size image
Fig. 13
figure 13

Actual and predicted values of monthly liquor law violations counts

Full size image

4.3 Forecasting

The minimum mean square error is one of the most common procedures for optimally forecasting future values of a model. The conditional mean finds a forecast, \(\hat{X}_{t+k}\) of \(X_{t+k}\) that minimizes the expected squared error given a sample. Using Eqs. (2.16) and (2.17), the one- and k-step-ahead forecasts of \(X_{t+1}\) and \(X_{t+k}\) are, respectively, given by

$$\begin{aligned} \hat{X}_{t+1}=E(X_{t+1}|X_{t})=(p\alpha ) X_{t}+(1-(p\alpha ))\lambda (1-\phi e^{-\lambda }), \end{aligned}$$

where \(\hat{X}_{1}=(1-(p\alpha ))\lambda (1-\phi e^{-\lambda })\) and

$$\begin{aligned} \hat{X}_{t+k}=E(X_{t+k}|X_{t})=(p\alpha )^{k} X_{t}+(1-(p\alpha )^{k})\lambda (1-\phi e^{-\lambda }), k\ge 1. \end{aligned}$$

In practice, the parameters \(p, \alpha , \lambda \), and \(\phi \) are replaced by their ML estimates. Therefore

$$\begin{aligned} \hat{X}_{t+1}=E(X_{t+1}|X_{t})=(\hat{p}\hat{\alpha }) X_{t}+(1-(\hat{p}\hat{\alpha }))\hat{\lambda }(1-\hat{\phi } e^{-\hat{\lambda }}), \end{aligned}$$
(4.2)

and

$$\begin{aligned} \hat{X}_{t+k}=E(X_{t+k}|X_{t})=(\hat{p}\hat{\alpha })^{k} X_{t}+(1-(\hat{p}\hat{\alpha })^{k})\hat{\lambda }(1-\hat{\phi } e^{-\hat{\lambda }}), k\ge 1. \end{aligned}$$
(4.3)

The two actual data sets and their predicted values in the classical way using Eq. (4.2) are displayed and plotted in Figs. 12 and 13 to show the predictive ability of the OMP-EMPT(1) process, where \(\hat{\alpha }, \hat{\phi }, \hat{p}, \ \text {and} \ \hat{\lambda }\) are presented in Tables 4 and 5. From these figures, we observe that the predicted values are close to the original ones in the data sets, indicating that the OMP-EMPT(1) process can provide a good forecast for these data sets.