Abstract
We consider flat differential control systems for which there exist flat outputs that are part of the state variables and study them using Jacobi bound. We introduce a notion of saddle Jacobi bound for an ordinary differential system of n equations in \(n+m\) variables. Systems with saddle Jacobi number equal to 0 generalize various notions of chained and diagonal systems and form the widest class of systems admitting subsets of state variables as flat output, for which flat parametrization may be computed without differentiating the initial equations. We investigate apparent and intrinsic flat singularities of such systems. As an illustration, we consider the case of a simplified aircraft model, providing new flat outputs and showing that it is flat at all points except possibly in stalling conditions. Finally, we present numerical simulations showing that a feedback using those flat outputs is robust to perturbations and can also compensate model errors, when using a more realistic aerodynamic model.












Similar content being viewed by others
Data availability
Simulation data for Maple implementations are available with the Maple packages.
Code availability
The most recent implementation in Maple for aircraft motion planning, including generalized flatness, is available at http://www.lix.polytechnique.fr/~ollivier/GFLAT/.
Notes
Allowing change of independent variable, i.e., in control change of time, so that Monge problem is more precisely to test orbital flatness (Fliess et al. 1999)
From the Greek
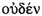 “nothing”, or “zero” for Iamblichus, and
“nothing”, or “zero” for Iamblichus, and  , “saddle”.
, “saddle”.Or Lie-Bäcklund transform.
In the case of a system \(X'=AX\), the characteristic polynomial of A is the determinant of \(M-\lambda \textrm{Id}\).
The general case is more complicated, already for time-varying linear systems (see Ritt 1935). Then, there exists an analog of Smith normal form, due to Jacobson (1937), but no suitable notion of divisors, as factorization in \(\mathbb {R}(t)[\textrm{d}/\textrm{d}t]\) is not unique. Indeed, \((\textrm{d}/\textrm{d}t)^{2}\) is equal to \((\textrm{d}/\textrm{d}t+1/(x+\alpha ))(\textrm{d}/\textrm{d}t-1/(x+\alpha ))\), for any \(\alpha \in \mathbb {R}\) (Chyzak et al. 2022). One must also notice that \(\textrm{diag}(\textrm{d}/\textrm{d}t, (\textrm{d}/\textrm{d}t)(\textrm{d}/\textrm{d}t+1))(x_{1}x_{2})^{\textrm{t}}\) is a Smith normal form with \(\mathbb {R}[\textrm{d}/\textrm{d}t]\) as the base ring, but not a Jacobson normal form with base ring \(\mathbb {R}(t)[\textrm{d}/\textrm{d}t]\), as then the quotient module may be generated by a single element \(x_{1}+tx_{2}\).
This convention, introduced by Ritt (see Ollivier 2023, § 4 for details), is known as the strong bound. The convention \(\textrm{ord}_{x_{j}}P_{i}=0\) is the weak bound.
Here, \(\sharp A\) denotes the number of elements of a set A.
Jacobi named it determinans mancum sive determinans mutilatum, because only the terms \(\partial P_{i}/\partial x_{j}^{(a_{i,j})}\), such that \(a_{i,j}=\alpha _{i}+\beta _{j}\) appear in it.
The algebraic ideal is a proper subset of the differential ideal.
Considering the system as a system in the variables of Y only, and the remaining variables as parametric variables, we reduce to a system of differential dimension 0 that is indeed block triangular, according to the definition in (Ollivier 2023, 4.3).
We denote for brevity sets of rows or columns by the sets of corresponding indices.
Wing span a and mean aerodynamic chord b are, respectively, denoted by b and c in Grauer and Morelli (2014).
More precisely, such angles are known as Tait–Bryan angles.
The angles are not physical angles, but rather measures related to some physical angles and that are calibrated by the aircraft producer.
References
Adel’son-Vel’skii GM, Landis EM (1962) An algorithm for the organization of information. Sov Math Doklady 3:1259–1263
Asselin M (1997) An Introduction to Aircraft Performance. American Institute of Aeronautics and Astronautics, Reston, Virginia
Beaver LE, Malikopoulos AA (2024) Optimal Control of Differentially Flat Systems is Surprisingly Easy Automatica Volume 159, January 2024, 111404
Board NTS (1973) Aircraft Accident Report NTSB/AAR-73-02: American Airlines, Inc. McDonnell Douglas DC-10-10, N103AA. Near Windsor, Ontario, Canada. 12 June 1972
Board NTS (2010) Loss of Thrust in Both Engines After Encountering a Flock of Birds and Subsequent Ditching on the Hudson River US Airways Flight 1549 Airbus A320-214, N106US Weehawken, New Jersey January 15, 2009
Buccieri D, Perritaz D, Mullhaupt P, Jiang Z-P, Bonvin D (2009) Velocity-scheduling control for a unicycle mobile robot: Theory and experiments. IEEE Trans Robot 25(2):451–458. https://doi.org/10.1109/TRO.2009.2014494
Burkard R, Dell’Amico M, Martello S (2012) Assignment Problems. Society for Industrial and Applied Mathematics, Philadelphia. https://doi.org/10.1137/1.9781611972238. https://epubs.siam.org/doi/abs/10.1137/1.9781611972238
Cartan É (1914) Sur l’équivalence absolue de certains systèmes d’équations différentielles et sur certaines familles de courbes. Bull Soc Math France 42:12–48
Cartan É (1915) Sur l’intégration de certains systèmes indéterminés d’équations différentielles. J für die reine und angewandte Mathematik 145:86–151
Chèze G, Combot T (2020) Symbolic computations of first integrals for polynomial vector fields. Found Comput Math 20:681–752. https://doi.org/10.1007/s10208-019-09437-9
Chrystal G (1897) A fundamental theorem regarding the equivalence of systems of differential equations, and its application to the determination of the order and the systematic solution of a determinate system of such equations. Trans R Soc Edinburgh 38:163–178
Chyzak F, Goyer A, Mezzarobba M (2022) Numeric factorization of differential operators. In: In Proceedings of the 2022 Int’l Symposium on Symbolic and Algebraic Computation (ISSAC ’22), pp. 73–82. ACM Press, New York. https://doi.org/10.1145/3476446.3535503
Duffin RJ (1963) Chrystal’s theorem on differential equation systems. J Math Anal Appl 8:325–331
Faulwasser T, Hagenmeyer V, Findeisen R (2011) Optimal exact path-following for constrained differentially flat systems. IFAC Proceedings Volumes 44(1):9875–9880. https://doi.org/10.3182/20110828-6-IT-1002.03132. 18th IFAC World Congress
Fliess M, Lévine J, Martin P, Rouchon P (1993) Défaut d’un système non linéaire et commande haute fréquence. C R Acad Sci Paris Autom 316:513–518
Fliess M, Lévine J, Martin P, Rouchon P (1995) Flatness and defect of non-linear systems: introduction theory and examples. Int J Control 61(6):1327–1361
Fliess M, Lévine J, Martin P, Rouchon P (1995) Flatness and defect of non-linear systems: introduction theory and examples. Int J Control 61(6):1327–1361
Fliess M, Lévine J, Martin P, Rouchon P (1999) A lie-bäcklund approach to equivalence and flatness of nonlinear systems. IEEE Trans Autom Control 44(5):922–937
Fliess M, Lévine J, Martin P, Rouchon P (1999) A Lie-Bäcklund approach to equivalence and flatness of nonlinear systems. IEEE Trans Autom Control 44(5):922–937
Flores ME, Milam MB (2006) Trajectory generation for differentially flat systems via nurbs basis functions with obstacle avoidance. 2006 American Control Conference, 7
Franch J, Agrawal S, Oh S, Fattah A (2003) Design of differentially flat planar space robots: a step forward in their planning and control. In: Proceedings 2003 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS 2003) (Cat. No.03CH37453), vol. 3, pp. 3053–3058. https://doi.org/10.1109/IROS.2003.1249625
Frobenius FG (1917) Über zerlegbare determinanten. Sitzungsberichte der Königlich Preußischen Akademie der Wissenschaften zu Berlin, 274–277
Grauer JA, Morelli EA (2014) A generic nonlinear aerodynamic model for aircraft. In: AIAA Atmospheric Flight Mechanics Conference
Gstöttner C, Kolar B, Schöberl M (2022) A structurally flat triangular form based on the extended chained form. Int J Control 95(5):1144–1163. https://doi.org/10.1080/00207179.2020.1841302
Gudmundsson S (2014) General Aviation Aircraft Design: Applied Methods and Procedures. Butterworth-Heinemann (Elsevier), Oxford
Hilbert D (1912) Über den Begriff der Klasse von Differentialgleichungen. Math Annal 73:95–108
Hopcroft JE, Karp RM (1973) An \(n^{5/2} \) algorithm for maximum matchings in bipartite graphs. SIAM J Comput 2(4):225–231. https://doi.org/10.1137/0202019
Hueschen RM (2011) Development of the transport class model (tcm) aircraft simulation from a sub-scale generic transport model (gtm) simulation. Technical Memorandum 217169, NASA, Langley Research Center, Hampton, VA
Jacobi CGJ (2009) Looking for the order of a system of arbitrary ordinary differential equations. de investigando ordine systematis aequationum differentialum vulgarium cujuscunque. AAECC 20(1):7–32
Jacobi CGJ (2009) The reduction to normal form of a non-normal system of differential equations. de aequationum differentialum systemate non normali ad formam normalem revocando. AAECC 20(1):33–64
Jacobson N (1937) Pseudo-linear transformations. Ann Math 38(2):484–507
Kaminski Y, Lévine J, Ollivier F (2018) Intrinsic and apparent singularities in differentially flat systems, and application to global motion planning. Syst Control Lett 113:117–124
Kaminski Y, Lévine J, Ollivier F (2020) On singularities of flat affine systems with n states and \(n - 1\) controls, international journal of robust and nonlinear control. Int J Robust Nonlinear Control 30(9):3547–3565
Knuth DE (1998) The Art of Computer Programming, , Volume III, “sorting and Searchin”, 2nd Edition. Addison-Wesley. https://www.worldcat.org/oclc/312994415
Kokotović PV, O’Reilly J, Khalil HK (1986) Singular Perturbation Methods in Control: Analysis and Design. Academic Press Inc, USA
Kolar B, Schöberl M, Schlacher K (2015) Remarks on a triangular form for 1-flat faffian systems with two inputs. IFAC-PapersOnLine 48(11):109–114. https://doi.org/10.1016/j.ifacol.2015.09.168
Kondratieva MV, Mikhalev AV, Pankratiev EV (2009) Jacobi’s bound for independent systems of algebraic partial differential equations. AAECC 20(1):65–71. https://doi.org/10.1007/s00200-009-0092-6
Kőnig D (1931) Gráfok és mátrixok. Matematikai és Fizikai Lapok 38:116–119
Krasil’shchik VV, Lychagin VV, Vinogradov AM (1986) Geometry of Jet Spaces and Nonlinear Partial Differential Equations. Gordon and Breach, New York
Kuhn HW (2012) A tale of three eras: The discovery and rediscovery of the hungarian method. Eur J Oper Res 219(3):641–651
Lévine J (2009) Analysis and Control of Nonlinear Systems: A Flatness-based Approach. Mathematical Engineering. Springer, Berlin Heidelberg
Lévine J (2011) On necessary and sufficient conditions for differential flatness. Appl Algebra Eng Commun Comput 22(1):47–90
Li S-J, Respondek W (2010) A kinematic model of the nonholonomic n-bar system: Geometry and flatness. IFAC Proceedings Volumes 43(14):689–694. https://doi.org/10.3182/20100901-3-IT-2016.00292. 8th IFAC Symposium on Nonlinear Control Systems
Li S-J, Respondek W (2012) Flat outputs of two-input driftless control systems. ESAIM: COCV 18(3):774–798. https://doi.org/10.1051/cocv/2011181. 8th IFAC Symposium on Nonlinear Control Systems
Li S, Nicolau F, Respondek W (2016) Multi-input control-affine systems static feedback equivalent to a triangular form and their flatness. Int J Control 89(1):1–24. https://doi.org/10.1080/00207179.2015.1056232
Lockwood GH (1985) Final report of the board of inquiry into air canada boeing 767 c-gaun accident — gimli, manitoba, july 23, 1983. Technical report, Canadian Government Publishing Center. https://reports.aviation-safety.net/1983/19830723-0_B762_C-GAUN.pdf
Martin P (1992) Contribution à l’étude des systèmes différentiellement plats. PhD thesis, Ecole Nationale Supérieure des Mines de Paris, Paris, France
Martin P (1996) Aircraft control using flatness. CESA’96 - Symposium on Control. Optimization and Supervision. IMACS/IEEE-SMC Multiconference, Lille, France, pp 194–199
McLean D (1990) Automatic Flight Control Systems. Prentice Hall, New York
Monge G (1787) Supplément où l’on fait savoir que les équations aux différences ordinaires, pour lesquelles les conditions d’intégrabilité ne sont pas satisfaites sont susceptibles d’une véritable intégration et que c’est de cette intégration que dépend celle des équations aux différences partielles élevées. Histoire de l’Académie royale des sciences, année MDCCLXXXIV, 502–576
NATOPS (1978) NATOPS flight manual, navy model, F-4F aircraft
Oldenburg J, Marquardt W (2002) Flatness and higher order differential model representations in dynamic optimization. Comp Chem Eng 26:385–400
Ollivier F (2022) Extending flat motion planning to non-flat systems. experiments on aircraft models using maple. In: Maza MM, Zhi L (eds.) ISSAC ’22: International Symposium on Symbolic and Algebraic Computation, Villeneuve-d’Ascq, France, July 4 - 7, 2022, pp. 499–507. ACM, New York. https://doi.org/10.1145/3476446.3536179
Ollivier F (2023) Jacobi’s bound: Jacobi’s results translated in könig’s, egerváry’s and ritt’s mathematical languages. AAECC 34 https://doi.org/10.1007/s00200-022-00547-6
Ollivier F (1998) A negative answer to the \(\delta \)-lüroth problem in two variables. C R Acad Sci 327(10):881–886. https://doi.org/10.1016/S0764-4442(99)80037-8
Ollivier F (1999) Une réponse négative au problème de noether différentiel. C R Acad Sci 328(2):99–104. https://doi.org/10.1016/S0764-4442(99)80145-1
Ollivier F (2009) Looking for the order of a system of arbitrary ordinary differential equations. AAECC 20(1):7–32. https://doi.org/10.1007/s00200-009-0087-3
Ollivier F (2009) The reduction to normal form of a non-normal system of differential equations. AAECC 20(1):33–64. https://doi.org/10.1007/s00200-009-0088-2
Ollivier F, Sadik B (2009) Jacobi’s bound for a diffiety defined by a quasi-regular system. Comptes Rendus Mathematique 345(3), 139–144. DOI: https://doi.org/0.1016/j.crma.2007.06.010
Ollivier F, Sedoglavic A (2001) A generalization of flatness to nonlinear systems of partial differential equations. application to the command of a flexible rod. IFAC Proceedings Volumes 34(6):219–223. https://doi.org/10.1016/S1474-6670(17)35177-7. 5th IFAC Symposium on Nonlinear Control Systems 2001, St Petersburg, Russia, 4-6 July 2001
Petitot M (1992) Polynômes non commutatifs et applications à l’automatique. Talk at the seminar Aleph et Géode, Polytechnique, Palaiseau, France
Ren W, Jiang B, Yang H (2016) A survey on singular perturbation theory in aerospace application. In: 2016 IEEE Chinese Guidance, Navigation and Control Conference (CGNCC), pp. 675–680. https://doi.org/10.1109/CGNCC.2016.7828867
Ritt JF (1935) Jacobi’s problem on the order of a system of differential equations. Ann Math 36:303–312
Ritt JF (1950) Differential Algebra. American Mathematical Society, Rhode Island
Ross IM, Fahroo F (2002) Pseudospectral methods for optimal motion planning of differentially flat systems. In: Proceedings of the 41st IEEE Conference on Decision and Control, 2002., vol. 1, pp. 1135–11401. https://doi.org/10.1109/CDC.2002.1184665
Rouchon PMP (1994) Feedback linearization and driftless systems. Mathematics of Control, Signals, and Systems (MCSS) 1994-sep vol. 7 iss. 3 7https://doi.org/10.1007/bf01212271
Rouchon P, Fliess M, Lévine J, Martin P (1993) Flatness and motion planning: the car with n trailers. In: IN PROC. EUROPEAN CONTROL CONFERENCE, pp. 1518–1522
Rouchon P, Fliess M, Levine J, Martin P (1993) Flatness, motion planning and trailer systems. In: Proceedings of 32nd IEEE Conference on Decision and Control, pp. 2700–27053. https://doi.org/10.1109/CDC.1993.325686
Silveira HB (2010) Formas triangulares para sistemas não-lineares com duas entradas e controle de sistemas sem arrasto em su(n) com aplicações em mecânica quântica. PhD thesis, Escola Politécnica, Universidade de São Paulo, São Paulo, Brasil. https://doi.org/10.11606/T.3.2010.tde-13082010-163547
Silveira HB, Silva PS, Rouchon P (2015) A flat triangular form for nonlinear systems with two inputs: Necessary and sufficient conditions. Eur J Control 22:17–22. https://doi.org/10.1016/j.ejcon.2015.01.001
Ströhle T, Betsch P (2022) A simultaneous space-time discretization approach to the inverse dynamics of geometrically exact strings. International Journal for Numerical Methods in Engineering 123(11) https://doi.org/10.1002/nme.6951
Szárnyas G (2020) Graphs and matrices: A translation of “Graphok és matrixok” by Dénes Kőnig (1931). arXiv. arXiv:2009.03780
Yueksel B, Buondonno G, Franchi A (2016) Differential flatness and control of protocentric aerial manipulators with any number of arms and mixed rigid-/elastic-joints. In: 2016 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), pp. 561–566. https://doi.org/10.1109/IROS.2016.7759109
Zerar M, Zolghadri A, Cazaurang F (2009) Coupled linear parameter varying and flatness-based approach for space re-entry vehicles guidance. IET Control Theory & Applications 3https://doi.org/10.1049/iet-cta.2008.0057
Zharinov VV (1992) Geometrical Aspects of Partial Differential Equations. Series on Soviet and East European Mathematics. World Scientific, Singapore
Acknowledgements
The authors thank Jean Lévine for advices and inspiration.
Funding
F. Ollivier thanks the French ANR project ANR-22-CE48-0016 NODE (numeric-symbolic resolution of differential equations) and the ANR project ANR-22-CE48-0008 OCCAM (theory and practice of differential elimination).
Author information
Authors and Affiliations
Contributions
Y. J. Kaminski is responsible for Python implementations and F. Ollivier for Maple implementations. Y.J. Kaminski and F. Ollivier have contributed to the study conception and realization or to the writing and typesetting process.
Corresponding author
Ethics declarations
Conflict of interest
No fundings or relations between the authors and companies or entities having interests in space or aircraft industries or control devices or softwares is likely to call into question the objectivity of this work.
Additional information
Communicated by Nadhir Messai.
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.
About this article
Cite this article
Kaminski, Y., Ollivier, F. Flat singularities of chained systems, illustrated with an aircraft model. Comp. Appl. Math. 43, 135 (2024). https://doi.org/10.1007/s40314-024-02605-w
Received:
Revised:
Accepted:
Published:
DOI: https://doi.org/10.1007/s40314-024-02605-w
Keywords
- Differentially flat systems
- Flat singularities
- Flat outputs
- Aircraft aerodynamics models
- Gravity-free flight
- Engine failure
- Rudder jam
- Differential thrust
- Forward slip landing
- Jacobi’s bound
- Hungarian method





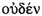 “nothing”, or “zero” for Iamblichus, and
“nothing”, or “zero” for Iamblichus, and  , “saddle”.
, “saddle”.