Oscillatory traveling waves for a population diffusion model with two age classes and nonlocality induced by maturation delay

Abstract

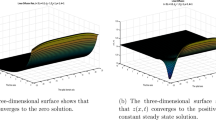
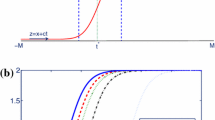
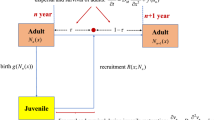
Considering the traveling wave solutions of an age-structured population model, we study the propagation patterns of a single species with respect to the diffusion rates of mature and immature population. Depending on the slope of the birth function at the positive equilibrium, the monotonic wave may change to an oscillatory wave solution, when the diffusion ratio of immature versus mature population exceeds a threshold value. This has been confirmed with numerical exploration of the traveling wave solutions.

Appendix A: The monotone iterative method

Considering the integral term in the wave Eq. (13), the functional $H: C(\mathbb {R},\mathbb {R})\rightarrow C(\mathbb {R},\mathbb {R})$ is defined by

$$\begin{aligned} H(\phi )(t) =\epsilon \int ^{\infty }_{-\infty } b(\phi (t+y-c\tau )) f_{\alpha }(y) dy, \phi \in C(\mathbb {R},\mathbb {R}),t\in \mathbb {R}. \end{aligned}$$

(38)

Then the wave Eq. (13) connecting the equilibria $\phi _{1}$ and $\phi _{2}$ at the two ends is represented by the Cauchy problem

$$\begin{aligned} c\phi ^{'}(t)&= D_{m}\phi ^{''}(t) -d_{m}\phi (t) +H(\phi )(t),\end{aligned}$$

(39)

$$\begin{aligned} \lim _{t\rightarrow -\infty }\phi (t)&= \phi _{1},\quad \lim _{t\rightarrow \infty }\phi (t)=\phi _{2}. \end{aligned}$$

(40)

As in So et al. (2001) a function $\phi \in C(\mathbb {R},\mathbb {R})$ is called an upper (respectively, lower) solution of (39) if it is differentiable and it satisfies (39) with the sign $\ge$ (respectively, $\le$). Define the wave profile of traveling wave solutions as

$$\begin{aligned} \Gamma =\left\{ \phi \in C(\mathbb {R},\mathbb {R})\left| \phi (t) \text{ is } \text{ non-decreasing } \text{ in } t\in \mathbb {R},\lim _{t\rightarrow \infty }=\phi _{2}, \lim _{t\rightarrow -\infty }=\phi _{1}\right. \right\} .\qquad \end{aligned}$$

(41)

It can be shown So et al. (2001) that if $b(\phi )$ is increasing in the interval $\left[ \phi _{1},\phi _{2}\right]$, then $H(\phi )(t)\ge 0$ for all $t\in \mathbb {R}$, $H(\phi )(t)$ is non-decreasing with respect to $t\in \mathbb {R}$ and also with respect to $\phi \in C(\mathbb {R},\mathbb {R})$. Using these properties of $H(\phi )(t)$ and the iterative technique, the problem of constructing a traveling wavefront is reduced to the problem of finding an upper $\overline{\phi }$ and lower $\underline{\phi }$ solutions of (39), which satisfy the three conditions: (1) $\overline{\phi }\in \Gamma ,$ (2) $\phi _{1}\le \underline{\phi }(t)\le \overline{\phi }(t)\le \phi _{2}$ for all $t\in \mathbb {R},$ and (3) $\underline{\phi }(t)\ne 0$. Specifically, under monotonicity condition (i.e., $\phi _{2}<\phi _{M}$, where $\phi _{M}$ is the local maximum of $b(\phi )$), the solution of (39), (40) is obtained by solving the following equation iteratively,

$$\begin{aligned} cv^{'}_{n}(t) =D_{m}v^{''}_{n}(t)-d_{m}v_{n}(t) +H(v_{n-1})(t),\quad t\in \mathbb {R}, n=1,2,\ldots , \end{aligned}$$

(42)

with boundary conditions

$$\begin{aligned} \lim _{t\rightarrow -\infty } v_{n}(t) =\phi _{1} \quad \text{ and }\quad \lim _{t\rightarrow \infty } v_{n}(t) =\phi _{2}, \end{aligned}$$

(43)

where $v_{0}(t) =\overline{\phi }(t)$, $t\in \mathbb {R}$.

In other words, $\underline{\phi }(t)\le v_{n}(t)\le v_{n-1}(t)\le \overline{\phi }(t)$ for all $n=1,2,\ldots$ and $\phi (t)=\lim _{n\rightarrow \infty }v_{n}(t)$ is the solution of (39), (40). Noting that $H(v_{n-1})(t)$ is a known function of $t$, Eq. (42) is a non-homogeneous second-order linear differential equation with the following solution.

$$\begin{aligned} v_{n}(t) =\frac{1}{D_{m}(\beta _{+}-\beta _{-})} \left[ \int ^{t}_{-\infty } e^{\beta _{-}(t-s)} H(v_{n-1}) (s) \mathrm{d}s +\int ^{\infty }_{t} e^{\beta _{+}(t-s)} H(v_{n-1}) (s) \mathrm{d}s \right] ,\qquad \end{aligned}$$

(44)

where $t\in \mathbb {R}$, $n=1,2,\ldots$ and $\beta _{\pm }=\frac{c\pm \sqrt{c^{2}+4D_{m}d_{m}}}{2D_{m}}$. Then it can be shown [see Theorem 4.3 of So et al. (2001)] that $v_{n}\in \Gamma$, $\underline{\phi }(t)\le v_{n}(t)\le v_{n-1}(t)\le \overline{\phi }(t)$. For all $n=1,2,\ldots ,$ each $v_{n}$ is an upper solution and $\lim _{n\rightarrow \infty }v_{n}(t) = \phi (t)$.

The work by So et al. (2001) suggests that

$$\begin{aligned} \overline{\phi }(t)=\min \left\{ \phi _{2},\phi _{2}e^{\lambda _{1}t}\right\} , \end{aligned}$$

(45)

and

$$\begin{aligned} \underline{\phi }(t)=\max \left\{ 0,\phi _{2}(1-Ne^{\delta t}) e^{\lambda _{1}t}\right\} , \end{aligned}$$

(46)

are a pair of upper and lower solutions when the birth function $b_{1}(\phi )$ is considered and $\frac{\epsilon p}{d_{m}}<e$, which is for the monotonicity of the wave solution. Nevertheless the upper and lower solutions should be differentiable Wu and Zou (2008). Here $N>1$ and $\delta >0$ are, respectively, large and small constants and $\lambda _{1}$ is a real positive root of

$$\begin{aligned} \Delta _{c}(\lambda )= \epsilon b^{'}_{i}(0) e^{\alpha \lambda ^{2}-\lambda c\tau } -(c\lambda +d_{m}-D_{m}\lambda ^{2}), \end{aligned}$$

(47)

which is the characteristic equation of the wave Eq. (39). The iterative method is also employed in the work by Liang and Wu (2003) where the authors have considered the same pair of upper and lower solutions when other birth functions are employed.