Skip to main content
SpringerLink
Log in

Structural Stability of the Financial Market Model: Continuity of Superhedging Price and Model Approximation

  • Published:
Journal of the Operations Research Society of China Aims and scope Submit manuscript

Abstract

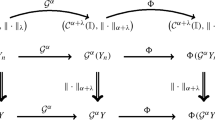
The present paper continues the topic of our recent paper in the same journal, aiming to show the role of structural stability in financial modeling. In the context of financial market modeling, structural stability means that a specific “no-arbitrage” property is unaffected by small (with respect to the Pompeiu–Hausdorff metric) perturbations of the model’s dynamics. We formulate, based on our economic interpretation, a new requirement concerning “no arbitrage” properties, which we call the “uncertainty principle”. This principle in the case of no-trading constraints is equivalent to structural stability. We demonstrate that structural stability is essential for a correct model approximation (which is used in our numerical method for superhedging price computation). We also show that structural stability is important for the continuity of superhedging prices and discuss the sufficient conditions for this continuity.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

Notes

  1. We believe, however, that this mistake is of “local” character, so it cannot have any implications for the other results in [16].

  2. In probabilistic terminology, this corresponds to the predictability of \(H_t\) with respect to the filtration, generated by asset prices process.

  3. If \(h=(h^1,\cdots ,h^n)\) and \(y=(y^1,\cdots ,y^n)\) then \(hy=h^1y^1 + \cdots + h^ny^n\).

  4. See the definition of this metric, e.g., in [35, Subsection 1.1, Chapter 1].

  5. In the probabilistic setting, this geometric criterion, understood almost surely, was found in [22].

  6. This recurrence relation is the starting point of our research and, in principle, can also be regarded as a kind of axiom.

  7. The sufficient conditions for the validity of (BI), that are formulated in [19, Theorem 3.1], are discussed in [19, Remark 3.1].

  8. Specifically, a particular case of this statement is needed, namely, the support function of a set is non-negative iff the point 0 belongs to closure of convex hull of this set.

  9. Recall that \(\mathop {\textrm{cl}}\limits \bigl (\mathop {\textrm{conv}}\limits (K_t(\cdot ))\bigr )= \mathop {\textrm{conv}}\limits (K_t(\cdot ))\) for compact \(K_t(\cdot )\).

  10. Continuity with respect to the Pompeiu–Hausdorff metric.

  11. Note that in this case RNDSAUP is equivalent to RNDAO.

  12. In this case \(D_t(\cdot )\equiv \mathbb {R}^n\), so that the condition 3) of Theorem 1 is satisfied.

  13. In fact, in [30] we prove a more general result (with constructive estimates of uniform approximation).

  14. Recall that for a non-empty set B in a linear space X, the recession cone of B (denoted \(\mathop {\textrm{rec}}\limits (B)\)) is the set of all vectors \(y\in X\) such that the half-lines \(\{x+\lambda y, \lambda \in [0, + \infty ) \}\) lie in B for all \(x \in B\). If B is convex, its recession cone is convex as well. Refer e. g. to [24, Section 8].

  15. The domain \(\mathcal {A}\) of Q, i. e., the \(\sigma \)-algebra of all subsets of \(\mathbb {R}^n\), can be chosen depending on a particular class \(\mathcal {P}_t(\cdot )\). For example, we can take as \(\mathcal {A}\) the class of all subsets if \(\mathcal {P}_t(\cdot )\) consists of probability measures concentrated in a finite set of points. In other cases, we can take, e.g., a Borel \(\sigma \)-algebra, which is natural when the functions \(v^*_t\) are upper semicontinuous.

  16. Hedger’s mixed strategies make no sense because the bracketed expression in (8) is a linear function of h (due to no transaction costs), and the set \(D_t(\cdot )\) is convex.

  17. Note that the following inequality always holds: \(\rho _t(\cdot ) \geqslant \rho '_t(\cdot )\).

  18. For example, as \(\mathcal {P}_t(\cdot )\) we can choose the class \(\mathcal {P}^*(K_t(\cdot ))\) of measures concentrated in a finite set of points from \(K_t(\cdot )\) (to avoid additional requirements on the functions \(v^*_t\)). An alternative approach involves, e.g., the universal measurability of \(v^*_t\) (or any other smoothness property, e.g., semicontinuity).

  19. Recall that \(\mathop {\textrm{ri}}\limits (A)\) is the relative interior of convex set A.

  20. That is, for every closed \(C \subseteq \mathbb {R}^n\), the set \(L^-(C)= \{ x \in X:\, L(x) \cap C \ne \varnothing \}\) is closed.

  21. In the case of one risky asset, i.e., \(n=1 \), the condition NDAO is tantamount to RNDAO.

  22. Note that Proposition 3.8 of [16] is nevertheless valid, since in one-dimensional case the condition RNDAO is equivalent to NDAO, so that the condition of structural stability is fulfilled.

  23. We are referring here to a theorem from [39]; although it is about countable products of measurable spaces, it holds for finite products as well.

  24. Under a martingale measure the (discounted) price process is a martingale.

  25. Recall that \(\delta _x \) stand for a Dirac measure (see Definition 6).

  26. Recall that according to our assumptions about trading constraints the vector 0 must lie in \(D_t(\cdot )\). Moreover, the sets \(D_t(\cdot )\) are convex.

  27. More intuitively clear arguments follows from the alternative geometric criterion of RNDSAUP, as proven in [21, Theorem 2]: in our case it is evident that \(\mathop {\textrm{bar}}\limits (D_t(\cdot ))\) and \(\mathop {\textrm{conv}}\limits (K_t (\cdot ) )\) intersect transversally; therefore, RNDSAUP holds.

References

  1. Smirnov, S.N.: Realistic models of financial market and structural stability. J. Math. (2021). https://doi.org/10.1155/2021/6651324

  2. Schachermayer, W.: The fundamental theorem of asset pricing under proportional transaction costs in finite discrete time. Math. Financ. 14(1), 19–48 (2004)

    Article  MathSciNet  Google Scholar 

  3. Bayraktar, E., Zhang, Y., Zhou, Z.: A note on the fundamental theorem of asset pricing under model uncertainty. Risks 2(4), 425–433 (2014)

    Article  Google Scholar 

  4. Ostrovski, V.: Stability of no-arbitrage property under model uncertainty. Stat. Probab. Lett. 83, 89–92 (2013)

    Article  MathSciNet  Google Scholar 

  5. Hou, Z., Obłój, J.: Robust pricing-hedging dualities in continuous time. Finance Stoch. 22, 511–567 (2018)

    Article  MathSciNet  Google Scholar 

  6. Smirnov, S.N.: A guaranteed deterministic approach to superhedging: no arbitrage properties of the market. Autom. Remote. Control. 82, 172–187 (2021)

    Article  MathSciNet  Google Scholar 

  7. Davis, M., Hobson, D.: The range of traded option prices. Math. Finance 17, 1–14 (2007)

    Article  MathSciNet  Google Scholar 

  8. Acciaio, B., Beiglböck, M., Penkner, F., Schachermayer, W.: A model-free version of the fundamental theorem of asset pricing and the super-replication theorem. Math. Financ. 26, 233–251 (2013)

    Article  MathSciNet  Google Scholar 

  9. Bouchard, B., Nutz, M.: Arbitrage and duality in nondominated discrete-time models. Ann. Appl. Probab. 25, 823–859 (2015)

    Article  MathSciNet  Google Scholar 

  10. Burzoni, M., Frittelli, M., Maggis, M.: Universal arbitrage aggregator in discrete-time markets under uncertainty. Finance Stoch. 20, 1–50 (2016)

    Article  MathSciNet  Google Scholar 

  11. Burzoni, M., Frittelli, M., Maggis, M.: Model-free superhedging duality. Ann. Appl. Probab. 27, 1452–1477 (2017)

    Article  MathSciNet  Google Scholar 

  12. Burzoni, M., Frittelli, M., Hou, Z., Maggis, M., Obłój, J.: Pointwise arbitrage pricing theory in discrete time. Math. Oper. Res. 44, 1034–1057 (2018)

  13. Kolokoltsov, V.N.: Nonexpansive maps and option pricing theory. Kybernetika 34, 713–724 (1998)

    MathSciNet  Google Scholar 

  14. Bernhard, P., Engwerda, J.C., Roorda, B., et al.: The Interval Market Model in Mathematical Finance: Game-Theoretic Methods. Springer, New York (2013)

    Book  Google Scholar 

  15. Smirnov, S.N.: A guaranteed deterministic approach to superhedging: sensitivity of solutions of Bellman–Isaacs equations and numerical methods. Comput. Math. Model. 31, 384–401 (2020)

    Article  MathSciNet  Google Scholar 

  16. Carassus, L., Obłój, J., Wiesel, J.: The robust superreplication problem: a dynamic approach. SIAM J. Financ. Math. 10, 907–941 (2019)

    Article  MathSciNet  Google Scholar 

  17. Carassus, L., Obłój, J., Wiesel, J.: Erratum to “The Robust Superreplication Problem: A Dynamic Approach”. SIAM Journal on Financial Mathematics 13, 653–655 (2022)

  18. Smirnov, S.N.: Guaranteed deterministic approach to superhedging: the semicontinuity and continuity properties of solutions of the Bellman–Isaacs equations. Autom. Remote. Control. 82, 2024–2040 (2021)

    Article  MathSciNet  Google Scholar 

  19. Smirnov, S.N.: A guaranteed deterministic approach to superhedging: financial market model, trading constraints, and the Bellman–Isaacs equations. Autom. Remote. Control. 82, 722–743 (2021)

    Article  MathSciNet  Google Scholar 

  20. Carassus, L., Vargiolu, T.: Super-replication price: It can be OK. ESAIM Proc. Surv. 65, 241–281 (2018)

    Google Scholar 

  21. Smirnov, S.N.: Geometric criterion for a robust condition of no sure arbitrage with unlimited profit. Mosc. Univ. Comput. Math. Cybern. 44, 146–150 (2020)

    Article  MathSciNet  Google Scholar 

  22. Jacod, J., Shiryaev, A.N.: Local martingales and the fundamental asset pricing theorems in the discrete-time case. Finance Stoch. 2, 259–273 (1998)

    Article  MathSciNet  Google Scholar 

  23. Carassus, L., Lépinette, E.: Pricing without no-arbitrage condition in discrete time. J. Math. Anal. Appl. 505, 125441 (2022)

    Article  MathSciNet  Google Scholar 

  24. Rockafellar, R.T.: Convex Analysis. Princeton University Press, Princeton (1970)

    Book  Google Scholar 

  25. Cherif, D., Lépinette, E.: No-arbitrage conditions and pricing from discrete-time to continuous-time strategies. Ann. Finance 19, 141–168 (2023)

    Article  MathSciNet  Google Scholar 

  26. Gerhold, S., Krühner, P.: Dynamic trading under integer constraints. Finance Stoch. 2018(22), 919–957 (2018)

    Article  MathSciNet  Google Scholar 

  27. Smirnov, S.N.: The guaranteed deterministic approach to superhedging: Lipschitz properties of solutions of the Bellman–Isaacs equations. In: Frontiers of Dynamics Games: Game Theory and Management, Birkhäuser, St. Petersburg. pp. 267–288 (2019)

  28. Smirnov, S.N.: A guaranteed deterministic approach to superhedging: relation between “deterministic" and “stochastic” settings in the case of no trading constraints. Theory Probab. Appl. 67, 548–569 (2023)

  29. Smirnov, S.N.: Structural stability threshold for the condition of robust no deterministic sure arbitrage with unbounded profit. Mosc. Univ. Comput. Math. Cybern. 45, 34–44 (2021)

    Article  MathSciNet  ADS  Google Scholar 

  30. Smirnov, S.N.: A guaranteed deterministic approach to superhedging: structural stability and approximation. Comput. Math. Model. 32, 129–146 (2021)

    Article  MathSciNet  ADS  Google Scholar 

  31. Goberna, M.A., González, E., Martínez-Legaz, J.E., Todorov, M.I.: Motzkin decomposition of closed convex sets. J. Math. Anal. Appl. 364, 209–221 (2010)

    Article  MathSciNet  Google Scholar 

  32. Smirnov, S.N.: Guaranteed deterministic approach to superhedging: mixed strategies and game equilibrium. Autom. Remote. Control. 83, 2019–2036 (2022)

    Article  Google Scholar 

  33. Smirnov, S.N.: A note on transition kernels for the most unfavourable mixed strategies of the market. J. Oper. Res. Soc, China (2023). https://doi.org/10.1007/s40305-023-00490-4

  34. Leichtweiß, K.: Konvexe Mengen. Springer-Verlag, Berlin Heidelberg (1979)

    Google Scholar 

  35. Hu, S., Papageorgiou, N.: Handbook of Multivalued Analysis: Theory, Mathematics and Its Applications, vol. I. Springer, Berlin (1997)

    Book  Google Scholar 

  36. Smirnov, S.N.: A guaranteed deterministic approach to superhedging: a game equilibrium in the case of no trading constraints. J. Math. Sci. 248, 105–115 (2020)

    Article  MathSciNet  Google Scholar 

  37. Aliprantis, C.D., Border, K.C.: Infinite Dimensional Analysis A Hitchhiker’s Guide, 3rd edn. Springer-Verlag, Berlin (2006)

    Google Scholar 

  38. Karlin, S.: Extreme points of vector functions. Proc. Am. Math. Soc. 4, 603–610 (1953)

    Article  MathSciNet  Google Scholar 

  39. Tulcea, C., Ionescu, T.: Mesures dans les espaces produits. Atti Accad. Naz. Lincei Rend., 7, pp. 208–211 (1949)

  40. Föllmer, H., Schied, A.: Stochastic Finance. An Introduction in Discrete Time, 4nd edition, Walter de Gruyter, New York (2016)

  41. Engelking, R.: General Topology. Heldermann, Berlin (1989)

    Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Faculty of Computational Mathematics and Cybernetics, Lomonosov Moscow State University, Moscow, 119991, Russian Federation

    Sergey N. Smirnov

Authors
  1. Sergey N. Smirnov
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Sergey N. Smirnov.

Ethics declarations

Conflicts of interest

The author declares that he has no conflict of interest.

Additional information

The work was published with the financial support of the Ministry of Education and Science of the Russian Federation as part of the program of the Moscow Center for Fundamental and Applied Mathematics under the agreement No75-15-2022-284.

Rights and permissions

Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Smirnov, S.N. Structural Stability of the Financial Market Model: Continuity of Superhedging Price and Model Approximation. J. Oper. Res. Soc. China 12, 215–241 (2024). https://doi.org/10.1007/s40305-023-00524-x

Download citation

  • Received:

  • Revised:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s40305-023-00524-x

Keywords

Mathematics Subject Classification

Search

Navigation