Introduction

The consumption of energy has always been the major difficulty battling man. Renewable energy has been receiving serious attention as the solution to the current global energy crisis [1]. Solar energy is the most available and least expensive source of energy but the fabrication of solar cells is sometimes not economically feasible either due to the lack of these materials (poisonous or not readily available) or the use of increasing the efficiency per unit area of solar cells to increase efficiency which leads to increase in the cost of installation [2,3,4,5,6]. Solar cells, as an energy converter, works on the Photovoltaic effect, which aids in the direct conversion of sunlight into electricity, with the potential to meet future energy demands [7]. Thin-film photovoltaics provides low-cost energy to humanity while having a high market penetration [8]. Despite the numerous advantages identified with photovoltaic devices, acquiring materials with cheap cost but high efficiency has emerged as a research priority. Among all the materials used in photovoltaic device manufacture, compound semiconductor materials play critical roles in the design and fabrication of solar devices. Compound semiconductor materials have been receiving a lot of attention as a result of their flexibility and wide variation of their tun-ability, ranging from binary compound semiconductor material (involving two elements) to ternary compound semiconductor material (involving three elements) to quaternary compound semiconductor material (involving four elements) [9, 10]. Among the various forms of compound semiconductor materials, ternary compounds have received considerable attention owing to their non-linear susceptibility and suitability in optics, electronics, photovoltaic detectors, light-emitting diodes, and solar cells [11]. Ternary compound semiconductor materials, being chalcogenide materials have offered overwhelming improvement in the performance of the nanomaterials-based optoelectronics devices, and effective materials properties tunability for specific device applications [12]. Despite the numerous advantages offered by ternary materials in photovoltaic applications, lattice mismatch and degradation have been identified as major bottlenecks that have received much research attention [11,12,13,14]. However, in this study, we have carefully selected different semiconductor elements and studied the combination numerically having identified their little lattice mismatch. Recently, copper indium sulfur has received considerable research attention owing to its direct energy band gap, large absorption coefficient, and photostability capable of replacing cadmium telluride (CdTe) while forming an heterostructure of cadmium sulfide [15, 16]. The compound has high affinity for the absorption of photon which perhaps require a material with wider energy band gap to prevent front surface recombination [17,18,19]. Since CdS possesses the required energy band gap with promising optical characteristics, we therefore chose the two materials in the study. CIS ternary compound semiconductor material (CuInS2) is made up of three elements as denoted by its name “ternary” which are copper, indium, and sulfur with a band gap of 1.530 eV, research has observed the introduction of gallium in to the ternary compound semiconductor material with a removal of Indium forming an alloy composition of Cu(In(1−x) Gax)S2, with this alloy composition this material would eventually change from CIS (CuInS2) there was no gallium in the material to CGS (CuGaS2) when gallium is fully introduced with complete removal of indium from the material, in between this transition that’s when a CIGS material would be formed and its energy band gap would range from 1.50–2.50 eV as that of transition range of CIS-CGS obeying the Vegard’s law [20,21,22]. The structural characterization of CIS compound semiconductor material has showed that the films have a strong preferred growth direction when it was observed using X-ray diffraction [23]. Due to the low energy band gap of CIS material, it is a suitable material to act as our P-type compound semiconductor material in this research. CdS is a binary compound semiconductor material which is made up of two elements as denoted from its name “binary” which are cadmium and sulfur. CdS compound semiconductor material is one of the most commonly used buffer layer material even with the fact that cadmium is poisonous [24]. CdS compound semiconductor material has a direct energy band gap of 2.4 eV, and from the study of the structural characterization of CdS, it was observed that it has a cubic sphalerite structure and a hexagonal wurtzite structure [25, 26], with very little lattice mismatch coefficient with CIGS which is a family of CIS compound semiconductor material which would be utilized as the P- type material for this study [27]. We studied the electrical properties of the heterostructured CIS/CdS based photovoltaic extensively by numerically model the structure through the application of SCAPS with the aim of providing and discussing insight into the possible degradation mechanism, and also leveraging on the study could provide photovoltaic degradation remediation. The obtained parameters reveal that J–V properties are not the only factors hindering the performance of the materials but also the generation and recombination current. We have successfully established many electrical parameters and their contributive factors to the degradation of the devices’ efficiency based on the materials.

Materials and methods

Numerical modeling

Provision of hypotheses for practical and experiment solutions has been one the advantages of numerical modeling since time in memorial. Numerical modeling has been used to analyzed practical solutions to solar cells and they have proved useful by helping in the creation of effective solar cells over time, most especially the application of SCAPS [28,29,30]. The electrical characterization of heterostructured CIS/CdS material was investigated with the usage of the SCAP-1D simulation tool. The SCAPS-1D simulation program solves the fundamental one-dimensional semiconductor equations of continuity, Poisson's equation, and carrier density with respect to electrons and holes. Various properties were observed during the observation of the electrical characterization of the heterostructured CIS/CdS compound semiconductor material. Equations (1) and (2) which are known as Poisson’s equations for holes and electrons [31, 32].

$$\frac{{\mathrm{d}}^{2}\Psi }{{\mathrm{d}x}^{2}}=\frac{\mathrm{d}E}{\mathrm{d}x}=\frac{\rho }{{\varepsilon }_{0}{\varepsilon }_{\mathrm{r}}}$$
(1)
$$\frac{{\mathrm{d}}^{2}\Psi }{{\mathrm{d}x}^{2}}=\frac{q}{{\varepsilon }_{0}{\epsilon }_{\mathrm{r}}} [p\left(x\right)-n(x)+{N}_{\mathrm{D}}-{N}_{\mathrm{A}}+{\rho }_{p}-{\rho }_{n}]$$
(2)

The drift current for both electrons and holes can be attributed to the electric field, from Maxwell’s equations

$${\text{Drift current density}}={\text{Charge}} \times \mathrm{flux}$$
(3)
$${J_n}_{\mathrm{drift}}=qn{V}_{\mathrm{d}}$$
(4)
$${J_p}_{\mathrm{drift}}=-qp{V}_{\mathrm{d}}$$
(5)

From Maxwell’s equations

$$J= \sigma F$$
(6)

Conductivity in the Maxwell’s equation Eq. (6) is

$$\sigma =qn\mu$$
(7)

Therefore comparing Eq. (6) and Eq. (7).

$$J=qn\mu F$$
(8)

Comparing Eq. (8) with Eqs. (4) and (5).

$${V}_{\mathrm{d}}=\mu F\quad (\mathrm{Drift})$$
(9)

The diffusion current for both the electrons and holes would be derived from the Einstein relation at when the energy band diagram of the material is at equilibrium (when there is no field, no current flowing) [28]:

$${\text{Drift current density}}={\text{Diffusion current density}}$$
(10)

At this time, the summation of both the drift current density and the diffusion current density would be zero [33]. This is given by Eqs. (11)–(14).

$${J}_{\mathrm{drift}}+{J}_{\mathrm{diffusion}}=0$$
(11)
$$q{D}_{n}\frac{\mathrm{d}n}{\mathrm{d}x}=-qn\mu F$$
(12)
$$q{D}_{p}\frac{\mathrm{d}p}{\mathrm{d}x}=-qp\mu F$$
(13)

After the evaluation of Eq. (12):

$$D_n={\mu }_{n}\frac{kT}{q}, D_p={\mu }_{p}\frac{kT}{q} \quad ({\text{Einstein relation}})$$
(14)

The current density for holes and electrons is the addition of the drift current and the diffusion current as represented in Eqs. (14) and (15) [32]:

$${J}_{n}=q\left({D}_{n}\frac{\mathrm{d}n}{\mathrm{d}x}+{\mu }_{n}n\frac{\mathrm{d}\Psi }{\mathrm{d}x}\right)$$
(15)
$${J}_{p}=-q\left({D}_{p}\frac{\mathrm{d}p}{\mathrm{d}x}+{\mu }_{p}p\frac{\mathrm{d}\Psi }{\mathrm{d}x}\right)$$
(16)

Continuity equation explains the flow of electrons with respect to time [34]:

$$\frac{\mathrm{d}n}{\mathrm{d}t}=({\text{current flowing out}}-{\text{current flowing in}})+G-R$$
(17)

G is the net generation rate and R is the net recombination rate given by Eqs. (18) and (19).

$${R}_{n}=\frac{\Delta n}{\tau }$$
(18)
$${R}_{p}=\frac{\Delta p}{\tau }$$
(19)

Device structure

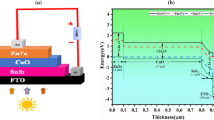
The structure of this research is a heterostructured CIS/CdS compound semiconductor material as shown in Fig. 1, in which the CIS compound semiconductor material with a band of 1.530 eV acts as the P-type material and the CdS compound semiconductor material with a band gap of 2.4 eV acts as the N-type material. The method of introduction of heterojunction into the device structure for optimization has produced good results and that is why more research attention has been given to this method.

Fig. 1
figure 1

Model of the solar cell device structure

Full size image

The parameters and values of CdS and CIS are presented in Table 1.

Table 1 Parameters and values of CdS and CIS
Full size table

In this research paper, influence of shunt resistance and series resistance was not taken into consideration likewise defects the illumination condition global AM 1.5 standard, the working point bias voltage is set at 0.000 V, and the frequency is \({10}^{6} \; \mathrm{Hz}\).

Results and discussion

J–V characteristics of CIS/CdS compound semiconductor

The J–V curve as depicted in Fig. 2 reveals the J–V characteristics of the simulated heterostructured CIS/CdS based photovoltaic and the extracted parameters are shown in Table 2. Semiconductor materials can be characterized in to four quadrants which are indicated in an ideal graph and the quadrants also helped in the extraction of the structure electrical parameters.

Fig. 2
figure 2

J–V curve depicting the recombination and generation current density with respect to the voltage

Full size image
Table 2 Extracted solar cell parameters at room temperature (300 K)
Full size table

This fourth quadrant shows that the semiconductor material (solar cells) is generating current with respect to voltage but the moment it leaves the fourth quadrant entering the second quadrant which indicates the usage of current with respect to voltage, the semiconductor material is no more generating current with respect to voltage but it’s already absorbing or utilizing current with respect to voltage to serve its use, example LED. The various stages of the quadrant indicates the conductivity of the materials [35].

Generation of electron–hole pair

In the Fig. 2, the generation current density Jgen is revealed to be constant until after the Voc at 0.8978 where a steep decrease was observed, this is because after the Voc the semiconductor material stopped working as a solar cell and one of the major processes involved in solar cells is generation of electron–hole pair which leads to the generation current density of the material and this generation of electron–hole pair is constant depending on material unless the such semiconductor material stops being a solar cell. Such generation of electron–hole pair as a result of photon absorption due to built-in-voltage at open circuit voltage beyond 0.8978 V is slightly different from the result obtained in the research works reported by authors in [36] and [37]. However, such discrepancy in the result could be attributed to the materials of study.

Recombination of electron–hole pair

Due to the absorption of photon by absorber layer materials, front surface recombination is imminent and in order to prevent such a recombination, materials with energy band gap is required. Given this, SCAPS simulation is utilized to study the recombination current density of the materials as depicted in Fig. 2. The recombination of electron–hole pair is the major influence in the recombination current density and it is often an exponential increase. A lot of factors can influence the recombination of electron–hole pairs ranging from temperature to charge density to the thickness of the material [37]. Such increase in the recombination current density within the limit breakdown voltage is in agreement with the previous work on heterostructured based devices [35]. The total current density is basically the difference between the recombination current density from the generation current density.

Electron current density, hole current density and total current density

The thickness of the CIS/CdS material is depicted in Fig. 3, with the N-type CdS from 1.1 to 1.0 µm while the P-type CIS material from 1.0 to 0.0 µm, the depletion region is in the P-type 0.9 µm thickness where the holes current density crosses the electron current density, at this region both the electrons and holes are equal, this leads to equal current density from both the electrons and the holes. The total current density present in any material is always uniform through a material from metals to semiconductor, there might be a in current density from the electrons or the holes but the total current density is always equal throughout the semiconductor material as also depicted in this CIS/CdS material [38].

Fig. 3
figure 3

Total current density, electron current density and hole current density with respect to the thickness of the CIS/CdS material

Full size image

Energy band diagram of the CIS/CdS compound semiconductor

In Fig. 4, we observed that Energy band diagram of the CIS/CdS material with respect to the thickness of the CIS/CdS material. Noting that CIS/CdS, from 1.1 to 1.0 µm is the N-type CdS material while from 1.0 to 0.0 µm is the P-type CIS material. The P–N junction is at 1.0 µm. This heterostructured material was done with the intention of high efficiency solar cells. The depletion layer can be seen to be at 0.9 µm thickness as already depicted by the Fig. 2, while the built-in voltage is also depicted as 0.25 eV from the Fig. 4.

Fig. 4
figure 4

Energy band diagram of CIS/CdS material with respect to thickness

Full size image

Generation rate and generation current density of the CIS/CdS compound semiconductor

From the Fig. 5, with an exponential growth of the net generation rate, more generation of the electron–hole pair happens around the P–N junction than at the tail end of the P-type CIS material from 1.0 to 0.0 µm while that of the N-type CdS material from 1.1 to 1.0 µm, more generation of electron–hole pairs happens at the surface of the CdS material which is the first contact the incident photons interact with in the heterostructured material, also facing an exponential increase just like the P-type CIS material.

Fig. 5
figure 5

Net generation rate of the CIS/CdS material with respect to thickness

Full size image

In Fig. 6, the total or cumulative generation of current density as a result of the generation of the electron–hole pairs, more current density is generated at the tail end of the P-type CIS material 1.1–1.0 µm as a result of the electron–hole pair than what is generated at the P–N junction (1.0 µm). Similar traits were observed in the N-type CdS material. The cumulative generation current density is inversely proportional to the net generation rate denoted in Fig. 5 due to the thickness of the CIS/CdS material.

Fig. 6
figure 6

Cumulative generation current density with respect to the thickness

Full size image

Recombination current density of the CIS/CdS compound semiconductor

Unlike cumulative generation current density in Fig. 6, the recombination current density Fig. 7 flows in two ways, recombination current density is achieved as a result of the movement of electrons and holes, electrons move in the opposite direction of holes and electric field, Due to the movements of electrons and holes that means recombination of electron–hole pairs happens from left to right and also from right to left depending on the flow of the electric field. As the recombination occurs the as result of the movement of electrons or the holes, current density would be generated from left to right and right to left. The total current density as a result of recombination of the electrons-holes pairs should be equal throughout the thickness of the CIS/CdS material since a loss in the left to right recombination current density is a gain in the right to left recombination current density of the CIS/CdS material’s thickness. The highest recombination rate is at 0.4 µm thickness in Fig. 14 and it is also where left to right recombination current density crosses the right to left recombination current density, at this point they are both equal.

Fig. 7
figure 7

Cumulative recombination left to right in blue and cumulative recombination right to left in red with respect to thickness of the CIS/CdS material

Full size image

Effect of temperature on J–V characteristics of the CIS/CdS compound semiconductor

From Fig. 8, the Table 3 has clearly been vindicated, variation of temperature on CIS/CdS majorly influences the open circuit voltage of the material, no significant changes was noticed for the short circuit current density but there a very minute difference in the short circuit current density. These influences on the short circuit current density and open circuit voltage have a ripple effect on the fill factor, power conversion efficiency, maximum power point voltage, maximum power point current of the solar cell. These parameters were depicted from Fig. 7. From the Table 2 it was observed an increase in temperature reduces the power conversion efficiency of the solar cell, as 400 K gives a 12% efficiency while 250 K gives a 21% efficiency. The fill factor which indicates the degradation of the CIS/CdS material which depicts that the solar cells would best at 300 K which gives a fill factor of 64.8% as compared to 400 K which gives a fill factor of 60.1% and 250 K which gives a fill factor of 63.6%. Observation from the table was a steady increase in the Voc and the Vmpp, similar increase was noticed in the Jsc and Jmpp but it is very little and sometimes not noticeable.

Fig. 8
figure 8

Effect of temperature variation on the J–V curve

Full size image
Table 3 Effect of temperature variation on the solar cell parameters of CIS/CdS compound semiconductor
Full size table

Effect of temperature on recombination current density of the CIS/CdS compound semiconductor

In the Fig. 9, recombination of electrons–holes pairs is one of the major processes of solar cells, and unlike generation of electrons–holes pair in which temperature is not a major determinant in its operations, temperature play a lot of roles in recombination of electrons-holes pairs. During recombination electron and holes could recombine to form a photon, such an event is called a radiative recombination. A phonon could also be formed during the recombination process, such an occurrence is called non radiative recombination. A free electron moving in the material could also absorb the photon s to acquire more kinetic energy and this might lead to the electron colliding with an atom to generate electron–hole pair, this occurrence is called auger recombination. These three events or occurrences either causes a loss or a gain in recombination current density of the solar cells. As it is observed increase in temperature eases the movement of electrons but due to recombination that happens as a result of either radiative recombination, non-radiative recombination or auger recombination which would be triggered as a result of increase in the thermal energy of the electrons as a result of the temperature. The generation current density is not affected by the variation of temperature but the recombination current density is clearly affected. Increase in the temperature increases the recombination current density of the CIS/CdS material.

Fig. 9
figure 9

Effect of temperature variation on the recombination current with respect to the voltage

Full size image

Effect of temperature on capacitance–voltage plot of the CIS/CdS compound semiconductor

Capacitance is the ability of the material to store electric charges. Increase in the temperature increases the capacitance of the CIS/CdS material as depicted in Fig. 10. Also increase in temperature makes changes to the dielectric properties of both the P-type CIS material and the N-type CdS material, which in turn shows an increase in the capacitance of the CIS/CdS material as temperature increases. The temperature is therefore directly proportional to the capacitance of the CIS/CdS material.

Fig. 10
figure 10

Effect of temperature variation on the C–V plot of the CIS/CdS material

Full size image

Effect of temperature on the electron current density, hole current density and total current density

Figure 11 depicts the effects of temperature on the electron current density Jn of the CIS/CdS material with observing the thickness of the material, as temperature increases the electron current density decreases, from 1.0 to 0.4 µm thickness of the CIS/CdS material temperature is not making any noticeable changes in terms of the electron current density of the CIS/CdS material. Going to the N-type CdS material 1.1–1.0 µm, the electron current density increases as the temperature increases. Therefore, it can be safe to say that the electron current density in tail end of the P-type CIS material is inversely proportional to temperature while electron current density in the N-type CdS material is directly proportional to temperature.

Fig. 11
figure 11

Effect of temperature variation on the electron current density with respect to the thickness of the CIS/CdS material

Full size image

Figure 12, the hole current density Jp of the CIS/CdS material reacts in an opposite way to how the electron current density of the CIS/CdS material reacts to temperature variation. Looking at the holes current density as being opposite to the electron current density, increase in temperature leads to an increase in holes current density of the CIS/CdS material while no noticeable changes can be seen with variation of temperature at 0.9 µm thickness of the P-type CIS material. While the inverse of the occurrence in the P-type CIS material is what is happening at the N-type CdS material at 1.1–1.0 µm thickness of the CIS/CdS material.

Fig. 12
figure 12

Effect of temperature variation on the holes current density with respect to the thickness of the CIS/CdS material

Full size image

The current density in any material is always uniform throughout the material [38]. From the Fig. 13, current density is constant throughout the thickness of the CIS/CdS material for each temperature, and as it has noticed again increase in temperature results to increase in the total current density of the CIS/CdS material. Current is the flow of electrons, increase in temperature leads to availability of thermal energy which excites the electrons, giving the electrons more kinetic energy, this in turn increases the total current density of the CIS/CdS material.

Fig. 13
figure 13

Effect of temperature on the total current density with respect to the thickness of the CIS/CdS material

Full size image

Effect of temperature on net recombination rate of the CIS/CdS compound semiconductor

From Fig. 14, The net recombination rate of the CIS/CdS material is highest at 0.4 µm thickness of P-type CIS material, with increasing temperature the rate at which the electrons-holes recombine increases, therefore, it is safe to say that increase in temperature results in increase in the net recombination rate of the P-type CIS material with the highest recombination happening in the P-type material while little recombination rate which is not noticeable is happening at the N-type material.

Fig. 14
figure 14

Effect of temperature on the net recombination rate with respect to the thickness of CIS/CdS material

Full size image

Effect of temperature on electric field strength

In Fig. 15, increase in the temperature leads to an increase in the electric field strength in the 1.1–1.0 µm N-type CdS material with an increasing electric field strength for all the variation of temperature from the P–N junction at 1.0 µm on the thickness of the CIS/CdS material. While for the P-type material from 0.6 to 1.0 µm thickness of the P-type material there is increase in the electric field strength as the temperature increases with also a steady decrease in the electric field with respect to the thickness of the P-type CIS material, at 0.4 µm, there is no changes in the electric field strength of the material upon getting to 0.3 µm, the low temperature deflects upwards while the high temperatures deflect downwards. This can be called electrostatic deflection.

Fig. 15
figure 15

Effect of temperature on the electric field strength with respect to the thickness of the CIS/CdS material

Full size image

Effect of temperature on the energy band diagram of the CIS/CdS compound semiconductor

From Fig. 16, effect of temperature on the band diagram, observing the band diagram of the material at varied temperatures, it could be depicted that the energy band gap of the material decreases with increasing temperature, therefore the temperature is inversely proportional to the energy band gap of the material. Decrease in the energy band gap of the CIS/CdS material majorly influences the Open circuit voltage of the CIS/CdS material [23].

Fig. 16
figure 16

Effect of temperature on the band diagram with respect to the Thickness of the CIS/CdS material

Full size image

Conclusion

The presented research work established that a loss in electron current density gives a corresponding gain in holes current density because the electrons and holes in the current density are factors responsible for such loss and gain in electrons current density and holes current density, respectively. The invariance of current in the selected material was affirmed in this study through the investigation of electrical characteristic of CIS/CdS compound semiconductor material and also the influence of temperature on the materials’ electrical properties was investigated to ascertain the materials electrical behavior. Since the average temperature climate condition ranges from 288 to 323 K. Any loss incurred by the electrons current density as a result of the electrons is a gain by the holes current density as a result of the holes. While the total current density remains constant throughout the CIS/CdS material. The major changes incurred in the current density of the CIS/CdS material can be attributed to the current density as a result of the net recombination rate, which is the recombination current density of the CIS/CdS material, net generation rate is independent of temperature due to this the generation current density is also independent of temperature. Recombination current density occurs in both directions of the CIS/CdS material with both the left to right recombination current density and the right to left recombination current density crossing each other at the region with the highest net recombination rate in the CIS/CdS material. From the observation of the Solar cell parameters extracted, the CIS/CdS material is most efficient at 300 K. Upon the observation of the electric field strength with respect to the thickness of the CIS/CdS material and the net recombination rate with respect to the thickness of the CIS/CdS material, it was observed that at the region of where there is highest recombination of electron–hole pair, the electric field strength of the CIS/CdS material is equal for all temperatures. Understanding the materials properties, especially, the electrical characteristics is very important for the application of materials at micro and nano scales and it also helps in providing remedies to the degradation mechanism.