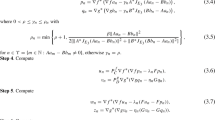An observation on $\alpha$-type F-contractions and some ordered-theoretic fixed point results

Abstract

We observe that all the results involving $\alpha$-type F-contractions are not correct in their present forms. In this article, we prove some fixed point results for extended F-weak contraction mappings in metric and ordered-metric spaces. Our observations and the usability of our results are substantiated by using suitable examples. As an application, we prove an existence and uniqueness result for the solution of a first-order ordinary differential equation satisfying periodic boundary conditions in the presence of either its lower or upper solution.

Introduction and preliminaries

In 2012, Wardowski [1] generalized Banach contraction principle in a novel way by introducing a new type of contraction called F-contraction:

Definition 1.1

[1] A self-mapping f on a metric space (X, d) is said to be F-contraction if there exists $\tau >0$ such that

$$\begin{aligned} d(fx,fy)>0\Rightarrow \tau +F(d(fx,fy))\le F(d(x,y)), \end{aligned}$$

(1.1)

for all $x,y\in X,$ where $F:\mathbb {R}_+\rightarrow \mathbb {R}$ is a mapping satisfying the following conditions:

• F1: F is strictly increasing,

• F2: for every sequence $\{s_n\}$ of positive real numbers,

  $$\begin{aligned} \lim \limits _{n\rightarrow \infty }s_n=0 \Leftrightarrow \lim \limits _{n\rightarrow \infty }F(s_n)=-\infty , \end{aligned}$$

• F3: there exists $k\in (0,1)$ such that $\lim \limits _{s\rightarrow 0^+}s^kF(s)=0.$

Let us denote by $\mathcal {F}$, the family of all functions F satisfying conditions F1–F3. Some well-known members of $\mathcal {F}$ are $F(s)=\ln s$, $F(s)=s+\ln s$, $F(s)=\frac{-1}{\sqrt{s}}$ and $F(s)=\ln (s^2+s)$. Moreover, Wardowski [1] proved that every F-contraction mapping on a complete metric space possesses a unique fixed point. Further, on varying the elements of $\mathcal {F}$ suitably, a variety of known contractions in the literature can be deduced.

Example 1.1

[1] Consider $F\in \mathcal {F}$ given by $F(s)=\ln s$. Then each self-mapping f on X satisfying inequality (1.1) is an F-contraction such that

$$\begin{aligned} d(fx,\, fy)\le e^{-\tau }d(x,y), \end{aligned}$$

where $x,y\in X$ and $x\ne y$. Observe that this inequality holds trivially if $x=y$.

Using Ćirić-type generalized contraction in Definition 1.1, Wardowski and Van Dung [2] (also independently Mnak et al. [3]) introduced the notion of F-weak contraction and utilize the same to generalize the main result of [1] as well as several other results of the existence literature.

Definition 1.2

[2, 3] Let $(X,d),~\tau$ and F be as in Definition 1.1. A self-mapping f on X is said to be F-weak contraction if

$$\begin{aligned} \tau +F(d(fx,fy))\le F(M_f(x,y)), \end{aligned}$$

(1.2)

for all $x,y\in X$ whenever $d(fx,fy)>0$ where

$$\begin{aligned} M_f(x,y)=\mathrm{max}\left\{ d(x,y),d(x,fx),d(y,fy),\frac{d(x,fy)+d(y,fx)}{2}\right\} . \end{aligned}$$

Usually, the following abbreviation, also, is utilized in the literature:

$$\begin{aligned} m_f(x,y)=\mathrm{max}\left\{ d(x,y),\frac{d(x,fx)+d(y,fy)}{2},\frac{d(x,fy)+d(y,fx)}{2}\right\} . \end{aligned}$$

Theorem 1.1

[2, 3] Let (X, d) a complete metric space and $f: X \rightarrow X$ be an F-weak contraction for some $F\in \mathcal {F}$. Then f has a unique fixed point $x\in X$ and for every $x_0\in X$, the Picard sequence $\{f^nx_0\}$ converges to x provided either

• (a) F is continuous or

• (b) f is continuous.

In 2016, Gopal et al. [4] introduced the concept of $\alpha$-type F-contraction (for simplicity we write $\alpha F$-contraction) as follows:

Definition 1.3

[4] Let $(X,d),~\tau$ and F be as in Definition 1.1. A mapping $f:X\rightarrow X$ is said to be an $\alpha F$-weak contraction if there exists $\alpha :X\times X\rightarrow \{-\infty \}\cup (0,+\infty )$ such that

$$\begin{aligned} \tau +\alpha (x,y)F(d(fx,fy))\le F(M_f(x,y)), \end{aligned}$$

(1.3)

for all $x,y\in X$ whenever $d(fx,fy)>0$.

Employing Definition 1.3, Gopal et al. [4] proved the following result:

Theorem 1.2

[4] Let (X, d) be a complete metric space and $f: X \rightarrow X$ an $\alpha F$-weak contraction satisfying the following conditions:

• (a) there exists $x_0\in X$ such that $\alpha (x_0,fx_0)\ge 1$,

• (b) f is $\alpha$-admissible, i.e., $\alpha (fx,fy)\ge 1$ whenever $\alpha (x,y)\ge 1$,

• (c) f is continuous (or F is continuous and if a sequence $\{x_n\}\in X$ such that $\alpha (x_n,x_{n+1})\ge 1$ for all $n\in \mathbb {N}$ and $x_n\rightarrow x$ as $n\rightarrow \infty$, then $\alpha (x_n,x)\ge 1$).

Then f has a unique fixed point $x\in X$ and for every such $x_0\in X$, the Picard sequence $\{f^nx_0\}$ converges to x.

In recent years, the idea of F-contraction has attracted the attention of several researchers and by now there exists a considerable literature on and around this concept (see [5,6,7,8,9,10,11,12,13,14,15,16,17,18] and references therein).

Definition 1.4

A metric space (X, d) together with a partially order “$\preceq$” on it is called ordered metric space and denoted by $(X,d,\preceq )$. Further, for arbitrary elements x, y of X and a self-mapping f on X we say that

• (i) x, y are comparable if either $x\preceq y$ or $y\preceq x$.

• (ii) f is increasing if $fx\preceq fy$ whenever $x\preceq y$.

• (iii) (X, d) is f-orbitally complete if every Cauchy sequence $\{f^nx\}$ converges in X.

• (iv) X is regular if for every increasing sequence $\{x_n\}$ in X with $x_n\rightarrow x$, we have $x_n\preceq x$ for all $n\in \mathbb {N}$.

Though Turinici [19, 20] initiated some order-theoretic results in 1986, yet it is often referred to be indicated in 2004 wherein Ran and Reurings [21] presented a more natural result which was well-followed by Nieto and Rodríguez-López [22, 23]. For the work of this kind, one can be referred to [24,25,26,27,28,29,30,31].

Remark 1.1

In the setting of ordered metric spaces, the conditions (1.1–1.3) are required to hold merely for all comparable pairs of elements $x, y \in X$.

Abbas et al. [32] utilized the idea of F-contraction to obtain order-theoretic common fixed point results. Very recently, Durmaz et al. [33] proved the following result which can be obtained by setting $g=I:X\rightarrow X$ in Theorem 2 of [32]:

Theorem 1.3

[33] Let $(X,\preceq ,d)$ be a complete ordered metric space and $f:X\rightarrow X$ an F-contraction for some $F\in \mathcal {F}$. If the following conditions hold:

• (a) there exists $x_0\in X$ such that $x_0\preceq fx_0$,

• (b) f is increasing,

• (c) either f is continuous (or F is continuous and X is regular),

then f has a fixed point.

Further, the authors in [33] gave the following condition to ensure the uniqueness of the fixed point in Theorem 1.3:

• B: Every pair of elements of X has a lower bound and upper bound.

Remark 1.2

Very recently, Vetro [34] enlarged the class $\mathcal {F}$ (and denote the same $\mathbb {F}$) by withdrawing the condition F3 and replacing the constant $\tau$ by a function $\sigma :\mathbb {R}_+\rightarrow \mathbb {R}_+$ with $\lim \inf _{t\rightarrow s^+}\sigma (t)>0$ for all $s\ge 0$. Obviously, $\mathcal {F}\subseteq \mathbb {F}$ and $F(s)=-1/s$ is a member of $\mathbb {F}$ which is not in $\mathcal {F}$. We denote with $\mathbb {S}$ the family of all functions $\sigma$.

The aim of this article is to point out that all the existing results regarding $\alpha$-type F-contraction are not correct in their existing forms. We also generalize Theorem 1.3 utilizing Ćirić-type contraction in two directions wherein $\sigma \in \mathbb {S}$ is utilized rather than the constant $\tau .$ In doing so, we obtain a slightly sharpened form of Theorem 1.1. We support our results by suitable examples and an application.

An observation on $\alpha$-type F-contractions

We begin our observation with [4] wherein authors enlarged the co-domain of $\alpha$ to include $-\infty$ and at the same time assumed that the expression $-\infty$ . 0 has the value $-\infty$ which is quite unnatural. Inspired by this substitution, we are able to furnish the following counterexamples:

Example 2.1

Let $X=\{0,\frac{1}{4},\frac{1}{2},1\}$ equipped with usual metric d. Then (X, d) is a complete metric space. Define $\alpha :X\times X\rightarrow \{-\infty \}\cup (0,\infty )$ by

$$\begin{aligned} \alpha (x,y)={\left\{ \begin{array}{ll} -\infty , &{} \text {for }\; x,y\in \{0,1\},x\ne y;\\ 2-\frac{\ln 3}{\ln 4}, &{} \text {for }\; x,y\in \{\frac{1}{4},\frac{1}{2}\},x\ne y;\\ 1, &{} \text { otherwise. } \end{array}\right. } \end{aligned}$$

Let f be a self-mapping on X defined as $f0=1,f\frac{1}{4}=\frac{1}{2},f\frac{1}{2}=\frac{1}{4}$, and $f1=0$. Then f is continuous as well as $\alpha$-admissible. By a routine calculation, one can verify that f satisfies the contraction condition (1.3) for $F(s)=\ln s$ and $\tau =\ln \frac{4}{3}$. Especially, for $x=0$ and $y=1$, we have

$$\begin{aligned} -\infty =\ln \big (4/3\big )+(-\infty )\ln (1)&\le \ln \big (\ \mathrm{max}\big \{1,1,1,0\big \}\big ) = 0. \end{aligned}$$

Observe that, f is fixed point free which disproves Theorem 1.2.

Even if we restrict the co-domain of $\alpha$ to $(0,\infty )$ in Definition 1.3 with a view to recover Theorem 1.2, still the theorem continues to be erroneous. The following example exhibits this fact:

Example 2.2

Consider $X=[1,\infty )$ equipped with the discrete metric D, that is,

$$\begin{aligned} D(x,y)={\left\{ \begin{array}{ll} 0, &{} \text {for }\; x=y;\\ 1, &{} \text { otherwise.} \end{array}\right. } \end{aligned}$$

Take $fx=ax,$ for all $x\in X$ where $a\in (1,\infty )$. Then with $\alpha (x,y)=2,$ for all $x,y\in X$ and $F(s)=-\frac{1}{\sqrt{s}}$, f satisfies all the requirements of Theorem 1.2 (for $\tau <1$) but f is a fixed point free.

Indeed, in all the proofs of the results on $\alpha F$-contractions, e.g. in [4, line 4, page 962] and also in [12, equation (2.4)], the authors assumed that $F(s)\le \alpha (x,y)F(s)$, for $\alpha (x,y)\ge 1$ which is not true in general (as F may have negative values).

Main results

In order to generalize Theorem 1.3, the following definitions are required:

Definition 3.1

Let (X, d) be a metric space and $\sigma \in \mathbb {S}$. A mapping $f:X\rightarrow X$ is said to be an extended F-weak contraction if for all $x,y\in X$, we have

$$\begin{aligned} \sigma (d(x,y))+F(d(fx,\,fy))\le F(M_f(x,y)) \end{aligned}$$

(3.1)

whenever $d(fx,\,fy)>0$, where $F\in \mathbb {F}$.

Definition 3.2

An ordered metric space $(X,d,\preceq )$ is said to be $\preceq$-regular if for every increasing sequence $\{x_n\}$ in X with $x_n\rightarrow x$, there exists a subsequence $\{x_{n_k}\}$ of $\{x_n\}$ and a positive integer $k_0$ such that $x_{n_k}\preceq x$ for all $k\ge k_0$.

First, we prove the following result:

Theorem 3.1

Let $(X,\preceq ,d)$ be an ordered metric space and $f:X\rightarrow X$ an extended F-weak contraction for some function $F\in \mathbb {F}$. If (X, d) is f-orbitally complete such that the following conditions hold:

• (a) there exists $x_0\in X$ such that $x_0\preceq fx_0$,

• (b) f is increasing,

• (c) F is continuous and X is $\preceq$-regular

Then f has a fixed point $x\in X$. Moreover, for every $x_0\in X$ satisfies (a), the sequence $\{f^nx_0\}$ converges to x.

Proof

Let $x_0\in X$ be such that $x_0\preceq fx_0$. Define a sequence $\{x_n\}$ in X by $x_{n+1}=:fx_n$ for all $n\in \mathbb {N}_0=:\mathbb {N}\cup \{0\}$. If $x_n=x_{n+1}$ for some $n\in \mathbb {N}_0$, then we are done. Otherwise, we assume $d(x_n,x_{n+1})>0$ for all $n\in \mathbb {N}$ . As $x_0\preceq fx_0$ and f is increasing, we have

$$\begin{aligned} x_0\preceq x_1\preceq x_2\preceq \cdots \preceq x_n\preceq x_{n+1}\preceq \cdots~. \end{aligned}$$

Now, on setting $x=x_{n-1}$ and $y=x_{n}$ in (3.1), we have

$$\begin{aligned} \sigma (d(x_{n-1},x_{n}))+F(d(x_{n},x_{n+1}))\le & {} F(M_f(x_{n-1},x_n))\nonumber \\= & {} F\big (\mathrm{max}\left\{ d(x_{n-1},x_n),d(x_n,x_{n+1})\right\} \big ). \end{aligned}$$

If $d(x_{n-1},x_n) \le d(x_n,x_{n+1})$ for some $n\in \mathbb {N}$, then

$$\begin{aligned} F(d(x_{n},x_{n+1}))\le F(d(x_{n},x_{n+1})) -\sigma (d(x_{n-1},x_{n})), \end{aligned}$$

a contradiction as $\sigma (d(x_{n-1},x_{n}))>0$. Therefore,

$$\begin{aligned} F(d(x_{n},x_{n+1}))\le & {} F(d(x_{n-1},x_n)-\sigma (d(x_{n-1},x_{n})), \end{aligned}$$

which, in turn, yields

$$\begin{aligned} F(d(x_{n},x_{n+1}))\le F(d(x_0,x_{1}))-n\sigma (d(x_0,x_{1})), \end{aligned}$$

(3.2)

for all $n\in \mathbb {N}.$ On letting $n\rightarrow \infty$ in (3.2), we get $\lim \limits _{n\rightarrow \infty }F(d(x_{n},x_{n+1}))=-\infty .$ Therefore, (due to F2)

$$\begin{aligned} \lim \limits _{n\rightarrow \infty }d(x_{n},x_{n+1})=0. \end{aligned}$$

(3.3)

We assert that $\{x_n\}$ is a Cauchy sequence . Let us assume that $\{x_n\}$ is not so. Then there exists $\epsilon >0$ and two subsequences $\{x_{n_k}\}$ and $\{x_{m_k}\}$ of $\{x_{n}\}$ such that

$$\begin{aligned} n_k>m_k \ge k,~~d(x_{n_k},x_{m_k})\ge \epsilon \text { and }d(x_{{n_k}-1},x_{m_k})<\epsilon \text { for all } k\in \mathbb {N}. \end{aligned}$$

Now, we have

$$\begin{aligned} \epsilon \le d(x_{n_k},x_{m_k})\le d(x_{n_k},x_{{n_k}-1})+d(x_{{n_k}-1},x_{m_k})\le d(x_{n_k},x_{{n_k}-1})+ \epsilon \end{aligned}$$

so that

$$\begin{aligned} \lim \limits _{k\rightarrow \infty }d(x_{n_k},x_{m_k})=\epsilon . \end{aligned}$$

Again, we have

$$\begin{aligned} \epsilon \le d(x_{n_k},x_{{n_k}+1})+ d(x_{{n_k}+1},x_{{m_k}+1})+d(x_{{m_k}+1},x_{m_k}) \end{aligned}$$

so that (on letting $k\rightarrow \infty$)

$$\begin{aligned} \epsilon \le \liminf _{k\rightarrow \infty }d(x_{{n_k}+1},x_{{m_k}+1}). \end{aligned}$$

Similarly, we can deduce that

$$\begin{aligned} \epsilon \le \liminf _{k\rightarrow \infty }d(x_{{n_k}+1},x_{m_k}) \text { and } \epsilon \le \liminf _{k\rightarrow \infty }d(x_{{m_k}+1},x_{n_k}). \end{aligned}$$

It follows that there exists $l\in \mathbb {N}$ with $d(x_{{n_k}+1},x_{{m_k}+1})>0$, $d(x_{{n_k}+1},x_{m_k})>0$ and $d(x_{{m_k}+1},x_{n_k})>0$ for all $k \ge l.$ Then for all $k\ge l$, we have (on setting $x=x_{n_k}$ and $y=x_{m_k}$ in (3.1))

$$\begin{aligned} \sigma (d(x_{n_k},x_{m_k}))+F(d(x_{{n_k}+1},x_{{m_k}+1}))\le & {} F(M_f(x_{n_k},x_{n_k})),\nonumber \end{aligned}$$

(3.4)

where

$$\begin{aligned} M_f(x_{n_k},x_{m_k})= & {} \max \bigg \{d(x_{n_k},x_{m_k}),d(x_{n_k},x_{{n_k}+1}),d(x_{m_k},x_{{m_k}+1}),\\&\frac{d(x_{n_k},x_{{m_k}+1})+d(x_{m_k},x_{{n_k}+1})}{2}\bigg \}\\ {}\le & {} \max \bigg \{d(x_{n_k},x_{m_k}),d(x_{n_k},x_{{n_k}+1}),d(x_{m_k},x_{{m_k}+1}),\\&\frac{d(x_{n_k},x_{m_k})+d(x_{m_k},x_{{m_k}+1})+d(x_{m_k},x_{n_k})+d(x_{n_k},x_{{n_k}+1})}{2}\bigg \}. \end{aligned}$$

Letting $k\rightarrow \infty$ in presiding inequality and in view of the definition of $\sigma$ and the continuity of F, we get

$$\begin{aligned} F(\epsilon )<\liminf _{k\rightarrow \infty }\sigma (d(x_{m_k},x_{n_k}))+F(\epsilon )\le F(\epsilon ), \end{aligned}$$

a contradiction so that $\{x_n\}$ is a Cauchy sequence and having a limit $x\in X$. Next, we show that x is a fixed point. Suppose that $x_n=fx$ for infinitely many $n\in \mathbb {N}$, then there exists a subsequence of $\{x_n\}$ which converges to fx and the uniqueness of the limit finish the proof. Henceforth, we assume that $fx_n\ne fx$ for all $n\in \mathbb {N}_0$. On using the $\preceq$-regularity of X, there exists a subsequence $\{x_{n_k}\}$ of $\{ x_n\}$ and a positive integer $k_0$ such that $x_{n_k}\preceq \ x$ for all $n_k\ge k_0$. Now, for $n_k\ge k_0$, we can set $x=x_{{n_k}}$ and $y=x$ in (3.1) so that

$$\begin{aligned} \sigma (d(x_{{n_k}},x))+F(d(x_{{n_k}+1},fx))\le & {} F(M(x_n,x)) \nonumber \\\le & {} F\bigg (\mathrm{max}\Big \{d(x_{{n_k}},x),d(x_{{n_k}},x_{{n_k}+1}),d(x,fx),\nonumber \\&\frac{1}{2}[d(x_{{n_k}},x)+d(x,fx)+d(x,x_{{n_k}+1})]\Big \}\bigg ). \end{aligned}$$

(3.5)

Let it be on the contrary that $d(x,fx)>0$. Making $n\rightarrow \infty$ in (3.4), one gets

$$\begin{aligned} \gamma +F(d(x,fx))\le F(d(x,fx)), \end{aligned}$$

where $0<\gamma =\lim \inf _{d(x_n,x)\rightarrow 0^+}\sigma (d(x_n,x)),$ a contradiction so that $d(x,fx)=0$ which concludes the proof. $\square$

The following result is yet another version of Theorem 3.1 :

Theorem 3.2

Theorem 3.1 remains true if the condition (c) is replaced by the continuity of f whenever $F\in \mathcal {F}$.

Proof

The proof is identical to the proof of Theorem 3.1 up to (3.3), i.e.,

$$\begin{aligned} \lim \limits _{n\rightarrow \infty }d(x_{n},x_{n+1})=0. \end{aligned}$$

Due to (F3), there exists $k\in (0,1)$ such that

$$\begin{aligned} \lim \limits _{n\rightarrow \infty }(d(x_{n},x_{n+1}))^kF(d(x_{n},x_{n+1}))=0. \end{aligned}$$

(3.6)

Now, from (3.2), we have

$$\begin{aligned} d(x_{n},x_{n+1})^k\left[ F(d(x_{n},x_{n+1})) -F(d(x_0,x_{1}))\right] \le -n\sigma (d(x_0,x_{1})) d(x_{n},x_{n+1})^k\le 0. \end{aligned}$$

(3.7)

On using (3.3), (3.5) and letting $n\rightarrow \infty$ in (3.6), we get

$$\begin{aligned} \lim \limits _{n\rightarrow \infty }n\sigma (d(x_0,x_{1})) d(x_{n},x_{n+1})^k=0. \end{aligned}$$

Hence, there exists $m\in \mathbb {N}_0$ such that $n d(x_{n},x_{n+1})^k\le 1$ for all $n\ge m,$ so that

$$\begin{aligned} d(x_{n},x_{n+1})\le \frac{1}{n^{\frac{1}{k}}} \text { for all }n\ge m. \end{aligned}$$

(3.8)

We assert that $\{x_n\}$ is a Cauchy sequence. Consider $s,t\in \mathbb {N}_0$ with $s>t\ge m$. Using the triangle inequality and (3.7), we have

$$\begin{aligned} d(x_t,x_s)\le & {} \sum _{i=t}^{s-1}d(x_i,x_{i+1})\nonumber \\\le & {} \sum _{i=t}^{\infty }d(x_i,x_{i+1})\nonumber \\\le & {} \sum _{i=t}^{\infty }\frac{1}{i^{\frac{1}{k}}}. \end{aligned}$$

As $\sum _{i=1}^{\infty }\frac{1}{i^{\frac{1}{k}}}$ is convergent, letting $s,t\rightarrow \infty$ gives rise to

$$\begin{aligned} \lim \limits _{s,t\rightarrow \infty } d(x_s,x_t)=0 \end{aligned}$$

so that the assertion is established. Since X is f-orbitally complete, there exists $x\in X$ such that $\lim \limits _{n\rightarrow \infty } x_n=x.$ The continuity of f implies

$$\begin{aligned} x=\lim \limits _{n\rightarrow \infty } x_{n+1}=f(\lim \limits _{n\rightarrow \infty } x_n)=fx. \end{aligned}$$

This concludes the proof. $\square$

Remark 3.1

Theorem 3.5 carries some advantage over Theorem 3.6 as $\mathbb {F}$ remains a relatively larger class as compared to $\mathcal {F}$, and at the same time most of the utilized functions in $\mathcal {F}$ are already continuous.

Corollary 3.1

Theorem 1.3 follows from Theorems 3.1 and 3.2.

The following example exhibits that Theorem 3.1 is a proper generalization of Theorem 1.3:

Example 3.1

Let $X=A\cup B\cup C$ where $A=[0,1],B=(1,\frac{3}{2}]$ and $C=(\frac{3}{2},2]$. Then, $(X,d,\preceq )$ is an ordered metric space wherein d is the usual metric and the partial order ’$\preceq$’ on X is defined by

$$\begin{aligned} x\preceq y\Leftrightarrow \text { either } x=y \text { or }\big \{x\le y:(x\in A \text { and }y\in B) \text { or } (x\in B\text { and } y\in C)\}. \end{aligned}$$

Consider $F\in \mathbb {F}$ given by $F(s)=\frac{-1}{\sqrt{s}}$, for $s>0$ and $\sigma (t)=\frac{1}{4},$ for all $t\in \mathbb {R}_+$. Define a self-mapping f on X by

$$\begin{aligned} f(x)={\left\{ \begin{array}{ll} 1, &{} \text {for } x\in A;\\ \frac{3}{2}, &{} \text {for } x\in B;\\ 2, &{} \text {for }x\in C. \end{array}\right. } \end{aligned}$$

Now, in order to verify inequality (3.1), we distinguish the following two cases:

Case 1: $x\in A$ and $y\in B$. Here, we have

$$\begin{aligned} F\Big (\inf _{x\in A,y\in B }M_f(x,y)\Big )= & {} F\Big (\inf _{x\in A,y\in B} \Big \{\mathrm{max}\Big \{y-x,1-x,\frac{3}{2}-y,\frac{y-x}{2}+\frac{1}{4}\Big \}\Big \}\Big )\\= & {} F\Big (\inf _{y\in B} \Big \{\mathrm{max}\Big \{y-1,\frac{3}{2}-y,y-\frac{1}{4}\Big \}\Big \}\Big )\\= & {} F\Big (\frac{3}{4}\Big )\\ {}= & {} -\frac{2}{\sqrt{3}}. \end{aligned}$$

Since $\sigma (d(x,y)) +F\big ( d(fx,fy)\big )=\frac{1}{4} +F\big (\frac{1}{2}\big )=\frac{1}{4}-\sqrt{2}$, f verifies (3.1).

Case 2: $x\in B$ and $y\in C$. Here, we have

$$\begin{aligned} F\Big (\inf _{x\in B,y\in C}M_f(x,y)\Big )= & {} F\Big (\inf _{x\in B,y\in C} \Big \{\mathrm{max}\Big \{y-x,x-\frac{3}{2},2-y,\frac{y-x}{2}+\frac{1}{4}\Big \}\Big \}\Big )\\= & {} F\Big (\inf _{y\in C} \Big \{\mathrm{max}\Big \{y-\frac{3}{2},2-y,y-\frac{1}{2}\Big \}\Big \}\Big )\\= & {} F(1)\\ {}= & {} -1. \end{aligned}$$

Since $\sigma (d(x,y)) +F\big ( d(fx,fy)\big )=\frac{1}{4} +F\big (\frac{1}{2}\big )=\frac{1}{4}-\sqrt{2}$, f verifies (3.1) in this case too. Therefore, in all, f is an F-contraction ensuring the existence of some fixed point of f.

Observe that for $x=\frac{3}{2}$ and $y=2$, the right-hand side of (1.1) gets us $F(1/2)=-\sqrt{2}$. As $\frac{1}{4}+F(d(f(3/2),f2))=\frac{1}{4}-\sqrt{2},$ the inequality (1.1) does not hold so that Theorem 1.3 is not applicable in the context of present example.

Now we prove the following uniqueness result corresponding to Theorems 3.1 and 3.2:

Theorem 3.3

If in addition to the hypotheses of Theorem 3.1 (or Theorem 3.2), the following condition is satisfied, then f has a unique fixed point:

• B: $Fix(f):=\{x\in X, fx=x\}$ is a totally ordered set.

Proof

We prove the conclusion for Theorem 3.1 (for Theorem 3.2, the proof is similar). If $F\in \mathcal {F}$ the proof is similar with $\sigma (d(x,y))\equiv \tau$. Let x, y be two elements of Fix(f) such that $d(x,y)>0$. Then,

$$\begin{aligned} \sigma (d(x,y))+F(d(x,y))\le & {} \sigma (d(x,y))+F(d(fx,fy))\\\le & {} F\bigg (\mathrm{max}\left\{ d(x,y),d(x,fx),d(y,fy),\right. \\&\left. \frac{d(x,fy)+d(y,fx)}{2}\right\} \bigg )\\= & {} F(d(x,y)), \end{aligned}$$

a contradiction so that $d(x,y)=0.$ $\square$

In the following uniqueness result, we weaken the condition (B) at the cost of a relatively more stronger contraction condition.

Theorem 3.4

If in addition to the hypotheses of Theorem 3.1, the condition (B) is satisfied, then f has a unique fixed point provided $M_f(x,y)$ in the contraction condition (3.1) is replaced by $m_f(x,y)$.

Proof

Let x, y be two elements of Fix(f). Then there exists $z\in X$ such that z is comparable to both x and y. For $x\prec \succ z$, we may assume that $z\preceq x$ (similar arguments for $y\prec \succ z$). Since f is increasing, we deduce that

$$\begin{aligned} f^nz\preceq x, f^nz\preceq y. \end{aligned}$$

Let $\xi _n=:d(x,f^nz)$. We assert that $\lim \limits _{n\rightarrow \infty }\xi _n=0$. For substitution $x=x, y=f^{n}z$ in the contraction condition, we have

$$\begin{aligned} F(\xi _{n+1})\le & {} \sigma (\xi _n)+F(\xi _{n+1})\\\le & {} F(m_f(x,f^nz))\nonumber \\= & {} F\bigg (\mathrm{max}\left\{ \xi _{n},\frac{0+d(f^nz,f^{n+1}z)}{2},\frac{\xi _{n+1}+\xi _{n}}{2}\right\} \bigg )\nonumber \\= & {} F\bigg (\mathrm{max}\left\{ \xi _{n},\frac{\xi _{n+1}+\xi _{n}}{2}\right\} \bigg ).\\\nonumber \end{aligned}$$

(3.9)

Now, if $\xi _{n}<\xi _{n+1}$, then (3.9) becomes

$$\begin{aligned} F(\xi _{n+1})\le F\Big (\frac{\xi _{n+1}+\xi _{n}}{2}\Big ), \end{aligned}$$

and since F is strictly increasing, we have $\xi _{n+1}\le \xi _{n}$ which is a contradiction. Therefore, $\xi _{n}\ge \xi _{n+1}$ so that $\xi _n$ is a decreasing sequence of nonnegative reals such that $\lim \limits _{n\rightarrow \infty }\xi _n=r\ge 0$. If $r>0$, then on letting n tends to infinity in (3.8), we get $F(r)< F(r)$ which is not possible. Thus, in all situations, $\lim \nolimits _{n\rightarrow \infty }d(x,f^nz)=0.$ Similarly, we can prove that $\lim \nolimits _{n\rightarrow \infty }d(y,f^nz)=0.$ Since $d(x,y)\le d(x,f^nz)+d(f^nz,y)\rightarrow 0$ as $n\rightarrow \infty$, the uniqueness of the fixed point is established. This concludes the proof. $\square$

Remark 3.2

As 1 and 2 are not comparable elements, in the context of Example 3.1, the fixed point is not unique supporting our uniqueness results.

The following result is immediate. Observe that by widening the class of functions $\mathcal {F}$ in Definition 1.2, one can derive the following result which remains a metric-version of Theorem 3.1:

Theorem 3.5

Let (X, d) be a metric space and $f:X\rightarrow X$ an extended F-weak contraction for some function $F\in \mathbb {F}$. If (X, d) is f-orbitally complete and the following condition holds:

• (a) F is continuous.

Then f has a unique fixed point $x\in X$. Moreover, for every $x_0\in X$, the Picard sequence $\{f^nx_0\}$ converges to x.

Proof

The proof of existence part is very similar to that one of Theorem 3.1 and the uniqueness follows from Theorem 3.3 . Only we mention here that the extra conditions therein ensure the comparability between the element in which we apply to inequality (3.1). $\square$

Remark 3.3

With a view to check the validity of Theorem 3.5 in the context of Example 3.1 (without any partial order on X), observe that for $x=1$ and $y=2$, (3.1) gives rise

$$\begin{aligned} -\frac{1}{2}=\frac{1}{2}+F(d(f1,f2))\ge F(1)=-1 \end{aligned}$$

so that the inequality (3.1) is not satisfied. This demonstrates the utility of proving an ordered-version of Theorem 3.5.

The following is yet another version of Theorem 3.5 which remains a slightly sharpened form of Theorem 1.1 (proved for continuous mapping f).

Theorem 3.6

Let (X, d) be a metric space and $f:X\rightarrow X$ an extended F-weak contraction for some function $F\in \mathcal {F}$. If (X, d) is f-orbitally complete and

• (a) f is continuous,

then f has a unique fixed point $x\in X$. Moreover, for every $x_0\in X$, the Picard sequence $\{f^nx_0\}$ converges to x.

The proof is omitted as it is very similar to that of [18, Theorem 2.4] and [3, Theorem 2.2] where the completeness of the whole space is utilized rather than the completeness of the orbit of f.

Corollary 3.2

Theorem 1.1 follows from Theorems 3.5 and 3.6.

Corollary 3.3

Let (X, d) be a complete metric space and $f:X\rightarrow X$. Assume there exists $F\in \mathbb {F}$ and $\sigma \in \mathbb {S}$ such that f is F-contraction of Hardy-Rogers, i.e.,

$$\begin{aligned} \sigma (d(x,y))+F(d(fx,fy))\le & {} F\big (a_1d(x,y)+a_2d(x,fx)+a_3d(y,fy)\\&+\,a_4d(x,fy)+a_5d(y,fx)\big ), \end{aligned}$$

for all $x,y\in X$ whenever $d(fx,fy)>0$, where $a_i\in [0,\infty ) ~\forall i$, $a_1+a_2+a_3+2a_4=1$, $a_3\ne 1$ and $a_1+a_3+a_5\le 1$. Then f has a unique fixed point $x\in X$.

Proof

For all $x,y\in X$, we have

$$\begin{aligned}&a_1d(x,y)+a_2d(x,fx)+a_3d(y,fy)+a_4d(x,fy)+a_5d(y,fx) \\&\le (a_1+a_2+a_3+2a_4)\max \bigg \{ d(x,y),d(x,fx),d(y,fy),\frac{d(x,fy)+d(y,fx)}{2}\bigg \}\\&=\max \bigg \{ d(x,y),d(x,fx),d(y,fy),\frac{d(x,fy)+d(y,fx)}{2}\bigg \}. \end{aligned}$$

$\square$

Applications

Inspired by [22], we establish the existence and uniqueness solution for the following first-order periodic boundary value problem with respect to its lower or upper solution:

$$\begin{aligned} {\left\{ \begin{array}{ll}u^{\prime }(s)=f(s,u(s)),\;\;\;s\in I=[0,S]\\ u(0)=u(S),\\ \end{array}\right. } \end{aligned}$$

(4.1)

where $S>0$ and $f:I\times \mathbb {R}\rightarrow \mathbb {R}$ is a continuous function.

Let $\mathcal {C}(I)$ denote the space of all continuous functions defined on I. We recall the following two definitions:

Definition 4.1

[22] A function $\gamma \in \mathcal {C}^1(I)$ is called a lower solution of (4.1), if

$$\begin{aligned} {{\left\{ \begin{array}{ll}\gamma ^{\prime }(s)\le f(s,\gamma (s)),\;\;\;s\in I\\ \gamma (0)\le \gamma (S).\\ \end{array}\right. }} \end{aligned}$$

Definition 4.2

[22] A function $\gamma \in \mathcal {C}^1(I)$ is called an upper solution of (4.1), if

$$\begin{aligned} {{\left\{ \begin{array}{ll}\gamma ^{\prime }(s)\ge f(s,\gamma (s)),\;\;\;s\in I\\ \gamma (0)\ge \gamma (S).\\ \end{array}\right. }} \end{aligned}$$

Now, we prove the following result on the existence and uniqueness of solution of the problem described by (4.1) in the presence of a lower solution (or an upper solution).

Theorem 4.1

In respect of the problem (4.1), suppose that the following conditions hold:

• (i) there exists $\tau >0$ such that for all $x,y\in \mathbb {R}$ with $x\le y$

  $$\begin{aligned} 0\le f(s,y)+e^{-\tau } y-[f(s,x)+e^{-\tau } x]\le e^{-\tau } (y-x). \end{aligned}$$

  (4.2)

• (ii) there exists a function $\omega :\mathbb {R}^2\rightarrow \mathbb {R}$ such that for all $s\in I$ and for all $a,b\in \mathbb {R}$ with $\omega (a,b)\ge 0$,

  $$\begin{aligned} \omega \Big (\int _{0}^{S}G(s,t)[f(t,u(t))+ e^{-\tau } u(t)]\mathrm{d}t,\gamma (s)\Big )\ge 0, \end{aligned}$$

  where $\gamma \in \mathcal {C}^1(I)$ is a lower solution of (4.1).

• (iii) for all $s\in I$ and all $x,y \in \mathcal {C}^1(I)$, $\omega (x(s),y(s))\ge 0$ implies

  $$\begin{aligned} \omega \Big (\int _{0}^{S}G(s,t)[f(t,x(t))+e^{-\tau } x(t)]\mathrm{d}t,\int _{0}^{S}G(s,t)[f(t,y(t))+e^{-\tau } y(t)]\mathrm{d}t\Big )\ge 0, \end{aligned}$$

• (iv) if $x_n\rightarrow x\in \mathcal {C}^1(I)$ and $\omega (x_{n+1},x_n)\ge 0,$ then $\omega (x_n,x)\ge 0$ for all $n\in \mathbb {N}$. Then the existence of a lower solution of problem (4.1) ensures the existence and uniqueness of a solution of problem (4.1).

Proof

The problem described by (4.1) can be rewritten as

$$\begin{aligned} {\left\{ \begin{array}{ll} u^{\prime }(s)+e^{-\tau } u(s)=f(s,u(s))+e^{-\tau } u(s)\;\;\;\forall ~s\in I\\ u(0)=u(S)\\ \end{array}\right. } \end{aligned},$$

which is equivalent to the integral equation

$$\begin{aligned} u(s)=\int _{0}^{S}G(s,t)[f(t,u(t))+e^{-\tau } u(t)]\mathrm{d}t, \end{aligned}$$

(4.3)

where Green function G(s, t) is given by

$$\begin{aligned} G(s,t)={{\left\{ \begin{array}{ll}\frac{e^{e^{-\tau }(S+t-s)}}{e^{e^{-\tau } S}-1}\;\;\;0\le t<s\le S,\\ \frac{e^{e^{-\tau }(t-s)}}{e^{e^{-\tau } S}-1}\;\;\;\;\;\;0\le s <t\le S.\\ \end{array}\right. }}\end{aligned}$$

Define a function $\mathcal {X}:\mathcal {C}(I)\rightarrow \mathcal {C}(I)$ by

$$\begin{aligned} (\mathcal {X}u)(s)=\int _{0}^{S}G(s,t)[f(t,u(t))+e^{-\tau } u(t)]\mathrm{d}t\;\;\forall ~s\in I. \end{aligned}$$

(4.4)

Clearly, if $u\in \mathcal {C}(I)$ is a fixed point of $\mathcal {X}$, then $u\in \mathcal {C}^1(I)$ is a solution of (4.3) and hence of (4.1). Now, define a metric d on $\mathcal {C}(I)$ by

$$\begin{aligned} d(u,v)=\sup \limits _{s\in I}|u(s)-v(s)|\;\;\;\forall ~u,v\in \mathcal {C}(I). \end{aligned}$$

(4.5)

On $\mathcal {C}(I)$, define a partial order $\preceq$ given by

$$\begin{aligned} u,v\in \mathcal {C}(I); u\preceq v\Longleftrightarrow u(s)\le v(s)\;\;\forall ~s\in I. \end{aligned}$$

(4.6)

Clearly, $(\mathcal {C}(I),d,\preceq )$ is a complete ordered metric space. We check that all other conditions of Theorem 3.4:

First, let $\gamma \in \mathcal {C}^1(I)$ be a lower solution of (4.1); we have

$$\begin{aligned} \gamma ^{\prime }(s)+e^{-\tau }\gamma (s)\le f(s,\gamma (s))+e^{-\tau }\gamma (s)\;\;\forall ~s\in I. \end{aligned}$$

Multiplying both the sides by $e^{e^{-\tau } s}$, we get

$$\begin{aligned} (\gamma (s)e^{e^{-\tau } s})^{\prime }\le [f(s,\gamma (s))+e^{-\tau }\gamma (s)]e^{e^{-\tau } s}\;\;\forall ~s\in I, \end{aligned}$$

which implies that

$$\begin{aligned} \gamma (s)e^{e^{-\tau } s}\le \gamma (0)+\int _{0}^{s}[f(t,\gamma (t))+e^{-\tau } \gamma (t)]e^{e^{-\tau } t}\mathrm{d}t\;\;\forall ~s\in I. \end{aligned}$$

(4.7)

As $\gamma (0)\le \gamma (S)$, we have

$$\begin{aligned} \gamma (0)e^{e^{-\tau } S}\le \gamma (S)e^{e^{-\tau } S}\le \gamma (0)+\int _{0}^{S}[f(t,\gamma (t))+e^{-\tau } \gamma (t)]e^{e^{-\tau } t}\mathrm{d}t \end{aligned}$$

so that

$$\begin{aligned} \gamma (0)\le \int _{0}^{S}\frac{e^{e^{-\tau } t}}{e^{e^{-\tau } S}-1}[f(t,\gamma (t))+e^{-\tau } \gamma (t)]\mathrm{d}t. \end{aligned}$$

(4.8)

On using (4.7) and (4.8), we obtain

$$\begin{aligned} \gamma (s)e^{e^{-\tau }s}\le & {} \int _{0}^{S}\frac{e^{e^{-\tau }t}}{e^{e^{-\tau } S}-1}[f(t,\gamma (t))+e^{-\tau }\gamma (t)]\mathrm{d}t\\&+\int _{0}^{s}e^{e^{-\tau }t}[f(t,\gamma (t))+e^{-\tau }\gamma (t)]\mathrm{d}t\\\le & {} \int _{0}^{s}\frac{e^{e^{-\tau }(S+t)}}{e^{e^{-\tau }S}-1}[f(t,\gamma (t))+e^{-\tau } \gamma (t)]\mathrm{d}t\\&+\int _{s}^{S}\frac{e^{e^{-\tau }t}}{e^{e^{-\tau }S}-1}[f(t,\gamma (t))+e^{-\tau } \gamma (t)]\mathrm{d}t \end{aligned}$$

so that

$$\begin{aligned} \gamma (s)\le & {} \int _{0}^{s}\frac{e^{e^{-\tau }(S+t-s)}}{e^{e^{-\tau } S}-1}[f(t,\gamma (t))+e^{-\tau } \gamma (t)]\mathrm{d}t\\&+\int _{s}^{S}\frac{e^{e^{-\tau } (t-s)}}{e^{e^{-\tau } S}-1}[f(t,\gamma (t))+e^{-\tau } \gamma (t)]\mathrm{d}t\\= & {} \int _{0}^{S}G(s,t)[f(t,\gamma (t))+e^{-\tau } \gamma (t)]\mathrm{d}t\\= & {} (\mathcal {X}\gamma )(s) \end{aligned}$$

for all $s\in I$, which implies that $\gamma \preceq \mathcal {X}(\gamma )$.

Second, take $u,v\in \mathcal {C}(I)$ such that $u\preceq v$; then by (4.2), we have

$$\begin{aligned} f(s,u(s))+e^{-\tau } u(s)\le f(s,v(s))+e^{-\tau } v(s)\;\;\forall ~s\in I. \end{aligned}$$

(4.9)

On using (4.4), (4.9) and the fact that $G(s,t)>0$ for $(s,t)\in I\times I$, we get

$$\begin{aligned} (\mathcal {X}u)(s)= & {} \int _{0}^{S}G(s,t)[f(t,u(t))+e^{-\tau } u(t)]\mathrm{d}t\\\le & {} \int _{0}^{S}G(s,t)[f(t,v(t))+e^{-\tau } v(t)]\mathrm{d}t\\= & {} (\mathcal {X}v)(s)\;\;\;\forall ~s\in I, \end{aligned}$$

which, owing to (4.6), implies that $\mathcal {X}(u)\preceq \mathcal {X}(v)$ so that $\mathcal {X}$ is increasing.

Finally, take an increasing sequence $\{u_n\}\subset \mathcal {C}(I)$ such that $u_n\rightarrow u\in \mathcal {C}(I)$; then for each $s\in I$, $\{u_n(s)\}$ is a sequence in $\mathbb {R}$ converging to u(s). Hence, for all $n\in \mathbb {N}$ and for all $s\in I$, we have $u_n(s)\le u(s)$ for all $n\in \mathbb {N}_0$ so that $\mathcal {C}(I)$ is $\preceq$-regular.

Now we show that $\mathcal {X}$ is F-contraction for some $F\in \mathbb {F}$. Take $u,v\in \mathcal {C}(I)$ such that $u\preceq v$, using (4.2), (4.4) and (4.5), we have

$$\begin{aligned} d(\mathcal {X}u,\mathcal {X}v)= & {} \sup \limits _{s\in I}|(\mathcal {X}u)(s)-(\mathcal {X}v)(s)|=\sup \limits _{s\in I}\big ((\mathcal {X}v)(s)-(\mathcal {X}u)(s)\big )\\\le & {} \sup \limits _{s\in I}\int _{0}^{S}G(s,t)[f(t,v(t))+e^{-\tau } v(t)-f(t,u(t))-e^{-\tau } u(t)]\mathrm{d}t\\\le & {} \sup \limits _{s\in I}\int _{0}^{S}G(s,t)e^{-\tau }(v(t)-u(t))\mathrm{d}t\\ {}= & {} e^{-\tau } d(u,v)\sup \limits _{s\in I}\int _{0}^{S}G(s,t)\mathrm{d}t\\= & {} e^{-\tau } d(u,v)\sup \limits _{s\in I}\frac{1}{e^{e^{-\tau } S}-1}\Big (\frac{1}{e^{-\tau }}e^{e^{-\tau } (S+t-s)}\Big ]_0^s+\frac{1}{e^{-\tau }}e^{e^{-\tau } (t-s)}\Big ]_s^S\Big )\\= & {} e^{-\tau } d(u,v)\frac{1}{(e^{e^{-\tau } S}-1)}(e^{e^{-\tau } S}-1)\\= & {} e^{-\tau } d(u,v)\\\le & {} e^{-\tau } \mathrm{max}\left\{ d(u,v),\frac{d(u,\mathcal {X}u)+d(v,\mathcal {X}v)}{2},\frac{d(u,\mathcal {X}v)+d(v,\mathcal {X}u)}{2}\right\} , \end{aligned}$$

for all $u,v \in X$ with $u\preceq v$. Hence, $\mathcal {X}$ is F-weak contraction for $\tau$ chosen as in (i) and $F(s)=\ln s$. Thus, all the conditions of Theorem 3.1 are satisfied ensuring the existence of some fixed point of $\mathcal {X}$. Observe that, for arbitrary $u,v\in \mathcal {C}(I)$, $w:=\max \{u,v\}\in \mathcal {C}(I)$ is comparable to both u and v. Therefore, by Theorem, 3.4, $\mathcal {X}$ has a unique fixed point which means that problem (4.1) has a unique solution. $\square$

Theorem 4.2

Theorem 4.1 remains true if we replace the existence of the lower solution of (4.1) by the existence of an upper solution