Introduction

Search for energy forms that reduce or eliminate the carbon dioxide emission to the atmosphere has encouraged the renewable energy sector development, with the wind energy being highlighted. According to the World Wind Energy Association, the installed capacity of wind power in the world reached 486.661 MW at the end of 2016, 54.846 MW more than in 2015, representing a growth rate of 11.8%.

Wind resource analysis is a key step in the wind power generation projects development. Reducing errors in this step brings significant reliability gains for the project. One of the most important information in the wind resource analysis is the characterization of the wind regime according to a probability distribution, which aims to transform the discrete data collected in a measurement campaign into continuous data. In this procedure, velocities are grouped in intervals and a probability distribution function is fitted to this histogram. Depending on the wind conditions, the curve to be adjusted may follow the Gauss, Rayleigh or, more commonly, two parameters k and c Weibull distributions [35].

One of the challenges in applying the Weibull distribution to represent the region wind regime is the estimation of the parameters k and c, and an adjustment must be obtained with the smallest possible error. Dorvlo [12] used the Chi-square method to determine the Weibull parameters in four locations in Oman and Saudi Arabia. Silva [32] presented the equivalent energy method, where the parameters are found from the square error minimization power. Akdag and Dinler [1] proposed the energy pattern factor method, with which it would be possible to determine the k and c parameters from the power density and average velocity. Rocha et al. [28] dealt with the analysis and comparison of seven numerical methods for the assessment of effectiveness in determining the parameters for the Weibull distribution, using wind data collected for Camocim and Paracuru cities in the northeast region of Brazil. Also in the Brazilian northeastern region, Andrade et al [3] compared the graphical method, moment, pattern energy, maximum likelihood, empirical and equivalent energy and evaluated the efficiency through the predicted and measured power available.

However, in some cases, these methods cannot represent satisfactorily the wind speed distribution. Therefore, a favorable condition for the study of the heuristic method applications has been applied in more recent studies in the field of wind energy. Rahmani et al. [27] estimated, applying the Particle Swarm Optimization, the wind speed and the power produced in the Binaloud Wind Farm. Barbosa [6] estimated the Weibull curve parameters through the Harmony Search for two Brazilian regions. Wang et al. [36] used the Cuckoo Search Optimization and Ant Colony Optimization methods to evaluate wind potential and predict wind speed in four locations in China. Gonzlez et al. [17] presented a new approach for optimizing the layout of offshore wind farms comparing the behavior of two metaheuristic optimization algorithms, the genetic algorithm and Particle Swarm Optimization. Hajibandeh et al. [18] used the multicriteria multi-objective heuristic method to propose a new model for wind energy and DR integration, optimizing supply and demand side operations by the time to use (TOU) or incentive with the emergency DR program (EDRP), as well as combining TOU and EDRP together. Salcedo-Sanz et al. [29] addressed a problem of representative selection of measurement points for long-term wind energy analysis, as the objective of selecting the best set of N measurement points, such that a measure of wind energy error reconstruction is minimized considering a monthly average wind energy field, for which the metaheuristic algorithm, Coral Reef Optimization with Substrate Layer, was used, which is an evolutionary type method capable of combining different search procedures within a single population. Faced with the inconsistent relationship between China’s economy and the distribution of wind power potential that caused unavoidable difficulties in wind power transport and even network integration, Jiang et al. [19] studied, by optimization methods, among them the Cuckoo Search and the Particle Swarm, the establishment of an integrated electric energy system with low-speed wind energy. Marzband et al. [23] used four heuristically optimized optimization algorithms to implement a market structure based on transactional energy, to ensure that market participants can obtain a higher return.

Considering the presented works, this study aims to analyze four heuristic optimization methods and compare them with four other deterministic numerical methods, to suggest which is the most efficient to determine the parameters of the Weibull probability distribution curve for Petrolina, Triunfo and São Martinho da Serra regions.

Weibull distribution

Wind speed is a random variable, and it is useful to use statistical analysis to determine the wind potential of a region [2, 9, 35]. Commonly, the two parameters Weibull distribution is the one that presents the best fit and is therefore the most used to estimate this potential. [8, 22].

The Weibull distribution for the velocity v is expressed by the probability density function, wind velocity frequency curve, shown in Eq. 1. Equation 2 expresses its cumulative probability function [10, 24].

$$\begin{aligned} f(v)= & {} \left( \frac{k}{c}\right) \cdot \left( \frac{v}{c}\right) ^{(k-1)}\cdot e^{-\left( \frac{v}{c}\right) ^{k}}, \end{aligned}$$
(1)
$$\begin{aligned} F(v)= & {} \int _0^v f(v) \mathrm {d}v = 1 - e^{-(\frac{v}{c})^{k}} \quad v, \, k \, \mathrm{and} \, c > 0, \end{aligned}$$
(2)

where c is the scaling factor with unit \(m \cdot s^{-1}\), k is the shape factor (dimensionless) and F(v) denotes the probability of velocities smaller than or equal to v.

Among the methods already studied with the purpose of Weibull curves estimating parameters for the regions studied in this paper, or with similar characteristics, the maximum likelihood method, moment method, empirical method and the equivalent energy method were shown to be the most effective [3, 5, 28].

Maximum likelihood method (MLM)

In the maximum likelihood method, numerical iterations are required to determine the Weibull distribution parameters [15]. In this method [28], the parameters k and c are determined according to the Eqs. 3 and 4.

$$\begin{aligned} k= & {} \left[ \frac{\sum _{i=1}^{n}{v_i^k}\mathrm{ln}{(v_i)}}{\sum _{i=1}^{n}{v_i^k}}- \frac{\sum _{i=1}^{n}\mathrm{ln}{(v_i)}}{n}\right] ^{-1}, \end{aligned}$$
(3)
$$\begin{aligned} c= & {} \left( \frac{1}{n}\sum _{i=1}^{n}{v_i^k}\right) ^{\frac{1}{k}}, \end{aligned}$$
(4)

where n is the number of observed data and \(v_{i}\) is the wind speed measured in the interval i.

Moment method (MM)

The moment method may be used as an alternative to the maximum likelihood method and it is recommended when the mean and standard deviation of the elements are known and are initially on an appropriate scale [21]. In this case [28], the k and c parameters are determined by Eqs. 5 and 6.

$$\begin{aligned} \sigma= & {} c\cdot \sqrt{\varGamma \left( 1+\frac{2}{k}\right) -\varGamma ^2\left( 1+\frac{2}{k}\right) }, \end{aligned}$$
(5)
$$\begin{aligned} {\overline{v}}= & {} c\cdot \varGamma \left( 1+\frac{1}{k}\right) , \end{aligned}$$
(6)

where \({\bar{v}}\), \(\sigma\), \(\varGamma\) are, respectively, the average wind speed, the standard deviation of the observed wind speed data, and the gamma function.

Empirical method (EM)

The empirical method [10, 28] is considered a simplified form of the moment method, in which the determination of the k parameter follows Eq. 7 and the c parameter Eq. 8.

$$\begin{aligned} k= & {} \left( \frac{\sigma }{{\overline{v}}}\right) ^{-1,086} \end{aligned}$$
(7)
$$\begin{aligned} {\overline{v}}= {} c\cdot \varGamma (1+\frac{1}{k}), \end{aligned}$$
(8)

where \({\bar{v}}\) and \(\sigma\) are, respectively, the mean wind speed and the standard deviation of the observed wind speed data.

Equivalent energy method (EEM)

The equivalent energy method seeks the equivalence between the energy density of the observations and the theoretical Weibull curve. For this, the k parameter is estimated from the third moment of the velocity, by minimizing the square error related to the adjustment, represented by Eq. 9 and the c parameter is adjusted by using Eq. 10 [3, 32].

$$\begin{aligned} \epsilon ^2= & {} \sum \limits _{i=1}^{n}\left\{ {W_i}-e^{- \left[ \frac{(v_i- 1)(\varGamma (1+\frac{3}{k}))^{1/3}}{(\overline{v^3})^{1/3}}\right] ^{k}}+e^{-\left[ \frac{(v_i)(\varGamma (1+\frac{3}{k}))^{1/3}}{(\overline{v^3})^{1/3}}\right] ^{k}}\right\} ^2, \end{aligned}$$
(9)
$$\begin{aligned} c= & {} \left[ \frac{\overline{v^3}}{\varGamma \left( 1+\frac{3}{k}\right) }\right] ^{1/3}. \end{aligned}$$
(10)

Heuristic methods

Heuristics encompasses a set of methods where, to solve a problem, the variables in question use the experience gained over the iterations. Heuristic methods combine different concepts intelligently to explore the search space, so that learning strategies are used to structure information and find efficient and almost optimal solutions [25]. Many of the heuristic approaches depend on probabilistic decisions made during the algorithm run. The main difference against pure random search is that in heuristic algorithms, randomness is not used blindly but intelligently and biased [34]. It is valid to emphasize that every optimization procedure searches for the best result of a function for the desired scenario. This function is called the objective function. In this paper, the objective function is the one presented in Eq. 11, which represents the minimization of the square error sum applied to the frequency of occurrence values found by the curve adjusted by the method and the observed frequency of occurrence in the histogram of the data.

$$\begin{aligned} \epsilon ^2 = \sum \limits _{i=1}^{n} (f_{\mathrm{adjustment}} - f_{\mathrm{observed}})^2, \end{aligned}$$
(11)

where n is the number of histogram velocity intervals and \(f_{\mathrm{adjustment}}\) and \(f_{\mathrm{observed}}\) are the occurrence frequencies from the adjusted curve and that observed in the histogram, respectively.

Harmony search (HS)

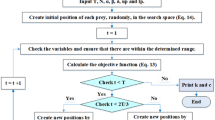
The Harmony Search is a heuristic algorithm based on the analogy of the artificial phenomenon of a musical group in search of the best harmony. This search occurs by the combination of existing elements and the generation of new elements that are combined to form possible solutions [16]. The search process begins with the formation of a harmony memory (HM), by the memorization of a series of possible solutions, denominated harmonies. At each iteration, a new harmony is formed and compared to the harmonies stored in the HM. The algorithm is presented by the following steps [4]:

  1. 1.

    initialize the HARMONY MEMORY;

  2. 2.

    improvise a new harmony from HM;

  3. 3.

    if the new harmony is better than the minimum harmony in HM, include the new harmony in HM and exclude the minimum harmony from HM. If not, the new harmony is excluded;

  4. 4.

    if the stopping criteria are not satisfied, go to step 2.

Figure 1 shows the flowchart of the Harmony Search algorithm, summarizing all steps described previously.

Fig. 1
figure 1

Flowchart of the HS algorithm

Full size image

Cuckoo search optimization (CSO)

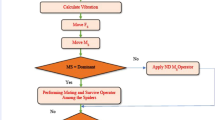
Cuckoos are birds with an aggressive breeding strategy. Some species such as Ani and Guira cuckoos place their eggs in communal nests, and sometimes remove other species’ eggs to increase the hatching probability of their own eggs. Other species lay their eggs in nesting host birds (often of other species). New World brood-parasitic Tapera species have evolved in such a way that the female parasitic cuckoos are often very specialized in the mimicry of the color and pattern of the eggs of a few chosen host species. This ability reduces the probability of their eggs being abandoned and thus increasing their reproductivity [26].

The CSO has its origin inspired by the behavior of the cuckoo in the process of finding nests, in which a nest is a possible solution. First, an initial population of nests is randomly generated. Later, new solutions are generated via Lévy flights. and from these the best solutions are stored in comparison to the current solutions. There are several ways to implement the distribution of Lévy distribution, the simplest is the Mantegna\('\)s algorithm [37], and its distribution takes the form presented by Eq. 12 [20].

$$\begin{aligned} x_i^{t+1}=x_i^{(t)} + \alpha _0 \cdot \frac{\phi \cdot u}{|v|^\frac{1}{\beta }} \cdot (x_i^{(t)}-x_{\mathrm{best}}^{(t)} ), \end{aligned}$$
(12)

where \(X_i^{(t)}\) is the previous solution from which the new solution \(X_i^{(t+1)}\) has been generated, \(\alpha _0\) is a constant, usually 0.01, \(X_{\mathrm{best}}^{(t)}\) represents the best actual solution, u and v are drawn from normal distributions, \(\beta\) is the scale factor which has an assigned value of 1.5 and \(\phi\) is calculated according to Eq. 13, where \(\varGamma\) is the gamma function.

$$\begin{aligned} \phi = \left\{ \frac{\varGamma (1+\beta ) \cdot \sin \left( \frac{\pi \cdot \beta }{2}\right) }{\varGamma \bigg [\frac{(1+ \beta )}{2}\bigg ]\cdot \beta \cdot 2^\frac{(\beta -1)}{2}} \right\} ^\frac{1}{\beta } . \end{aligned}$$
(13)

Then, the solution subset is discarded according to the probability of detection \(P_a\) \(\in\) [0,1] and new solutions are obtained, according to Eq. 14, with the same quantity of solutions abandoned [20, 30].

$$\begin{aligned} x_i^{t+1}=x_i^{(t)} + r \cdot \left( x_{i,c}^{(t)}-x_{i,k}^{(t)} \right) . \end{aligned}$$
(14)

In Eq. 14, r is a uniformly distributed random number from 0 to 1, and \(X_{(i,c)}\) and \(X_{(i,k)}\) denote the two random solutions of the ith generation.

Figure 2 shows the flowchart of the Cuckoo Search Optimization algorithm, summarizing all steps described previously.

Fig. 2
figure 2

Flowchart of the CSO algorithm

Full size image

Particle swarm optimization (PSO)

In a PSO system, each particle “flies” through the multidimensional search space, adjusting its position in space according to its own experience, however, also considering the experience of the neighboring particle. A particle uses the best position found by itself and the best position of its neighbors to position itself toward an ideal solution. The effect is that the particles “fly” toward a global optimum, while still investigating an area around the best current solution [14]. For each particle k positioned in a two-dimensional plane and for each iteration i, the positions and the best individual results \((x_k^{\mathrm{best}},y_k^{\mathrm{best}})\) are recorded. Then, the best result among the k particles is recorded \((x_{\mathrm{global}}^{\mathrm{best}},y_{\mathrm{global}}^{\mathrm{best}})\). Each particle’s movement will be proportional to the distance between the current position of the particle and the resulting point of the weighted average between the best individual position of the particle and the best position of the swarm, according to Eqs. 15 and 16 [13].

$$\begin{aligned} x_k^{(i+1)}= {} x_k^{(i)}+V_{x,k}^{(i)} , \end{aligned}$$
(15)
$$\begin{aligned} y_k^{(i+1)}= {} y_k^{(i)}+V_{y,k}^{(i)} , \end{aligned}$$
(16)

where

$$\begin{aligned} V_{x,k}^{(i+1)}= {} \omega ^{(i)}\cdot V_{x,k}^{(i)} +c_1\cdot \lambda \cdot [x_k^{\mathrm{(best)}} - x_k^{(i)}] + c_2\cdot \mu \cdot [x_{\mathrm{(global)}}^{\mathrm{(best)}} - x_k^{(i)}], \end{aligned}$$
(17)
$$\begin{aligned} V_{y,k}^{(i+1)}= {} \omega ^{(i)}\cdot V_{y,k}^{(i)} +c_1\cdot \eta \cdot [y_k^{\mathrm{(best)}} - y_k^{(i)}] + c_2\cdot \epsilon \cdot [x_{\mathrm{(global)}}^{\mathrm{(best)}} - y_k^{(i)}]. \end{aligned}$$
(18)

In these, \(\lambda\), \(\mu\), \(\eta\) and \(\epsilon\) are random numbers belonging to the set [0, 1] and \(\omega\) is the particle inertia term, defined by Eq. 19 [31].

$$\begin{aligned} \omega ^{(i)}=\omega _{\mathrm{initial}}+(\omega _{\mathrm{final}}-\omega _{\mathrm{initial}})\cdot \Big (\frac{i}{m}\Big ), \end{aligned}$$
(19)

where m is the maximum number of iterations.

Figure 3 shows the flowchart of the Particle Search Optimization algorithm, summarizing all steps described previously.

Fig. 3
figure 3

Flowchart of the PSO algorithm

Full size image

Ant colony optimization (ACO)

In an ant colony, the communication between individuals, or between the individuals and the environment, is based on the pheromone produced by them. The trail pheromone is a specific type of pheromone that some ant species use to mark paths on the ground. When detecting pheromone trails, forage ants may follow the path trodden by other ants to the food source. The first ants when sniffing the pheromone tend to choose, probabilistically, the trails marked with stronger concentrations of pheromone. The second group of ants will notice more intense the shortest path due to the shorter evaporation time. With the continuation of this procedure by all the ants, at one point in this process, one of the paths stands out for being the most frequented, being indicated by the intensity of ants’ pheromone and density superior to the others. At this point, the best path found by the ants is defined. This behavior inspired the optimization method by ant colonies [11].

In the ACO method, the parameters k and c of the Weibull curve form a Cartesian plane that is divided into N equal parts. The center point of each new area will be an ordered pair (k, c) where the curve fit will be evaluated [5]. The probability of occurrence of each reticulum is defined by Eq. 20.

$$\begin{aligned} P_{r}= \frac{\tau _r}{\sum _{r=1}^{R} \tau _r}, \end{aligned}$$
(20)

where \(\tau _r\) is the pheromone intensity for the reticle r.

Each ant is then randomly positioned in the plane through a roulette draw, where each slice of the roulette represents a reticle and is defined by the probability of occurrence. The visited quadrants are indicated by the pheromone deposit according to Eq. 21. At each iteration, the amount of the hormone is also reduced at a constant rate to simulate the hormone volatility, according to Eq. 22.

$$\begin{aligned} \tau _{i, r}= & {} \tau _{i-1, r} + \bigg (\frac{\mu }{{\mathrm{err}}_f} \bigg ) \end{aligned}$$
(21)
$$\begin{aligned} \tau _{i, r}= & {} \rho \cdot \tau _{i,r}, \end{aligned}$$
(22)

where \(\tau _{i, r}\) is the pheromone intensity for the reticle r, at iteration i, \({\mathrm{err}}_f\) is the error evaluated by the ant f, \(\mu\) is the deposition constant and \(\rho\) is the evaporation constant [33].

While the iterations follow up, some reticles will be more attractive to ants because they have a large amount of pheromone, this attraction being symbolized by the larger slices of the roulette, until most of the ants follow the same path.

Figure 4 shows the flowchart of the Ant Colony Optimization algorithm, summarizing all steps described previously.

Fig. 4
figure 4

Flowchart of the ACO algorithm

Full size image

Parameters applied to the heuristic methods

Each heuristic method depends on a certain number of parameters, with its adjustment being necessary to reduce the computational time response that leads to convergence to the optimal values. The parameters applied here, presented in Table 1, were extracted from the works whose authors used the proposed methods in wind energy applications [6, 7, 27, 36].

Table 1 Parameters applied to the heuristic methods
Full size table

Statistical tests

The performance evaluation of the applied methods was realized by the following tests:

Root mean square error (RMSE) (Eq, 23):

$$\begin{aligned} \mathrm{RMSE}\, = \sqrt{\frac{\sum _{i=1}^{n}(y_i^{\text {calculated}} - y^{\text {measured}} )^2}{n}}. \end{aligned}$$
(23)

Mean absolute error (MAE) (Eq. 24):

$$\begin{aligned} MAE = \frac{1}{n}\displaystyle \sum _{i=1}^{n} {\left| y_i^{\text {calculated}} - y_i^{\text {measured}}\right| }. \end{aligned}$$
(24)

Determination coefficient R\(^2\) (Eq. 25):

$$\begin{aligned} R^2 = \frac{\sum _{i=1}^{n}(y_i^{\text {measured}} - {\bar{y}}^{\text {measured}} )^2 - \sum _{i=1}^{n}(y_i^{\text {measured}} - y_i^{\text {calculated}})^2 }{\sum _{i=1}^{n}(y_i^{\text {measured}} - {\bar{y}}^{\text {measured}})^2}, \end{aligned}$$
(25)

where n is the number of observations, \(y_i^{\mathrm{calculated}}\) is the frequency of Weibull, \({\bar{y}}_i^{\mathrm{measured}}\) is the mean wind speed and \(y_i^{\mathrm{measured}}\) is the frequency of observations.

The percentage value of the wind production deviation (WPD) between the obtained Weibull probability distribution curve and the data histogram was evaluated as in Eq. 26.

$$\begin{aligned} WPD= & {} \bigg (\frac{WPD_{\mathrm{estimated}} -WPD_{\mathrm{measured}}}{WPD_{\mathrm{measured}}}\bigg )\cdot 100, \end{aligned}$$
(26)
$$\begin{aligned} WPD_{\mathrm{measured}}= & {} \frac{1}{2}\cdot \rho \cdot v^3 \end{aligned}$$
(27)
$$\begin{aligned} WPD_{\mathrm{estimated}}= & {} \frac{1}{2}\cdot \rho \cdot c^3 \cdot \varGamma \bigg (1 + \frac{3}{k} \bigg ), \end{aligned}$$
(28)

where \(\rho\) is the specific mass of the air, v is the wind speed, \(\varGamma\) is the gamma function and k and c are the estimated Weibull curve parameters.

Wind site data processing

The data of each location were separated into intervals with a variation of 1 m/s, and to fit the interval, the velocity should be higher than the lower value of the interval and less than or equal to the upper value, except the first interval where: 0 m/s \(\le\) V  \(\le\) 1 m/s. Once separated, the data size within each interval was evaluated, and this amount of each interval was divided by the data size, thus generating a relative frequency value for each interval. The data is validated by a SONDA project methodology, which does not change the databases, eliminating data considered invalid by the process. However, this only indicates the data considered as suspicious for the user to decide whether or not to use them. Data collected by the SONDA project for the Triunfo, Petrolina and São Martinho da Serra accounted for a total of 52,560 for the three stations, although, after the processing, a total of 52,560, 52,514 and 52,366 data were considered, representing a use of 100%, 99.91% and 99.63%. (Figs. 5, 6, 7, 8, 9, 10)

Results and discusssion

The results of the statistical tests for the TRI23 station located in Triunfo, PTR11 station located in Petrolina and SMS08 located in São Martinho da Serra are presented in Tables  2, 3 and 4. Figures 5, 8, 11, 6, 9 and 12 present the Weilbull distribution curves for deterministic numerical methods and heuristic methods. Figures  7 and 13compare the results obtained by ACO and the EM for Triunfo and São Martinho da Serra and Figure 10 compares the results obtained by CSO and the EM for Petrolina

Table 2 Statistical analysis: Triunfo, year 2010
Full size table
Fig. 5
figure 5

Weibull curve adjustment for TRI23-deterministic numerical methods

Full size image
Fig. 6
figure 6

Weibull curve adjustment for TRI23-heuristic methods

Full size image
Fig. 7
figure 7

Weibull curve adjustment for TR23 station in Triunfo

Full size image
Table 3 Statistical analysis: PTR11, year 2006
Full size table
Fig. 8
figure 8

Weibull curve adjustment for PTR11-deterministic numerical methods

Full size image
Fig. 9
figure 9

Weibull curve adjustment for PTR11-heuristic methods

Full size image
Fig. 10
figure 10

Weibull curve adjustment for PTR11 station in Petrolina

Full size image
Table 4 Statistical analysis: SMS08, year 2006
Full size table
Fig. 11
figure 11

Weibull curve adjustment for SMS08—deterministic numerical methods

Full size image
Fig. 12
figure 12

Weibull curve adjustment for SMS08—heuristics methods

Full size image
Fig. 13
figure 13

Weibull curve adjustment for SMS08 station in São Martinho da Serra

Full size image

Graphically, it was observed that the methods EM, MLM, MM, ACO, CSO, PSO and HS, to determine the shape parameter k and the scale parameter c of the Weibull distribution, presented a better curve fit with the histogram of the wind speed for the cities Triunfo, Petrolina and São Martinho da Serra. Moreover, it was further observed that the heuristic methods Ant Colony Optimization and Cuckoo Search Optimization were completely adequate to estimate the Weibull parameters. This fact was clearly validated by means of the statistical tests, i.e., RMSE, MAE and R\(^2\), and by the WPD test. Tables 2, 3 and 4 show the statistical tests results for all deterministic and heuristic methods and WPD test considered in the analysis. It was also observed from the statistical and wind production deviation analysis that the values of RMSE, MAE, R\(^2\) and WPD have low variation magnitudes to each other for all the methods.

It can be concluded that the ACO method for Triunfo and São Martinho da Serra and the CSO method for Petrolina have a good performance, since the results among all the used methods obtained the lowest values of RMSE, MAE and WPD, highlighting the WPD test values less than 2%, which was below the acceptable limit for the wind production deviation. It can also be concluded that the EEM for Triunfo, Petrolina and São Martinho da Serra has the worst performance, since it obtained the highest values of RMSE and MAE, and the lowest value of R\(^2\) among all methods, although this method presented great performance of the WPD test, since it obtained negligible values of wind production deviation. Among the heuristic methods, PSO for Triunfo and São Martinho da Serra had the worst performance, since it obtained WPD value higher than 2%.

Conclusion

The following conclusions can be drawn from the preceding analysis:

  1. 1.

    Graphically, the EEM method was the least effective to fit Weibull distribution curves for wind speed data from the region of Pernambuco and Rio Grande do Sul, respectively, using the data analyzed for the cities of Triunfo, Petrolina and São Martinho da Serra.

  2. 2.

    Regarding the parameter k, it was observed that its values range from 2 to 3 for the cities of Triunfo, Petrolina and São Martinho da Serra, showing less constancy of the wind speed for that location. The values of c for Petrolina and São Martinho da Serra cities range from 3 to 6 and for Triunfo range 13 to 16 for the mean wind speed occurring in those aforementioned places.

  3. 3.

    Ant Colony Optimization was an efficient method to determine the Weibull distribution parameters, k and c, for Triunfo and São Martinho da serra, and Cuckoo Search Optimization was an efficient method for Petrolina.

  4. 4.

    A suggestion for future work is to evaluate more periods of time and use the predicted values for k and c to calculate the average wind speed and its standard deviation to achieve a rank for each method.