Effect of obliqueness and external magnetic field on the characteristics of dust acoustic solitary waves in dusty plasma with two-temperature nonthermal ions

Abstract

In this paper, a theoretical investigation has been made of obliquely propagating dust acoustic solitary wave (DASW) structures in a cold magnetized dusty plasma consisting of a negatively charged dust fluid, electrons, and two different types of nonthermal ions. The Zakharov–Kuznetsov (ZK) and modified Zakharov–Kuznetsov (MZK) equations, describing the small but finite amplitude DASWs, are derived using a reductive perturbation method. The combined effects of the external magnetic field, obliqueness (i.e. the propagation angle), and the presence of second component of nonthermal ions, which are found to significantly modify the basic features (viz. amplitude, width, polarity) of DASWs, are explicitly examined. The results show that the external magnetic field, the propagation angle, and the second component of nonthermal ions have strong effects on the properties of dust acoustic solitary structures. The solitary waves may become associated with either positive potential or negative potential in this model. As the angle between the direction of external magnetic field and the propagation direction of solitary wave increases, the amplitude of the solitary wave (for both positive potential and negative potential) increases. With changing this angle, the width of solitary wave shows a maximum. The magnitude of the external magnetic field has no direct effect on the solitary wave amplitude. However, with decreasing the strength of magnetic field, the width of DASW increases.

Introduction

Dusty plasma is an ionized gas containing small particles of solid matter which acquire a large electric charge by collecting electrons and ions from the plasma. This state of plasma is ubiquitous in the universe, e.g., in interstellar clouds, in interplanetary space, in cometary tails, in ring systems of giant planets (like Saturn F-ring’s), in mesospheric noctilucent clouds, as well as in many Earth bound plasma [1, 2].

Recently, nonlinear wave propagation in plasmas has become one of the most important subjects of plasma. One of the most common and most fascinating eigen-modes that exist in space and laboratory dusty plasmas is dust acoustic wave (DASW), which was first theoretically predicted by Rao et al. [3] and experimentally verified by Barkan et al. [4]. The properties of these nonlinear plasma waves can be described by different nonlinear differential equations, e.g., the Korteweg–de Vries (KdV) equation, Zakharov–Kuznetsov (ZK) equation, and so on [5–7].

Over the last few years, a great deal of attention has been paid to non-Maxwellian particle distributions. The Maxwellian distribution is applicable to systems in thermodynamic equilibrium. However, astrophysical systems and space plasmas are observed to have particle distributions that depart from the Maxwellian distribution due to non-equilibrium stationary state. This state may arise due to a number of physical mechanisms such as external force field present in natural space plasma environments, wave–particle interaction, and turbulence. Spatial observations revealed the existence of non-Maxwellian distribution functions with high-energy tails or pronounced shoulders. Such type of distributions is frequently called superthermal or nonthermal distributions and occurs in space/astrophysical environments. Many authors studied solitary wave propagation in such non-Maxwellian distributions.

For example, Lin and Duan [8] considering the nonthermal ion in a dusty plasma derived a Korteweg–de Vries (KdV) equation for DA wave and it was found that the nonthermal ions have very important effect on the propagation of DA solitary waves. In a recent report Dorranian and Sabetkar [9] reported that with increasing nonthermal ion population, the amplitude of solitary wave decreases, while the width of solitary waves increases. It is also reported that in nonthermal dusty plasmas, the DASW have larger amplitude, smaller width, and higher propagation velocity than those involving adiabatic ions. Zhang and Wang [10] in their report observed the possibility of co-existence of both compressive and rarefactive solitary wave depending on a critical value of nonthermal ion population.

In continuation of that a number of theoretical investigations have been made on DASWs. Recently, the effects of the dust fluid temperature on the DASWs have been investigated by a number of authors [11, 12]. Sayed and Mamun [13] assumed a dusty plasma containing the adiabatic dust fluid and non-adiabatic (isothermal) inertialess electron and ion fluid, and studied the effect of the dust fluid temperature on the DASWs.

Many authors derived the ZK equation to study the solitary wave structures in magnetized plasma in different environments [14–16]. Recently, Mahmood et al. [17] have derived the ZK equation for nonlinear acoustic waves in dense magnetized electron–positron (e–p) plasmas. They showed that an increase in the strength of the magnetic field may lead to a significant decrease of the width of the solitons. More recently Shahmoradi et al. [18] have investigated the effect of dust size, mass, and charge distributions on the characteristics of nonlinear dust acoustic solitary waves (DASWs) in magnetized dusty plasma. They found that at each strength of the external magnetic field, there is an optimum magnitude for its direction at which the width of DASW is maximum.

This paper is organized in the following fashion. Following the introduction in Sect. 1, the governing equations and model description of dusty plasma system are presented in Sect. 2. The Zakharov–Kuznetsov (ZK) equation and its modified form with their solitary wave solution are derived by employing the reductive perturbation method in Sects. 3 and 4, respectively. Results and discussion are presented in Sects. 5 and 6 is devoted to conclusion.

Model description

We consider a three-component dusty plasma system, which consists of negatively charged dust fluid, Boltzmann distributed electrons, and two-temperature nonthermal ions with fast particles in the presence of external static magnetic field B = $B_0\hat{z}$, where $\hat{z}$ is the unit vector along $z$ direction. Charge neutrality at equilibrium reads

$$\begin{aligned} n_{\mathrm{e0}}+n_{\mathrm{d0}}Z_{\mathrm{d0}}=n_{i {\mathrm l0}}+n_{i {\mathrm h0}} \end{aligned}$$

(1)

where $n_{i \mathrm lo}$ ($n_{i \mathrm h0}$), $n_\mathrm{e0}$, and $n_\mathrm{d0}$ are the unperturbed lower (higher) temperature ion, electron, and dust number densities, respectively, and $Z_\mathrm{d0}$ is the unperturbed number of charges residing on the dust grain measured in the unit of electron charge. The normalized equations governing the dust acoustic wave dynamics are

$$\begin{aligned}&\frac{\partial n_\mathrm{d}}{\partial t}+ \nabla \cdot ({n_\mathrm{d}\mathbf{u }_\mathrm{d}})=0\end{aligned}$$

(2a)

$$\begin{aligned}&\frac{\partial \mathbf{u }_\mathrm{d}}{\partial t}+(\mathbf{u }_\mathrm{d}\cdot \nabla )\mathbf{u }_\mathrm{d}={\nabla \phi }-\omega _\mathrm{cd}(\mathbf{u }_\mathrm{d}\times \hat{z})\end{aligned}$$

(2b)

$$\begin{aligned}&{\nabla ^2\phi }=n_\mathrm{d}+n_\mathrm{e}-n_{i \mathrm l}-n_{i \mathrm h} \end{aligned}$$

(2c)

where u $_\mathrm{d}=(u_{\mathrm{d}x}, u{_{\mathrm{d}y}},u{_{\mathrm{d}z}})$. The time and space variables are normalized by the dust plasma period $\omega _\mathrm{pd}^{-1}=\sqrt{m_\mathrm{d}/4\pi n_\mathrm{d0}Z_\mathrm{d0}^2e^2}$ and the Debye length $\lambda _\mathrm{d}=\sqrt{T_\mathrm{eff}/4\pi n_\mathrm{d0} Z_\mathrm{d0}e^2},$ respectively. $n_\mathrm{d}$ is the dust particle number density normalized to $n_\mathrm{d0}$; u $_\mathrm{d}$ is the dust fluid velocity normalized to the dust acoustic speed $C_\mathrm{d}=\sqrt{Z_\mathrm{d0}T_\mathrm{eff}/m_\mathrm{d}}$ in which $T_\mathrm{eff}$ is the effective temperature which is defined below and $m_\mathrm{d}$ is the mass of the dust particles. $\phi$ is the electrostatic potential of plasma medium normalized by $T_\mathrm{eff}/e$ and $n_i$ is the ion number density normalized to $n_{i0}$. For the case of dusty plasma with two kinds of ions at different temperatures, the effective temperature is

$$\begin{aligned} T_{\mathrm{eff}}=\left[ \frac{1}{n_{\mathrm{d0}}Z_{\mathrm{d0}}}\left( \frac{n_{\mathrm{e0}}}{T_{\mathrm{e}}}+\frac{n_{i {\mathrm l0}}}{T_{i {\mathrm l}}}+\frac{n_{i {\mathrm h0}}}{T_{i {\mathrm h}}}\right) \right] ^{-1} \end{aligned}$$

(3)

in which $T_\mathrm{e}$, $T_{i \mathrm l}$, and $T_{i \mathrm h}$ are the plasma electron temperature and the temperatures of plasma ions at lower and higher temperatures, respectively. $\omega _\mathrm{cd}=Z_\mathrm{d0}eB_0/m_\mathrm{d}\omega _\mathrm{pd}$ is the dust cyclotron frequency normalized to $\omega _\mathrm{pd}$. The distribution function that was chosen by Cairns et al. [19] is chosen to model an ion distribution with a population of fast particles. Therefore, the lower temperature ion density, $n_{i \mathrm l}$, and higher temperature ion density, $n_{i \mathrm h}$, are directly given by

$$\begin{aligned} {n_{i \mathrm l}} &= \frac{\delta _{1}}{\delta _{1}+\delta _{2}-1}\left( 1+\mu \left( s\phi +s^2\phi ^2\right) \right) \exp (-s\phi ),\end{aligned}$$

(4a)

$$\begin{aligned} n_{ih}&= \frac{\delta _{2}}{\delta _{1}+\delta _{2}-1}\left( 1+\mu \left( {\beta }s\phi +\beta ^2s^2\phi ^2\right) \right) \exp (-{\beta }s\phi ),\end{aligned}$$

(4b)

$$\begin{aligned} n_{e}&= \frac{1}{\delta _{1}+\delta _{2}-1}\exp \left( \beta _1 s\phi \right) \!, \end{aligned}$$

(4c)

where $\mu =4\alpha /(1+3\alpha )$, $\alpha$ is parameter determining the number of fast (nonthermal) ions.

It should be noted here that if we neglect the number of nonthermal ions in comparison with that of thermal ions, i.e. we put $\alpha =0$, this dusty plasma model reduces to the model considered by Rao et al. [3]. From Eq. 1 one can write

$$\begin{aligned} \delta _{1}+\delta _{2}-1\ge 0. \end{aligned}$$

(5)

In above equations $\beta _{1}=\frac{T_{il}}{T_e}$, $\beta _{2}=\frac{T_{ih}}{T_e}$, $\frac{\beta _{1}}{\beta _{2}}=\frac{T_{il}}{T_{ih}}$, $\delta _{1}=\frac{n_{il}}{n_e}$, $\delta _{2}=\frac{n_{ih}}{n_e}$, and $S=\frac{T_{eff}}{T_{il}}=\frac{\delta _{1}+\delta _{2}-1}{\delta _{1}+\delta _{2}\beta +\beta _{1}}$.

Zakharov–Kuznetsov (ZK) equation

Derivation of the ZK equation

To investigate the nonlinear propagation of DASWs in magnetized plasma, we employ the standard RPM [7] to obtain the appropriate ZK equation. The independent variables are stretched as

$$\begin{aligned}&x'=\varepsilon ^{1/2}x\end{aligned}$$

(6a)

$$\begin{aligned}&y'=\varepsilon ^{1/2}y\end{aligned}$$

(6b)

$$\begin{aligned}&z'=\varepsilon ^{1/2}(z-\lambda t),\end{aligned}$$

(6c)

$$\begin{aligned}&t'=\varepsilon ^{3/2}t, \end{aligned}$$

(6d)

where $\varepsilon$ is a small parameter measuring the strength of nonlinearity and $\lambda$ the phase velocity of waves normalized by the dust acoustic speed $C_\mathrm{d}$, which is determined later. The physical quantities are expanded about their equilibrium values in a power series of $\varepsilon$ as

$$\begin{aligned} f&= f^{(0)}+\sum _{i=1}^\infty \epsilon ^mf^{(m)}\end{aligned}$$

(7a)

$$\begin{aligned} u_{\mathrm{d}x,y}&= \sum _{i=1}^\infty \epsilon ^{1+m/2}u_{\mathrm{d}x,y}^{(m)}. \end{aligned}$$

(7b)

The variables $f = (n_\mathrm{d},\phi ,u_{\mathrm{d}z})$ describe the state of the system with $f^{(0)}=(1,0,0)$. Substituting Eqs. 6 and 7 into the basic set of Eq. 2 and then equating the coefficient powers of $\epsilon$ in the lowest order, i.e. $O(\epsilon ^{3/2})$, we obtain the followings:

$$\begin{aligned} n_\mathrm{d}^{(1)}&= \frac{u_{\mathrm{d}z}^{(1)}}{\lambda }\end{aligned}$$

(8a)

$$\begin{aligned} u_{\mathrm{d}z}^{(1)}&= \frac{-\phi ^{(1)}}{\lambda }\end{aligned}$$

(8b)

$$\begin{aligned} u_{\mathrm{d}y}^{(1)}&= \frac{1}{\omega _\mathrm{cd}}\frac{\partial \phi ^{(1)}}{\partial x'}\end{aligned}$$

(8c)

$$\begin{aligned} u_{\mathrm{d}x}^{(1)}&= \frac{-1}{\omega _\mathrm{cd}}\frac{\partial \phi ^{(1)}}{\partial y'} \end{aligned}$$

(8d)

Now, substituting Eq. 8 into the lowest order Poisson equation, we get the phase velocity of DASWs as

$$\begin{aligned} \lambda =\left[ \frac{\left( \delta _1+\delta _2\beta +\beta _1\right) \left( 1+3\alpha \right) }{\left( \delta _1+\delta _2\beta \right) \left( 1-\alpha \right) +\beta _1\left( 1+3\alpha \right) }\right] ^{1/2} \end{aligned}$$

(9)

which agrees exactly with the phase velocity of the perturbation mode derived by Dorranian et al. [9]. Similarly, to the next higher order of $\epsilon$, i.e. $O(\epsilon ^2)$ we obtain the second-order $x$ and $y$ components of the momentum and Poisson equation as

$$\begin{aligned} u_{\mathrm{d}y}^{(2)}&= \frac{-\lambda }{\omega _\mathrm{cd}^2}\frac{\partial ^2\phi ^{(1)}}{\partial z'\partial y'}\end{aligned}$$

(10a)

$$\begin{aligned} u_{\mathrm{d}x}^{(2)}&= \frac{-\lambda }{\omega _\mathrm{cd}^2}\frac{\partial ^2\phi ^{(1)}}{\partial z'\partial x'}\end{aligned}$$

(10b)

$$\begin{aligned} \left( \frac{\partial ^2}{\partial x'^2}+\frac{\partial ^2}{\partial y'^2}+\frac{\partial ^2}{\partial z'^2}\right) \phi ^{(1)}&= n_\mathrm{d}^{(2)}+\frac{1}{\lambda ^2}\phi ^{(2)}+\left( \frac{-1}{2}\frac{\left( \delta _{1}+\delta _{2}\beta ^2-\beta _{1}^2\right) s^2}{\delta _{1}+\delta _{2}-1}\right) \left( \phi ^{(1)}\right) ^2 \end{aligned}$$

(10c)

Also, following the same procedure, we can obtain the next higher-order continuity equation and $z$ component of momentum equation as, i.e. $O(\epsilon ^{5/2})$

$$\begin{aligned}&\frac{\partial n_\mathrm{d}^{(1)}}{\partial t'}-\lambda \frac{\partial n_\mathrm{d}^{(2)}}{\partial z'}+\frac{\partial u_{\mathrm{d}x}^{(2)}}{\partial x'}+\frac{\partial u_{\mathrm{d}y}^{(2)}}{\partial y'}+\frac{\partial }{\partial z'}(u_{\mathrm{d}z}^{(2)}+n_\mathrm{d}^{(1)}u_{\mathrm{d}z}^{(1)})=0\end{aligned}$$

(11a)

$$\begin{aligned}&\frac{\partial u_{\mathrm{d}z}^{(1)}}{\partial t'}-\lambda \frac{\partial u_{\mathrm{d}z}^{(2)}}{\partial z'}+u_{\mathrm{d}z}^{(1)}\frac{\partial u_{\mathrm{d}z}^{(1)}}{\partial z'}-\frac{\partial \phi ^{(2)}}{\partial z'}=0 \end{aligned}$$

(11b)

Solving the system of Eq. 11, with the aid of Eqs. 8, 9, and 10, we can readily obtain

$$\begin{aligned} \frac{\partial \phi ^{(1)}}{\partial t'}+AB\phi ^{(1)}\frac{\partial \phi ^{(1)}}{\partial z'}+\frac{A}{2}\frac{\partial ^3\phi ^{(1)}}{\partial z'^3}+\frac{AD}{2}\left( \frac{\partial ^3\phi ^{(1)}}{\partial z'x'^2}+\frac{\partial ^3\phi ^{(1)}}{\partial z'y'^2}\right) =0 \end{aligned}$$

(12)

where

$$\begin{aligned} A&= \lambda ^3\end{aligned}$$

(13a)

$$\begin{aligned} D&= \frac{\omega _\mathrm{cd}^2+1}{\omega _\mathrm{cd}^2}\end{aligned}$$

(13b)

$$\begin{aligned} B&= \frac{1}{2}\frac{\left( \delta _1+\delta _2\beta ^2-\beta _1^2\right) \left( \delta _1+\delta _2-1\right) }{\left( \delta _1+\delta _2\beta +\beta _1\right) ^2} -\frac{3}{2\lambda ^4}. \end{aligned}$$

(13c)

Equation 12 is known as the Zakharov–Kuznetsov (ZK) equation or the Korteweg–de Vries (KdV) equation in three dimensions.

Solitary wave solution of the ZK equation

To study the propagation of DASWs in a direction making an angle $\theta$ with the external magnetic field B, lying in the $x'-z'$ plane, we transform the coordinate system $x',y',z'$ into the new coordinate system $\zeta ,\xi ,\eta$ by a rotation around the $y'$ axis through an angle $\theta$. The relations between the new and old coordinates become

$$\begin{aligned} \zeta&= x'\cos \theta -z'\sin \theta \end{aligned}$$

(14a)

$$\begin{aligned} \eta&= y'\end{aligned}$$

(14b)

$$\begin{aligned} \xi&= x'\sin \theta +z'\cos \theta \end{aligned}$$

(14c)

$$\begin{aligned} \tau&= t' \end{aligned}$$

(14d)

Under these changes of the independent variables, the ZK Eq. 12 becomes

$$\begin{aligned}\frac{\partial \phi ^{(1)}}{\partial \tau }&+h_1\phi ^{(1)}\frac{\partial \phi ^{(1)}}{\partial \xi }+h_2\frac{\partial ^3\phi ^{(1)}}{\partial \xi ^3}+h_3\phi ^{(1)}\frac{\partial \phi ^{(1)}}{\partial \zeta }\\ &+h_4\frac{\partial ^3\phi ^{(1)}}{\partial \zeta ^3}+h_5\frac{\partial ^3\phi ^{(1)}}{\partial \xi ^2\partial \zeta }+h_6\frac{\partial ^3\phi ^{(1)}}{\partial \xi \partial \zeta ^2}\nonumber \\ &+h_7\frac{\partial ^3\phi ^{(1)}}{\partial \xi \partial \eta ^2}+h_8\frac{\partial ^3\phi ^{(1)}}{\partial \zeta \partial \eta ^2}=0. \end{aligned}$$

(15)

Coefficients of Eq.15 are

$$\begin{aligned}&h_1=AB\cos \theta ,\qquad h_2=\frac{A}{2}\cos \theta \left( \cos ^2\theta +D\sin ^2\theta \right) \!,\qquad h_3=-AB\sin \theta ,\\&h_4=-\frac{A}{2}\sin \theta \left( \sin \theta +D\cos ^2\theta \right) \!,\qquad h_5=A\sin \theta \left( D\left( \cos ^2\theta -\frac{1}{2}\sin ^2\theta \right) -\frac{3}{2}\cos ^2\theta \right) \!,\\&h_6=A\cos \theta \left( D\left( \frac{1}{2}\cos ^2\theta -\sin ^2\theta \right) +\frac{3}{2}\sin ^2\theta \right) \!,\qquad h_7=\frac{AD}{2}\cos \theta ,\qquad h_8=-\frac{AD}{2}\sin \theta . \end{aligned}$$

Defining the new variables $Z=\xi -u_0\tau$ and $\phi ^{(1)}=\phi ^{(0)}(Z)$ in Eq. 15, the ZK equation in a steady state can be written as

$$\begin{aligned} h_2\frac{d^3\phi ^{(0)}}{dZ^3}-\left( u_0-h_1\phi ^{(0)}\right) \frac{d\phi ^{(0)}}{dZ}=0 \end{aligned}$$

(16)

in which $u_0$ is the constant velocity normalized to the dust acoustic speed. Using the appropriate boundary conditions ($\phi ^{(0)}$ and its two successive derivatives tend to zero when $Z\rightarrow \infty$) the solution of the Eq. 16 is given by

$$\begin{aligned} \phi ^{(0)}(Z)=\phi _m^{(0)}\mathrm{sech}^2\left( \frac{Z}{W}\right) \end{aligned}$$

(17)

where $\phi _m^{(0)}$ and $W$ are the amplitude and width of the DAWs, respectively, given by

$$\begin{aligned}&\phi _m^{(0)}=\frac{3u_0}{AB\cos \theta }\end{aligned}$$

(18a)

$$\begin{aligned}&W=\left( \frac{2A\cos \theta \left( \cos ^2\theta +D\sin ^2\theta \right) }{u_0}\right) ^{1/2} \end{aligned}.$$

(18b)

Modified Zakharov–Kuznetsov (MZK) equation

Derivation of the MZK equation

It is obvious that the propagation of compressive and rarefactive solitons depends on the sign of the nonlinear coefficient, $AB$, of the ZK equation. If we assume that the dispersion coefficient of the ZK equation $AB > 0$ ($AB < 0$), the dust acoustic solitary waves are compressive (rarefactive) waves. When the density of low (high) temperature ions $\delta _1$($\delta _2$) reaches the so-called $\delta _\mathrm{1c}$($\delta _\mathrm{2c}$) critical density of low- (high-) temperature ions, the nonlinear coefficient of the ZK equation vanishes, i.e., $AB=0$. Therefore, ZK equation breaks down and one has to seek for another equation suitable for describing the evolution of the system. At the critical density of low- (high-) temperature ions, the general method of the reductive perturbation method introduces the modified stretched variables defined by

$$\begin{aligned} x'&= \epsilon x\end{aligned}$$

(19a)

$$\begin{aligned} y'&= \epsilon y\end{aligned}$$

(19b)

$$\begin{aligned} z'&= \epsilon (z-\lambda t)\end{aligned}$$

(19c)

$$\begin{aligned} t'&= \varepsilon ^3t. \end{aligned}$$

(19d)

The dependent variables $n_\mathrm{d}$, $u_{\mathrm{d}z},$ and $\phi$ are expanded the same as Eq. 7 but $u_{\mathrm{d}y}$ and $u_{\mathrm{d}x}$ are expanded as follows:

$$\begin{aligned} u_{\mathrm{d}x}&= \epsilon ^2u_{\mathrm{d}x}^{(1)}+\epsilon ^3u_{\mathrm{d}x}^{(2)}+\epsilon ^4u_{\mathrm{d}x}^{(3)}+\cdots \end{aligned}$$

(20a)

$$\begin{aligned} u_{\mathrm{d}y}&= \epsilon ^2u_{\mathrm{d}y}^{(1)}+\epsilon ^3u_{\mathrm{d}y}^{(2)}+\epsilon ^4u_{\mathrm{d}y}^{(3)}+\cdots . \end{aligned}$$

(20b)

Using Eqs. 19, 20, and 7 in the main Eq. 2 and collecting terms with the same powers of expanding parameter $\epsilon$ we have Eqs. 8 and 9 again, for the lowest order, i.e. $O(\epsilon ^2)$. Similarly, to the next higher order of $\epsilon$, i.e. $O(\epsilon ^3)$ we obtain the second-order $x,y,$ and $z$ components of the momentum and continuity equation and Poisson equation as

$$\begin{aligned} u_{\mathrm{d}x}^{(2)}&= \frac{-\lambda }{\omega _\mathrm{cd}^2}\frac{\partial ^2\phi ^{(1)}}{\partial z'\partial x'}-\frac{1}{\omega _\mathrm{cd}^2}\frac{\partial \phi ^{(2)}}{\partial y'}\end{aligned}$$

(21a)

$$\begin{aligned} u_{\mathrm{d}y}^{(2)}&= \frac{-\lambda }{\omega _\mathrm{cd}^2}\frac{\partial ^2\phi ^{(1)}}{\partial z'\partial y'}+\frac{1}{\omega _\mathrm{cd}^2}\frac{\partial \phi ^{(2)}}{\partial x'}\end{aligned}$$

(21b)

$$\begin{aligned} u_{\mathrm{d}z}^{(2)}&= \frac{(\phi ^{(1)})^2}{2\lambda ^3}-\frac{\phi ^{(2)}}{\lambda }\end{aligned}$$

(21c)

$$\begin{aligned} n_\mathrm{d}^{(2)}&= \frac{(\phi ^{(1)})^2}{2\lambda ^4}-\frac{\phi ^{(2)}}{\lambda ^2}\end{aligned}$$

(21d)

$$\begin{aligned}& \left( \frac{\partial ^2}{\partial x'^2}+\frac{\partial ^2}{\partial y'^2}+\frac{\partial ^2}{\partial z'^2}\right) \phi ^{(1)}= n_\mathrm{d}^3+\frac{\phi ^{(3)}}{\lambda ^2}\nonumber \\&\quad +\frac{\left( \delta _1+\delta ^2-1\right) ^2}{\left( \delta _1+\delta ^2\beta +\beta _1\right) ^3}\frac{(1+15\alpha ) \left( \delta _1+\delta _2\beta ^3\right) +(1+3\alpha )\beta _1^3}{6(1+3\alpha )}(\phi ^{(1)})^3\nonumber \\&\quad +\frac{\left( \delta _1+\delta ^2-1\right) }{\left( \delta _1+\delta _2\beta +\beta _1\right) ^2}\left( \beta _1^2-\delta _1-\delta _2\beta ^2\right) \phi ^{(1)}\phi ^{(2)}. \end{aligned}$$

(21e)

Following the same procedure, we can obtain the next higher-order continuity equation and $z$ component of momentum equation as, i.e. $O(\epsilon ^4)$.

$$\begin{aligned}&\frac{\partial n_\mathrm{d}^{(1)}}{\partial t'}-\lambda \frac{\partial n_\mathrm{d}^{(3)}}{\partial z'}+\frac{\partial }{\partial x'}(u_{\mathrm{d}x}^{(2)}+n_\mathrm{d}^{(1)}u_{\mathrm{d}x}^{(1)})+\frac{\partial }{\partial y'}(u_{\mathrm{d}y}^{(2)}+n_\mathrm{d}^{(1)}u_{\mathrm{d}y}^{(1)})\nonumber \\&\qquad \quad \;+\frac{\partial }{\partial z'}(u_{\mathrm{d}z}^{(3)}+n_\mathrm{d}^{(1)}u_{\mathrm{d}z}^{(2)}+n_\mathrm{d}^{(2)}u_{\mathrm{d}z}^{(1)})=0\end{aligned}$$

(22a)

$$\begin{aligned}&\frac{\partial u_{\mathrm{d}z}^{(1)}}{\partial t'}-\lambda \frac{\partial u_{\mathrm{d}z}^{(3)}}{\partial z'}+u_{\mathrm{d}x}^{(1)}\frac{\partial u_{\mathrm{d}z}^{(1)}}{\partial x'}+u_{\mathrm{d}y}^{(1)}\frac{\partial u_{\mathrm{d}z}^{(1)}}{\partial y'}+u_{\mathrm{d}z}^{(1)}\frac{\partial u_{\mathrm{d}z}^{(2)}}{\partial z'}\nonumber \\&\qquad \quad \;+u_{\mathrm{d}z}^{(2)}\frac{\partial u_{\mathrm{d}z}^{(1)}}{\partial z'}-\frac{\partial \phi ^{(3)}}{\partial z'}=0. \end{aligned}$$

(22b)

Solving the system of Eq. 22, using Eqs. 8, 9, and 21, we finally obtain the modified Zakharov–Kuznetsov (MZK) equation:

$$\begin{aligned} \frac{\partial \phi ^{(1)}}{\partial t'}+AE\left( \phi ^{(1)}\right) ^2\frac{\partial \phi ^{(1)}}{\partial z'}+\frac{A}{2}\frac{\partial }{\partial z'}\left( \frac{\partial ^2}{\partial z'^2}+D\left( \frac{\partial ^2}{\partial x'^2}+\frac{\partial ^2}{\partial y'^2}\right) \right) \phi ^{(1)}=0 \end{aligned}$$

(23)

$A$ and $D$ were introduced in the previous section and $E$ is

$$\begin{aligned} E=\frac{15}{4\lambda ^6}-\frac{1}{4}\frac{\left( \delta _{1}+\delta _{2}-1\right) ^2\left( (1+15\alpha )\left( \delta _{1}+\delta _{2}\beta ^3\right) + (1+3\alpha )\beta _{1}^3\right) }{\left( \delta _{1}+\delta _{2}\beta +\beta _{1}\right) ^3(1+3\alpha )} \end{aligned}$$

(24)

Solitary wave solution of the MZK equation

To study the propagation of DASW in a direction making an angle $\theta$ with the external magnetic field B, lying in the $x'-z'$ plane, we transform the coordinate system $x',y',z'$ into the new coordinate system $\zeta ,\xi ,\eta$ by a rotation around the $y'$ axis through an angle $\theta$. The relations between the new and old coordinates were introduced in Eq. 14. In this case, the new form of Eq. 23 will be

$$\begin{aligned}&\frac{\partial \phi ^{(1)}}{\partial \tau }+\Omega _{1}\left( \phi ^{(1)}\right) ^2\frac{\partial \phi ^{(1)}}{\partial \xi }+\Omega _{2}\frac{\partial ^3\phi ^{(1)}}{\partial \xi ^3}\nonumber \\&\qquad \quad \; +\Omega _{3}\left( \phi ^{(1)}\right) ^2\frac{\partial \phi ^{(1)}}{\partial \zeta }+\Omega _{4}\frac{\partial ^3\phi ^{(1)}}{\partial \zeta ^3} +\Omega _{5}\frac{\partial ^3\phi ^{(1)}}{\partial \xi ^2\partial \zeta }+\Omega _{6}\frac{\partial ^3\phi ^{(1)}}{\partial \xi \partial \zeta ^2}\nonumber \\&\qquad \quad \; +\Omega _{7}\frac{\partial ^3\phi ^{(1)}}{\partial \xi \partial \eta ^2}+\Omega _{8}\frac{\partial ^3\phi ^{(1)}}{\partial \zeta \partial \eta ^2}=0. \end{aligned}$$

(25)

where

$$\begin{aligned}&\Omega _{1}=AE\cos \theta ,\qquad \Omega _{2}=\frac{1}{2}A\cos \theta \left( \cos ^2\theta +D\sin ^2\theta \right) , \qquad \Omega _{3}=-AE\sin \theta \\&\Omega _{4}=-\frac{1}{2}A\sin \theta \left( \sin ^2\theta +D\cos ^2\theta \right) ,\qquad \Omega _{5}=A\sin \theta \left( D\left( \cos ^2\theta -\frac{1}{2}\sin ^2\theta \right) -\frac{3}{2}\cos ^2\theta \right) \\&\Omega _{6}=A\cos \theta \left( D\left( \frac{1}{2}\cos ^2\theta -\sin ^2\theta \right) +\frac{3}{2}\sin ^2\theta \right) ,\qquad \Omega _{7}=\frac{1}{2}AD\cos \theta , \qquad \Omega _{8}=\frac{-1}{2}AD\sin \theta .\\ \end{aligned}$$

Using again the new variables $Z=\xi -u_0\tau$ and $\phi ^{(1)}=\phi ^{(0)}(Z)$ in Eq. 25, the MZK equation in a steady-state forms as

$$\begin{aligned} \Omega _{2}\frac{d^3\phi ^{(0)}}{dZ^3}-\left( u_{0}-\Omega _{1}\left( \phi ^{(0)}\right) ^2\right) \frac{d\phi ^{(0)}}{dZ}=0 \end{aligned}$$

(26)

in which $u_0$ is constant velocity normalized to the dust acoustic speed. Now, using the appropriate boundary conditions ($\phi ^{(0)}$ and its two successive derivatives tend to zero when $Z\rightarrow \infty$) the solution of the Eq. 26 is given by

$$\begin{aligned} \phi ^{(0)}(Z)=\phi _{m}^{(0)}\mathrm{sech}\left( \frac{Z}{W}\right) \end{aligned}$$

(27)

where $\phi _m^{(0)}$ and $W$ are the amplitude and width of the DASWs, respectively, given by

$$\begin{aligned}&\phi _{m}^{(0)}=\left( \frac{6u_{0}}{AE\cos \theta }\right) ^{1/2}\end{aligned}$$

(28a)

$$\begin{aligned}&W=\left( \frac{A\cos \theta \left( \cos ^2\theta +D\sin ^2\theta \right) }{2u_{0}}\right) ^{1/2} \end{aligned}$$

(28b)

Solitons exist when $E>0$.

Results and discussion

The nonlinear propagation of dust acoustic solitary waves (DASW) in a magnetized dusty plasma which consists of two different types of nonthermal ions, electrons, and mobile negatively charged dust particles is studied. The Zakharov–Kuznetsov (ZK) and modified Zakharov–Kuznetsov (MZK) equations, describing the small but finite amplitude DASW, are derived using a reductive perturbation method. The combined effects of the external magnetic field, obliqueness (i.e., the propagation angle), and the presence of second component of nonthermal ions, which are found to significantly modify the basic properties of DASWs, are explicitly examined. For $\alpha =0$, and by assuming collisionless dusty plasma systems (such as outside ionopause of Halley’s comet, Saturn’s F-ring, Saturn’s spokes, zodiacal dust disc (IAU) and supernovae shells), our results would coincide with the results obtained by Moslem [20]. It is obvious that if we neglect the contributions of external magnetic field, $\omega _\mathrm{cd}=0$, our present dusty plasma model corresponds to the dusty plasma system considered in a recent published work by Dorranian et al. [9]. As $u_0 > 0$, it is clear from Eqs. 13 and 18 that depending on whether $AB$ is positive or negative, the solitary waves will be associated with either positive potential $\phi _m^{(0)} > 0$ or negative potential $\phi _m^{(0)} < 0$. Therefore, there exist solitary waves associated with positive (negative) potential when $AB > 0$ ($AB < 0$).

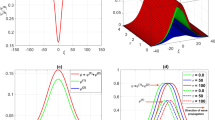
Figure 1 shows the variation of the nonlinear coefficient $AB$, with $\delta _1$ and $\delta _2$ for $u_0=1$, $\alpha =0.4$, $\beta _1=0.1$, and $\beta _2=0.4$. This figure also indicates the critical value of $\delta _1$ and $\delta _2$ (which are $\delta _\mathrm{2c}$ = 0.93, and $\delta _\mathrm{1c}$ = 0.57). For the region of positive nonlinear coefficient AB, the nonlinear coefficient $AB$ decreases as the values of both $\delta _1$ and $\delta _2$ decrease. $AB$ is effectively changed with $\delta _1$ and $\delta _2$ when they are smaller than 5 and for larger magnitudes of $\delta _1$ and $\delta _2$, the nonlinear coefficient is almost constant. It is observed from Eqs. 13 and 18 that the amplitude of DASW $\phi _m^{(0)}$ is a nonlinear function of $\delta _1$, $\delta _2$, $\beta _1$, $\beta$, $\theta$, and $\alpha$. The variation of $\phi _m^{(0)}$ (for positive and negative potential) with $\delta _2$, $\beta _2$, $\theta$, and $\alpha$ are shown in Figs. 2–7. Figure 2(3) shows the variation of the amplitude of the negative solitary waves (positive solitary waves) with $\delta _2$ and $\alpha$ for $u_0 = 1$,$\delta _1 = 0.1,$ $\beta _1 = 0.1,$ $\beta _2 = 0.4$, and $\theta = 30^o$ (for $u_0 = 1$, $\delta _1 = 1.9,$ $\beta _1 = 0.1,$ $\beta _2 = 0.4,$ and $\theta =30^{\circ }$). Figure 2 shows that the amplitude increases as the values of both $\delta _2$ and $\alpha$ increase. Figure 3 shows that the amplitude increases as the values of both $\delta _2$ and $\alpha$ decrease. With decreasing the nonthermal coefficient $\alpha$, the amplitude of soliton increases, while with decreasing $\delta _2$ amplitude increases very slightly. In other words, the influence of nonthermal coefficient on the amplitude is more larger. This effect was observed in Ref. [9].

Fig. 1

The variation of the nonlinear coefficient $AB$ with $\delta _1$ and $\delta _2$ for $u_0 = 1, \alpha = 0.4, \beta _1 = 0.1$ and $\beta _2 = 0.4$

Fig. 2

The variation of the amplitude of the negative ZK solitary potential $\left( \phi _m^{(0)}<0\right)$ with $\delta _2$ and $\alpha$ for $u_0 = 1, \delta _1 = 0.1, \beta _1 = 0.1, \beta _2 = 0.4,$ and $\theta = 30^{\circ }$

Fig. 3

The variation of the amplitude of the positive ZK solitary potential $\left( \phi _m^{(0)}>0\right)$ with $\delta _2$ and $\alpha$ for $u_0 = 1, \delta _1 = 1.9, \beta _1 = 0.1, \beta _2 = 0.4,$ and $\theta = 30^{\circ }$

Fig. 4

The variation of the amplitude of the negative ZK solitary potential $\left( \phi _m^{(0)}<0\right)$ with $\beta _2$ and $\theta$ for $u_0 = 1, \delta _1 = 0.1, \delta _2 = 2.1, \beta _1 = 0.1$, and $\alpha = 0.1$

Fig. 5

The variation of the amplitude of the positive ZK solitary potential $\left( \phi _m^{(0)}>0\right)$ with $\beta _2$ and $\theta$ for $u_0 = 1, \delta _1 = 1.2, \delta _2 = 2.1, \beta _1 = 0.1$, and $\alpha = 0.5$

Fig. 6

The variation of the amplitude of the positive MZK solitary potential $\left( \phi _m^{(0)}>0\right)$ with $\delta _2$ and $\alpha$ for $u_0 = 1, \delta _1 = 0.4, \beta _1 = 0.1, \beta _2 = 0.4$, and $\theta = 30^{\circ }$

Fig. 7

The variation of the amplitude of the positive MZK solitary potential $\left( \phi _m^{(0)}>0\right)$ with $\beta _2$ and $\theta$ for $u_0 = 1, \delta _1 = 1.1, \beta _1 = 0.1, \delta _2 = 2.1$, and $\alpha = 0.1$

Figure 4(5) shows the variation of the amplitude of the negative solitary waves (positive solitary waves) with $\beta _2$ and $\theta$ for $u_0 = 1$, $\alpha = 0.1, \beta _1 = 0.1, \delta _1 = 0.1$, and $\delta _2 = 2.1$ (for $u_0 = 1$, $\alpha = 0.5, \beta _1 = 0.1, \delta _1 = 1.2$, and $\delta _2 = 2.1$). In Fig. 4 the rate of the increase is low (high) in the region about $48^{\circ }<\theta <70^{\circ }$ ($70^{\circ }<\theta <89^{\circ }$) for all of $\beta _2$. In Fig. 5 the rate of the increase is low (high) in the region at about $50^{\circ }<\theta <77^{\circ }$ ($77^{\circ }<\theta <89^{\circ }$) for all $\beta _2$. Amplitude of solitons are directly proportional with the angle of propagation, but in the region $0^{\circ }<\theta <50^{\circ }$, the soliton amplitude changes very slightly both ZK and MZK solitons. For the propagation angle almost greater than $50^{\circ }$, variation of amplitude is noticeable in Figs. 4 and 5.

By considering $u_0 > 0$, it is clear from Eqs. 24 and 28 that MZK solitons exist when $E>0$. Therefore, there always exist solitary waves associated with positive potential. In Fig. 6(7), the variation of the amplitude of the positive solitary waves with $\delta _2$ and $\alpha$ is presented for $u_0 = 1$, $\delta _1 = 0.4$, $\beta _1 = 0.1$, $\beta _2 = 0.4,$ and $\theta = 30^{\circ }$ (with $\beta _2$ and $\theta$ for $u_0 = 1$, $\delta _1 = 1.1$, $\beta _1 = 0.1$, $\alpha = 0.1$ and $\delta _2 = 2.1$). Figure 6 shows that the amplitude decreases for the lower regions of $\delta _2$ (for about $\delta _2 <$0.76), its magnitude increases rapidly with increasing the value of $\delta _2$ (for the region $\delta _2 >$0.76) to 3.05 and this figure also indicates that the amplitude increases with increasing $\alpha$. Figure 7 shows that the amplitude increases slowly as the value of $\beta _2$ increases. The rate of increase is very high in the region at about $84^{\circ }<\theta <89^{\circ }$.

The magnitude of the external magnetic field has a significant effect only on the width, but not on the amplitude of solitary waves. It is found from Eqs. 18 and 28 that the width is a nonlinear function of $\delta _1, \delta _2, \beta _2, \beta , \theta , \alpha ,$ and $\omega _\mathrm{cd}$. The variation of the width (for positive and negative solitary waves) with $\delta _2$, $\beta _2$, $\theta ,$ and $\omega _\mathrm{cd}$ is presented in Figs. 8, 9, 10, 11 and Fig. 12. Dependence of soliton width on $\theta$ and $\alpha$ ($\delta _2$ and $\beta _2$) is shown in Fig. 8(9). In Fig. 8(9) we have $u_0=1, \delta _1=0.6, \beta _1=0.1, \beta _2=0.4, \delta _2=2.1$, and $\omega _\mathrm{cd}=0.6$ ($u_0=1, \delta _1=0.4, \beta _1=0.1, \alpha =0.2, \theta =30^{\circ },$ and $\omega _\mathrm{cd}=0.3$). Figure 8 shows that the width increases with $\theta$ for the lower range, i.e. $0<\theta <53.6^{\circ }$, but decreases for its higher range, i.e. $53.6^{\circ }<\theta <89^{\circ }$, and as $\theta \rightarrow 90^{\circ }$, the width goes to $0$. The maximum of width is at $\theta =53.6^{\circ }$. This also shows that the width increases with increasing $\alpha$. The width increases slowly with increasing (decreasing) $\delta _2$ ($\beta _2$) as shown in Fig. 9.

Figure 10(11) shows variation of soliton width with $\theta$ and $\alpha$ ($\delta _2$ and $\beta _2$) for $u_0=1, \delta _1=0.6, \beta _1=0.1, \beta _2=0.4, \delta _2=2.1$, and $\omega _\mathrm{cd}=0.6$ (for $u_0=1, \delta _1=0.6, \beta _1=0.1, \alpha =0.1, \theta =30^{\circ }$, and $\omega _\mathrm{cd}=0.4$). Figure 10 shows that the width increases with $\theta$ for the lower range, i.e., $0^{\circ }<\theta <55.11^{\circ }$, but decreases for its higher range, i.e., $55.11^{\circ }<\theta <89^{\circ }$ and as $\theta$ tends to 90$^{\circ }$, the width goes to 0. This also shows that the width increases with increasing $\alpha$. Figure 11 shows that the width remains almost unchanged for all value of $\beta _2$, but increases rapidly with increasing $\delta _2$. Figure 12 shows the variation of width with $\theta$ and $\omega _\mathrm{cd}$. In this figure we have $u_0=1, \delta _1=0.1, \beta _1=0.1, \beta _2=0.4, \delta _2=2.1$, and $\alpha =0.5$. The width of soliton for the case of MZK solution is half of the ZK solitons. Amplitude of soliton is independent of magnetic field intensity while is influenced by the direction of applied external magnetic field. The effective variation of $\omega _\mathrm{cd}$ on the width of soliton is when $\omega _\mathrm{cd}\le 0.01$. In the case of larger magnitude, width of solitons does not change with $\omega _\mathrm{cd}$ noticeably, and the same results have been reported by Sabetkar et al. [21]. Figure 12 shows that the width increases with $\theta$ for the lower range, i.e., $0^{\circ } <\theta < 56.5^{\circ }$, but decreases for its higher range, i.e., $56.5^{\circ }, <\theta < 89^{\circ }$ and as $\theta$ tends to $90^{\circ }$, the width tends to a constant value. Also, with decreasing $\omega _\mathrm{cd}$, the width of soliton increases.

Fig. 8

The variation of the width of positive ZK solitary potential $\left( \phi _m^{(0)}>0\right)$ with $\theta$ and $\alpha$ for $u_0=1, \delta _1=0.6, \delta _2=2.1, \beta _1=0.1, \beta _2=0.4$, and $\omega _\mathrm{cd}=0.6$

Fig. 9

The variation of the width of positive ZK solitary potential $\left( \phi _m^{(0)}>0\right)$ with $\delta _2$ and $\beta _2$ for $u_0=1, \delta _1=0.4, \beta _1=0.1, \alpha =0.2, \theta =30^o$, and $\omega _\mathrm{cd}=0.3$

Fig. 10

The variation of the width of negative MZK solitary potential $\left( \phi _m^{(0)}<0\right)$ with $\theta$ and $\alpha$ for $u_0=1, \delta _1=0.6, \delta _2=2.1, \beta _1=0.1, \beta _2=0.4$, and $\omega _\mathrm{cd}=0.6$

Fig. 11

The variation of the width of negative MZK solitary potential $\left( \phi _m^{(0)}<0\right)$ with $\delta _2$ and $\beta _2$ for $u_0=1, \delta _1=0.6, \beta _1=0.1, \alpha =0.1, \theta =30^{\circ }$, and $\omega _\mathrm{cd}=0.4$

Fig. 12

The variation of the width of positive ZK solitary potential $\left( \phi _m^{(0)}>0\right)$ with $\omega _\mathrm{cd}$ and $\theta$ for $u_0=1, \delta _1=0.1, \delta _2= 2.1, \beta _1=0.1, \beta _2=0.4$, and $\alpha =0.5$

Conclusion

In present paper, nonlinear propagating dust acoustic solitary waves (DASWs) in a cold magnetized dusty plasma containing negatively charged dust particles, electrons, high- and low-temperature nonthermal ions in the presence of an external static magnetic field are investigated. For this purpose, a reasonable normalization of the hydrodynamic and Poisson equations is used to derive the Zakharov–Kuznetsov (ZK) and (MZK) equation for our dusty plasma system. We have found that depending on the values of $\delta _1, \delta _2, \beta _1, \beta _2,$ and $\alpha$, the solitary waves may become associated with either positive potential or negative potential. We have seen that as the values of $\delta _2$ and $\alpha$ increase, the amplitude of the positive (negative) solitary waves decreases (increases). The width of soliton also increases with the increasing $\delta _2$ and $\alpha$. For higher-order approximation, i.e. MZK case, we have found that the amplitude of the positive solitary waves increases with increasing $\alpha$. The amplitude of solitary waves decreases with $\delta _2$ when $\delta _2<$ 0.76 and increases rapidly for $\delta _{2}>$0.76.

We have found that as the angle between the direction of external magnetic field with the propagation direction of solitary wave, $\theta$, increases, the amplitude of the solitary wave (for both positive potential and negative potential) increases. The width of solitary wave has a maximum magnitude when $\theta = 55.11^{\circ }$. As $\theta$ tends to 90$^{\circ }$, the width goes to 0, and the amplitude goes to infinity. It is found that (for both positive potential and negative potential) the amplitude increases slowly as the value of $\beta _2$ increases, but the width increases slowly. Taking into account the higher order of $\epsilon$ (i.e. MZK equation) the width remains almost unchanged for all values of $\beta _2$. The magnitude of the external magnetic field has no direct effect on the solitary wave amplitude. However, it has a direct effect on the width of the solitary waves, and also with decreasing $\omega _\mathrm{cd}$, the width of DASW increases. In fact, the external magnetic field makes the solitary structures more spiky.