Computing Bredon homology of groups

Abstract

We describe the basic ingredients of a general computational framework for performing machine calculations in the cohomology of groups. This has been implemented in the GAP system for computational algebra and the paper is intended to aid those wishing to extend that implementation to their own needs.

1 Introduction

Explicit calculations play a role in the theoretical development of the cohomology of groups and it is becoming more common for such calculations to be derived with the aid of a computer. In this paper we describe a basic framework for performing machine computations in the cohomology of groups. This has been implemented in the HAP package [16] for the GAP system for computational algebra [21] and the paper is intended to aid those wishing to extend that implementation to their own needs. The framework is extremely simple, involving just two ingredients: (i) a data type for a computer representation of Bredon modules that permits the easy implementation and easy combination of a range of homological algorithms; (ii) an emphasis on explicit homotopies as a means of translating non-constructive homological proofs into constructive homological algorithms. The paper is thus no more than a description of a single data type reflecting a particular choice of approach—the explicit homotopy approach—to implementing homological algorithms.

Given an implementation of our Bredon module data type it is a triviality to extract the corresponding Bredon homology. We view the standard Eilenberg–MacLane homology of a group as a special instance of Bredon homology. The data type has been used in [3, 11, 12, 19, 25] to calculate the low dimensional integral group homology $H_n(G,\mathbb Z)$ of groups such as $PSL_4(\mathbb Z)$, $M_{24}$, $SL_2(\mathbb Z[1/6])$, various Artin groups and various Bieberbach groups. In [17] the data type is used to provide examples of infinite families of finite p-groups G for which a single finite computation determines the mod-p homology $H_n(G,\mathbb Z_p)$ for all $n\ge 0$ and all G in a family. These papers describe the mathematics underlying the calculations and omit details of the data type. Other calculations in the literature can also be recovered using the data type. We are grateful to Alexander Rahm and Rubén Sánchez-García for contributing to the HAP package implementations of the data type that allow package users to recover calculations on the Bredon homology of a group G with coefficients in the complex representation ring, for G equal to $SL_3(\mathbb Z)$ [32] and G equal to various Bianchi groups [26] and Coxeter groups [28, 31]. We are grateful to Sebastian Schönnenbeck for contributing further implementations for Bianchi groups [33]. We are grateful to Mathieu Dutour-Sikirić for contributing implementations for groups such as $PSL(3,\mathbb {Z}[i]), PSL(3,\mathcal {O}_{Eis})$ with $\mathcal {O}_{Eis}$ the Eisenstein integers, $PSL(4,\mathbb {Z}), Sp(4,Z)$. The first author has contributed an implementation of the data type for calculating Bredon homology of crystallographic groups.

The paper is structured as follows. In Sect. 2 we indicate more clearly the kind of homological computations covered by our computational framework. These include standard Eilenberg-MacLane homology of a group G with coefficients in a finitely generated $\mathbb ZG$-module, as well as Bredon homology of the classifying space for proper actions $\underline{E}G$ with coefficients in a Bredon module such as the complex representation ring or the Burnside ring. In Sect. 3 we recall some basic definitions from the cohomology of groups. In Sect. 4 we describe our data type for representing Bredon modules; this incorporates a data type for representing rigid G-CW spaces. In Sect. 5 we review some implementations of this Bredon module data type that are currently available in HAP. In Sect. 6 we summarize the role of explicit homotopies in constructive homological algebra. Section 7 details methods for rigidifying G-CW spaces so that they can be used in implementations of the Bredon module data type.

2 Some typical homological computations

We use the term G -CW space to mean a CW space X on which a discrete group G acts in such a way that the action induces a permutation of the cells of X. We say the space is rigid if each element in the stabilizer of any cell fixes the cell pointwise. (Our terminology differs slightly from standard usage where rigidity is required of all G-CW spaces.) A family of subgroups of G is any collection $\mathcal{F}$ of subgroups of G that is closed under conjugation and taking subgroups. Thus $H\in \mathcal F$ implies that $gHg^{-1}\in \mathcal F$ for all $g\in G$ and that all subgroups of H are in $\mathcal F$. We say that a G-CW space X is an $\mathcal F$ -space if it is rigid and for each cell $e\subset X$ the stabilizer group $Stab_G(e) =\{g\in G~|~{^ge}=e\}$ belongs to $\mathcal F$. By a morphism $\phi :X\rightarrow Y$ between two G-CW spaces we mean a cellular map satisfying $\phi (^gx)={^g\phi (x)}$ for $g\in G, x\in X$. For any subgroup $H\subseteq G$ the set of left cosets G / H can be viewed as a discrete G-CW space. For a family $\mathcal{F}$ of subgroups of G let $\mathcal{O_F}$ denote the category with one object G / H for each subgroup $H\in \mathcal F$ and with maps $\phi :G/H \rightarrow G/H'$ the morphisms of G-CW spaces. A map $\phi$ is determined by its image $\phi (H) = gH'$ and we have $g^{-1}Hg\subseteq H'$. The map $\phi$ is completely determined by g, and any $g\in G$ determines such a map. A functor $\mathcal{M}:\mathcal{O_F}\rightarrow {\mathcal {AB}}$ to the category of abelian groups is called a left Bredon module. Given any $\mathcal{F}$-space X and left Bredon module $\mathcal{M}:\mathcal{O_F}\rightarrow {\mathcal {AB}}$ one can define the Bredon homology groups $H_n^\mathcal{F}(X,\mathcal{M})$ for $n\ge 0$. The definition is recalled in Sect. 3 along with that of Bredon cohomology.

Our aim is to present a data type for representing Bredon modules in a way that facilitates the computation of Bredon homology and cohomology of a range of G-CW spaces. The data type is implemented in the HAP package for GAP and the following GAP commands illustrate how it can be used in the computation of $H_1^\mathcal{F}(K,\mathcal{B})=0$ for K the Quillen simplicial complex at the prime $p=3$ for the symmetric group of degree 9 and $\mathcal{B}$ the Burnside module; the definitions of this K and $\mathcal{B}$ are recalled in Sect. 3. The cellular chain complex $R_*=C_*(K)$ is used in the computation.

This computation is essentially just a routine transcription of classical mathematical definitions into computational data types, but may be of interest since the computation of Bredon cohomology of finite simplicial complexes K constructed from families of subgroups of G has recently been shown in [23] to be relevant to the gluing problem in certain fusion systems.

In Sect. 5 we review a selection of practical algorithms for constructing models of two particular $\mathcal F$-spaces EG and $\underline{E}G$. For the definition of EG and $\underline{E}G$ we say that an $\mathcal F$-space X is a model for $E_\mathcal{F}$ if the G-CW space $X^H =\{x\in X~|~{^hx}=x \mathrm{~for~all~} h\in H\}$ is contractible for each $H\in \mathcal F$ and empty for each subgroup $H\notin \mathcal F$. In the special case when the family $\mathcal{F}=\{1\}$ consists of just the identity subgroup we say that such a model is a total space for G and denote it by EG. Thus a total space EG is any contractible CW space on which G acts freely by permuting cells; the quotient space $BG=EG/ G$ obtained from an EG by identifying x with $^gx$ for $x\in EG, g\in G$ is said to be a classifying space for G. In the special case when the family $\mathcal{F}={\mathfrak {F}in}$ consists of all finite subgroups of G we say that a model for $E_\mathcal{F}$ is a proper total space for G and denote it by $\underline{E}G$. Some authors refer to $\underline{E}G$ as a classifying space for proper actions [24]. If G is torsion free then a proper total space $\underline{E}G$ is the same thing as a total space EG.

If $\mathcal{F} = \{1\}$ then a left Bredon module $\mathcal{M}$ is just a $\mathbb ZG$-module and the classical homology (also known as the Eilenberg-MacLane homology) of the group G with coefficients in $\mathcal{M}$ can be defined as $H_n(G,\mathcal{M})=H_n^\mathcal{F}(EG,\mathcal{M})$. For $\mathcal{F}={\mathfrak {F}in}$ there is a well-defined analogue $\underline{H}_n(G,\mathcal{M})=H_n^\mathcal{F}(\underline{E}G,\mathcal{M})$ which we refer to as the Bredon homology of G. In order to implement these two homology definitions on a computer we need a practical method for constructing finitely many dimensions of the spaces EG and $\underline{E}G$ on a computer. One approach is to take some theoretical descriptions of the spaces and simply transcribe them into a suitable data type. The following GAP commands illustrate this approach to computing the Eilenberg-MacLane homology with integer coefficients $H_2(SL_3(\mathbb Z),\mathbb Z)= \mathbb Z_2\oplus \mathbb Z_2$ and the Bredon homology $\underline{H}_0(SL_3(\mathbb Z),\mathcal{R}) =\mathbb Z^8$ with coefficients in the complex representation ring $\mathcal R$. The definition of the Bredon module $\mathcal R$ is recalled in Sect. 3.

The computation involves the cellular chain complex $R_*=C_*(X)$ of the model X for $\underline{E}SL_3(\mathbb Z)$ constructed by Soulé [34] and used in [32]. The algebraic structure of $C_*(X)$ has been transcribed into a suitable data type and stored in GAP. For the Eilenberg–MacLane homology the computation uses an algorithmic procedure to construct a free $\mathbb ZSL_3(\mathbb Z)$-resolution $F_*$ from $C_*(X)$. A spectral sequence argument [32] shows that in examples such as this, with Bredon homology $\underline{H}_n(G,\mathcal{R})$ trivial for $n\ge 2$, there is an isomorphism $K_n^G(\underline{E}G)\cong \underline{H}_n(G,\mathcal{R})$, $n=0,1$, where $K_n^G(\underline{E}G)$ denotes equivariant K-theory. Interest in Bredon homology in this context stems from the Baum–Connes conjecture [5] asserting that $K_n^G(\underline{E}G)$ should be isomorphic to the K-theory of the reduced $C^*$-algebra of G.

A second approach to computing with EG and $\underline{E}G$ is to design and implement algorithms that input generators (and possibly other group-theoretic information) for G and return the low-dimensional algebraic structure of $C_*(EG)$ and $C_*(\underline{E}G)$. The following GAP commands illustrate this approach to computing $H_2(G,\mathbb Z)=\mathbb Z_2\oplus \mathbb Z_2$ and $\underline{H}_2(G,\mathcal{B})=\mathbb Z^4 \oplus \mathbb Z_2$ for G the Euclidean crystallographic group arising as the 32nd group of dimension 3 in the Cryst [14] library of crystallographic groups available as part of the GAP system.

The algorithm for constructing $\underline{E}G$ in this example is new and is detailed in Sect. 7.2.

3 Review of Bredon homology

Fix a group G, a family $\mathcal F$ of subgroups of G, an $\mathcal F$-space X, and a left Bredon module $\mathcal{M}:\mathcal{O_F}\rightarrow {\mathcal {AB}}$. Let $\{e^n_\alpha \}$ denote a minimal set of representatives of the G-orbits of n-cells in X. Write $S^n_\alpha =Stab_G(e^n_\alpha )\in \mathcal F$. The terms in the cellular chain complex $C_*(X)$ have the form

$$\begin{aligned} C_n(X)\ \cong \ \bigoplus _{\{e^n_\alpha \}} \mathbb ZG \otimes _{S^n_\alpha } \mathbb Z \ \cong \ \bigoplus _{\{e^n_\alpha \}} \mathbb Z[G/S^n_\alpha ]\ . \end{aligned}$$

We set

$$\begin{aligned} M_n=\bigoplus _{\{e^n_\alpha \}} \mathcal{M}(G/S^n_\alpha ) \end{aligned}$$

and note that the boundary homomorphism $\partial _n:C_n(X) \rightarrow C_{n-1}(X)$ induces a homomorphism of abelian groups $d_n:M_n \rightarrow M_{n-1}$ for which $M_*= (M_n,d_n)_{n\ge 0}$ is a chain complex. If $\partial _n(e^n_\alpha )= \sum _{\{e^{n-1}_\beta \}} m_\beta g_\beta e^{n-1}_\beta$, with $m_\beta \in \mathbb Z, g_\beta \in G$, then the inclusions $g_\beta ^{-1}S^{n}_\alpha g_\beta \hookrightarrow S^{n-1}_\beta$ induce homomorphisms $\iota ^n_{\alpha ,\beta }:\mathcal{M}(G/S^{n}_\alpha ) \rightarrow \mathcal{M}(G/S^{n-1}_\beta )$. The homomorphism $d_n:M_n\rightarrow M_{n-1}$ is $d_n =\sum _{\{e^{n-1}_\beta \}} m_\beta \iota ^n_{\alpha ,\beta }$.

Definition 1

The Bredon homology of X with coefficients in the Bredon module $\mathcal{M}$ is defined as

$$\begin{aligned} H_n^\mathcal{F}(X,\mathcal{M}) = H_n(M_*). \end{aligned}$$

The family $\mathcal F$ doesn’t play much of a role in this definition but it is useful to retain $\mathcal F$ in the notation.

The following example of an $\mathcal F$-space is among those implemented in [16].

Example 1

The order complex of a partially ordered set $\mathcal A$ is the simplicial complex $\Delta (\mathcal A)$ with vertex set $\mathcal A$ and with k-simplices the chains $A_0< A_1< \cdots < A_k$ of $k + 1$ distinct elements $A_i \in \mathcal A$. When $\mathcal A$ is a collection of subgroups of some group G which is closed under conjugation, $gA_ig^{-1} \in \mathcal A$ for all $A_i\in \mathcal A$ and $g\in G$, then conjugation induces an action of G on $\Delta (\mathcal{A})$. The simplicial complex $\Delta (\mathcal A)$ is a rigid G-CW space with respect to this action. When $\mathcal{A}=\mathcal{A}_p$ is the poset of all non-trivial elementary abelian p-subgroups of G the G-CW space $\Delta (\mathcal{A}_p)$ is called the Quillen complex of G at the prime p. This is an example of an $\mathcal{F}$-space for $\mathcal{F}$ the family of all subgroups of G.

The following three examples of left Bredon modules are implemented in [16].

Example 2

For any family $\mathcal F$ of subgroups of G, and any abelian group A, we have the constant Bredon module $A:\mathcal{O_F}\rightarrow {\mathcal {AB}}$ which sends each object G / H to the abelian group A and each morphism $\phi :G/H\rightarrow G/H'$ to the identity homomorphism $1:A \rightarrow A$. Of particular interest is the abelian group $A=\mathbb Z$ and the corresponding homology theories $H_n(G,\mathbb Z)$ and $\underline{H}_n(G,\mathbb Z)$.

Example 3

For a group G and $\mathcal{F}={\mathfrak {F}in}$ we define the complex representation ring to be the left Bredon module $\mathcal{R}:\mathcal{O_F}\rightarrow {\mathcal {AB}}$ that sends an object G / H to the vector space $R_{\mathbb C}(H)$ of complex representations of the finite group H. For a G-map $\phi :G/H\rightarrow G/H'$ we have $g^{-1}Hg \subset H'$ for some $g\in G$ and define $\mathcal{R}(\phi ):R_{\mathbb C}(H)=R_{\mathbb C}(g^{-1}Hg) \rightarrow R_{\mathbb C}(H')$ to be induction.

Example 4

For a group G and $\mathcal{F}={\mathfrak {F}in}$ we define the Burnside ring to be the left Bredon module $\mathcal{B}:\mathcal{O_F}\rightarrow {\mathcal {AB}}$ that sends an object G / H to the free abelian group BS(H) with isomorphism types of transitive H-sets as basis. For a G-map $\phi :G/H\rightarrow G/H'$ with $g^{-1}Hg \subset H'$, $g\in G$, we again define $\mathcal{B}(\phi ):BS(H) = BS(g^{-1}Hg) \rightarrow BS(H')$ to be induction.

Another readily implemented example for $\mathcal{F}={\mathfrak {F}in}$ is the left Bredon module that sends G / H to the integral homology group $H_n(H,\mathbb Z)$.

Definition 2

For a family $\mathcal F$ of subgroups of G and for a left Bredon module $\mathcal{M}$ we define the $\mathcal{F}$-Bredon homology of G to be

$$\begin{aligned} H_n^\mathcal{F}(G,\mathcal{M}) = H_n^\mathcal{F}(X,\mathcal{M}) \end{aligned}$$

where X is any model for $E_\mathcal{F}G$. It is readily shown [5] that this definition does not depend on the choice of model X and so we can write $H_n^\mathcal{F}(E_\mathcal{F}G,\mathcal{M})$ instead of $H_n^\mathcal{F}(X,\mathcal{M})$.

For $\mathcal{F}=\{1\}$ we write $H_n(G,\mathcal{M}) = H_n(E_\mathcal{F}G,\mathcal{M})$ and refer to this as the classical homology, or Eilenberg–MacLane homology, of G. For $\mathcal{F}={\mathfrak {F}in}$ we write $\underline{H}_n(G,\mathcal{M}) = H_n(E_\mathcal{F}G,\mathcal{M})$ and refer to this as the Bredon homology of G.

A right Bredon module is a contravariant functor $\mathcal{M}:\mathcal{O}_\mathcal{F} \rightarrow {\mathcal AB}$. Such modules give rise to the definition of Bredon cohomology in the obvious way.

4 A data type for Bredon modules

We now specify data types for: (i) chain complexes and maps, (ii) cellular chain complexes and maps of $\mathcal F$-spaces, and (iii) Bredon modules. These are used in [16] to implement the examples of the preceding section.

The GAP language supports a form of object oriented programming which we use in our specification. We say that an object X is a component object if it is a collection of components X.component_1, X.component_2,....

Data Type 41 Let $C_*: \cdots \rightarrow C_j \rightarrow C_{j-1} \rightarrow \cdots \rightarrow C_0 \rightarrow 0$ be a chain complex of free modules over a ring $\mathbb K$. Suppose that all modules in negative degrees are zero, and suppose that ordered bases for modules in non-negative degrees have been specified. We represent this data as a component object C with the following components:

• C!.dimension(k) is a function which enters an integer $k\ge 0$ and returns the rank of the free module $C_k$. (This rank could be infinite.)

• C!.boundary(k,j) is a function which enters integers $k\ge 0$, $1 \le j \le \mathrm{rank}_{\mathbb K}(C_k)$ and returns the image in $C_{k-1}$ of the jth free generator of $C_k$. Elements in $C_{k-1}$ are represented as vectors (i.e. lists) over $\mathbb K$ of length equal to the rank of $C_{k-1}$.

• C!.properties is a list of properties of the complex, each property stored as a pair such as $[``characteristic'',0]$.

The associated function IsHAPChainComplex(C) returns the boolean true when C is of this data type. A morphism $f_*:C_*\rightarrow C'_*$ of such chain complexes over $\mathbb K$ is represented as a component object f with the following components:

• f.source is a representation of the chain complex $C_*$.

• f.target is a representation of the chain complex $C'_*$.

• f.fun(k,j) is a function which inputs integers k, $1 \le j \le \mathrm{rank}_{\mathbb K}(C_k)$ and returns the image in $C'_{k}$ of the jth free generator of $C_k$ under the homomorphism $f_k$.

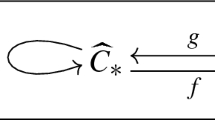
The boundary homomorphisms in a chain complex are represented by functions, rather than by matrix arrays, to allow for lazy evaluation: an implementation can opt to compute boundaries of generators only at the point when they are required. To illustrate why one might wish to compute in this way, consider some classifying space $BG=EG/G$ of a group G which has been constructed with only finitely many cells in each degree. Then standard Smith Normal Form algorithms can be used to compute the homology group $H_n(G,\mathbb Z) =H_n(C_*(BG))$. Given a homomorphism $\phi :G\rightarrow G'$ of such groups we may wish to compute the induced homomorphism $H_n(\phi ):H_n(C_*(BG)) \rightarrow H_n(C_*(BG'))$. For this we would first need to compute an induced chain map $\phi _*:C_*(BG) \rightarrow C_*(BG')$. One approach is to consider the bar chain complex $C_*(B^\mathrm{bar}G)$ where $B^\mathrm{bar}G=\mathrm{Nerve}(G)$ is the simplicial nerve of the category G. There is a readily implemented functorial chain map $\phi ^\mathrm{bar}_*:C_*(B^\mathrm{bar}G) \rightarrow C_*(B^\mathrm{bar}G')$. One could try to compute $\phi _*$ as a composite

$$\begin{aligned}C_*(BG) \mathop {\rightarrow }\limits ^{\alpha } C_*(B^\mathrm{bar}G) \mathop {\rightarrow }\limits ^{\phi ^\mathrm{bar}_*} C_*(B^\mathrm{bar}G') \mathop {\rightarrow }\limits ^{\beta } C_*(BG')\end{aligned}$$

in which $\alpha$ and $\beta$ are chain equivalences. The chain complexes $C_*(B^\mathrm{bar}G)$ and $C_*(B^\mathrm{bar}G')$ will have an extremely large number of free generators in each degree, and for infinite groups will have infinitely many free generators in each degree. For this reason these chain complexes would need to be implemented using lazy evaluation. This approach to induced homology homomorphisms is one of the methods implemented in [16] and relies on the availability of explicitly defined contracting homotopies on the universal covers $\widetilde{B(G)} =EG$ and $\widetilde{\mathrm{Nerve}(G)}$ as explained in Sect. 6.

Data Type 42 Let $R_*=C_*(X)$ be the cellular chain complex of a G-CW space X. The space X need not be rigid. Each chain group $R_k=C_k(X)$ is free abelian with $\mathbb Z$-basis corresponding to the k-cells of X. We suppose that some ordering of the k-cells has been chosen and fixed, and that for each k-cell some orientation has also been chosen and fixed. Each $R_k$ is also a $\mathbb ZG$-module. The action of G permutes the free abelian generators, and the boundary homomorphisms are G-equivariant. We suppose that some minimal set $\{e^k_j\}$ of representatives of G-orbits of the k-cells has been chosen. We represent $R_*$ as a component object R with the following components.

• R!.dimension(k) is a function which inputs an integer $k\ge 0$ and returns the cardinality $r_k$ of the set $\{e^k_j\}$.

• R!.elts is a list of some elements of G. Not all elements of G need to be in this list, and a given element of G may appear several times in the list. Furthermore, elements of G can be appended to the list during the course of a computation. If G is a small finite group then typically the list would be a full listing of all the elements of G. (This approach to referring to elements allows for: (i) certain computations with groups, such as finitely presented groups, where no algorithm for solving the word problem is available; (ii) easy implementation of topological constructions that combine G-equivariant chain complexes involving groups G represented in different ways, such as matrix groups, finitely presented groups, permutation groups, ....)

• R!.boundary(k,j) is a function which inputs integers $k\ge 0$, $1\le j\le r_k$ and returns the image in $R_{k-1}$ of the jth $\mathbb ZG$-generator $e^k_j$ of the $\mathbb ZG$-module $R_k$. An element $w\in R_{k-1}$ can be expressed, in a non-unique way, as a sum

  $$\begin{aligned} w= \epsilon _1g_{1}e^{k-1}_{i_1} + \epsilon _2g_{2}e^{k-1}_{i_2} +\cdots + \epsilon _n g_{n}e^{k-1}_{i_n} \in R_{k-1},\quad (g_i\in G, \epsilon _i=\pm 1). \end{aligned}$$

  We represent this sum as a list of integer pairs

  $$\begin{aligned} w=[ [\epsilon _1i_1,i'_1], [\epsilon _2i_2,i'_2], \ldots , [\epsilon _n i_n,i'_n] ] \end{aligned}$$

  with $\textsf {R!.elts}[i'_m]=g_m$ for $m=1,2,\ldots ,n$.

• R!.stabilizer(k,j) is a function which inputs integers $k\ge 0$, $1\le j\le r_k$ and returns the subgroup of G consisting of those elements that fix, up to sign, the jth $\mathbb ZG$-generator $e^k_j\in R_k$.

• R!.action(k,j,i) is a function which inputs integers $k\ge 0$, $1\le j\le r_k$, $1\le i \le \ell$ where $\ell$ is the current length of the list R!.elts and returns $\pm 1$ according to how the group element R!.elts[i] acts on the orientation of the jth $\mathbb ZG$-generator $e^k_j\in R_k$.

• R!.group is the GAP representation of the group G. This representation could be, for instance, as a finitely presented group, or as a polycyclically presented group, or as a permutation group, or as a matrix group and so forth.

• R!.homotopy is, in many cases, the boolean variable fail. In cases where the space X is contractible, and where an explicit contracting chain homotopy $h_k:C_k(X) \rightarrow C_{k+1}(X)$ ($k\ge 0$) is available, R!.homotopy(k,[j,i]) is a function which inputs integers $k\ge 0$, $1 \le j\le r_k$, $1\le i\le \ell$. This function returns the image $h( g e^k_j)\in R_{k+1}$ for $g=$ R!.elts[i] $\in G$. The elements of the form $g e^k_{j}$ freely generate $R_k$ as an abelian group and so the value of $h_k(w)$ can be evaluated for arbitrary elements $w\in R_k$. (The role of contracting homotopies in computational homological algebra is explained in Sect. 6.)

• R!.properties is a list of properties of the complex, each property stored as a pair such as [“characteristic”, 0].

The associated function IsHAPGChainComplex(R) returns the boolean true when R is of this data type.

Let $f:X\rightarrow X'$ be a cellular map from a G-CW space X to a $G'$-CW space Y, and let $f_\#:G\rightarrow G'$ be a group homomorphism such that $f(gx) =(f_\#g)f(x)$. The induced $f_\#$-equivariant chain map $f_*:R_*=C_*X \rightarrow R'_*=C_*X'$ is represent as a component object f with the following components:

• f.source is a representation of the G-chain complex $R_*$.

• f.target is a representation of the $G'$-chain complex $R'_*$.

• f.fun(k,w) is a function which inputs an integer $k\ge 0$ and list w representing a word $w\in R_k$, and returns a list representing the image $f_k(w)\in R'_{k}$.

Data Type 42 has evolved over several years of development of the HAP package. A realization of the importance of storing homotopies dates back to conversations with Ronnie Brown and Larry Lambe some twenty years ago regarding the Homological Perturbation Lemma [7]. The choice of method for storing group actions is based on discussions with Mathieu Dutour-Sikirić and was first used in [12].

It is useful to record certain mathematical properties that may be known to hold for a given instance R of Data Type 42. In particular, the function IsHAPNonFreeResolution(R) returns the boolean true when R is known to correspond to an acyclic $\mathbb ZG$-chain complex $R_*$ with $H_0(R_*)\cong \mathbb Z$; we refer to such an $R_*$ as a non-free resolution or non-free $\mathbb ZG$ -resolution. The function IsHAPResolution(R) returns the boolean true when R is known to correspond to an acyclic and $\mathbb ZG$-free chain complex $R_*$ with $H_0(R_*)\cong \mathbb Z$; we refer to such an $R_*$ as a free resolution or free $\mathbb ZG$ -resolution. In this latter case the components R!.stabilizer(k,j) and R!.action(k,j,g) may be omitted. Note that our terminology allows for a non-free resolution to be a free resolution.

It is possible to algorithmically test whether certain properties hold for a given instance R of data type 42. In particular, let us say that the $\mathbb ZG$-chain complex $R_*=C_*(X)$ described in 42 is rigid if the following property holds for each $\mathbb ZG$-generator $e^k_\alpha \in R_k$, $k\ge 1$.

Chain rigidity property Suppose $\partial _k(e^k_\alpha )= \sum _{\beta \in I} m_\beta g_\beta e^{k-1}_\beta$, where the indices $\beta$ are distinct and the integers $m_\beta$ are non-zero for $\beta \in I$. Then $Stab_G(e_\alpha ^{k}) \le Stab_G(g_\beta e_\beta ^{k-1})$ for $\beta \in I$ and, at the chain level, $ge^k_\alpha \ne -e^k_\alpha$ for $g\in Stab_G(e_\alpha ^{k})$.

The function IsRigid(R) returns the boolean true if the chain rigidity property holds for all $e^k_\alpha$, $k\ge 1$, and false otherwise.

The following is the main data type of the paper.

Data Type 43 A left Bredon module $\mathcal{M}:\mathcal{O_F}\rightarrow {\mathcal {AB}}$ is represented as a function M that inputs a rigid G-chain complex R with stabilizer groups in the family $\mathcal{F}$ (represented using Data Type 42) and returns a chain complex M(R) over $\mathbb Z$ (represented using Data Type 41).

By an implementation of Data Type 43 we actually mean an implementation M of 43 together with an implementation R of Data Type 42, since the former is redundant without the latter. Given implementations of M and R it is straightforward to compute the homology of the chain complex $\textsf {M}(\textsf {R})$ using the Smith Normal Form algorithm.

The HAP package currently contains implementations of the following Bredon functors M: tensor with the integers $-\otimes _{\mathbb ZG}\mathbb Z$; tensor with the integers modulo a prime $-\otimes _{\mathbb ZG}\mathbb Z/pZ$; tensor with a finitely generated $\mathbb ZG$-module $-\otimes _{\mathbb ZG}A$; the complex representation ring $\mathcal R$; and the Burnside ring $\mathcal B$.

The main implementations of rigid G-chain complexes R in HAP are of complexes that are (not necessarily free) $\mathbb ZG$-resolutions of the ring $\mathbb Z$.

5 Review of algorithms for resolutions

The HAP package includes implementations of a range of algorithms which input an integer $n\ge 0$ and information about a group G in some given class and, at least in principle, use the information to output in finite time the first $n+1$ terms of a free $\mathbb ZG$-resolution $R_*$ of $\mathbb Z$ with $R_k$ a finitely generated free $\mathbb ZG$-module in each degree $0\le k\le n$. For the purposes of this section, let us say that a class of groups is HAP-resolvable if HAP contains an implementation of such an algorithm that applies to all groups in the class.

The following classes of groups are HAP-resolvable (where references give details of the implemented resolutions/algorithms): finite groups [15]; finitely generated nilpotent groups and, more generally, any group G admitting a subnormal chain of subgroups $N_1 \le N_2 \le \cdots \le N_k=G$ where each quotient $N_{i+1}/N_i$ is HAP-resolvable [18]); Bieberbach groups [29]; crystallographic groups [1, 2, 29]; Coxeter groups [10, 18]; Artin groups for which the $K(\pi ,1)$ conjecture is known to hold [19, 30, 35]; a few finite simple groups such as the Mathieu groups [11]; $PSL_4(\mathbb Z)$ and a few related arithmetic groups [12]; $SL_2(\mathcal{O})$ and $GL_2(\mathcal{O})$ for a few rings $\mathcal{O}$ of integers in an imaginary quadratic field [27, 33]; $SL_2(\mathbb Z[1/m])$ for any integer $m\ge 1$ [3]; finite p-groups (yielding a minimal resolution over the field of p elements) [8]; graphs of HAP-resolvable groups; finite index subgroups of HAP-resolvable groups; direct products of HAP-resolvable groups.

Let us say that a class of groups is HAP-properly resolvable if HAP contains an implementation of an algorithm that inputs any integer $n\ge 0$ and group G in the class and, at least in principle, returns in finite time the first $n+1$ terms of a $\mathbb ZG$-resolution of the form $R_*=C_*(\underline{E}G)$ with $R_k$ finitely generated as a $\mathbb ZG$-module for each $0\le k\le n$.

For a finite group G one can take $\underline{E}G$ to be a single point, and for torsion free infinite groups G one can take $\underline{E}G =EG$ and $R_*$ to be any free $\mathbb ZG$-resolution of $\mathbb Z$. Thus explicit constructions of $\underline{E}G$ are of particular interest for infinite groups G with torsion. For any discrete group G one can take $\underline{E}G$ to be the simplicial complex with k-simplices all $k+1$-element subsets of G [24], though $R_k=C_k(\underline{E}G)$ will then not be finitely generated if G is infinite.

As a first approximation to $\underline{E}G$ we denote by $\underline{E}'G$ any G-CW space X such that $X^H =\{x\in X~|~{^hx}=x \mathrm{~for~all~} h\in H\}$ is contractible for each finite subgroup H in G. The important distinction between $\underline{E}'G$ and $\underline{E}G$ is that the latter is required to be rigid.

At present HAP contains implementations of algorithms for returning a $\mathbb ZG$-resolution $C_*(\underline{E}'G)$ for just two classes of groups: Coxeter groups [31]; crystallographic groups [1, 2, 29]. It also includes a resolution $C_*(\underline{E}'G)$ for a number of specific groups including: $G=SL_3(\mathbb Z)$ (obtained by transcribing data from [32]); $PGL_3(\mathbb Z[\mathbf{i}])$, $PSL_4(\mathbb Z)$, $Sp_4(\mathbb Z)$ (obtained by transcribing data from [13]); $GL_2({\mathcal O}_{-m})$ and $SL_2({\mathcal O}_{-m})$ for $m=1,2,3,5,6,7,10,11,13,14,$ 15, 17, 19, 21, 22, 23,  26, 43 with ${\mathcal O}_{-m}$ the ring of integers in the field $\mathbb Q(\sqrt{-m})$ [33].

By subdividing cells it is often practical to convert a resolution $C_*(\underline{E}'G)$ into a rigid resolution $C_*(\underline{E}G)$. We discuss this in Sect. 7.

6 Homotopies and discrete vector fields

Various constructions in the cohomology of groups require the following element of choice.

$$\begin{aligned}&\hbox {Given a} \, \hbox {ZG-resolution} \,{\mathbb R_*}\, \hbox {and an element}\, x\in \ker (\partial _k :R_k \rightarrow R_{k-1})\nonumber \\&\quad \hbox {choose an element}\, \tilde{x}\in R_{k+1} \,\hbox {such that}\, \partial _{k+1}(\tilde{x}) = x. \end{aligned}$$

(1)

In order to translate such constructions into procedures that can be implemented on a computer one needs a method of performing (1) algorithmically. In particular, these comments apply to the construction of (co)homology homomorphisms induced by group homomorphisms, the construction of cup products and other cohomology operations, the construction of explicit cocycles, and various constructions that express a resolution for a group in terms of simpler resolutions for its subgroups and quotient groups.

It is sometimes possible to choose $\tilde{x}$ by solving a system of equations using elementary linear algebra or by using more sophisticated techniques from Gröbner basis theory. If the resolution $R_*$ is endowed with a contracting homotopy, i.e. a family of $\mathbb Z$-linear homomorphisms $h_k:R_k \rightarrow R_{k+1}$ satisfying

$$\begin{aligned} h_{k-1}\partial _k + \partial _{k+1}h_k =1 \end{aligned}$$

for $k\ge 0$ with $h_{-1}=0$, then one can very quickly solve (1) as follows.

$$\begin{aligned}&\hbox {Given a}\, \hbox {ZG-resolution}\, \mathbb R_*\,\hbox {and an element}\, x\in \ker (\partial _k :R_k \rightarrow R_{k-1})\, \hbox {then}\nonumber \\&\mathrm{the\, equation} \, \partial _{k+1}(\tilde{x}) = x \, \hbox {is satisfied by setting}\, \tilde{x} := h_k(x) \in R_{k+1}. \end{aligned}$$

(2)

The following notion can be useful in designing explicit contracting homotopies on cellular chain complexes of contractible CW spaces. Recall that a CW space X is said to be regular if the attaching map of each cell is a homeomorphism on its boundary.

Definition 3

A discrete vector field on a regular CW-space X is a collection of formal arrows $s \rightarrow t$ where

• 1. s, t are cells of X with $\dim (t) =\dim (s) +1$ and with s lying in the boundary of t. We say that s and t are involved in the arrow, that s is the source of the arrow, and that t is the target of the arrow.

• 2. any cell is involved in at most one arrow.

The term discrete vector field is due to Forman [20]. In an earlier work [22] Jones calls this concept a marking.

By a chain in a discrete vector field we mean a sequence of arrows

$$\begin{aligned} \ldots , s_1 \rightarrow t_1, s_2 \rightarrow t_2, s_3 \rightarrow t_3, \ldots \end{aligned}$$

where $s_{i+1}$ lies in the boundary of $t_i$ for each i. A chain is a circuit if it is of finite length with source $s_1$ of the initial arrow $s_1\rightarrow t_1$ lying in the boundary of the target $t_n$ of the final arrow $s_n\rightarrow t_n$. A discrete vector field is said to be admissible if it contains no circuits and no chains that extend infinitely to the right. A cell in X is said to be critical if it is not involved in any arrow.

Fig. 1

A contracting vector field on a tessellation of $X=\mathbb R^2$

We say that a discrete vector field on a regular CW space X is a contracting vector field if it is admissible and if it has only one critical cell, the critical cell being of dimension 0. Figure 1 illustrates a contracting vector field on a CW structure on the plane $X=\mathbb R^2$ arising from a tessellation of the plane by unit squares.

We identify the cells of X with free $\mathbb Z$-linear generators of the cellular chain complex $C_*(X)$, the k-cells corresponding to a basis of $C_k(X)$. We denote this basis by $B_k(X) \subset C_k(X)$. A discrete vector field on X then induces a partial pairing between the sets $B_k(X)$ and $B_{k+1}(X)$ for $k\ge 0$. A pairing involving $s\in B_k(X)$ and $t\in B_{k+1}(X)$ is again denoted by an arrow $s\rightarrow t$. For an element $w\in C_k(X)$ and basis element $e\in B_k(X)$ we write |w : e| for the coefficient of e in the unique expression of w as a linear combination of basis elements. The following proposition is routine to verify.

Proposition 1

A contracting vector field on a regular CW space X induces a contracting homotopy on the cellular chain complex $C_*(X)$. The $\mathbb Z$-linear homomorphisms $h_k:C_k(X) \rightarrow C_{k+1}(X)$ of the contracting homotopy are given on generators $e\in B_k(X)$ by the following recursive formulae.

$$\begin{aligned} h_k(e)= \left\{ \begin{array}{ll} 0, &{}\quad \textit{ if e is critical or if e is the target of an}\\ &{}\quad \mathrm{arrow.}\\ f+h_k(\partial _{k+1}f - e) &{}\quad \textit{ if e is the source of an arrow e }\rightarrow \textit{ f and}\\ &{}\quad |\partial f:e|=1.\\ -f-h_k(\partial _{k+1}f + e) &{}\quad \textit{ if e is the source of an arrow e }\rightarrow \textit{f and} \\ &{}\quad |\partial f:e|=-1. \end{array}\right. \end{aligned}$$

The recursion stops due to the admissibility of the discrete vector field.

Suppose now that the regular CW space X is a G-CW space for some group G. If X admits a contracting vector field then the chain complex $C_*(X)$ is a $\mathbb ZG$-resolution of $\mathbb Z$ and Proposition 1 provides formulae for a contracting homotopy on $C_*(X)$.

As an example, consider the finitely presented group $G=\langle a,b\ |\ aba=b\rangle$. An action of G on the plane $X=\mathbb R^2$ is defined by $a:\mathbb R^2 \rightarrow \mathbb R^2, (x,y) \mapsto (x+1,-y)$ and $b:\mathbb R^2 \rightarrow \mathbb R^2, (x,y) \mapsto (x,y+1)$. It is readily checked that this is a free action admitting the unit square $[0,1]\times [0,1]$ as a fundamental domain. The quotient X / G is the Klein bottle. The regular CW structure and contracting vector field illustrated in Fig. 1 provide a free $\mathbb ZG$-resolution $C_*(X)$ with explicit contracting homotopy. This resolution is implemented in HAP and can be used to recover the calculations $H^1(G,\mathbb Z)=\mathbb Z$, $H^2(G,\mathbb Z)=\mathbb Z_2$, $H^n(G,\mathbb Z)=0$ for $n\ge 3$. Moreover, the contracting homotopy on $C_*(X)$ and the standard contracting homotopy on the bar resolution $C_*(\widetilde{\mathrm{Nerve}(G)})$ are implemented and can be used to construct chain equivalences

$$\begin{aligned} \phi _*:C_*(X)\otimes _{\mathbb ZG}\mathbb Z \rightleftarrows C_*(\mathrm{Nerve}(G)):\psi _*\end{aligned}$$

between a finitely generated chain complex and a chain complex that is infinitely generated in each degree. The larger chain complex is of interest because it is functorial and thus good for theoretical descriptions of certain constructions; the smaller chain complex is of interest because its homology is quickly calculated using the Smith Normal Form algorithm. Section 7.2 contains an explanation of how this example extends to certain other crystallographic groups.

7 Rigidification of G-CW spaces

The cellular structure of a regular CW space is captured, up to homotopy of attaching maps, by the cellular chain complex $C_*X$.

For any regular CW space X one defines sd(X) to be the simplicial complex with one vertex for each cell in X, and with one k-simplex for each sequence $e^0 , e^1 , \ldots , e^k$ of cells of X with $e^i$ of dimension i for $0\le i\le k$ and with $e^{i-1}$ in the boundary of $e^i$ for $1\le i\le k$. The geometric realization |sd(X)| is called the barycentric subdivision of X.

Any regular CW space X is homeomorphic to the geometric realization |sd(X)| of its barycentric subdivision. If X is a G-CW space then the action of G on X induces an action of G on |sd(X)|, and the latter action is clearly rigid. We thus have the following computationally useful result.

Lemma 1

Let X be a G-CW space with regular cell structure. Then the homeomorphic space |sd(X)| is a rigid G-CW space.

The following GAP commands apply barycentric subdivision to a non-rigid contractible G-CW space X for the group $G=SL_2({\mathcal O_{-3}})$. The 2-dimensional space X is obtained from [27, 33] and the subdivided space sd(X) is used to compute the Bredon homology

$$\begin{aligned} \underline{H}_0( SL_2( {\mathcal O_{-3}} ), {\mathcal R}) = \mathbb Z_2 \oplus \mathbb Z^9 , \end{aligned}$$

$$\begin{aligned} \underline{H}_1(SL_2({\mathcal O_{-3}} ), {\mathcal R}) = \mathbb Z \end{aligned}$$

with coefficients in the complex representation ring $\mathcal R$. The analogous Bredon homology for $PSL_2({\mathcal O_{-3}})$ has been calculated in [26] using the same space X.

7.1 Coxeter groups

A Coxeter matrix is a symmetric $n\times n$ matrix whose entries m(i, j) are either positive integers or the symbol $\infty$, with $m(i,j)=1$ if and only if $i=j$. Such a matrix is represented by an n-vertex labelled graph D (called a Coxeter graph) with edge joining vertices i and j if and only if $m(i,j)\ge 3$; the edge is labelled by m(i, j). The Coxeter group $W_D$ is defined to be the group generated by the set of symbols $S=\{x_1,\ldots , x_n\}$ subject to relations $x_i^2=1$ and $(x_i x_j)_{m(i,j)} = (x_j x_i)_{m(i,j)}$ for all $i\ne j$, where $(xy)_m$ denotes the word $xyxyx\ldots$ of length m. There is a faithful matrix representation $\rho :W_D \rightarrow GL_n(\mathbb R)$ obtained by constructing a vector space V over $\mathbb R$ with basis $\{\alpha _i\}_{x_i\in S}$ and inner product

$$\begin{aligned} \langle \alpha _i, \alpha _j\rangle = -\cos (\pi /m_{ij}) \end{aligned}$$

where we interpret $\cos (\pi /\infty )=1$. The representation $\rho$ is defined on generators $x_i\in S$ by letting $\rho (x_i)$ be the matrix of the linear map

$$\begin{aligned} V\rightarrow V, v\mapsto v - 2\langle \alpha _i,v\rangle \alpha _i . \end{aligned}$$

Assume for the moment that the Coxeter group $W_D$ is finite. The representation $\rho$ realizes $W_D$ as a group of orthogonal transformations of $\mathbb R^n$ with generators $\rho (x_i)$ equal to reflections [9]. For convenience we identify $W_D=\rho (W_D)$ and $x_i=\rho (x_i)$. Let $\mathcal{A}$ be the set of hyperplanes corresponding to all the reflections in $W_D$. For any point v in $\mathbb R^n{\setminus }\mathcal{A}$ we denote by $P_D$ the convex hull of the orbit of v under the action of $W_D$. The face lattice of the n-dimensional convex polytope $P_D$ depends only on the graph D. (To see this, first note that the vertices of $P_D$ are the points $g\cdot v$ for $g\in W_D$ and that there is an edge between $g\cdot v$ and $g'\cdot v$ if and only if $g^{-1}g' \in S$. Thus the combinatorial type of the 1-skeleton of $P_D$ does not depend on the choice of point v. Furthermore, each vertex of the n-dimensional polytope $P_D$ is incident with precisely n edges; hence $P_D$ is simple and the face lattice of the polytope is determined by the combinatorial type of the 1-skeleton [6].) The polytope $P_D$ is a G-CW space for $G=W_D$. The contractible simplicial space $|sd(P_D)|$ is called the Davis complex for the finite group $G=W_D$.

To define the Davis complex for an arbitrary Coxeter group $W_D$ we first consider the Cayley graph $\Gamma _D$ consisting of one vertex for each $g\in W_D$ and one undirected edge connecting the pair of vertices $\{g,gx\}$ for each $g\in W_D$ and $x\in S$. We can consider any subset of generators $T\subset S$ that generates a finite subgroup $\langle T\rangle \le W_D$. This subgroup can be shown to be a Coxeter group $W_{D^T}=\langle T\rangle$ where $D^T$ is the full subgraph of D on those vertices corresponding to generators in T. The 1-skeleton of the convex polytope $P_{D^T}$ can be identified with the Cayley graph $\Gamma _{D^T}$. We view $\Gamma _{D^T}$ as a full subgraph of $\Gamma _D$. For each coset $gW_{D^T}$ in $W_D$ there is a corresponding subgraph $g\Gamma _{D^T} \subset \Gamma _D$. We take $X_D$ to be the union of the graph $\Gamma _D$ with the polytopes $gP_{D^T}$ where T ranges over all maximal subsets $T\subset S$ that generate a finite subgroup, and g ranges over a set of coset representative for $W_{D^T}$, and where any two polytope faces with identical 1-skeleta in $\Gamma _D$ are identified. The space $X_D$ is a G-CW space for $G=W_D$ and is known to be a model for $\underline{E}'G$ [9]. The contractible simplicial space $|sd(X_D)|$ is called the Davis complex for G and is a model for $\underline{E}G$.

The following GAP commands use the data types of Sect. 3 to compute the non-rigid G-CW space $X_D$ for the infinite Coxeter group $G=W_D$ corresponding to the diagram D of Fig. 2. The figure follows convention in omitting to print the number 3 on those edges of D labelled by $m(i,j)=3$. The $\mathbb ZG$-chain complex $R_*=C_*(X_D)$ is converted to a free $\mathbb ZG$-resolution $F_*$ and used to compute $H_2(W_D,\mathbb Z)= \mathbb Z_2 \oplus \mathbb Z_2 \oplus \mathbb Z_2$. Barycentric subdivision could be applied to $R_*$ to obtain the rigid chain complex $C_*=C_*(|sd(X_D)|)$ from which the Bredon homology group $\underline{H}_0(W_D,\mathcal{R})= \mathbb Z^{21}$ with coefficients in the complex representation ring is computed. The GAP session instead uses the implementation [28] to compute $C_*$ directly from D.

Fig. 2

Coxeter graph of an infinite Coxeter group W$_\mathrm{D}$

7.2 Cubical crystallographic groups

In [1, 2] a procedure is given which inputs an n-dimensional crystallographic group G and attempts to return a G-CW structure on $\mathbb R^n$ with just one orbit of n-dimensional cells for which a representative n-cell has the CW structure of an n-cube $I^n$. To be precise, here $I=[0,1]$ is understood to have the CW structure involving two 0-cells and one 1-cell, and the n-cube $I^n$ has the product CW structure. We refer to such a G-CW structure on $\mathbb R^n$ as a cubical G -CW space. The procedure succeeds on 12 of the 17 two-dimensional crystallographic groups; it succeeds on 114 of the 219 three-dimensional crystallographic groups; it succeeds on 1996 of the 4783 four-dimensional crystallographic groups. When the procedure succeeds the n-dimensional analogue of the contracting vector field of Fig. 1 can be used to implement a contracting homotopy on $C_*(\mathbb R^n)$. In many cases where the procedure fails one can prove that no cubical G-CW structure exists on $\mathbb R^n$.

The procedure begins by constructing a cubical T-CW structure on $\mathbb R^n$ for the translation subgroup $T\le G$. This can always be done. The procedure then considers the order |G / T| of the (finite) point group and tries to decompose a representative cubical n-cell for T into |G / T| or fewer smaller cubical n-cells such that the smaller n-cells form a G-CW structure on $\mathbb R^n$.

In some cases where the procedure succeeds the resulting cubical G-CW space is rigid and can be used as a model for $\underline{E}G$. In other cases where the procedure succeeds the resulting space is non-rigid and thus a model only for $\underline{E}'G$. A problem with using barycentric subdivision $\underline{E}G=|sd(\underline{E}'G)|$ is the prohibitively large number of cells involved for very modest dimensions n. A compromise is to use a cubical subdivision based on the CW space $J=[0,1]$ involving three 0-cells 0, 1 / 2, 1 and two 1-cells (0, 1 / 2), (1 / 2, 1). The product $J^n$ has just $5^n$ cells, compared to the $3^n$ cells in $I^n$. We denote by $bcsd(\underline{E}'G)$ the resulting binary cubical subdivision of $\underline{E}'G$. This subdivision will not always be rigid, but in many cases it is.

The following GAP code constructs $R_*=C_*(\underline{E}'G)$ for the second group of dimension 4 in the Cryst [14] library of crystallographic groups and determines that $R_*$ is not rigid. The commands then use binary cubical subdivision to construct a rigid resolution $S_*=C_*(bcsd(\underline{E}'G))$.

There are many ways to subdivide an n-cube into equally sized sub cubes. In general we can let $J_i=[0,1]$ be the CW space involving $m_i+1$ equally spaced 0-cells and $m_i$ equally long 1-cells. Then the product $J_1\times \cdots \times J_n$ is a CW structure on the n-cube involving $m_1\times \cdots \times m_n$ equally sized sub cubes. To apply this general cubical subdivision to a cubical space $\underline{E}'G$ for an n-dimensional crystallographic group G one can proceed as follows. First, represent G so that its translation subgroup $T\le G$ is generated by n orthogonal unit translations $x \mapsto x+t_1, \ldots , x\mapsto x+t_n\in T$. This can be done using a change of basis for $\mathbb R^n$ if necessary. Then consider the crystallographic group H generated by the generators of G together with the translations

$$\begin{aligned} x\mapsto x+\frac{1}{m_1}t_1,\ \ldots ,\ x\mapsto x+\frac{1}{m_n}t_n. \end{aligned}$$

The group G is a finite index subgroup of H of index $m_1\times \cdots \times m_n$. We can attempt to use the function CrystGcomplex to construct $R_*=C_*(\underline{E}'H)$. If the attempt is successful then $R_*$ can be viewed as a $\mathbb ZG$-resolution corresponding to a general cubical subdivision of a cubical G-CW structure on $\mathbb R^n$.

7.3 Simplification of barycentric subdivision

Two disadvantages to cubical subdivison are: it applies only to G-CW spaces whose cells are cubes; it is not guaranteed to yield a rigid space. A naive algorithm for converting an arbitrary G-CW space X with regular CW structure into a homotopy equivalent rigid G-CW space is to first construct the barycentric subdivision |sd(X)| and then to simplify the cell structure on |sd(X)| while preserving rigidity. We describe one method for simplifying the cell structure below. The method has not yet been fully implemented.

Let Y denote any rigid G-CW space X with regular CW structure. For instance, Y could be the barycentric subdivision |sd(X)|. Rigidity ensures that the quotient space $W=Y/G$ is a regular CW space. Let $\rho :Y\twoheadrightarrow W$ denote the quotient map. On any given cell $e\subset Y$ this quotient map restricts to a homeomorpism $e \rightarrow \rho (e)$. For any cell $f =\rho (e) \subset W$ the preimage $\rho ^{-1}(f)$ is $e \times G/Stab_G(e)$. By writing $G_f = Stab_G(e)$ we associate to each cell $f=\rho (e) \subset W$ a finite group $G_f\le G$.

We are interested in cases where W has only finitely many cells. Such a regular CW space is stored in [16] using the following data type.

Data Type 71 A finite regular CW space is represented as a component object W with the following components:

• W!.boundaries[n+1][k] is a list of integers $[t,a_1,\ldots ,a_t]$ recording that the $a_i$th cell of dimension $n-1$ lies in the boundary of the kth cell of dimension n.

• W!.coboundaries[n+1][k] is a list of integers $[t,a_1,\ldots ,a_t]$ recording that the kth cell of dimension n lies in the coboundary of the $a_i$th cell of dimension $n-1$.

• W!.nrCells(n) is a function returning the number of cells in dimension n.

• W!.properties is a list of properties of the complex, each property stored as a pair such as [“dimension”, 4].

The associated boolean valued function IsHAPRegularCWComplex(W) returns true when W is of this data type.

Our proposed simplification procedure for a regular CW space W is based on the observation that if W contains a k-cell $e^k$ lying in the boundary of precisely two $(k+1)$-cells $e^{k+1}_1, e^{k+1}_2$ with identical coboundaries then these three cells can be removed and replaced by a single cell of dimension $k+1$. The topological space W is unchanged; only its CW-structure changes. The resulting CW-structure will not in general be regular. However, it will be regular if the sets of cells $V_0, V_1, V_2$ lying in the boundaries of $e^k, e^{k+1}_1, e^{k+1}_2$ respectively are such that $V_1\cap V_2=V_0\cup \{e^k\}$. Thus by repeatedly replacing three cells by a single cell we will arrive at a potentially smaller CW space V; as topological spaces W and V will be identical.

As an illustration of this simplification procedure consider the 2-dimensional CW space S consisting of a $9\times 9$ array of unit squares with interior of the central square removed. Thus S is of the homotopy type of a circle. Now consider $W=S\times S$. The following GAP commands construct this regular CW space W and then applies an implementation of the simplification procedure to obtain a small regular CW space V. The space W involves 129,600 cells and the space V involves 224 cells.

Returning now to the rigid G-CW space Y and quotient map $\rho :Y\twoheadrightarrow W$ we note that if $G_f$ is the trivial group for all cells $f\subset W$ then $\rho$ is a covering map. In this case it is possible to lift the simplified CW-structure from W to Y and hence to $C_*Y$. In order to lift the simplified structure in the general case the simplification procedure needs one easily implemented refinement: only replace the three cells $e^k$, $e^{k+1}_1, e^{k+1}_2$ by a single cell if $G_{e^k} = G_{e^{k+1}_1} = G_{e^{k+1}_2}$.

Further algorithmic approaches to rigidification of G-CW spaces are developed in [4].