Rigidity of terminal simplices in persistent homology

Abstract

Given a filtration function on a finite simplicial complex, stability theorem of persistent homology states that the corresponding barcode is continuous with respect to changes in the filtration function. However, due to the discrete setting of simplicial complexes, the simplices terminating matched bars cannot change continuously for arbitrary perturbations of filtration functions. In this paper we provide a sufficient condition for rigidity of a terminal simplex, i.e., a condition on $\varepsilon >0$ implying that the terminal simplex of a homology class or a bar in persistent homology remains constant through $\varepsilon$-perturbations of filtration function. The condition for a homology class or a bar in dimension n depends only on the barcodes in dimensions n and $n+1$.

1 Introduction

Let K be a finite simplicial complex. A filtration function assigns to each simplex in K a unique real value, such that for each simplex, the values of its faces are lower than the value of the simplex. For each $r\in \mathbb {R}$ we define $K_r$ as the subcomplex of K consisting of all the simplices whose values are at most r. The collection of subcomplexes $\{K_r\}_{r\in \mathbb {R}}$ connected by the natural inclusions $K_r \rightarrow K_{r'}$ for each $r \le r'$ is called a filtration of K.

Persistent homology [9, 10] is a parameterized version of homology, with the parameter arising from a filtration function of a simplicial complex. It is obtained by applying a homology to a filtration, which yields a collection of homology groups $\{H_n(K_r)\}_{r\in \mathbb {R}}$ and inclusion-induced maps between them. One of its fundamental features as compared to homology is stability [8]. In particular, small perturbations of filtration functions induce small perturbations to the lifespans (along parameter r) of homology classes. However, the terminal simplices and the corresponding homology representatives of persistent homology cannot change continuously with arbitrary perturbations of filtration functions.

As simplices keep appearing in a filtration, non-trivial homology classes are either appearing (if the boundary of the added simplex is homologically trivial) or terminating. A simplex terminating a homology class (i.e., identifying the class with the trivial class) is called a terminal simplex. A corresponding homology representative, appearing at the first possible scale of the filtration, can be obtained from the boundary of the terminal simplex. As such, the terminal simplices allow us to localize and determine a geometric manifestation of homology terminating with the simplex. While finding a suitable homology representative in persistent homology is by itself challenging [7], the fact that small perturbations of a filtration function may yield completely different terminal simplices results in unstable representatives. There has been an attempt to circumvent this issue in practice [5].

In this paper we study the region of parameter $\varepsilon$ for which the terminal simplex of a persistent homology class $[\alpha ]$ of an injective filtration function f is rigid (i.e., constant) through $\varepsilon$-perturbations of f. Let [a, b) be the lifespan interval of an n-dimensional homology class $[\alpha ].$ Our main results are the following (under suitable assumptions).

• (1) Theorem 9: The terminal $(n+1)$-dimensional simplex of $[\alpha ]$ is rigid for $\varepsilon$-perturbations of f if

  • no class of $H_{n+1}$ is born on $(b,b+2\varepsilon ]$ and

  • no class of $H_n$ terminates on $[b-2\varepsilon ,b)$.

• (2) Theorem 11: A version of Theorem 9 for significant bars in the barcode. One of the main advantages of this result is that rigidity can be deduced solely from the barcode, without looking at the underlying filtration. (For details on barcodes of persistent homology see Preliminaries.)

Theorem 9 describes the two ways in which non-rigidity of a terminal simplex may occur: either via sequentially critical pair of simplices or independently critical pair of simplices. As a result, we are not only able to provide bounds on the region of rigidity, but also to locate a simplex ($\Delta _2$ in Theorem 9) appearing as a new terminal simplex for $[\alpha ]$ in the region of non-rigidity. For a demonstration within the context of persistence diagrams and barcodes (defined in Preliminaries) see Figs. 4 and 5 following Theorem 11.

On the other hand, our results contribute to a new interpretation of the structure of persistent homology. So far, persistent homology has been known to encode topological information of the space at small scales [11, 12, 20], intrinsic combinatorial structure of filtrations (such as Rips complexes) [1, 2], proximity of spaces via the stability result [18], geometric properties of spaces [19], shortest homology basis [17], spaces of contraction [16], filling radius [13], curvature [6], width of homology class [3], and more. Our results imply that, to a degree, persistent homology encodes rigidity of terminal simplices.

2 Preliminaries

We first introduce the setup of persistent homology, see [9] for details. Throughout this paper we assume that K is a finite simplicial complex and $f:K \rightarrow \mathbb {R}$ is an injective filtration function on K (if $\sigma$ is a face of $\tau$ then $f(\sigma )< f(\tau )$ for all $\sigma , \tau \in K$). As such f encodes an order on the simplices of K. For example, in the original persistent homology algorithm [10] such an order is used to arrange simplices in the boundary matrix. A simplex in K is (inclusion) maximal if it is not a proper face of any simplex.

Given two injective filtration functions f and g, we define the distance between them as

$$\begin{aligned} ||f-g||_\infty = \max _{\sigma \in K}|f(\sigma )-g(\sigma )|. \end{aligned}$$

Function g corresponds to some permutation of the ordering of simplices encoded by f.

The sublevel sets of f are subcomplexes of K defined for all $r\in \mathbb {R}$ as the pre-images $K_r^f = f^{-1}((-\infty , r])$. We can also define $K^f_\infty = f^{-1}((-\infty , \infty )) = K$. The notation $K^f$ denotes the standard sublevel filtration of K obtained through f, i.e., the collection of subcomplexes $\{K^f_r\}_{r\in \mathbb {R}}$ along with the natural inclusions

$$\begin{aligned} \iota _{q,r} :K^f_q \rightarrow K^f_r \end{aligned}$$

for all $q\le r$. Applying homology $H_n$ as a functor to a filtration we obtain a persistence module, i.e., a collection of vector spaces $\{H_n(K^f_r)\}_{r\in \mathbb {R}}$ along with the inclusions induced linear maps

$$\begin{aligned} \iota ^*_{q,r} :H_n(K^f_q) \rightarrow H_n(K^f_r) \end{aligned}$$

for all $q\le r$. All homology groups are assumed to be with coefficients in a fixed field $\mathbb {F}$ and therefore not mentioned in the notation for homology.

Given a non-trivial homology element $[\alpha ]\in H_n(K^f_r)$ for some r, we define:

• birth $a\in \mathbb {R}$ of $[\alpha ]$ as the infimum of levels $q \le r$, for which there exists $[\alpha _q]\in H_n(K^f_q)$ such that $\iota ^*_{q,r} [\alpha _q]=[\alpha ]$. We say that $[\alpha ]$ is born at a.

• termination scale $b\in \mathbb {R}\cup \{\infty \}$ of $[\alpha ]$ as the infimum of levels $q \ge r$, for which $\iota ^*_{r,q} [\alpha ]=0$, or $\infty$ if such levels do not exist. We say that $[\alpha ]$ is terminated at b.

Note that the termination scale is defined differently than death in [9]. Given our setup of sublevel complexes defined through preimages of closed intervals, the infima in the definition of birth and termination scale are always attained if finite. Since f is injective, at most one simplex is added at each level r. Consequently each $(n+1)$-simplex either gives birth to a non-trivial homology class in dimension $n+1$ or terminates a non-trivial homology class in dimension n.

We next state the stability theorem and introduce the corresponding notation, see [4] for details. Each persistence module obtained in our setting decomposes as a finite direct sum of interval modules $\mathbb {F}_{[a_i,b_i)}$, where persistence module $\mathbb {F}_{[a,b)}$ for $a<b$ is a collection of vector spaces $\{V_r\}_{r\in \mathbb {R}}$, with:

• $V_r=\mathbb {F}$ for $r\in [a,b)$,

• $V_r=0$ for $r\notin [a,b)$ and

• the bonding linear maps $V_r \rightarrow V_{r'}$ being identities for parameters $r<r'$ from [a, b).

Note that the type of endpoints of intervals (closed on the left, open on the right) is a consequence of our setup of a filtration, i.e., a sublevel filtration of an injective filtration function on a finite simplicial complex. The collection of intervals $[a_i,b_i)$ is called a barcode and a single interval in this setting is referred to as a bar.

Given injective filtration functions f and g and $n\in \{0,1,\ldots \}$, assume

$$\begin{aligned} \mathcal {M}=\{H_n(K^f_r)\}_{r\in \mathbb {R}} = \bigoplus _{i\in I} \mathbb {F}_{[a_i,b_i)} \end{aligned}$$

and

$$\begin{aligned} \mathcal {M}'=\{H_n(K^g_r)\}_{r\in \mathbb {R}} = \bigoplus _{j\in J} \mathbb {F}_{[a'_j,b'_j)} \end{aligned}$$

are decompositions of persistence modules $\mathcal {M}$ and $\mathcal {M}'$ into interval modules. The bottleneck distance between $\mathcal {M}$ and $\mathcal {M}'$ is the infimum of $\varepsilon >0$, for which there exists a bijection $\varphi :I' \rightarrow J'$ for subsets $I' \subseteq I$ and $J' \subseteq J$ such that:

• $|a_i - a'_{\varphi (i)}| \le \varepsilon$ and $|b_i - b'_{\varphi (i)}| \le \varepsilon$ for all $i\in I'$,

• $|a_i-b_i | \le 2\varepsilon$ for all $i\in I\setminus I'$ and

• $|a'_j-b'_j | \le 2\varepsilon$ for all $j\in J\setminus J'$.

The stability theorem states that if $||f-g||_\infty \le \varepsilon$, then the bottleneck distance between $\mathcal {M}$ and $\mathcal {M}'$ is at most $\varepsilon$, see [9] for details.

2.1 Filtration manipulation

The following propositions explain local adjustments to filtration functions that result in a predetermined permutation of a collection of simplices.

Proposition 1

Let $\sigma _1$ and $\sigma _2$ be two n-dimensional simplices in a finite simplicial complex K and let f be an injective filtration function on K. Assume that for some $\varepsilon > 0$ we have

$$\begin{aligned} f(\sigma _1)< f(\sigma _2)< f(\sigma _1)+2\varepsilon . \end{aligned}$$

Then there exists an injective filtration function g on K such that $||f-g||_\infty \le \varepsilon$ and $g(\sigma _2) < g(\sigma _1)$.

Proof

Without loss of generality we can slightly decrease $\varepsilon$ so that the assumptions of the proposition still hold and that

$$\begin{aligned} \varepsilon \notin \{|f(\sigma )- f(\tau )| \;;\; \sigma , \tau \in K\} \text { and }2\varepsilon \notin \{|f(\sigma )- f(\tau )| \;;\; \sigma , \tau \in K\}. \end{aligned}$$

(1)

Let $U={\textrm{Upper}}(\sigma _1)\subseteq K$ denote the subset of all simplices in K that contain $\sigma _1$ as a face (the upper set of $\sigma _1$ in the Hasse diagram of K), and let $L={\textrm{Lower}}(\sigma _2)\subseteq K$ denote the subset of all faces of $\sigma _2$ (the lower set of $\sigma _2$ in the Hasse diagram of K). Note that $\sigma _1\in U$ and $\sigma _2\in L$.

If $\mu \in U$, set $g(\mu ) = f(\mu )+\varepsilon$. If $\mu \in L$, set $g(\mu ) = f(\mu )-\varepsilon$. For all other simplices $\mu$ let $g(\mu ) = f(\mu )$.

Since $\sigma _1$ and $\sigma _2$ are two distinct simplices of the same dimension, we have $U\cap L = \emptyset$, so g is well-defined. It is also obvious that $|g(\mu )-f(\mu )|\le \varepsilon$ for all $\mu \in K$, so $||g-f||_\infty \le \varepsilon$. Finally, if the value at a simplex $\mu$ has decreased (or increased) by $\varepsilon$, then the same was true for all the faces (or cofaces) of $\mu$, so g is a filtration function. The function g defined this way is injective by the condition (1). $\square$

Given a collection of k simplices of dimension n and an arbitrary permutation $\pi \in S_k$, we do not have to switch the order of one pair at a time but can instead mix them up all at once. Corollary 2 shows one way of doing this.

Corollary 2

Let $\sigma _1,\ldots ,\sigma _k$ be a selection of n-dimensional simplices in a finite simplicial complex K, $\pi \in S_k$ an arbitrary permutation of the indices $\{1,2,\ldots ,k\}$ and f an injective filtration function on K. Assume that for some $\varepsilon > 0$ we have

$$\begin{aligned} f(\sigma _1)< f(\sigma _2)< \cdots< f(\sigma _k) < f(\sigma _1)+2\varepsilon . \end{aligned}$$

Then there exists an injective filtration function g on K such that $||f-g||_\infty \le \varepsilon$ and

$$\begin{aligned} g(\sigma _{\pi (1)})< g(\sigma _{\pi (2)})< \ldots < g(\sigma _{\pi (k)}). \end{aligned}$$

Proof

If we write $a = f(\sigma _k)-\varepsilon$ and $b = f(\sigma _1)+\varepsilon$, then $(a,b\,]$ is an interval of length $\delta < 2\varepsilon$. Divide this interval into $k+1$ equal pieces of length $\frac{\delta }{k+1}$ and define

$$\begin{aligned} g(\sigma _{\pi (1)})= & {} a +\frac{\delta }{k+1},\\ g(\sigma _{\pi (2)})= & {} a +\frac{2\delta }{k+1},\\ {}&\vdots&\\ g(\sigma _{\pi (k-1)})= & {} a +\frac{(k-1)\delta }{k+1},\\ g(\sigma _{\pi (k)})= & {} a +\frac{k\delta }{k+1}. \end{aligned}$$

It is not difficult to show that $|g(\sigma _{i})-f(\sigma _{i})| \le \varepsilon - \frac{\delta }{k+1}$. Define

$$\begin{aligned} I^+= & {} \{i\in \{1,2,\ldots ,k\};\; g(\sigma _i)-f(\sigma _i) > 0\},\\ I^-= & {} \{i\in \{1,2,\ldots ,k\};\; g(\sigma _i)-f(\sigma _i) < 0\},\\ \varepsilon ^+= & {} \max \{g(\sigma _i)-f(\sigma _i);\; i\in I^+\},\\ \varepsilon ^-= & {} \max \{|g(\sigma _i)-f(\sigma _i)|;\; i\in I^-\},\\ U= & {} \bigcup _{i\in I^+}{\textrm{Upper}}(\sigma _i)\quad \text {and}\quad L = \bigcup _{i\in I^-}{\textrm{Lower}}(\sigma _i). \end{aligned}$$

It is easy to see that $\varepsilon ^+ <\varepsilon$ and $\varepsilon ^- <\varepsilon$. For all $\mu \in U{\setminus }\{\sigma _1,\ldots ,\sigma _k\}$ let $g(\mu ) = f(\mu )+\varepsilon ^+$. For all $\mu \in L{\setminus }\{\sigma _1,\ldots ,\sigma _k\}$ let $g(\mu ) = f(\mu )-\varepsilon ^-$. Finally, for all other $\mu \in K$ set $g(\mu ) = f(\mu )$. Then g is a filtration function with all the desired properties except (perhaps) injectivity, but it can be made injective either with a small perturbation of values (upholding the property of being a filtration function), or with a minor decrease in $\varepsilon$ at the beginning (as was done in the proof of Proposition 1). $\square$

3 Rigidity for homology classes

As before, let f be an injective filtration function on a simplicial complex K and let n be a positive integer. Assume that an n-cycle $\alpha$ is created when its last n-dimensional simplex is added at level a, and that the homology class $[\alpha ]\in H_n(K_a^f)$ is born at a and terminated at b. A nullhomology of $\alpha$ at b is an $(n+1)$-chain in $K_b^f$, whose boundary is $\alpha$.

Choose $\varepsilon <\frac{b-a}{2}$. Then for each $\varepsilon$-perturbation g of f the class $[\alpha ]$ exists and is non-trivial in $H_n(K_r^g)$ at least for $r\in [a+\varepsilon , b-\varepsilon )$.

For every injective filtration function g at distance at most $\varepsilon <\frac{b-a}{2}$ from f let $\Delta _{g,\alpha }$ denote the $(n+1)$-simplex in $K^g$ that terminates $[\alpha ]$. Define

$$\begin{aligned} \Sigma _{\varepsilon } = \{\Delta _{g,\alpha };\; g \text { an injective } \varepsilon -\text { perturbation of } f\}. \end{aligned}$$

Note that $g(\Delta _{g,\alpha })\in [b-\varepsilon , b+\varepsilon ]$ and $f(\Delta _{g,\alpha })\in [b-2\varepsilon ,b+2\varepsilon ]$. We say that $[\alpha ]$ is $\varepsilon$-terminally-rigid if $|\Sigma _{\varepsilon }|=1$.

Since f is injective and K is finite, we can define

$$\begin{aligned} {\textrm{ir}}(f) = \min \{|f(\sigma )-f(\tau )|;\;\sigma \ne \tau \in K\}>0, \end{aligned}$$

the injectivity radius of f.

The aim of this paper is to study algebraic effects of terminal non-rigidity. Homology class $[\alpha ]$ as defined above is $\varepsilon$-terminally-rigid for small $\varepsilon$, certainly for $\varepsilon <\frac{{\textrm{ir}}(f)}{2}$ since $\frac{{\textrm{ir}}(f)}{2}$-perturbations of f retain the order of simplices appearing in the filtration of K. For larger $\varepsilon$ the class $[\alpha ]$ is typically not terminally-rigid. We intend to focus on the region of $\varepsilon$ in which the initial form of non-rigidity occurs.

Let $d = \dim (K)$ and let $\sigma _j^{(i)}$ for $j=1,\ldots ,k_i$ be the simplices of K of dimension i. Then f determines a linear ordering on the set

$$\begin{aligned} \{\sigma _1^{(0)},\ldots ,\sigma _{k_0}^{(0)},\ldots ,\sigma _1^{(d)},\ldots ,\sigma _{k_{d}}^{(d)}\} \end{aligned}$$

of all simplices of K. We can encode this ordering as a permutation $\overline{\pi }^f\in S_{k_0+k_1+\ldots +k_d}$ of the pre-determined ordering of simplices given above. A different injective filtration function h defines a potentially different ordering of the simplices of K, corresponding to a potentially different permutation $\overline{\pi }^h$. Note that not all permutations in the symmetric group $S_{k_0+k_1+\ldots +k_d}$ correspond to filtration functions.

If we limit ourselves to only the simplices of a single dimension, however, all possible permutations of those simplices can be realized by Corollary 2. Our filtration function f determines a permutation $\pi _{n+1}^f\in S_{k_{n+1}}$, defined by the induced linear ordering of the set

$$\begin{aligned} \left\{ \sigma _1^{(n+1)},\ldots ,\sigma _{k_{n+1}}^{(n+1)}\right\} \end{aligned}$$

of $(n+1)$-dimensional simplices of K. We will assume that the simplices of K have been ordered in such a way that $\pi _{n+1}^f$ is the identity permutation. To unburden the notation we will write $\pi _{n+1}^f = \pi ^f$ and $m=k_{n+1}$ from now on.

Any injective filtration functions that correspond to the same permutation generate the same boundary matrices in the classical matrix reduction algorithm for persistent homology, although the labels (function values) of simplices generally differ.

Also recall that for each $\varepsilon \in D=(0,\frac{b-a}{2}]$ and each injective filtration function g with $||f-g||_\infty \le \varepsilon$ the class $[\alpha ]$ has a non-trivial lifespan in $K^g$.

Now, let us consider

• the function $\varepsilon \mapsto \Sigma _\varepsilon$ defined on D that returns the collection of all terminal simplices of $\varepsilon$-perturbations of f that terminate $[\alpha ]$ and

• the function $\varepsilon \mapsto \Pi _\varepsilon$ defined on D that returns the collection of all permutations corresponding to $\varepsilon$-perturbations of f.

The functions $\varepsilon \mapsto |\Sigma _\varepsilon |$ and $\varepsilon \mapsto |\Pi _\varepsilon |$ defined on D

• (1) are increasing,

• (2) have values in the discrete sets $\{1,2,\ldots , m\}$ and $\{1,2,\ldots , m!\}$, respectively, and

• (3) attain the value of 1 for small $\varepsilon$ (at least for all $\varepsilon <\frac{{\textrm{ir}}(f)}{2}$).

As a result, both functions are increasing step functions on D as each of them partitions D into finitely many intervals, such that the function is constant on each interval of that partition. It is also apparent that a change in $\Sigma _\varepsilon$ may occur at some $\varepsilon$ only if $\Pi _\varepsilon$ also changes at the same parameter. The next lemma shows that $|\Sigma _\varepsilon |$ and $|\Pi _\varepsilon |$ are lower semi-continuous (the intervals of the two partitions of D are open on the left and closed on the right).

Lemma 3

Assume f is an injective filtration function on a finite simplicial complex K and assume that for the n-cycle $\alpha$ appearing in the filtration at level a the homology class $[\alpha ]\in H_n(K^f_a)$ is born at a and terminated at b. For each $t\in D = \left( 0,\frac{b-a}{2}\right]$ there exists $\delta >0$ such that $\Sigma _\varepsilon$ and $\Pi _\varepsilon$ are constant on $(t-\delta ,t]$.

Proof

Choose finitely many injective filtration functions generating $\Pi _t$. Each of them can be brought a bit closer to f because of injectivity. $\square$

We next discuss potential points of discontinuity of $|\Sigma _\varepsilon |$ and $|\Pi _\varepsilon |$. The following lemma shows that they always correspond to exactly half the distance between two (not necessarily consecutive) values of f.

Lemma 4

Assume f is an injective filtration function on a finite simplicial complex K and assume that for the n-cycle $\alpha$ appearing in the filtration at level a the homology class $[\alpha ]\in H_n(K^f_a)$ is born at a and terminated at b. Suppose $t\in D\left( 0,\frac{b-a}{2}\right]$ is a point of discontinuity of $\Pi _\varepsilon$. Then there exist $i\ne j$ such that $2t=|f(\sigma _i)-f(\sigma _j)|$.

Proof

As a consequence of Lemma 3 there exists a $\delta >0$ such that $\Pi _\varepsilon$ is constant on $(t,t+\delta ]$. Since t is the point of discontinuity, there exists a permutation $\nu \in \Pi _{t+\delta }{\setminus } \Pi _t$. For each $N\in \mathbb {N}$ choose an injective filtration function $g_N$ inducing $\nu$ and satisfying $||f-g_N||_\infty \le t+ 1/N$. Without loss of generality we may assume that $\{g_N(\sigma _i)\}_{N\in \mathbb {N}}$ converges for each i and define $f_\infty$ as the limiting function (if any of them do not converge we can choose a converging subsequence). Note that while $f_\infty$ is a filtration function, it cannot be injective, because it would have corresponded to the premutation $\nu$ which is not in $\Pi _t$ while $||f-f_\infty ||_\infty \le t$ by definition. Let us try fixing the values of $f_\infty$ to make it injective and see where exactly that fails.

Assume that q is a value attained by $f_\infty$ at more than one simplex. Let $A_q$ denote the collection of such simplices. If there exist two distinct $\sigma _i, \sigma _j$ such that $q = f(\sigma _i)-t = f(\sigma _j)+t$, then we have found two simplices that satisfy the desired condition. If not, there are two possible reasons for that.

• If there is no i such that $q=f(\sigma _i)-t$, then the f-values of all simplices in $A_q$ lie on $[q-t,q+t)$. In this case the $f_\infty$ values of all the simplices in $A_q$ can be slightly decreased by Corollary 2 so that:

  • $f_\infty (\sigma )\ne f_\infty (\sigma ')$ for all $\sigma \ne \sigma '$ in $A_q$,

  • the relative position of each simplex of $A_q$ to the simplices outside of $A_q$ is the same as in $\nu$,

  • simplices of $A_q$ appear in the same order as in $\nu$ and

  • the resulting filtration function $f'_\infty$ satisfies $||f-f'_\infty ||_\infty \le t$.

  Since this would make $f_\infty$ injective, it cannot happen for all q and there must be a simplex $\sigma _i$ such that $q = f(\sigma _i)-t$.

• The case where there is no j such that $q = f(\sigma _j)+t$ and the f-values of simplices from $A_q$ all lie on $(q-t,q+t]$ can be handled similarly by a small local increase of the values of $f_\infty$.

We can conclude that there exist $i\ne j$ such that $q = f(\sigma _i)-t = f(\sigma _j)+t$. $\square$

Definition 5

An injective filtration function f is called generic if

$$\begin{aligned} |f(\sigma _i)-f(\sigma _j)|=|f(\sigma _{i'})-f(\sigma _{j'})| \end{aligned}$$

implies $\{i,j\}=\{i',j'\}$.

Proposition 6

Let f be a generic injective filtration function on a finite simplicial complex K. Assume that for the n-cycle $\alpha$ appearing in the filtration at level a the homology class $[\alpha ]\in H_n(K^f_a)$ is born at a and terminated at b and let $D\left( 0,\frac{b-a}{2}\right]$. Let $t_0=\max \{x\in D; |\Sigma _x|=1\}$ and $\Sigma _{t_0}=\{\Delta _1\}$. By Lemma 4 there exist indices i, j satisfying $q=f(\sigma _{j})-t_0=f(\sigma _{i})+t_0$. Choose $t>t_0$ such that $|\Sigma _{t}|$ is as small as possible, i.e., $|\Sigma _{t}|=\lim _{x \searrow t_0} |\Sigma _x|$. Then:

• (1) $\Delta _1\in \{\sigma _{i}, \sigma _{j}\}$.

• (2) $\Delta _1$ is a maximal simplex in $K^f_{f(\Delta _1)+2s}$ for all $s<t_0$.

• (3) $\Delta _1=\sigma _{j}$ implies $\{\sigma _{i}, \sigma _{j}\} \subseteq \Sigma _{t}$ and $\sigma _{i}$ terminates a class in $H_*(K^f)$.

• (4) $\Delta _1=\sigma _{i}$ implies $\{\sigma _{i}, \sigma _{j}\} \subseteq \Sigma _{t}$ and $\sigma _{j}$ creates a class in $H_*(K^f)$.

Definition 7

In case (3) of Proposition 6 (i.e., when $\Delta _1=\sigma _j$) we say simplices $\sigma _i$ and $\sigma _j$ are sequentially critical, see Fig. 1.

In case (4) of Proposition 6 (i.e., when $\Delta _1=\sigma _i$) we say simplices $\sigma _i$ and $\sigma _j$ are independently critical, see Fig. 2.

Proof

Without loss of generality we may choose t so that no element of the form $\frac{1}{2}|f(\sigma _i)-f(\sigma _j)|$ lies on $(t_0,t]$. We will further develop the limiting argument presented in Lemma 4. Choose $\nu \in \Pi _{t}{\setminus } \Pi _{t_0}$. For each $N\in \mathbb {N}$ choose a filtration function $g_N$ inducing $\nu$ and satisfying $||f-g_N||_\infty \le t_0+1/N$. Without loss of generality we may assume $\{g_N(\sigma _i)\}_{N\in \mathbb {N}}$ converges for each i and define $f_\infty$ as the limiting function. Using local modifications as in the proof of Lemma 4 we may assume that $f_\infty ^{-1}(x)$ contains at most one simplex for each $x \ne q$. Define $A_q=f_\infty ^{-1}(q)$. Choose an open interval H around q such that

$$\begin{aligned} H \subseteq \left( \bigcap _{\sigma \in \{\sigma _i, \sigma _j\}} (f(\sigma )-t,f(\sigma )+t)\right) \ \cap \ \left( \bigcap _{\sigma \in A_q\setminus \{\sigma _{i}, \sigma _{j}\}} (f(\sigma )-t_0,f(\sigma )+t_0)\right) \end{aligned}$$

and $H \cap \textrm{im}(f_\infty )=\{q\}$.

Redefining $f_\infty$ on $A_q$ by any injective assignment of values in H respecting dimension (i.e., faces of a simplex are assigned smaller values than the simplex) we obtain an injective filtration function at a distance at most t from f. As a result, any dimension-respecting permutation of elements in $A_q$, nested between other simplices as determined by $f_\infty$, determines a permutation in $\Pi _{t}$. We will call such a permutation a local $A_q$-perturbation of $\nu$. On the other hand, redefining $f_\infty$ on $A_q$ by any injective assignment of values in H respecting dimension such that $f_\infty (\sigma _{i})< q < f_\infty (\sigma _{j})$, we obtain an injective filtration function at distance at most $t_0$ from f. As a result, any dimension respecting permutation of elements in $A_q$ nested between other simplices as determined by $f_\infty$, in which $\sigma _{i}$ appears before $\sigma _{j}$, determines a permutation in $\Pi _{t_0}$. We will call such a permutation a restricted local $A_q$-perturbation of $\nu$. Roughly speaking, the difference between $\Pi _{t_0}$ and $\Pi _{t}$ is that the later may swap $\sigma _{i}$ and $\sigma _{j}$. Observe also that $f(A_q) \subset [f(\sigma _i), f(\sigma _j)]$.

Recall that $\Sigma _{t_0}=\{\Delta _1\}$ and fix a permutation $\nu \in \Pi _{t} \setminus \Pi _{t_0}$ (and the corresponding adjusted limit $f_\infty$ of filtration functions) such that the corresponding simplex terminating $\alpha$ is $\Delta _2\ne \Delta _1$. Observe that $\nu$ swaps $\sigma _{i}, \sigma _{j}$, i.e., $\sigma _{i}$ appears after $\sigma _{j}$ in this permutation.

• (1) We will now show that $\Delta _1\in \{\sigma _{i}, \sigma _{j}\}.$ Assume that $\Delta _1\notin \{\sigma _{i}, \sigma _{j}\}.$

  • (a) Then $\Delta _1$ may appear as the first of the simplices of $A_q$ in some restricted local $A_q$ perturbation of $\nu$. In particular, $\Delta _1$ and the simplices appearing before $A_q$ contain a nullhomology of $[\alpha ]$.

  • (b) On the other hand, $\Delta _1$ may appear as the last of the simplices of $A_q$ in some restricted local $A_q$ perturbation of $\nu$. In particular, $A_q\setminus \{\Delta _1\}$ and the simplices appearing before $A_q$ do not contain a nullhomology of $[\alpha ]$.

  As a result, $\Sigma _{t}$ can only contain $\Delta _1$ as in permutation $\nu$, class $[\alpha ]$ becomes trivial by the time $\Delta _1$ is added (by (a)) but not before (by (b)). This is a contradiction. This proves our claim.

• (2) If $\Delta _1$ was not maximal but rather a codimension 1 face of a simplex ${{\widehat{\Delta }}}$ in $K^f_{f(\Delta _1)+2s}$, then by Corollary 2 we could construct an injective filtration function g of K with $||f-g||_\infty < t_0$ in which the boundary of ${{\widehat{\Delta }}}$ would appear before $\Delta _1$, while the simplices in $K^f$ appearing before $\Delta _1$ would also appear before $\Delta _1$ in $K^g$. This would mean that $\Delta _1$ would not be the simplex terminating $[\alpha ]$ in $K^g$ as it could be replaced by the same-dimensional simplices of $\partial {{\widehat{\Delta }}}$. This contradicts the fact that $\Sigma _{t_0}=\{\Delta _1\}$.

• (3) Let $\Delta _1=\sigma _{j}$.

  • (a) There is a restricted local $A_q$ perturbation of $\nu$ in which $\sigma _{j}$ appears as the last simplex. As $\Sigma _{t_0}=\{\sigma _{j}\}$, the simplices of $A_q\setminus \{\sigma _{j}\}$ and all the simplices appearing before them do not contain a nullhomology of $\alpha$, i.e., each nullhomology induced by a local $A_q$-perturbation of $\nu$ contains $\sigma _{j}$.

  • (b) On the other hand, there is a restricted local $A_q$ perturbation of $\nu$ in which $\sigma _{j}$ appears as the second simplex, right after $\sigma _{i}$. This means that $\sigma _{i}, \sigma _{j}$ and the simplices appearing before $A_q$ contain a nullhomology of $\alpha$.

  • (c) There is a local $A_q$-perturbation of $\nu$ in which $\sigma _{i}$ appears as the second simplex, right after $\sigma _{j}$. By (2) the terminal simplex of $\alpha$ in this perturbation is either $\sigma _i$ or $\sigma _j$. If $\sigma _{j}$ was the terminal simplex of $\alpha$ in this perturbation, $\sigma _{j}$ and the simplices appearing before $A_q$ would contain a nullhomology of $\alpha$. Consequently (a) would imply the terminal simplex of $\alpha$ in any local $A_q$ perturbation of $\nu$ is $\sigma _j$ implying $|\Sigma _{t}|=1,$ a contradiction. According to (b), $\sigma _{i}$ appears as the terminal simplex for this permutation implying $\{\sigma _{i}, \sigma _{j}\} \subseteq \Sigma _{t}$.

  If $\sigma _{i}$ was a birth simplex, the term $\partial \sigma _{i}$ could have been replaced by a combination of boundaries of simplices appearing before $A_q$. We would thus transform the nullhomology mentioned in (c), which consists of terms containing $\sigma _{i}, \sigma _{j}$ and simplices appearing before $A_q$, into a nullhomology consisting of terms $\sigma _{j}$ and simplices appearing before $A_q$. Such a nullhomology does not exist, as was mentioned in (c), so $\sigma _{i}$ must be a terminal simplex in $K^f$.

• (4) Let $\Delta _1=\sigma _{i}$.

  • (a) There is a restricted local $A_q$-perturbation of $\nu$ in which $\sigma _{j}$ appears as the last simplex and $\sigma _{i}$ appears as the second simplex from the last. As $\Sigma _{t_0}=\{\sigma _{i}\}$, the simplices of $A_q\setminus \{\sigma _{i}, \sigma _{j}\}$ and all the simplices appearing before them do not contain a nullhomology of $\alpha$, i.e., each nullhomology induced by a local $A_q$-perturbation of $\nu$ contains $\sigma _{j}$ or $\sigma _{i}$.

  • (b) On the other hand, there is a restricted local $A_q$-perturbation of $\nu$ in which $\sigma _{i}$ appears as the first simplex. This means that $\sigma _{i}$ and the simplices appearing before $A_q$ contain a nullhomology of $\alpha$.

  • (c) There is a local $A_q$-perturbation of $\nu$ in which $\sigma _{i}$ appears as the last simplex and $\sigma _{j}$ appears as the second simplex from the last. By (a) the terminal simplex of $\alpha$ in this perturbation is either $\sigma _i$ or $\sigma _j$. If $\sigma _{i}$ was the terminal simplex of $\alpha$ in this perturbation, then simplices of $A_q\setminus \{\sigma _{i}\}$ and all the simplices appearing before them do not contain a nullhomology of $\alpha$. By (b) this would mean $|\Sigma _{t}|=1,$ a contradiction. Thus $\sigma _{j}$ appears as the terminal simplex for this permutation implying $\{\sigma _{i}, \sigma _{j}\} \subseteq \Sigma _{t}$.

  It remains to prove that $\sigma _{j}$ is a birth simplex in $K^f$. By (b) we have

  $$\begin{aligned} \alpha = \partial \mu _1 \sigma _i +\partial \sum _{k} \lambda _k \tau _k, \end{aligned}$$

  with $\mu _1 \ne 0$ and $\tau _k$ being simplices appearing before $A_q$. On the other hand, (c) implies

  $$\begin{aligned} \alpha = \partial \mu _2 \sigma _j +\partial \sum _{l} \lambda '_l \tau '_l, \end{aligned}$$

  with $\mu _2 \ne 0$ and each $\tau '_l$ being a simplex from $A_q$ or appearing before $A_q$. Subtracting the equations we obtain

  $$\begin{aligned} \partial \mu _2 \sigma _j =\partial \Big (- \sum _{l} \lambda '_l \tau '_l+ \mu _1 \sigma _i + \sum _{k} \lambda _k \tau _k\Big ). \end{aligned}$$

  Recall that $f(A_q) \subset [f(\sigma _i), f(\sigma _j)]$ and thus the f-values of simplices $\tau _k$, $\tau '_l$ and $\sigma _i$ are below $f(\sigma _j)$. The last equality thus implies $\sigma _{j}$ is a birth simplex in $K^f$.

$\square$

Fig. 1

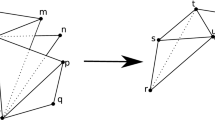
Consider the filtrations $K^f$ and $K^g$ shown above. Let $\alpha = [B-A]\in H_{0}(K)$, $\Delta _1 = DF$ and $\Delta _2 = EF$. Assume that $|f-g|<\varepsilon$, $t_2-t_1<2\varepsilon$ and $t'_2-t'_1<2\varepsilon$. Then $\Sigma _{\varepsilon } = \{\Delta _{1},\Delta _{2}\}$. In the first case $\alpha$ is terminated by $\Delta _1$ at $t = t_2$. In the second case $\alpha$ is terminated by $\Delta _2$ at $t = t'_2$. We say that $\Delta _1$ and $\Delta _2$ are sequentially critical: both need to be present to terminate $\alpha$, the one that appears first terminates another class in the same dimension and the one that appears second is the one that terminates $\alpha$

Fig. 2

Consider the filtrations $K^f$ and $K^g$ shown above. Let $\alpha = [B-A]\in H_{0}(K)$, $\Delta _1 = AB$ and $\Delta _2 = DE$. Assume that $|f-g|<\varepsilon$, $t_2-t_1<2\varepsilon$ and $t'_2-t'_1<2\varepsilon$. Then $\Sigma _{\varepsilon } = \{\Delta _{1},\Delta _{2}\}$. In the first case $\alpha$ is terminated by $\Delta _1$ at $t = t_1$. In the second case $\alpha$ is terminated by $\Delta _2$ at $t = t'_1$. We say that $\Delta _1$ and $\Delta _2$ are independently critical. One of them terminates $\alpha$ and the other creates a new class in dimension above

Example 8

Consider the following example with $\alpha = [B-A]$, $\Delta _1 = AB$, $\Delta _2 = AC$ and $\Delta _3 = BC$. If the order of the simplices is

$$\begin{aligned} A,B,C,AB,BC,AC, \end{aligned}$$

then $\alpha$ is terminated by $\Delta _1$. If we assume f assigns to the simplices the values 1, 2, 3, 4, 5 and 6 in this order, then for $\varepsilon \le 1$ we have $\Sigma _\varepsilon = \{\Delta _1\}$. If the another function changes the order to any where $\Delta _1$ occurs after $\Delta _2$ and $\Delta _3$, namely

$$\begin{aligned} A,B,C,BC,AC,AB\quad \text { or }\quad A,B,C,AC,BC,AB, \end{aligned}$$

then $\alpha$ is terminated by $\Delta _2$ and $\Delta _3$, respectively, and in both cases $\Sigma _\varepsilon = \{\Delta _1, \Delta _2, \Delta _3\}$ when $\varepsilon >1$. In this case it is not possible for $\Sigma _\varepsilon$ to have exactly two elements and $|\Sigma _\varepsilon |$ jumps from 1 to 3. An analoguous example with $n+2$ vertices and $n+2$ edges (see Fig. 3) shows that $|\Sigma _\varepsilon |$ can jump from 1 to $n+2$ for any positive integer n.

Fig. 3

Example 8: $|\Sigma _\varepsilon |$ can increase by more than 1

3.1 Sufficient conditions for rigidity of homology classes

Theorem 9

Given an injective filtration function f on a simplicial complex K and a homology class $[\alpha ]\in H_n(K^f_a)$ born at a and terminating at b, let:

• $R_u =\min \{|f(\tau )-b|;\; \tau \text { a birth}$(n+1)$-\text {simplex with } f(\tau )>b\}$ or $\infty$ if undefined;

• $R_l =\min \{|f(\tau )-b|;\; \tau \text { a terminal}$(n+1)$-\text {simplex with } f(\tau )<b\}$ or $\infty$ if undefined.

Then $[\alpha ]$ is $\varepsilon$-terminally-rigid for $\varepsilon =\frac{1}{2}\min \{b-a, R_u, R_l\}.$

Proof

For a generic f the conclusion follows from Proposition 6.

Assume f is not generic. For a positive $\delta < \max \{{\textrm{ir}}(f)/2,\varepsilon /2 \}$ choose a generic function $f_\delta$ such that $||f-f_\delta || \le \delta$. Quantities $b-a, R_u, R_l$ for this new function are at most $2\delta$ smaller than the original quantities for f and hence $[\alpha ]$ in $K^{f_\delta }$ is $(\varepsilon -\delta )$-terminally-rigid. As any $(\varepsilon -2\delta )$-perturbation of f is also an $(\varepsilon -\delta )$-perturbation of $f_\delta$, we conclude f is $(\varepsilon -2\delta )$-terminally-rigid. As $\delta$ may be arbitrarily small, Lemma 3 concludes the proof. $\square$

4 Rigidity for barcodes

In the previous sections we assumed $\varepsilon < (b-a)/2$, which ensures that any $\varepsilon$-perturbation g of f still contains a non-trivial homology class $[\alpha ]$ in $K^g$. Our main results so far described the change of the terminal simplex of $[\alpha ]$ with $\varepsilon$-perturbations. The situation is a bit more problematic with barcodes. While the barcodes induced by f and g are at the bottleneck distance at most $\varepsilon$, there is no natural way to define the underlying matching [4]. In particular, if $[\alpha ]$ represents a bar, the bar matched to it by the isometry theorem may not be represented by $[\alpha ]$. On a similar note, given a homology class $[\alpha ]$ that is born at a and terminates at b, there may be no bar of the form [a, b), see Remark 10 for more details.

Remark 10

Let f be an injective filtration function on a simplicial complex K and let n be a positive integer. Assume that for some $a,b\in \mathbb {R}$ an n-cycle $\alpha$ is created, so that the corresponding homology class $[\alpha ]\in H_n(K_r^f)$ is born at a and terminates at b. The creation of $\alpha$ causes the birth of a bar in the persistence diagram. A while later, $\alpha$ might become homologuous to an older cycle $\alpha '$ at a time $c\in (a,b)$, at which point the bar born at a would be terminated according to the elder rule. The class $[\alpha ]$ becomes trivial in $H_n(K^f_{b})$ however, so there must exist a bar in the persistence diagram that begins at or before a and dies exactly at b. In other words, the starting point of such a bar might be ambiguous, but the moment of its termination is certain.

This leads us to focus on a setting in which the same homology class determines the endpoint of a designated bar and of its matched bar arising from $\varepsilon$-perturbation.

Theorem 11

Let f be an injective filtration function on a simplicial complex K. Assume [a, b) is a bar of $\{H_n(K^f_r)\}_{r\in \mathbb {R}}$ represented by $[\alpha ]\in H_n(K^f_a)$ (a homology class born at a and terminating at b). Choose $\varepsilon < (b-a)/4$ and assume that for all other bars $[a_i,b_i)$ of $\{H_n(K^f_r)\}_{r\in \mathbb {R}}$ either $a_i > a+2\varepsilon$ or $b_i < b-2\varepsilon$. Let g be an injective filtration function satisfying $||f-g||_\infty \le \varepsilon$, and assume the induced matching matches the bar [a, b) of $\{H_n(K^f_r)\}_{r\in \mathbb {R}}$ to a bar $[a',b')$ of $\{H_n(K^g_r)\}_{r\in \mathbb {R}}$. Then

• (1) $[\alpha ]$ as a homology class in $\{H_n(K^g_r)\}_{r\in \mathbb {R}}$ terminates at $b'$ and

• (2) the simplex in $K^f$ terminating the bar [a, b) is the same as the simplex in $K^g$ terminating the bar $[a',b')$ if $\varepsilon \le \frac{1}{2} \min \{R_u,R_l\},$ where:

  • $R_u =\min \{|f(\tau )-b|;\; \tau \text { a birth (n+1)-simplex with } f(\tau )>b\}$ or $\infty$ if undefined;

  • $R_l =\min \{|f(\tau )-b|;\; \tau \text { a terminal (n+1)-simplex with } f(\tau )<b\}$ or $\infty$ if undefined.

Proof

Let

$$\begin{aligned} \{H_n(K^g_r)\}_{r\in \mathbb {R}} = \bigoplus _{j\in J} \mathbb {F}_{[a'_j,b'_j)} \end{aligned}$$

be the decomposition into interval modules, indexed so that $[a',b')$ corresponds to $[a'_0,b'_0)$. Our assumption on the barcode of $\{H_n(K^f_r)\}_{r\in \mathbb {R}}$ and the stability theorem imply the following: if $a + \varepsilon \in [a'_j,b'_j)$ then either $j=0$ or $b'_j <b - \varepsilon$. For each j let $[\alpha _j]$ be the homology class corresponding to the bar $[a'_j,b'_j)$, i.e., $[\alpha _j]$ is born at $a'_j$ and terminates at $b'_j$.

The homology class

$$\begin{aligned}{}[\beta ] = \sum _{j\in J} \lambda _j [\alpha _j]\in H_n(K^g_{a + \varepsilon }) \end{aligned}$$

terminates either at:

• $b'$, if $\lambda _0 \ne 0$, or

• before $b - \varepsilon$, if $\lambda _0 = 0$.

We now apply this observation to $[\alpha ]$. By stability theorem it represents an element of $H_n(K^g_{a + \varepsilon })$ and does not terminate before $b - \varepsilon$, so it terminates at $b'$ and this concludes the proof of (1).

Bars [a, b) of $\{H_n(K^f_r)\}_{r\in \mathbb {R}}$ and $[a',b')$ of $\{H_n(K^g_r)\}_{r\in \mathbb {R}}$ both terminate when $[\alpha ]$ terminates. Conclusion (2) now follows from Theorem 9. $\square$

Remark 12

Theorem 11 provides a sufficient condition on the structure of the barcode that guarantees that the simplex terminating the bar matched to the designated bar [a, b) remains constant through $\varepsilon$-perturbations of the filtration function f. Going beyond the region of unique terminal simplex within the setting of Theorem 11, let $\varepsilon _0$ be the maximal $\varepsilon$ for which the terminal simplex terminating the bar matched to the designated bar [a, b) remains unique $\Delta _1$ through $\varepsilon$-perturbations of the filtration function f. Proposition 6 allows us to deduce at least one additional simplex $\Delta _2$ that appears as the terminal simplex terminating the bar matched to the designated bar [a, b) for some $\varepsilon$-perturbations of the filtration function f with $\varepsilon > \varepsilon _0$. Namely, $\Delta _2$ is an n-simplex with the function value $f(\Delta _1) \pm 2\varepsilon _0$. If f is generic there is only one such simplex.

To put it differently, we may identify potential simplices generating non-rigidity from the structure of the barcode. For a demonstration see Figs. 4 and 5.

Fig. 4

The figure represents persistent homology barcodes of filtration $K^f$ in dimensions n and $n+1$. From the barcodes we can deduce (using Theorem 11) that the critical simplex terminating the bar matched with the bar [a, b) is constant (rigid) through all $\varepsilon$-perturbation of the filtration function f. This conclusion follows from the following facts: (i) no $(n+1)$-dimensional bar is born (in the green area) between b and $b+2\varepsilon$, (ii) no n-dimensional bar ends (in the blue area) between $b-2\varepsilon$ and b (except $\alpha$ at b), and (iii) $\alpha$ is the only bar that lives through $a+2\varepsilon$ and $b-2\varepsilon$

Fig. 5

If $\varepsilon$ is the scale by which rigidity is broken, we can find a bar in dimension $n+1$ starting at $b+2\varepsilon$ or a bar in dimension n ending at $b-2\varepsilon$. In this case, for each $\varepsilon '>\varepsilon$ at least one of the corresponding simplices (appearing at the black dots) appears as the terminal simplex of a bar matched with [a, b) in some $\varepsilon '$ perturbation of f

5 Related work

After the publication of the first version of this paper we were made aware that a precise relationship with [8] and [14] would be helpful. In these works the authors consider what in our terminology would be phrased as a rigidity of persistence pairs (birth simplex, death simplex) with respect to transpositions of adjacent simplices. On the other hand, we consider rigidity of the terminal simplex of a homology class or a bar with respect of $\varepsilon$-perturbations of filtration functions. The concepts are different insofar as the first one depends only on the permutation of simplices, treats single transpositions of simplices and looks to preserve pairing in persistent homology; on the other hand, our concept treats only the terminal simplices of a homology class, and considers all homology classes (not just the ones generating bars) and all $\varepsilon$-perturbations. The mentioned concepts of rigidity are different, as is demonstrated by Fig. 6.

The approach of [8] and [14] is algorithmic, has been used to demonstrate change in persistence diagrams via one-parameter modification of filtration functions and yields a proof of stability theorem. The technical treatment is based on the analysis of the matrix reduction based persistence algorithm.

Our approach is to look more generally at any single homology class and consider all $\varepsilon$-perturbations within our direct treatment of homology classes. Along the way we describe how $\varepsilon$-perturbations affect permutations of simplices (Sect. 2.1), at what values of $\varepsilon$ do terminal simplices potentially change and how (Proposition 6), and demonstrate that their number might increase by more than one despite a “single new transposition” in an incremental increase of $\varepsilon$ (Example 8).

Different rigidity concepts understandably generate different results. Sufficient conditions for rigidity of pairings are given by Nested-Disjoint Lemma in [14], while sufficient conditions for rigidity of terminal simplices in barcodes are presented in Theorem 11. Note that example in Fig. 4 satisfies only the conditions of Theorem 11. We do believe though that the treatment of [14] could be expanded and combined with our results on $\varepsilon$-perturbations to yield another proof of Theorem 11. On the other hand, such treatment would not suffice for our main and most general result: Theorem 9.

Fig. 6

Two simplicial complexes with the labels above the simplices indicating filtration values. Let $\varepsilon \in (0,1)$. The only persistence pair in the left filtration is (A, AB) while an $\varepsilon$-perturbation may change it to (B, AB). On the other hand, the only homology class that is terminated is $[A]-[B]$ and its terminal simplex is always AB, hence $[A]-[B]$ is $\varepsilon$-rigid. On the right we see a filtration whose two persistence pairs are rigid with respect to $\varepsilon$-perturbations despite the terminal simplex of $[A]-[C]$ changing from AB to AC. The concepts of rigidity of persistence pairs and rigidity of the terminal simplex of a homology class thus differ

A different treatment of instability of information provided by persistent homology is given in [5]. There, the authors recast an unstable output of persistent homology as a real valued function and average it over small perturbations to obtain a stable output. For example, while the cycle generating a persistent homology class is unstable, the approach of [5] yields, roughly speaking, a distribution of generating cycles over small perturbations. As such, this approach is aimed at stabilizing the potentially unstable outputs of persistent homology. On the other hand, our work aims to detect the instability of terminal simplices from the structure of filtration or persistence diagram.

6 Conclusions and further work

In this paper we have established sufficient conditions for the rigidity of terminal simplices. One of the main advantages of our result is that the conditions only depend on the persistence diagram. In our subsequent work we intend to extend our approach to a more geometric setting, treating persistence diagrams arising from the popular Vietoris-Rips filtrations on metric spaces. In this setting the instability of terminal simplices should be measured by the distance between terminal simplices in the metric space, as opposed to “combinatorial” proximity of this paper. In particular we plan to explore the instability in case of persistence diagrams arising from Vietoris-Rips filtrations of geodesic spaces. Recent results on $S^1$ [1, 15] indicate that in this case, the terminal simplices of 1-dimensional homology form a 1-parameter family which consequently generates a 3-dimensional homology class. We intend to provide a general treatment of this phenomenon.