Causal structure of spacetime and Scott topology

Abstract

In this paper we establish the spacetime manifold as a partially ordered set via the casual structure. We show that these partially ordered sets are naturally continuous as a suitable way below relation can be established via the chronological order. We further consider those classes of spacetimes on which a lattice structure can be endowed by physically defining the joins and meets. By considering the physical properties of null geodesics on the spacetime manifold we show that these lattices are necessarily distributive. These lattices are then continuous as a result of the equivalence between the way below relation and chronology. This enables us to define the Scott topology on the spacetime manifold and describe it on an equal footing as any other continuous lattice. We further show that the Scott topology is a proper subset of Alexandroff topology, which must be the manifold topology for the strongly causal spacetimes, (and hence a coarser topology than Alexandroff). In the process we find some interesting results on the sobriety of these manifolds. We prove that they are necessarily not sober under the Scott topology but regain their sobriety under Alexandroff topology. We also define a dual Scott topology on these manifolds by endowing them with bicontinuous poset structure and show that the join of the Scott topology with the dual is the Alexandroff topology. We also discuss the previous works done in this topic and how the present work generalises those results to some extent.

1 Introduction

The physical universe is considered to be a spacetime continuum where three dimensional space and one dimensional time are intertwined in a four dimensional spacetime. This spacetime is a continuum of all events, the primitive absolute quantities of relativistic kinematics. Further to this, via the Principle of Equivalence, it is well established that locally the spacetime can always be mapped to a flat Minkowski spacetime by choosing a suitable frame of reference. Therefore, naturally the spacetime can be given a manifold structure. Hence in general relativity (GR), the spacetime is considered to be a real four-dimensional connected $C^{\infty }$ Hausdorff manifold $(\mathcal {M},g)$ endowed with a globally defined and at least $C^2$ metric tensor field ‘g’ of type (0, 2), which is non-degenerate and Lorentzian (or hyperbolic normal) [3, 7, 8, 11, 18]. This implies that at any point $x\in \mathcal {M}$, the tangent space $T_x(\mathcal {M})$ has a basis with respect to which g has the matrix ‘$\mathrm{{diag}}(-1,1,1,1)$.

Any relativistic theory of the physical world has an important property, the absence of instantaneous interaction between two events that are separated in space and time. This has been strongly verified by experiments. Therefore, there is a finite maximum velocity of the propagation of any interaction, which is taken to be a universal constant and that corresponds to the velocity of light in vacuum ($c=2.998\times 10^8$ m/s). The finite maximum velocity of propagation of interaction has an important consequence: there always exist a well defined subset of all events which defines the set of events that a given event can be causally affected by or can causally affect. This gives rise to the causal structure of the spacetime manifold. In special relativity, where the metric is constant throughout the manifold, these subsets are described by past and future light cones from the given event. However, in general relativity the metric g, that defines the light cone at every point, may vary from point to point. Also the topology of the spacetime manifold may not be that of the Euclidean space $\mathbb {R}^4$. This allows much more possibilities and a much richer structure. The causal structure of spacetime has been widely studied under very general and physically realistic conditions (which do not allow time travel to future or past). See for example [2,3,4, 7, 8, 11, 12, 18, 21] and the references therein.

The theory of continuous lattices is of relatively recent origin and has arisen more or less independently in a variety of mathematical contexts like computational theory, general topology, analysis, category theory and logic [5, 6, 9, 13,14,15, 17]. In all of these fields, applications of theory of continuous lattices were extremely useful, and hence these provided truly interdisciplinary tools. Initially the major areas of application were the theory of computing and computability. In fact, the order theoretical foundations of computer science was the main motivation for the creation of the unifying theory of continuous lattices. Continuous lattices have also appeared in general topology, in the context of the category of all topological spaces or of topological spaces satisfying $T_0$ separation axiom. Such spaces have been the objects of renewed interest with the emergence of spectral theory. A continuous lattice can be naturally endowed with a $T_0$ topology which is defined from the lattice structure and this topology is called the Scott topology. Spaces for which the lattice of open sets is a continuous lattice provides a number of interesting results. For Hausdorff spaces, the locally compact spaces have this property, and in more general spaces analogs of this result remain true.

Continuous lattices are also of importance when one studies topology from the point-free context, that is, when one considers the lattice of open sets of a topological space as the primitive objects of study rather than the points of the space themselves. The lattice of open sets of a topological space form what is called a frame or locale [10, 19]. The latter refers to any lattice that is complete and satisfies the infinite distributive law. Continuous lattices that are also distributive form an important class of frames, and, in the language of category theory can be recognised as being dually equivalent to the category of locally compact sober topological spaces.

In this paper we investigate yet another application of theory of continuous lattices. We consider the causal structure of spacetime manifold and using that, recast it into a partially ordered set or poset [1]. We further assume that these posets are continuous and have a lattice structure. We show the equivalence of the lattice theoretic way below relation to the chronological order on the spacetime manifold. Noting that the class of spacetimes, that have these characteristics locally, are non-empty, we define the Scott topology on these posets and show explicitly that the Scott topology is a subset of Alexandrov topology, (which is the manifold topology for all strongly causal spacetimes). This makes the Scott topology to be a coarser topology than Alexandroff. We find some interesting results on the sobriety of these manifolds. We prove that they are necessarily not sober under the Scott topology but regain their sobriety under Alexandroff topology. The fact that space-time structure with the Scott topology is not sober is we believe mathematically interesting. Since the introduction of the Scott topology by Dana Scott in his seminal work on continuous lattices, a question was raised whether the Scott topology is necessarily sober. This was shown to be negative by Johnstone in [9], where he constructs a particular counterexample. The interesting aspect for us is that the non-sobriety of the Scott topology comes out in the natural course of analysing space-time structure. We also define a dual Scott topology on these manifolds by endowing them with bicontinuous poset structure and show that the join of the Scott topology with the dual is the Alexandroff topology.

We also discuss the similarity and the differences of the approaches in our paper and the earlier works [15, 16], where the authors considered a globally hyperbolic spacetime $\mathcal {M}$. and defined a globally hyperbolic poset which is bicontinuous and the closure of the interval of two spacetime points is compact in the interval topology. This compactness enabled them to construct the directed complete posets (dcpos) and domains.

2 Spacetime as a POSET with a lattice structure

Definition 2.1

The spacetime manifold is a real four-dimensional connected $C^{\infty }$ Hausdorff manifold $(\mathcal {M},g)$, which is paracompact and endowed with a globally defined and at least $C^2$ metric tensor field ‘g’ of type (0, 2), which is non-degenerate and Lorentzian (or hyperbolic normal). This implies that at any point $x\in \mathcal {M}$, the tangent space $T_x(\mathcal {M})$ has a basis with respect to which g has the matrix ‘$\mathrm{{diag}}(-1,1,1,1)$.

Definition 2.2

Any tangent vector $\mathbb {X}\in T_x(\mathcal {M})$ is said to be timelike, spacelike or null, according as $g_x(\mathbb {X},\mathbb {X})$ is negative, positive or zero. The null cone at x is the set of all null vectors in $T_x(\mathcal {M})$.

Definition 2.3

If at every point x, if there exist two disjoint equivalence classes in $T_x(\mathcal {M})$, which between them contains all non-spacelike vectors, then the space-time is time-orientable. We can arbitrarily call one of these classes as future directed and the other as past directed. Physically this corresponds to the choice of arrow of time at a given point. The spacetime is clearly time orientable if there exist a nowhere vanishing timelike vector field on $\mathcal {M}$, and the converse is also true.

Remark 2.4

Physically realistic spacetimes are time orientable. The next obvious question is, whether space-time is space-orientable. That is, whether it is possible to divide bases of the spacelike axes into right handed and left handed bases into a continuous manner. Geroch [3] established an important relation between these two orientibilities, by considering experiments of elementary particles, whose interactions are always invariant under the combination of charge, parity and time reversals (CPT Theorem). This leads us to believe that if the spacetime is time-orientable then it is also space-orientable.

Definition 2.5

On the spacetime manifold $\mathcal {M}$, a future directed smooth causal curve is a smooth mapping $\mu :\Sigma \rightarrow \mathcal {M}$ with the following conditions:

• 1. $\Sigma$ is a connected subset of $\mathbb {R}$ containing more than one point.

• 2. The mapping $\mu$ is smooth (at least $C^2$) with non-vanishing $d\mu$.

• 3. At every point $x\in \mathcal {M}$ on the curve $\gamma$, which is the image of the map $\mu$, the tangent vector $\mathbb {X}$ is future directed and non-spacelike ($g_x(\mathbb {X},\mathbb {X})\leqslant 0$).

Definition 2.6

A point $x\in \mathcal {M}$ is said to causally precede another point $y\in \mathcal {M}$ if there exist a future directed smooth causal curve $\gamma$ from x to y and we write $x \leqslant y$. If the future directed causal curve is null at every point, we write $x\nearrow y$.

Definition 2.7

The spacetime is said to be causal, if there are no closed causal curves in the spacetime. Further to this the spacetime is said to be strongly causal if for any neighbourhood U of $p\in \mathcal {M}$, there exist a neighbourhood $V\subset U$, $p\in V$, such that there exists no timelike curve that passes through V more than once.

2.1 Spacetime as a POSET

In the following lemma we would establish that the causal structure on the spacetime manifold, naturally makes it a partially ordered set.

Lemma 2.8

The spacetime manifold $\mathcal {M}$ together with the order relation ‘$\leqslant$ ’constitute a partially ordered set (poset).

Proof

From Definitions 2.5 and 2.6 it is clear that:

• 1. $x\leqslant x$, as degenerate causal curves are allowed.

• 2. Also $x\leqslant y$ and $y\leqslant z$ automatically imply $x\leqslant z$. Since the causal curves from x to y and y to z are both smooth, we can always round off the corner at y in a causal manner to obtain a single casual curve from x to z.

• 3. As we will be considering only strongly causal spacetimes in this investigation, we must have $x\leqslant y$ and $y\leqslant x$ $\Rightarrow$ $x=y$, as otherwise there will be closed causal curves, which is not allowed by strong causality conditions.

The above points establish that the order relation ‘$\leqslant$’ satisfies the reflexive, transitive and anti-symmetry conditions respectively. Thus the set of points $\mathcal {M}$, together with the order relation ‘$\leqslant$’ constitute a poset. $\square$

Definition 2.9

Any subset $A\subseteq \mathcal {M}$ is called an up set denoted by $\uparrow A$ if $x\in A$ and $x\leqslant y$ imply $y\in A$ Dually, $A\subseteq \mathcal {M}$ is called an down set denoted by $\downarrow A$ if $x\in A$ and $y\leqslant x$ imply $y\in A$.

We can define the future/past sets of any point or subset of $\mathcal {M}$ in the following way:

Definition 2.10

Let $x \in \mathcal {M}$. Then the causal future of x, denoted by $J^+(x)$ or $\uparrow x$ is defined by:

$$\begin{aligned} \uparrow x \equiv J^+(x) = \{y \in \mathcal {M}|\; x\leqslant y\} \end{aligned}$$

Dually we define the causal past of x as:

$$\begin{aligned} \downarrow x \equiv J^-(x) = \{y \in \mathcal {M}|\; y \leqslant x\} \end{aligned}$$

Definition 2.11

Let $S \subset \mathcal {M}$, then the causal future (past) of S is defined as:

$$\begin{aligned} \uparrow S \equiv J^+(S) = \bigcup _{x\in S}J^+(x);\;\downarrow S \equiv J^-(S) = \bigcup _{x\in S}J^-(x) \end{aligned}$$

Lemma 2.12

Any subset $A\subseteq \mathcal {M}$ is a down set iff the complement $\mathcal {M}{\setminus } A$ is an up set. Dually, A is an up set iff $\mathcal {M}{\setminus } A$ is a down set.

Proof

First consider $A\subseteq \mathcal {M}$ to be a down set and let $x\in \mathcal {M}{\setminus } A$ and $x \leqslant y$. Hence $x\notin A$ and that implies $y\notin A$, as $y\in A$ would force $x\in A$ as A is a down set. Therefore $y\in \mathcal {M}{\setminus } A$. Thus $x\in \mathcal {M}{\setminus } A$ and $x \leqslant y$ imply $y\in \mathcal {M}{\setminus } A$, making $\mathcal {M}{\setminus } A$ an up set.

Conversely, let $\mathcal {M}{\setminus } A$ be an up set. Let $x\in A$ and $y\leqslant x$. If $y\in \mathcal {M}{\setminus } A$, then x must be in $\mathcal {M}{\setminus } A$, as that is an upset, but that is a contradiction. Hence $y\in A$. Therefore for any $x\in A$, $y\leqslant x$ implies $y\in A$. Therefore A is a down set. The dual part can be proved similarly. $\square$

Remark 2.13

From Definitions 2.10, 2.9 it is easy to see that $\uparrow x$ is an up set and $\downarrow x$ is a down set. Therefore, for all $y \in \uparrow x$ we have $\uparrow y \subseteq \uparrow x$. Similarly, for all $y \in \downarrow x$ we have $\downarrow y \subseteq \downarrow x$. This immediately shows that

$$\begin{aligned} \uparrow x = \bigcup _{y\in \uparrow x}\uparrow y;\;\downarrow x = \bigcup _{y\in \downarrow x}\downarrow y \end{aligned}$$

2.2 Spacetimes with Lattice structure

Now that we have established the spacetime manifold $\mathcal {M}$ to be a poset, we would like to impose some further restriction of $\mathcal {M}$ by giving it a lattice structure via the following definition.

Definition 2.14

(The Lattice structure) For any two points $x,y\in \mathcal {M}$, both $x\vee y$ and $x\wedge y$ exist, which have the properties $\uparrow (x\vee y)=\uparrow x\, \cap \uparrow y$ and $\downarrow (x\wedge y)=\downarrow x\, \cap \downarrow y$

Remark 2.15

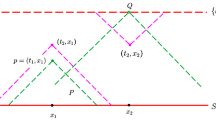
It can be easily seen, that for comparable points this definition is straightforward. For non-comparable points, we can visualise the join by considering Huygen’s wavefront construction. Let p and q are two no-comparable spacetime points. If a light pulse is emitted from both points, they will form moving spherical wavefronts. The point in the future of p and q, where these spherical wavefronts touch each other will be denoted by $p\vee q$.

We caution here that although any general strongly causal spacetime will definitely be a poset, but may not have the lattice structure defined above. Obviously Minkowski spacetime is globally endowed with this lattice structure, and so are the open sets of many other physically reasonable spacetimes. The key idea here is that the open sets should not have singularities or points removed and/or other similar pathologies like conjugate points for null geodesics, trapped surfaces etc.

With the lattice structure defined above, one can immediately check that the lattice algebra for the binary operators ‘$\vee$’ and ‘$\wedge$’, stated below are satisfied.

Lemma 2.16

(The Connecting Lemma) For any two points $x,y\in \mathcal {M}$, the following statements are equivalent:

• 1. $x\leqslant y$.

• 2. $x\vee y = y$.

• 3. $x\wedge y=x$.

Proof

Let $x\leqslant y$, which implies that $\uparrow y \subseteq \uparrow x$. Hence $\uparrow (x\vee y)\equiv \uparrow x\, \cap \uparrow y= \uparrow y$, which implies that $x\vee y = y$. Conversely, if $x\vee y = y$, we have $\uparrow x\, \cap \uparrow y= \uparrow y$ which means that $\uparrow y \subseteq \uparrow x$ and hence $x\leqslant y$. Thus the statements (1) and (2) are equivalent. The equivalence between (1) and (3) can be proved dually. $\square$

Remark 2.17

The above lemma gives an important result for spacetimes having a lattice structure as defined in Definition 2.14. If the point x is in the causal future of y, then y must be in the causal past of x. This is the stronger version of the reflecting spacetime condition [11], as applicable to these spacetime lattices.

Lemma 2.18

(The lattice algebra) For any three points $x,y,z\in \mathcal {M}$, and the operators ‘$\vee$’ and ‘$\wedge$’ as defined in Definition 2.14, the following are satisfied:

• 1. Associative Law: $x\vee (y\vee z)=(x\vee y)\vee z$ and $x\wedge (y\wedge z)=(x\wedge y)\wedge z$.

• 2. Commutative Law: $x\vee y=y\vee x$ and $x\wedge y=y\wedge x$.

• 3. Idempotency Law: $x\vee x=x$ and $x\wedge x=x$.

• 4. Absorption Law: $x\vee (x\wedge y)=x$ and $x\wedge (x\vee y)=x$.

Proof

The proofs of (1)–(3) are trivial as the binary intersection operator ‘$\cap$’ obeys associative, commutative and idempotency laws. To prove (4), we note that $\downarrow x\,\cap \downarrow y\subseteq \downarrow x$ and hence $x\wedge y \leqslant x$. Now using the connecting lemma gives the required results. The dual statement can be proved dually. $\square$

Proposition 2.19

Let $t, x, y, z \in \mathcal {M}$, where $\mathcal {M}$ has the lattice structure as defined in Definition 2.14, then we have the following:

• 1. $x \leqslant y,\;\Rightarrow \; x \vee z \leqslant y\vee z\; \;\textrm{and} \;\; x \wedge z \leqslant y\wedge z$.

• 2. $x\leqslant y\;\;\textrm{and}\;\; z\leqslant t\; \;\Rightarrow \;\; x \vee z \leqslant y\vee t\;\;\textrm{and}\;\; x \wedge z \leqslant y\wedge t$.

Proof

To show (1), let $x, y, z \in \mathcal {M}$ and suppose $x \leqslant y$. Then $\uparrow y \subseteq \uparrow x$. Which implies that $\uparrow y \,\cap \uparrow z \subseteq \uparrow x\,\cap \uparrow z$, which implies that $\uparrow (y\vee z) \subseteq \uparrow (x\vee z)$. Therefore, $y\vee z \in \uparrow (x\vee z)$. Thus, $x\vee z \leqslant y\vee z$ as required. Dually one can show that $x\wedge z \leqslant y\wedge z$. To show (2), let $t, x, y, z \in \mathcal {M}$ and suppose that $x \leqslant y$ and $z \leqslant t$. Then, by (1) we have $x \vee z \leqslant y\vee z$ and $y\vee z \leqslant y\vee t$, which implies that $x\vee z \leqslant y\vee t$. Dually $x \wedge z \leqslant y\wedge t$. $\square$

Remark 2.20

This shows that if y is in the causal future of x, then the common causal future of y and any other point z will lie inside the common causal future of x and the same point z.

Proposition 2.21

Let $x, y, z \in \mathcal {M}$, then we have the following:

$$\begin{aligned} y\leqslant x \leqslant y\vee z\; \Rightarrow \; x \vee z = y \vee z \end{aligned}$$

Proof

Let $x, y, z \in \mathcal {M}$ and suppose that $y\leqslant x \leqslant y\vee z$. Since, $z \leqslant y\vee z$ and $\vee$ is associative, then $(y \vee z)\vee z = y \vee z$. Also since, $y \leqslant x$ then $y \vee z \leqslant x \vee z$. Again since, $x \leqslant y\vee z$ then $x \vee z \leqslant (y \vee z)\vee z$. So we see that, $y \vee z \leqslant x \vee z \leqslant (y \vee z)\vee z = y \vee z$. Therefore, $y \vee z \leqslant x \vee z \leqslant y \vee z$. This is only possible if $x \vee z = y \vee z$. $\square$

Remark 2.22

This shows that when the common causal future of two points are fixed, then the common causal future of one point with an intermediate point is forced.

2.3 Properties of null geodesics: distributive lattice

We would now, impose certain physical restrictions for null geodesics (the path traced by a photon on the spacetime manifold) in the spacetime lattice $\mathcal {M}$ defined above. First and foremost, we will assert that the spacetime does not contain any closed trapped surface. We can explain this using the Huygen’s wavefront construction. Let us consider that at any given instant a sphere emits a flash of light. At any later time the light from a point on the sphere will envelop two spherical wavefronts, one ingoing with surface area strictly less than the original sphere, and other outgoing with surface area strictly greater than the original sphere. We note that this is not possible if the original sphere was a closed trapped surface, in which case the surface area of both ingoing and outgoing wavefronts would be less than the original sphere. Absence of closed trapped surfaces will then enable us to assert the following propositions.

Proposition 2.23

The future (or past) directed null geodesics from a given point $x\in \mathcal {M}$, can be uniquely assigned one of the two spatial parities, “ingoing" or “outgoing".

Proposition 2.24

If two points $x,y\in \mathcal {M}$ are not comparable, then these points lies on two different past directed (future directed) null geodesics from their join (meet), having opposite spatial parities.

Remark 2.25

From the above proposition it is clear that more than two non-comparable points cannot have a common join (or meet) as there are only two different spatial parities. This immediately tells us, that any sublattice of $\mathcal {M}$ will not have a “diamond" structure.

Further to the above, there is another important physical property of null geodesics which we state below:

Proposition 2.26

If a null geodesic exists between two points $x,y\in \mathcal {M}$, then this null geodesic is the unique causal curve between x and y.

Remark 2.27

The above proposition then immediately assures us, that there are no conjugate points for the congruence of null geodesics in the spacetime.

Proposition 2.28

If x and y are points in two different past directed (or two different future directed) null geodesics from another point z, then x and y must be non-comparable.

Proof

Suppose x and y are comparable and $x\leqslant y$. Then we can construct a continuous causal curve from x to z via y which contradicts the null geodesic from x to z being the unique causal curve. Hence x and y must be non comparable. $\square$

Proposition 2.29

Let $x,y,z\in \mathcal {M}$, such that x and z are non-comparable and so is y and z. Also given that $x\leqslant y$ and $x\vee z=y\vee z =a$ (or dually $x\wedge z=y\wedge z =a$). Then x and y are points on the same past directed (or dually future directed) null geodesic from a.

Proof

Since x and z are non-comparable and so is y and z, then by Proposition 2.24x and z are points on two different past directed null geodesics from a with opposite spatial parities (and so is y and z). On the other hand since $x\leqslant y$, they cannot lie in two different null geodesics by Proposition 2.28. Hence x and y are points on the same past directed null geodesic from a. The dual statement can be proved likewise. $\square$

Proposition 2.30

Let $x,y,z\in \mathcal {M}$, such that x and z are non-comparable and so is y and z, and given that $x\leqslant y$. Then x, y and z cannot have a common join and meet simultaneously.

Proof

Let us suppose x, y and z have a common join and meet simultaneously. Then by the previous proposition, there must be two different null geodesics joining x and y, (one past directed from the common join and other future directed from the common meet), which contradicts Proposition 2.26. $\square$

Remark 2.31

The above proposition assures that there will not be any sublattice of $\mathcal {M}$ that has a “pentagonal" structure.

Theorem 2.32

From the definition of ‘$\vee$’ and ‘$\wedge$’, as defined in Definition 2.14, the spacetime lattice $\mathcal {M}$ has the distributive property: $\forall a,b,c \in \mathcal {M}$

$$\begin{aligned} a\vee (b\wedge c)=(a\vee b)\wedge (a\vee c)\;;\;\; a\wedge (b\vee c)=(a\wedge b)\vee (a\wedge c) \end{aligned}$$

Proof

A lattice is distributive if and only if none of it’s sublattices have a diamond or pentagonal structure [1], and hence the spacetime lattice $\mathcal {M}$ is distributive. $\square$

3 Chronology, Directed Sets and Way Below relation

Definition 3.1

On the spacetime manifold $\mathcal {M}$, a point x chronologically precedes another point y, if there is a smooth, future directed and timelike curve (a curve whose tangent vector norm at every point is strictly negative) from x to y. Set of all points that x chronologically precedes is denoted by $I^+(x)$. Similarly the set of all points that chronologically precedes x is denoted by $I^-(x)$.

Definition 3.2

The relation “chronology precedes" is transitive. If x chronologically precedes y and y chronologically precedes z, then one can always find a smooth timelike curve from x to z, by smoothing off the corner at y and hence x chronologically precedes z. Therefore if x chronologically precedes y, we must have $I^+(y)\subseteq I^+(x)$ and the dual is also true. However, in a causal spacetime x cannot chronologically precede x, as that would necessarily require a closed timelike curve from x to x.

Definition 3.3

A spacetime is called reflecting if for all $x,y\in \mathcal {M}$, $I^+(x)\subseteq I^+(y)\iff I^-(x)\subseteq I^-(y)$.

Proposition 3.4

[8] For any $x \in \mathcal {M}$, $I^-(x)\subseteq \downarrow I^+(x)$ and $I^+(x)\subseteq \uparrow I^-(x)$.

Remark 3.5

Proposition 3.4 is true in general, a spacetime $\mathcal {M}$ need not to be reflecting. Hawking and Sachs in [8] proved the following important characterisation of a reflecting spacetime.

Proposition 3.6

[8] The following conditions are equivalent.

• 1. $\mathcal {M}$ is reflecting.

• 2. For any $x, y \in \mathcal {M}$, $x \in \overline{J^+(y)}$ iff $y \in \overline{J^-(x)}$.

• 3. For all $x \in \mathcal {M}$, $\downarrow I^+(x) = I^-(x)$ and $\uparrow I^-(x) = I^+(x)$.

Remark 3.7

Since we are dealing with spacetimes that have a lattice structure, the spacetimes that we consider here must be reflecting. In fact they obey a stronger condition due to the connecting lemma in the previous section.

Definition 3.8

From the definitions it is clear that in general $I^\pm (x)\subseteq J^\pm (x)$. In fact $I^\pm (x)=J^\pm (x){\setminus }\partial J^\pm (x)$, where $\partial J^\pm (x)$ is the topological boundary of $J^\pm (x)$. For the spacetimes with the lattice structure this boundary is generated by the future (past) directed null geodesics from the point $x\in \mathcal {M}$.

Lemma 3.9

For all $x,y\in \mathcal {M}$, if x chronologically precedes y, then the causal past of x chronologically precedes y. In other words, $x\in I^-(y)\Rightarrow J^-(x)\subset I^-(y)$. The dual statement is also true, $x\in I^+(y)\Rightarrow J^+(x)\subset I^+(y)$

Remark 3.10

This lemma was originally proven by Penrose [18]. The key idea is, if there exists a smooth causal curve from z to x and a smooth timelike curve from x to y, one can always smoothen out the corner at x (by covering the causal path by a finite number of convex normal regions) to generate a single smooth timelike curve from z to y.

In the next part of this section we will now define the concepts of Directed sets and Way below relation in the context of theory of continuous lattices and prove the equivalence with the chronological structure of strongly causal spacetimes that have a lattice structure.

Definition 3.11

[1, 5] (Directed sets) Let us consider any poset P equipped with a given order relation. A subset D of P is called a directed set if it is not empty and every pair of elements has an upper bound in D.

Remark 3.12

In context of the spacetime poset $\mathcal {M}$, clearly any causal curve (with or without endpoints) will be a directed set. Further to that, if we assume the lattice structure on $\mathcal {M}$, then $\downarrow x$ is directed for all $x\in \mathcal {M}$. This is because, if $a\leqslant x$ and $b\leqslant x$, then by the Proposition 2.19 we have $a\vee b \leqslant x$. hence for every pair of points in $\downarrow x$, their least supper bound is also in $\downarrow x$.

Definition 3.13

[1, 5] (Way below relation) Let P be a poset and $x,y\in P$. We say that x is “way below" y or $x\ll y$, iff for all directed subsets $D\subseteq P$ for which $\sup D$ exists, the relation $y\leqslant \sup D$ always implies the existence of a $d\in D$ such that $x\leqslant d$.

Remark 3.14

Since we are working with a poset $\mathcal {M}$ which is also a lattice, therefore If $D\subseteq \mathcal {M}$ is a directed set which has a supremum we will write this as $\bigvee D$ rather than $\sup D$.

Proposition 3.15

Let $x, y, z, w \in \mathcal {M}$, then

• 1. $x\ll y \Rightarrow x \leqslant y$.

• 2. $z \leqslant x\ll y\leqslant w\Rightarrow z\ll w$.

• 3. $x\ll y,\; y\ll z\Rightarrow x\ll z$.

Proof

To show (1), suppose $x\ll y$ and let $D = \{y\}$. It is clear that D is directed with $\bigvee \{y\} = y$. Now since $y \leqslant \bigvee \{y\} = y$ and $x\ll y$, then by definition there exists $d \in \{y\}$ such that $x \leqslant d = y$. Thus, $x \leqslant y$. To show (2), suppose $z \leqslant x\ll y\leqslant w$ and let D be a directed subset of $\mathcal {M}$ with $w \leqslant \bigvee D$. Since $y \leqslant w$, then $y \leqslant \bigvee D$. Now, since $x \ll y$ and $y \leqslant \bigvee D$, then there exists $d \in D$ such that $x \leqslant d$. Again, since $z \leqslant x$ it follows that $z \leqslant d$ which implies that $z \ll w$ as required. The proof of (3) trivially follows from (1) and (2). $\square$

We will now prove an important theorem showing the equivalence of poset theoretic “way below" relation with the chronological structure of the spacetime. We note that for this equivalence to hold we don’t need a lattice structure on the continuous posets and in this respect this equivalence is one of fundamental properties of a spacetime manifold that is strongly causal.

Theorem 3.16

For the spacetime manifold $\mathcal {M}$ that has a lattice structure, the “chronologically precede" relation is equivalent to the “ way below relation".

Proof

Let us suppose $x,y\in \mathcal {M}$ and $x\ll y$. Consider a smooth future directed timelike curve $\gamma$ from any point in $I^-(y)$ to y. Let $D=\gamma {\setminus } y$. Obviously D is directed with $\bigvee D=y$. Therefore there must be a $d\in D\subset I^-(y)$ such that $x\in \,\downarrow d$. But then by Lemma 3.9, it is clear that $x\in I^-(y)$. Thus $x\ll y$ implies that there exist a smooth timelike curve from x to y or x chronologically precedes y.

Conversely, let us suppose $x,y\in \mathcal {M}$ and x chronologically precedes y. Then $y\in I^+(x)$ and hence $y\notin \partial J^+(x)$. Therefore for any directed set D for which $y\leqslant \bigvee D$, we must have $\bigvee D\in I^+(x)$ by Lemma 3.9 and hence $\bigvee D\notin \partial J^+(x)$. Now, if none of the elements of D are in $\uparrow x$, then $\bigvee D$ will either not be in $\uparrow x$ or be in $\partial J^+(x)$, which leads to a contradiction. This makes $\uparrow x \cap D\ne \emptyset$. Therefore, there must exist a $d\in D$ such that $x\leqslant d$. Hence chronologically precedes imply way below relation. $\square$

From the above theorem, we can consider the following definitions of chronological future and past sets of a point or a subset of $\mathcal {M}$

Definition 3.17

Let $x \in \mathcal {M}$. Then the chronological future of x, is defined by:

$$\begin{aligned} \Uparrow x \equiv I^+(x) = \{y \in \mathcal {M}|\; x\ll y\} \end{aligned}$$

Dually we define the chronological past of x as:

$$\begin{aligned} \Downarrow x \equiv I^-(x) = \{y \in \mathcal {M}|\; y \ll x\} \end{aligned}$$

Definition 3.18

Let $S \subset \mathcal {M}$, then the chronological future (past) of S is defined as:

$$\begin{aligned} \Uparrow S \equiv I^+(S) = \bigcup _{x\in S}I^+(x);\;\Downarrow S \equiv I^-(S) = \bigcup _{x\in S}I^-(x) \end{aligned}$$

Further to this, we impose the continuous lattice condition on $\mathcal {M}$, by the following definition.

Definition 3.19

For all points $x\in \mathcal {M}$ the following holds:

$$\begin{aligned} x=\bigvee \{y\in \mathcal {M}| y\ll x\}\equiv \bigvee I^-(x) \end{aligned}$$

That is, every spacetime point is the supremum of it’s chronological past, although it is not a member of it’s chronological past.

Proposition 3.20

For the spacetime manifold $\mathcal {M}$, that has a lattice structure, $I^-(x)\equiv \Downarrow x$ is directed.

Proof

Assume $a, b \in \Downarrow x$. We show $a\vee b \ll x$. Take D directed such that $x\leqslant \bigvee D$. Since $a\ll x$ there exists $d_1 \in D$ such that $a \leqslant d_1$, and similarly $b\leqslant d_2$ for some $d_2 \in D$. Therefore by Proposition 2.19 we have $a\vee b\leqslant d_1\vee d_2$. Now since D is directed, there exists $d_3\in D$ such that $d_1\leqslant d_3$ and $d_2 \leqslant d_3$. Therefore $d_1\vee d_2\leqslant d_3$. Therefore we have $a\vee b \leqslant d_3\in D$, so $a\vee b \ll x$. Since for every pair of element in $\Downarrow x$, their join or the least upper bound is also in $\Downarrow x$, hence $\Downarrow x$ is directed. $\square$

4 Scott topology on the spacetime manifold with a lattice structure

To define the Scott topology on the spacetime manifold $\mathcal {M}$, let us briefly recall the basic assumptions on the manifold:

• 1. $\mathcal {M}$ is a poset which is also a lattice.

• 2. Each element $x\in \mathcal {M}$ is a join of elements way below x, that is $x=\bigvee \{y\in \mathcal {M}| y\ll x\}$

• 3. Conditions (1) and (2) make $\mathcal {M}$ a continuous poset (in the language of the theory of posets), but which also has a lattice structure. In general continuous posets need not have any lattice structure.

• 4. If $x\in \mathcal {M}$, then there exists $y\in \mathcal {M}$ such that $x\ll y$. In general continuous posets with a lattice structure need not necessarily satisfy this condition, so this is a special condition on the poset $\mathcal {M}$ imposed by the physical condition being modelled.

Proposition 4.1

In a lattice $\mathcal {M}$, if every element a can be written as

$$\begin{aligned} a=\bigvee \{x\in \mathcal {M}| x\ll a\} \end{aligned}$$

then the relation $\ll$ interpolates, that is, whenever $a\ll b$, there exists $c\in \mathcal {M}$ such that $a\ll c\ll b$.

Proof

Suppose $a\ll b$. Now $b=\bigvee \{y\in \mathcal {M}| y\ll b\}$. Also for each $y\ll b$, $y=\bigvee \{x\in \mathcal {M}| x\ll y\}$. Let us define a subset $T\subset \mathcal {M}$ in the following way: $T= \{x\in \mathcal {M}| x\ll y\ll b$, for some $y \in \mathcal {M}\}$.

Firstly, we will show that T is directed: Take $x_1, x_2 \in T$, and find $y_1, y_2$ in $\mathcal {M}$ such that $x_1\ll y_1\ll b$ and $x_2\ll y_2\ll b$. From the Proposition 3.20 we can immediately see that $y_1\vee y_2 \ll b$. Let $y_3=y_1\vee y_2$. So we have $y_3\ll b$. Now $x_1\ll y_1\leqslant y_3$ implies $x_1\ll y_3$ (by Proposition 3.15). Similarly, $x_2 \ll y_3$. From the Proposition 3.20 again we get $x_3=x_1\vee x_2 \ll y_3 \ll b$, showing that $x_3 \in T$. Hence T is directed.

Now we claim that: $b = \bigvee T$:

Firstly, $x\in T$ implies $x\ll y\ll b$, hence by Proposition 3.15 we have $x\ll b\Rightarrow x\leqslant b$, so b is an upper bound for T. To show that this is the least upper bound, let $z\in \mathcal {M}$ such that $x\leqslant z$ for every $x\in T$. We will now show that $b\leqslant z$. Take any y such that $y\ll b$. Now $y=\bigvee \{x\in \mathcal {M}| x\ll y\}$. Each such x making up this join for y must be in T, so $x\leqslant z$. Hence $y=\bigvee \{x | x\ll y\} \leqslant z$. We have shown $y\leqslant z$ for every y such that $y\ll b$. Now $b=\bigvee \{y | y\ll b\}$, hence $b\leqslant z$. Hence b is the least upper bound of T, proving the claim.

Now by initial assumption $a\ll b =\bigvee T$, and T is directed, so from the definition of way below relation, there exists $t\in T$ such that $a\leqslant t$. Also, since $t\in T$, by definition of T above, there exists c such that $t\ll c \ll b$. Since $a\leqslant t$ and $t\ll c$, by Proposition 3.15 this implies $a\ll c\ll b$, as required. $\square$

Definition 4.2

[5] (Scott open sets) A subset $U\subset \mathcal {M}$ is Scott open if the following hold:

• 1. U is an up set, that is, whenever $x\in U$ and $x\leqslant y$ then $y\in U$.

• 2. U is inaccessible by directed joins, that is, if $D\subset \mathcal {M}$ is directed, and $\bigvee D \in U$, then $U\cap D \ne \emptyset$.

Theorem 4.3

For every $x\in \mathcal {M}$, $I^+(x)$ is Scott open.

Proof

$I^+(x)$ is clearly an upper set of $\mathcal {M}$. Now, let $D\subseteq \mathcal {M}$ be directed such that $y= \bigvee D \in I^+(x)$. Then $x\ll y$, so by the Proposition 4.1 there exists $z\in \mathcal {M}$ such that $x\ll z\ll y$. Now $z\ll y=\bigvee D$ $\Rightarrow$ $z\leqslant d$ for some $d\in D$. Therefore we have $x\ll z\leqslant d$, which implies $x\ll d$ by Proposition 3.15. Therefore $d\in I^+(x)$. Then $d\in D\cap I^+(x)$, so $I^+(x)$ is Scott-open. $\square$

Proposition 4.4

The collection $\{I^+(x) | x\in \mathcal {M}\}$ forms a base for the Scott topology on P.

Proof

Let U be any Scott-open subset of $\mathcal {M}$. Let us consider any $x\in U$ and $y\in I^+(x)$. Then $x\ll y \Rightarrow x\leqslant y$. Therefore $y\in U$ as U is an up set. Hence $\bigcup _{x\in U}I^+(x) \subseteq U$. Also, if $z\in U$ then since $z=\bigvee \{x | x\ll z\}$ and $\Downarrow z$ is directed, therefore because of unaccessibility by directed joins, we have $x\in U$ for some $x\ll z$. Hence $z\in I^+(x)$ and $U\subseteq \bigcup _{x\in U}I^+(x)$. Therefore we must have $U=\bigcup _{x\in U}I^+(x)$. $\square$

Proposition 4.5

If U is Scott open in $\mathcal {M}$ and $x\in U$ then there exists $y\in U$ such that $y\ll x$.

Proof

In $\mathcal {M}$, $x=\bigvee \{y | y\ll x\}$. From Proposition 3.20$\{y\in \mathcal {M}| y\ll x\}$ is directed, hence since U is Scott open there exists $y\in U$ such that $y\ll x$. $\square$

Proposition 4.6

• (a) $\overline{I^+(x)}=\overline{J^+(x)} = \mathcal {M}$.

• (b) Int $(J^+(x))= I^+(x)$, where Int refers to the (topological) interior.

Proof

(a) Since ‘$\ll \;\;\Rightarrow \;\;\leqslant$’ but the converse is not true, we have $I^+(x) \subseteq J^+(x)$ and hence $\overline{I^+(x)} \subseteq \overline{J^+(x)}$. On the other hand, let $y\in \overline{J^+(x)}$ and take any Scott-open $U\subseteq \mathcal {M}$ such that $y\in U$. Since y is a limit point of $J^+(x)$, therefore $U\cap J^+(x) \ne \emptyset$. So there exists $z\in U,\; x\leqslant z$. Take any $t\in \mathcal {M}$ such that $z\ll t$. Then $t\in U$ as U is an up set. Then $x\ll t, t\in U$. Therefore $U\cap I^+(x) \ne \emptyset$. Hence any limit point of $J^+(x)$ is also a limit point of $I^+(x)$. Therefore $\overline{J^+(x)} \subseteq \overline{I^+(x)}$. This shows that $\overline{I^+(x)} = \overline{J^+(x)}$.

It is obvious that $\overline{I^+(x)} \subseteq \mathcal {M}$ for any $x \in \mathcal {M}$. To show the reverse inclusion, suppose $a \in \mathcal {M}$ and let $a \in U$ for some Scott open set U. Since U must be an up set by definition, hence $a\vee x\in U$ and $I^+(a\vee x)\subset U$. But $I^+(a\vee x)\subset I^+(x)$. Therefore $U\cap I^+(x) \ne \emptyset$. Thus a is a limit point of $I^+(x)$ and hence $a\in \overline{I^+(x)}$. Since this is true $\forall a\in \mathcal {M}$, therefore $\mathcal {M}\subseteq \overline{I^+(x)}$. Hence $\overline{I^+(x)}=\mathcal {M}=\overline{J^+(x)}$.

(b) $I^+(x) \subseteq J^+(x)$ and $I^+(x)$ is Scott open, so $I^+(x)\subseteq Int (J^+(x))$. For the reverse, suppose $z\in Int (J^+(x))$. Then there exists open U such that $z\in U \subseteq J^+(x)$. From Proposition 4.5 we can find $y\in U$ such that $y\ll z$. Now $y\in J^+(x)$, so $x\leqslant y\ll z$, hence $z\in I^+(x)$. $\square$

Remark 4.7

It is interesting that the above result is also true for the Alexandroff topology [15], which is the spacetime manifold topology for strongly causal spacetimes. However, the key difference that arises in the Scott topology is that the complete manifold $\mathcal {M}$ is the closure of the chronological and causal future of any spacetime point. Thus, for the Scott topology, the boundary of the chronological future of any point $x\in \mathcal {M}$ is $\mathcal {M}{\setminus } I^+(x)$. In the next proposition we prove some important connections between Alexandroff and Scott topologies.

Proposition 4.8

Let $\sigma (\mathcal {M})$ denote the Scott topology, $\alpha (\mathcal {M})$ the Alexandroff topology and $\tau (\mathcal {M})$ the manifold topology. We have $\sigma (\mathcal {M}) \subseteq \alpha (\mathcal {M}) \subseteq \tau (\mathcal {M})$. Also $\sigma (\mathcal {M}) \ne \alpha (\mathcal {M})$, otherwise this would violate causality.

Proof

That $\alpha (\mathcal {M}) \subseteq \tau (\mathcal {M})$, is well-known since the basis members of $\alpha (\mathcal {M})$ are sets of the type $I^+(a)\cap I^-(b)$ and these are in $\tau (\mathcal {M})$. To see that $\sigma (\mathcal {M}) \subseteq \alpha (\mathcal {M})$ it suffices to show $I^+(x) \in \alpha (\mathcal {M})$ for all $x\in \mathcal {M}$. Now $I^+(x)=\bigcup \{I^+(x) \cap I^-(y) | x\ll y\}$: If $z\in I^+(x)$ then $x\ll z$, and we can take any y such that $z\ll y$ thereby giving $z\in I^+(x)\cap I^-(y)$. Thus $I^+(x) \in \alpha (\mathcal {M})$ as required.

If $\sigma (\mathcal {M}) = \alpha (\mathcal {M})$ then $I^+(x)\cap I^-(y)$ would be an upper set whenever $x\ll y$. By interpolation find z such that $x\ll z\ll y$. Then $z\in I^+(x)\cap I^-(y)$, so $y\in I^+(x)\cap I^-(y)$ since $z\leqslant y$. This implies $y\ll y$, violating causality. $\square$

Remark 4.9

It was shown by Penrose [7, 18] that for strongly causal spacetimes $\alpha (\mathcal {M})=\tau (\mathcal {M})$.

5 Scott Spacetime lattices: some results

Definition 5.1

[5] (The S-property) A subset $X\subseteq \mathcal {M}$ has the property (S) provided the following is true:

(S): If $D\subseteq \mathcal {M}$ is directed and it has a supremum with $\bigvee D \in X$, then there is a $y\in D$ such that $x\in X$ for all $x\in D$ with $y\leqslant x$.

Proposition 5.2

The following is true for the spacetime $\mathcal {M}$:

• 1. $F\subseteq \mathcal {M}$ is Scott closed iff F is a down set closed under all directed sups that exist.

• 2. $\downarrow x =\overline{\{x\}}$ (closure in $\sigma (\mathcal {M})$, the Scott topology) for all $x\in \mathcal {M}$.

• 3. $\sigma (\mathcal {M})$ is $T_0$.

• 4. Every up set is the intersection of its Scott open neighbourhoods.

• 5. A set is Scott open iff it is an up set satisfying (S).

• 6. Every downset has property (S).

• 7. The collection of all subsets of $\mathcal {M}$ having property (S) is a topology on $\mathcal {M}$.

Proof

• 1. $(\Rightarrow )$: Assume F is Scott closed. Then it’s complement $\mathcal {M}{\setminus } F$ is open and hence is an up set. Therefore by Lemma 2.12F is a down set. Let $D\subseteq F$ be directed and $\bigvee D$ exists. If $\bigvee D \in \mathcal {M}{\setminus } F$, then there exists $d\in D$ such that $d\in \mathcal {M}{\setminus } F$ (since $\mathcal {M}{\setminus } F$ is Scott open), a contradiction. So $\bigvee D \in F$.

  $(\Leftarrow )$: We show $\mathcal {M}{\setminus } F$ is Scott open if F is a down set closed under all directed sups that exist. By Lemma 2.12$\mathcal {M}{\setminus } F$ is an up set. Now assume $D\subseteq \mathcal {M}$ is directed, has a supremum, and $\bigvee D \in \mathcal {M}{\setminus } F$. If for all $d\in D$ we have $d\in F$, then $D\subseteq F$ and hence $\bigvee D \in F$ (since F is closed under directed sups), a contradiction. Hence there exists $d\in D$ such that $d\in \mathcal {M}{\setminus } F$, so $\mathcal {M}{\setminus } F$ is Scott open.

• 2. Take $y\in \downarrow x$ (that is $y\leqslant x$), $y\in U$, U Scott open. If $x\notin U$, then $x\in \mathcal {M}{\setminus } U$ which is a down set by Lemma 2.12. So $y\leqslant x$ implies $y\in \mathcal {M}{\setminus } U$, which is a contradiction. So $x\in U$. Therefore y is a limit point of x, that is $y\in \overline{\{x\}}$. Now suppose $y\in \overline{\{x\}}$ and we need to show $y\leqslant x$. If $y\nleqslant x$ then $y\notin \downarrow x$. Now $\downarrow x$ is a down set by definition. Further to that if all elements d of a directed set D are in $\downarrow x$ (i.e. $d\leqslant x,\; \forall d\in D$), then by Proposition 2.19 we must have $\bigvee D\leqslant x$, or $\bigvee D\in \downarrow x$. Thus $\downarrow x$ is closed under directed joins. Therefore by (1) above we know that $\downarrow x$ is Scott closed. So $\mathcal {M}{\setminus } {\downarrow x}$ is Scott open, and $y\in \mathcal {M}{\setminus } \downarrow x$. Hence $(\mathcal {M}{\setminus } \downarrow x)\cap \{x\} \ne \emptyset$ (as y is a limit point of x). This gives $x\notin \downarrow x$, a contradiction. Thus $y\leqslant x$.

• 3. Assume $x\ne y$. Then either $x\nleqslant y$ or $y\nleqslant x$. Suppose $x\nleqslant y$. Then $x\in \mathcal {M}{\setminus } \downarrow y$ which is Scott open (as $\downarrow y$ is Scott closed as shown in (2) above), but $y\notin \mathcal {M}{\setminus } \downarrow y$. Similarly if $y\nleqslant x$, there is the Scott open set containing y but not x. Hence $\sigma (\mathcal {M})$ is $T_0$.

• 4. Let A be an up set. To show $A=\bigcap \{U | U { \text{ is } \text{ Scott } \text{ open }}\;,U\supseteq A\}$. Obviously intersection of Scott open sets (which are up sets) is an up set. Conversely let A be an up set and take $x\notin A$.Then for all $y\in A$ we have $y\nleq x$, that is, $y\notin \downarrow x$. Hence $y\in \mathcal {M}{\setminus } \downarrow x$ which is Scott open. Therefore $A\subseteq \mathcal {M}{\setminus } \downarrow x,\;\forall x\notin A$. Now $\bigcap \{\mathcal {M}{\setminus } \downarrow x | x\notin A\}= \mathcal {M}{\setminus }\bigcup \{\downarrow x | x\notin A\}=A$.

• 5. $(\Rightarrow )$: Suppose U is Scott open. Then U is an upper set. If D is a directed set with supremum, and $\bigvee D \in U$, then $D\cap U \ne \emptyset$. Let $y\in D\cap U$. Then $x\in D, y\leqslant x \implies x\in U$, so (S) is satisfied. $(\Leftarrow )$: Let U be an upper set satisfying (S). If $D\subseteq Q$ is directed with a supremum, and $\bigvee D \in U$, then there exists $y\in D$ with the (S) property. But $y\geqslant y$, so $y\in U$, i.e. $D\cap U \ne \emptyset$, so U is Scott open.

• 6. Let A be a downset. Let D be directed with supremum and $\bigvee D \in A$. Since all $d\in D \leqslant \bigvee D$ hence all $d \in A$. Fix a $y\in D$. Take any $x\in D$ with $y\leqslant x$. Now $x\leqslant \bigvee D$ so $x\in A$, hence A satisfies property (S).

• 7. Let $\mathcal {G}= \{G\subseteq \mathcal {M}| G \;\text{ has }\;\text{ property }\;S\}$. Clearly $\emptyset$ and $\mathcal {M}$ satisfy property (S). Now suppose $G_1$ and $G_2$ have property (S). Take $D\subseteq \mathcal {M}$ directed with supremum, and $\bigvee D\in G_1\cap G_2$. Then there exists $y_1\in D$ such that $x\in D, x\geqslant y_1 \implies x\in G_1$, and there exists $y_2\in D$ such that $x\in D, x\geqslant y_2 \implies x\in G_2$. Find $y_3 \in D$ such that $y_1, y_2 \leqslant y_3$ (By definition of a directed set, this is always possible). Then $x\in D, x\geqslant y_3 \implies x\in G_1\cap G_2$, so $G_1\cap G_2 \in \mathcal {G}$. Now suppose $G_\alpha \in \mathcal {G}$ for each $\alpha \in I$. To show $G=\bigcup G_\alpha \in \mathcal {G}$. Let D be directed with supremum such that $\bigvee D \in G$. Then there exists $\alpha _{0}$ such that $\bigvee D \in G_{\alpha _0}$. Since $G_{\alpha _0}$ has property (S) there exists $y\in D$ such that $x\in D, x\geqslant y \implies x\in G_{\alpha _0}$, so $x\in G$ proving that $G\in \mathcal {G}$.

$\square$

5.1 Scott closure and causal past

Proposition 5.3

In $\mathcal {M}$, $J^{-}(a)$ is Scott closed, and $\overline{I^{-}(a)}=J^{-}(a)$ (Closure in the Scott topology).

Proof

We use (i) of Proposition 5.2. $J^{-}(a) = \downarrow a$, which is a downset. Now suppose $D\subseteq J^{-}(a)$, D directed and $\bigvee D$ exists. Then $d\leqslant a$ for all $d\in D$, so $\bigvee D \leqslant a$, i.e. $\bigvee D \in J^{-}(a)$. Thus $J^{-}(a)$ is Scott closed.

Now $I^{-}(a)\subseteq J^{-}(a)$, and $J^{-}(a)$ is closed, so $\overline{I^{-}(a)}\subseteq J^{-}(a)$. For the reverse, take $x\in J^{-}(a)$ and U Scott open, $x\in U$. Then $x\leqslant a$. From the Proposition 4.5 we can find $y\in U$ such that $y\ll x$. Then $y\ll a$, so $y\in I^{-}(a)$ and $y\in U$, i.e. $U\cap I^{-}(a) \ne \emptyset$. Thus $x\in \overline{I^{-}(a)}$. Thus $J^{-}(a)\subseteq \overline{I^{-}(a)}\subseteq J^{-}(a)$. This is possible iff $\overline{I^{-}(a)}=J^{-}(a)$. $\square$

Proposition 5.4

$J^{-}(a)=\downarrow a =\overline{\{a\}}$ for every $a\in (\mathcal {M}, \sigma (\mathcal {M}))$.

Proof

This follows from (ii) Proposition 5.2. $\square$

Remark 5.5

The above proposition is extremely interesting in cosmological scenario. It says that the complete region within the cosmological horizon of a given spacetime point (observer at a given instant of time), constitutes the Scott closure of the point. Hence Scott closure of a point is the set of all points from which information can reach to the given point.

5.2 Irreducible sets and Sobriety

Definition 5.6

[19] A topological space $\mathcal {M}$ is called irreducible if whenever U and V are non-empty open subsets of $\mathcal {M}$ then $U\cap V \ne \emptyset$.

Proposition 5.7

$J^{-}(a)$ is an irreducible closed set in $(\mathcal {M},\sigma (\mathcal {M}))$, i.e. $J^{-}(a)$ cannot be written as a union of two proper closed sets.

Proof

Suppose not. Then there exists Scott closed sets $F_1$ and $F_2$ with $F_1\ne J^{-}(a), F_2\ne J^{-}(a)$ and $J^{-}(a)=F_1 \cup F_2$. Pick $x_1\in J^{-}(a), x_1\notin F_1$ and $x_2\in J^{-}(a), x_2\notin F_2$. Now $x_1\le a, x_2\le a \implies x_1\vee x_2 \le a \implies x_1\vee x_2 \in J^{-}(a) \implies x_1 \vee x_2 \in F_1$, say. This implies $x_1 \in F_1$ since $F_1$ is a down set. This is a contradiction. Similarly, we get a contradiction if $x_1\vee x_2 \in F_2$. Thus $J^{-}(a)$ is irreducible closed. $\square$

Proposition 5.8

  If there were an element $a\in \mathcal {M}$ such that $J^{-}(a)=\{a\}$, then $a\leqslant x$ for all $x\in \mathcal {M}$, i.e. a would be the smallest element in $\mathcal {M}$ and we can denote $a=0$. Moreover, a is the unique element with the property $J^{-}(a)=\{a\}$.

Proof

Assume $J^{-}(a)=\{a\}$. Take any $x\in \mathcal {M}$. Then $a\wedge x \leqslant a$, so $a\wedge x \in J^{-}(a) =\{a\}$. Hence $a\wedge x =a$, and this implies $a\leqslant x$. If $b\in \mathcal {M}$ were also an element such that $J^{-}(b)=\{b\}$, then $a\leqslant b$ and $b\leqslant a$, hence $b=a$, proving uniqueness of a. $\square$

Definition 5.9

[20] A topological space $\mathcal {M}$ is called a $T_1$ space if whenever $x\ne y$ there exists an open set U such that $x \in U$ but $y\notin U$, and there exists an open set V such that $y\in V$ but $x\notin V$. All Hausdorff spaces are $T_1$. An equivalent condition of $T_1$ is that all singleton sets are closed.

Theorem 5.10

$(\mathcal {M}, \sigma (\mathcal {M}))$ can never be $T_1$.

Proof

If it were, then for all $x\in \mathcal {M}$ we will have $J^{-}(x)=\overline{\{x\}}=\{x\}$. From the above Proposition 5.8 we would have $x=0$ for all x, hence $\mathcal {M}=\{0\}$ which is impossible. $\square$

Definition 5.11

  [20] A topological space $\mathcal {M}$ is called connected if it cannot be written as the disjoint union of two non-empty open sets. It is said to be locally connected at a point $p\in \mathcal {M}$ if whenever $p\in U, U$ open, there exists open connected V such that $p\in V\subseteq U$. $\mathcal {M}$ is said to be locally connected if it is locally connected at each of its points.

Remark 5.12

One can see from the Definitions 5.6 and 5.11 that in an irreducible space $\mathcal {M}$ every non-empty open set U must be connected. Thus an irreducible space is always connected and locally connected.

Proposition 5.13

$(\mathcal {M}, \sigma (\mathcal {M}))$ is an irreducible space, hence is connected and locally connected.

Proof

Take any two basic Scott open sets $I^+(a)$ and $I^+(b)$. Find $x\in \mathcal {M}$ such that $a\vee b\ll x$. Then $x\in I^+(a) \cap I^+(b)$, so $I^+(a) \cap I^+(b) \ne \emptyset$. This implies that if U and V are non-empty open sets in $\mathcal {M}$ then $U\cap V \ne \emptyset$. Hence $\mathcal {M}$ is irreducible. $\square$

Definition 5.14

[19] (Sobriety) A topological space is called sober if it is $T_0$ and every irreducible closed set is the closure of a unique point.

Proposition 5.15

$(\mathcal {M}, \sigma (\mathcal {M}))$ is not sober.

Proof

We show that the closed set $\mathcal {M}$ itself is an irreducible set, but there is no point $x\in \mathcal {M}$ such that $\mathcal {M}=\overline{\{x\}}$. So suppose $\mathcal {M}=F_1\cup F_2$ where $F_1$ and $F_2$ are closed subsets of $\mathcal {M}$. Then $(\mathcal {M}{\setminus } F_1)\cap (\mathcal {M}{\setminus } F_2)=\emptyset$. Since $\mathcal {M}$ is an irreducible topological space, we must have either $\mathcal {M}{\setminus } F_1 =\emptyset$ or $\mathcal {M}{\setminus } F_2 =\emptyset$. Thus either $F_1=\mathcal {M}$ or $F_2=\mathcal {M}$. Thus $\mathcal {M}$ cannot be written as a union of two proper closed subsets. Hence $\mathcal {M}$ is a closed irreducible set. If $\mathcal {M}=\overline{\{x\}}$ for some $x\in \mathcal {M}$, then from Proposition 5.4 we get $\mathcal {M}=J^-(x)$. This is impossible since if $y\in \mathcal {M}$ with $x\ll y$, then $y\notin J^-(x)$. Thus $\mathcal {M}$ is not sober. $\square$

Remark 5.16

The above result immediately shows that in $(\mathcal {M}, \sigma (\mathcal {M}))$, the spacetime points cannot be uniquely identified via the open sets or the irreducible closed set they are in. Thus the spacetime points do not have unique limit.

6 The dual Scott spacetime lattice: some results

Definition 6.1

A subset $S\subseteq \mathcal {M}$ is called filtered if whenever $a, b\in S$ then there exists $c\in S$ such that $c\leqslant a$ and $c\leqslant b$. This is the dual notion of a directed set. Let $\sigma _d(\mathcal {M})$ consist of all $L\subseteq \mathcal {M}$ with the following properties:

• (a) L is a downset.

• (b) Whenever $S\subseteq \mathcal {M}$ is filtered and has an infimum $\bigwedge S$ such that $\bigwedge S \in L$, then $L\cap S \ne \emptyset$.

Proposition 6.2

The collection $\sigma _d(\mathcal {M})$ is a topology on $\mathcal {M}$.

Proof

• (i) Clearly $\mathcal {M}\in \sigma _d(\mathcal {M})$, and $\emptyset \in \sigma _d(\mathcal {M})$ vacuously.

• (ii) Suppose $L_1$ and $L_2$ are in $\sigma _d(\mathcal {M})$. Then clearly $L_1\cap L_2$ is a downset. Suppose $S\subseteq \mathcal {M}$ is filtered, $\bigwedge S$ exists, and $\bigwedge S \in L_1\cap L_2$. Then $\bigwedge S \in L_1$ implies $L_1\cap S \ne \emptyset$, and $\bigwedge S \in L_2$ implies $L_2\cap S \ne \emptyset$. Pick $a\in S, a\in L_1$ and $b\in S, b\in L_2$. Since S is filtered, there exists $c\in S$ such that $c\leqslant a, c\leqslant b$. Thus $c\in L_1\cap L_2$, and hence $(L_1\cap L_2)\cap S \ne \emptyset$. Hence $L_1\cap L_2 \in \sigma _d(\mathcal {M})$.

• (iii) Assume $L_\alpha \in \sigma _d(\mathcal {M})$ for each $\alpha$ in some index set I, and let $L=\bigcup _{\alpha \in I}L_\alpha$. Then L is a downset. Now take $S\subseteq \mathcal {M}$ filtered having an infimum, and suppose $\bigwedge S \in L$. Then $\bigwedge S \in L_\alpha$ for some $\alpha$. This implies $L_\alpha \cap S \ne \emptyset$, and hence $L\cap S \ne \emptyset$. Thus $L\in \sigma _d(\mathcal {M})$. Thus $\sigma _d(\mathcal {M})$ is a topology on $\mathcal {M}$. $\square$

Let us refer to this topology as the dual Scott topology on $\mathcal {M}$.

Definition 6.3

[15] A continuous poset $(\mathcal {M},\leqslant )$ is called bicontinuous if:

• (i) For all $x,y \in \mathcal {M}$, $x\ll y$ iff for all filtered $S\subseteq \mathcal {M}$ with an infimum,

  $$\begin{aligned} \bigwedge S \leqslant x \implies \;\text{ there } \text{ exists }\; s\in S \;\text{ such } \text{ that }\;s\leqslant y. \end{aligned}$$

• (ii) For each $a\in \mathcal {M}$, $I^+(a)$ is filtered and $a=\bigwedge \{x | a\leqslant x\}$.

Proposition 6.4

$I^-(a)$ is open in the dual Scott topology $\sigma _d(\mathcal {M})$ for all $a\in \mathcal {M}$ iff $\mathcal {M}$ is bicontinuous.

Proof

$(\Leftarrow )$ Assume $\mathcal {M}$ is bicontinuous. We know that $I^-(a)$ is a downset. Suppose $S\subseteq \mathcal {M}$ is filtered, has an infimum, and $\bigwedge S \in I^-(a)$. Then $\bigwedge S \ll a$, so by interpolation there exists y such that $\bigwedge S \ll y \ll a$. By bicontinuity there exists $s\in S$ such that $s\leqslant y$. Hence $s\ll a$, so $s\in I^-(a)$. Thus $I^-(a)$ is open.

$(\Rightarrow )$ Assume $I^-(a)$ is open for all $a\in \mathcal {M}$. We need only show the first condition of bicontinuity. Suppose then that $x\ll y$, $S\subseteq \mathcal {M}$ is filtered, has an infimum, and $\bigwedge S\leqslant x$. Then $\bigwedge S \ll y$, so $\bigwedge S \in I^-(y)$. Since $I^-(y)$ is open, there exists $s\in S$ such that $s\in I^-(y)$. This implies $s\leqslant y$. Now suppose for all filtered $S\subseteq \mathcal {M}$ with infimum, $\bigwedge S \leqslant x$ implies there exists $s\in S$ such that $s\leqslant y$. We have to show $x\ll y$. Now $x=\bigwedge \{w | x\ll w\}$, and we know $I^+(x)$ is filtered, so there exists $w\in I^+(x)$ such that $w\leqslant y$. Then $x \ll w\leqslant y$ implies $x\ll y$, and we are done. $\square$

Similar to the fact that the sets $I^+(a)$, $a\in \mathcal {M}$, forms a base for the Scott topology on $\mathcal {M}$, we have:

Proposition 6.5

If $\mathcal {M}$ is bicontinuous, then the collection $\{I^-(a) | a\in \mathcal {M}\}$ forms a base for the dual Scott topology on $\mathcal {M}$.

Proof

We have seen from the above proposition that the sets $I^-(a)$, $a\in \mathcal {M}$ are all open in the dual Scott topology. To show these sets form a base for $\sigma _d(\mathcal {M})$, take any $L \in \sigma _d(\mathcal {M})$. We show that $L=\bigcup _{a\in L}I^-(a)$. Take any $a\in L$ and $x\in I^-(a)$. Then $x\ll a$, so $x\leqslant a$ and hence $x\in L$ since L is a downset. Thus $\bigcup _{a\in L}I^-(a) \subseteq L$. Now suppose $x\in L$. Now $x=\bigwedge \{a\in \mathcal {M}| x\ll a\}$. Since $I^+(x)$ is filtered and $x\in L$, there exists $a\in L$ such that $x\ll a$. Hence $x\in I^-(a)$, and we are done. $\square$

6.1 Relation with Alexandroff topology and strong causality

Remark 6.6

If $\tau _1$ and $\tau _2$ are topologies on a set $\mathcal {M}$, then the supremum $\tau _1 \vee \tau _2$ of these topologies exists, and is given as the intersection of all topologies on $\mathcal {M}$ that contain both $\tau _1$ and $\tau _2$. There is always a topology containing both of them, namely the discrete topology, and it can be checked that any intersection of topologies is also a topology.

Proposition 6.7

If $\mathcal {M}$ is bicontinuous then $\sigma (\mathcal {M})\vee \sigma _d(\mathcal {M}) =\alpha (\mathcal {M})$, the Alexandroff topology on $\mathcal {M}$.

Proof

We have seen earlier that $\sigma (\mathcal {M}) \subseteq \alpha (\mathcal {M})$. Now take any basic open set $I^-(a)$ in the dual Scott topology. Then $I^-(a) =\bigcup \{ I^+(x)\cap I^-(a) | x\ll a\}$: To see this, take any $z\in I^-(a)$. Then $z\ll a$. Take any x such that $x\ll z$. Then $z\in I^+(x)\cap I^-(a)$. Thus $I^-(a) \in \alpha (\mathcal {M})$ and hence $\sigma _d(\mathcal {M}) \subseteq \alpha (\mathcal {M})$. Therefore $\sigma (\mathcal {M})\vee \sigma _d(\mathcal {M}) \subseteq \alpha (\mathcal {M})$. For the other direction, take any basic open set $I^+(x)\cap I^-(y) \in \alpha (\mathcal {M})$. Now $I^+(x) \in \sigma (\mathcal {M})$, so $I^+(x)\in \sigma (\mathcal {M}) \vee \sigma _d (\mathcal {M})$. Similarly, $I^-(y)\in \sigma (\mathcal {M})\vee \sigma _d (\mathcal {M})$. Hence $I^+(x)\cap I^-(y) \in \sigma (\mathcal {M}) \vee \sigma _d (\mathcal {M})$, showing that $\alpha (\mathcal {M})\subseteq \sigma (\mathcal {M}) \vee \sigma _d (\mathcal {M})$. $\square$

Definition 6.8

[18] An open set $Q\subseteq \mathcal {M}$ is said to be causally convex if for every $x, y \in Q, \;x\ll z\ll y \implies z\in Q$.

Definition 6.9

[18] $\mathcal {M}$ is said to be strongly causal at p if p has arbitrarily small causally convex neighbourhoods, i.e. if $p \in U$, U open in $\mathcal {M}$, then there exists open Q such that $p\in Q\subseteq U$ and Q is causally convex.

Theorem 6.10

[18] The following three restrictions on a spacetime M are equivalent:

• (a) $\mathcal {M}$ is strongly causal;

• (b) the Alexandroff topology agrees with the manifold topology;

• (c) the Alexandroff topology is Hausdorff.

Remark 6.11

It seems that in the absence of the strong causality restriction, the Alexandroff topology should be $T_1$ at least, as we now show.

Proposition 6.12

$(\mathcal {M}, \alpha (\mathcal {M}))$ is $T_1$.

Proof

We will show that every singleton set $\{a\}$ is closed by showing that $\overline{\{a\}} =\{a\}$, where the closure is with respect to $\alpha (\mathcal {M})$. Let $b \in \overline{\{a\}}$. Then whenever $b \in I^+(x)\cap I^-(y)$ we have $a\in I^+(x)\cap I^-(y)$, i.e. whenever $x\ll b\ll y$, then $x\ll a\ll y$. Fix any y such that $b\ll y$. Then $x\ll b \implies x\ll b\ll y \implies x\ll a\ll y \implies x\ll a \implies x\leqslant a$. Thus $b=\bigvee \{x | x\ll b\} \leqslant a$.

Now fix x such that $x\ll b$. Then $b\ll y \implies x\ll b\ll y \implies x\ll a\ll y \implies a\ll y$. Now $a=\bigwedge \{y | a\ll y\} \leqslant \bigwedge \{y | b\ll y\} = b$, so $a\leqslant b$. Hence $b=a$, and therefore $\overline{\{a\}} =\{a\}$. Thus $(\mathcal {M}, \alpha (\mathcal {M}))$ is $T_1$. $\square$

Proposition 6.13

If spacetime $\mathcal {M}$ is strongly causal, then $(\mathcal {M},\alpha (\mathcal {M}))$ is sober.

Proof

From the above Theorem 6.10 the Alexandroff topology is Hausdorff, and it is well known that any Hausdorff topological space is sober. $\square$

7 Discussion

In this paper we treated the spacetime manifold in the same footing as a continuous lattice and established the following important results:

• 1. In the absence of any trapped surfaces, singularities and conjugate points for non-spacelike geodesics (e.g. spacetimes similar to Minkowski spacetime), it was shown that the spacetime manifold can be endowed with a natural lattice structure via the causal properties. It was further shown that this lattice will then be necessarily distributive.

• 2. We further explored this spacetime lattice in the light of continuous lattices and domain theory, via establishing an equivalence between the chronology and way-below relation.This enabled us to define the Scott topology on the spacetime manifold and explore the relationship between the Scott topology and Alexandroff topology (which is the manifold topology of a strongly causal spacetime). We could demonstrate that the Scott topology is a courser topology than that of Alexandroff, and it is necessarily contained in the Alexandroff topology. Although these two topologies can never be equal as that would definitely amount to breakdown of causality via closed timelike curves.

• 3. We further excavated some interesting results for the spacetime manifold endowed with the Scott topology, in terms of the closure of singleton points or it’s sobriety. It was interesting to note that although the manifold is sober under Alexandroff topology, it ceases to be sober under Scott topology.

• 4. Finally, we could also define a bicontinuous poset structure on the spacetime manifold and define a dual Scott topology on it. It is an important result that in the spaces of all manifold topologies (which is a lattice via the inclusion order), the join of Scott topology and it’s dual, is the Alexandroff topology.

It would be extremely interesting to explore these constructions, when trapped surfaces are present in the spacetimes. Especially studying the evolution of horizons, via the lattice theoretic picture. We keep this for our future work.

In contrast to the work done in [15], the authors considered a globally hyperbolic spacetime $\mathcal {M}$. By definition, a spacetime $\mathcal {M}$ is globally hyperbolic if it is strongly causal and the set $\uparrow {x} \cap \downarrow {y}$ is compact in the manifold topology for any $x, y \in \mathcal {M}$. Then the same authors in [16] proved a fundamental result, that a spacetime $\mathcal {M}$ is globally hyperbolic if it is a bicontinuous poset with point $a \in \mathcal {M}$ lying in the intersection of the chronological future of x and chronological past of y, i.e., $x \ll a \ll y$. On a bicontinuous poset, this is an open interval: $(x, y) = \{a \in \mathcal {M}| x \ll a \ll y \}$ and it forms a basis in the interval topology. This motivated the definition of a globally hyperbolic poset, that is, a poset is globally hyperbolic if it is bicontinuous and the closure of the interval $(x, y) = [x, y] = \{a \in \mathcal {M}| x \leqslant a \leqslant y\}$ is compact in the interval topology. Hence, any point $a \in \mathcal {M}$ lies in a closed and bounded set $\uparrow {x} \cap \downarrow {y}$. So in other words the authors have taken the compact interval [x, y] to be the casual diamonds of the spacetime manifold and these casual diamonds are compact in a spacetime manifold. Furthermore, the authors in [15] considered the interval poset from which they defined the interval domain which is also compact in the Scott topology (Scott compact). Then the authors established the equivalence between a globally hyperbolic spacetime and the interval domain and they obtained some results.

It is clear from the outset that both papers establishes the spacetime manifold as partially ordered set in the context of order theory and both papers have considered the concept of Scott topology. But the authors in [15] considered the interval topology which is the manifold topology on a globally hyperbolic spacetime and investigated the globally hyperbolic spacetime manifold under this interval topology. It is easy in that case to consider directed complete posets (dcpos) and domains, since the intervals are compact in the interval topology. In this paper we have taken an approach of not confining the spacetime to global hyperbolicity. Rather, we have considered the spacetime manifold under the standard manifold topology, which possesses difficulties in exploring the spacetime in the context of domain theory.