Modeling of MHD Casson Fluid Flow Across an Infinite Vertical Plate with Effects of Brownian, Thermophoresis, and Chemical Reactivity

Abstract

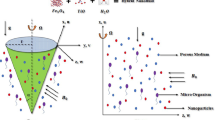
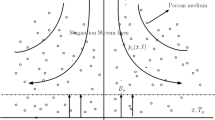
The current study presented here demonstrates the magnetohydrodynamics (MHD) Casson fluid flow within an infinite vertical plate with consequences of Brownian, thermophoresis, and chemically responsive systems. The governing equations are numerically computed by employing a sixth-order Runge–Kutta (R–K) algorithm, whereas Nachtsheim–Swigert (N–S) shooting iteration technique has been used as the main tool for calculating the current statement. The novelty of this study is dealing with the impression of Brownian and thermophoresis effect using shooting technique. The nonlinear governing problems have been transformed into coupled nonlinear ordinary differential equations using a suitable transformation. Numerical simulation is presented for the various interesting profiles. The velocity, temperature, and concentration profiles along with skin fraction, Nusselt, and Sherwood number take into account with the varying contributions of the parameters and deployed through graphs and tables. However, one of the current study’s key findings is that skin friction improves with expanding values of the thermal convective parameter while diminishing with increasing values of the Casson term, magnetic factor, and Eckert number. The current research has an enormous demand for Brownian and thermophoresis effects within the fields involving cosmology, power systems, ionized studies, and nanotechnology.

Appendix

When we differentiate E with regard to ${g}_{1}, {g}_{2}$ and ${g}_{3}$, we get

$$\delta_{1} \frac{{\partial \delta_{1} }}{{\partial g_{1} }} + \delta_{2} \frac{{\partial \delta_{2} }}{{\partial g_{1} }} + \delta_{3} \frac{{\partial \delta_{3} }}{{\partial g_{1} }} + \delta_{4} \frac{{\partial \delta_{4} }}{{\partial g_{1} }} + \delta_{5} \frac{{\partial \delta_{5} }}{{\partial g_{1} }} + \delta_{6} \frac{{\partial \delta_{6} }}{{\partial g_{1} }} = 0\quad ({\text{A)}}$$

$$\delta_{1} \frac{{\partial \delta_{1} }}{{\partial g_{2} }} + \delta_{2} \frac{{\partial \delta_{2} }}{{\partial g_{2} }} + \delta_{3} \frac{{\partial \delta_{3} }}{{\partial g_{2} }} + \delta_{4} \frac{{\partial \delta_{4} }}{{\partial g_{2} }} + \delta_{5} \frac{{\partial \delta_{5} }}{{\partial g_{2} }} + \delta_{6} \frac{{\partial \delta_{6} }}{{\partial g_{2} }} = 0\quad ({\text{B}})$$

$$\delta_{1} \frac{{\partial \delta_{1} }}{{\partial g_{3} }} + \delta_{2} \frac{{\partial \delta_{2} }}{{\partial g_{3} }} + \delta_{3} \frac{{\partial \delta_{3} }}{{\partial g_{3} }} + \delta_{4} \frac{{\partial \delta_{4} }}{{\partial g_{3} }} + \delta_{5} \frac{{\partial \delta_{5} }}{{\partial g_{3} }} + \delta_{6} \frac{{\partial \delta_{6} }}{{\partial g_{3} }} = 0\quad ({\text{C}})$$

By combining Eqs. (21) to (26), and (A), the following equation was created:

$$\left[ {\left( {\frac{{\partial f^{\prime}}}{{\partial g_{1} }}} \right)^{2} + \left( {\frac{\partial \theta }{{\partial g_{1} }}} \right)^{2} + \left( {\frac{\partial \varphi }{{\partial g_{1} }}} \right)^{2} + \left( {\frac{{\partial f^{\prime\prime}}}{{\partial g_{1} }}} \right)^{2} + \left( {\frac{{\partial \theta^{\prime}}}{{\partial g_{1} }}} \right)^{2} + \left( {\frac{{\partial \varphi^{\prime}}}{{\partial g_{1} }}} \right)^{2} } \right]\Delta g_{1} + \left( {\frac{{\partial f^{\prime}}}{{\partial g_{2} }}\frac{{\partial f^{\prime}}}{{\partial g_{1} }} + \frac{\partial \theta }{{\partial g_{2} }}\frac{\partial \theta }{{\partial g_{1} }} + \frac{\partial \varphi }{{\partial g_{2} }}\frac{\partial \varphi }{{\partial g_{1} }} + \frac{{\partial f^{\prime\prime}}}{{\partial g_{2} }}\frac{{\partial f^{\prime\prime}}}{{\partial g_{1} }} + \frac{{\partial \theta^{\prime}}}{{\partial g_{2} }}\frac{{\partial \theta^{\prime}}}{{\partial g_{1} }} + \frac{{\partial \varphi^{\prime}}}{{\partial g_{2} }}\frac{{\partial \varphi^{\prime}}}{{\partial g_{1} }}} \right)\Delta g_{2} + \left( {\frac{{\partial f^{\prime}}}{{\partial g_{3} }}\frac{{\partial f^{\prime}}}{{\partial g_{1} }} + \frac{\partial \theta }{{\partial g_{3} }}\frac{\partial \theta }{{\partial g_{1} }} + \frac{\partial \varphi }{{\partial g_{3} }}\frac{\partial \varphi }{{\partial g_{1} }} + \frac{{\partial f^{\prime\prime}}}{{\partial g_{3} }}\frac{{\partial f^{\prime\prime}}}{{\partial g_{1} }} + \frac{{\partial \theta^{\prime}}}{{\partial g_{3} }}\frac{{\partial \theta^{\prime}}}{{\partial g_{1} }} + \frac{{\partial \varphi^{\prime}}}{{\partial g_{3} }}\frac{{\partial \varphi^{\prime}}}{{\partial g_{1} }}} \right)\Delta g_{3} = - \left[ {\frac{{\partial f^{\prime}}}{{\partial g_{1} }}f^{\prime}_{c} + \frac{\partial \theta }{{\partial g_{1} }}\theta_{c} + \frac{\partial \varphi }{{\partial g_{1} }}\varphi_{c} + \frac{{\partial f^{\prime\prime}}}{{\partial g_{1} }}f^{\prime\prime}_{c} + \frac{{\partial \theta^{\prime}}}{{\partial g_{1} }}\theta^{\prime}_{c} + \frac{{\partial \varphi^{\prime}}}{{\partial g_{1} }}\varphi^{\prime}_{c} } \right] \quad ({\text{D}})$$

Again, implementing Eqs. (21) to (26) in equations (B), the gained equation is as follows:

$$\left[ {\left( {\frac{{\partial f^{\prime}}}{{\partial g_{2} }}} \right)^{2} + \left( {\frac{\partial \theta }{{\partial g_{2} }}} \right)^{2} + \left( {\frac{\partial \varphi }{{\partial g_{2} }}} \right)^{2} + \left( {\frac{{\partial f^{\prime\prime}}}{{\partial g_{2} }}} \right)^{2} + \left( {\frac{{\partial \theta^{\prime}}}{{\partial g_{2} }}} \right)^{2} + \left( {\frac{{\partial \varphi^{\prime}}}{{\partial g_{2} }}} \right)^{2} } \right]\Delta g_{2} + \left( {\frac{{\partial f^{\prime}}}{{\partial g_{2} }}\frac{{\partial f^{\prime}}}{{\partial g_{1} }} + \frac{\partial \theta }{{\partial g_{2} }}\frac{\partial \theta }{{\partial g_{1} }} + \frac{\partial \varphi }{{\partial g_{2} }}\frac{\partial \varphi }{{\partial g_{1} }} + \frac{{\partial f^{\prime\prime}}}{{\partial g_{1} }}\frac{{\partial f^{\prime\prime}}}{{\partial g_{2} }} + \frac{{\partial \theta^{\prime}}}{{\partial g_{1} }}\frac{{\partial \theta^{\prime}}}{{\partial g_{2} }} + \frac{{\partial \varphi^{\prime}}}{{\partial g_{1} }}\frac{{\partial \varphi^{\prime}}}{{\partial g_{2} }}} \right)\Delta g_{1} + \left( {\frac{{\partial f^{\prime}}}{{\partial g_{3} }}\frac{{\partial f^{\prime}}}{{\partial g_{2} }} + \frac{\partial \theta }{{\partial g_{3} }}\frac{\partial \theta }{{\partial g_{2} }} + \frac{\partial \varphi }{{\partial g_{3} }}\frac{\partial \varphi }{{\partial g_{2} }} + \frac{{\partial f^{\prime\prime}}}{{\partial g_{2} }}\frac{{\partial f^{\prime\prime}}}{{\partial g_{3} }} + \frac{{\partial \theta^{\prime}}}{{\partial g_{2} }}\frac{{\partial \theta^{\prime}}}{{\partial g_{3} }} + \frac{{\partial \varphi^{\prime}}}{{\partial g_{2} }}\frac{{\partial \varphi^{\prime}}}{{\partial g_{3} }}} \right)\Delta g_{3} = - \left[ {\frac{{\partial f^{\prime}}}{{\partial g_{2} }}f^{\prime}_{c} + \frac{\partial \theta }{{\partial g_{2} }}\theta_{c} + \frac{\partial \varphi }{{\partial g_{2} }}\varphi_{c} + f^{\prime\prime}_{c} \frac{{\partial f^{\prime\prime}}}{{\partial g_{2} }} + \theta^{\prime}_{c} \frac{{\partial \theta^{\prime}}}{{\partial g_{2} }} + \varphi^{\prime}_{c} \frac{{\partial \varphi^{\prime}}}{{\partial g_{2} }}} \right] \quad ({\text{E}})$$

Similarly, employing Eqs. (21) to (26) in equations (C), the collected equation is as follows:

$$\left[ {\left( {\frac{{\partial f^{\prime}}}{{\partial g_{3} }}} \right)^{2} + \left( {\frac{\partial \theta }{{\partial g_{3} }}} \right)^{2} + \left( {\frac{\partial \varphi }{{\partial g_{3} }}} \right)^{2} + \left( {\frac{{\partial f^{\prime\prime}}}{{\partial g_{3} }}} \right)^{2} + \left( {\frac{{\partial \theta^{\prime}}}{{\partial g_{3} }}} \right)^{2} + \left( {\frac{{\partial \varphi^{\prime}}}{{\partial g_{3} }}} \right)^{2} } \right]\Delta g_{3} + \left( {\frac{{\partial f^{\prime}}}{{\partial g_{2} }}\frac{{\partial f^{\prime}}}{{\partial g_{3} }} + \frac{\partial \theta }{{\partial g_{2} }}\frac{\partial \theta }{{\partial g_{3} }} + \frac{\partial \varphi }{{\partial g_{2} }}\frac{\partial \varphi }{{\partial g_{3} }} + \frac{{\partial f^{\prime\prime}}}{{\partial g_{3} }}\frac{{\partial f^{\prime\prime}}}{{\partial g_{2} }} + \frac{{\partial \theta^{\prime}}}{{\partial g_{3} }}\frac{{\partial \theta^{\prime}}}{{\partial g_{2} }} + \frac{{\partial \varphi^{\prime}}}{{\partial g_{3} }}\frac{{\partial \varphi^{\prime}}}{{\partial g_{2} }}} \right)\Delta g_{3} + \left( {\frac{{\partial f^{\prime}}}{{\partial g_{3} }}\frac{{\partial f^{\prime}}}{{\partial g_{1} }} + \frac{\partial \theta }{{\partial g_{3} }}\frac{\partial \theta }{{\partial g_{1} }} + \frac{\partial \varphi }{{\partial g_{3} }}\frac{\partial \varphi }{{\partial g_{1} }} + \frac{{\partial f^{\prime\prime}}}{{\partial g_{1} }}\frac{{\partial f^{\prime\prime}}}{{\partial g_{3} }} + \frac{{\partial \theta^{\prime}}}{{\partial g_{1} }}\frac{{\partial \theta^{\prime}}}{{\partial g_{3} }} + \frac{{\partial \varphi^{\prime}}}{{\partial g_{1} }}\frac{{\partial \varphi^{\prime}}}{{\partial g_{3} }}} \right)\Delta g_{1} = - \left[ {f^{\prime}_{c} \frac{{\partial f^{\prime}}}{{\partial g_{3} }} + \theta_{c} \frac{\partial \theta }{{\partial g_{3} }} + \varphi_{c} \frac{\partial \varphi }{{\partial g_{3} }} + \frac{{\partial f^{\prime\prime}}}{{\partial g_{3} }}f^{\prime\prime}_{c} + \frac{{\partial \theta^{\prime}}}{{\partial g_{3} }}\theta^{\prime}_{c} + \frac{{\partial \varphi^{\prime}}}{{\partial g_{3} }}\varphi^{\prime}_{c} } \right]\quad ({\text{F}})$$