1 Introduction

In a wire coating (WC) process, the wire is placed into a fluid bath containing a polymer molten, then into a mold that wipes the fluid and produces a coating of the required shape. In a manner, its the movement of the air that flows via the polymer and brings it into the mold. The flux in the die is a pull flux by a fixed cross-sectional equivalent to the state of the pivotal loop withdrawal flow or a flight Couette flow. Very Little information is present in the existing research on the topic of the WC problem about its solution through stochastic techniques. Maximum literature on the WC system solution methodologies is based on deterministic infrastructure, i.e., Denn [1] and Middleman’s [2] books are provided the fundamental design of WC problem simulation in a viscous fluid. Akter and Hashmi [3, 4] introduced a WC mathematical paradigm where the non-Newtonian fluid follows the constituent systems of energy rule fluid. They studied the impact of viscosity change through the illustration of the WC operation. The attention in the research of non-Newtonian fluids has grown in the last few years. The equations governing these fluids’ movement present many defies for engineers, mathematicians, physicists, and modelers. Non-Newtonian mathematical models for WC analysis are based on stiff nonlinear differential equations and normally exact analytical solutions of complex mathematical models are not available in the literature. Therefore, a variety of numerical as analytical techniques is introduced by the research community to handle the complexities of the system by finding approximate solutions [5,6,7,8,9,10,11,12,13]. Moreover, Mitsoulis [14] investigated the flow of WC with heat transfer. Sajid et al. [15] applied Sisko fluid for the WC system by using the homotopy analysis method. The Oldroyd 8–constant fluid was utilized for analysis of WC by Shah et al. [16]. Sajid et al. [17] studied the MHD flow of an Oldroyd 8–constant fluid for analysis of WC in a pressure–type coating die. Zeeshan et al. [18] developed the differential type non-Newtonian system for WCA. Shah et al. [19] also studied the WC system for differential type fluidic system in the presence of heat transfer. The existing literature on WC analysis is deeply investigated by using numerical and analytical deterministic approaches for the solution of the WC system subjected to different types of Newtonian and non-Newtonian fluids. On the other hand, artificial intelligence-based numerical soft computing solver is comparatively less discovered and analyzed in the WC system-related problems, especially for WC systems in different flow dynamics.

The artificial intelligence-based numerical solvers are established primarily by the modeling artificial neural networks (ANN) and different back-propagation search approaches for solving a range of problems centered on ordinary and partial differential systems. Recent applications based on the soft computing solvers include nonlinear systems emerging in the fluid dynamics [20,21,22], biological mathematics [21, 23, 24], financial system model [25], neuro-fuzzy model [26], pantograph system [27,28,29], mathematical models in plasma physics [30], COVID-19 virus spread model [31], Lane–Emden model [21], magnetohydrodynamics problem [32], delay differential equation system [33], and Heat conduction model [34] are little under significant examples of these solutions. Such facts inspire the authors to explore and incorporate soft computing architectures as an alternative, precise, and feasible computational approach for solving the fluid mechanic’s systems associated with the WC system. In this research work, a stochastic solver based on the back-propagation of the Levenberg–Marquardt method is exploited for solving the WC mathematical system by performing a parametric analysis to investigate the influences or different physical parameters on the velocity profile. Mathematica and MATLAB applications are used for numerical analysis. The creative ideas into the suggested computing models are illustrated as follows:

  • A new implementation centered intelligent computing of the artificial intelligence is introduced using Levenberg–Marquardt back-propagation based supervised neural network (LMB-SNN) for interpreting the analysis of MHD-TGFWCA.

  • The original mathematical formulation in terms of PDEs for MHD-TGFWCA is converted into a dimensionless nonlinear system of ODEs.

  • A dataset for proposed LMB-SNN is produced for the analysis of fluidic flow system MHD-TGFWCA based physical quantities associated with the system consist of ODEs using state-of-the-art Adams numerical technique.

  • The training, validation, and testing operations of the LMB-SNN are developed for MHD-TGFWCA in terms of different scenarios, and comparison with the reference results confirms the accuracy of the suggested LMB-SNN.

  • Mean squared-based convergence analysis, regression plots, and histograms representations are constructed for the cases of MHD-TGFWCA, which further validate the accuracy and convergence of the designed solver.

The remaining parts of the manuscript are organized as follows: The problem formulation of magnetohydrodynamic flux (MHD) of a viscoelastic fluid for the examination of WC is described in Sect. 2. The solution methodology of the suggested LMB-SNN on various variables of MHD-TGFWCA is briefly explained in Sect. 3. The results and discussion are presented in Sect. 4. The final fifth section consists of the conclusion of the study.

2 Mathematical Model

Fig. 1
figure 1

Wire-coating operations

Full size image

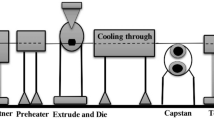
Here, let us discuss a WC process in which the flow reaches a control leak unit connected to the melting chamber. The flow joins the pressure unit after moving through the melting chamber. In this situation, the pressure put the coating on the wire. Then, a speed control motor powers the bull-block next, injuring a coated wire. The typical dynamics system of the problem can be seen in Figs. 1 and 2. Where L is mold length, and \(R_w\) is the wire radius. We suppose in our problem the following:

  • The flux of the molten polymer is laminar.

  • The third grade is the fluid under study.

  • The flow is concentric.

  • At every point z, the axial fluid pressure is independent on the radial length r.

Fig. 2
figure 2

Geometry of the problem

Full size image

We consider the momentum and continuity equations for third grade fluid as following [29]:

$$\begin{aligned}&\nabla \cdot \overrightarrow{{\varvec{V}}}=0, \end{aligned}$$
(1)
$$\begin{aligned}&\rho \frac{D \overrightarrow{{\varvec{V}}}}{D t}=J \times B+\nabla \cdot T. \end{aligned}$$
(2)

The velocity domain and the nonzero stress are

$$\begin{aligned} \overrightarrow{{\varvec{V}}}=0 i+0 j+w^*(r) k, \quad P=P(r). \end{aligned}$$
(3)

The Maxwell’s equations for electrically conducting fluid are

$$\begin{aligned}&\nabla \cdot E=0, \end{aligned}$$
(4)
$$\begin{aligned}&\nabla \times E=0, \end{aligned}$$
(5)
$$\begin{aligned}&\nabla \times B=\mu J. \end{aligned}$$
(6)

Moreover, the Ohm’s law as following:

$$\begin{aligned} J=\sigma (E+w^* \times B), \end{aligned}$$
(7)

where E is the electric field, J is current density, \(\sigma \) is electric conductivity, and \(\mu \) is magnetic permeability. The magnetic field \(B=b+B_o\) is perpendicular to the velocity domain \(w^*\), and the induced magnetic force b is insignificant compared to the applied magnetic force, resulting in a reduced magnetic Reynolds number (Re). Relying on these considerations, especially for low magnetic Re, the magnetohydrodynamic force is

$$\begin{aligned} J \times B=- B_{o}^{2} \sigma w^*. \end{aligned}$$
(8)

From Eqs. 1, 2, 3, and 8, supposing there is no pressure gradient along the flow path, the momentum Eq. 2 transform to the dimensional governing equation of the proposed WC as follows:

$$\begin{aligned}&2\left( \tau _{1}+\tau _{2}\right) \frac{d}{d r}\left[ r\left( \frac{d w^{*}}{d r}\right) ^{3}\right] +\frac{\eta }{r} \frac{d}{d r}\left( r \frac{d w^{*}}{d r}\right) \nonumber \\&\quad -\sigma B_{o}^{2} w^{*}=0, \end{aligned}$$
(9)

with boundary conditions

$$\begin{aligned} \begin{array}{l} w^*\left( R_{\mathrm {w}}\right) =V_1, \quad w^*\left( R_{d}\right) =V_2, \end{array} \end{aligned}$$
(10)

where \(\tau _1\) and \(\tau _2\) are constants, \(w^*\) denotes the dimensional velocity in the trend of \(\mathbf {r}\), \(R_d\) is the radius of the mold, \(\eta \) represents the viscosity coefficient of the fluid, and \(V_2\) is the speed of the gas around the coated wire.

The dimensionless variables/parameters as following:

$$\begin{aligned}&w^{`}=\frac{w^*}{V_{1}}, \quad r^{`}=\frac{r}{R_{w}}, \quad \tau _{o}=\tau _{1}+\tau _{2}, \quad \frac{R_{d}}{R_{w}}=\delta >1, \nonumber \\&\beta =\frac{\tau _{o}}{\mu \left( \frac{R_{w}^{2}}{V_{1}^{2}}\right) }, \quad \frac{V_{2}}{V_{1}}=U, \quad M^{2}=\frac{\sigma B_{o}^{2} R_{w}}{\mu }. \end{aligned}$$
(11)

Using Eq. 11, we get:

$$\begin{aligned}&r \frac{d^{2} w}{d r^{2}}+\frac{d w}{d r}+2 \beta \left[ 3 r \frac{d^{2} w}{d r^{2}}\left( \frac{d w}{d r}\right) ^{2}+\left( \frac{d w}{d r}\right) ^{3}\right] \nonumber \\&\quad -M^{2} w =0, \end{aligned}$$
(12)

with boundary conditions

$$\begin{aligned} w(1)=1, \,w(\delta )=u, \end{aligned}$$
(13)

where w denotes the dimensionless velocity in the trend of \(\mathbf {r}\), third grade fluid parameter \(\beta \), magnetic parameter M, and the velocity ratio u.

3 Solution Methodology

There are two techniques for neural network training: unsupervised and supervised. Unsupervised learning requires the neural network to make a perception of the inputs values without the help and guidance of a user. In the present study are used supervised learning which both the input values and the output values are given. The neural network then procedures the input data and relates the consequent outputs to the target values. Errors are then propagated back via the scheme, allow the scheme to modify the weights that regulate the neural network.

The complete design of the operations flow paradigm can be seen in Fig. 3. The suggested LMB-SNN is carried out using the ’nftool’ routine in MATLAB, whereas training the neural network weight is carried out using the Levenberg–Marquardt Backpropagation Method.

Numerical simulation for LMB-SNN is provided here for the WC analysis model with third grade fluid shown in Eqs. 12 and 13. The suggested LMB-SNN is implemented for three different scenarios by the impact of \(\beta \), M, and u, for all cases of MHD-TGFWCA as shown in Table 1, i.e., every parameter given in Eqs. 12 and 13 has four cases using different values of the MHD flow analysis of a third grade fluid for wire coating process have been numerically solved by the SNN-LMB scheme.

Dataset for LMB-SNN is determined for inputs between 1 and 2 with a time interval of 0.001 by using the solutions of state-of-the-art numerical technique throughout the ’NDSolve’ a numerical solver for differential equations in the Mathematica software package for every variant of the WC analysis model with third grade fluid as shown in Table 1. The reference solutions for w(r) for 1001 input points are chosen randomly to create and design a set with 40 is the number of hidden neurons and 80 \(\%\) of data values for training, 10 \(\%\) validation, and 10 \(\%\) for testing, respectively. The LMB-SNN-based computational model structure of neural networks with Levenberg–Marquardt back-propagation of the designed network is presented in Fig. 4.

Table 1 Detailing of scenarios along with cases for MHD-TGFWCA
Full size table
Fig. 3
figure 3

Scheme process of the suggested LMB-SNN for the WC analysis model with third grade fluid

Full size image
Fig. 4
figure 4

Design of suggested Neural network

Full size image
Fig. 5
figure 5

Performance of the LMB-SNN for testing, validation, and training procedures of Case 4 in the wire coating analysis model with third grade fluid

Full size image
Fig. 6
figure 6

Performance of LMB-SNN in terms of Gradient, Mu, and validation checks of Case 4 in the wire coating analysis model with third grade fluid

Full size image
Fig. 7
figure 7

Error-Histogram views of the LMB-SNN procedures for Case 4 in the wire coating analysis model with third grade fluid

Full size image
Fig. 8
figure 8

Regression views of the LMB-SNN results for Case 4 of scenario 3 in the WC analysis model with third grade fluid, The top left and right sub-figures are results for training and validation samples, respectively, while bottom left and right sub-figures are for the results of testing and all samples, respectively

Full size image
Fig. 9
figure 9

Comparison of reference solutions with LMB-SNN outcomes for case 4 in the wire coating analysis model with third grade fluid

Full size image
Table 2 Results of LMB-SNN for Scenario1 of the WC analysis model with third grade model fluid
Full size table
Table 3 Outcomes of LMB-SNN for second Scenario of the WC analysis model for third grade fluid
Full size table
Table 4 Outcomes of LMB-SNN for third Scenario of the WC analysis model for third grade fluid
Full size table
Fig. 10
figure 10

Comparison between suggested LMB-SNN with results of numerical reference for scenario 1 in the wire coating analysis model with third grade fluid

Full size image
Fig. 11
figure 11

Comparison between suggested LMB-SNN with results of numerical reference for scenario 2 in the wire coating analysis model with third grade fluid

Full size image
Fig. 12
figure 12

Comparison between suggested LMB-SNN with results of numerical reference for scenario 3 in the wire coating analysis model with third grade fluid

Full size image

4 Results and Discussion

The outputs of LMB-SNN for each case of all variants involved in MHD-TGFWCA in terms of performance are shown in Fig. 5, while states are shown in Fig. 6. Also, diagrams of histograms are given in Fig. 7, whereas Fig. 8 demonstrated regression parameters of MHD-TGFWCA. The explanation related to fitting parameters is illustrated in Fig. 9. Moreover, the convergence achieved in terms of performance index, MSE, back-propagation mechanism, completed epochs, and time participations are listed in Tables 2, 3, and 4 for scenarios 1-3 of MHD-TGFWCA.

The best fit is characterized by training lost, validation lost, and testing lost that lower to a stability point with a small gap between the three final lost worth’s. The loss of the LMB-SNN model is almost always lesser on the dataset than on the testing and validation datasets. This implies that a gap between the train, test, and validation lost learning curves should be expected. Fig. 5a–c provides a convergence of mean square error for a train, test, and validation best curves are given for the fourth case of scenarios 1, 2, and 3 of MHD-TGFWCA. It can be seen that the lost training curve lowers to the stability point. Also, the testing and validation loss plots reduce to a stability point and have a tiny gap with the training lost curve, indicating that a learning curves plot show the best fit and the most perfect and united execution is carried out at 91, 101, and 57 epochs with MSE in the range \(10^{-13}\), \(10^{-13}\), and \(10^{-12}\), respectively. The gradient and Mu parameters of Levenberg–Marquardt back-propagation are (\(9.71\times 10^{-08}\), \(9.97\times 10^{-08}\), and \(9.20\times 10^{-08}\)) and (\(10^{-14}\)) as given in Fig. 6a–c. The results indicate the precision and convergence efficiency of the LMB-SNN procedure for every case of MHD-TGFWCA.

The dynamics of the performance is further analyzed by error histogram as shown in Fig. 7a–c for scenarios 1, 2, and 3, respectively, of MHD-TGFWCA. The average error value closed to zero axes or at \(8.24\times 10^{-09}\), \(-3\times 10^{-08}\), and \(7.5\times 10^{-08}\)) for respective 1, 2, and 3 scenarios of MHD-TGFWCA. The investigation throughout regression training is performed by means of co-relation analyses. Figure 8 is the regression outputs of one variation of MHD-TGFWCA given in Eqs. 12 and 13. It can be seen that the worths of correlation index R are closed to unity, i.e., good modeling scenario, in a situation of training, testing as well as validation, which approved the correctness of LMB-SNN methodology for MHD-TGFWCA.

The efficacy of LMB-SNN-based outputs obtained is identified with matching results of Adams numerical solver for scenarios 1, 2, and 3 of MHD-TGFWCA, as illustrated in Fig. 9 and further supported by graphs of error. The maximum error for testing, training, and validation inputs of the structure LMB-SNN are around \(1\times 10^{-5}\), \(1\times 10^{-5}\), \(2\times 10^{-6}\), and \(1\times 10^{-6}\) for different cases of system MHD-TGFWCA.

Moreover, Tables 2, 3, and 4 present results of the process of LMB-SNN for solving each case of all three scenarios of MHD-TGFWCA using ‘nftool,’ i.e., a routine used for neural network fitting tool in Matlab software which lists the details of the study with varying number of epochs, grad, Mu (i.e., step-size of back-propagation), time participations, MSE for testing, training, and validation of learning algorithm and their performance. The respective numerical values established in Tables 2, 3, and 4 for scenarios 1-3 of the velocity parameter of MHD-TGFWCA show that performance on MSE for the suggested LMB-SNN process is around \(10^{-13}\), \(10^{-13}\), and \(10^{-12}\) to \(10^{-13}\) for MHD-TGFWCA. All numerical outputs and illustrations provided in Tables 2, 3, and 4 confirm the robust, consistent, and accurate performance of LMB-SNN for solving the variants of MHD-TGFWCA.

As a result, the LMB-SNN outcomes are analyzed for the dimensionless velocity distribution for all three scenarios of the MHD-TGFWCA as seen in Figs. 10, 11, and 12. The outcomes of the LMB-SNN corresponded to the numerical solutions of the Adams numerical method for each scenario. It can be seen from Fig. 10a that the rise of the third grade fluid parameter and the velocity ratio slightly increase the fluid velocity w(r) in the flow dynamics of MHD-TGFWCA, while the velocity profile is decreasing by the rise of the magnetic parameter as shown in Fig. 11a. Furthermore, Fig. 12a describes that the high value of the velocity ratio increases the velocity profile. Figures 10b, 11b, and 12b indicate that the A–E is about \(10^{-5}\) to \(10^{-9}\), \(10^{-6}\) to \(10^{-8}\), and \(10^{-5}\) to \(10^{-9}\) for all scenarios of MHD-TGFWCA, respectively. The numerical and graphical diagrams show the validity and worth of the solver LMB-SNN based on the precise accuracy, convergence, and powerful performance analysis for the solution of MHD-TGFWCA.

5 Conclusion

In this work, the integrated stochastic numerical computing solver is discussed for finding the solution of fluid mechanics problem representing the WC process using magneto–hydrodynamic (MHD) flow of a third grade fluid based on various scenarios for the parameter of third grade fluid, the parameter of magnetic, and the velocity ratio. The training (\(80\%\)), validation (\(10\%\)), and testing (\(10\%\)) are exploited to create structured LMB-SNNs with 40 number of hidden neurons. The MSE level \(10^{-05}\) to \(10^{-09}\) accessed the accuracy of the suggested design based on LMB-SNNs. In addition, the correctness is verified by numerical and graphical illustrations for the convergence plots on MSE index, error histograms as well as regression dynamics. We found that the rise of the third grade fluid parameter (\(\beta \)) and the velocity ratio (u) enhances the velocity fluid in the flow dynamics of the proposed problem, while the rise of the magnetic parameter (M) reduces the magnetohydrodynamic flow impact near the surface.

In the future, one may utilize the intelligent computing of backpropagated with the Levenberg–Marquardt method to clarify and better solve fluid mechanics problems [13, 35, 36].