Skip to main content
SpringerLink
Log in

Design, Modelation and Numerical Simulation of a Novel Artefact for Coordinate Measuring Machines Calibration Based on Laser Trilateration

  • Research Article - Mechanical Engineering
  • Published:
Arabian Journal for Science and Engineering Aims and scope Submit manuscript

Abstract

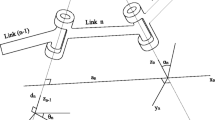
There are several methods and corresponding artefacts to assess Coordinate Measuring Machine (CMM) errors. In this paper, we present a novel method based on a designed new artefact that can be seen as a simplification of the hexapod machine, commonly used in several contexts in engineering, to determine the CMM’s global errors. The artefact is constituted by a set of three fixed spheres connected by telescopic links to a moving sphere which is the reference for CMM calibration. By comparison of the coordinates of the center of the moving sphere measured by the artefact system against the correspondent coordinates measured by the CMM, the global errors of the machine are determined. Shifting the moving sphere, the links’ variations are measured by laser interferometry using the laser interferometers installed in the interior of the telescopic links. Applying the equations of trilateration, the coordinates of the moving sphere center are determined. However, it is necessary prior knowledge of the artefact geometry and of the initial links length which should be done by calibrating the artefact. To avoid the difficult and expensive artefact calibration, we develop a method which performs the self-calibration of the artefact, by shifting the moving sphere on the same plane defined by the other three. The self-calibration of the artefact is done solving a nonlinear problem both with and without constraints. Finally, we present some results obtained from extensive simulations.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

References

  1. Bartscher, M.; Busch, K.; Schwenke, H.; Trapet E.; Wäldele, F.: Artefact based traceability concept for large co-ordinate measuring machines (CMMs), Proceedings of the 9th Metrologie Conference, Bordeaux, France. pp. 158–161 (1999)

  2. International Organization for Standardization, ISO Guide to the Expression of Uncertainty in Measurement (GUM). Geneva, Switzerland (1995)

  3. Facas Vicente, M.A.: Numerical Simulation of New 3-Dimensional Coordinate Measuring Machine’s Calibration Artefacts, Ph.D. Thesis, University of Coimbra, Department of Mathematics of the Faculty of Sciences and Technology, Coimbra, Portugal (2007) (in Portuguese)

  4. Facas Vicente M.A.: A new artefact, hexapod based, for local calibration of coordinate measuring machines. Arab. J. Sci. Eng. 36, 355–373 (2011)

    Article  Google Scholar 

  5. Cauchick-Miguel, P.; King T.; Davis, J.: CMM verification: a survey, Measurement, 17(1), 1–16 (1996)

  6. Sartori, S.; Zhang, G.X.: Geometric error measurement and compensation of machines. Ann. CIRP 44/2 (1995)

  7. Caskey, G.W.; Phillips, S.D.; Borchardt, B.R.; Ward, D.E.; Sawyer, D.S.: A users guide to NIST SRM 2084: CMM probe performance standard, Technical Report NIST Special Publication pp. 260–120, National Institute of Standards and Technology, USA (1994)

  8. Trapet, E.: Asseguramiento de la Calidad para Máquinas de Medir por Coordenadas, Physikalisch Technische Bundesantalt (1991)

  9. Knapp W.: Circular test for three-coordinate measuring machines and machine tools. Precis. Eng. 5(3), 115–124 (1983)

    Article  MathSciNet  Google Scholar 

  10. Knapp, W.: Accuracy of length measurement and positioning statistical measurement and contouring mode. Ann. CIRP 37 (1988)

  11. Knapp W., Tschudi U., Bucher A.: Comparison of different artefacts for interim coordinate measuring machine checking. Precis. Eng. 13(4), 277–291 (1991)

    Article  Google Scholar 

  12. Kunzmann H., Wäldele F.: On testing coordinate measuring machines (CMM) with kinematics references standards. Ann. CIRP. 32, 465–468 (1983)

    Article  Google Scholar 

  13. Woolet M.: Rapid error correction of CMM for squareness, twist and scaling errors. Adv. Manuf. Eng. 1, 35–41 (1988)

    Google Scholar 

  14. Kunzmann H., Trapet E., Wäldele F.: An uniform concept for calibration, acceptance test, and periodic inspection of coordinate measuring machines using reference objects. Ann. CIRP 39, 561–564 (1990)

    Article  Google Scholar 

  15. Trapet E., Wäldele F.: Determination of the parametric error of CMMs and machine tools using reference objects. VDI Berichte. 761, 163–175 (1989)

    Google Scholar 

  16. Schussler, H.H.: Quadrangular test body for the acceptance and monitoring of coordinate measuring instruments, PTB Me-38, pp. 93–118 (1983)

  17. Rohde, J.: Laser calibration for the 90s. Quality Today 16 (1991)

  18. Schussler, H.H.: Automatic bidirectional laser-step gauge, in 1st IMEKO TC 14, Budapest, pp. 49–69 (1986)

  19. Tasic T., Acko B.: Integration of a laser interferometer and a CMM into a measurement system for measuring internal dimensions. Measurement 44, 426–433 (2011)

    Article  Google Scholar 

  20. Nafi A., Mayer J.R.R., Wozniak A.: Novel CMM-based implementation of the multi-step method for the separation of machine and probe errors. Precis. Eng. 35, 318–328 (2011)

    Article  Google Scholar 

  21. Dang Q.C., Yoo S., Kim S.-W.: Complete 3-D self-calibration of coordinate measuring machines. CIRP Ann. Manuf. Technol. 55(1), 527–530 (2006)

    Article  Google Scholar 

  22. Antunes, S.D.; Antunes, P.M.V.C.D.; Vicente, M.A.F.: Local and Global Calibration of Coordinate Measuring Machines, Advanced Mathematical and Computational Tools in Metrology V, Series on Advances in Mathematics for Applied Sciences, vol. 57, World Scientific, Singapore (2001), pp. 16–22

  23. Antunes, S.D.; Vicente, M.A.F.: Estimation of Precision and Uncertainty of a Calibration Artefact for CMMs, Advanced Mathematical and Computational Tools in Metrology VI, Series on Advances in Mathematics for Applied Sciences, vol. 66, World Scientific, Singapore (2004), pp. 1–15

  24. Schmitz T., Ziegert J.: A new sensor for the micrometre-level measurement of three-dimensional dynamic contours. Meas. Sci. Technol. 10, 51–62 (1999)

    Article  Google Scholar 

  25. Takamasu, K.; Murui, I.; Sato, O.; Olea, G.; Furutani, R.: Calibration of Three Dimensional Mechanism - Novel Calibration Method for 3DOF Parallel Mechanism, IEEE ICIT’02, Bangkok, Thailand (2002)

  26. Bosscher, P.; Ebert-Uphoff, I.: A Novel Mechanism for Implementing Multiple Collocated Spherical Joints, Proceedings of the 2003 IEEE International Conference on Robotics & Automation, Taipei, Taiwan, September 14–19 (2003)

  27. Nocedal J., Wright S.J.: Numerical Optimization. Springer, New York (1999)

    Book  MATH  Google Scholar 

  28. Frandsen, P.E.; Jonasson, K.; Nielsen, H.B.; Tingleff, O.: Unconstrained Optimization, Informatics and Mathematical Modelling. Technical University of Denmark, Copenhagen (2004)

  29. Hart G.W.: Multidimensional Analysis: Algebras and Systems for Science and Engineering. Springer, New York (1995)

    Book  MATH  Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Department of Mathematics, Faculty of Sciences and Technology, University of Coimbra, Apartado 3008, 3001-454, Coimbra, Portugal

    M. A. Facas Vicente

Authors
  1. M. A. Facas Vicente
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to M. A. Facas Vicente.

Additional information

Supported by INESC-C—Instituto de Engenharia de Sistemas e Computadores—Coimbra, Rua Antero de Quental, 199, 3000-033 Coimbra, Portugal.

Work carried within the agreement between the Department of Mathematics of the University of Coimbra and IPQ—Instituto Português da Qualidade (Portuguese Institute for Quality).

Rights and permissions

Reprints and permissions

About this article

Cite this article

Facas Vicente, M.A. Design, Modelation and Numerical Simulation of a Novel Artefact for Coordinate Measuring Machines Calibration Based on Laser Trilateration. Arab J Sci Eng 38, 1519–1528 (2013). https://doi.org/10.1007/s13369-013-0537-x

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s13369-013-0537-x

Keywords

Search

Navigation