1 Introduction

The promise of aeroelastic tailoring was to develop a design framework that could enhance aircraft structural performance at large. The idea sees great recognition in the research community in the 1980s with important works by Shirk et al. [1] and Weisshaar et al. [2], and recent developments by Stanford et al. [3], and Stodiek et al. [4]. State-of-the-art aeroelastic tailoring practices have developed frameworks to solve the problem at a wing level. The results in terms of weight saving, load alleviation and/or range optimization are very promising, thus justifying the further development in this field.

The early studies [1, 2] explored the potential of aeroelastic tailoring using a single-fiber angle, thus describing most of the fundamental phenomena observed in composite wings and how to prevent them by inducing a beneficial bend-twist coupling.

In the late 1990s, aeroelastic tailoring research started to focus on laminates with different fiber angles through the thickness, an approach that increased the level of complexity of the models to describe more realistic composite structures. There are three main approaches to this problem found in literature, namely using (1) laminates with a fixed thickness, but varying fiber angles, (2) laminates with a fixed set of fiber angles, and varying thickness and (3) laminates with both varying fiber angles and varying thickness.

The first approach, where the thickness is kept constant, has been solved with evolutionary algorithms [5,6,7] or fiber steering [3, 4, 8] to maximize flutter speed. Both approaches already show significant improvements in overall aeroelastic performance due to varying stiffness along the span of the wing compared to the classic approach with straight fibers.

The second approach, with a fixed set of discrete ply angles, provides a solution to comply with certification requirements, reduce the number of design variables [9,10,11] and improve aeroelastic performance under different set of constraints including buckling, strains and aileron effectiveness.

The aeroelastic framework developed by De Breuker et al. [12] focuses on the third approach where both fiber angles and thickness are modeled as design variables to explore the full potential of aeroelastic tailoring and simplify the formulation of the optimization problem. In contrast to working with fiber angles directly, the formulation where both thickness and fiber angles are varying can be described in the continuous domain using lamination parameters thus making this problem fit for gradient-based solvers and optimization frameworks. The first description in lamination parameters was introduced by Kameyama et al. [13]. The approach was first proved for a flat composite panel, where the set of lamination parameters and thickness was calculated for maximum flutter speed. The work of Jin et al. [14], and Dillinger et al. [15] has scaled this approach to solve a similar problem for the whole wing, modeled as a multitude of chordwise and spanwise panels for a more detailed description of a composite wingbox and its structural elements.

In view of a more complete analysis, it is important to understand the classic aeroelastic phenomena in the context of the whole aircraft, in particular with respect to the interaction of the wing with fuselage and tails. The first problem encompasses the solution to the flow around the full-aircraft configuration, in particular in the area near the wing–body junction. A very extensive explanation of the fuselage aerodynamics, including the effects of the wing–body interaction and its importance, is found in the work of Singh et al. [16]. The main contributions of the fuselage aerodynamics are a large pitching moment and a destabilizing neutral point shift upstream. A minor contribution is the increase of effective angle of attack at the root of the wing. The lift generated by the fuselage itself is negligible. Further details regarding the interaction phenomena in a full-aircraft configuration are found in the work of Rusak et al. [17]. Another important point to discuss is the vortex shedding of the body. According to Rusak et al. [17], although there is no comprehensive model to describe the phenomenon, experimental evidence shows how the effect of the body wake on the longitudinal aerodynamic coefficient is of orders of magnitude smaller, thus negligible.

To summarize, the advancement in low- and medium-fidelity physical models for the description of the aeroelastic framework has made new solutions available at the preliminary design level. Already in the early phases of the design process, it is possible to develop a framework for analysis and optimization which is capable to select an improved design candidate for the more detailed phases ahead. Certification aspects and manufacturability constraints are also important parts of the problem that can be incorporated at this level. The benefit of the low-fidelity approach is in the capability of exploring a wide range of the design space at a relative small computational effort or cost. A preliminary study of this size would be almost unfeasible with any 2D or 3D finite element description.

In that spirit, the aim of this paper is to build on the state-of-the-art aeroelastic framework developed at Delft University of Technology by De Breuker et al. [12] and explore the effects of a full-aircraft aerodynamic model on a structurally optimized design via aeroelastic tailoring including material failure, buckling and aileron effectiveness constraints. After an introduction to the aeroelastic framework in Sect.  2, we will discuss the fuselage aerodynamic model (Sect.  3), the full-aircraft aerodynamics (Sect.  5) and aeroelastic solution (Sect. 6). The optimization framework and results are discussed in Sect.  7, while conclusions and recommendation are in Sect. 8.

2 Aeroelastic framework

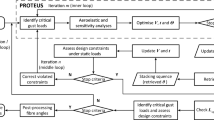
This works builds upon the aeroelastic framework (PROTEUS) developed at Delft University of Technology initiated by De Breuker et al. [12]. The framework serves as an analysis and optimization tool for preliminary design of composite wings. The flow is described by means of a continuous-time state-space model, as extensively described in the work of Werter et al. [18]. The three-dimensional composite wing structure is idealized by a Timoshenko beam by means of a cross-sectional modeler.

The function of the cross-sectional modeler is twofold. First, it is used to calculate the equivalent one-dimensional beam properties starting from the three-dimensional wing model. This is done by means of a thin-walled cross-sectional modeler that was developed based on the work by Willaert et al. [19] and Ferede et al. [20]. The cross-section is discretized in linear Hermitian beam elements having constant properties and can be any arbitrary open or closed, thin-walled, composite cross-section. Using a variational asymptotic approach, the Timoshenko cross-sectional stiffness and mass properties can be determined. The second function of the cross-sectional modeler is the strain recovery. This process converts the one-dimensional beam strains into surface strains. These surface strains include both the Euler–Bernoulli strains and the second-order free warping solution.

The strain field is then used in the assessment of the material failure by means of the failure envelope derived by Ijsselmuiden et al. [21]. The main challenge during the optimization is that the classic composite strength failure criteria cannot be used since the stacking sequence of the laminates is unknown. The failure enveloped is a Tsai–Wu-based criterion that ensures no failure regardless of the ply angle. The derivation of the failure envelope criterion as a function of the principal strains is found in Khani et al. [22].

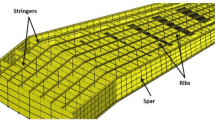
The surface strains are also used to calculate the buckling solution and the buckling index. In a conventional wingbox structure, the buckling panels are defined as the area between two stringers and two ribs. Structural stability is thus assessed in a local sense. Stringers and ribs are assumed to be stiff enough to prevent global buckling. The analytical model is based on the work of Dillinger et al. [23], where the individual panels are assumed to be flat and the bending displacement solution is approximated with two-dimensional shape functions obtained from Lobatto (bubble) polynomials.

The aerodynamic and structural models are closely coupled into a unified framework for analysis and optimization. More details regarding the framework and its functionalities are found in the work of Werter et al. [24, 25]. The analytical formulation of the buckling and aileron effectiveness constraint is extensively discussed in Dillinger et al. [15]. The main additions to the state-of-art aeroelastic framework, namely the fuselage aerodynamics (Sect. 3) and the full-aircraft trim solution (Sect. 6), are presented in this paper.

3 Fuselage aerodynamics

The aerodynamics of the fuselage is described by means of a source panel distribution. The work by Hess et al. [26] and Katz and Plotkin [27] discusses the two main options for body aerodynamics, namely (1) a source distribution along the center line and (2) a source distribution on the fuselage wetted surface. The first model is more appropriate for bodies of revolution, while for more complex body shapes the second one is preferred. For the purposes of this work, a source distribution on the wetted surface has been adopted.

The fuselage aerodynamics is described by potential flow theory. Flow separation, turbulence and the wake shed by the body are not included in this work. Furthermore, the source panel distribution does not allow for wake modeling. The work by Rusak et al. [17] discusses the challenges of modeling such a physical phenomena should this be of interest to the reader.

The different theories behind the source distribution is given in the work by Katz and Plotkin [27]. A distribution of constant strength source panels has been chosen to describe the aerodynamics of the fuselage. The method is based on the Laplacian of the disturbance velocity potential \(\varPhi\),

$$\begin{aligned} \nabla ^2\varPhi = 0, \end{aligned}$$
(1)

with flow tangency condition,

$$\begin{aligned} \nabla \varPhi \cdot \mathbf{n } = \mathbf{0 }, \end{aligned}$$
(2)

and the far-field condition as

$$\begin{aligned} \lim _{r\rightarrow \infty }\nabla \varPhi =0, \end{aligned}$$
(3)

where r refers to the distance from the body. The velocity potential at an arbitrary point P due to a constant strength quadrilateral source \(\sigma\) is:

$$\begin{aligned} \varPhi (\mathbf{P }) = \dfrac{\sigma }{4\pi }\int _s\dfrac{\mathrm{d}S}{\sqrt{(x - x_0)^2 + (y - y_0)^2 + z^2}}, \end{aligned}$$
(4)

while the local velocity can be derived from the potential \(\varPhi\) as

$$\begin{aligned} \mathbf{u } = \dfrac{\partial \varPhi }{\partial \mathbf{P }}. \end{aligned}$$
(5)

By solving Eq.  4, and differentiating with respect to P, one can obtain the expressions for the local velocity components (u, v and w) in each segments, as derived in Katz and Plotkin [27].

Force calculation Hereby the system of equations that describes the flow around the body is given. Neumann boundary conditions are adopted, with the far-field condition being satisfied by definition of the quadrilateral constant strength source panels, and the flow tangency condition enforced. For a single panel, the flow is described by the following equation:

$$\begin{aligned} \mathbf{v }\cdot \mathbf{n } + \mathbf{v }_\infty \cdot \mathbf{n } = 0, \end{aligned}$$
(6)

where \(\mathbf{v }^T = \{v_x, v_y, v_z\}\) is the velocity at the collocation point, and \(\mathbf{v }_\infty\) is the far-field velocity vector in the body reference frame; thus,

$$\begin{aligned} \mathbf{v }_\infty = \left[ V_\infty \cos \alpha ,\,\,\,0,\,\,\,V_\infty \sin \alpha \right] . \end{aligned}$$
(7)

Applying the same logic to the rest of the body panels, the following system of equations is written as

$$\begin{aligned} \mathbf{A }\varvec{}{\sigma } = - \mathbf{B }, \end{aligned}$$
(8)

with \(\mathbf{A }\) being the aerodynamic influence coefficient matrix, \(\varvec{}{\sigma }\) the source strength, and B the vector with its \(i\text {th}\) element being the product \(\left( \mathbf{v }_i\cdot \mathbf{n }_i\right)\) for the \(i\text {th}\) panel.

Once the source strength distribution is known, the panel velocities can be calculated. The equations are written for the velocity components of one panel. Assembling the equations for all the panels leads to a system of equations in matrix format for each velocity component; thus,

$$\begin{aligned} {\left\{ \begin{array}{ll} \mathbf{v }_x = \mathbf{A }_x\,\varvec{}{\sigma }\\ \mathbf{v }_y = \mathbf{A }_y\,\varvec{}{\sigma }\\ \mathbf{v }_z = \mathbf{A }_z\,\varvec{}{\sigma }, \end{array}\right. } \end{aligned}$$
(9)

where v\(_x\), v\(_y\) and v\(_z\) are vectors containing, respectively, the x, y and z components of the velocity in each panel. The pressure distribution is then derived as a function of the panel velocities. The pressure coefficient is generally expressed as

$$\begin{aligned} C_\mathrm{p} = 1 - \dfrac{V^2}{V_\infty ^2}. \end{aligned}$$
(10)

For a single panel k, let \(\mathbf{R }_k\) be the transformation matrix from the body-frame to the local panel coordinates, the local velocity vector can be written as

$$\begin{aligned} \mathbf{v }_k = \mathbf{R }_k \left( \mathbf{v }_\infty + \mathbf{v }_k\right) , \end{aligned}$$
(11)

thus,

$$\begin{aligned} C_\mathrm{p} = 1 - \dfrac{||\mathbf{v }_k||^2}{V_\infty }. \end{aligned}$$
(12)

The force vector F, normal to the panel, is then given by

$$\begin{aligned} \mathbf{F } = -\dfrac{1}{2}\rho _\infty C_\mathrm{p} S V_\infty ^2 \cdot \mathbf{n }, \end{aligned}$$
(13)

with S being the surface area.

Wing–body interaction problem

Fig. 1
figure 1

Detail of wing–fuselage intersection. Diamond collocation points, circle corner points

Full size image

Interrupting the wing at the fuselage intersection would result in a discontinuity in the vortex distribution which will not end at the symmetry plane. The discontinuity will lead to a strong vortex being generated at the root of the wing, that is not counteracted by its symmetric part thus influencing the neighboring body panels. This condition is also not realistic since a vortex at the midplane is not representative of the physical phenomena.

A possible solution is discussed by Rusak et al. [17] which entails extending the wing panels to the midplane. The extension of the panels will immediately solve the problem of the discontinuity at the midplane shedding no extra vortices within the body. The tangency condition is omitted from the wing panels within the body, and the collocation point is removed. This modification to describe the physics of the wing–body interaction is illustrated in Figs. 1, 2.

Fig. 2
figure 2

Fuselage model used for verfification

Full size image

4 Verification with literature

The implementation has been validated against the work by Singh et al. [16], proving both analytical and experimental reference results on the model shown in Fig. 3a, with the wing located at 4.0 m along the fuselage symmetry line. The wing is rectangular with a 8.8-m span and a 1.5-m chord. An extensive description of the model is found in Singh et al. [16]. The results of the comparison are shown in Fig. 3, where the pressure coefficient is sampled at different radial positions \(\theta\). The sign convention chosen for the radial position is shown in Fig. 3b.

The overall trends are in good agreement. There are two main differences between the model used in the present work and the one by Singh et al. [16] that ultimately cause the differences observed in the results. The differences are due to (1) the wing models used in the studies, and (2) the different models for the wing–body interaction. In particular,

  • in the work by Singh et al. [16], the wing collocation points are defined on the wetted surface, with the panels modeling the 3D airfoil, whereas in the present work, the airfoil is reduced to its camber line thus not modeling the airfoil thickness. In the former case, the forces are thus perpendicular to the local airfoil wetted surface, as opposed to being perpendicular to the camber line (locally) as in the latter case. This explains the slight shift observed in the peak force;

  • the wing–body interaction model used in the present work is not needed if the full 3D wing is modeled. In the numerical model in Singh et al., the wing panels will end at the junction meeting the fuselage panels. A discussion with regard to the differences with the experimental data presented in Singh et al. [16] has not been found.

Fig. 3
figure 3

Fuselage \(C_p\), in comparison with the work of Singh et al. [16]

Full size image

5 Full-aircraft aerodynamic model

The aerodynamic models of wing, horizontal tail and fuselage are hereby summarized:

$$\begin{aligned} {\left\{ \begin{array}{ll} \mathbf{A }_\text {W}\varvec{}{\varGamma _\text {W}} &{}= \mathbf{B }_\mathbf{W }\\ \mathbf{A }_\text {HT}\varvec{}{\varGamma _\text {HT}} &{}= \mathbf{B }_\mathbf HT \\ \mathbf{A }_\text {F}\varvec{}{\sigma } &{}= \mathbf{B }_\mathbf{F }, \end{array}\right. } \end{aligned}$$
(14)

with \(\mathbf{A }\) being the aerodynamic influence coefficients of fuselage (F), wing (W) and horizontal tail (HT), \(\varvec{}{\sigma }\) the fuselage source strength, and \(\varvec{}{\varGamma }\) the vortex strength.

The derivation of the vortex-lattice models for wing and horizontal tail is extensively discussed in the work of Werter et al. [24, 25].

To couple the three equations and obtain the full-aircraft aerodynamic model, the following aerodynamic influence coefficients are needed, namely

  • wing on fuselage, and horizontal tail (\(\mathbf{A }_\text {W,F}\), \(\mathbf{A }_\text {W,HT}\)),

  • horizontal tail on fuselage, and wing (\(\mathbf{A }_\text {HT,F}\), \(\mathbf{A }_\text {HT,W}\)),

  • fuselage on wing, and horizontal tail (\(\mathbf{A }_\text {F,W}\), \(\mathbf{A }_\text {F,HT}\)).

The system of equations can then be written as

$$\begin{aligned} \left[ \begin{array}{ccc} \mathbf{A }_\text {W} &{} \mathbf{A }_\text {W,HT} &{} \mathbf{A }_\text {W,F}\\ \mathbf{A }_\text {HT,W} &{} \mathbf{A }_\text {HT} &{} \mathbf{A }_\text {HT,F}\\ \mathbf{A }_\text {F,W} &{} \mathbf{A }_\text {F,HT} &{} \mathbf{A }_\text {F} \end{array} \right] \left[ \begin{array}{c} \varvec{}{\varGamma }_\mathbf{W }\\ \varvec{}{\varGamma }_\mathbf HT \\ \varvec{}{\sigma } \end{array} \right] = \left[ \begin{array}{c} \mathbf{B }_\mathbf{W }\\ \mathbf{B }_\mathbf HT \\ \mathbf{B }_\mathbf{F } \end{array} \right] . \end{aligned}$$
(15)

Once the source and vortex strength distribution is known across all the panels, the forces are calculated. The force distribution along the fuselage is given by Eq. 13. For wing and horizontal tail, the force is given by the Kutta–Jukowski theorem. With i and j being the spanwise and chordwise indexes, the lift expression for a single panel (identified with the indexes i, j) is given by

$$\begin{aligned} L_{i,j} = {\left\{ \begin{array}{ll} \rho V_\infty \varGamma _{i,j}\varDelta y_{i,j}, &{} \text {if } j = 1\\ \rho V_\infty \left( \varGamma _{i,j}-\varGamma _{i,j-1}\right) \varDelta y_{i,j}, &{} \text {if } j \ne 1, \end{array}\right. } \end{aligned}$$
(16)

where \(\varDelta y_{i,j}\) is the width of the i, j panel. The pressure difference is then given by

$$\begin{aligned} \varDelta p_{i,j} = \dfrac{L_{i,j}}{S_{i,j}}, \end{aligned}$$
(17)

with \(S_{i,j}\) being the area of the panel.

6 Static aeroelastic solution

The fully non-linear aeroelastic solution is given by

$$\begin{aligned} {\left\{ \begin{array}{ll} \mathbf{F }_s = \mathbf{F }_a + \mathbf{F }_\text {ext}\\ L = W\\ M_\text {CG} = 0, \end{array}\right. } \end{aligned}$$
(18)

where the subscripts s, a and ext refer to the internal, aerodynamic and external forces, respectively.

The solution to the static problem is described by the displacement vector p, the trim angle of attack \(\alpha\) and the horizontal tail angle of attack \(\delta\). Expanding the non-linear system with a first-order Taylor series with respect to p, \(\alpha\) and \(\delta\), the system of equation can be written as

$$\begin{aligned} {\left\{ \begin{array}{ll} \dfrac{\partial \mathbf{F }_s}{\partial \mathbf{p }}\varDelta \mathbf{p } + \mathbf{F }_{s,0} = \mathbf{F }_{a,0} + \mathbf{F }_{\text {ext},0} + \dfrac{\partial (\mathbf{F }_a+\mathbf{F }_\text {ext})}{\partial \mathbf{p }}\varDelta \mathbf{p } +\dfrac{\partial (\mathbf{F }_a+\mathbf{F }_\text {ext})}{\partial \alpha }\varDelta \alpha +\dfrac{\partial (\mathbf{F }_a+\mathbf{F }_\text {ext})}{\partial \delta }\varDelta \delta \\ L_0 + \dfrac{\partial L}{\partial \mathbf{p }}\varDelta \mathbf{p } + \dfrac{\partial L}{\partial \alpha } \varDelta \alpha + \dfrac{\partial L}{\partial \delta } \varDelta \delta = \mathbf{W }\\ \mathbf{M }_{\text {CG},0} + \dfrac{\partial \mathbf{M }_\text {CG}}{\partial \mathbf{p }}\varDelta \mathbf{p } + \dfrac{\partial \mathbf{M }_\text {CG}}{\partial \alpha }\varDelta \alpha + \dfrac{\partial \mathbf{M }_\text {CG}}{\partial \delta }\varDelta \delta = \mathbf{0 }, \end{array}\right. } \end{aligned}$$
(19)

where the subscript 0 refers to the initial value of the forces.

It is important to notice that (1) the internal forces (\(\mathbf{F }_s\)) do not depend on the angle of attack of the wing, nor the horizontal tail deflection, and (2) the weight is independent of all three state variables.

The linearized equations can be now written in matrix format. Remembering that the derivatives of the forces F\(_s\), F\(_a\) and F\(_\text {ext}\) with respect to p are nothing other than the definition of the stiffness matrices, the system can also be written as

$$\begin{aligned} \left[ \begin{array}{ccc} \mathbf{K }_s-(\mathbf{K }_a+\mathbf{K }_\text {ext}) &{} -\dfrac{\partial \mathbf{F }_a}{\partial \alpha } -\dfrac{\partial \mathbf{F }_\text {ext}}{\partial \alpha } &{} -\dfrac{\partial \mathbf{F }_a}{\partial \delta } -\dfrac{\partial \mathbf{F }_\text {ext}}{\partial \delta }\\ \dfrac{\partial \mathbf{L }}{\partial \mathbf{p }} &{} \dfrac{\partial \mathbf{L }}{\partial \alpha } &{} \dfrac{\partial \mathbf{L }}{\partial \delta }\\ \dfrac{\partial \mathbf{M }_\text {CG}}{\partial \mathbf{p }} &{} \dfrac{\partial \mathbf{M }_\text {CG}}{\partial \alpha } &{} \dfrac{\partial \mathbf{M }_\text {CG}}{\partial \delta }\\ \end{array} \right] \left[ \begin{array}{c} \varDelta \mathbf{p }\\ \varDelta \alpha \\ \varDelta \delta \end{array} \right] = \left[ \begin{array}{c} \mathbf{F }_{a,0} + \mathbf{F }_{\text {ext},0} - \mathbf{F }_{s,0}\\ \mathbf{W } - \mathbf{L }_0\\ -\mathbf{M }_{\text {CG},0} \end{array} \right] \end{aligned}$$
(20)

or in a more compact format

$$\begin{aligned} \mathbf{J }\mathbf{x } = \mathbf{R }_0, \end{aligned}$$
(21)

where \(\mathbf{x }^T = \{\mathbf{p },\,\,\,\alpha ,\,\,\,\delta \}\), J referred to as the Jacobian of the system, and R\(_0\) is the residual. The states of the trim condition can be thus calculated as

$$\begin{aligned} \mathbf{x } = \mathbf{J }^{-1}\mathbf{R }_0. \end{aligned}$$
(22)

This approach is suitable for non-linear methods provided the stiffness matrices and force vectors are updated. For linear static aeroelasticity the system can be solved in a single iteration.

In case the configuration is not to be trimmed, the solution becomes trivial since \(\varDelta \alpha\) and \(\varDelta \delta\) are prescribed. The solution can be derived from the first line of Eq. 20.

7 Aeroelastic tailoring studies

7.1 Objective and constraints

Table 1 Details of constraint limits and margins of safety
Full size table

The objective of the optimizations is minimizing the structural mass of the composite wing by optimizing its thickness and stiffness distribution, described as a function of lamination parameters. As discussed in Sect. 1, the formulation in terms of lamination parameters is continuous and is thus suitable for gradient-based optimizers. The present work uses the globally convergent method of moving asymptotes (GCMMA) as presented by Svanberg [28].

The constraints adopted for the aeroelastic tailoring optimization and their relative margins of safety (MS) or limits are summarized in Table 1. The margins of safety combine both certification aspects (according to CS25) and knockdown factors, with reference to the work of Kassapoglou [29].

7.2 Optimization set-up

The aircraft model used for the aeroelastic tailoring studies hereby discussed is based on the NSRFootnote 1 benchmark aircraft. The geometric description of the wing and the non-structural mass, taken into account for the purposes of these studies, are shown in Fig.  4. The loadcases adopted for the study can be found in Table  2.

Fig. 4
figure 4

Details of the NSR wing model. MLG main landing gear

Full size image
Table 2 Overview of static load cases
Full size table

The NSR aircraft has been modeled with a flexible composite wing, a rigid horizontal tail and rigid fuselage. At the start of the optimization, the wing has a zero-dominated layup (60% in 0, 10% in 90 and 30% in \(\pm\,\, 45\)) for top and bottom skin and quasi-isotropic (QI) spars. Such stiffness distribution is widely used as a reference in aeroelastic tailoring, as discussed in Dillinger et al. [23], for more realistic estimation of the weight-saving potential of aeroelastic tailoring as opposed to a QI initial design which is highly over-designed.

Three aeroelastic tailoring optimizations have been run on the NSR-wing model: (1) using a wing aerodynamic model as shown in Fig. 5, (2) a wing–tail aerodynamic model, Fig. 6 and (3) a full-aircraft aerodynamic description as in Fig. 7. The design variables for each of the three optimizations are the lamination parameters and the thickness of the composite wing. The goal of the study is to observe the difference in optimum design due to a change in loads because of (1) the moment equilibrium due to the horizontal tail, and (2) the extra lift generated by the fuselage.

Fig. 5
figure 5

Wing aerodynamic model (ID = 0)

Full size image
Fig. 6
figure 6

Wing–tail aerodynamic model (ID = 1)

Full size image
Fig. 7
figure 7

Aircraft aerodynamic mode (ID = 2)

Full size image

7.3 Optimization results

Table 3 Converged objective in comparison
Full size table
Fig. 8
figure 8

Convergence of the objective functions

Full size image

The wing-only optimization (ID = 0) converged to a final structural mass of 1700 kg, which will be used as a reference for this discussion. As shown in Table 3, the wing–tail (ID = 1) is 2.5% lighter, whereas the aircraft (ID = 2) shows an increase in structural mass of approximately 11%. The convergence history of the objective function is shown in Fig. 8. These results can be explained by looking at the physics behind aeroelastic tailoring, and some of the results shown in Appendices A through C.

Fuselage influence The first effect of the fuselage aerodynamic model is a drop of lift at the root of the wing, namely the area at the midline that lies within the fuselage. Since the aircraft is to remain trimmed at a given flight point, the wing has to generate more lift, hence its resultant will shift outboard. For a swept back wing, an outboard shift of the lift resultant also implies that its application point moves towards the rear of the aircraft. The shift of the aerodynamic center alters its relative position with respect to the center of gravity, thus changing the dynamics of the whole aircraft.

The fuselage is also responsible for inducing a relatively large nose-up moment (assumed positive in this paper). The reason behind the introduction of this moment has to do with the shape of the fuselage and its rotational asymmetry. This nose-up moment is important for two reasons:(1) it affects the lift distribution significantly since it plays an important role in the moment equation, (2) the pitching moment is unstable as discussed in the work by Singh et al. [16].

Horizontal tail influence The influence of the tail is particularly on the moment equilibrium and it depends on the relative position between the wing aerodynamic center (AC) and the aircraft center of gravity (CG).

In case the CG is in front of the AC, the horizontal tail generates a negative lift to balance the moment. As a result, the lift the wing has to generate is equal to the weight plus the lift generated by the tail:

$$\begin{aligned} L_\text {wing} = W + L_\text {tail}; \end{aligned}$$
(23)

hence,

$$\begin{aligned} L_\text {wing}> W. \end{aligned}$$
(24)

The opposite scenario, where the AC is in front of the CG, the horizontal tail generates positive lift; thus,

$$\begin{aligned} L_\text {wing} < W. \end{aligned}$$
(25)

Combined effects The effects caused by the fuselage and tail individually are to be weighted against the effect the practices of aeroelastic tailoring have on the aircraft. The objective of the optimization via aeroelastic tailoring is weight minimization that is usually achieved by shifting the lift inboard and reducing the root bending moment at high-load factors. For a swept back wing, an inboard shift of the lift resultant also implies a forward shift of the aerodynamic center. At the same time, since the structural mass of the wing is descreasing, the CG is moving aft, towards the rear of the aircraft.

In optimization 1 (wing-tail aerodynamics), the configuration where the AC is in front of the CG is reached as a consequence of weight minimization and load alleviation due to aeroelastic tailoring. This explains the lower structural mass (approximately 2% compared to the wing reference) since at a given flight points, the loads on the wing are reduced.

The physics is different for optimization 2 (full-aircraft aerodynamics). Due to the high nose-up moment induced by the fuselage, and the drop of lift at the midline, the AC remains aft of the center of gravity thus explaining the increase in lift generated by the wing. The overall increase in the stress state in the wing explains the increase of the optimum structural mass up to app. 11%.

Tailoring The results on stiffness and thickness tailoring are summarized in Appendix A. In all three optimization cases, we can see the following trends:

  • a beneficial wash-out effect is induced by controlling the stiffness and thickness distribution. An example of wash-out control through thickness design is observed in the spar thickness distribution in Fig. 11 in Appendix A where the front spar is thicker than the rear spar. This allows the rear spar to deform more, compared to the front spar, and thus reduce the local angle of attack. The stiffness tailoring, on the other hand, controls the local twist distribution by rotating the principal direction of the design patches. This phenomenon can be observed in the optimized stiffness distribution of both top and bottom skin in Figs. 9 and 10 in Appendix A.

  • the optimized stiffness distribution is a result of the particular active constraint associated with every patch. For example, the patches where the buckling failure index is closer to the critical value of 1.0, the optimized stiffness approaches almost a cross-ply stiffness distribution that is most suitable for a buckling driven design. On the other hand, a very defined principal direction is typical of patches where the strain failure index is critical.

Margins This paragraph discusses the results in terms of margins calculated during the optimization via aeroelastic tailoring. An overview of the strain and buckling failure indexes of the design configurations used for this study is shown in Appendices B and C. Both measures are conservative to account for material imperfections, damage and scatter.

The outcome of the optimization shows two main trends regarding the sizing constraints for the final design, shown in Fig. 12 on Appendix B, namely:

  • aileron effectiveness, found in Table 4, is active in the load case at dive speed (LC1),

  • buckling and/or strains are active in the maneuver loadcases (LC2, LC3).

Table 4 Overview of aileron effectiveness
Full size table

The aileron effectiveness constraint is active under high-speed loading conditions at 1g. The lower bound set to the constraint, namely 0.15, is a very conservative measure and can vary depending on the type of aircraft and mission. The interesting trade-off is to compare the wing designed for a minimum level of aileron effectiveness within the flight envelope, to a wing where the aileron is actively controlled also beyond reversal.

The strain and buckling failure indexes are active in maneuver loadcases. The failure indexes are influenced by the internal load distribution, and consequently both the material and stiffness distribution of the optimized design will determine whether strain or buckling failure occurs first. In particular:

  • in optimization 1, we see that the wing has more severe strain buckling failure indices compared to optimization 0. This means that the in-plane stiffness distribution induces more wash-out to control the local twist distribution as a result of the higher deformations, whereas more patches have the out-of-plane stiffness closer to a cross-ply distribution to avoid buckling.

  • in optimization 2, the wing is less critical in buckling and mainly sized by strain failure. This happens because the drop of lift at the root caused by the presence of the fuselage induces higher strains on the wing. As a result, the principal direction is aligned with the wing trailing edge for enhanced stiffness while the cross-ply distributions are less pronounced.

8 Conclusions

The recent progress in aeroelasticity, in terms of both fundamental research and numerical solutions, has allowed the development of novel integrated frameworks to describe the tailoring optimization problem at aircraft level for more complete analyses compared to the classic aeroelastic tailoring solutions developed for a clamped wing. The assumptions and methodologies behind the classic aeroelastic tailoring practices are valid within certain levels of flexibility such that the interactions between the different parts of the aircraft are negligible.

The present work builds upon the aeroelastic tailoring framework developed by De Breuker et al. [12] to study the effects of a full-aircraft aerodynamic model on a tailored composite wing. This paper has shown the importance of a representative load description on the aeroelastic tailored design. The changes in lift distribution, center of gravity and aerodynamic center are driving the optimizer in different design regions with changes up to 11% in the mass of the final design.

It is important to realize that the changes in lift distribution are caused by the process of aeroelastic tailoring itself. By operating on the mass and stiffness properties of the wing, the load distribution changes in each iteration of the optimization loop. This also implies that both the center of gravity and the aerodynamic center are moving during the optimization, a phenomenon that has implication of the overall aircraft stability.

These observations will surely be of relevance in a future integrated approach to aeroelastic tailoring for composite aircraft design since they will affect other disciplines, for example, the flight dynamic performance, maneuverability and controllability of the aircraft.

The integrated approach for aircraft aeroelasticity and aeroelastic tailoring serves as a tool for design selection in the preliminary design phase. This concept is found already in the early work by Weisshaar et al. [2] where aeroelastic tailoring is recognized as an effective tool to scan the design space and select the best candidates for the subsequent phases. More applications of aeroelastic tailoring practices will be made feasible by development of both more efficient high-fidelity solutions, especially from the computational standpoint, and modular multidisciplinary frameworks for design purposes.