Introduction

Accurate flow measurement is one of the essential parameters for water resources management and the management of water systems such as irrigation and drainage networks and hydropower plants (Mohammadzadeh-Habili et al. 2016; Sarvarinezhad et al. 2022). Typically, to measure flow in open channels, only the depth of flow upstream and, in some cases, the depth of flow downstream of a given section is measured (Bos 1976; Chen 2015). According to open channel hydraulics, this reach must have a critical depth, because in this reach, regardless of the geometric characteristics, the discharge is directly related to the flow depth. Therefore, the flow energy must reach its minimum value to create a critical reach. This can be achieved by changing the bed elevation, narrowing the flow cross section, or both at the same time (Subramanya 2009; Akan and Iyer 2021; Moglen 2022). Based on these approaches in sub-critical flows, the design and construction of various hydraulic structures such as weirs, gates and flumes have been proposed (Haghiabi et al. 2018; Afaridegan et al. 2023). The installation of weirs and gates causes some problems, such as sediment deposition and accumulation of floating material, which reduces the discharge capacity of flumes and causes significant errors in flow measurement (Ogden et al. 2017; Mohammadzadeh-Habili et al. 2018; Vatankhah and Khalili 2020). Energy dissipation is another important parameter in the selection of flow measurement structures (Ghaderi et al. 2020; Daneshfaraz and Najibi 2021; Haghiabi et al. 2022; Salmasi and Abraham 2022). This is because the high energy dissipation of cross-sectional structures (such as weirs and gates) limits the design criteria. Another method of creating a critical depth, mainly used in irrigation and drainage channels, is to narrow the flow cross section. If the narrowing is gradual, very little energy is lost. Based on this approach, various types of flow measurement flumes have been proposed. More than 100 years have passed since the introduction of the first flume by Parshall, called the "Parshall flume". A review of the research carried out on this structure shows that its performance is only adequate and acceptable under free-flow conditions. Prismatic piers located in the centre and semi-cylindrical piers attached to the side walls of the channel have been proposed to narrow the channel width (Carollo et al. 2016; Carollo and Pampalone 2021). The developed flumes based on the use of a central prismatic pillar are called "Central Baffle Flumes": CBF" and the use of side cylinders is called "SMBF". The name "SMBF" is derived from the first letter of the surname of the designers of this type of flumes (Samani et al. 1991; Samani and Magallanez 1993, 2000; Baiamonte and Ferro 2007; Samani 2017). Different shapes have been proposed for the CBF, such as cylindrical, regular pentagonal, and hydrofoil. Shapes such as hydrofoil, semicircle and triangle have also been proposed for the lateral prism pillars. Samani and Magallanez (1993) used circular flumes to measure flow, in which a vertical cylindrical pier of diameter (d) was installed inside a horizontal pipe of larger diameter (D). They also developed and applied a cylindrical pier in a trapezoidal channel. Peruginelli and Bonacci (1997) used a prismatic pier instead of a cylindrical pier to create control sections in rectangular channels. They formulated the stage-discharge relationship for this structure. Samani and Magallanez (2000) introduced the SM flume for flow measurement. In this flume, two half-cylinders of dare diameter are installed on the side walls of a rectangular channel to narrow the cross section of the channel.

Badar and Ghare (2012), Ghare and Badar (2014), and Ghare et al. (2020) studied the CBF structure and derived the dimensionless parameters and then proposed a mathematical model for the stage-discharge relationship of this structure using the data published by the researchers (Samani and Magallanez 1993). They also studied the CBF structure experimentally and, according to the dimensionless parameters derived from Buckingham's theorem, proposed a mathematical formula for the rating curve of such structures. Aminpour et al. (2020) with a theoretical and laboratory study of a wide range of SMBF structures to derive a general relationship for the Ashle discharge curve of such structures.

A review of the literature shows that most studies have focused on the rating curve relationship of CBF and SMBF; therefore, this study investigates the discharge coefficient of the SMBF flume under free and submerged flow conditions. For this purpose, the dimensionless parameters involved are derived using П Buckingham's theorem, and then, their internal relationship is justified with the published data by Aminpour et al. (2020), Vatankhah and Mohammadi (2020), and Baiamonte and Ferro (2007).

Material and methods

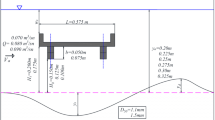
A schematic of the SMBF flume is shown in Fig. 1. As shown in this figure, an SMBF flume consists of a rectangular channel whose width (throat) is constricted by two lateral semi-cylindrical piers. In this figure, the flow rate is defined by (\(Q\)), \(B\) is the width of the channel, \(h\) and \(h_{{\text{s}}}\) are the upstream flow depths under free and submerged flow conditions. The \(W\) is the width of the throat of the SMBF, \(R\) is the radius of the half-cylinders, and \(h_{{\text{t}}}\) is the downstream flow depth in submerged flow conditions.

Fig. 1
figure 1

The schematic of the SMBF flume and its hydraulic and geometric parameters (Aminpour et al. 2020)

Full size image

According to open channel hydraulics, the discharge in a critical section is proportional to the critical depth. Equation (1) defines the relationship between the discharge and the depth of flow at the critical location. Equation (2) gives the total discharge, and Qt is the total discharge of the flow.

$$ \left\{ \begin{gathered} q = \sqrt {gy_{{\text{c}}}^{3} } \hfill \\ y_{{\text{c}}} = \frac{2}{3}H \hfill \\ \end{gathered} \right. \Rightarrow q = \sqrt {g\left( {\frac{2}{3}H} \right)^{3} } = \frac{2}{3}\sqrt {\frac{2}{3}g\left( H \right)^{3} } $$
(1)
$$ Q_{{\text{t}}} = Wq $$
(2)

where q is the flow rate per width, H is the total upstream head. Qt is obtained by multiplying q by the width of the orifice (W). By inserting Eq. (1) into (2), the Qt in terms of total upstream head is given by Eq. (3) (Subramanya 2009; Akan and Iyer 2021).

$$ Q_{{\text{t}}} = \frac{2}{3}W\sqrt {g\frac{2}{3}H^{3} } $$
(3)

The theoretically based Eq. (3) is derived by avoiding local head losses, so the flow discharge values may differ from the calculated flow discharge. Therefore, a coefficient called the discharge coefficient (Cd) is defined as the ratio of the actual discharge to the calculated discharge [Eq. (4)].

$$ \begin{aligned} & C_{{\text{d}}} = \frac{{Q_{{\text{m}}} }}{{Q_{{\text{t}}} }} \\ & Q_{{\text{m}}} = \frac{2}{3}C_{{\text{d}}} W\sqrt {g\frac{2}{3}H^{3} } \\ \end{aligned} $$
(4)

In the following, the calculation of Cd and the investigation of the factors influencing it will be focused on. It appears that under free-flow conditions, the hydraulic factors of the upstream head, which include the depth (h) and the head of the flow velocity (V), and the geometric factors, which include the radius of the half-cylinders (R) and the width of the throat (W), are influential. These parameters, in addition to the fluid properties (μ, σ, and ρ), are summarised in Eq. (5). In the submerged state, the hydraulic parameters of the downstream part, such as (ht), are added to them [parameters given in Eq. (5)] [Eq. (6)].

$$ C_{{\text{d - free}}} = \psi \left( {B,W,L,V,h,g,\mu ,\rho ,\sigma } \right) $$
(5)
$$ C_{{\text{d - submerge}}} = \varphi \left( {B,W,L,V,h_{{\text{s}}} ,h_{{\text{t}}} ,g,\mu ,\rho ,\sigma } \right) $$
(6)

where L is the curvature length [L = R × θ (θ = π (= 3.14))], hS is used instead of \(h\) in the submerged state. Considering the W, ρ, and g parameters as repetitive parameters, the dimensionless parameters are derived as Eq. (7), and Eqs. (8) and (9) are proposed for the free and submerged flow conditions, respectively.

$$ C_{{\text{d - free}}} = \psi \left( {r_{{{\text{crn}}}} = \frac{W}{B},r_{{{\text{srt}}}} = \frac{L}{W},\frac{h}{W},{\text{Fr}},{\text{Re}},{\text{We}}} \right) $$
(7)

where \({r}_{\mathrm{crn}}\) and \({\mathrm{r}}_{\mathrm{srt}}\) _ are the contraction and expansion ratios. As the flow in nature is often turbulent, the flow in the water supply channels is sub-critical; therefore, the effects of Froude and Reynolds are neglected. Examination of the values related to the depth of flow shows that the minimum depth of flow is 25 mm, so the effect of Weber's number is worth considering.

$$ \begin{aligned} & C_{{\text{d - free}}} = \psi \left( {r_{{{\text{crn}}}} ,r_{{{\text{srt}}}} ,\frac{h}{W}} \right) \\ & C_{{\text{d - submerge}}} = \varphi \left( {r_{{{\text{crn}}}} ,r_{{{\text{srt}}}} ,\frac{{h_{{\text{s}}} }}{W},\frac{{h_{{\text{t}}} }}{{h_{{\text{s}}} }}} \right) \\ \end{aligned} $$
(8)

To investigate Cd, the parameters involved in free and submerged flow conditions, the data published by Aminpour et al. (2020), Vatankhah and Mohammadi (2020), and Baiamonte and Ferro (2007) are used. The range of data collected in free and submerged flow conditions is given in Tables 1 and 2, respectively.

Table 1 The range of geometric and hydraulic variables of collected data used in free-flow condition
Full size table
Table 2 The range of geometric and hydraulic variables of data used in submerged flow condition
Full size table

Results and discussion

This section presents the results of calculating Cd according to Eq. (4) and discusses the effects of the involved parameters. To achieve this, Fig. 2 displays the rating curves of four SMBF models tested under both free and submerged conditions.

Fig. 2
figure 2

The rating curves of SMBF models in the free, threshold, and submerged flow conditions

Full size image

According to Fig. 2, under submerged conditions, the flow rate exhibits horizontal changes with variations in both upstream and downstream heads. This implies two things: firstly, a greater upstream head is needed to achieve a given flow rate, and the degree of submergence (ht/hS) correlates positively with the required upstream head. Secondly, the flow rate changes horizontally with head (both upstream and downstream heads), indicating that under submerged conditions, the flow rate is influenced solely by head.

To mathematically express the rating curve of SMBFs (relationship between flow rate and upstream head) under free-flow conditions, the general form of Eq. (3), which is \(Q={\alpha h}^{1.5}\), is fitted to the rating curve data of each laboratory model. The values of the α coefficient for each model are given in Table 3, and its variation with contraction ratio (\({r}_{\mathrm{crn}}\)) and stretch ratio (\({r}_{\mathrm{srt}}\)) are shown in Table 3 and Fig. 3. Upon examination of this figure and table, it can be observed that an increase in the ratios (rcrn and rsrt) leads to a decrease in the α coefficient.

Table 3 The range of \(r_{{{\text{srt}}}}\), \(r_{{{\text{crn}}}}\) and α
Full size table
Fig. 3
figure 3

The variation of the α coefficient versus the \(r_{{{\text{srt}}}}\), \(r_{{{\text{crn}}}}\)

Full size image

The Cd was calculated for each model under free and submerged flow conditions and the results are shown in Fig. 4. As can be seen from this figure, in the free-flow condition, for the range of relative head (h/W) between 0.4 and 1.8, the \({C}_{\mathrm{d}}\) varies between 1.20 and 0.75 and with increasing \(h/W\), the \({C}_{\mathrm{d}}\) decreases. It is noteworthy that this decreasing trend of Cd is observed in all models. This decrease is due to the higher head loss at high relative heads. In other words, the smothering phenomenon is much more pronounced at high relative heads. At high submergence ratios, it is sometimes necessary to increase the upstream depth to 50% in order to maintain the \({C}_{\mathrm{d}}\).

Fig. 4
figure 4

The Cd of SMBF models in the free, threshold, and submerged flow conditions

Full size image

The effect of submergence intensity on \({C}_{\mathrm{d}}\) at different ratios of the \({r}_{\mathrm{crn}}\) and \({r}_{\mathrm{srt}}\) is shown in Fig. 5. As shown in this figure, there is no clear relationship between the intensity of flow submergence and \({C}_{\mathrm{d}}\). As stated above, the intensity of submergence affects the discharge capacity, not the \({C}_{\mathrm{d}}\).

Fig. 5
figure 5

The effect of intensity of submergence on Cd of models of SMBF flume

Full size image

The \(C_{{\text{d}}}\) was calculated for models with different \(r_{{{\text{crn}}}}\) and \(r_{{{\text{srt}}}}\) under free and submerged conditions and the results are shown in Figs. 6 and 7. The purpose of presenting these figures was to investigate the effect of \(r_{{{\text{crn}}}}\) and \(r_{{{\text{srt}}}}\) on \(C_{{\text{d}}}\) under free flow and submerged conditions. As can be seen from this figure, as \(r_{{{\text{crn}}}}\) is increased, more h/W is required to have a given value of \(C_{{\text{d}}}\) and this requirement becomes more acute at higher relative heads. For example, to have a \(C_{{\text{d}}}\) of about 0.9, at \(r_{{{\text{crn}}}}\) ≈ 27%, it is only necessary to provide \(h / W \approx 0.6\), while increasing the \(r_{{{\text{crn}}}}\) up to 65%, it is necessary to provide h⁄W up to 1.15. In other words, by doubling the \(r_{{{\text{crn}}}}\) (increase from 27 to 65%), the h/W should also be at least doubled (increase from 0.6 to 1.15).

Fig. 6
figure 6

The Cd of models of SMBF flume versus the relative upstream depth under the free-flow condition

Full size image
Fig. 7
figure 7

The Cd of models of SMBF flume versus the relative upstream depth under submerged flow condition

Full size image

The same is true in submerged conditions. Of course, it is worth noting that the submergence ratio will exacerbate this problem. By increasing the \({r}_{\mathrm{crn}}\), to achieve a given \(C_{{\text{d}}}\), a relative upstream head (\({h}_{\mathrm{s}}/\)W) is required that is greater than in a free-flow condition. Due to the submerged condition (\({h}_{\mathrm{t}}\)⁄\({h}_{\mathrm{s}}\)) acts as a flow resistance factor. In order to achieve a \(C_{{\text{d}}}\) of 0.9, in the case of \({r}_{\mathrm{crn}}\) of 27%, the relative head (\({h}_{\mathrm{s}}\)/W) of 0.6 is required, while providing the same \(C_{{\text{d}}}\) in, in the case of \({r}_{\mathrm{crn}}\) of 53%, \({h}_{\mathrm{s}}\)⁄W of 1.4 is required, which is about 130% more than the previous state and 20% more than the free-flow condition, and this reason is flow resistance due to flow submergence.

Conclusion

In this study, the \(C_{{\text{d}}}\) of the SMBF was calculated to measure the flow rate in the open channel under free and submerged conditions. The results of dimensional analysis based on П Buckingham's theorem showed that dimensionless parameters such as relative head and strength ratio in free-flow condition and submergence ratio in submerged condition are also involved in \(C_{{\text{d}}}\). The results declared that the \(C_{{\text{d}}}\) of SMBF in free-flow condition changes between 1.2 and 0.75 considering the range of upstream relative head between 0.4 and 1.8. With the increase in relative head from 0.4 to 1.8, the \(C_{{\text{d}}}\) decreases from 1.2 to 0.75. The relationship between \({C}_{d}\) and relative head is inverse. The submerged condition reduces the discharge capacity of the SMBF structure to 50%. It is worth noting that submersion has no effect on \(C_{{\text{d}}}\). However, its effect on the increase of the upstream head is obvious.