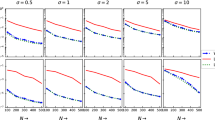
Appendix A: Preliminaries
To establish the consistency and asymptotic normality of the WLSEs we need some trigonometric and number theoretic results and one famous number theoretic conjecture. We explicitly mention it here for easy reference.
Result A.1: If \(\alpha , \beta \in (0,\pi )\), and \(\alpha \ne \beta \), then the following results hold.
$$\begin{aligned}\lim _{N \rightarrow \infty } \frac{1}{N} \sum _{n=1}^N \cos (\alpha n)= & {} \lim _{N \rightarrow \infty } \frac{1}{N} \sum _{n=1}^N \sin (\alpha n) = 0, \\ \lim _{N \rightarrow \infty } \frac{1}{N^{k+1}} \sum _{n=1}^N n^k \cos ^2(\alpha n)= & {} \frac{1}{2 (k+1)}, \\ \lim _{N \rightarrow \infty } \frac{1}{N^{k+1}} \sum _{n=1}^N n^k \sin ^2(\alpha n)= & {} \frac{1}{2 (k+1)}, \\ \lim _{N \rightarrow \infty } \frac{1}{N^{k+1}} \sum _{n=1}^N n^k \cos (\alpha n) \sin (\alpha n)= & {} 0, \\ \lim _{N \rightarrow \infty } \frac{1}{N^{k+1}} \sum _{n=1}^N n^k \sin (\alpha n) \sin (\beta n)= & {} \lim _{N \rightarrow \infty } \frac{1}{N^{k+1}} \sum _{n=1}^N n^k \cos (\alpha n) \cos (\beta n) \!=\! 0, \end{aligned}$$
where \(k = 0, 1, 2, \ldots \).
Proof
The proofs can be found in Mangulis (1965). \(\square \)
Result A.2: If \(\alpha , \beta \in (0,\pi )\), and \(\alpha \ne \beta \), then except for countable number of points, the following results hold.
$$\begin{aligned}\lim _{N \rightarrow \infty } \frac{1}{N} \sum _{n=1}^N \cos (\alpha n^2)= & {} \lim _{N \rightarrow \infty } \frac{1}{N} \sum _{n=1}^N \sin (\alpha n^2) = 0, \\ \lim _{N \rightarrow \infty } \frac{1}{N^{k+1}} \sum _{n=1}^N n^k \cos ^2(\alpha n^2)= & {} \frac{1}{2 (k+1)}, \\ \lim _{N \rightarrow \infty } \frac{1}{N^{k+1}} \sum _{n=1}^N n^k \sin ^2(\alpha n^2)= & {} \frac{1}{2 (k+1)}, \\ \lim _{N \rightarrow \infty } \frac{1}{N^{k+1}} \sum _{n=1}^N n^k \cos (\alpha n^2) \sin (\beta n^2)= & {} 0, \\ \lim _{N \rightarrow \infty } \frac{1}{N^{k+1}} \sum _{n=1}^N n^k \sin (\alpha n^2) \cos (\beta n)= & {} \lim _{N \rightarrow \infty } \frac{1}{N^{k+1}} \sum _{n=1}^N n^k \cos (\alpha n^2) \sin (\beta n)\\= & {} 0, \\ \lim _{N \rightarrow \infty } \frac{1}{N^{k+1}} \sum _{n=1}^N n^k \sin (\alpha n^2) \sin (\beta n)= & {} \lim _{N \rightarrow \infty } \frac{1}{N^{k+1}} \sum _{n=1}^N n^k \cos (\alpha n^2) \cos (\beta n) \\= & {} 0. \end{aligned}$$
In addition if \(\alpha \ne \beta \), then for \(k = 0,1,2, \ldots \),
$$\begin{aligned}\lim _{N \rightarrow \infty } \frac{1}{N^{k+1}} \sum _{n=1}^N n^k \sin (\alpha n^2) \sin (\beta n^2)= & {} \lim _{N \rightarrow \infty } \frac{1}{N^{k+1}} \sum _{n=1}^N n^k \cos (\alpha n^2) \cos (\beta n^2)\\= & {} 0. \\ \end{aligned}$$
where \(k = 0, 1, 2, \ldots \).
Proof
The proofs can be obtained from Vinogradov ’s (1954) results. See Lahiri et al. (2015) for details.
The following well known number theoretic conjecture, see for example Montgomery (1990), can not be established formally. But extensive numerical experiments indicate that it holds true.
Conjecture A: If \(\alpha , \beta \in (0,\pi )\), then except for countable number of points, for \(k = 0,1,2, \ldots \),
$$\begin{aligned}\lim _{N \rightarrow \infty } \frac{1}{\sqrt{N} N^k} \sum _{n=1}^N n^k \cos (\alpha n^2) \sin (\beta n^2)= & {} 0, \\ \lim _{N \rightarrow \infty } \frac{1}{\sqrt{N} N^k} \sum _{n=1}^N n^k \cos (\alpha n^2) \sin (\beta n)= & {} 0, \\ \lim _{N \rightarrow \infty } \frac{1}{\sqrt{N} N^k} \sum _{n=1}^N n^k \sin (\alpha n^2) \cos (\beta n)= & {} 0. \\ \end{aligned}$$
In addition if \(\alpha \ne \beta \), then for \(k = 0,1,2, \ldots \),
$$\begin{aligned}\lim _{N \rightarrow \infty } \frac{1}{\sqrt{N} N^k} \sum _{n=1}^N n^k \cos (\alpha n^2) \cos (\beta n^2)= & {} 0, \\ \lim _{N \rightarrow \infty } \frac{1}{\sqrt{N} N^k} \sum _{n=1}^N n^k \sin (\alpha n^2) \sin (\beta n^2)= & {} 0. \\ \lim _{N \rightarrow \infty } \frac{1}{\sqrt{N} N^k} \sum _{n=1}^N n^k \sin (\alpha n^2) \sin (\beta ^2)= & {} 0, \end{aligned}$$
Appendix B: Proof of Theorem 1
We need the following lemmas to prove Theorem 1.
Lemma
B-1: Let \(\{e(n)\}\) be a sequence of i.i.d. random variables with mean zero and finite fourth moment, w(t) satisfies Assumption 1, then
$$ E \left| \sum _{n=1}^{N} w \left( \frac{n}{N} \right) w^2\left( \frac{n+1}{N} \right) w \left( \frac{n+2}{N} \right) e(n) e^2(n+1)e(n+2) \right| = O(N^{\frac{1}{2}}). $$
Proof
$$\begin{aligned}{} & {} E \left| \sum _{n=1}^{N} w \left( \frac{n}{N} \right) w^2\left( \frac{n+1}{N} \right) w \left( \frac{n+2}{N} \right) e(n) e^2(n+1)e(n+2) \right| \\{} & {} \quad \le \left[ E \left( \sum _{n=1}^{N} w \left( \frac{n}{N} \right) w^2\left( \frac{n+1}{N} \right) w \left( \frac{n+2}{N} \right) e(n) e^2(n+1)e(n+2) \right) ^2 \right] ^{\frac{1}{2}}\\{} & {} \quad = O(N^{\frac{1}{2}}). \end{aligned}$$
Similarly, it follows that
$$\begin{aligned}{} & {} E \left| \sum _{n=1}^{N} w \left( \frac{n}{N} \right) w \left( \frac{n+1}{N} \right) w \left( \frac{n+k}{N} \right) w \left( \frac{n+k+1}{N} \right) e(n) e(n+1) e(n+k) e(n+k+1) \right| \\{} & {} \quad = O(N^{\frac{1}{2}}), \end{aligned}$$
for some fixed k, where \(k = 2,3,\ldots \).
Lemma
B-2: Let \(\{e(n)\}\) be a sequence of i.i.d. random variables with mean zero and finite fourth moment, w(t) satisfies Assumption 1, then for arbitrary integers \(m,k \ge 1\),
$$ E \sup _\theta \left| \sum _{n=1}^N w \left( \frac{n}{N} \right) w \left( \frac{n+k}{N} \right) e(n) e(n+k) e^{i m \theta n} \right| = O(N^{\frac{3}{4}}). $$
Proof
$$\begin{aligned}{} & {} E \sup _\theta \left| \sum _{n=1}^N w \left( \frac{n}{N} \right) w \left( \frac{n+k}{N} \right) e(n) e(n+k) e^{i m \theta n} \right| \le \\{} & {} \left[ E \sup _\theta \left| \sum _{n=1}^N w \left( \frac{n}{N} \right) w \left( \frac{n+k}{N} \right) e(n) e(n+k) e^{i m \theta n} \right| ^2 \right] ^{\frac{1}{2}} = \\{} & {} \left[ E \sup _\theta \left( \sum _{n=1}^N w \left( \frac{n}{N} \right) w \left( \frac{n+k}{N} \right) e(n) e(n+k) e^{i m \theta n} \right) \right. \\{} & {} \hspace{1in}\left. \left( \sum _{n=1}^N w \left( \frac{n}{N} \right) w \left( \frac{n+k}{N} \right) e(n) e(n+k) e^{-i m \theta n} \right) \right] ^{\frac{1}{2}} \\\le & {} \left[ E \sum _{n=1}^N w^2 \left( \frac{n}{N} \right) w^2 \left( \frac{n+k}{N} \right) e^2(n) e^2 (n+k) + \right. \\{} & {} 2 E \left| \sum _{n=1}^{N-1}w \left( \frac{n}{N} \right) w \left( \frac{n+k}{N} \right) w \left( \frac{n+1}{N} \right) w \left( \frac{n+k+1}{N} \right) e(n) e(n+k) e(n+1) e(n+k+1) \right| + \\{} & {} \left. \ldots + 2E \left| w \left( \frac{1}{N} \right) w \left( \frac{1+k}{N} \right) w \left( 1 \right) w \left( \frac{N+k}{N} \right) e(1) e(1+k)e(N) e(N+k) \right| \right] ^{\frac{1}{2}} \\= & {} O(N + N.N^{\frac{1}{2}})^{\frac{1}{2}} = O(N^{\frac{3}{4}}). \end{aligned}$$
Lemma
B-3: Let \(\{e(n)\}\) be a sequence of i.i.d. random variables with mean zero and finite fourth moment, w(t) satisfies Assumption 1, then
$$ E \sup _{\beta } \left| \sum _{n=1}^N w \left( \frac{n}{N} \right) e(n) e^{i \beta n^2}\right| ^2 = O(N^{\frac{7}{4}}). $$
Proof
$$\begin{aligned}{} & {} E \sup _{\beta } \left| \sum _{n=1}^N w \left( \frac{n}{N} \right) e(n) e^{i \beta n^2}\right| ^2 = \\{} & {} E \sup _{\beta } \left( \sum _{n=1}^N w \left( \frac{n}{N} \right) e(n) e^{i \beta n^2}\right) \left( \sum _{n=1}^N w \left( \frac{n}{N} \right) e(n) e^{-i \beta n^2}\right) = O(N+N.N^{\frac{3}{4}})\\{} & {} \quad = O(N^{\frac{7}{4}}) \end{aligned}$$
Lemma
B-4: Let \(\{e(n)\}\) be a sequence of i.i.d. random variables with mean zero and finite fourth moment, w(t) satisfies Assumption 1, then
$$ E \sup _{\beta } \left| \frac{1}{N} \sum _{n=1}^N w \left( \frac{n}{N} \right) e(n) e^{i \beta n^2} \right| \le O(N^{-\frac{1}{8}}). $$
Proof
$$ E \sup _{\beta } \left| \frac{1}{N} \sum _{n=1}^N w \left( \frac{n}{N} \right) e(n) e^{i \beta n^2} \right| \le \left[ E \sup _{\beta } \left| \frac{1}{N} \sum _{n=1}^N w \left( \frac{n}{N} \right) e(n) e^{i \beta n^2} \right| ^2 \right] ^{\frac{1}{2}} = O(N^{-\frac{1}{8}}). $$
Lemma
B-5: Let \(\{e(n)\}\) be a sequence of i.i.d. random variables with mean zero and finite fourth moment, w(t) satisfies Assumption 1, and \(\{X(n)\}\) is same as defined in (4), then
$$ E \sup _{\beta } \left| \frac{1}{N} \sum _{n=1}^N w \left( \frac{n}{N} \right) X(n) e^{i \beta n^2} \right| \le O(N^{-\frac{1}{8}}). $$
Proof
$$\begin{aligned}{} & {} E \sup _{\beta } \left| \frac{1}{N} \sum _{n=1}^N w \left( \frac{n}{N} \right) X(n) e^{i \beta n^2} \right| = \\{} & {} E \sup _{\beta } \left| \frac{1}{N} \sum _{n=1}^N \sum _{k=-\infty }^{\infty } a(k) e(n-k) w \left( \frac{n}{N} \right) e^{i \beta n^2} \right| \le \\{} & {} \sum _{k=-\infty }^{\infty } |a(k)| \left[ E \sup _{\beta } \left| \frac{1}{N} \sum _{n=1}^N e(n-k) w \left( \frac{n}{N} \right) e^{i \beta n^2} \right| \right] = O(N^{-\frac{1}{8}}). \end{aligned}$$
Since \(\displaystyle E \sup _{\beta } \left| \frac{1}{N} \sum _{n=1}^N e(n-k) w \left( \frac{n}{N} \right) e^{i \beta n^2} \right| \) is independent of k, the result follows from Lemma B-4.
Lemma
B-6: Let \(\{e(n)\}\) be a sequence of i.i.d. random variables with mean zero and finite fourth moment, w(t) satisfies Assumption 1, and \(\{X(n)\}\) is same as defined in (4), then
$$ \sup _{\beta } \left| \frac{1}{N} \sum _{n=1}^N w \left( \frac{n}{N} \right) X(n) e^{i \beta n^2} \right| \longrightarrow 0, \ \ \ \ a.s. $$
Proof
Consider the sequence \(N^9\), then we obtain
$$ E \sup _{\beta } \left| \frac{1}{N^9} \sum _{n=1}^{N^9} w \left( \frac{n}{N} \right) X(n) e^{i \beta n^2} \right| \le O(N^{-\frac{9}{8}}). $$
Therefore, using Borel Cantelli lemma, it follows that
$$ \sup _{\beta } \left| \frac{1}{N^9} \sum _{n=1}^{N^9} w \left( \frac{n}{N} \right) X(n) e^{i \beta n^2} \right| \longrightarrow 0, \ \ \ \ a.s. $$
Now consider J, such that \(N^9 < J \le (N+1)^9\), then
$$\begin{aligned}\sup _{\beta } \sup _{N^9< J \le (N+1)^9} \left| \frac{1}{N^9} \sum _{n=1}^{N^9} w \left( \frac{n}{N} \right) X(n) e^{i \beta n^2} - \frac{1}{J} \sum _{n=1}^{J} w \left( \frac{n}{N} \right) X(n) e^{i \beta n^2} \right| = \\ \sup _{\beta } \sup _{N^9< J \le (N+1)^9} \left| \frac{1}{N^9} \sum _{n=1}^{N^9} w \left( \frac{n}{N} \right) X(n) e^{i \beta n^2} - \frac{1}{N^9} \sum _{n=1}^{J} w \left( \frac{n}{N} \right) X(n) e^{i \beta n^2} + \right. \\ \left. \frac{1}{N^9} \sum _{n=1}^{J} w \left( \frac{n}{N} \right) X(n) e^{i \beta n^2} - \frac{1}{J} \sum _{n=1}^{J} w \left( \frac{n}{N} \right) X(n) e^{i \beta n^2} \right| \le \\ \sup _{\beta } \sup _{N^9< J \le (N+1)^9} \left| \frac{1}{N^9} \sum _{n=1}^{N^9} w \left( \frac{n}{N} \right) X(n) e^{i \beta n^2} - \frac{1}{N^9} \sum _{n=1}^{J} w \left( \frac{n}{N} \right) X(n) e^{i \beta n^2} \right| + \\ \sup _{\beta } \sup _{N^9 < J \le (N+1)^9} \left| \frac{1}{N^9} \sum _{n=1}^{J} w \left( \frac{n}{N} \right) X(n) e^{i \beta n^2} - \frac{1}{J} \sum _{n=1}^{J} w \left( \frac{n}{N} \right) X(n) e^{i \beta n^2} \right| \le \\ \frac{K}{N^9} \sum _{n=N^9+1}^{(N+1)^9} |X(n)| + K \sum _{n=1}^{(N+1)^9} |X(n)| \left( \frac{1}{N^9} - \frac{1}{(N+1)^9} \right) \end{aligned}$$
Note that the mean squared error of the first term is of the order \(O \left( \frac{1}{N^{18}} \times ((N+1)^9-N^9)^2 \right) = O(N^{-2})\). Similarly, the mean squared error of the second term is of the order \(\displaystyle O \left( N^{18} \times \left( \frac{(N+1)^9 - N^9}{N^{18}} \right) ^2 \right) = O(N^{-2})\). Therefore, both the terms converge to zero almost surely.
Along the same line the following result follows.
Lemma
B-7: Let \(\{e(n)\}\) be a sequence of i.i.d. random variables with mean zero and finite fourth moment, w(t) satisfies Assumption 1, and \(\{X(n)\}\) is same as defined in (4), then
$$ \sup _{\alpha } \left| \frac{1}{N} \sum _{n=1}^N w \left( \frac{n}{N} \right) X(n) e^{i \alpha n} \right| \longrightarrow 0, \ \ \ \ a.s. $$
Lemma
B-8: Let us denote
$$ S_c = \{{\varvec{\theta }}: {\varvec{\theta }} = (A,B,C,D,\alpha ,\beta )^{\top }, |{\varvec{\theta }}-{\varvec{\theta }}^0| \ge 6c\}. $$
If there exists a \(c > 0\),
$$\begin{aligned} \underline{\lim } \inf _{{\varvec{\theta }} \in S_c} \frac{1}{N} [Q(\varvec{\theta }) - Q(\varvec{\theta }^0)] > 0 \ \ \ \ a.s. \end{aligned}$$
(21)
then \(\widehat{\varvec{\theta }}\), the WLSE of \({\varvec{\theta }}^0\), is a strongly consistent estimator of \({\varvec{\theta }}^0\).
Proof
It follows using simple arguments by contradiction, exactly similar to the lemma by Wu (1981). \(\square \)
Proof of Theorem 1:
Let us denote
$$\begin{aligned} \mu (n;{\varvec{\theta }}) = A \cos (\alpha n) + B \sin (\alpha n) + C \cos (\beta n^2) + D \sin (\beta n^2). \end{aligned}$$
(22)
Consider
$$\begin{aligned}\frac{1}{N} [Q(\varvec{\theta }) - Q({\varvec{\theta }}^0)]= & {} \frac{1}{N} \left[ \sum _{n=1}^N w \left( \frac{n}{N} \right) (y(n) - \mu (n;{\varvec{\theta }}))^2 - \sum _{n=1}^N w \left( \frac{n}{N} \right) X^2(n) \right] \\= & {} \frac{1}{N} \left[ \sum _{n=1}^N w \left( \frac{n}{N} \right) (\mu (n;{\varvec{\theta }}^0) - \mu (n;{\varvec{\theta }}))^2 \right] \\{} & {} + \frac{2}{N} \left[ \sum _{n=1}^N w \left( \frac{n}{N} \right) X(n)(\mu (n;{\varvec{\theta }}^0) - \mu (n;{\varvec{\theta }})) \right] \\{} & {} = f_1(\varvec{\theta }) + f_2(\varvec{\theta }). \end{aligned}$$
Here
$$\begin{aligned}{} & {} f_1(\varvec{\theta }) = \frac{1}{N} \left[ \sum _{n=1}^N w \left( \frac{n}{N} \right) (\mu (n;{\varvec{\theta }}^0) - \mu (n;{\varvec{\theta }}))^2 \right] , \\{} & {} f_2(\varvec{\theta }) = \frac{2}{N} \left[ \sum _{n=1}^N w \left( \frac{n}{N} \right) X(n)(\mu (n;{\varvec{\theta }}^0) - \mu (n;{\varvec{\theta }})) \right] . \end{aligned}$$
Consider
$$\begin{aligned}S_{c,1}= & {} \{{\varvec{\theta }}:{\varvec{\theta }} = (A,B,C,D,\alpha ,\beta )^{\top }, |A-A^0| \ge c\} \\ S_{c,2}= & {} \{{\varvec{\theta }}: {\varvec{\theta }} = (A,B,C,D,\alpha ,\beta )^{\top }, |B-B^0| \ge c\} \\ S_{c,3}= & {} \{{\varvec{\theta }}: {\varvec{\theta }} = (A,B,C,D,\alpha ,\beta )^{\top }, |C-C^0| \ge c\} \\ S_{c,4}= & {} \{{\varvec{\theta }}: {\varvec{\theta }} = (A,B,C,D,\alpha ,\beta )^{\top }, |D-D^0| \ge c\} \\ S_{c,5}= & {} \{{\varvec{\theta }}: {\varvec{\theta }} = (A,B,C,D,\alpha ,\beta )^{\top }, |\alpha -\alpha ^0| \ge c\} \\ S_{c,6}= & {} \{{\varvec{\theta }}: {\varvec{\theta }} = (A,B,C,D,\alpha ,\beta )^{\top }, |\beta -\beta ^0| \ge c\}. \end{aligned}$$
Now \(\displaystyle S_c \in \cup _{j=1}^6 S_{c,j} = S\). Therefore,
$$\begin{aligned} \underline{\lim } \inf _{\theta \in S_c} f_1(\varvec{\theta }) \ge \underline{\lim } \inf _{{\varvec{\theta }} \in S} f_1(\theta ) = \underline{\lim } \inf _{{\varvec{\theta }} \in \cup _j S_{c,j}} f_1(\theta ). \end{aligned}$$
Now
$$\begin{aligned}\underline{\lim } \inf _{{\varvec{\theta }} \in S_{c,1}} f_1(\theta )= & {} \underline{\lim } \inf _{|A-A^0| \ge c} (A-A^0)^2 \frac{1}{N} \sum _{n=1}^N w \left( \frac{n}{N} \right) \cos ^2(\alpha ^0 n) \\\ge & {} \gamma \ \ \underline{\lim } \inf _{|A-A^0| \ge c} (A-A^0)^2 \frac{1}{N} \sum _{n=1}^N \cos ^2(\alpha ^0 n) > 0,\\{} & {} \ \ \ \ \ (\hbox {using Result A.1}). \end{aligned}$$
Similarly using Results A.1 and A.2, it can be shown for \(S_{c,2}, \ldots , S_{c,6}\) also. Therefore,
$$ \underline{\lim } \inf _{{\varvec{\theta }} \in S_c} f_1(\varvec{\theta }) > 0. $$
Using Lemma B-7, it follows that
$$ \lim \sup _{{\varvec{\theta }}} |f_2(\varvec{\theta })| = 0, $$
therefore
$$ \underline{\lim } \inf _{{\varvec{\theta }} \in S_c} \frac{1}{N} [Q(\varvec{\theta }) - Q({\varvec{\theta }}^0)] > 0 \ \ \ \ a.s. $$
Using Lemma B-8, the result follows. \(\square \)
Appendix C: Proof of Theorem 2.
We need the following lemmas to prove Theorem 2.
Lemma
C-1: If \(0< \alpha , \beta < \pi \), and w(t) satisfies Assumption 1, then for \(k = 0,1,2, \ldots \),
$$\begin{aligned}&\hbox {(a)}&\lim _{N \rightarrow \infty } \frac{1}{N} \sum _{n=1}^N w \left( \frac{n}{N} \right) \sin ^2(\alpha n) = \lim _{N \rightarrow \infty } \frac{1}{N} \sum _{n=1}^N w \left( \frac{n}{N} \right) \cos ^2(\alpha n)\\{} & {} = \frac{1}{2} \int _0^1 w(t) dt> \frac{\gamma }{2}, \\&\hbox {(b)}&\lim _{N \rightarrow \infty } \frac{1}{N^{k+1}} \sum _{n=1}^N n^k w\! \left( \frac{n}{N} \right) \!\sin (\alpha n)\\{} & {} = \lim _{N \rightarrow \infty } \frac{1}{N^{k+1}} \sum _{n=1}^N n^k w \left( \frac{n}{N} \right) \cos (\alpha n) = 0, \\&\hbox {(c)}&\lim _{N \rightarrow \infty } \frac{1}{N^{k+1}} \sum _{n=1}^N n^k w \left( \frac{n}{N} \right) \sin ^2(\alpha n) = \lim _{N \rightarrow \infty } \frac{1}{N^{k+1}} \sum _{n=1}^N n^k w \!\left( \frac{n}{N} \right) \! \cos ^2(\alpha n) \\{} & {} \hspace{2.42 in} = \frac{1}{2} \int _0^1 t^k w(t) dt = \frac{c_{k+1}}{2} > 0, \\&\hbox {(d)}&\lim _{N \rightarrow \infty } \frac{1}{N^{k+1}} \sum _{n=1}^N n^k w \left( \frac{n}{N} \right) \sin (\alpha n) \cos (\alpha n) \\{} & {} = \lim _{N \rightarrow \infty } \frac{1}{N^{k+1}} \sum _{n=1}^N n^k w \left( \frac{n}{N} \right) \sin (\alpha n) \cos (\beta n) = 0, \\{} & {} \hbox {In addition if } \alpha \ne \beta , \hbox { then,} \\&\hbox {(e)}&\lim _{N \rightarrow \infty } \frac{1}{N^{k+1}} \sum _{n=1}^N n^k w \left( \frac{n}{N} \right) \sin (\alpha n) \sin (\beta n) \\{} & {} = \lim _{N \rightarrow \infty } \frac{1}{N^{k+1}} \sum _{n=1}^N n^k w \left( \frac{n}{N} \right) \cos (\alpha n) \cos (\beta n) = 0. \end{aligned}$$
Proof of Lemma C-1:
Proof of (a). First we will show
$$ \lim _{N \rightarrow \infty } \frac{1}{N} \sum _{n=1}^N w \left( \frac{n}{N} \right) \cos ^2 (\alpha n) = \frac{1}{2} \int _0^1 w(t) dt. $$
For \(\epsilon > 0\), there exists a polynomial \(p_{\epsilon }(x)\), such that \(\displaystyle |w(x) - p_{\epsilon }(x)| \le \epsilon \), for all \(x \in [0,1]\). Hence,
$$ \int _0^1 w(x) dx - \epsilon \le \int _0^1 p_{\epsilon }(x) dx \le \int _0^1 w(x) dx + \epsilon . $$
Further
$$\begin{aligned}{} & {} \frac{1}{N} \sum _{n=1}^N p_{\epsilon } \left( \frac{n}{N} \right) \cos ^2(\alpha n) - \frac{\epsilon }{N} \sum _{n=1}^N \cos ^2(\alpha t ) \le \frac{1}{N} \sum _{n=1}^N w \left( \frac{n}{N} \right) \cos ^2(\alpha n) \le \\{} & {} \frac{1}{N} \sum _{n=1}^N p_{\epsilon } \left( \frac{n}{N} \right) \cos ^2(\alpha n) + \frac{\epsilon }{N} \sum _{n=1}^N \cos ^2(\alpha n). \end{aligned}$$
Suppose
$$ p_{\epsilon }(x) = a_0 + a_1 x + \cdots + a_k x^k \ \ \ \ \ \Rightarrow \ \ \ \int _0^1 p_{\epsilon }(x) dx = a_0 + \frac{a_1}{2} + \cdots + \frac{a_k}{k+1}. $$
Now due to Result A.1,
$$\begin{aligned}\frac{1}{N} \sum _{n=1}^N p_{\epsilon } \left( \frac{n}{N} \right) \cos ^2(\alpha n)= & {} \frac{1}{N} \sum _{n=1}^N \left\{ a_0 + \frac{a_1n}{N} + \cdots + \frac{a_k n^k}{N^k} \right\} \cos ^2(\alpha n) \\\longrightarrow & {} \frac{1}{2} \left[ a_0 + \frac{a_1}{2} + \cdots + \frac{a_k}{k+1} \right] = \frac{1}{2} \int _0^1 p_{\epsilon }(x) dx. \end{aligned}$$
Therefore,
$$\begin{aligned}{} & {} \lim _{N \rightarrow \infty } \frac{1}{N} \sum _{n=1}^N p_{\epsilon } \left( \frac{n}{N} \right) \cos ^2(\alpha n) - \frac{\epsilon }{2} \le \lim _{N \rightarrow \infty } \frac{1}{N} \sum _{n=1}^N w \left( \frac{n}{N} \right) \cos ^2(\alpha n) \le \\{} & {} \lim _{N \rightarrow \infty } \frac{1}{N} \sum _{n=1}^N p_{\epsilon } \left( \frac{n}{N} \right) \cos ^2(\alpha n) + \frac{\epsilon }{2}. \end{aligned}$$
Hence
$$ \frac{1}{2} \int _0^1 w(t) dt - \frac{\epsilon }{2} \le \lim _{N \rightarrow \infty } \frac{1}{N} \sum _{n=1}^N w \left( \frac{n}{N} \right) \cos ^2(\alpha n) \le \frac{1}{2} \int _0^1 w(t) dt + \frac{\epsilon }{2}. $$
Since \(\epsilon \) is arbitrary, the result follows.
The result involving \(\sin ^2(\alpha n)\) will go through exactly in the same way. Note that using (a), Result A.2 and by properly choosing \(w(\cdot )\), (b), (c), (d) and (e) follow. \(\square \)
Lemma
C-2: If \(0< \alpha , \beta < \pi \), and w(t) satisfies Assumption 1, then except for countable number of points, for \(k = 0,1,2, \ldots \),
$$\begin{aligned}&\hbox {(a)}&\lim _{N \rightarrow \infty } \frac{1}{N} \sum _{n=1}^N w \left( \frac{n}{N} \right) \sin ^2(\beta n^2) = \lim _{N \rightarrow \infty } \frac{1}{N} \sum _{n=1}^N w \left( \frac{n}{N} \right) \cos ^2(\beta n^2) \\{} & {} = \frac{1}{2} \int _0^1 w(t) dt> \frac{\gamma }{2}, \\&\hbox {(b)}&\lim _{N \rightarrow \infty } \frac{1}{N^{k+1}} \sum _{n=1}^N n^k w \left( \frac{n}{N} \right) \sin ^2(\beta n^2) \\ {}{} & {} = \lim _{N \rightarrow \infty } \frac{1}{N^{k+1}} \sum _{n=1}^N n^k w \left( \frac{n}{N} \right) \cos ^2(\beta n^2) = \frac{1}{2} \int _0^1 t^k w(t) dt = \frac{c_{k+1}}{2} > 0, \\&\hbox {(c)}&\lim _{N \rightarrow \infty } \frac{1}{N^{k+1}} \sum _{n=1}^N n^k w \left( \frac{n}{N} \right) \sin (\alpha n^2)\\{} & {} =\lim _{N \rightarrow \infty } \frac{1}{N^{k+1}} \sum _{n=1}^N n^k w \left( \frac{n}{N} \right) \cos (\alpha n^2) = 0, \\&\hbox {(d)}&\lim _{N \rightarrow \infty } \frac{1}{N^{k+1}} \sum _{n=1}^N n^k w \left( \frac{n}{N} \right) \sin (\alpha n^2) \cos (\alpha n^2)\\{} & {} = \lim _{N \rightarrow \infty } \frac{1}{N^{k+1}} \sum _{n=1}^N w \left( \frac{n}{N} \right) \sin (\alpha n^2) \cos (\beta n^2) = 0, \\&\hbox {(f)}&\lim _{N \rightarrow \infty } \frac{1}{N^{k+1}} \sum _{n=1}^N n^k w \left( \frac{n}{N} \right) \sin (\alpha n^2) \sin (\beta n) \\{} & {} = \lim _{N \rightarrow \infty } \frac{1}{N^{k+1}} \sum _{n=1}^N w \left( \frac{n}{N} \right) \cos (\alpha n^2) \cos (\beta n) = 0, \\&\hbox {(g)}&\lim _{N \rightarrow \infty } \frac{1}{N^{k+1}} \sum _{n=1}^N n^k w \left( \frac{n}{N} \right) \sin (\alpha n^2) \cos (\beta n) \\{} & {} = \lim _{N \rightarrow \infty } \frac{1}{N^{k+1}} \sum _{n=1}^N w \left( \frac{n}{N} \right) \cos (\alpha n^2) \sin (\beta n) = 0, \\{} & {} \hbox {In addition if } \alpha \ne \beta , \hbox { then,} \\&\hbox {(e)}&\lim _{N \rightarrow \infty } \frac{1}{N^{k+1}} \sum _{n=1}^N n^k w \left( \frac{n}{N} \right) \sin (\alpha n^2) \sin (\beta n^2) \\{} & {} = \lim _{N \rightarrow \infty } \frac{1}{N^{k+1}} \sum _{n=1}^N w \left( \frac{n}{N} \right) \cos (\alpha n^2) \cos (\beta n^2) = 0. \\ \end{aligned}$$
Proof of Lemma C-2:
The proof follows along the same line as the proof of Lemma C-1. \(\square \)
Lemma
C-3: If \(\alpha , \beta \in (0,\pi )\), and if Conjecture A is true, then except for countable number of points, for \(k = 0,1,2, \ldots \),
$$\begin{aligned}\lim _{N \rightarrow \infty } \frac{1}{\sqrt{N} N^k} \sum _{n=1}^N n^k w \left( \frac{n}{N} \right) \cos (\alpha n^2) \sin (\beta n^2)= & {} 0. \\ \end{aligned}$$
In addition if \(\alpha \ne \beta \), then
$$\begin{aligned}\lim _{N \rightarrow \infty } \frac{1}{\sqrt{N} N^k} \sum _{n=1}^N n^k w \left( \frac{n}{N} \right) \cos (\alpha n^2) \cos (\beta n^2)= & {} 0, \\ \lim _{N \rightarrow \infty } \frac{1}{\sqrt{N} N^k} \sum _{n=1}^N n^k w \left( \frac{n}{N} \right) \sin (\alpha n^2) \sin (\beta n^2)= & {} 0, \\ \lim _{N \rightarrow \infty } \frac{1}{\sqrt{N} N^k} \sum _{n=1}^N n^k w \left( \frac{n}{N} \right) \cos (\alpha n^2) \cos (\beta n)= & {} 0, \\ \lim _{N \rightarrow \infty } \frac{1}{\sqrt{N} N^k} \sum _{n=1}^N n^k w \left( \frac{n}{N} \right) \sin (\alpha n^2) \sin (\beta n)= & {} 0, \\ \lim _{N \rightarrow \infty } \frac{1}{\sqrt{N} N^k} \sum _{n=1}^N n^k w \left( \frac{n}{N} \right) \sin (\alpha n^2) \cos (\beta n)= & {} 0, \\ \lim _{N \rightarrow \infty } \frac{1}{\sqrt{N} N^k} \sum _{n=1}^N n^k w \left( \frac{n}{N} \right) \cos (\alpha n^2) \sin (\beta n)= & {} 0. \end{aligned}$$
Proof of Lemma C-3:
If Conjecture A is true, then proof follows along the same line as the proof of Lemma C-1. \(\square \)
Proof of Theorem 2:
This proof can be obtained by expanding \(Q({\varvec{\theta }})\) around the point \({\varvec{\theta }}^0\). We will use the structure of the weight function w(t), Lemmas C-1 and C-2 and the Central Limit Theorem of the stochastic process to obtain the asymptotic distribution of \(\widehat{\varvec{\theta }}\). The criterion function is
$$ Q({\varvec{\theta }}) = \sum _{n=1}^N w \left( \frac{n}{N} \right) \left( y(n) - A\cos (\alpha n) - B\sin (\alpha n) - C\cos (\beta n^2) - D\sin (\beta n^2) \right) ^2, $$
therefore, the vector of first order derivatives is
$$\begin{aligned} Q'({\varvec{\theta }}^0)= & {} \left[ \begin{array}{c} \frac{\partial Q({\varvec{\theta }})}{\partial A} \\ \frac{\partial Q({\varvec{\theta }})}{\partial B} \\ \frac{\partial Q({\varvec{\theta }})}{\partial \alpha } \\ \frac{\partial Q({\varvec{\theta }})}{\partial C} \\ \frac{\partial Q({\varvec{\theta }})}{\partial D} \\ \frac{\partial Q({\varvec{\theta }})}{\partial \beta } \end{array} \right] _{{\varvec{\theta }} = {\varvec{\theta }}^0}\\ {}= & {} -2 \left[ \begin{array}{c} \sum _{n=1}^N w \left( \frac{n}{N} \right) X(n) \cos (\alpha ^0 n) \\ \sum _{n=1}^N w \left( \frac{n}{N} \right) X(n) \sin (\alpha ^0 n) \\ \sum _{n=1}^N n w \left( \frac{n}{N} \right) X(n) (B^0 \cos (\alpha ^0 n) - A^0 \sin (\alpha ^0 n)) \\ \sum _{n=1}^N w \left( \frac{n}{N} \right) X(n) \cos (\beta ^0 n^2) \\ \sum _{n=1}^N w \left( \frac{n}{N} \right) X(n) \sin (\beta ^0 n^2) \\ \sum _{n=1}^N n^2 w \left( \frac{n}{N} \right) X(n) (D^0 \cos (\beta ^0 n^2) - C^0 \sin (\beta ^0 n^2)) \end{array} \right] \end{aligned}$$
and the matrix of second order derivatives is
$$ Q^{''}({\varvec{\theta }}^0) = \left[ \begin{array}{cccccc} \frac{\partial ^2 Q({\varvec{\theta }})}{\partial A^2} &{} \frac{\partial ^2 Q({\varvec{\theta }})}{\partial A \partial B} &{} \frac{\partial ^2 Q({\varvec{\theta }})}{\partial A \partial \alpha } &{} \frac{\partial ^2 Q({\varvec{\theta }})}{\partial A \partial C} &{} \frac{\partial ^2 Q({\varvec{\theta }})}{\partial A \partial D} &{} \frac{\partial ^2 Q({\varvec{\theta }})}{\partial A \partial \beta } \\ \frac{\partial ^2 Q({\varvec{\theta }})}{\partial B \partial A} &{} \frac{\partial ^2 Q({\varvec{\theta }})}{\partial B^2} &{} \frac{\partial ^2 Q({\varvec{\theta }})}{\partial B \partial \alpha } &{} \frac{\partial ^2 Q({\varvec{\theta }})}{\partial B \partial C} &{} \frac{\partial ^2 Q({\varvec{\theta }})}{\partial B \partial D} &{} \frac{\partial ^2 Q({\varvec{\theta }})}{\partial B \partial \beta } \\ \frac{\partial ^2 Q({\varvec{\theta }})}{\partial \alpha \partial A} &{} \frac{\partial ^2 Q({\varvec{\theta }})}{\partial \alpha \partial B} &{} \frac{\partial ^2 Q({\varvec{\theta }})}{\partial \alpha ^2} &{} \frac{\partial ^2 Q({\varvec{\theta }})}{\partial \alpha \partial C} &{} \frac{\partial ^2 Q({\varvec{\theta }})}{\partial \alpha \partial D} &{}\frac{\partial ^2 Q({\varvec{\theta }})}{\partial \alpha \partial \beta } \\ \frac{\partial ^2 Q({\varvec{\theta }})}{\partial C \partial A} &{} \frac{\partial ^2 Q({\varvec{\theta }})}{\partial C \partial B} &{} \frac{\partial ^2 Q({\varvec{\theta }})}{\partial C \partial \alpha } &{} \frac{\partial ^2 Q({\varvec{\theta }})}{\partial C^2} &{} \frac{\partial ^2 Q({\varvec{\theta }})}{\partial C \partial D} &{} \frac{\partial ^2 Q({\varvec{\theta }})}{\partial C \partial \beta } \\ \frac{\partial ^2 Q({\varvec{\theta }})}{\partial D \partial A} &{} \frac{\partial ^2 Q({\varvec{\theta }})}{\partial D \partial B} &{} \frac{\partial ^2 Q({\varvec{\theta }})}{\partial D \partial \alpha } &{} \frac{\partial ^2 Q({\varvec{\theta }})}{\partial D \partial C} &{} \frac{\partial ^2 Q({\varvec{\theta }})}{\partial D^2} &{} \frac{\partial ^2 Q({\varvec{\theta }})}{\partial D \partial \beta } \\ \frac{\partial ^2 Q({\varvec{\theta }})}{\partial \beta \partial A} &{} \frac{\partial ^2 Q({\varvec{\theta }})}{\partial \beta \partial B} &{} \frac{\partial ^2 Q({\varvec{\theta }})}{\partial \beta \partial \alpha } &{} \frac{\partial ^2 Q({\varvec{\theta }})}{\partial \beta \partial C} &{} \frac{\partial ^2 Q({\varvec{\theta }})}{\partial \beta \partial D} &{}\frac{\partial ^2 Q({\varvec{\theta }})}{\partial \beta ^2} \end{array} \right] _{{\varvec{\theta }} = {\varvec{\theta }}^0}. $$
The elements of \(Q^{''}({\varvec{\theta }}^0)\) are given in Appendix D. Consider the following diagonal matrix
$$\begin{aligned} {\varvec{D}} = \text {diag}(N^{-1/2},N^{-1/2},N^{-3/2},N^{-1/2},N^{-1/2},N^{-5/2}) = \left( \begin{array}{cc} {\varvec{D}}_1^{-1} &{} \textbf{0} \\ \textbf{0} &{} {\varvec{D}}_2^{-1} \end{array} \right) , \end{aligned}$$
(23)
where \({\varvec{D}}_1\) and \({\varvec{D}}_2\) are same as used in the statement of Theorem 2. Then using Lemmas C-1 and C-2, it follows that
$$\begin{aligned} {\varvec{D}} Q'({\varvec{\theta }}^0) {\mathop {\longrightarrow }\limits ^{d}} N_6({\varvec{0}}, \sigma ^2 \ \mathbf{\Sigma }), \end{aligned}$$
(24)
where
$$ {\varvec{\Sigma }} = \left( \begin{array}{cc}\zeta {\varvec{\Sigma }}_1 &{} \textbf{0} \\ \textbf{0} &{} \eta {\varvec{\Sigma }}_2 \end{array} \right) . $$
Here \({\varvec{\Sigma }}_1\) and \({\varvec{\Sigma }}_2\) are same as defined in equation (10) and
$$ \zeta = \left| \sum _{k=-\infty }^{\infty } a(k) e^{i \alpha ^0 k} \right| ^2, \;\;\; \eta = \left| \sum _{k=-\infty }^{\infty } a(k) e^{i 3\beta ^0 k^2.} \right| ^2. $$
Now expanding \(Q'(\widehat{\varvec{\theta }})\) around \({\varvec{\theta }}^0\) using multivariate Taylor series expansion, we obtain
$$ Q'(\widehat{\varvec{\theta }}) = Q'({\varvec{\theta }}^0) + Q''(\bar{\varvec{\theta }})(\widehat{\varvec{\theta }}-{\varvec{\theta }}^0), $$
where \(\bar{\varvec{\theta }}\) lies on the line joining \(\widehat{\varvec{\theta }}\) and \({\varvec{\theta }}^0\). Since \(\widehat{\varvec{\theta }}\) minimizes \(Q({\varvec{\theta }})\), we have \(Q'(\widehat{\varvec{\theta }}) = {\varvec{0}}\), therefore
$$\begin{aligned} {\varvec{D}} Q'({\varvec{\theta }}^0) = - {\varvec{D}} Q''(\bar{\varvec{\theta }}){\varvec{D}}{\varvec{D}}^{-1}(\widehat{\varvec{\theta }}-{\varvec{\theta }}^0). \end{aligned}$$
(25)
Theorem 1 implies that \(\widehat{\varvec{\theta }} {\mathop {\longrightarrow }\limits ^{a.s.}}{\varvec{\theta }}^0\). Therefore, using the continuous mapping theorem and repeated use of Lemmas C-1 and C-2, we observe that
$$\begin{aligned} \lim _{N \rightarrow \infty } {\varvec{D}} Q^{''}(\bar{\varvec{\theta }}) {\varvec{D}} = \lim _{N \rightarrow \infty } {\varvec{D}} Q^{''}(\theta ^0) {\varvec{D}} = {\varvec{G}}, \end{aligned}$$
(26)
where
$$ {\varvec{G}} = \left( \begin{array}{cc} {\varvec{G}}_1 &{} \textbf{0} \\ \textbf{0} &{} {\varvec{G}}_2 \end{array} \right) . $$
with \({\varvec{G}}_1\) and \({\varvec{G}}_2\) same as defined in (11). Now using (24) and (26) in (25), we obtain
$$ {\varvec{D}}^{-1}(\widehat{\varvec{\theta }}-{\varvec{\theta }}^0) {\mathop {\longrightarrow }\limits ^{d}} N_6({\varvec{0}}, \sigma ^2 \ \mathbf{\Sigma }^{-1} {\varvec{G}} \mathbf{\Sigma }^{-1}). $$
Hence, the result follows. \(\square \)
Appendix D
The second order derivatives of \(Q({\varvec{\theta }})\) with respect to elements of \({\varvec{\theta }}\) at \({\varvec{\theta }}^0\) are provided in this Appendix.
$$\begin{aligned}\frac{\partial ^2 Q({\varvec{\theta }}^0)}{\partial A^2}= & {} 2 \sum _{n=1}^N w \left( \frac{n}{N} \right) \cos ^2(\alpha ^0 n), \\ \frac{\partial ^2 Q({\varvec{\theta }}^0)}{\partial A \partial B}= & {} 2 \sum _{n=1}^N w \left( \frac{n}{N} \right) \cos (\alpha ^0 n) \sin (\alpha ^0 n), \\ \frac{\partial ^2 Q({\varvec{\theta }}^0)}{\partial A \partial \alpha }= & {} 2 \sum _{n=1}^N n \ w \left( \frac{n}{N} \right) (B^0 \cos (\alpha ^0 n) - A^0 \sin (\alpha ^0 n))\cos (\alpha ^0 n ) \\{} & {} + 2 \sum _{n=1}^N n \ w \left( \frac{n}{N} \right) X(n) \sin (\alpha ^0 n ), \\ \frac{\partial ^2 Q({\varvec{\theta }}^0)}{\partial A \partial C}= & {} 2 \sum _{n=1}^N w \left( \frac{n}{N} \right) \cos (\alpha ^0 n) \cos (\beta ^0 n^2), \\ \frac{\partial ^2 Q({\varvec{\theta }}^0)}{\partial A \partial D}= & {} 2 \sum _{n=1}^N w \left( \frac{n}{N} \right) \cos (\alpha ^0 n) \sin (\beta ^0 n^2), \end{aligned}$$
$$\begin{aligned}\frac{\partial ^2 Q({\varvec{\theta }}^0)}{\partial A \partial \beta }= & {} 2 \sum _{n=1}^N n^2 w \left( \frac{n}{N} \right) \cos (\alpha ^0 n) (D^0 \cos (\beta ^0 n^2) - C^0 \sin (\beta ^0 n^2)) \\ \frac{\partial ^2 Q({\varvec{\theta }}^0)}{\partial B^2}= & {} 2 \sum _{n=1}^N w \left( \frac{n}{N} \right) \sin ^2(\alpha ^0 n), \\ \frac{\partial ^2 Q({\varvec{\theta }}^0)}{\partial B \partial \alpha }= & {} 2 \sum _{n=1}^N n \ w \left( \frac{n}{N} \right) (B^0 \cos (\alpha ^0 n) - A^0 \sin (\alpha ^0 n ))\sin (\alpha ^0 n) \\{} & {} - 2 \sum _{n=1}^N n \ w \left( \frac{n}{N} \right) X(n) \cos (\alpha ^0 n ), \\ \frac{\partial ^2 Q({\varvec{\theta }}^0)}{\partial B \partial C}= & {} 2 \sum _{n=1}^N w \left( \frac{n}{N} \right) \sin (\alpha ^0 n) \cos (\beta ^0 n^2), \\ \frac{\partial ^2 Q({\varvec{\theta }}^0)}{\partial B \partial D}= & {} 2 \sum _{n=1}^N w \left( \frac{n}{N} \right) \sin (\alpha ^0 n) \sin (\beta ^0 n^2), \\ \frac{\partial ^2 Q({\varvec{\theta }}^0)}{\partial B \partial \beta }= & {} 2 \sum _{n=1}^N n^2 w \left( \frac{n}{N} \right) \sin (\alpha ^0 n) (D^0 \cos (\beta ^0 n^2) - C^0 \sin (\beta ^0 n^2)) \\ \frac{\partial ^2 Q({\varvec{\theta }}^0)}{\partial \alpha ^2}= & {} 2 \sum _{n=1}^N n^2 w \left( \frac{n}{N} \right) \left( B^0 \cos (\alpha ^0 n) - A^0 \sin (\alpha ^0 n)\right) ^2 \\ \hspace{.5in}{} & {} + 2 \sum _{n=1}^N n^2 w \left( \frac{n}{N} \right) X(n) \left\{ A^0 \cos (\alpha ^0 n) + B^0 \sin (\alpha ^0 n)\right\} , \\ \frac{\partial ^2 Q({\varvec{\theta }}^0)}{\partial \alpha \partial C}= & {} 2\sum _{n=1}^N n \ w \left( \frac{n}{N} \right) \cos (\beta ^0 n^2) (B^0 \cos (\alpha ^0 n) - A^0 \sin (\alpha ^0 n)), \\ \frac{\partial ^2 Q({\varvec{\theta }}^0)}{\partial \alpha \partial D}= & {} 2\sum _{n=1}^N n \ w \left( \frac{n}{N} \right) \sin (\beta ^0 n^2) (B^0 \cos (\alpha ^0 n) - A^0 \sin (\alpha ^0 n)), \\ \frac{\partial ^2 Q({\varvec{\theta }}^0)}{\partial \alpha \partial \beta }= & {} 2 \sum _{n=1}^N n^3 w \left( \frac{n}{N} \right) (B^0 \cos (\alpha ^0 n) - A^0 \sin (\alpha ^0 n)) (D^0 \cos (\beta ^0 n^2) \\{} & {} - C^0 \sin (\beta ^0 n^2)) \\ \frac{\partial ^2 Q({\varvec{\theta }}^0)}{\partial C^2}= & {} 2 \sum _{n=1}^N w \left( \frac{n}{N} \right) \cos ^2(\beta ^0 n^2), \\ \frac{\partial ^2 Q({\varvec{\theta }}^0)}{\partial C \partial D}= & {} 2 \sum _{n=1}^N w \left( \frac{n}{N} \right) \cos (\beta ^0 n^2) \sin (\beta ^0 n^2), \\ \frac{\partial ^2 Q({\varvec{\theta }}^0)}{\partial C \partial \beta }= & {} 2 \sum _{n=1}^N n^2 w \left( \frac{n}{N} \right) (D^0 \cos (\beta ^0 n^2) - C^0 \sin (\beta ^0 n^2))\cos (\beta ^0 n^2 ) \\{} & {} + 2 \sum _{n=1}^N n w \left( \frac{n}{N} \right) X(n) \sin (\beta ^0 n^2 ), \\ \frac{\partial ^2 Q({\varvec{\theta }}^0)}{\partial D^2}= & {} 2 \sum _{n=1}^N w \left( \frac{n}{N} \right) \sin ^2(\beta ^0 n^2), \\ \frac{\partial ^2 Q({\varvec{\theta }}^0)}{\partial D \partial \beta }= & {} 2 \sum _{n=1}^N n^2 w \left( \frac{n}{N} \right) (D^0 \cos (\beta ^0 n^0) - C^0 \sin (\beta ^0 n^2))\sin (\beta ^0 n^2) \\{} & {} - 2 \sum _{n=1}^N n^2 w \left( \frac{n}{N} \right) X(n) \cos (\beta ^0 n^2 ), \\ \frac{\partial ^2 Q({\varvec{\theta }}^0)}{\partial \beta ^2}= & {} 2 \sum _{n=1}^N n^4 w \left( \frac{n}{N} \right) \left( D^0 \cos (\beta ^0 n^2) - C^0 \sin (\beta ^0 n^2)\right) ^2 \\ \hspace{.5in}{} & {} + 2 \sum _{n=1}^N n^4 w \left( \frac{n}{N} \right) X(n) \left\{ C^0 \cos (\beta ^0 n^2) + D^0 \sin (\beta ^0 n^2)\right\} . \end{aligned}$$
Now consider the \((1,1)^{th}\) element of \(\textbf{D} Q({\varvec{\theta }}^0) \textbf{D}\) for large N.
$$\begin{aligned}\lim _{N\rightarrow \infty } \frac{1}{N} \frac{\partial ^2 Q({\varvec{\theta }}^0)}{\partial A^2}= & {} \lim _{N\rightarrow \infty }\frac{2}{N} \sum _{n=1}^N w \left( \frac{n}{N} \right) \cos ^2(\alpha ^0 n) \\= & {} \lim _{N\rightarrow \infty } \frac{2}{N} \sum _{n=1}^N \Bigl (1 + a_1 \frac{n}{N} + a_2 \frac{n^2}{N^2} + \cdot + a_m \frac{n^m}{N^m} \Bigr )\cos ^2(\alpha ^0 n) \\= & {} \bigl (1 + \frac{a_1}{2} + \frac{a_2}{3} + \cdots + \frac{a_m}{m+1} \bigr )= c_1, \end{aligned}$$
using Result A.1. Here \(c_{k+1}, k=0, 1,\ldots \) are same as defined in (8). Similarly the other elements of \(\displaystyle \lim _{N\rightarrow \infty } \textbf{D} Q({\varvec{\theta }}^0) \textbf{D}\) can be obtained using Lemmas C-1 and C-2.