Optimal control of the SEIR epidemic model using a dynamical systems approach

Abstract

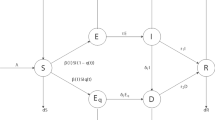
We consider the susceptible-exposed-infected-removed (SEIR) epidemic model and apply optimal control to it successfully. Here three control inputs are considered, so that the infection rate is decreased and exposed or infected individuals are removed. Our approach is to reduce the computation of the optimal control input to that of the stable manifold of an invariant manifold in a Hamiltonian system. Some numerical examples in which the computer software AUTO is used to numerically compute the stable manifold are given to demonstrate the usefulness of our approach for the optimal control in the SEIR model. Our study suggests how we can decrease the number of infected individuals quickly before a critical situation occurs while keeping social and economic burdens small. Our results for the SEIR model are very different from the previous one for the SIR model, which is similar but simpler than the present one.

Appendix A: Dynamics of (1.3)

In this appendix we collect necessary information on the SEIR model (1.3). As stated in Sect. 1, for any $c\ge 0$ $(S,E,I)=(c,0,0)$ is an equilibrium in (1.3). Moreover, these equlilibria construct a one-dimensional invariant manifold in the three-dimensional phase space. The Jacobian matrix of the right hand side of (1.3) at (c, 0, 0) becomes

$$\begin{aligned} \begin{pmatrix} 0 &{} 0 &{} -rc\\ 0 &{} -b &{} rc\\ 0 &{} b &{} -a \end{pmatrix} \end{aligned}$$

and has eigenvalues at

$$\begin{aligned} \lambda =0\quad \text {and}\quad \tfrac{1}{2}\left( -(a+b)\pm \sqrt{(a+b)^2+4b(rc-a)}\right) , \end{aligned}$$

for which the eigenvectors are given by

$$\begin{aligned} \begin{pmatrix} 1\\ 0\\ 0 \end{pmatrix} \quad \text{ and }\quad \begin{pmatrix} \displaystyle \frac{-2rbc}{-(a+b)\pm \sqrt{(a+b)^2+4b(rc-a)}}\\ a+\tfrac{1}{2}\left( -(a+b)\pm \sqrt{(a+b)^2+4b(rc-a)}\right) \\ b \end{pmatrix}, \end{aligned}$$

(A.1)

respectively. So the equilibrium (c, 0, 0) is unstable when $c>a/r$. On the other hand, when $c<a/r$, since it has a one-dimensional center manifold which coincides with the S-axis and consists of equilibria along with a two-dimensional stable manifold, the equilibrium is not asymptotically stable but stable.

On the other hand, we add the second and third equations of (1.3) to obtain

$$\begin{aligned} {\dot{E}}+{\dot{I}}=(rS-a)I. \end{aligned}$$

This means $E+I$ is monotonically increasing or decreasing for $S>a/r$ and $S<a/r$, respectively. We also easily see that Eq. (1.1) or (1.3) has a first integral, i.e., a conservative quantity,

$$\begin{aligned} F(S,E,I)=S\exp \left( -\frac{r}{a}(S+E+I)\right) . \end{aligned}$$

Since $F(S,E,I)=S\exp (-rS/a)$ is not a constant on the S-axis which is its center manifold, we see that the equilibrium (c, 0, 0) is stable, again. Moreover, it is shown to be non-integrable unlike the SIR model (1.2). See [22] for the details.