1 Introduction

Porous media consists of numerous irregular pores of different sizes panning several orders of magnitude in length scales (Feng et al 2004). Fractal theory (Mandelbrot 1983) has been widely employed for characterizing the geometrical micro-structure of porous media and assessing the physical properties and processes derived from them. The irregular nature of porous media exhibit fractal characteristics, and thus, fractal theory is a useful tool for describing its porosity (Wei et al. 2015) and the apparent randomness in its geometric properties (Sufian and Russell 2013). Consequently, fractal framework allows both characterizing differences in complex structural properties of porous media from different perspectives (Xia et al. 2019) and describing the degree of irregularity of natural shapes, taking the advantage that this analysis is independent of scale.

The pioneer work dealing with the fractal description of a porous media was developed by Katz and Thompson (1985) by using scanning electron microscopy and optical data in pore spaces of sandstones. Later, fractal analysis have been conducted in porous media of rocks and stones (Krohn and Thompson 1986; Krohn 1988), soils (Perfect and Kay 1991; Rieu and Sposito 1991; Young and Crawford 1991), and textile fabrics (Yu et al. 2001, 2002), to cite a few. Fractal dimension is the main parameter for fractal analysis. It is known that, on the one hand, fractal dimension reflects the complexity of the pore structure, and on the other, that this parameter increases when the pore ratios increases (Peng et al. 2011). Beside the characterization of complex geometries in porous media, fractal dimension has also been employed for characterizing processes and modelling physical properties in them, mainly in percolation and permeability (Schlueter et al. 1997; Yu and Cheng 2002; Yu et al. 2002, 2003; Yu and Liu 2004; Feng et al 2004; Xu et al. 2013; Pia and Sanna 2014; Cai et al. 2015; Liu et al. 2019), thermal conductivity (Thovert et al. 1990; Feng et al 2004), electrical conductivity (Wei et al. 2015), transport (Adler 1996; Cai et al. 2018), hydraulic properties (Giménez et al. 1997), flow simulation (Smidt and Monro 1998; Xiao et al 2018) imbibition process (Cai et al. 2010), water retention (Bird et al. 2000) and gas transport (Wang et al. 2019), among others.

Even so, different methods for fractal measurements can be found. Thompson (1991) distinguished three types of fractal measurements in sedimentary rocks. On the one hand, discrete methods, which are based on the digitisation of an object and the subsequent analysis of the data in a spatial domain. Second, the spectral and scattering methods, in which the fractality of the object is explored by means of a previous transformation to the spatial frequency of the wave number domain. Third, the adsorption methods, which are based on the idea that molecules of various sizes can be used as measuring rods on a molecular scale to quantify the area of a fractal surface as a function of measuring rod size. Within each typology, there are different methods that might generate uncertainty in the estimation of the fractal dimension, as in the case of surface roughness measured from isotherm data (Wood 2021). In addition, there is not a single fractal dimension, i.e., several fractal dimensions can be defined in porous structures by applying a specific method, such as the mass fractal dimension (Bartoli et al. 1991; Rieu and Sposito 1991; Young and Crawford 1991), the volume fractal dimension (Hansen and Skjeltorp 1988; Jacquin and Adler 1987), the surface fractal dimension (Avnir et al. 1985; Hansen and Skjeltorp 1988; Katz and Thompson 1985), the fragmentation fractal dimension, and the fractal dimension of connectivity (Giménez et al. 1997), to cite a few. This work explore fractality by means of the box-counting method, which is included in the discrete methods.

Moreover, the generation of synthetic images for the study of fractal properties has been widely performed. For example, synthetic images of known fractal dimension were compared with real topography images, being their results very consistent (Huang and Turcotte 1989, 1990). In these cases, images were considered as gray-scales, as well as in the study developed by Liu et al. (2014), in which different box-counting algorithms were compare by using a set of synthetic texture-like images. Even in psychology, correlations have been established between fractal dimension of synthetic noise images and artworks with their preference aesthetic value (Viengkham and Spehar 2018). However, pore size distribution often exhibits fluctuations at different scales, and thus, local variations in the internal distribution of pore sizes cannot be explained by a single fractal dimension (Gao et al. 2014; Li et al. 2015). In fact, for irregular distributions of pore sizes, a single fractal dimension would describe the irregularity within limited size intervals. In these cases, different pore size intervals show different types of self-similarity and, therefore, the fractal dimension would only characterize the average properties of an ensemble (Vázquez et al. 2008). These complex microstructures are found in many existing distributions in nature, they being more accurately described by considering them as multifractal structures (Li et al. 2015; San José Martínez et al. 2010).

Multifractality arises when a single fractal dimension is not enough to completely characterize a complex and heterogeneous behavior, i.e., when the simple fractal is not able to describe the geometry of the system (Kravchenko et al. 1999; Jouini et al. 2011). Thus, a multifractal structure is considered as a superposition of subsets of monofractal structures intertwined by a hierarchy of scale exponents that characterizes the local variability and heterogeneity of the studied variables (Bird et al. 2000; Kravchenko et al. 1999; Posadas et al. 2003). Multifractal analysis provides more parameters to quantitatively conveys the internal scaling behavior of pore size distributions (Li et al. 2015), taking the advantage of characterizing more sophisticated pore space distributions (Kong et al. 2019a).

Multifractal analysis of synthetic images, which is subsequent to fractal analysis, has been used for describing synthetic and real images in the last decades, such as rough surfaces (Decoster et al. 2000; Hosseinabadi et al. 2012), crack patterns in structures (Ebrahimkhanlou et al. 2016), and soil porosity images (Torre et al. 2020), among others. The generalization of this analysis is evident in the generation of programs for fractal and multifractal analysis of binary images (Perrier et al. 2006) and fast a and efficient procedures to perform accurate analysis of the scaling and multifractal properties of images (Wendt et al. 2009). More recently, scanning electron microscope (SEM) has allowed the digital analysis of two-dimensional images with high accuracy, characterizing and quantifying the pore space of porous media using both fractal and multifractal methods (Kong et al. 2019b; Tian et al. 2021; Wang et al. 2016; Xie et al. 2010). On the other hand, fractal and multifractal analysis of images has been extended to volume textures, this being previously tested on synthetic data (Lopes et al. 2011).

Summarizing, fractal and multifractal analysis are powerful tools for describing porous media at different spatial scales. For this reason, it is common to use these scaling analysis as comparative descriptors among images of porous media. However, these techniques are complex to discern why certain images show more or less fractal dimension or to motivate the shape of the generalized multifractal function. For this reason, a global analysis considering fractal, lacunarity and multifractal properties of synthetic images of porous media is performed in this work. Pore size and pore distribution are used as parameters in order to assess the influence of porosity variables on (multi-)fractality. The influence of deterministic versus random pore distributions has also been evaluated, as well as the role of different pore size mixtures. It is also noted that these synthetic images obey to the relationship among fractal dimension and porosity stated by Yu and Li (2001). The findings of the work are useful to better understand and describe the fractal and multifractal properties of real porous media, in accordance to their pore size and distribution.

The remainder of this work is structured as follows: Sect. 2 describe the fractal and multifractal methods employed (Sect. 2.1), along with the description of the generation of synthetic images (Sect. 2.2). The results obtained are shown and discussed in Sect. 3. Finally, Sect. 4 concludes the work.

2 Methods

This section is comprised by 2 subsections. Section 2.1 describes the algorithms and method employed for the determination of the fractal, multifractal and lacunarity parameters, along with porosity. Section 2.2 describes the procedure for generating the synthetic images analyzed in this work and their main parameters.

2.1 Fractal and multifractal methods

2.1.1 Fractal analysis

In Euclidean geometry, the measure of an object does not depend on the scale of measurement, i.e, the measure is invariant respect to the measurement unit employed. As consequence, the total length of an object (L) can be easily computed as the amount of times (N) that the scale of measurement \((\delta )\) is required, according to \(L=N \cdot \delta \). By contrast, many objects existing in nature exhibit irregular, rough and disordered shapes and contours (Mandelbrot 1983) and do not follow an Euclidean description. Therefore, their measures depend on the scale of measurement according to Eq. 1:

$$\begin{aligned} L(\delta )=N(\delta ) \cdot \delta \ \end{aligned}$$
(1)

When the relationship between \(L(\delta )\) and \(\delta \) follows a power law, it is said that the object exhibits fractal properties, and thus, by taking logarithms in Eq. 1, the relationship between both variables becomes linear. The scaling of \(ln[L(\delta )]\) versus \(ln[\delta ]\) is characterized by the slope of the linear fit, the slope being the value of the fractal dimension (\(D_f\)). The box-counting method (Barnsley 1993; Falconer 2004; Feder 2013) is the most common and efficient method for estimating the fractal dimension of binary images (Xia et al. 2019), because it can be accurately estimated in Euclidean spaces when working with a finite range of scales (FernándezspsMartínez and SánchezspsGranero 2016). Due to its simplicity and high degree of computability (Wang et al. 2012), the box-counting method is an effective procedure to complete porosity analysis, specifically to describe pore distribution and heterogeneity (Wang et al. 2016).

The box-counting method is conducted on a square binary image of side L comprised by both a solid phase and a porous phase. Subsequently, a set of square boxes of side a divisor of L is chosen: \(\delta = \{L/1, L/2, L/4, L/8, L/8, L/16\,...\}\), so that smaller and smaller box sizes are taken each time. For each box size, the image is completely covered without any overlapping among the boxes. The choice of images of side a power of 2 facilitates this task. Then, the existence of pores in each covering box is checked and the amount of boxes containing at least one pixel belonging to the porous phase, \(N(\delta )\), is counted. The procedure is repeated by varying the observation scale, that is, by covering the image with boxes of different size \((\delta )\). If the image shows fractal properties, the variables \(N(\delta )\) and \((\delta )\) obey the following relationship:

$$\begin{aligned} N(\delta ) \approx k\cdot \delta ^{-D_f} \end{aligned}$$
(2)

where \(D_f\) is the box-counting fractal dimension and k is a trivial constant. \(D_f\) is estimated from the absolute value of the slope of the linear regression of \(ln[N(\delta )]\) vs \(ln[\delta ]\) (Wang et al. 2016). For 2D images, the fractal dimension of the pore is between 1 and 2, agreeing with the capacity of a porous media to cover a plane. As seen, computing the fractal dimension is relatively simple and has a very intuitive physical meaning (Peng et al. 2011).

2.1.2 Analytical relationship between fractal dimension and porosity

Porosity (\(\phi \)) is a measure of the void of a image, which is represented as a fraction of void space over the total space. Porosity is defined in Eq. 3.

$$\begin{aligned} \phi = \frac{Pixel \ Pores}{Total \ Pixels} \end{aligned}$$
(3)

So, the greater amount of pixel pores in a image, the greater value of \(\phi \). It oscillates in the range [0, 1]. \(\phi = 0\) when the image contains no pores and \(\phi = 1\) when the whole image is a void.

On the other hand, Yu and Li (2001) stated a logarithmic relationship among fractal dimension (\(D_f\)), porosity (\(\phi \)), and self-similarity scale in porous media, as follows in Eq. 4:

$$\begin{aligned} D_f = d_E - \frac{ln(\phi )}{ln\frac{\lambda _{min}}{\lambda _{max}}} \end{aligned}$$
(4)

with \(d_E\) being the Euclidean dimension (2 for a plane) and \(\lambda _{min}\) and \(\lambda _{max}\) the minimum and maximum pore sizes in a unit cell for fractal porous media (Feng et al 2004). As can be deduced, when the porosity is \(\phi = 1\), the numerator of the fraction is equal to 0, so the \(D_f\) equals to the Euclidean dimension \(d_E\). Anyway, Eq. 4 is applicable not only for strictly self-similar fractal geometries, but also for fractal geometries, such as random or disordered porous media. The only difference is that \(\lambda _{max}\) is the side length for exactly self-similar fractal geometries and the maximum pore size in a unit cell (representative cell) in random/disordered porous media (Yu and Li 2001).

2.1.3 Lacunarity analysis

Several porous media works have highlighted that fractal dimension need to be complemented by further analysis in some cases. Whereas Tian et al. (2021) found significant differences in the fractal dimension among different images obtained from the same section, Xia et al. (2019) discovered that fractal dimension was not an accurate predictor of the variation of permeability on its own. For this reason, it is usual to complete the fractal dimension with other fractal parameters that overcome these drawbacks. One of them is the lacunarity (\(\Lambda \)) (Allain and Cloitre 1991), which describes the degree of aggregation of pores in a porous media, according to higher values of lacunarity, implying high degrees of pore aggregation.

Lacunarity is computed by using the gliding-box method, which is similar to the box-counting detailed in Sect. 2.1.1, but requires the complete covering of the image by means of the overlapping of the boxes. For each size box \(\delta \), the amount of pore pixels falling into the box is computed as M, and then, the amount of boxes containing M pore pixels is marked as \(n(M,\delta )\). Later, \(n(M,\delta )\) is divided by the total amount of gliding boxes of size \(\delta \) in order to obtain the probability density function \(Q(M,\delta )\). From the probability density function, the function of statistical moments is constructed as shown in Eq 5:

$$\begin{aligned} \ Z_Q^{(q)}(\delta ) = \sum _M{M^q}Q(M,\delta ) \end{aligned}$$
(5)

Finally, lacunarity (\(\Lambda \)) is defined for each \(\delta \) as the quotient between the statistical moment functions when \(q=2\) and the square of statistical moment function when \(q=1\), as follows in Eq. 6:

$$\begin{aligned} \Lambda (\delta )= \frac{Z_Q^{(q=2)}(\delta )}{[Z_Q^{(q=1)}(\delta )]^2} \end{aligned}$$
(6)

Thus, lacunarity is a function that varies with \(\delta \). The minimum value is obtained when the side of the gliding-box is equal to the size of the image, i.e., \(\Lambda _{min}=\Lambda (\delta =L)=1\). Conversely, the maximum of lacunariry is reached when the side of the gliding-boxes are 1, so \(\Lambda _{max}=\Lambda (\delta =1)=1/\phi \). Due to the dependece of \(\Lambda _{max}\) respect to \(\phi \), lacunarity is not comparable between two images with different porosity. To overcome this drawback, normalized lacunarity \(\Lambda ^*\) (Roy et al. 2010) is defined in the interval [0, 1] by means of Eq. 7:

$$\begin{aligned} \ \Lambda ^*(\delta )= \frac{\Lambda (\delta )-\Lambda _{min}}{\Lambda _{max}-\Lambda _{min}}=\phi \frac{\Lambda (\delta )-1}{1-\phi } \end{aligned}$$
(7)

2.1.4 Multifractal analysis

Conversely to fractal objects, which are mainly characterized by means of a single value (Vega and Jouini 2015), multifractals are mathematical measures completely characterized by a function, i.e., the multifractal spectrum or spectrum of generalized fractal dimensions. Both functions allow to describe complex structures with subsets of regions that exhibit different properties (Grau et al. 2006; Jouini et al. 2011; Dănilă et al. 2018). Definitely, a multifractal is a non-uniform fractal that exhibits local density fluctuations (Grau et al. 2006; Ge et al. 2015). Multifractal analysis solves local densities in order to capture the internal variations of a system (Posadas et al. 2003; Vázquez et al. 2008; Li et al. 2015). This means that multifractal analysis allows a more specific characterization of pore space distributions (Kravchenko et al. 1999; Gao et al. 2014; Kong et al. 2019a).

In this work, multifractal analysis is conducted through the box-counting method and the method of moments (Evertsz and Mandelbrot 1992) for computing the generalized fractal dimensions D(q) (Grassberger 1983; Hentschel and Procaccia 1983). In the box-counting method for multifractal analysis, the domain is subsequently divided into non-overlapping square boxes that completely cover the entire domain. For each box size \(\delta \), the mass probability function (\(c_i(\delta )\)), is computed as the portion of the pore pixels contained in each box i of size \(\delta \), respect to the total amount of pore pixels of the image, according to Eq. 8:

$$\begin{aligned} \ c_i(\delta ) = \frac{N_i(\delta )}{\sum _{i=1}^{M(\delta )}N_i(\delta )} \end{aligned}$$
(8)

For binary images, \(c_i(\delta )\) can be understood as the probability of existence of pore pixels in the box ith, where \(N_i(\delta )\) is the amount of pore pixels inside the ith box of size \(\delta \), and \(M(\delta )\) is the total number of boxes containing at least one pore pixel Ebrahimkhanlou et al. (2016). Later, the mass probability function is calculated by employing the method of moments (Evertsz and Mandelbrot 1992), where the partition function (\(\chi (q,\delta )\)) is computed from the values of \(c_i(\delta )\) as follows:

$$\begin{aligned} \ \chi (q,\delta ) = \sum _{i=1}^{n}(c_i(\delta ))^q \end{aligned}$$
(9)

where n is the number of boxes of size \(\delta \) and q is a real number ranging from \(-\infty \) to \(+\infty \). In this analysis, whereas negative q moments emphasize boxes with low pore densities, positive q moments emphasize boxes with high pore densities. In any case, it is well known that multifractality appears when the existence of a power law between \(\chi (q,\delta )\) and \(\delta \) is trusted. Thus, for multifractal measures the partition function exhibits the scaling property described in Eq. 10:

$$\begin{aligned} \ \chi (q,\delta ) \approx \delta ^{\tau (q)} \end{aligned}$$
(10)

\(\tau (q)\), which is called the mass exponent function, is estimated from the slope of the linear segment of the log-log plot of \(\chi (q,\delta )\) versus \(\delta \). Finally, generalized fractal dimensions, D(q) (also called Rényi Dimensions), are computed from \(\tau (q)\) using the following relationship:

$$\begin{aligned} \ D(q) = \frac{\tau (q)}{q-1} \end{aligned}$$
(11)

It should be noted that generalized dimension function exhibits a multifractal behaviour when D(q) is a monotonically decreasing function versus q. Multifractal parameters are considered useful tools for characterizing the structure and topological properties of porous media (Ge et al. 2015; Posadas et al. 2003). Most common of them are the generalized dimensions, D(q), and the multifractal degree, \(\Delta D(q)\). For the generalized dimension functions three values are spotlighted: the capacity dimension \(D(q=0)\), the information dimension \(D(q=1)\), and the correlation dimension \(D(q=3)\). Generally, for multifractal measures, it is satisfied that \(D(0)> D(1) > D(2)\), being the dimension function decreasing with respect to q. By contrast, when the distribution is statistical or exactly monofractal, equality between these three dimensions occurs, and thus, D(q) is independent of q. On the other hand, multifractal degree, which allows to characterize the dimension function, is used as a heterogeneity indicator (Ge et al. 2015). It is defined as:

$$\begin{aligned} \ \Delta D(q) = D(q_{min}) - D(q_{max}) \end{aligned}$$
(12)

In general, the higher the values of \(\Delta D(q)\), the wider the structural variability, the less homogeneous the distribution patterns and, therefore, the stronger the multifractality of the system (Dănilă et al. 2018; Xie et al. 2010).

2.2 Synthetic images

In this section, deterministic and random synthetic images are generated by controlling two parameters: pore size and pore location. Images are square with \(L \cdot L = 512 \cdot 512\) = 262,144 pixels. Thus, \(\delta \) values for box-counting and gliding-box are established as \(\delta \) = 1, 2, 4, 8, 16, 32, 64, 128, 256, and 512.

2.2.1 Regular grid images

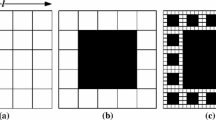
For generating the regular grid images, the pore location is fixed and the pore size varies. These images are regular grids comprised by 21 rows and 21 columns of pores (441 voids). Pore sizes are considered as squares of side 1, 2, 4, 6, 10, 15 and 20 pixels. In Fig. 1 these 7 regular grid images are depicted along with the pore surface and porosity (\(\phi \)), which ranges between \(\phi = 0.0016\) to \(\phi = 0.6103\).

Fig. 1
figure 1

Regular grid images with pore size: a \(1 \times 1\), b \(2 \times 2\), c \(4 \times 4\), d \(6 \times 6\), e \(10 \times 10\), f \(15 \times 15\), and g \(20 \times 20\)

Full size image

2.2.2 Fixed pore size random images

Regular grid images with a random component are generated by means of a random location of fixed-size pores. To compare them with the regular grid images, random images were generated with square pores of side 1, 2, 4, 6, 10, 15 and 20 pixels. Notice that the amount of pores of random images is also equal to the regular grid ones, that is 441 pores. On the other hand, random images exhibit a drawback related to a pore overlapping which influences on the final size of the pores, and thus, on the image porosity. However, avoiding overlapping presents a disadvantage, mainly for images with large pore sizes. For large pores, it is computationally complex to obtain images with 441 non-overlapping pores randomly distributed. Therefore, the approach taken was to perform hundreds of iterations for each pore size, and then, choosing the 5 of them that ensure the same porosity (or as close as possible) to their regular grid counterpart. The selection of 5 images for each pore size is due to the use of random images, and thus, results are the average of them. To illustrate, one of the 5 images selected for each pore size is shown in Fig. 2. By comparing Figs. 1 and 2, it is observed that the porosity of the regular grid images (\(\phi \)) is equal than the average porosity of the fixed pore size random ones (\(\overline{\phi }\)) for \(1 \times 1\) and \(2 \times 2\) pore size. For larger pore size, (\(\overline{\phi }\)) is lower than the porosity of the regular grid images according to the larger the pore size, the grater difference between \(\phi \)-\(\overline{\phi }\). This is due to the fact that pore overlapping in random images causes a lower porosity than in regular grid images.

Fig. 2
figure 2

Fixed pore size random images with pore size: a \(1 \times 1\), b \(2\times 2\), c \(4 \times 4\), d \(6 \times 6\), e \(10 \times 10\), f \(15 \times 15\), and g \( 20\times 20\)

Full size image

2.2.3 Mixed pore size random images

Mixed pore size random images are characterized by combining different pore sizes. 11 set of images have been generated by mixing different pore distributions from 5 pore sizes established (\(2 \times 2\) pixel, \(4 \times 4\) pixel, \(6 \times 6\) pixel, \(10 \times 10\) pixel and \(15 \times 15\) pixel). Each image contains 440 pores according to a default pore size distribution. The mixtures are organized into three groups, as summarizes Table 1.

Group 1 is comprised by 3 kinds of mixtures in which the ratio of pores is equal to \(15\%\) for each pore size. However, one pore size is magnified over the others with a percentage of \(40\%\): In mixture I the main percentage of pore size are the smallest (\(2 \times 2\) pixel), in mixture II are the medium size (\(6 \times 6\) pixel) and in mixture III are the largest one (\(15 \times 15\) pixel) (see Fig. 3a–c). In group 2 the overall ratio of pores is \(10\%\), with the importance of the dominant pore size being even higher than in group 1. Thus, \(60\%\) of the pores correspond to the smallest pore size (\(2 \times 2\) pixel) for mixture IV, the medium (\(6 \times 6\) pixel) for mixture V and the largest (\(15 \times 15\) pixel) for mixture VI (see Fig. 3d–f). Group 3 is comprised by 5 mixtures, which represent a more gradual transition among the different pore sizes distributions. Mixture VII concentrates 40% of the smaller pore sizes, decreasing to 25%, 20%, 10% and 5% for the larger sizes. Conversely, mixture XI contains \(40\%\) of large pore sizes (\(15 \times 15\)), decreasing towards smaller pore sizes. Mixture IX has \(40\%\) medium-sized pores, decreasing in a balanced way towards larger and smaller pores. Whereas mixture VIII is an intermediate situation between VII and IX, mixture X is the intermediate between IX and XI (see Fig. 3g–k).

Since random process to generate these images, there is an overlapping among pores, as explained in Sect. 2.2.2. For this reason, the ideal porosity is previously computed (ideal porosity is computed from a theoretical image with no pore overlapping). Thus, hundreds of iterations must be performed for selecting the 5 images that best ensure the ideal porosity of each mixture.

Fig. 3
figure 3

Mixed pore size random images: Group 1 (a Mixture I, b Mixture II, c Mixture III); Group 2 (d Mixture IV, e Mixture V, f Mixture VI), and Group 3 (g Mixture VII, h Mixture VIII, i Mixture IX, j Mixture X and k Mixture XI)

Full size image
Table 1 Pore size ratio for mixed pore size random images
Full size table

3 Results and discussion

3.1 Fractal and lacunarity analysis

Fractal dimensions (\(D_f\)) are estimated for each set of images from the box-counting method described in Sect. 2.1.1, and the normalized lacunarity \(\Lambda ^*(\delta )\) according to 2.1.3.

3.1.1 Regular grid images

Fractal dimensions for regular grid images are obtained from the slope of the linear regression of ln[N] vs \(ln[\delta ]\) between \(\delta _{min} = 1\) to \(\delta _{max} = 16/32\), with a \(R^2\) greater than 0.950 for most cases. It is noted that the value of the fractal dimension for the \(1 \times 1\)-regular grid image exhibit a low \(R^2\) (0.429), which evinces a high uncertainty in the estimation of \(D_f\) in regular grid images with tiny pore size.

Figure 4a depicts the fractal dimension against the pore size for each regular grid images. As seen, the grater the pore size, the higher the value of \(D_f\). On the one hand, regular grid image of \(1 \times 1\) pore size exhibits a fractal dimension close to zero (0.112) and \(2 \times 2\) and \(4 \times 4\) grid images reach fractal dimension lower than 1. Finally, fractal dimensions greater than 1 are found for regular grid images of pore size larger than \(6 \times 6\). This is in agreement with the understanding of the \(D_f\) as a measure of the capacity of the pores for filling the geometric support. On the other hand, in Fig. 4b fractal dimension is related to the porosity of the image. According to this figure, \(D_f\) increases with the porosity following a non-linear relationship. The logarithmic fit between both variables evinces that grid regular images follows the Eq. 4 established by Yu et al. (2001) with a \(R^2>0.996\).

Fig. 4
figure 4

Fractal dimension of regular grid images versus a pore size and b porosity

Full size image

Regarding to pore clustering of these images, normalized lacunarity is computed and depicted in Fig. 5a. As expected, normalized lacunarity is a decreasing function according to \(\delta \), which takes values from 1 to 0. As observed, lacunarity functions of each of the images almost overlap, taking very close \(\Lambda ^*\) values as \(\delta \) values increase. For this reason, the central region of the Figure has been zoomed in. In the extended region, lacunarity values decrease as the pore size of the image decreases for a given \(\delta \). According to Xia et al. (2019), normalized lacunarity values were selected from the median (\(\delta = 16\)) of the different scales with the aim of establishing comparisons among the lacunarity values of the different images. Normalized lacunarity varies according to the pore size of the images by following the trend showed in 5c. Gray dots depict \(\Lambda ^*(\delta = 16)\) for each pore size. As expected, pore clustering degree increases as pore size increases up to a maximum for pore sizes of \(15 \times 15\). For greater pore size (\(20 \times 20\)), pore clustering degree decreases. Thus, conversely to \(D_f\), which is always an increasing function, normalized lacunarity reaches a maximum for a certain pore size when image is a regular grid.

Fig. 5
figure 5

Normalized lacunarity for a regular grid images, b fixed pore size random images, and c different pore size of the regular grid (gray) and fixed pore size random (black) images for \(\delta = 16\)

Full size image

3.1.2 Fixed pore size random images

According to the generation of the fixed pore size random images, the results shown below correspond to the average values of the 5 images of each typology selected for the analysis. Fractal dimensions are obtained from the slope of the linear regression of ln[N] vs \(ln[\delta ]\) between \(\delta _{min} = 1\) to \(\delta _{max} = 64\), with a \(R^2\) greater than 0.925 for each case. As described in Sect. 3.1.1, linearity is trusted for a limited range of scales from \(\delta _{min} = 1\) to \(\delta _{max} = 16/32\) for regular grid images. This fact evinces that fractal properties exits for a wider range of scales when pores are randomly distributed. Similar to the regular grid one, the estimation of \(D_f\) for \(1 \times 1\)-fixed pore size random image has a low \(R^2\) (0.636). Thus, the uncertainty of \(D_f\) for images with tiny pore size exists and it is independent of the pore distribution. As observed in the black dots of Fig. 6(a), the grater the pore size, the higher the value of \(\overline{D_f}\). Error bars depict the standard deviation of the \(\overline{D_f}\) for the random images. The standard deviation is very low for all cases, indicating that pore size is more important for \(D_f\) than pore distribution in a random images. Additionally, \(D_f\) is higher for fixed pore size random images than for regular grid ones, as can be seen by comparing the black and gray dots in this Figure. For example, random \(4 \times 4\) pore size image exhibit a \(D_f\) close to 1, whereas for the regular grid one, \(D_f\) was lower than 1 (0.898). In general, the larger the pore size, the lower the difference between \((D_f)_{\text {random}}\) - \((D_f)_{\text {regular grid}}\). In fact, for large pores sizes, \(D_f\) of the regular grid is similar to that of the fixed pore size random (\(15 \times 15\)); and even slightly higher for \(20 \times 20\) pore size. Therefore, the effect of the random distribution is diluted as the pore size increases, and thus, when pore size is huge, fractal dimension is mainly determined by the pore size and not by the pore distribution.

On the other hand, fractal dimension is related to the porosity in Fig. 6b. Notice that the generation of random images produces overlap among pores, resulting in images with lower porosity compared to regular grid ones. This fact is evident in Fig. 6b, where porosity is lower for fixed pore size random images than for regular grid ones, mainly in huge pore size images (\(20 \times 20\) pixel). In this case, the porosity is 0.5028 and 0.6103 for fixed pore size random images and regular grid images, respectively. Nevertheless, assuming that porosity is identical for a certain pore size, it is found that fractal dimension is larger for fixed pore size random images according to the logarithmic fits in Fig. 6b.

Fig. 6
figure 6

Fractal dimension of fixed pore size random images versus a pore size and b porosity. To compare, gray dots depict the aforementioned values for the regular grid images

Full size image

Finally, pore clustering degree of these images is computed by means of the normalized lacunarity, which are depicted in Fig. 5b. Zoomed region shows that for a fixed \(\delta \) value, lacunarity increases as pore size increases, this being more evident that for the regular grid image (see Fig. 5a), indicating that pore clustering depends on pore size, this dependence being more evident when pores are randomly distributed in the image. Figure 5c supports this finding through a comparison between both kind of images. Normalized lacunarity for fixed pore size random images (black dots) exhibit two relevant differences with respect to regular grid images (gray dots). On the one hand, the function is always increasing and, on the other hand, the difference between the lacunarity values of both images increases as the pore size increases. For random images of fixed pore size, both \(D_f\) and \(\overline{\Lambda ^*}\) are increasing functions depending on pore size.

3.1.3 Mixed pore size random images

In this case, three groups of mixtures have been performed in order to assess the influence of the combination of different pore sizes on the fractal dimension of a binary image. Fractal dimensions are obtained from the value of the slope of the linear regression of ln[N] vs \(ln[\delta ]\) between \(\delta _{min} = 1\) to \(\delta _{max} = 64\), with a \(R^2\) greater than 0.989 for each case. Since 5 samples were selected from each image typology, the fractal dimension values shown are the average values for each typology.

The first result is that all the proposed mixtures show a \(D_f\) value greater than 1, which was not the case for the images with very tiny pore sizes (both in grid and random cases). This indicates that the presence of medium and large pore size promotes fractal dimensions greater than 1 (see Fig. 7). Black dots in Fig. 7a depict the fractal dimension of the mixtures of group 1. In group 1 the main pore size represent the 40% of image pores according to small, medium and large pore size for mixtures 1, 2 and 3, respectively. As seen, \(D_f\) increases in the order mixture 1 < mixture 2 < mixture 3, which implies that the fractal dimension increases as the ratio of large pores in the mixture increases. In addition, in Fig. 7a, a comparison between groups 1 and 2 is made. It is noted that mixtures of group 2 emphasizes the percentage of majority pore size. That is, the majority pore ratio increases from 40 to 60% according to small, medium and large pore size for mixtures 4, 5 and 6, respectively. Consequently, the most infrequent pore sizes in group 2 are 10%

Fig. 7
figure 7

Fractal dimension of mixed pore size random images versus a mixture and b porosity. Comparison between group 1 and group 2

Full size image

On the other hand, the mixtures of group 3 are depicted in Fig. 8. As in the previous cases, the greater the number of large pores, the higher the fractal dimension, as can be seen in Fig. 8a. This fact also being notable for mixtures with grater percentages of large pores (mixtures X and XI). Similarly, as porosity increases, \(D_f\) also increases according to a logarithmic relationship with \(R^2\) greater than 0.999 (see Fig. 8b).

Fig. 8
figure 8

Fractal dimension of mixed pore size random images versus a mixture and b porosity. Group 3

Full size image
Fig. 9
figure 9

Normalized lacunarity for a Mixture images of Group 1, b mixture images of Group 2, c mixture images of Group 3, and (d) \(\delta = 16\) grouped by mixtures groups: light gray for group 1, dark gray for group 2, and black for group 3

Full size image

Finally, pore clustering degree is measured by using the normalized lacunarity for each of the mixtures. As expected, normalized lacunarity are decreasing functions taking values from 1 to 0 (see Fig. 9a–c). As observed in the zoomed regions, \(\overline{\Lambda ^*}\) do not follow the expected order according to the ratio of pore sizes. In fact, \(\overline{\Lambda ^*}\) is medium for images with a majority of very small pores, lower for medium pores and higher for large pores, which is evident in Fig. 9d. This means that clustering degree decreases significantly when the ratio of medium-sized pores is predominant in the image. Furthermore, comparing groups 1 and 2, it can be observed that the clustering degree is higher when the ratio of large pores prevails. This happens in mixture 1 versus mixture 4, as well as in mixture 2 versus mixture 5, since the ratio of large and very large pores is 15% in the former and 10% in the latter (see Table 1). In the case of mixture 3 and mixture 6, the clustering degree is higher for the mixture with a greater ratio of large pores, i.e., mixture 6 (60%). For understanding the role of small pore sizes, we focus on mixtures of group 3 depicted in Fig. 9d. As seen, the greatest values of \(\Lambda ^*\) are found for mixtures X and XI, in which the ratio of large pores is higher. However, \(\Lambda ^*\) decreases in the order mixture VII, VIII and IX, which means that the presence of high percentages of very small pores also increases the clustering degree, and thus, the predominance of medium-sized pores reduces the clustering coefficient.

3.2 Multifractal analysis

After applying the multifractal method detailed in Sect. 2.1.4 to the set of synthetic binary images, results are described below

3.2.1 Regular grid images

Partition functions from the regular grid images are showed in Fig. 10. As observed, they are characterized by different linear regions with crossovers located at different scales (\(\delta \)). Generally, there is a main crossover at \(\delta = 32\) and a secondary crossover linked to the pore size, which moves from small to high scales. So, three linear regions are found. This, being evident for pore size from \(2 \times 2\) to \(6 \times 6\) (see Fig. 10b–d). For higher pore sizes (see Fig. 10f–g), the secondary crossover depending on the pore size disappears, and only two linear regions are defined. Therefore, the shape of the partition functions strongly depends on the pore size in regular grid images. On the other hand, negative moments only exists from \(\delta \ge 32\), which implies that dimension functions (D(q)) only can be completely reconstructed for greater scales.

Fig. 10
figure 10

Partition functions from the regular grid images with pore size: a \(1 \times 1\), b \(2 \times 2\), c \(4 \times 4\), d \( 6 \times 6\), e \(10 \times 10\), f \(15 \times 15\), and g \( 20 \times 20\)

Full size image

According to this, dimension functions are constructed from the linear regions of the partitions functions, i.e., from \(\delta \) = 32 to \(\delta \) = 512. Linear fits are trusted by means linear regressions with goodness-fits greater than 0.996 for all the cases. Figure 11 depicts the dimension functions, D(q), for each pore size. As seen in Table 2, multifractal degree varies from \(\Delta D(q)\) = 0.316 to \(\Delta D(q)\) = 0.097, according to the larger the pore size, the lower multifractality. Thus, whereas regular grid with small pores exhibit multifractal properties, regular grid with very large pores tend to be monofractal due to the value of \(\Delta D(q)\) close to zero (0.097).

Fig. 11
figure 11

Dimension functions, \(D_q\) for regular grid images

Full size image
Table 2 Multifractal parameters obtained from regular grid and fixed pore size random images
Full size table

3.2.2 Fixed pore size random images

Figure 12 depicts the partition functions corresponding to the fixed pore size random images. They are the average function of the five images for each pore size. As in the previous case, they are characterized by different linear regions with crossovers located at different scales (\(\delta \)). Thus, as before, the shape of the partition functions strongly depends on the pore size. From larger pore sizes (see Fig. 12f–g), only two linear regions are found, i.e., from \(\delta \) = 1 to \(\delta \) = 64, where only positive q moments can be considered, and from \(\delta \) = 64 to \(\delta \) = 512, where all q moments are defined. Therefore, right region allows a complete reconstruction of the dimension functions (D(q)).

Fig. 12
figure 12

Partition functions from the fixed pore size random images with pore size: a \(1 \times 1\), b \(2 \times 2\), c \(4 \times 4\), d \(6 \times 6\), e \(10 \times 10\), f \(15 \times 15\), and g \(20 \times 20\)

Full size image

According to this, dimension functions are represented in Fig. 13. Linear fits are trusted by means linear regressions with goodness-fits greater than 0.998 for all the cases.

Fig. 13
figure 13

Dimension functions, \(D_q\) for fixed pore size random images

Full size image

As seen in Table 2, multifractal degree varies from \(\Delta D(q)\) = 0.407 to \(\Delta D(q)\) = 0.166. Whereas fixed pore size random images with small pores exhibit multifractal properties, fixed pore size random images with high pores tend to monofractality due to the lower slopes of D(q). Thus, the larger the pore size, the lower multifractal degree of the image. In addition, by comparing \(\Delta D(q)\) between regular grid and random images for a certain pore size, it is found that a random pore distribution implies a grater degree of multifractality than a deterministic distribution. This is because a random pore distribution shows a higher degree of complexity than a regular one. Therefore, the degree of multifractality is a measure of the complexity of the porosity distribution in the image.

3.2.3 Mixed pore size random images

After applying the multifractal method described in Sect. 2.1.4, the corresponding partition functions were obtained for the mixture images. Specifically, Fig. 14 depicts a representative partition function from the mixed pore size random images. As seen in the aforementioned Figure, three regions are found. One of them is clearly differentiated by the presence of negative q moments, with the range of scales being from \(\delta _{min} = 64\) to \(\delta _{max} = 512\). Thus, multifractal analysis focus on region 3, as it allows a complete reconstruction of the dimension function (considering all q moments). According to this, dimension functions are constructed from the linear regions of the partitions functions for larger scales, i.e., from \(\delta \) = 64 to \(\delta \) = 512. Linear fits are trusted by means linear regressions with goodness-fits greater than 0.995 for all the cases.

Fig. 14
figure 14

Representative partition function from the mixed pore size random images. Average of the five iterations of each mixture

Full size image

Figure 15 depicts the dimension functions, D(q), for each group of the mixed pore size random images. As observed in Fig. 15a and b, it is satisfied that, the greater the ratio of small pores, the greater multifractality. Therefore, multifractality decreases when larger pores become more frequent. The same applies in Group 3 (see Fig. 15c), where it is noted that images exhibit a high degree of multifractality when small pores are predominant. As seen in Table 3, multifractal degree varies from \(\Delta D(q)\) = 0.544–1.077 for Group 1, from \(\Delta D(q)\) = 0.331–1.256 for Group 2 and from \(\Delta D(q)\) = 0.523–0.975 for Group 3. Thus, it can be established that multifractality decreases as pore size increases. However, this happens up to a limit, where large pores start to merge into macropores (the image collapses) and an increase in multifractality occurs (Mixture XI).

Table 3 Multifractal parameters obtained from mixed pore size random images
Full size table
Fig. 15
figure 15

Dimension functions, \(D_q\) for mixed pore size random images

Full size image

4 Conclusions

For grid regular images, the pore size determines the fractal dimension and the normalized lacunarity. On the one hand, fractal dimension increases when pore size increases, and on the other, normalized lacunarity increases when pore size increases until a maximum. This implies that, from a scaling perspective, the capacity of filling the space is determined by the pore size, but the clustering degree saturates for medium-large pore sizes. For small and medium pore sizes, fractal dimension is mainly determined by the distribution of the pores. By contrast, for large pore sizes, fractal dimension mainly depends on the pore size, which is deducted from the comparison between the regular grid and the random images. Accordingly to results, the main difference between both kind of images is found in the normalized lacunarity analysis. When pores are randomly distributed, the clustering degree always increases according to the pore size. Conversely, for grid images, this is trusted for small and medium pore sizes, since the clustering degree decreases for large pores. Results of images generated from mixtures of pore sizes evince that fractal dimension is completely linked to the pore size. Conversely, lacunarity analysis provides differences in the clustering degree of this images. Mixtures with greater ratio of large pore sizes show greater clustering degree. However, when medium pore size are emphasized clustering degree is reduced, and increases when the predominant pore size are small. Finally, multifractal analysis completes these findings, revealing that small pores generate heterogeneity in the images, this being the reason because multifractality increases from large to small pores. This fact is stronger when the distribution is governed by randomness.