Abstract
This work presents an enriched Galerkin (EG) discretization for the two-dimensional shallow-water equations. The EG finite element spaces are obtained by extending the approximation spaces of the classical finite elements by discontinuous functions supported on elements. The simplest EG space is constructed by enriching the piecewise linear continuous Galerkin space with discontinuous, element-wise constant functions. Similar to discontinuous Galerkin (DG) discretizations, the EG scheme is locally conservative, while, in multiple space dimensions, the EG space is significantly smaller than that of the DG method. This implies a lower number of degrees of freedom compared to the DG method. The EG discretization presented for the shallow-water equations is well-balanced, in the sense that it preserves lake-at-rest configurations. We evaluate the method’s robustness and accuracy using various analytical and realistic problems and compare the results to those obtained using the DG method. Finally, we briefly discuss implementation aspects of the EG method within our MATLAB / GNU Octave framework FESTUNG.
Similar content being viewed by others
1 Introduction
The two dimensional shallow-water equations (SWE) are used for a wide range of applications in environmental and hydraulic engineering, oceanography, and many other areas. They are discretized on computational domains that can be very large and often feature complex geometries; therefore, the numerical schemes must be computationally efficient and robust. The nonlinearity and hyperbolic character of the SWE system constitute additional challenges for designing discretizations and solution algorithms, while other application-specific aspects such as local conservation of unknown quantities and well-balancedness represent further desirable properties [see Hinkelmann et al. (2015)] for a brief overview of key requirements for SWE models).
The aforementioned issues led to a large number of studies dedicated to the development, analysis, and practical evaluation of various numerical techniques for solving the SWE. The earliest models used finite differences on structured grids, but, with the emergence of unstructured-mesh models [e.g. TELEMAC (Galland et al. 1991) or ADCIRC (Luettich et al. 1992)], finite elements and finite volumes became the de-facto standard. A big advantage of the finite element approach is its potential to naturally accommodate higher-order discretizations on unstructured meshes; in this vein, various methods based on the continuous Galerkin (CG) and discontinuous Galerkin (DG) approximation spaces (or mixtures of both) have been described and compared in the literature (Hanert et al. 2003; Comblen et al. 2010). The results of these comparisons can be summarized (in a somewhat oversimplified fashion) as follows:
-
Using CG for elevation and velocity is computationally very efficient (at least the low-order schemes) but tends to have stability issues usually represented by spurious elevation or velocity modes that arise from the LBB condition or from too large elevation spaces;
-
Using DG spaces for both unknowns is robust and needs no additional stabilization but may turn out to be computationally expensive [up to a factor of four to five longer serial execution times compared to CG for piecewise linears on the same mesh (Dawson et al. 2006)]. However, DG discretizations deliver higher accuracy than their CG counterparts (Kubatko et al. 2009), are locally conservative, have better support for adaptive and non-conforming meshes, and can partially offset their computational costs by more efficient parallel scaling (Kubatko et al. 2009);
-
Some combinations of continuous and discontinuous spaces such as the lowest-order Raviart–Thomas spaces are robust and computationally efficient (Hanert et al. 2003) but difficult to generalize to higher orders on triangular meshes.
The idea of the enriched Galerkin (EG) method is to enhance the CG approximation space using element-local discontinuous functions and, by relying on a solution procedure nearly identical to that of the DG method (i.e. edge fluxes, Riemann solvers, etc.), produce a robust, locally conservative discretization with fewer unknowns than a DG discretization of the same order.
In its original form, the EG method adds a piecewise constant DG component to a continuous piecewise linear or multilinear CG space and uses the DG bilinear form. This method was introduced for the linear advection–diffusion–reaction equation in Becker et al. (2003) and was proved there to be stable and to converge at the same rate as the piecewise linear DG discretization. The piecewise constant enrichment of the linear CG approximation makes the scheme intrinsically stable and imparts the local conservation property (Sun and Liu 2009). Since then, the EG method has been generalized to CG spaces of the polynomial order k augmented by discontinuous, element-wise constant functions (Sun and Liu 2009; Lee et al. 2016) and even to arbitrary enrichments with polynomials of degree m with \(-1 \le m \le k\) (\(m=-1\) indicates no enrichment at all) as discussed in Rupp and Lee (2020). Arbitrary enrichments allow to consider EG as a generalization of both CG and DG since EG uses the same bilinear and linear forms as DG.
While inheriting many advantages of DG, the EG method in multiple dimensions needs fewer degrees of freedom (DOF) than the DG method if \(m < k\). The standard EG method (with \(m = 0\)) has been developed to solve general elliptic and parabolic problems with dynamic mesh adaptivity (Choi and Lee 2019; Lee et al. 2018; Lee and Wheeler 2017, 2018) and was extended to address multiphase fluid flow problems (Lee and Wheeler 2018). Recently, the EG method has been applied to solve the nonlinear poroelastic problem (Choo and Lee 2018; Kadeethum et al. 2019), and its performance has been compared to other two- and three-field methods (Kadeethum et al. 2019). Another generalization of the EG approach considers enrichments by discontinuous polynomials defined on a subcell mesh (Rupp et al. 2020).
The EG methodology should not be confused with numerous other approximation space enrichment approaches such as bubble functions or eXtended Finite Element Method (XFEM) schemes. Main differences are the purpose (robustness and local conservation for EG vs. higher accuracy for bubbles and XFEM) and the underlying framework (DG vs. CG). Similarly to DG, the EG method also appears to be well-suited for computational enhancements such as hybridization or static condensation—this topic deserves a separate study.
In the context of convection-dominated problems, additional stabilization techniques are often required. Classical stabilizations include the streamline upwind Petrov–Galerkin (SUPG) method, weighted essentially non oscillatory (WENO) schemes, as well as provably bound-preserving alternatives [e.g. Brooks and Hughes (1982), Shu (2009), Cockburn and Shu (1998), Zhang and Shu (2011), Dumbser et al. (2014)]. Popular methods designed particularly for DG discretizations include the edge-based Barth–Jesperson limiter (Barth and Jespersen 1989), and its vertex-based counterparts (Kuzmin 2010; Aizinger 2011). Limiters for an EG discretization of the linear advection equation have recently been proposed in Kuzmin et al. (2020). The approach therein deviates from classical DG slope limiters but rather fits in the framework of algebraic flux correction (Kuzmin 2012), which only recently has been extended to the DG setting (Anderson et al. 2017; Hajduk et al. 2020). Numerical solutions based on the methods in Kuzmin et al. (2020) can be proven to satisfy discrete maximum principles under CFL-like time step restrictions, which makes the approach superior to geometrical slope limiting.
The main focus of the present work is to formulate and evaluate an EG scheme for the SWE and to compare the quality of the EG and DG discretizations. The method is implemented in the FESTUNG framework (Frank et al. 2015; Reuter et al. 2016; Jaust et al. 2018; Reuter et al. 2020) by modifying our DG implementation for the SWE presented in Reuter et al. (2019), Hajduk et al. (2018). The same scheme was initially introduced in our UTBEST solver (Dawson and Aizinger 2002; Aizinger and Dawson 2002) and later extended to three dimensions in UTBEST3D (Dawson and Aizinger 2005; Aizinger et al. 2013; Reuter et al. 2015).
The paper is structured as follows. The mathematical model and its discretization using the EG method are presented in Sect. 2, a brief description of the implementation using our MATLAB / GNU Octave framework FESTUNG is the subject of Sect. 3. In Sect. 4, we demonstrate the accuracy and robustness of our EG scheme using an analytical convergence test, a supercritical flow example with discontinuous solution, and a realistic tidal flow scenario for Bahamas islands. A short conclusions and outlook section wraps up this work.
2 EG formulation for the SWE
2.1 Governing equations
The SWE in conservative form are given by
They are considered on a two-dimensional, polygonally-bounded domain \(\Omega \) and finite time interval \(\left( t_0,\,t_\mathrm {end}\right) \). By \(\xi \), we denote the free surface elevation of the water body with respect to a certain zero level (e.g., the mean sea level). The quantity \(H = \xi - z_\mathrm {b}\) represents the total fluid depth with \(z_\mathrm {b}\) denoting the bathymetry. \(\varvec{q} :=(U,V)^\mathsf {T}\) is the depth integrated horizontal velocity field, \(f_\mathrm {c}\) the Coriolis coefficient, g the gravitational acceleration, and \(\tau _{\text {bf}}\) the bottom friction coefficient. Wind stress, the atmospheric pressure gradient, and tidal potential are combined in the body force term \(\varvec{F} :=(F_x,F_y)^\mathsf {T}\).
Defining \(\varvec{c} :=(\xi , U,V)^\mathsf {T}\), system (1) can be rewritten in the following compact form:
with
and
In this work, we use several types of boundary conditions for the SWE (1). Following the standard approach, interior values are used as boundary values at parts of the boundary, on which the corresponding unknowns are not prescribed. By \(\hat{\cdot }\) , we denote prescribed boundary values of the respective unknowns. The following types of boundary conditions are used in this work:
Dirichlet boundary: Here, all unknowns are specified:
Land boundary: Denoting by \(\varvec{n}\) the exterior unit normal to \(\partial \Omega \), we set the normal flux to zero:
Open sea boundary: We prescribe the free surface elevation:
Radiation boundary: No unknowns are specified (free outflow). Finally, initial conditions are set for elevation and depth integrated velocity
2.2 Enriched Galerkin discretization
Let \(\{\mathcal {T}_\Delta \}_{\Delta >0}\) be a simplicial, shape-regular, quasi uniform, geometrically conformal family of triangulations of \(\Omega \subset \mathbb {R}^2\) with \(\# T\) denoting the total number of elements of \(\mathcal {T}_\Delta \). We obtain the local variational formulation of system (2) by multiplying with smooth test functions \(\varvec{\phi } \in C^\infty (\Omega )^3\) and integrating by parts on each element \(T \in \mathcal {T}_\Delta \) yielding
where we write \((\cdot ,\cdot )_{T}\) and \(\langle \cdot ,\cdot \rangle _{\partial T}\) for the \(L^2\)-scalar products on elements and their boundaries, and denote by \(\varvec{n}=(n_x, n_y)^\mathsf {T}\) an exterior unit normal to \(\partial T\).
Defining the broken polynomial spaces of order \(m \in \mathbb {N}_0\) as
and setting \(\mathbb P_{-1}(\mathcal T_\Delta ) :=\{0\}\), we specify the EG test and trial spaces as
for integers \(-1 \le m \le k\), \(k > 0\). Obviously, \(\mathbb P_m(\mathcal T_\Delta ) \subset \mathbb P_{k,m}(\mathcal T_\Delta ) \subset \mathbb P_k(\mathcal T_\Delta )\). Here, ‘+’ denotes the sum of subspaces which is not a direct sum if \(m \ne -1\). Examples of spaces are given in Fig. 1.
From (10) it follows immediately that
This dimension formula will come handy in Sect. 3 for defining EG shape functions. More details about these spaces and their properties can be found in Rupp and Lee (2020).
To obtain the semi-discrete EG formulation of (9), \(\varvec{c}\) and \(\varvec{\phi }\) are replaced by their discrete counterparts \(\varvec{c}_\Delta ,\varvec{\phi }_\Delta \in \mathbb P_{k,m}(\mathcal T_\Delta )^3\). Since the values of a discontinuous function are not unique on element edges, we replace the boundary term \(\varvec{A}(\varvec{c})\cdot \varvec{n}\) by a numerical flux \(\varvec{\hat{A}}(\varvec{c}_\Delta ,\varvec{c}^+_\Delta , \varvec{n})\) that depends on the discontinuous values of the solution on element T (without superscript) and its edge neighbor (superscript \(^+\)). On domain boundaries, the specified boundary values of free surface elevation and velocity are utilized in place of \(\varvec{c}^+_\Delta \) for the flux computation. Finally, summing up over all elements \(T \in \mathcal {T}_\Delta \) yields
In this work, we use the Lax–Friedrichs flux combined with the Roe–Pike averaging (Aizinger and Dawson 2002; Roe 1981; Roe and Pike 1984) defined as
where \(\lambda = \lambda (\varvec{c}_\Delta ,\varvec{c}_\Delta ^+,\varvec{n})\) is given by
with \(H_\Delta ^+ :=\xi _\Delta ^+ - z_\mathrm {b}\) (note that the bathymetry \(z_\mathrm {b}\) is assumed to be continuous).
Discrete initial conditions are obtained using suitable projections of \(\xi _0\) and \(\varvec{q}_0\) into the discrete function space (10) (cf. Rupp and Lee (2020), (Sect. 5) for a comparison of reasonable choices for such projections). For the temporal discretization, we use strong stability preserving (SSP) explicit Runge–Kutta methods (Gottlieb et al. 2001).
This study uses the inviscid system of SWE (1) (similarly to our DG scheme for the SWE (Hajduk et al. 2018), the EG formulation needs no viscous stabilization). Such terms can be easily added in the same way as in DG methods [see, e.g. Lee et al. (2016)].
3 Implementation aspects
Our implementation of the EG method is based on the DG code for the SWE realized within the FESTUNG framework (Reuter et al. 2019; Frank and Reuter 2020). To obtain the required EG operators, we use a simple strategy of modifying the DG code that exploits the fact that the EG (or, for that matter, also the CG) approximation spaces are embedded in the DG spaces of the same order. Therefore, all EG or CG basis functions can be represented as linear combinations of DG basis functions. This representation can be written in the form of a (generally rectangular) system of linear equations, which can then be used to convert an available DG operator into the corresponding one for EG or CG spaces. This trick is by no means restricted to the SWE system; it can be just as easily applied to any linear or nonlinear PDE. The downside of this approach is that a full DG discretization must be assembled first—thus limiting the efficiency gain due to a smaller approximation space of the EG method. While simplifying switching between different DG, EG, and CG schemes, this approach is not recommended if a dedicated EG scheme were to be implemented from scratch. However, our implementation uses for this purpose multiplication with a time-independent matrix (highly optimized operation in MATLAB / GNU Octave) that only incurs a negligible runtime overhead.
In this work, we utilize finite element spaces of polynomial degree \(k \le 2\). First consider the DG space \(\mathbb P_k(\mathcal T_\Delta )\) and denote by \(N:=\dim \mathbb P_k(\mathcal T_\Delta )\) the number DG unknowns for a scalar quantity. We have \(\dim \mathbb P_1(\mathcal T_\Delta ) = 3\,\#T\) and \(\dim \mathbb P_2(\mathcal T_\Delta ) = 6\,\#T\). For fixed k, let \(\left\{ \varphi _i: i\in \{1,\ldots ,N\}\right\} \) be the element-wise continuous nodal basis of the DG method, where the nodal property is local to every element \(T \in \mathcal T_\Delta \). Moreover, we denote by \(\left\{ \phi _i: i\in \{1,\ldots ,M\}\right\} \) with \(M:=\dim \mathbb P_{k,m}(\mathcal T_\Delta )\) a basis of the EG space.
In the following, we construct bases for various EG spaces from CG and DG basis functions. Here, one has to be careful since, in general, simply combining a CG basis with element-wise DG basis functions produces a linearly-dependent set. For the admissible combinations of k and m with \(-1\le m< k \le 2\) considered in our work, the EG bases can be constructed as follows:
-
\(k \in \{1,2\},~m=-1\): The space \(\mathbb P_{k,-1}(\mathcal {T}_\Delta )\) coincides with the CG ansatz space of order at most k. Therefore, we can simply choose the CG basis functions.
-
\(k=1,~m=0\): The union of characteristic functions of all elements \(T \in \mathcal T_\Delta \) and the continuous, piecewise linear interpolation functions for all but one mesh vertex form a basis.
-
\(k=2,~m=0\): We obtain a basis from the union of characteristic functions of all elements and all but one of the shape functions for the quadratic CG space.
-
\(k = 2,~m=1\): We use the standard linear DG basis and extend it by the nodal quadratic shape functions equal to 1 at one edge midpoint, but omit the ones corresponding to cell vertices. The functions are linearly independent and are contained in the space \(\mathbb P_{2,1}(\mathcal {T}_\Delta )\). As the number of basis functions equals \(\dim \mathbb P_{2,1}(\mathcal {T}_\Delta ) = 3\,\#T+\,\#E\), it must be a basis of \(\mathbb P_{2,1}(\mathcal {T}_\Delta )\). Here, \(\#T\) and \(\#E\) denote the number of triangles and edges of \(\mathcal {T}_\Delta \), respectively. The dimension formula (11) ensures that this, in fact, constitutes a basis of \(\mathbb P_{2,1}(\mathcal T_\Delta )\).
3.1 Assembling nonlinear EG operators from DG operators
Next, we show how to obtain an EG from the corresponding DG operator. To simplify the presentation, we formulate our approach for the scalar case noting that the generalization to vector fields is straightforward. DG discretizations of nonlinear PDEs such as the SWE feature nonlinear operators of the form
where \(b: \mathbb P_k(\mathcal T_\Delta ) \times \mathbb P_k(\mathcal T_\Delta ) \rightarrow \mathbb {R}\) is linear in the second argument. Our goal is to form the EG operator
by making use of (14). Since \(\mathbb P_{k,m}(\mathcal T_\Delta )\subset \mathbb P_{k}(\mathcal T_\Delta )\), it is possible to express the EG basis functions as linear combinations of the DG basis
Next, we insert (16) into (15), obtaining
for \(i \in \{1,\ldots ,M\}\). By defining \(\varvec{C} :=\left( C_{kl}\right) _{kl}\), \(k \in \{ 1,\ldots ,M\}\), \(l \in \{ 1,\ldots ,N\}\), we can thus write
Employing (17), we assemble the terms corresponding to (15) by modifying an existing DG discretization of the operator (14) and computing the matrix \(\varvec{C}\). Due to the above choice of EG and DG basis functions, the matrix \(\varvec{C}\) can be determined from simple geometric considerations during preprocessing.
3.2 Assembly of the EG mass matrix
We consider the operator \(b_\mathrm M\) defined by \(b_\mathrm M(u_{\Delta },v_{\Delta }) :=\left( u_{\Delta }\,,\,v_{\Delta }\right) _{\Omega }\). Since \(b_\mathrm M\) is a bilinear form, we can write its induced operator (mass matrix) as
with \(\left( B_\mathrm {M}^{\mathrm {DG}}\right) _{ij} = \int _{\Omega } \varphi _j \varphi _i\, dx\) for \(i,j \in \{1,..,N\}\). The corresponding EG mass matrix
can be obtained from (17), and, in operator form, is given by
That is, for operators induced by bilinear forms, the assembly can be preprocessed.
4 Numerical results
In this section, we investigate the performance of the EG method using artificial and realistic test problems for the SWE. The main goals of these numerical studies can be summarized as follows:
-
Verify the expected rate of convergence against a manufactured analytical solution;
-
evaluate the solution quality for realistic benchmarks;
-
compare the EG and DG methods in terms of accuracy, stability, and robustness.
We denote the results obtained for different combinations of k and m by the corresponding finite element spaces as illustrated in Fig. 1. To simplify notation, we omit their dependency on \(\mathcal {T}_\Delta \). Hence, we write \(\mathbb P_{k,m}\) instead of \(\mathbb P_{k,m}(\mathcal T_\Delta )\) and use the convention that \(\mathbb P_{k,k}\) is the DG space of polynomial degree k. As temporal discretization, we use SSP Runge–Kutta time stepping schemes described in Aizinger et al. (2000) with \(s = k+1\) stages. The time step size depends on the specific test problem.
4.1 Analytical convergence test
In our first numerical experiment, we approximate a smooth solution of the SWE on the domain \(\Omega :=(0,1000) \times (0,1000)\). The coarsest mesh (corresponding to level one) consists of 16 triangular elements and is shown in Fig. 2 (left). To investigate the convergence behavior, we consider a total of five meshes obtained from the coarsest mesh by uniform refinement via edge bisection.
Setting \(\tau _{\mathrm {bf}}\) and \(f_\mathrm {c}\) to zero and prescribing the bathymetry by
we utilize the following analytical solution
Using the method of manufactured solution, we substitute (18) into (2)–(4) to obtain a forcing function for the right-hand side; in addition, Dirichlet boundary conditions for each unknown arising from (18) are imposed on all boundaries. We solve the SWE for the time interval (0, 1000) using the time step size \(\Delta t=1/4\) in all considered scenarios. This value of \(\Delta t\) is sufficiently small to make temporal discretization errors negligible compared to spatial approximation errors. Solution parameters are chosen as \(C_1=0.3,\, C_2=0.2,\, C_3=0.2\).
The projected initial surface elevation for \(\mathbb P_{1,0}\) on the coarsest mesh is shown in Fig. 2 (middle). Figure 2 (right) displays the numerical solution for the surface elevation using the same approximation (\(k=1,~m=0\)) on the finest mesh at the final time.
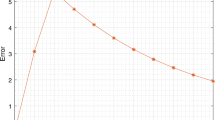
For all considered CG, EG, and DG methods (\(-1\le m\le k\le 2\)), we list the \(L^2(\Omega )\) discretization errors at the final time along with the corresponding convergence rates in Table 1 and plot them in Fig. 3. The results indicate that we obtain at least second order convergence for all methods. Third order convergence can be observed for \(k=2\) and \(m\in \{1,2\}\), but not for the CG approximation \(k=2, m=-1\). The results for \(k=2\) and \(m=0\) are slightly better than without the piecewise constant enrichment, but do not exhibit third order accuracy. In conclusion, the EG scheme converges almost exactly as well as the DG method if \(m=k-1\), \(k \in \{1,2\}\), although the absolute errors tend to be somewhat larger than for their DG counterparts. This is to be expected because EG has fewer unknowns, and even the projected exact solution in general becomes less accurate if the number of unknowns is reduced.
In Table 2, we list the total numbers of degrees of freedom for all configurations. Note that, the DOF for the EG method with element-wise constant enrichment \((k \in \{1,2\},~m=0)\) has approximately half as many DOF as the DG method of order k. EG with \(k=2,~m=1\) has ca. three quarters of the DOF for the quadratic DG method. In conclusion, the EG method performs similarly to DG for smooth solutions while having significantly fewer DOF.
Analytical convergence test: Logarithmic plots of the \(L^2(\Omega )\) errors at the final time for the surface elevation \(\xi \) (left) and the depth integrated velocity magnitude \(|\varvec{q}|\) (right) for CG, EG, and DG discretizations (see Fig. 1)
One has to note here that the relation between the computational cost (even in serial execution) and the number of degrees of freedom is not a simple one. In a time-explicit DG or EG scheme, main cost factors are element and edge integrals that are not significantly cheaper for the EG method than for the DG one. The situation is more complicated in time-implicit and semi-implicit cases (not evaluated in our study): The EG system is smaller than the DG one and whether it is faster to solve depends on a number of different aspects such as the condition number, sparsity structure, preconditioner, solver, etc.
The focus of the present study is an evaluation of the accuracy, stability, and robustness of the EG method for the SWE; any conclusions about the computational performance of this scheme are clearly outside of the scope—in particular, since our implementation is based on MATLAB / GNU Octave and rides on top of the DG assembly for the SWE solver. However, to give an indication of the computational costs associated with an EG scheme, we list in Table 3 the cumulative (summed over all time steps) solution times for systems with the DG mass matrix (\(\mathbb {P}_{1,1}\)), the EG mass matrix (\(\mathbb {P}_{1,0}\)), and the EG mass matrix (\(\mathbb {P}_{1,0}\)) lumped according to the scheme proposed in Becker et al. (2003). We see there that naively using the direct MATLAB solver (backslash operator that calls the Cholesky method) on the EG mass matrix produces a rather inefficient and poorly scaling implementation, whereas system solves with block-diagonal DG and lumped EG matrices scale much better. Another interesting point to note is the fact that lumping the mass matrix leads to some degradation of the method’s accuracy and its convergence.
4.2 Supercritical flow in a constricted channel
In order to demonstrate the stability and robustness of the EG method, we solve the supercritical flow problem proposed in Zienkiewicz and Ortiz (1995). The computational domain is a channel whose lateral boundary walls are constricted on both sides with an angle of five degrees (cf. Fig. 4). This benchmark uses constant bathymetry \(z_b \equiv -1\) while parameters \(\tau _{\mathrm {bf}},\) and \(f_\mathrm {c}\) are once more set to zero. The following initial and boundary conditions are prescribed for this problem: Initially, we set the surface elevation and momentum to \(\xi _0\equiv 0,\) \(\varvec{q}_0 = (1,0)^\mathsf {T}\), respectively. Land boundary conditions are imposed at the lateral (wall) boundaries, while at the inlet (left), free surface elevation as well as velocity are for all times specified to be identical to their corresponding initial values. Finally, at the outlet (right), radiation boundary conditions are used. Denoting by u and H the axial velocity and water depth at the inlet, respectively, the flow regime is made supercritical by choosing the inlet Froude number \(\mathrm {Fr}\)
achieved by setting the gravitational constant \(g=0.16~\frac{m}{s^2}\).
The solution to this problem converges to a steady-state, for which an analytical solution is available (Ippen 1951). Figure 4 illustrates the computational domain along with the unstructured mesh used in all computations.
We run all simulations to a steady-state using pseudo time stepping with a time step of \(\Delta t = 1/10\) and present the results for all schemes in Fig. 5. The steady-state surface elevation shown in Fig. 5 (top left) is discontinuous and displays interactions of waves reflected from the channel constrictions. Figure 5 (top right to bottom right) depicts the steady-state solutions for all considered EG and DG methods (\(0\le m\le k\le 2\)). Since no limiter was used, all approximations exhibit spurious oscillations close to the discontinuities. We expect the results to improve and the numerical solutions to become bound-preserving if a limiter, such as the one developed in Kuzmin et al. (2020), is utilized (at least) for the free surface elevation.
Supercritical flow in a constricted channel, free surface elevation, analytical solution (top left) and approximations (see Fig. 1) at steady-state for: \(\mathbb P_{1,1}\) (top right), \(\mathbb P_{1,0}\) (middle left), \(\mathbb P_{2,2}\) (middle right), \(\mathbb P_{2,0}\) (bottom left), \(\mathbb P_{2,1}\) (bottom right)
The specific type of enrichment appears to play a major role for the stability of EG schemes. Thus the results for enrichments with \(m=k-1,~k \in \{1,2\}\) are almost indistinguishable from the corresponding DG results. In particular, the characteristic wave features such as positions and magnitudes of discontinuities are in good agreement with the analytical solution. On the other hand, the EG solution for \(k=2,~m=0\) exhibits severe oscillations not only in the vicinity of the discontinuities but also in the remainder of the computational domain. This phenomenon indicates that a piecewise constant enrichment of the quadratic CG space may not be sufficient to obtain an intrinsically stable scheme. However, an enrichment by piecewise linear discontinuous functions seems to remedy this issue, which confirms the previous findings in Sect. 4.1 and (Rupp and Lee 2020). The results for this benchmark suggest that optimal EG schemes (\(m=k-1\)) possess similar stability properties to their DG counterparts while offering potential advantages in computational efficiency.
4.3 Tidal flow at Bahamas Islands
The next benchmark considered in this work involves a tidal flow scenario around the Bahamas Islands based on the configuration, parameter values, and mesh presented in Westerink et al. (1989) for the Bight of Abaco. The domain geometry, bathymetry as well as boundary types are depicted in Fig. 6 (left), and Fig. 6 (right) shows the unstructured mesh used in all simulations. Furthermore, four recording stations also shown in Fig. 6 (left) are placed at the following locations \((38\,667,49\,333)\), \((56\,098,9\,613)\), \((41\,263,29\,776)\), and \((59\,594,41\,149)\) (coordinates in meters) to monitor the temporal evolution of surface elevation and depth integrated velocity.
For bottom friction, we use the standard quadratic friction law \(\tau _{\text {bf}} = C_f | \varvec{q} | /H^2\) [see e.g. Vreugdenhil (1994)] with coefficient \(C_f = 0.009\). The constant Coriolis parameter is set to \(3.19 \times 10^{-5}~\mathrm {s}^{-1}\). The following tidal forcing is prescribed at the open sea boundary (Kolar et al. 1994):
with time t in hours. In real-life ocean simulations, the initial conditions are often unknown or very difficult to obtain, therefore a cold start initialization is performed: The flow domain is assumed to be at rest initially (\(\xi _0 \equiv 0\), \({\varvec{q}}_0 \equiv (0,0)^T\)). Then, starting immediately at initial time \(t=0\), the tidal forcing (19) is imposed at the open sea boundary.
The simulations are run for a total of 12 days using constant time step \(\Delta t = 15\) seconds for EG and DG discretizations corresponding to \(0\le m \le k \le 2\). In Figs. 7, 8 and 9, we compare the numerical solutions for all considered EG and DG methods at the four recording stations.
Tidal flow at Bahamas Islands: Free surface elevation for days eleven and twelve at stations one to four (left to right, top to bottom) (see Fig. 1 for legend explanation)
Tidal flow at Bahamas Islands: x-velocity component for days eleven and twelve at stations one to four (left to right, top to bottom) (see Fig. 1 for legend explanation)
Tidal flow at Bahamas Islands: y-velocity component for days eleven and twelve at stations one to four (left to right, top to bottom) (see Fig. 1 for legend explanation)
Surface elevation results in Fig. 7 demonstrate excellent agreement for all EG and DG methods. The curves lie nearly on top of each other and no differences can be visually detected at this resolution. The differences in the surface elevation between the EG and DG approximations at the recording stations are on the order of \(10^{-4}\) meters.
In Figs. 8 and 9, we plot both velocity components at the recording stations. For the station two (Figs. 8, 9 top right), one can observe slight differences between the approximations of orders one and two. Such behavior is fully consistent with the station comparisons performed in Aizinger and Dawson (2002). The effect of approximation order has greater magnitude than the differences between the EG and DG discretizations. Small differences between EG and DG discretizations of the same order can be observed in the plots at some locations. The deviations at the recording stations are on the order of \(10^{-3}\) to \(10^{-4}~\mathrm {m\,s^{-1}}\).
In addition to testing the accuracy and robustness of the EG method, we also use the Bahamas example to verify the well-balancedness of the method. For this purpose, our simulation were run for the lake-at-rest configuration with open sea boundary condition set to zero. Just as expected, no spurious circulation emerged for any of the EG or DG configurations.
5 Conclusions and future work
In this work, we present the first enriched Galerkin discretization for the system of 2D shallow-water equations, evaluated its performance in analytical and realistic test problems, and compared the numerical results to those obtained using our discontinuous Galerkin solver. The results of our studies demonstrate that EG schemes with enrichments using discontinuous spaces of order one less than the order of the continuous space display accuracy and robustness on a par with the corresponding DG discretizations. Similarly to DG, the EG method guarantees local conservation of all primary unknowns while the total number of degrees of freedom is substantially lower than that for the DG space of the same order. This makes the enriched Galerkin method a very attractive candidate for solving the shallow-water equations and other nonlinear hyperbolic PDE systems.
Several interesting avenues of future research concerning the development of an EG solver for the SWE present themselves at this time. Thus one could try the quadrature-free methodology to improve the computational efficiency of the method—similarly to our recent work for the DG SWE solver in Faghih-Naini et al. (2020). Formulating the EG method for the SWE as a time-implicit or a semi-implicit scheme—especially in a combination with an efficient linear solver such as the hierarchical scale separation method either directly (Aizinger et al. 2015) or in a hybridized setting (Schütz and Aizinger 2017) appears to be particularly attractive due to similarities with the DG method, on one hand, and a substantially smaller system size, on the other. Also EG schemes hold promise (perhaps even more so than the DG ones) for bathymetry reconstruction using modified shallow-water equations (Hajduk et al. 2020).
References
Aizinger, V.: A geometry independent slope limiter for the discontinuous Galerkin method. In: Krause, E., Shokin, Y., Resch, M., Kröner, D., Shokina, N. (eds.) Computational Science and High Performance Computing IV, Notes on Numerical Fluid Mechanics and Multidisciplinary Design, vol. 115, pp. 207–217. Springer, Berlin (2011). https://doi.org/10.1007/978-3-642-17770-5_16
Aizinger, V., Dawson, C.: A discontinuous Galerkin method for two-dimensional flow and transport in shallow water. Adv. Water Resour. 25(1), 67–84 (2002). https://doi.org/10.1016/S0309-1708(01)00019-7
Aizinger, V., Dawson, C., Cockburn, B., Castillo, P.: The local discontinuous Galerkin method for contaminant transport. Adv. Water Resour. 24(1), 73–87 (2000). https://doi.org/10.1016/S0309-1708(00)00022-1
Aizinger, V., Proft, J., Dawson, C., Pothina, D., Negusse, S.: A three-dimensional discontinuous Galerkin model applied to the baroclinic simulation of Corpus Christi Bay. Ocean Dyn. 63(1), 89–113 (2013). https://doi.org/10.1007/s10236-012-0579-8
Aizinger, V., Kuzmin, D., Korous, L.: Scale separation in fast hierarchical solvers for discontinuous Galerkin methods. Appl. Math. Comput. 266, 838–849 (2015). https://doi.org/10.1016/j.amc.2015.05.047.
Anderson, R., Dobrev, V., Kolev, T., Kuzmin, D., Quezada de Luna, M., Rieben, R., Tomov, V.: High-order local maximum principle preserving (MPP) discontinuous Galerkin finite element method for the transport equation. J. Comput. Phys. 334, 102–124 (2017). https://doi.org/10.1016/j.jcp.2016.12.031
Barth, T., Jespersen, D.: The design and application of upwind schemes on unstructured meshes. In: Proceedings of the AIAA 27th Aerospace Sciences Meeting, Reno (1989)
Becker, R., Burman, E., Hansbo, P., Larson, M.G.: A reduced P1-discontinuous Galerkin method. Chalmers Finite Element Center Preprint 2003–13 (2003)
Brooks, A.N., Hughes, T.J.: Streamline upwind/Petrov-Galerkin formulations for convection dominated flows with particular emphasis on the incompressible Navier-Stokes equations. Comput. Methods Appl. Mech. Eng. 32, 199–259 (1982). https://doi.org/10.1016/0045-7825(82)90071-8
Choi, W., Lee, S.: Optimal error estimate of elliptic problems with Dirac sources for discontinuous and enriched Galerkin methods. Appl. Numer. Math. 150, 76–104 (2019). https://doi.org/10.1016/j.apnum.2019.09.010
Choo, J., Lee, S.: Enriched Galerkin finite elements for coupled poromechanics with local mass conservation. Comput. Methods Appl. Mech. Eng. 341, 311–332 (2018). https://doi.org/10.1016/j.cma.2018.06.022
Cockburn, B., Shu, C.W.: The Runge-Kutta discontinuous Galerkin method for conservation laws V: multidimensional systems. J. Comput. Phys. 141(2), 199–224 (1998). https://doi.org/10.1006/jcph.1998.5892
Comblen, R., Lambrechts, J., Remacle, J.F., Legat, V.: Practical evaluation of five partly discontinuous finite element pairs for the non-conservative shallow water equations. Int. J. Numer. Methods Fluids 63(6), 701–724 (2010). https://doi.org/10.1002/fld.2094
Dawson, C., Aizinger, V.: The local discontinuous Galerkin method for advection-diffusion equations arising in groundwater and surface water applications. In: Chadam, J., Cunningham, A., Ewing, R.E., Ortoleva, P., Wheeler, M.F. (eds.) Resource Recovery, Confinement, and Remediation of Environmental Hazards, pp. 231–245. Springer, New York (2002). https://doi.org/10.1007/978-1-4613-0037-3_13
Dawson, C., Aizinger, V.: A discontinuous Galerkin method for three-dimensional shallow water equations. J. Sci. Comput. 22(1–3), 245–267 (2005). https://doi.org/10.1007/s10915-004-4139-3
Dawson, C., Westerink, J., Feyen, J., Pothina, D.: Continuous, discontinuous and coupled discontinuous-continuous Galerkin finite element methods for the shallow water equations. Int. J. Numer. Methods Fluids 52(1), 63–88 (2006). https://doi.org/10.1002/fld.1156
Dumbser, M., Zanotti, O., Loubère, R., Diot, S.: A posteriori subcell limiting of the discontinuous Galerkin finite element method for hyperbolic conservation laws. J. Comput. Phys. 278, 47–75 (2014). https://doi.org/10.1016/j.jcp.2014.08.009
Faghih-Naini, S., Kuckuk, S., Aizinger, V., Zint, D., Grosso, R., Köstler, H.: Quadrature-free discontinuous Galerkin method with code generation features for shallow water equations on automatically generated block-structured meshes. Adv. Water Resour. 138, 103552 (2020). https://doi.org/10.1016/j.advwatres.2020.103552
Frank, F., Reuter, B.: FESTUNG: The Finite Element Simulation Toolbox for UNstructured Grids (2020). https://github.com/FESTUNG
Frank, F., Reuter, B., Aizinger, V., Knabner, P.: FESTUNG: a MATLAB/GNU Octave toolbox for the discontinuous Galerkin method, Part I: diffusion operator. Comput. Math. Appl. 70(1), 11–46 (2015). https://doi.org/10.1016/j.camwa.2015.04.013
Galland, J.C., Goutal, N., Hervouet, J.M.: TELEMAC: a new numerical model for solving shallow water equations. Adv. Water Resour. 14(3), 138–148 (1991). https://doi.org/10.1016/0309-1708(91)90006-A
Gottlieb, S., Shu, C.W., Tadmor, E.: Strong stability-preserving high-order time discretization methods. SIAM Rev. 43, 89–112 (2001). https://doi.org/10.1137/S003614450036757X
Hajduk, H., Hodges, B.R., Aizinger, V., Reuter, B.: Locally filtered transport for computational efficiency in multi-component advection-reaction models. Environ. Model. Softw. 102, 185–198 (2018). https://doi.org/10.1016/j.envsoft.2018.01.003
Hajduk, H., Kuzmin, D., Aizinger, V.: Bathymetry reconstruction using inverse shallow water models: finite element discretization and regularization. In: van Brummelen, H., Corsini, A., Perotto, S., Rozza, G. (eds.) Numerical Methods for Flows: FEF 2017 Selected Contributions, pp. 223–230. Springer, Cham (2020). https://doi.org/10.1007/978-3-030-30705-9_20
Hajduk, H., Kuzmin, D., Kolev, T., Abgrall, R.: Matrix-free subcell residual distribution for Bernstein finite element discretizations of linear advection equations. Comput. Method. Appl. M. 359, 112658 (2020). https://doi.org/10.1016/j.cma.2019.112658
Hanert, E., Legat, V., Deleersnijder, E.: A comparison of three finite elements to solve the linear shallow water equations. Ocean Model. 5(1), 17–35 (2003). https://doi.org/10.1016/S1463-5003(02)00012-4
Hinkelmann, R., Liang, Q., Aizinger, V., Dawson, C.: Robust shallow water models. Environ. Earth Sci. 74(11), 7273–7274 (2015). https://doi.org/10.1007/s12665-015-4764-1. (editorial)
Ippen, A.: High-velocity flow in open channels: a symposium: mechanics of supercritical flow. Trans. Am. Soc. Civ. Eng. 116(1), 268–295 (1951)
Jaust, A., Reuter, B., Aizinger, V., Schütz, J., Knabner, P.: FESTUNG: a MATLAB/GNU Octave toolbox for the discontinuous Galerkin method, part III: hybridized discontinuous Galerkin (HDG) formulation. Comput. Math. Appl. 75(12), 4505–4533 (2018). https://doi.org/10.1016/j.camwa.2018.03.045
Kadeethum, T., Nick, H.M., Lee, S., Richardson, C.N., Salimzadeh, S., Ballarin, F.: A novel enriched Galerkin method for modelling coupled flow and mechanical deformation in heterogeneous porous media. In: 53rd US Rock Mechanics/Geomechanics Symposium. American Rock Mechanics Association, New York, NY, USA (2019). ARMA-2019-0228
Kadeethum, T., Nick, H., Lee, S.: Comparison of two-and three-field formulation discretizations for flow and solid deformation in heterogeneous porous media. In: 20th Annual Conference of the International Association for Mathematical Geosciences (2019)
Kolar, R., Westerink, J., Cantekin, M., Blain, C.: Aspects of nonlinear simulations using shallow-water models based on the wave continuity equation. Comput. Fluids 23(3), 523–538 (1994). https://doi.org/10.1016/0045-7930(94)90017-5
Kubatko, E., Bunya, S., Dawson, C., Westerink, J., Mirabito, C.: A performance comparison of continuous and discontinuous finite element shallow water models. J. Sci. Comput. 40(1), 315–339 (2009). https://doi.org/10.1007/s10915-009-9268-2
Kuzmin, D.: A vertex-based hierarchical slope limiter for adaptive discontinuous Galerkin methods. J. Comput. Appl. Math. 233(12), 3077–3085 (2010). https://doi.org/10.1016/j.cam.2009.05.028. Finite Element Methods in Engineering and Science (FEMTEC 2009)
Kuzmin, D.: Algebraic flux correction I. Scalar conservation laws. In: Kuzmin, R.L.D., Turek, S. (eds.) Flux-Corrected Transport: Principles, Algorithms, and Applications, vol. 2, pp. 145–192. Springer, New York (2012)
Kuzmin, D., Hajduk, H., Rupp, A.: Locally bound-preserving enriched Galerkin methods for the linear advection equation. Comput. Fluids 205(104525), 15 (2020). https://doi.org/10.1016/j.compfluid.2020.104525
Lee, S., Wheeler, M.F.: Adaptive enriched Galerkin methods for miscible displacement problems with entropy residual stabilization. J. Comput. Phys. 331, 19–37 (2017). https://doi.org/10.1016/j.jcp.2016.10.072
Lee, S., Wheeler, M.F.: Enriched Galerkin methods for two-phase flow in porous media with capillary pressure. J. Comput. Phys. 367, 65–86 (2018). https://doi.org/10.1016/j.jcp.2018.03.031
Lee, S., Lee, Y.J., Wheeler, M.F.: A locally conservative enriched Galerkin approximation and efficient solver for elliptic and parabolic problems. SIAM J. Sci. Comput. 38(3), A1404–A1429 (2016). https://doi.org/10.1137/15M1041109
Lee, S., Mikelic, A., Wheeler, M.F., Wick, T.: Phase-field modeling of two phase fluid filled fractures in a poroelastic medium. Multiscale Model. Simul. 16(4), 1542–1580 (2018). https://doi.org/10.1137/17M1145239
Luettich, R., Westerink, J., Scheffner, N.: ADCIRC: an advanced three-dimensional circulation model for shelves, coasts and estuaries, Report 1: theory and methodology of ADCIRC-2DDI and ADCIRC-3DL. Technical Report Dredging Research Program Technical Report DRP-92-6, US Army Engineers Waterways Experiment Station, Vicksburg, MS (1992)
Reuter, B., Hajduk, H., Rupp, A., Frank, F., Aizinger, V., Knabner, P.: FESTUNG 1.0: overview, usage, and example applications of the MATLAB/GNU Octave toolbox for discontinuous Galerkin methods. Comput. Math. Appl. (2020). https://doi.org/10.1016/j.camwa.2020.08.018
Reuter, B., Aizinger, V., Köstler, H.: A multi-platform scaling study for an OpenMP parallelization of a discontinuous Galerkin ocean model. Comput. Fluids 117, 325–335 (2015). https://doi.org/10.1016/j.compfluid.2015.05.020
Reuter, B., Aizinger, V., Wieland, M., Frank, F., Knabner, P.: FESTUNG: a MATLAB/GNU Octave toolbox for the discontinuous Galerkin method, Part II: advection operator and slope limiting. Comput. Math. Appl. 72(7), 1896–1925 (2016). https://doi.org/10.1016/j.camwa.2016.08.006
Reuter, B., Rupp, A., Aizinger, V., Frank, F., Knabner, P.: FESTUNG: a MATLAB/GNU Octave toolbox for the discontinuous Galerkin method. Part IV: generic problem framework and model-coupling interface. Commun. Comput. Phys. 28, 827–876 (2020). https://doi.org/10.4208/cicp.OA-2019-0132
Roe, P., Pike, J.: Efficient construction and utilisation of approximate Riemann solutions. In: R. Glowinski, J.L. Lions (Eds.) Computing Methods in Applied Sciences and Engineering, pp. 499–518 (1984)
Roe, P.: Approximate Riemann solvers, parameter vectors, and difference schemes. J. Comput. Phys. 43, 357–372 (1981)
Rupp, A., Hauck, M., Aizinger, V.: A subcell-enriched Galerkin method for advection problems. Submitted (2020). arXiv:2006.09041
Rupp, A., Lee, S.: Continuous Galerkin and enriched Galerkin methods with arbitrary order discontinuous trial functions for the elliptic and parabolic problems with jump conditions. J. Sci. Comput. 84(9), 25 (2020). https://doi.org/10.1007/s10915-020-01255-4
Schütz, J., Aizinger, V.: A hierarchical scale separation approach for the hybridized discontinuous Galerkin method. J. Comput. Appl. Math. 317, 500–509 (2017). https://doi.org/10.1016/j.cam.2016.12.018.
Shu, C.W.: High order weighted essentially nonoscillatory schemes for convection dominated problems. SIAM Rev. 51, 82–126 (2009). https://doi.org/10.1137/070679065
Sun, S., Liu, J.: A locally conservative finite element method based on piecewise constant enrichment of the continuous Galerkin method. SIAM J. Sci. Comput. 31(4), 2528–2548 (2009). https://doi.org/10.1137/080722953
Vreugdenhil, C.B.: Numerical Methods for Shallow-Water Flow. Springer, New York (1994). https://doi.org/10.1007/978-94-015-8354-1
Westerink, J.J., Stolzenbach, K.D., Connor, J.J.: General spectral computations of the nonlinear shallow water tidal interactions within the bight of abaco. J. Phys. Oceanogr. 19(9), 1348–1371 (1989). https://doi.org/10.1175/1520-0485(1989)019<1348:GSCOTN>2.0.CO;2
Zhang, X., Shu, C.W.: Maximum-principle-satisfying and positivity-preserving high-order schemes for conservation laws: survey and new developments. Proc. R. Soc. A Math. Phys. Eng. Sci. 467, 2752–2776 (2011). https://doi.org/10.1098/rspa.2011.0153
Zienkiewicz, O.C., Ortiz, P.: A split-characteristic based finite element model for the shallow water equations. Int. J. Numer. Methods Fluids 20(8–9), 1061–1080 (1995). https://doi.org/10.1002/fld.1650200823
Acknowledgements
This work is supported by the Deutsche Forschungsgemeinschaft (DFG, German Research Foundation) under Germany’s Excellence Strategy EXC 2181/1 - 390900948 (the Heidelberg STRUCTURES Excellence Cluster).
Funding
Open Access funding enabled and organized by Projekt DEAL.
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Hauck, M., Aizinger, V., Frank, F. et al. Enriched Galerkin method for the shallow-water equations. Int J Geomath 11, 31 (2020). https://doi.org/10.1007/s13137-020-00167-7
Received:
Accepted:
Published:
DOI: https://doi.org/10.1007/s13137-020-00167-7
Keywords
- Enriched Galerkin
- Finite elements
- Shallow-water equations
- Discontinuous Galerkin
- Local conservation
- Ocean modeling