Introduction

One of the most important models [1,2,3,4,5,6,7,8,9,10] that has been extensively studied in optics, for the past few decades, is the Lakshmanan–Porsezian–Daniel (LPD) equation. This model was considered with Kerr law of self–phase modulation (SPM) as well as power–Law of SPM. Thereafter, this model was extended to address soliton studies in birefringent fibers. Later, LPD was also studied after replacing the chromatic dispersion (CD) with a combination of third–order and fourth–order dispersion effects. These were referred to as cubic–quartic solitons. These cubic–quartic solitons for LPD were studied for the perturbed LPD equation where the perturbation terms are of Hamiltonian type. The semi–inverse variational principle recovered the soliton solutions under these circumstances.

Additionally, in the past the LPD model was also studied with nonlinear CD and Kerr law of SPM. In this context, the Kerr law of SPM was considered. The linear temporal evolution as well as the generalized temporal evolution were taken into consideration. The current paper addresses the LPD equation with power-law of SPM and having linear as well as generalized temporal evolution. The implicit quiescent optical solitons are recovered by Lie symmetry analysis. The results are presented with the respective parameter constraints. A very important observation was made pertaining to the nonlinearity parameters of CD and SPM to the model. This was not recoverable in the two prequel papers [1, 2].

Linear temporal evolution

The dimensionless form of the LPD equation with nonlinear CD and power-law of nonlinear SPM, for linear temporal evolution is given as:

$$\begin{aligned} iq_t + a\left( \left| q \right| ^n q\right) _{xx} + b \left| q \right| ^{2m} q = cq_{xxxx} + \alpha \left( q_x \right) ^2 q^{*} + \beta \left| q_x \right| ^2 q + \gamma \left| q \right| ^{2m} q_{xx} + \delta q^2 q^{*}_{xx} + \sigma \left| q \right| ^{2m+2} q. \end{aligned}$$
(1)

Here, in (1), q(x, t) represents the wave amplitude and is a complex-valued function. The first term is the linear temporal evolution and its coefficient is \(i = \sqrt{-1}\). The second term, with coefficient a, is the nonlinear CD with n being the nonlinearity parameter while the third term, with coefficient b, is the nonlinear form of SPM with the parameter m being the power-law of nonlinearity there. It needs to be noted that the parameter \(m=1\) collapses to Kerr law of SPM while if \(n=0\), one recovers linear CD. On the right hand side, the usual terms of the LPD equation are present except for the fact that the intensity terms are written with power-law of nonlinearity.

To solve (1), the following transformation is picked:

$$\begin{aligned} q \left( x,t \right) =\phi \left( x \right) {\textrm{e}^{i\lambda \,t}}. \end{aligned}$$
(2)

Upon substituting (2) into (1), one recovers the following relation for the amplitude portion \(\phi (x)\):

$$\begin{aligned}{} & {} a(n+1) \phi ^{\prime \prime } (x) \phi ^{n+1}(x) + an(n+1) \left\{ \phi ^{\prime }(x) \right\} ^2 \phi ^n (x) + b \phi ^{2m+2} (x) + c \phi ^{(iv)}(x) \phi (x) - \gamma \phi ^{\prime \prime } (x) \phi ^{2m+1} (x) \nonumber \\{} & {} \quad -\sigma \phi ^{2m+4} (x) - \left[ \lambda + \left( \alpha + \beta \right) \left\{ \phi ^{\prime }(x) \right\} ^2 \right] \phi ^2(x) - \delta \phi ^{\prime \prime }(x) \phi ^3(x) = 0. \end{aligned}$$
(3)

For integrability of (3), the following parameter restrictions must remain valid:

$$\begin{aligned} m = 1, \end{aligned}$$
(4)
$$\begin{aligned} n = 1, \end{aligned}$$
(5)
$$\begin{aligned} \alpha + \beta = 0, \end{aligned}$$
(6)
$$\begin{aligned} \delta + \gamma = 0, \end{aligned}$$
(7)
$$\begin{aligned} c=0. \end{aligned}$$
(8)

With the implementation of these parameter constraints, the governing model transforms to:

$$\begin{aligned} iq_t + a\left( \left| q \right| q\right) _{xx} + b \left| q \right| ^{2} q = \beta \left\{ \left| q_x \right| ^2 q - \left( q_x \right) ^2 q^{*} \right\} + \gamma \left\{ \left| q \right| ^{2} q_{xx} - q^2 q^{*}_{xx} \right\} + \sigma \left| q \right| ^4 q. \end{aligned}$$
(9)

Then, the ODE given by (3) shrinks to:

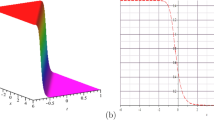
$$\begin{aligned} 2a \left[ \phi ^{\prime \prime }(x) \phi ^2(x) + \left\{ \phi ^{\prime }(x) \right\} ^2 \phi (x) \right] + b \phi ^4 (x) - \lambda \phi ^2 (x) - \sigma \phi ^6 (x) = 0. \end{aligned}$$
(10)

The above equation (10) admits a single Lie point symmetry, namely \(\frac{\partial }{\partial x}\). This symmetry when applied to (4) leads to its implicit solution in terms of Appell hypergeometric function of two variables as follows:

$$\begin{aligned} x=\pm 2 \phi ^{\frac{1}{2}} \sqrt{\frac{3 a}{\lambda }} F_1\left( \frac{1}{4};\frac{1}{2},\frac{1}{2};\frac{5}{4};-\frac{30 \sigma \phi ^2}{-21 b+\sqrt{441 b^2-2100 \lambda \sigma }},\frac{30 \sigma \phi ^2}{21 b+\sqrt{441 b^2-2100 \lambda \sigma }}\right) . \end{aligned}$$
(11)

The Appell hypergeometric function of two variables is defined as follows:

$$\begin{aligned} F_1\left( a;b_1,b_2;c;x,y\right) , \end{aligned}$$
(12)

which has a primary definition through the hypergeometric series

$$\begin{aligned} x^m y^n \left( \sum _{m=0}^{\infty } \sum _{n=0}^{\infty } \frac{(a)_{m+n} \left( b_1\right) _m \left( b_2\right) _n}{(c)_{m+n} m! n!}\right) , \end{aligned}$$
(13)

which is convergent inside the region

$$\begin{aligned} \max \left( \left| x \right| , \left| y \right| \right) < 1. \end{aligned}$$
(14)

Equation (14) for (11) transforms to

$$\begin{aligned} \max \left( \frac{30 \sigma \phi ^2}{-21b+\sqrt{441 b^2-2100 \lambda \sigma }}, \frac{30 \sigma \phi ^2}{-21b+\sqrt{441 b^2-2100 \lambda \sigma }} \right) < 1, \end{aligned}$$
(15)

together with

$$\begin{aligned} 21 b^2 > 100 \lambda \sigma , \end{aligned}$$
(16)

and

$$\begin{aligned} \sqrt{441 b^2-2100 \lambda \sigma } \ne \left| 21b \right| . \end{aligned}$$
(17)

The Pochhammer symbol in (13) is defined as follows:

$$\begin{aligned} (p)_n = \left\{ \begin{array}{ll} 1 &{} { n=0},\\ p(p+1)\cdots (p+n-1) &{} { n > 0}. \end{array} \right. \end{aligned}$$
(18)

Finally, the Appell hypergeometric function (11) is defined for:

$$\begin{aligned} a \lambda > 0. \end{aligned}$$
(19)

Generalized temporal evolution

The dimensionless form of LPD Eq. (1), with generalized temporal evolution, is written as:

$$\begin{aligned} iq^l_t + a\left( \left| q \right| ^n q^l\right) _{xx} + b \left| q \right| ^{2m} q^l = cq^l_{xxxx} + \alpha \left( q_x \right) ^2 \left( q^l \right) ^{*} + \beta \left| q_x \right| ^2 q^l + \gamma \left| q \right| ^{2m} \left( q^l \right) _{xx} + \delta q^2 \left( q^l \right) ^{*}_{xx} + \sigma \left| q \right| ^{2m+2}q^l. \end{aligned}$$
(20)

The constant l is the parameter for the generalized temporal evolution. For \(l=1\), Eq. (20) collapses to (1). Substituting the transform given by (2) into (20) the real and imaginary components reveal the following pair of relations:

$$\begin{aligned} \left\{ \alpha + \delta l(l-1) \right\} \left\{ \phi ^{\prime }(x) \right\} ^2 + \delta l \phi ^{\prime \prime }(x) \phi (x) = 0, \end{aligned}$$
(21)

and

$$\begin{aligned}{} & {} a\left\{ l^2 + l(2 n-1) + n(n-1)\right\} \left\{ \phi ^{\prime }(x) \right\} ^2 \phi ^{n+2}(x) + a(l+n) \phi ^{\prime \prime }(x) \phi ^{n+3}(x) + b\phi ^{m+4}(x) \nonumber \\{} & {} \quad - 6cl(l-1)(l-2) \phi ^{\prime \prime }(x) \left\{ \phi ^{\prime } (x) \right\} ^2 \phi (x) - c l(l-1)(l-2)(l-3) \left\{ \phi ^{\prime }(x) \right\} ^4 - cl \phi ^{(iv)}(x) \phi ^3 (x) \nonumber \\{} & {} \quad + cl(l-1) \left[ 3 \left\{ \phi ^{\prime \prime }(x) \right\} ^2 + 4 \phi ^{\prime \prime \prime }(x) \phi ^{\prime }(x) \right] \phi ^2(x) - \gamma l\phi ^{\prime \prime } (x) \phi ^{2m+3}(x) - \gamma l(1-l) \left\{ \phi ^{\prime } (x) \right\} ^2 \phi ^{2m+2}(x) \nonumber \\{} & {} \quad - \lambda l \phi ^4(x) - \sigma \phi ^{2m+6}(x) - \beta \left\{ \phi ^{\prime }(x) \right\} ^2 \phi ^4(x) = 0. \end{aligned}$$
(22)

For integrability, the same conditions given by (4)–(8) must hold. Therefore, the governing model (20) simplifies to:

$$\begin{aligned} iq^l_t + a\left( \left| q \right| q^l\right) _{xx} + b \left| q \right| ^{2} q^l = \beta \left\{ \left| q_x \right| ^2 q^l - \left( q_x \right) ^2 \left( q^l \right) ^{*} \right\} + \delta \left\{ q^2 \left( q^l \right) ^{*}_{xx} - \left| q \right| ^{2} \left( q^l \right) _{xx} \right\} + \sigma \left| q \right| ^{4}q^l, \end{aligned}$$
(23)

while Eq. (22) reduces to

$$\begin{aligned}{} & {} \left\{ \beta +\gamma l(l-1) \right\} \left\{ \phi ^{\prime }(x) \right\} ^2 \phi (x) + \gamma l \phi ^{\prime \prime }(x) \phi ^2(x) + a l(l+1) \left\{ \phi ^{\prime }(x) \right\} ^2 + a (l+1) \phi ^{\prime \prime }(x) \phi (x) \nonumber \\{} & {} \quad + b\phi ^3(x) - \gamma l \phi ^{\prime \prime } (x) \phi ^2(x) - \gamma l(l-1) \left\{ \phi ^{\prime } (x) \right\} ^2 \phi (x) - \lambda l \phi (x) - \beta \left\{ \phi ^{\prime }(x)\right\} ^2 \phi (x) - \sigma \phi ^5(x) = 0. \end{aligned}$$
(24)

The above equation admits a single Lie point symmetry, namely \(\frac{\partial }{\partial x}\). This symmetry will be used the integration process and it leads to the following implicit solution in terms of Appell hypergeometric function of two variables

$$\begin{aligned} x=\pm \phi ^{\frac{1}{2}} \sqrt{\frac{2 a (1+l) (1+2 l)}{l \lambda }} F_1\left( \frac{1}{4};\frac{1}{2},\frac{1}{2};\frac{5}{4};A_1,A_2\right) , \end{aligned}$$
(25)

where

$$\begin{aligned} A_1=\frac{2 \left( 4 l^2+8 l+3\right) \sigma \phi ^2}{b \left( 4 l^2+12 l+5\right) -\sqrt{\left( 4 l^2+12 l+5\right) \left\{ b^2 \left( 4 l^2+12 l+5\right) -4 \lambda l (2 l+3)^2 \sigma \right\} }}, \end{aligned}$$
(26)

and

$$\begin{aligned} A_2=\frac{2 \left( 4 l^2+8 l+3\right) \sigma \phi ^2}{\sqrt{\left( 4 l^2+12 l+5\right) \left\{ b^2 \left( 4 l^2+12 l+5\right) -4 \lambda l(2l+3)^2 \sigma \right\} }+b \left( 4 l^2+12 l+5\right) }. \end{aligned}$$
(27)

The condition (14), in this case translates to

$$\begin{aligned} \max \left( \left| A_1 \right| , \left| A_2 \right| \right) < 1, \end{aligned}$$
(28)

; while, the other constraints that naturally follow through are:

$$\begin{aligned} \left( 4 l^2+12 l+5\right) \left\{ b^2 \left( 4 l^2+12 l+5\right) -4 \lambda l(2l+3)^2 \sigma \right\} > 0, \end{aligned}$$
(29)

and

$$\begin{aligned} \left| \sqrt{\left( 4 l^2+12 l+5\right) \left\{ b^2 \left( 4 l^2+12 l+5\right) -4 \lambda l(2l+3)^2 \sigma \right\} }+b \left( 4 l^2+12 l+5\right) \right| \ne 0. \end{aligned}$$
(30)

Additionally, the condition (19) still holds true here as well.

An observation

The results of the current paper prove that quiescent solitons for LPD equation with power-law of SPM would exist only when the nonlinear CD parameter as well as the SPM parameter both shrink to unity. This fact was neither observed nor retrievable when the LPD equation with Kerr law nonlinearity was studied in the prequel papers [1, 2].

Conclusions

The current paper recovered the implicit quiescent optical solitons for the LPD model with power-law of SPM and having nonlinear CD. Both linear temporal evolution as well as generalized temporal evolution effects are considered. The recovered results are in terms of Appell hypergeometric functions. The respective parameter constraints are also considered. The paper unravels a mysterious situation with the power-law parameters. The study of the LPD model with power-law of SPM reveals the fact that the solitons would exist provided the parameter of nonlinearity for CD as well as SPM are both reduced to unity. This was never revealed in the prequel papers [1, 2]. This paper will be later studied for the same model but with differential group delay as well as in dispersion flattened fibers. The results of those research activities would be soon disclosed after aligning the results with the pre-existing reports [11,12,13,14,15,16,17,18,19,20,21,22,23,24,25,26,27].