Skip to main content
SpringerLink
Log in

Adaptive-Wave Alternative for the Black-Scholes Option Pricing Model

  • Published:
Cognitive Computation Aims and scope Submit manuscript

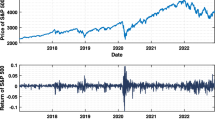
Abstract

A nonlinear wave alternative for the standard Black-Scholes option-pricing model is presented. The adaptive-wave model, representing controlled Brownian behavior of financial markets, is formally defined by adaptive nonlinear Schrödinger (NLS) equations, defining the option-pricing wave function in terms of the stock price and time. The model includes two parameters: volatility (playing the role of dispersion frequency coefficient), which can be either fixed or stochastic, and adaptive market potential that depends on the interest rate. The wave function represents quantum probability amplitude, whose absolute square is probability density function. Four types of analytical solutions of the NLS equation are provided in terms of Jacobi elliptic functions, all starting from de Broglie’s plane-wave packet associated with the free quantum-mechanical particle. The best agreement with the Black-Scholes model shows the adaptive shock-wave NLS-solution, which can be efficiently combined with adaptive solitary-wave NLS-solution. Adjustable ‘weights’ of the adaptive market-heat potential are estimated using either unsupervised Hebbian learning or supervised Levenberg–Marquardt algorithm. In the case of stochastic volatility, it is itself represented by the wave function, so we come to the so-called Manakov system of two coupled NLS equations (that admits closed-form solutions), with the common adaptive market potential, which defines a bidirectional spatio-temporal associative memory.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8
Fig. 9
Fig. 10
Fig. 11
Fig. 12
Fig. 13

Similar content being viewed by others

Notes

  1. Note that the domain of validity of the ‘quantum probability’ is not restricted to the microscopic world [27]. There are macroscopic features of classically behaving systems, which cannot be explained without recourse to the quantum dynamics (see [28] and references therein).

  2. For example, the general pendulum equation:

    $$ \alpha^{\prime \prime }(t,\phi )+\sin [\alpha (t,\phi )]=0 $$

    has the elliptic solution:

    $$ \alpha (t,\phi )=2\sin ^{-1}\left[ \sin \left( {\frac{\phi}{2}}\right) \right] \hbox{sn}\left[ t,\sin ^{2}\left( {\frac{\phi} {2}}\right) \right] . $$

  3. A shock wave is a type of fast-propagating nonlinear disturbance that carries energy and can propagate through a medium (or, field). It is characterized by an abrupt, nearly discontinuous change in the characteristics of the medium. The energy of a shock wave dissipates relatively quickly with distance and its entropy increases. On the other hand, a soliton is a self-reinforcing nonlinear solitary wave packet that maintains its shape while it travels at constant speed. It is caused by a cancelation of nonlinear and dispersive effects in the medium (or, field).

  4. A closely related solution of an anharmonic oscillator ODE:

    $$ \phi^{\prime \prime }(s)+\phi (s)+\phi^{3}(s)=0 $$

    is given by

    $$ \phi (s)=\sqrt{{\frac{2m}{1-2m}}} \hbox{cn}\left( \sqrt{1+{\frac{2m}{1-2m}}} s, m\right) . $$

  5. Controlled stochastic volatility here represents volatility evolving in a stochastic manner but within the controlled boundaries.

  6. The hypothesis that financial leverage can explain the leverage effect was first discussed by F. Black [61].

  7. The Manakov system (19)–(20) has the following Lax pair [86] representation:

    $$ \begin{aligned} \partial_{x}\phi &=M\phi \hbox{ and }\partial_{t}\phi =B\phi , \hbox{ or }\partial_{x}B -\partial_{t}M=[M,B],\qquad \hbox{with}\\ M(\lambda )&=\left( \begin{array}{ccc} \hbox{i}\lambda & \psi_{1} & \psi_{2}\\ -\psi_{1} & \hbox{i}\lambda & 0 \\ -\psi_{2} & 0 & \hbox{i}\lambda \end{array} \right) \qquad \hbox{and}\\ B(\lambda )&= -\hbox{i}\left( \begin{array}{ccc} 2\lambda ^{2}-|\psi_{1}|^{2}-|\psi_{2}|^{2} & 2i\psi_{1}\lambda -\partial_{x}\psi_{1} & 2i\psi_{2}\lambda -\partial_{x}\psi_{2}\\ -2i\psi_{1}^{\ast }\lambda -\partial_{x}\psi_{1}^{\ast } & -2\lambda ^{2}+|\psi_{1}|^{2} & \psi_{1}^{\ast }\psi_{2} \\ -2i\psi_{2}^{\ast }\lambda -\partial_{x}\psi_{2}^{\ast } & \psi_{1}\psi_{2}^{\ast } & -2\lambda ^{2}+|\psi_{2}|^{2} \end{array} \right). \end{aligned} $$
    (25)

References

  1. Hussain A (2009) Cognitive computation: an introduction. Cogn Comput 1:1–3

    Article  Google Scholar 

  2. Gurney KN (2009) Reverse engineering the vertebrate brain: methodological principles for a biologically grounded programme of cognitive modelling. Cogn Comput 1:29–41

    Article  Google Scholar 

  3. Haikonen POA (2009) The role of associative processing in cognitive computing. Cogn Comput 1:42–49

    Article  Google Scholar 

  4. Taylor JG (2009) Cognitive computation. Cogn Comput 1:4–16

    Article  Google Scholar 

  5. McClelland JL (2009) Is a machine realization of truly human-like intelligence achievable?. Cogn Comput 1:17–21

    Article  Google Scholar 

  6. Aleksander I (2009) Designing conscious systems. Cogn Comput 1:22–28

    Article  Google Scholar 

  7. Seth A (2009) Explanatory correlates of consciousness: theoretical and computational challenges. Cogn Comput 1:50–63

    Article  Google Scholar 

  8. Black F, Scholes M (1973) The pricing of options and corporate liabilities. J Pol Econ 81:637–659

    Article  Google Scholar 

  9. Merton RC (1973) Theory of rational option pricing. Bell J Econ Manage Sci 4:141–183

    Article  Google Scholar 

  10. Osborne MFM (1959) Brownian motion in the stock market. Oper Res 7:145–173

    Article  Google Scholar 

  11. Perello J, Porra JM, Montero M, Masoliver J (2000) Black-Scholes option pricing within Ito and Stratonovich conventions. Physica A 278(1–2): 260–274

    Article  Google Scholar 

  12. Fama E (1965) The behavior of stock market prices. J Bus 38:34–105

    Article  Google Scholar 

  13. Jensen MC (1978) Some anomalous evidence regarding market efficiency, an editorial introduction. J Finan Econ 6:95–101

    Article  Google Scholar 

  14. Wiener N (1923) Differential space. J Math Phys 2:131–174

    Google Scholar 

  15. Gardiner CW (1983) Handbook of stochastic methods. Springer, Berlin

    Google Scholar 

  16. Itô K (1951) On stochastic differential equations. Mem Am Math Soc 4:1–51

    Google Scholar 

  17. Stratonovich RL (1966) A new representation for stochastic integrals and equations. SIAM J Control 4:362–371

    Article  Google Scholar 

  18. Kadanoff LP (2000) Statistical physics: statics, dynamics and renormalization. World Scientific, Singapore

    Google Scholar 

  19. Kelly M (2009) Black-Scholes option model & European option Greeks. The Wolfram demonstrations project, http://www.demonstrations.wolfram.com/EuropeanOptionGreeks, (2009)

  20. Fouque JP, Papanicolau G, Sircar KR (2000) Derivatives in financial markets with stochastic volatility. Cambdrige University Press, Cambridge

    Google Scholar 

  21. Cont R (2001) Empirical properties of asset returns: stylized facts and statistical issues. Quant Financ 1:223–236

    Article  Google Scholar 

  22. Perello J, Sircar R, Masoliver J (2008) Option pricing under stochastic volatility: the exponential Ornstein-Uhlenbeck model. J Stat Mech P06010

  23. Masoliver J, Perello J (2008) The escape problem under stochastic volatility: the Heston model. Phys Rev E 78:056104

    Article  Google Scholar 

  24. Ivancevic V, Ivancevic T (2007) Complex dynamics: advanced system dynamics in complex variables. Springer, Dordrecht

    Google Scholar 

  25. Ivancevic V, Ivancevic T (2008) Quantum leap: from Dirac and Feynman, across the Universe, to human body and mind. World Scientific, Singapore

    Google Scholar 

  26. Voit J (2005) The statistical mechanics of financial markets. Springer, New York

    Google Scholar 

  27. Umezawa H (1993) Advanced field theory: micro macro and thermal concepts. Am Inst Phys, New York

  28. Freeman WJ, Vitiello G (2006) Nonlinear brain dynamics as macroscopic manifestation of underlying many–body field dynamics. Phys Life Rev 3(2):93–118

    Article  Google Scholar 

  29. Trippi RR (1995) Chaos & nonlinear dynamics in the financial markets. Irwin Prof. Pub.

  30. Rothman P (1999) Nonlinear time series analysis of economic and financial data. Springer, New York

    Google Scholar 

  31. Ammann M, Reich C (2001) VaR for nonlinear financial instruments—linear approximation or full Monte-Carlo?. Fin Mark Portf Manag 15(3)

  32. Ivancevic V, Ivancevic T (2007) High-dimensional chaotic and attractor systems. Springer, Dordrecht

    Google Scholar 

  33. Tse WM (1996) Policy implications in an adaptive financial economy. J Eco Dyn Con 20(8):1339–1366

    Article  Google Scholar 

  34. Ingber L (2000) High-resolution path-integral development of financial options. Physica A 283:529–558

    Article  Google Scholar 

  35. Ivancevic V, Ivancevic T (2006) Geometrical dynamics of complex systems. Springer, Dordrecht

    Book  Google Scholar 

  36. Ivancevic V, Ivancevic T (2008) Complex nonlinearity: chaos, phase transitions, topology change and path integrals. Springer, New York

    Google Scholar 

  37. Ivancevic V, Ivancevic T (2009) Quantum neural computation. Springer, New York

    Google Scholar 

  38. Lo AW (2004) The adaptive markets hypothesis: market efficiency from an evolutionary perspective. J Portf Manag 30:15–29

    Article  Google Scholar 

  39. Lo AW (2005) Reconciling efficient markets with behavioral finance: the adaptive markets hypothesis. J Inves Consult 7:21–44

    Google Scholar 

  40. Ivancevic V, Aidman E (2007) Life-space foam: a medium for motivational and cognitive dynamics. Physica A 382:616–630

    Article  Google Scholar 

  41. Ivancevic V, Ivancevic T (2008) Nonlinear quantum neuro-psycho-dynamics with topological phase transitions. Neuro Quantology 4:349–368

    Google Scholar 

  42. Ivancevic V, Aidman E, Yen L (2009) Extending Feynmans formalisms for modelling human joint action coordination. Int J Biomath 2(1):1–7

    Article  Google Scholar 

  43. Frost AJ, Prechter RR, Jr. (1978) Elliott wave principle: key to market behavior. Wiley, New York, 10th edn. Elliott Wave International, (2009)

  44. Steven P (2003) Applying Elliott wave theory profitably. Wiley, New York

    Google Scholar 

  45. Mandelbrot B (1999) A multifractal walk down Wall Street. Sci. Am. February

  46. Ivancevic V, Reid D (2009) Entropic geometry of crowd dynamics. In nonlinear dynamics, Intech, Vienna, (in press)

  47. Ivancevic V, Reid D, Aidman E (2010) Crowd behavior dynamics: entropic path-integral model. Nonlin Dyn 59(1):351

    Article  Google Scholar 

  48. Ivancevic V, Reid D (2009) Dynamics of confined crowds modelled using entropic stochastic resonance and quantum neural networks. Int J Intel Defence Sup Sys (in press)

  49. Kleinert H (2002) Path integrals in quantum mechanics, statistics, polymer physics, and financial markets, 3rd edn. World Scientific, Singapore

    Google Scholar 

  50. Liu S, Fu Z, Liu S, Zhao Q (2001) Jacobi elliptic function expansion method and periodic wave solutions of nonlinear wave equations. Phys Let A 289:69–74

    Article  CAS  Google Scholar 

  51. Liu G-T, Fan T-Y (2005) New applications of developed Jacobi elliptic function expansion methods. Phys Let A 345:161–166

    Article  CAS  Google Scholar 

  52. Abramowitz M, Stegun IA (eds) (1972) Jacobian elliptic functions and theta functions. Chapter 16 in Handbook of mathematical functions with formulas, graphs, and mathematical tables, 9th edn. Dover, New York, pp 567–581

  53. Griffiths DJ (2005) Introduction to quantum mechanics, 2nd edn. Pearson Educ. Int., UK

    Google Scholar 

  54. Thaller B (2000) Visual quantum mechanics. Springer, New York

    Google Scholar 

  55. Ivancevic V (2009) Adaptive wave models for option pricing evolution: nonlinear and quantum Schrodinger approaches. CEJP (submitted); arXiv:1001.0615v1 [q-fin.PR]

  56. Ivancevic V, Ivancevic T (2007) Neuro-fuzzy associative machinery for comprehensive brain and cognition modelling. Springer, Berlin

    Book  Google Scholar 

  57. Ivancevic V, Ivancevic T (2007) Computational mind: a complex dynamics perspective. Springer, Berlin

    Book  Google Scholar 

  58. Behera L, Kar I (2005) Quantum stochastic filtering. In: Proceedings of the IEEE International Conference of SMC 3:2161–2167

  59. Behera L, Kar I, Elitzur AC (2005) Recurrent quantum neural network model to describe eye tracking of moving target. Found Phys Let 18(4):357–370

    Article  Google Scholar 

  60. Behera L, Kar I, Elitzur AC (2006) Recurrent quantum neural network and its applications, Chapter 9. In:Tuszynski JA (ed.) The emerging physics of consciousness. Springer, Berlin

  61. Black F (1976) Studies of stock price volatility changes. In: Proc. 1976 Meet. Ame. Stat. Assoc. Bus. Econ. Stat. 177–181

  62. Roman HE, Porto M, Dose C (2008) Skewness, long-time memory, and non-stationarity: application to leverage effect in financial time series. EPL 84, 28001, (5pp)

    Google Scholar 

  63. Kosko B (1988) Bidirectional associative memory. IEEE Trans Sys Man Cyb 18:49–60

    Article  Google Scholar 

  64. Kosko B (1992) Neural networks, fuzzy systems, a dynamical systems approach to machine intelligence. Prentice–Hall, New York

    Google Scholar 

  65. Hanm S-H, Koh IG (1999) Stability of neural networks and solitons of field theory. Phys Rev E 60:7608–7611

    Article  Google Scholar 

  66. Manakov SV (1973) On the theory of two-dimensional stationary self-focusing of electromagnetic waves. Zh Eksp Teor Fiz 65:505–516 (in Russian); (1974) (transleted into English) Sov Phys JETP 38:248–253

  67. Haelterman M, Sheppard AP (1994) Bifurcation phenomena and multiple soliton bound states in isotropic Kerr media. Phys Rev E 49:3376–3381

    Article  Google Scholar 

  68. Yang J (1997) Classification of the solitary wave in coupled nonlinear Schrödinger equations. Physica D 108:92–112

    Article  Google Scholar 

  69. Benney DJ, Newell AC (1967) The propagation of nonlinear wave envelops. J Math Phys 46:133–139

    Google Scholar 

  70. Zakharov VE, Manakov SV, Novikov SP, Pitaevskii LP (1980) Soliton theory: inverse scattering method. Nauka, Moscow

    Google Scholar 

  71. Hasegawa A, Kodama Y (1995) Solitons in optical communications. Clarendon, Oxford

    Google Scholar 

  72. Radhakrishnan R, Lakshmanan M, Hietarinta J (1997) Inelastic collision and switching of coupled bright solitons in optical fibers. Phys Rev E 56:2213

    Article  CAS  Google Scholar 

  73. Agrawal G (2001) Nonlinear fiber optics, 3rd edn. Academic Press, San Diego

    Google Scholar 

  74. Yang J (2001) Interactions of vector solitons. Phys Rev E 64:026607

    Article  CAS  Google Scholar 

  75. Elgin J, Enolski V, Its A (2007) Effective integration of the nonlinear vector Schrödinger equation. Physica D 225(22):127–152

    Article  Google Scholar 

  76. Kaup DJ, Malomed BA (1993) Soliton trapping and daughter waves in the Manakov model. Phys Rev A 48:599–604

    Article  PubMed  Google Scholar 

  77. Radhakrishnan R, Lakshmanan M (1995) Bright and dark soliton solutions to coupled nonlinear Schrödinger equations. J Phys A 28:2683–2692

    Article  Google Scholar 

  78. Tratnik MV, Sipe JE (1988) Bound solitary waves in a birefringent optical fiber. Phys Rev A 38:2011–2017

    Article  PubMed  Google Scholar 

  79. Forest MG, Sheu SP, Wright OC (2000) On the construction of orbits homoclinic to plane waves in integrable coupled nonlinear Schrö dinger system. Phys Lett A 266(1):24–33

    Article  CAS  Google Scholar 

  80. Forest MG, McLaughlin DW, Muraki DJ, Wright OC (2000) Nonfocusing instabilities in coupled, integrable nonlinear Schrö dinger PDEs. J Nonl Sci 10:291–331

    Article  Google Scholar 

  81. Wright OC, Forest MG (2000) On the Bäcklund-gauge transformation and homoclinic orbits of a coupled nonlinear Schrö dinger system. Physica D Nonl Phenom 141(1–2):104–116

    Article  Google Scholar 

  82. Champneys A, Yang J (2002) A scalar nonlocal bifurcation of solitary waves for coupled nonlinear Schrödinger systems. Nonlinearity 15(6):2165–2192

    Article  Google Scholar 

  83. Landau LD, Lifshitz EM (1977) Quantum mechanics: non-relativistic theory, 3rd edn. Pergamon Press, Oxford

    Google Scholar 

  84. Pretorius F, Choptuik MW (2006) Adaptive mesh refinement for coupled elliptic-hyperbolic systems. J Comp Phys 218(1):246–274

    Article  Google Scholar 

  85. Mallet Y, Coomans D, Kautsky J, de Vel O (1997) Classification using adaptive wavelets for feature extraction. IEEE Trans Patt Anal Mach Intel 19(10):1058–1066

    Article  Google Scholar 

  86. Lax P (1968) Integrals of nonlinear equations of evolution and solitary waves. Comm Pure Applied Math 21:467–490

    Article  Google Scholar 

  87. Lazarides N, Tsironis GP (2005) Coupled nonlinear Schroedinger field equations for electromagnetic wave propagation in nonlinear left-handed materials. Phys Rev E 71:036614

    Article  CAS  Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Defence Science & Technology Organisation, Adelaide, Australia

    Vladimir G. Ivancevic

Authors
  1. Vladimir G. Ivancevic
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Vladimir G. Ivancevic.

Appendix: Manakov System

Appendix: Manakov System

Manakov’s own method was based on the Lax pair representation.Footnote 7

Alternatively, for normalized value of the market-heat potential, β = r = 1, Manakov system allows solutions of the form:

$$ \sigma (s,t)=\varphi (s) \hbox{e}^{{\rm i}w_\sigma^{2}t},\qquad \psi (s,t) =\phi (s) \hbox{e}^{{\rm i}w_\psi^{2}t}, $$
(26)

where φ, ϕ are real-valued functions and w σ, w ψ are positive wave parameters for volatility and option-price. Substituting (26) into the Manakov equations we get the ODE-system [68]

$$ \varphi^{\prime \prime }(s) =w_\sigma^{2}\varphi (s)-[\varphi^{2}(s)+\phi ^{2}(s)] \varphi (s), $$
(27)
$$ \phi^{\prime \prime }(s) =w_\psi^{2}\phi (s)-[\phi^{2}(s)+\varphi^{2}(s)] \phi (s). $$
(28)

For w σ = w ψ = w, Eqs. 27 and 28 have a one-parameter family of symmetric single-humped soliton solutions (see the left part of Fig. 14) given by

$$ \varphi (s)=\pm \phi (s)=w \hbox{sech}(w s), $$
(29)

as well as periodic solutions:

$$ \varphi (s)=A\cos (Bs)\qquad \hbox{and}\qquad \phi (s)=A\sin (Bs), $$
(30)

where \(A=\sqrt{w^{2}+B^{2}}\) (with B an arbitrary parameter). For 0 < w < 1 there is also another, in general asymmetric, one-parameter family of solutions for each fixed w [68]

$$ \begin{aligned} \varphi (s) &= \sqrt{2(1-w^{2})}\cosh (ws)/\kappa,\\ \phi (s) &= -w\sqrt{2(1-w^{2})}\sinh (s-s_0)/\kappa,\qquad \hbox{where}\\ \kappa &=\cosh (s)\cosh (w s)-w\sinh (s)\sinh (w s), \end{aligned} $$
(31)

in which φ is symmetric and ϕ antisymmetric.

Fig. 14
figure 14

Initial envelopes for volatility |σ0| and option-price |ψ0| within the Manakov solitons: (left) bright compound soliton (29), (middle) dark compound soliton (32), and (right) compound kink-shaped soliton (36). These initial envelopes can be used for numerical studies of the Manakov system and its various generalizations (modified and adapted from [87])

Full size image

On the other hand, for negative values of the potential β, the Manakov equations accept dark soliton solutions of the form [87]

$$ \sigma (s,t)=\psi (s,t)=k\left[ \tanh (ks)-\hbox{i}\right] \hbox{e}^{\hbox{i}(ks-5k^{2}t)}, $$
(32)

which are localized dips on a finite-amplitude background wave (see the middle part of Fig. 14). In this very interesting case, volatility and option-price fields are coupled together, forming a dark compound soliton. Note that their respective relative amplitudes are controlled by the corresponding nonlinearities and frequency. For β =  −1 the Manakov equations alow also solutions of the form:

$$ \sigma (s,t)=\varphi (s) \hbox{e}^{-iw_\sigma^{2}t},\qquad \psi (s,t)=\phi (s) \hbox{e}^{iw_\psi^{2}t}. $$
(33)

Introducing (33) into the Manakov equations, we get the ODE-system:

$$ \varphi^{\prime \prime }(s)= [\varphi^{2}(s)+\phi^{2}(s)] \varphi (s)-w_\sigma^{2}\varphi (s), $$
(34)
$$ \phi^{\prime \prime}(s) =[\phi ^{2}(s)+\varphi ^{2}(s)] \phi (s)-w_\psi^{2}\phi (s), $$
(35)

which, for w σ = w ψ = w, allow for kink-shaped localized soliton solutions (see the right part of Fig. 14) given by [87]

$$ \varphi (s)=\pm \phi (s)=({w}/\sqrt{2})\tanh ({w} s/\sqrt{2}), $$
(36)

as well as periodic solutions (30). Inserting (14) back into (33) gives the double-kink solution for the Manakov system:

$$ \sigma (s,t)=\pm({w}/\sqrt{2})\tanh ({w} s/\sqrt{2}) \hbox{e}^{-iw^{2}t},\qquad \psi (s,t)=\pm({w}/\sqrt{2})\tanh ({w} s/\sqrt{2}) \hbox{e}^{-iw^{2}t}. $$
(37)

Rights and permissions

Reprints and permissions

About this article

Cite this article

Ivancevic, V.G. Adaptive-Wave Alternative for the Black-Scholes Option Pricing Model. Cogn Comput 2, 17–30 (2010). https://doi.org/10.1007/s12559-009-9031-x

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s12559-009-9031-x

Keywords

Search

Navigation