Skip to main content
SpringerLink
Log in

Non-parametric Dual Control of Non-minimum Phase Linear Dynamic Plant Using Shunt Compensator

  • Regular Papers
  • Control Theory and Applications
  • Published:
International Journal of Control, Automation and Systems Aims and scope Submit manuscript

Abstract

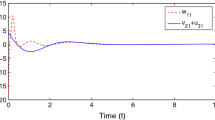
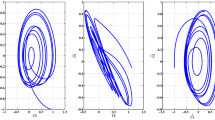
This article describes a new design approach of dual control systems for non-minimum phase dynamic systems which involve the use of shunt compensator, the type of which is determined by the non-parametric identification algorithm. In this study the dynamic system is represented with the observation data and the model whose analytical form is unknown and that has no a priori information. The identification algorithm is based on the rule of extracting essential variables in a non-parametric model which allows determining the order of the difference equation of the plant model. The information obtained is necessary to select the type of parallel compensator or shunt accurately. Both the shunt and the plant form an extended object that satisfies the conditions presented by the strict minimum-phase system. The use of the proposed control scheme for a linear dynamic plant makes it possible to synthesize a non-parametric dual control algorithm. An illustrative example of linear dynamic control system is presented to show the effectiveness of the proposed method. The identification of the plant was carried out preliminarily and the type of compensator was chosen. Further stage of non-parametric dual controller design was implemented to achieve control goals. The simulation results show that the application of the approach allows achieving better control efficiency indicators in comparison with the PID controller.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

References

  1. A. A. Feldbaum, “Dual control theory. I.,” Avtomatika i Telemekhanika, vol. 21, no. 9, pp. 1240–1249, 1960.

    MathSciNet  Google Scholar 

  2. T. A. N. Heirung, B. E. Ydstie, and B. Foss, “Dual adaptive model predictive control,” Automatica, vol. 80, pp. 340–348, 2017.

    Article  MathSciNet  MATH  Google Scholar 

  3. L. Gang and L. Ping, “Generalized dual-control system and its predictive control strategy with dual optimized horizon,” Proc. of 5th World Congress on Intelligent Control and Automation, vol. 1, pp. 698–701A, 2004.

    Article  Google Scholar 

  4. E. Žáčeková, S. Prívara, Z. Váňa, J. Cigler, and L. Ferkl, “Dual control approach for zone model predictive control,” Proc. of European Control Conference (ECC), pp. 1398–1403, 2013.

  5. A. V. Medvedev and A. V. Raskina, “On the nonparametric identification and dual adaptive control of dynamic processes,” Journal of Siberian Federal University. Mathematics and Physics, vol. 10, no. 1, pp. 96–107, 2017.

    Article  MATH  Google Scholar 

  6. A. Mesbah, “Stochastic model predictive control with active uncertainty learning: A survey on dual control,” Annual Reviews in Control, vol. 45, pp. 107–117, 2018.

    Article  MathSciNet  Google Scholar 

  7. A. V. Raskina, M. E. Kornet, E. A. Chzhan, A. A. Korneeva, and N. V. Kononova, “Design of multi loop control systems with decision makers under incomplete information,” Computer Science On-line Conference, Springer, Cham, pp. 1–8, 2021.

    Google Scholar 

  8. A. L. Fradkov, I. V. Miroshnik, and V. O. Nikiforov, Nonlinear and Adaptive Control of Complex Dynamical Systems, Springer Science and Business Media, p. 510, 2013.

  9. I. B. Furtat, “Robust control for a specific class of non-minimum phase dynamical networks,” Journal of Computer and Systems Sciences International, vol. 53, no. 1, pp. 33–46, 2014.

    Article  MathSciNet  MATH  Google Scholar 

  10. J. Li, S. Li, X. Chen, and J. Yang, “RBFNDOB-based neural network inverse control for non-minimum phase MIMO system with disturbances,” ISA Transactions, vol. 53, no. 4, pp. 983–993, 2014.

    Article  Google Scholar 

  11. Y. Ji, H. Zhou, and Q. Zong, “Approximate output regulation of non-minimum phase hypersonic flight vehicle,” Nonlinear Dynamics, vol. 91, no. 4, pp. 2715–2724, 2018.

    Article  Google Scholar 

  12. S. Zhou, M. K. Helwa, and A. P. Schoellig, “An inversion-based learning approach for improving impromptu trajectory tracking of robots with non-minimum phase dynamics,” IEEE Robotics and Automation Letters, vol. 3, no. 3, pp. 1663–1670, 2018.

    Article  Google Scholar 

  13. X. Hu, L. Wu, X. Si, and B. Xu, “Adaptive sliding mode control of non-linear non-minimum phase system with input delay,” IET Control Theory and Applications, vol. 11, no. 8, pp. 1153–1161, 2017.

    Article  MathSciNet  Google Scholar 

  14. X. Hu, B. Xu, X. Si, and C. Hu, “Nonlinear adaptive tracking control of non-minimum phase hypersonic flight vehicles with unknown input nonlinearity,” Nonlinear Dynamics, vol. 90, no. 2, pp. 1151–1163, 2017.

    Article  MATH  Google Scholar 

  15. R. Ramachandran, B. Madasamy, and V. Veerasamy, “Load frequency control of a dynamic interconnected power system using generalised Hopfield neural network based self-adaptive PID controller,” IET Generation, Transmission and Distribution, vol. 12, no. 21, pp. 5713–5722, 2018.

    Article  Google Scholar 

  16. W. Xue, Y. Huang, and Z. Gao, “On ADRC for non-minimum phase systems: Canonical form selection and stability conditions,” Control Theory and Technology, vol. 14, pp. 199–208, 2016.

    Article  MathSciNet  MATH  Google Scholar 

  17. Z. Liu, X. Hu, X. Wang, and Y. Guo, “Robust adaptive control for uncertain input delay MIMO nonlinear non-minimum phase system: A fuzzy approach,” IEEE Access, vol. 8, pp. 154143–154152, 2020.

    Article  Google Scholar 

  18. L. Wang and J. Su, “Disturbance rejection control for non-minimum phase systems with optimal disturbance observer,” ISA Transactions, vol. 57, pp. 1–9, 2015.

    Article  Google Scholar 

  19. G. R. G. da Silva, L. Campestrini, and A. S. Bazanella, “Multivariable virtual reference feedback tuning for non-minimum phase plants,” IEEE Control Systems Letters, vol. 2, no. 1, pp. 121–126, January 2018.

    Article  MathSciNet  Google Scholar 

  20. M. V. A. Fernandes, S. M. Dias, A. D. Araujo, J. B. Oliveira, and K. I. M. P. Queiroz, “Shunt indirect variable structure model reference adaptive controller for plants with arbitrary relative degree,” Proc. of 11th International Workshop on Variable Structure Systems (VSS), IEEE, pp. 283–288, 2010.

  21. E. L. Eremin and E. A. Shelenok, “Robust control for one class of multivariable dynamic plants,” Automation and Remote Control, vol. 78, no. 6, pp. 1046–1058, 2017.

    Article  MathSciNet  MATH  Google Scholar 

  22. K. Röbenack and S. Palis, “On the control of non-minimum phase systems using a parallel compensator,” Proc. of 23rd International Conference on System Theory, Control and Computing (ICSTCC), pp. 308–313, 2019.

  23. A. Selivanov and A. Fradkov, “Adaptive stabilization of minimum-phase systems under quantized measurements,” IFAC-PapersOnLine, Elsevier, vol. 53, no. 2, pp. 3761–3766, 2020.

    Article  Google Scholar 

  24. E. A. Parsheva and A. M. Tsykunov, “Adaptive control of an object with a delayed control and scalar input-output signals,” Automation and Remote Control, vol. 62, no. 1, pp. 124–131, 2001.

    Article  MathSciNet  MATH  Google Scholar 

  25. I. B. Furtat and A. M. Tsykunov, “Adaptive control of plants of unknown relative degree,” Automation and Remote Control, vol. 71, no. 6, pp. 1076–1084, 2010.

    Article  MathSciNet  MATH  Google Scholar 

  26. L. Denisova and V. Meshcheryakov, “Predictor-based adaptive control system with stability analysis,” IFAC-PapersOnLine, vol. 52, no. 13, pp. 486–491, 2019.

    Article  Google Scholar 

  27. S. Galeani, C. Possieri, and M. Sassano, “Asymptotic tracking for nonminimum phase linear systems via steady-state compensation,” IEEE Transactions on Automatic Control, vol. 66, no. 9, pp. 4176–4183, 2021.

    Article  MathSciNet  MATH  Google Scholar 

  28. R. Hmidi, A. B. Brahim, F. B. Hmida, and A. Sellami, “Proportional-derivative unknown input observer design using descriptor system approach for non-minimum phase systems,” International Journal of Control, Automation, and Systems, vol. 18, no. 9, pp. 2206–2219, 2020.

    Article  Google Scholar 

  29. N. Hovakimyan, B. J. Yang, and A. J. Calise, “Adaptive output feedback control methodology applicable to non-minimum phase nonlinear systems,” Automatica, vol. 42, no. 4, pp. 513–522, 2006.

    Article  MathSciNet  MATH  Google Scholar 

  30. H. Ting, J. Chang, and Y. Chen, “Proportional-derivative unknown input observer design using descriptor system approach for non-minimum phase systems,” International Journal of Control, Automation, and Systems, vol. 9, no. 5, pp. 850–856, 2011.

    Article  Google Scholar 

  31. S. P. Kruglov, “Adaptive control of a non-minimal-phase scalar object of the second order with the provision of specified characteristics of the transient process,” Scientific Bulletin of the Novosibirsk State Technical University, vol. 65, no. 4, pp. 33–53, 2016.

    Article  MathSciNet  Google Scholar 

  32. S. Yadav, S. K. Verma, and S. K. Nagar, “Design of an optimized PID controller for non-minimum phase system with delay,” Proc. of 39th National Systems Conference (NSC), IEEE, pp. 1–4, 2015.

  33. N. H. Jo, H. Shim, and Y. I. Son, “Disturbance observer for non-minimum phase linear systems,” International Journal of Control, Automation, and Systems, vol. 8, no. 5, pp. 994–1002, 2010.

    Article  Google Scholar 

  34. A. V. Medvedev, A. V. Raskina, E. A. Chzhan, A. A. Korneeva, and C. A. Videnin, “Determination of the order of stochastically linear dynamic systems by using non-parametric estimation of a regression function,” Journal of Physics: Conference Series — IOP Publishing, vol. 1399, no. 3, pp. 33–90, 2019.

    Google Scholar 

  35. A. L. Fradkov, B. Andrievsky, and M. S. Ananyevskiy, “Passification based synchronization of nonlinear systems under communication constraints and bounded disturbances,” Automatica, vol. 55, pp. 287–293, 2015.

    Article  MathSciNet  MATH  Google Scholar 

  36. W. K. Härdle and L. Simar, Applied Multivariate Statistical Analysis, Springer International Publishing, p. 581, 2019.

  37. J. Franke, W. K. Härdle, and C. M. Hafner, “Non-parametric and flexible time series estimators,” Statistics of Financial Markets, Springer, Cham, pp. 343–362, 2019.

    Chapter  MATH  Google Scholar 

  38. B. Wittenmark, “Adaptive dual control methods: An overview,” Adaptive Systems in Control and Signal Processing, pp. 67–72, 1995.

  39. D. Li, F. Qian, and P. Fu, “Optimal nominal dual control for discrete-time linear-quadratic Gaussian problems with unknown parameters,” Automatica, vol. 44, no 1, pp. 119–127, January 2008.

    Article  MathSciNet  MATH  Google Scholar 

  40. T. A. N. Heirung, B. E. Ydstie, and B. Foss, “Dual adaptive model predictive control,” Automatica, vol. 80, pp. 340–348, 2017.

    Article  MathSciNet  MATH  Google Scholar 

  41. S. Cao and X. Hu, “Adaptive control for stochastic systems with unknown parameters and input delay,” International Journal of Control and Automation, vol. 9, no. 7, pp. 211–220, 2016.

    Article  Google Scholar 

  42. M. K. Bugeja, S. G. Fabri, and L. Camilleri, “Dual adaptive dynamic control of mobile robots using neural networks,” IEEE Transactions on Systems, Man, and Cybernetics, Part B (Cybernetics), vol. 39, no. 1, pp. 129–141, 2008.

    Article  Google Scholar 

  43. Z. Nemec and R. Matousek, “Optimal criteria for non-minimal phase plants,” International Journal of Electrical and Computer Engineering, vol. 5, no. 11, pp. 1264–1268, 2011.

    Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Siberian Federal University, Svobodny pr., 79, Krasnoyarsk, Russia

    Anastasia Raskina, Ekaterina Chzhan, Darya Yareshchenko & Maria Videnina

Authors
  1. Anastasia Raskina
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Ekaterina Chzhan
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Darya Yareshchenko
    View author publications

    You can also search for this author in PubMed Google Scholar

  4. Maria Videnina
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Anastasia Raskina.

Additional information

The research was carried out within the state assignment of Ministry of Science and Higher Education of the Russian Federation (theme No. FSRZ-2020-0011).

Anastasia Raskina received her Ph.D. degree in computer science in 2018. Her research interests include dual control, adaptive control, and system identification.

Ekaterina Chzhan received her Ph.D. degree in computer science in 2018. Her research interests include data analysis, non-parametric algorithms, and dual control.

Darya Yareshchenko received her Ph.D. degree in computer science in 2020. Her research interests include non-parametric system identification and control algorithms.

Maria Videnina received her Master’s degree in computer science in 2019. Her research interests include data analysis and machine learning.

Publisher’s Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Raskina, A., Chzhan, E., Yareshchenko, D. et al. Non-parametric Dual Control of Non-minimum Phase Linear Dynamic Plant Using Shunt Compensator. Int. J. Control Autom. Syst. 20, 3614–3623 (2022). https://doi.org/10.1007/s12555-021-0254-2

Download citation

  • Received:

  • Revised:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s12555-021-0254-2

Keywords

Search

Navigation