Skip to main content
SpringerLink
Log in

Study of delay-independent decentralized guaranteed cost control for large scale systems

  • Regular Papers
  • Control Applications
  • Published:
International Journal of Control, Automation and Systems Aims and scope Submit manuscript

Abstract

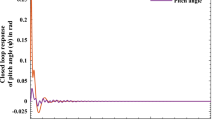
This study introduces delay independent decentralized guaranteed cost control design method based on two controller structures for nonlinear uncertain interconnected large scale systems with time delays. First, a set of equivalent Takagi-Sugeno (T-S) fuzzy models are extended to represent the systems. Then a decentralized state-feedback guaranteed cost performance controller is proposed for the fuzzy systems. Based on delay independent Lyapunov functional approach, some sufficient conditions for the existence of the controller can be cast into the feasible problem of LMIs irrespective of the sizes of the time delays so that the system can be asymptotically stabilized for all considered uncertainties whose sizes are not larger than their bounds. Finally, the minimizing approach is proposed to search the suboptimal upper bound value of guaranteed cost function. Moreover, the corresponding conditions are extended into the generalized dynamic output-feedback close-loop system. Finally, the better control performances of the proposed methods are shown by the simulation examples.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

References

  1. G. L. Yu, B. H. Zhang, H. Xie, B. G. Zou, and L. Y. Wang, “Design of a nonlinear global integrated controller based on wide-area information,” Proc. IEEE Conf. Power System Tech., pp. 23–29, 2006.

  2. S. Xie, L. Xie, Y. Wang, and G. Gao, “Decentralized control of multi-machine power systems with guaranteed performance,” IEE Proc.-Contr. Theory Appl., vol. 47, pp. 355–365, 2000.

    Article  Google Scholar 

  3. Q. Lu, S. W. Mei, W. Hu, F. F. Wu, Y. X. Ni, and T. L. Shen, “Nonlinear decentralized disturbance attenuation excitation control via recursive design for multi-machine power systems,” IEEE Trans. on Power Syst., vol. 16, pp. 729–735, 2001.

    Article  Google Scholar 

  4. Kamwa, R. Grondin, and Y. Hebert, “Wide-area measurement stabilizing control of large power systems- a decentralized /hierarchical approach,” IEEE Trans. on Power Syst., vol. 16, pp. 136–153, 2001.

    Article  Google Scholar 

  5. H. F. Wang, “Multiagent Co-ordination for the secondary voltage control in power system contingencies,” Proc. Inst. Elect. Eng. Generation Transm. Distrib, vol. 148, PP. 61–66, 2001.

    Article  Google Scholar 

  6. H. Hi, G. T. Heydt, and L. Mill, “Power system stability agents using robust wide area control,” IEEE Trans. on Power Syst., vol. 17, pp. 1123–1131, 2002.

    Article  Google Scholar 

  7. V. A. Ugrinovskii, I. R. Petersen, and A.V. Savkin, “Decentralized state-feedback stabilization and robust control of uncertain large-scale system with integrally constrained interconnections,” System & Control Letters, vol. 40, no. 2, pp. 107–119, 2000.

    Article  MathSciNet  MATH  Google Scholar 

  8. W. H. Gui, N. Chen, and M. Wu, “Robust decentralized reliable H ∞ control for uncertain large-scale systems,” Control Theory & Applications, vol. 19, no. 6, pp. 923–926, 2002.

    MathSciNet  MATH  Google Scholar 

  9. C. X. Dou, Q. Q. Jia, S. J. Jin, and Z. Q. Bo, “Delay-independent decentralized stabilizer design for large interconnected power systems based on WAMS,” Int. J. Electrical Power and Energy Syst., vol. 29, pp. 775–782, 2007.

    Article  Google Scholar 

  10. Y. M. Gan and Z. A. Wang, “Decentralized statefeedback robust H ∞ control design for uncertain interconnected large-scale systems,” Control Theory & Applications, vol. 19, no. 2, pp. 997–301, 2002.

    MathSciNet  Google Scholar 

  11. B. Labibi, B. Lohmann, and S. Khaki, “Robust decentralized stabilization of large-scale systems via eigenstructure assignment,” Int. J. of System Science, vol. 34, no. 6, pp. 389–393, 2003.

    Article  MATH  Google Scholar 

  12. Y. Y. Cao, Y. X. Sun, and W. J. Mao, “Outputfeedback decentralized stabilization: ILMI approach,” System & Control Letters, vol. 35, no. 3, pp. 183–194, 1998.

    Article  MathSciNet  MATH  Google Scholar 

  13. S. C. Tong, S. Tong, and Q. L. Zhang, “Robust stabilization of nonlinear time-delay interconnected systems via decentralized fuzzy control,” International Journal of Innovative Computing Information and Control, vol. 4, no. 7, pp. 1567–1582, 2008.

    MathSciNet  Google Scholar 

  14. G. S. Zhai, M. Ikeda, and Y. Fujisaki, “Decentralized H ∞ controller design: a matrix inequality approach using a homotopy method,” Automatica, vol. 37, no. 4, pp. 565–572, 2001.

    Article  MathSciNet  MATH  Google Scholar 

  15. M. Kown and J. H. Park, “Decentralized guaranteed cost control for uncertain large-scale systems using delayed feedback: LMI optimization approach,” Journal of Optimization Theory and Applications, vol. 129, no. 3, pp. 391–414, 2006.

    Article  MathSciNet  MATH  Google Scholar 

  16. R. J. Wang, “Nonlinear decentralized state feedback controller for uncertain fuzzy time-delay interconnected systems,” Fuzzy Sets and Systems, vol. 151, no. 1, pp. 191–204, 2005.

    Article  MathSciNet  MATH  Google Scholar 

  17. C. P. Guan and C. L. Chen, “Delay-dependent guaranteed cost control for T-S fuzzy systems with time delays,” IEEE Trans. on Fuzzy Syst., vol. 12, no. 2, pp. 236–248, 2004.

    Article  MATH  Google Scholar 

  18. Y. Zhang and A. H. Pheng, “Stability of fuzzy control systems with bounded uncertain delays,” IEEE Trans. on Fuzzy Syst., vol. 10, pp. 92–96, 2002.

    Article  MATH  Google Scholar 

  19. H. J. Lee, J. B. Park, and G. R. Chen, “Robust fuzzy control of nonlinear systems with parametric uncertainties,” IEEE Trans. on Fuzzy Syst., vol. 9, pp. 369–379, 2001.

    Article  Google Scholar 

  20. X. W. Liu and H. B. Zhang, “Delay-dependent robust stability of uncertain fuzzy large-scale systems with time-varying delays,” Automatica, vol. 44, no. 1, pp. 193–198, 2008.

    Article  MathSciNet  MATH  Google Scholar 

  21. H. B. Zhang and J. B. Yu, “LMI-based stability analysis of fuzzy large-scale systems with time delays,” Chaos Solitons and Fractals, vol. 25, no. 5, pp. 1193–1207, 2005.

    Article  MathSciNet  MATH  Google Scholar 

  22. C. Lin, Q. G. Wang, and T. H. Lee, “Less conservative stability conditions for fuzzy large-scale systems with time delays,” Chaos Solitons and Fractals, vol. 29, no. 5, pp. 1141–1154, 2006.

    Article  MathSciNet  Google Scholar 

  23. M. Kown and J. H. Park, “Guaranteed cost control for uncertain large-scale systems with time-delays via delayed feedback,” Chaos Solitons and Fractals, vol. 27, no. 3, pp. 800–812, 2006.

    Article  MathSciNet  Google Scholar 

  24. J. Q. Sun, K. Fujimoto, C. X. Dou, J. Q. Zhang, and S. W. Yuan, “H ∞ fuzzy tracking control for multimachine interconnected power system with model uncertainties,” International Journal of Innovative Computing Information and Control, vol. 2, no. 1, pp. 61–68, 2006.

    Google Scholar 

  25. V. A. Ugrinovskii, I. R. Petersen, and A.V. Savkin, “Decentralized state-feedback stabilization and robust control of uncertain large-scale system with integrally constrained interconnections,” System & Control Letters, vol. 40, no. 2, pp.107–119, 2000.

    Article  MathSciNet  MATH  Google Scholar 

  26. J. W. Cai, S. S. Hu, and H. F. Tao, “Fuzzy static output-feedback guaranteed cost reliable control for uncertain nonlinear systems with time-delay,” International Journal of Innovative Computing Information and Control, vol. 4, no. 12, pp. 3409–3420, 2008.

    Google Scholar 

  27. R. Petersen and C. V. Hollot, “A riccati equation approach to the stabilization of uncertain linear systems,” Automatica, vol. 22, no. 4, pp. 397–411, 1986.

    Article  MathSciNet  MATH  Google Scholar 

  28. S. Boyd, L. E. Ghaoui, E. Feron, and V. Balakrishan, “Linear Matrix inequality in system and control theory,” SIAM Studies in Applied Mathematics, Philadelphia: SIAM, 1994.

    Google Scholar 

  29. N. Yadaiah and R. N. Venkata, “Linearisation of multi- machine power system: modeling and control- a survey,” Int. J. Electrical Power and Energy Syst., vol. 29, pp. 297–311, 2007.

    Article  Google Scholar 

Download references

Author information

Authors and Affiliations

  1. College of Engineering, Peking University, Beijing, 100871, China

    Chun-Xia Dou

  2. Institute of Electrical Engineering, Yanshan University, Qinhuangdao City, 066004, P. R. China

    Chun-Xia Dou, Xing-Bei Jia & Pei-Feng Niu

  3. State Key Laboratory for Turbulence and Complex Systems and Dept. of Mechanics and Aerospace Engineering, College of Engineering, Peking University, Beijing, 100871, P. R. China

    Zhi-Sheng Duan

Authors
  1. Chun-Xia Dou
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Zhi-Sheng Duan
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Xing-Bei Jia
    View author publications

    You can also search for this author in PubMed Google Scholar

  4. Pei-Feng Niu
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Zhi-Sheng Duan.

Additional information

Recommended by Editorial Board member Ju Hyun Park under the direction of Editor Young Il Lee. This work is supported by the National Science Foundation of China under Grant 60874023 & 60974078 and the National Science Foundation of Hebei Province under Grant F2010001318.

Chun-Xia Dou received her B.S., M.S. and Ph.D. degrees from the Yanshan University, Qinhuangdao, China. She is currently a postdoctoral student at College of Engineering, Peking University, Beijing, China and is also a professor at the Institute of Electrical Engineering, Yanshan University. Her research interests include nonlinear robust control, adaptive control, fuzzy control, stability of wide-area power systems.

Zhi-Sheng Duan received his B.S. degree from the Inner Mongolia Normal University, an M.S. degree from Inner Mongolia University, and a Ph.D. degree from Peking University, Beijing, China. He is currently a professor at State Key Laboratory for Turbulence and Complex Systems and Department of Mechanics and Aerospace Engineering, College of Engineering, Peking University, Beijing, China. His research interests include stabilization of interconnected systems and robust control for complex large systems.

Xing-Bei Jia is currently pursuing a M.S. in the Institute of Electrical Engineering, Yanshan University, Qinhuangdao, China. Her research interests include nonlinear robust control, adaptive control, and transient stability control for power systems.

Pei-Feng Niu received his B.S. and M.S. degrees from the Northeast Electric Power University, Jilin, China, and his Ph.D. degree from Northeast University, Shenyang, China. He is currently a professor at the Institute of Electrical Engineering, Yanshan University, Qinhuangdao, China. His research interests include nonlinear robust control, adaptive control, fuzzy control, stabilization of large scale power systems.

Rights and permissions

Reprints and permissions

About this article

Cite this article

Dou, CX., Duan, ZS., Jia, XB. et al. Study of delay-independent decentralized guaranteed cost control for large scale systems. Int. J. Control Autom. Syst. 9, 478–488 (2011). https://doi.org/10.1007/s12555-011-0307-z

Download citation

  • Received:

  • Revised:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s12555-011-0307-z

Keywords

Search

Navigation