Return window decision for modular mass customization products in a two-echelon returnable supply chain

Abstract

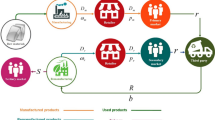
This paper considers a two-echelon returnable supply chain in which a manufacturer sells modular mass customization (MC) products via a retailer to rapidly satisfy the individual needs of consumers. The retailer offers consumers full refund when the unsuitable MC products are returned within a certain return window, and meanwhile the manufacturer provides the retailer with two return polices: no return and full return with partial or full refund. We explore how the manufacturer’s modular design and return policy affect the retailer’s optimal return window. With a wholesale price contract, we also compare the return window and consumer welfare between different supply chain systems. To the best of our knowledge, this is the first paper to study the return window for customized products. Findings show that as the modularity level increases, the return window tends towards the upper bound, which implies that modular design enables MC firms to lengthen return window. Compared to the centralized system, the decentralized system can offer a longer return window, but it fails in generating greater consumer welfare due to high retail price and low modularity level. This suggests that the resale channel may be better for the speculative consumers who just want to experience the customized products, whereas the direct sales channel may be better for the personalized consumers who seek better customized services. We also extend the model to the retailer’s partial refund policy to check the robustness, and apply a two-part tariff contract to coordinate the decentralized system. Numerical experiments verify the theoretical results.

Appendix

Proof of Lemma 1

In the centralized system, all decisions are decided by the supply chain, and whether the game sequence is simultaneous or sequential makes no mathematical difference. For interpretational convenience, we use the sequential game.

Since $\frac{{\partial }^{2}{\pi }_{s}^{C}}{\partial {p}^{2}}=-\frac{2{\left[1-\left(1-\beta \right)T\right]}^{2}}{\beta m}<0$, ${\pi }_{s}^{C}$ is strictly concave for $p$. Solving $\frac{\partial {\pi }_{s}^{C}}{\partial p}=0$, we obtain ${p}^{C0}=\frac{\beta m-\left(1-\beta \right)Tmv}{2[1-\left(1-\beta \right)T]}$ and ${D}^{C0}=\frac{\beta +\left(1-\beta \right)Tv}{2\beta }$. The supply chain profit can be rewritten as follows: ${\pi }_{s}^{C}=\frac{m{[\beta +\left(1-\beta \right)Tv]}^{2}}{4\beta }-k{m}^{2}-\left(1-\beta \right){T}^{2}$, where $\frac{{\partial }^{2}{\pi }_{s}^{C}}{\partial {T}^{2}}=-\frac{\left(1-\beta \right)[4\beta -\left(1-\beta \right)m{v}^{2}]}{2\beta }$. Thus, $\frac{{\partial }^{2}{\pi }_{s}^{C}}{\partial {T}^{2}}<0$ if $m<\frac{4\beta }{\left(1-\beta \right){v}^{2}}$; $\frac{{\partial }^{2}{\pi }_{s}^{C}}{\partial {T}^{2}}>0$ if $m>\frac{4\beta }{\left(1-\beta \right){v}^{2}}$. By solving $\frac{\partial {\pi }_{s}^{C}}{\partial T}=0$, we obtain ${T}^{C0}=\frac{\beta mv}{4\beta -\left(1-\beta \right)m{v}^{2}}$.

• (1) When $m<\frac{4\beta }{\left(1-\beta \right){v}^{2}}$,

  ${\pi }_{s}^{C}$ is strictly concave for $T$ and ${T}^{C0}>0$. (a) if $0<{T}^{C0}<1$ (i.e., $m<\frac{4\beta }{\beta v+\left(1-\beta \right){v}^{2}}$), then the optimal return window ${T}^{C*}={T}^{C0}$, and ${p}^{C*}=\frac{2{\beta }^{2}m-\beta \left(1-\beta \right){m}^{2}{v}^{2}}{4\beta -\left(1-\beta \right)m{v}^{2}-\beta \left(1-\beta \right)mv}$, ${D}^{C*}=\frac{2\beta }{4\beta -\left(1-\beta \right)m{v}^{2}}$, ${CS}^{C*}=\frac{2{\beta }^{3}m}{{[4\beta -\left(1-\beta \right)m{v}^{2}]}^{2}}$; (b) if $1<{T}^{C0}$ (i.e., $\frac{4\beta }{\beta v+\left(1-\beta \right){v}^{2}}<m<\frac{4\beta }{\left(1-\beta \right){v}^{2}}$), then the optimal return window ${T}^{C*}=1$, and ${p}^{C*}=\frac{\beta m-\left(1-\beta \right)mv}{2\beta }$, ${D}^{C*}=\frac{\beta +\left(1-\beta \right)v}{2\beta }$, ${CS}^{C*}=\frac{{[\beta m+\left(1-\beta \right)mv]}^{2}}{8\beta m}$.

• (2) When $\frac{4\beta }{\left(1-\beta \right){v}^{2}}<m$, ${\pi }_{s}^{C}$ is strictly convex for $T$ and ${T}^{C0}<0$. Since $0\le T\le 1$, then ${T}^{C*}=1$, which is the same as in $\frac{4\beta }{\beta v+\left(1-\beta \right){v}^{2}}<m<\frac{4\beta }{\left(1-\beta \right){v}^{2}}$. □

Proof of Corollary 1

The logic for deriving the impacts of modularity level on the optimal pricing and return window decisions is identical for Corollary 1, Corollary 2, and Corollary 3. Thus, we will outline it explicitly for Corollary 1 only.

Due to salvage value loss, the actual salvage value for each returned item cannot exceed the sales revenue for each new product, that is, ${mv<p}^{C*}=\frac{\beta m-\left(1-\beta \right)mv}{2\beta }$. Hence, the parameter $v$ should satisfy $v<\frac{\beta }{1+\beta }$.

• a. if $m<\frac{4\beta }{\beta v+\left(1-\beta \right){v}^{2}}$, then $\frac{\partial {T}^{C*}}{\partial m}=\frac{4v{\beta }^{2}}{{\left(4\beta -\left(1-\beta \right)m{v}^{2}\right)}^{2}}>0$ and $\frac{\partial {p}^{C*}}{\partial m}=\frac{\beta \left({v}^{2}\left(1-\beta \right)\left(\left(1-\beta \right)\left(\beta +v\right)mv-8\beta \right)m+8{\beta }^{2}\right)}{{\left({\beta }^{2}mv+\left(4+\left(2{v}^{2}-v\right)m\right)\beta -m{v}^{2}\right)}^{2}}>0$, where ${v}^{2}\left(1-\beta \right)\left(\left(1-\beta \right)\left(\beta +v\right)mv-8\beta \right)m+8{\beta }^{2}>\frac{8{\beta }^{2}\left(-{\left(1-\beta \right)}^{2}{v}^{2}-2{\beta }^{2}\left(1-\beta \right)v+{\beta }^{2}\right)}{{\left(\left(1-\beta \right)v+\beta \right)}^{2}}$ since $m<\frac{4\beta }{\beta v+\left(1-\beta \right){v}^{2}}$, and $-{\left(1-\beta \right)}^{2}{v}^{2}-2{\beta }^{2}\left(1-\beta \right)v+{\beta }^{2}>0$ because $v<\frac{\beta }{1+\beta }$.

• b. if $\frac{8\beta }{\beta v+\left(1-\beta \right){v}^{2}}<m$, then $\frac{\partial {T}^{C*}}{\partial m}=0$, $\frac{\partial {p}^{C*}}{\partial m}=\frac{\beta -\left(1-\beta \right)v}{2\beta }>0$. □

Similarly, Corollarys 2 and 3 can be proved, which are omitted.

Proof of Lemma 2

For solving the decentralized system, we first derive the retailer’s best response of return window and retail price to the wholesale price.

Since $\frac{{\partial }^{2}{\pi }_{r}^{N}}{\partial {p}^{2}}=-\frac{2{\left[1-\left(1-\beta \right)T\right]}^{2}}{\beta m}<0$, ${\pi }_{r}^{N}$ is strictly concave for $p$. By solving $\frac{\partial {\pi }_{r}^{N}}{\partial p}=0$, we obtain ${p}^{N0}=\frac{\beta m-\left(1-\beta \right)Tmv+w}{2[1-\left(1-\beta \right)T]}$ and ${D}^{N0}=\frac{\beta m+\left(1-\beta \right)Tmv-w}{2\beta m}$. The retailer’s profit function can be rewritten as ${\pi }_{r}^{N}=\frac{{[\beta m+\left(1-\beta \right)Tmv-w]}^{2}}{4\beta m}-\left(1-\beta \right){T}^{2}$, where $\frac{{\partial }^{2}{\pi }_{r}^{N}}{\partial {T}^{2}}=-\frac{\left(1-\beta \right)\left[4\beta -\left(1-\beta \right)m{v}^{2}\right]}{2\beta }$. Thus, $\frac{{\partial }^{2}{\pi }_{r}^{N}}{\partial {T}^{2}}<0$ if $m<\frac{4\beta }{\left(1-\beta \right){v}^{2}}$; $\frac{{\partial }^{2}{\pi }_{r}^{N}}{\partial {T}^{2}}>0$ if $m>\frac{4\beta }{\left(1-\beta \right){v}^{2}}$. By solving $\frac{\partial {\pi }_{r}^{N}}{\partial T}=0$, we obtain ${T}^{N0}=\frac{\beta mv-vw}{4\beta -\left(1-\beta \right)m{v}^{2}}$.

• (1) When $m<\frac{4\beta }{\left(1-\beta \right){v}^{2}}$, ${\pi }_{r}^{N}$ is strictly concave for $T$.

  • (a) if $0<{T}^{N0}\le 1$ (i.e., $\frac{\beta mv-4\beta +\left(1-\beta \right)m{v}^{2}}{v}\le w<\beta m$), then best response of return window ${T}^{N}={T}^{N0}$. Then, the best response of retail price and demand are: ${p}^{N}=\frac{2{\beta }^{2}m-\beta \left(1-\beta \right){m}^{2}{v}^{2}+2\beta w}{4\beta -\left(1-\beta \right)m{v}^{2}-\beta \left(1-\beta \right)mv+\left(1-\beta \right)vw}$ and ${D}^{N}=\frac{2\beta m-2w}{4\beta m-\left(1-\beta \right){m}^{2}{v}^{2}}$.

  • (b) if $1<{T}^{N0}$ (i.e., $w<\frac{\beta mv-4\beta +\left(1-\beta \right)m{v}^{2}}{v}$), the best response of return window ${T}^{N}=1$. Similarly, ${p}^{N}=\frac{\beta m-\left(1-\beta \right)mv+w}{2\beta }$ and ${D}^{N}=\frac{\beta m+\left(1-\beta \right)mv-w}{2\beta m}$.

  • (c) if ${T}^{N0}\le 0$ (i.e., $\beta m\le w$), the best response of return window ${T}^{N}=0$, and then ${p}^{N}=\frac{\beta m+w}{2}$ and ${D}^{N}=\frac{\beta m-w}{2\beta m}$. Due to the demand ${D}^{N}=\frac{\beta m-w}{2\beta m}<0$ under the condition of $\beta m\le w$, we exclude the case (c).

• (2) When $m>\frac{4\beta }{\left(1-\beta \right){v}^{2}}$, ${\pi }_{r}^{N}$ is strictly convex for $T$.

  • (a) if $0<{T}^{N0}<1$ (i.e., $\beta m<w<\frac{\beta mv-4\beta +\left(1-\beta \right)m{v}^{2}}{v}$). ${\pi }_{r}^{N}\left(T=0\right)-{\pi }_{r}^{N}\left(T=1\right)=\frac{\left(1-\beta \right)[-2\beta mv-\left(1-\beta \right)m{v}^{2}+2wv+4\beta ]}{4\beta }$. We find that: if $\frac{2\beta mv-4\beta +\left(1-\beta \right)m{v}^{2}}{2v}<w$, then ${\pi }_{r}^{N}\left(T=0\right)>{\pi }_{r}^{N}\left(T=1\right)$; if $w<\frac{2\beta mv-4\beta +\left(1-\beta \right)m{v}^{2}}{2v}$, then ${\pi }_{r}^{N}\left(T=0\right)<{\pi }_{r}^{N}\left(T=1\right)$. Thus, when $\frac{2\beta mv-4\beta +\left(1-\beta \right)m{v}^{2}}{2v}\le w<\frac{\beta mv-4\beta +\left(1-\beta \right)m{v}^{2}}{v}$, the best response of return window ${T}^{N}=0$. Similarly, according to ${D}^{N0}$, we can obtain the best response of demand ${D}^{N}=\frac{\beta m-w}{2\beta m}<0$, and thus we exclude this case. When $\beta m<w<\frac{2\beta mv-4\beta +\left(1-\beta \right)m{v}^{2}}{2v}$, the best response of return window ${T}^{N}=1$, and then ${p}^{N}=\frac{\beta m-\left(1-\beta \right)mv+w}{2}$ and ${D}^{N}=\frac{\beta m+\left(1-\beta \right)mv-w}{2\beta m}$.

  • (b) if ${T}^{N0}\le 0$ (i.e., $w\le \beta m$), the best response of return window ${T}^{N}=1$, and then ${p}^{N}=\frac{\beta m-\left(1-\beta \right)mv+w}{2}$ and ${D}^{N}=\frac{\beta m+\left(1-\beta \right)mv-w}{2\beta m}$.

  • (c) if $1\le {T}^{N0}$ (i.e., $\frac{\beta mv-4\beta +\left(1-\beta \right)m{v}^{2}}{v}\le w$), the best response of return window ${T}^{N}=0$, thus ${p}^{N}=\frac{\beta m+w}{2}$ and ${D}^{N}=\frac{\beta m-w}{2\beta m}$. Due to the demand ${D}^{N}=\frac{\beta m-w}{2\beta m}<0$ under the condition of $\beta m\le w$, we exclude the case (c).

To sum up, the best response functions in Model N are as follows: (1) When $m<\frac{4\beta }{\left(1-\beta \right){v}^{2}}$, if $\underset{\_}{w}\le w<\beta m$, then ${T}^{N}=\frac{\beta mv-vw}{4\beta -\left(1-\beta \right)m{v}^{2}}$, ${p}^{N}=\frac{2{\beta }^{2}m-\beta \left(1-\beta \right){m}^{2}{v}^{2}+2\beta w}{4\beta -\left(1-\beta \right)m{v}^{2}-\beta \left(1-\beta \right)mv+\left(1-\beta \right)vw}$, and ${D}^{N}=\frac{2\beta m-2w}{4\beta m-\left(1-\beta \right){m}^{2}{v}^{2}}$; if $w<\underset{\_}{w}$, then ${T}^{N}=1$, ${p}^{N}=\frac{\beta m-\left(1-\beta \right)mv+w}{2\beta }$, and ${D}^{N}=\frac{\beta m+\left(1-\beta \right)mv-w}{2\beta m}$. (2) When $m>\frac{4\beta }{\left(1-\beta \right){v}^{2}}$, if $w<\overline{w}$, then ${T}^{N}=1$, ${p}^{N}=\frac{\beta m-\left(1-\beta \right)mv+w}{2}$, and ${D}^{N}=\frac{\beta m+\left(1-\beta \right)mv-w}{2\beta m}$. Where $\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{w} = \frac{{\beta mv - 4\beta + \left( {1 - \beta } \right)mv^{2} }}{v}$ and $\overline{w}=\frac{2\beta mv-4\beta +\left(1-\beta \right)m{v}^{2}}{2v}$.

Second, according to the above best response, we derive the optimal wholesale price.

• (1) When $m<\frac{4\beta }{\left(1-\beta \right){v}^{2}}$,

  • (a) if $\underset{\_}{w}\le w<\beta m$, then ${\pi }_{m}^{N}=\frac{2\beta mw-2{w}^{2}}{4\beta m-\left(1-\beta \right){m}^{2}{v}^{2}}-k{m}^{2}$. Since $\frac{{\partial }^{2}{\pi }_{m}^{N}}{\partial {w}^{2}}=-\frac{4}{4\beta m-\left(1-\beta \right){m}^{2}{v}^{2}}<0$, ${\pi }_{m}^{N}$ is strictly concave for $w$. By solving $\frac{\partial {\pi }_{m}^{N}}{\partial w}=0$, we obtain ${w}_{1}^{N}=\frac{\beta m}{2}$. Then, we can obtain the optimal wholesale price: if $m<\frac{8\beta }{\beta v+2\left(1-\beta \right){v}^{2}}$, then ${w}^{N*}={w}_{1}^{N}$; if $m>\frac{8\beta }{\beta v+2\left(1-\beta \right){v}^{2}}$, then ${w}^{N*}=\underset{\_}{w}$.

  • (b) if $w<\underset{\_}{w}$, then ${\pi }_{m}^{N}=\frac{[\beta m+\left(1-\beta \right)mv]w-{w}^{2}}{2\beta m}-k{m}^{2}$. Since $\frac{{\partial }^{2}{\pi }_{m}^{N}}{\partial {w}^{2}}=-\frac{1}{\beta m}<0$, ${\pi }_{m}^{N}$ is strictly concave for $w$. By solving $\frac{\partial {\pi }_{m}^{N}}{\partial w}=0$, we obtain ${w}_{2}^{N}=\frac{\beta m+\left(1-\beta \right)mv}{2}$. Then, we can obtain the optimal wholesale price: if $m<\frac{8\beta }{\beta v+\left(1-\beta \right){v}^{2}}$, then ${w}^{N*}=\underset{\_}{w}$; if $m>\frac{8\beta }{\beta v+\left(1-\beta \right){v}^{2}}$, then ${w}^{N*}={w}_{2}^{N}$.

• (2) When $m>\frac{4\beta }{\left(1-\beta \right){v}^{2}}$,

  If $w<\overline{w}$, ${\pi }_{m}^{N}=\frac{[\beta m+\left(1-\beta \right)mv]w-{w}^{2}}{2\beta m}-k{m}^{2}$, then $\frac{{\partial }^{2}{\pi }_{m}^{N}}{\partial {w}^{2}}=-\frac{1}{\beta m}<0$. Thus, ${\pi }_{m}^{N}$ is strictly concave for $w$. By solving $\frac{\partial {\pi }_{m}^{N}}{\partial w}=0$, we obtain ${w}_{2}^{N}=\frac{\beta m+\left(1-\beta \right)mv}{2}$. We can obtain the optimal wholesale price: if $m>\frac{4\beta }{\left(1-\beta \right){v}^{2}}$, then ${w}^{N*}={w}_{2}^{N}$.

As a result, equilibrium solutions in Model N: if $m<\frac{8\beta }{\beta v+2\left(1-\beta \right){v}^{2}}$, then ${w}^{N*}=\frac{\beta m}{2}$, ${p}^{N*}=\frac{6{\beta }^{2}m-2\beta \left(1-\beta \right){m}^{2}{v}^{2}}{8\beta -2\left(1-\beta \right)m{v}^{2}-\beta \left(1-\beta \right)mv}$, ${T}^{N*}=\frac{\beta mv}{8\beta -2\left(1-\beta \right)m{v}^{2}}$, ${D}^{N*}=\frac{\beta }{4\beta -\left(1-\beta \right)m{v}^{2}}$, ${\pi }_{m}^{N*}=\frac{{\beta }^{2}m-k{m}^{2}\left(8\beta -2\left(1-\beta \right)m{v}^{2}\right)}{8\beta -2\left(1-\beta \right)m{v}^{2}}$, ${\pi }_{r}^{N*}=\frac{4{\beta }^{3}m-{\beta }^{2}\left(1-\beta \right){m}^{2}{v}^{2}}{4{[4\beta -\left(1-\beta \right)m{v}^{2}]}^{2}}$, and ${CS}^{N*}=\frac{{\beta }^{3}m}{2{[4\beta -\left(1-\beta \right)m{v}^{2}]}^{2}}$; if $\frac{8\beta }{\beta v+2\left(1-\beta \right){v}^{2}}<m<\frac{8\beta }{\beta v+\left(1-\beta \right){v}^{2}}$, then ${w}^{N*}=\frac{\beta mv-4\beta +\left(1-\beta \right)m{v}^{2}}{v}$, ${p}^{N*}=\frac{mv-2}{v}$, ${T}^{N*}=1$, ${D}^{N*}=\frac{2}{mv}$, ${\pi }_{m}^{N*}=\frac{2\beta mv-8\beta +2\left(1-\beta \right)m{v}^{2}-k{m}^{3}{v}^{2}}{m{v}^{2}}$, ${\pi }_{r}^{N*}=\frac{4\beta -\left(1-\beta \right)m{v}^{2}}{m{v}^{2}}$, and ${CS}^{N*}=\frac{2\beta }{m{v}^{2}}$; if $\frac{8\beta }{\beta v+\left(1-\beta \right){v}^{2}}<m$, then ${w}^{N*}=\frac{\beta m+\left(1-\beta \right)mv}{2}$, ${p}^{N*}=\frac{3\beta m-\left(1-\beta \right)mv}{4\beta }$, ${T}^{N*}=1$, ${D}^{N*}=\frac{\beta +\left(1-\beta \right)v}{4\beta }$, ${\pi }_{m}^{N*}=\frac{{[\beta +\left(1-\beta \right)v]}^{2}m-8\beta k{m}^{2}}{8\beta }$, ${\pi }_{r}^{N*}=\frac{{[\beta +\left(1-\beta \right)v]}^{2}m-16\beta \left(1-\beta \right)}{16\beta }$, and ${CS}^{N*}=\frac{{[\beta m+\left(1-\beta \right)mv]}^{2}}{32\beta m}$. □

Proof of Lemma 3

We first derive the retailer’s best response of return window and retail price to the wholesale price. Since $\frac{{\partial }^{2}{\pi }_{r}^{F}}{\partial {p}^{2}}=-\frac{2{\left[1-\lambda \left(1-\beta \right)T\right]}^{2}}{\beta m}<0$, ${\pi }_{r}^{F}$ is strictly concave for $p$. By solving $\frac{\partial {\pi }_{r}^{F}}{\partial p}=0$, we obtain ${p}^{F0}=\frac{\beta m+\left[1-\lambda \left(1-\beta \right)T\right]w}{2[1-\left(1-\beta \right)T]}$ and ${D}^{F0}=\frac{\beta m-\left[1-\lambda \left(1-\beta \right)T\right]w}{2\beta m}$. The retailer’s profit function can be rewritten as ${\pi }_{r}^{F}=\frac{{[\beta m-\left(1-\lambda \left(1-\beta \right)T\right)w]}^{2}}{4\beta m}$ where $\frac{{\partial }^{2}{\pi }_{r}^{F}}{\partial {T}^{2}}=\frac{{\left[\lambda \left(1-\beta \right)w\right]}^{2}}{2\beta m}>0$. Thus, ${\pi }_{r}^{F}$ is strictly convex for $T$. By solving $\frac{\partial {\pi }_{r}^{F}}{\partial T}=0$, we obtain ${T}^{F0}=\frac{W-\beta m}{\lambda \left(1-\beta \right)w}$.

Proof of Corollary 4

Note that, when the modularity level is exogenous, the optimal return window in Model C is as follows: if $m<\frac{4\beta }{\beta v+\left(1-\beta \right){v}^{2}}$, then ${T}^{C*}=\frac{\beta mv}{4\beta -\left(1-\beta \right)m{v}^{2}}$; otherwise, ${T}^{C*}=1$, where $1-\frac{\beta mv}{4\beta -\left(1-\beta \right)m{v}^{2}}>0$ under $m<\frac{4\beta }{\beta v+\left(1-\beta \right){v}^{2}}$. The optimal return window in Model F is always ${T}^{F*}=1$. Thus, ${T}^{C*}<{T}^{F*}$ under $m<\frac{4\beta }{\beta v+\left(1-\beta \right){v}^{2}}$. □

Proof of Corollary 5

• (1) when $m<\frac{4\beta }{\beta v+\left(1-\beta \right){v}^{2}}$,

  ${p}^{N*}-{p}^{C*}=\frac{\left(4\beta -\left(1-\beta \right)m{v}^{2}\right)\left(2-\left(1-\beta \right)mv\right)m{\beta }^{2}}{\left(8\beta -2\left(1-\beta \right)m{v}^{2}-\beta \left(1-\beta \right)mv\right)\left(4\beta -\left(1-\beta \right)m{v}^{2}-\beta \left(1-\beta \right)mv\right)}>0$, where $4\beta -\left(1-\beta \right)m{v}^{2}>\frac{4{\beta }^{2}}{\left(1-\beta \right)v+\beta }>0$ and $2-\left(1-\beta \right)mv>2{\beta }^{2}$ since $m<\frac{4\beta }{\beta v+\left(1-\beta \right){v}^{2}}$ and $v<\frac{\beta }{1+\beta }$.

• (2) when $\frac{4\beta }{\beta v+\left(1-\beta \right){v}^{2}}<m<\frac{8\beta }{\beta v+2\left(1-\beta \right){v}^{2}}$,

  $${p}^{N*}-{p}^{C*}=\frac{m\left(\left(-2\left(1-\beta \right){v}^{2}+\beta \left(1-3\beta \right)v+{\beta }^{2}\right)\left(1-\beta \right)mv+4\beta \left(2\left(1-\beta \right)v+\left(3\beta -2\right)\beta \right)\right)}{2\beta \left(8\beta -2\left(1-\beta \right)m{v}^{2}-\beta \left(1-\beta \right)mv\right)}$$
  $$>\frac{2 m\beta \left(v\left(1-\beta \right)+\beta \left(2\beta -1\right)\right)}{\left(\left(1-\beta \right)v+\beta \right)\left(8\beta -2\left(1-\beta \right)m{v}^{2}-\beta \left(1-\beta \right)mv\right)}>0, \text{w}\text{h}\text{e}\text{r}\text{e} \left(-2\left(1-\beta \right){v}^{2}+\beta \left(1-3\beta \right)v+{\beta }^{2}\right)>\frac{2{\beta }^{3}\left(1-\beta \right)}{{\left(1+\beta \right)}^{2}}>0 \text{s}\text{i}\text{n}\text{c}\text{e} v<\frac{\beta }{1+\beta }.$$

• (3) when $\frac{8\beta }{\beta v+2\left(1-\beta \right){v}^{2}}<m<\frac{8\beta }{\beta v+\left(1-\beta \right){v}^{2}}$,

  $${p}^{N*}-{p}^{C*}=\frac{mv-2}{v}-\frac{\beta m-\left(1-\beta \right)mv}{2\beta }=\frac{\left(\left(1-\beta \right)v+\beta \right)mv-4\beta }{2\beta v}>\frac{2\beta }{v\left(2\left(1-\beta \right)v+\beta \right)}>0.$$

• (4) when $\frac{8\beta }{\beta v+\left(1-\beta \right){v}^{2}}<m$,

  $${p}^{N*}-{p}^{C*}=\frac{3\beta m-\left(1-\beta \right)mv}{4\beta }-\frac{\beta m-\left(1-\beta \right)mv}{2\beta }=\frac{\left(\left(1-\beta \right)v+\beta \right)m}{4\beta }>0.$$

  Thus, we can conclude that ${p}^{C*}<{p}^{N*}$. Similarly, ${p}^{C*}<{p}^{F*}$, ${{CS}^{C*}>CS}^{N*}$, ${{CS}^{C*}>CS}^{F*}$, ${D}^{C*}>{D}^{N*}$, and ${D}^{C*}>{D}^{F*}$ can be derived. □

Proof of Corollary 6

• (1) when $m<\frac{8\beta }{\beta v+2\left(1-\beta \right){v}^{2}}$,

  $${\pi }_{m}^{N*}-{\pi }_{m}^{F*}=\frac{\left(1-\beta \right)\left[\beta mv\left(24\beta +\beta mv-6\left(1-\beta \right)m{v}^{2}\right)+4\beta \left(8\beta -3\left(1-\beta \right)m{v}^{2}\right)+{\left(1-\beta \right)}^{2}{m}^{2}{v}^{4}\right]}{4\beta \left[8\beta -2\left(1-\beta \right)m{v}^{2}\right]}>0.$$

• (2) when $\frac{8\beta }{\beta v+2\left(1-\beta \right){v}^{2}}<m<\frac{8\beta }{\beta v+\left(1-\beta \right){v}^{2}}$,

  $${\pi }_{m}^{N*}-{\pi }_{m}^{F*}=\frac{\left[16{\beta }^{2}v+24\beta \left(1-\beta \right){v}^{2}\right]m+\left[6\beta \left(1-\beta \right){v}^{3}-{\beta }^{2}{v}^{2}-{\left(1-\beta \right)}^{2}{v}^{4}\right]{m}^{2}-64{\beta }^{2}}{8\beta m{v}^{2}}$$
  $$>\frac{8\beta \left(1-\beta \right)[9\beta +\left(1-\beta \right)v]}{{[\beta -2\left(1-\beta \right)v]}^{2}mv}>0.$$

• (3) when

  $$\frac{8\beta }{\beta v+\left(1-\beta \right){v}^{2}}<m, {\pi }_{m}^{N*}-{\pi }_{m}^{F*}=\left(1-\beta \right)>0.$$

  Thus, ${\pi }_{m}^{N*}>{\pi }_{m}^{F*}$. Similarly, we can obtain that ${\pi }_{r}^{F*}>{\pi }_{r}^{N*}$. □

Proof of Lemma 4

To ensure the concavity of profit function, we assume $\frac{{v}^{2}\left(1-\beta \right){[\beta +\left(1-\beta \right)v]}^{3}}{{16\beta }^{3}}<k$. We first derive the optimal modularity level in Model C: when $m<\frac{4\beta }{\beta v+\left(1-\beta \right){v}^{2}}$, $\frac{\partial {\pi }_{s}^{C}}{\partial m}=\frac{4{\beta }^{3}}{{[4\beta -\left(1-\beta \right)m{v}^{2}]}^{2}}-2 km$. Then $\frac{{\partial }^{2}{\pi }_{s}^{C}}{\partial {m}^{2}}=\frac{8{\beta }^{3}\left(1-\beta \right){v}^{2}}{{[4\beta -\left(1-\beta \right)m{v}^{2}]}^{3}}-2k<0$ and thus ${\pi }_{s}^{C}$ is strictly concave for $m$. By solving $\frac{\partial {\pi }_{s}^{C}}{\partial m}=0$, the optimal modularity level ${m}^{C*}=\frac{\beta \left(8kX-{X}^{2}-16{k}^{2}\right)}{3\left(1-\beta \right)k{v}^{2}X}$, where $X={\left[{k}^{2}\left(\beta x-x+27\beta {v}^{2}-27{v}^{2}+64k\right)\right]}^{\frac{1}{3}}$ and $x=3v\sqrt{\frac{81\beta {v}^{2}-81{v}^{2}+384k}{\beta -1}}$; when $\frac{4\beta }{\beta v+\left(1-\beta \right){v}^{2}}<m$, $\frac{\partial {\pi }_{s}^{C}}{\partial m}=\frac{{[\beta +\left(1-\beta \right)v]}^{2}}{4\beta }-2 km$. Then $\frac{{\partial }^{2}{\pi }_{s}^{C}}{\partial {m}^{2}}=-2k<0$ and thus ${\pi }_{s}^{C}$ is strictly concave for $m$. By solving $\frac{\partial {\pi }_{s}^{C}}{\partial m}=0$, the optimal modularity level ${m}^{C*}=\frac{{[\beta +\left(1-\beta \right)v]}^{2}}{8\beta k}$. Hence, for Model C, the optimal decisions under endogenous modularity level are as follows: (1) when $\frac{v{[\beta +\left(1-\beta \right)v]}^{3}}{{32\beta }^{2}}<k$, then ${m}^{C*}=\frac{\beta (8kX-{X}^{2}-16{k}^{2})}{3(1-\beta )k{v}^{2}X}$, ${p}^{C*}=\frac{2{\beta }^{2}{m}^{C*}-\beta \left(1-\beta \right){{m}^{C*}}^{2}{v}^{2}}{4\beta -\left(1-\beta \right){m}^{C*}{v}^{2}-\beta \left(1-\beta \right){m}^{C*}v}$, and ${T}^{C*}=\frac{\beta {m}^{C*}v}{4\beta -\left(1-\beta \right){m}^{C*}{v}^{2}}$; (2) when $\frac{{v}^{2}\left(1-\beta \right){[\beta +\left(1-\beta \right)v]}^{3}}{{16\beta }^{3}}<k<\frac{v{[\beta +\left(1-\beta \right)v]}^{3}}{{32\beta }^{2}}$, then ${m}^{C*}=\frac{{[\beta +\left(1-\beta \right)v]}^{2}}{8\beta k}$, ${p}^{C*}=\frac{\beta {m}^{C*}-\left(1-\beta \right){m}^{C*}v}{2\beta }$, and ${T}^{C*}=1$.

Similarly, for Model N, the optimal decisions under endogenous modularity level are as follows: (1) when $\frac{v{[\beta +2\left(1-\beta \right)v]}^{3}}{{128\beta }^{2}}<k$, then ${m}^{N*}=\frac{\beta (48kY-{Y}^{2}-64{k}^{2})}{6\left(1-\beta \right)k{v}^{2}Y}$, ${w}^{N*}=\frac{\beta {m}^{N*}}{2}$, ${p}^{N*}=\frac{6{\beta }^{2}{m}^{N*}-2\beta \left(1-\beta \right){{m}^{N*}}^{2}{v}^{2}}{8\beta -2\left(1-\beta \right){m}^{N*}{v}^{2}-\beta \left(1-\beta \right){m}^{N*}v}$, and ${T}^{N*}=\frac{\beta {m}^{N*}v}{8\beta -2\left(1-\beta \right){m}^{N*}{v}^{2}}$; (2) when $\frac{v{[\beta +\left(1-\beta \right)v]}^{3}}{{128\beta }^{2}}<k<\frac{v{[\beta +2\left(1-\beta \right)v]}^{3}}{{128\beta }^{2}}$, then ${m}^{N*}=\sqrt[3]{\frac{4\beta }{k{v}^{2}}}$, ${w}^{N*}=\frac{\beta {m}^{N*}v-4\beta +\left(1-\beta \right){m}^{N*}{v}^{2}}{v}$, ${p}^{N*}=\frac{{m}^{N*}v-2}{v}$, and ${T}^{N*}=1$; (3) when $\frac{{v}^{2}\left(1-\beta \right){[\beta +\left(1-\beta \right)v]}^{3}}{{16\beta }^{3}}<k<\frac{v{[\beta +\left(1-\beta \right)v]}^{3}}{{128\beta }^{2}}$, then ${m}^{N*}=\frac{{[\beta +\left(1-\beta \right)v]}^{2}}{16\beta k}$, ${w}^{N*}=\frac{\beta {m}^{N*}+\left(1-\beta \right){m}^{N*}v}{2}$, ${p}^{N*}=\frac{3\beta {m}^{N*}-\left(1-\beta \right){m}^{N*}v}{4\beta }$, and ${T}^{N*}=1$.

For Model F, the optimal decisions under endogenous modularity level are as follows: ${m}^{F*}=\frac{{[\beta -\left(1-\beta \right)v]}^{2}-4\beta \left(1-\beta \right)v}{16\beta k}$, ${w}^{F*}=\frac{\beta {m}^{F*}-\left(1-\beta \right){m}^{F*}v}{2\beta }$, ${p}^{F*}=\frac{3\beta {m}^{F*}-\left(1-\beta \right){m}^{F*}v}{4\beta }$, and ${T}^{F*}=1$. □

Proof of Corollary 7

When the modularity level is endogenous, the optimal return window in Model C is as follows: if $\frac{v{[\beta +\left(1-\beta \right)v]}^{3}}{{32\beta }^{2}}<k$, then ${T}^{C*}=\frac{\beta {m}^{C*}v}{4\beta -\left(1-\beta \right){m}^{C*}{v}^{2}}$ where ${m}^{C*}=\frac{\beta \left(8kX-{X}^{2}-16{k}^{2}\right)}{3\left(1-\beta \right)k{v}^{2}X}$; otherwise, ${T}^{C*}=1$. Note that, $1-\frac{\beta {m}^{C*}v}{4\beta -\left(1-\beta \right){m}^{C*}{v}^{2}}>0$ under $\frac{v{[\beta +\left(1-\beta \right)v]}^{3}}{{32\beta }^{2}}<k$. The optimal return window in Model F is always ${T}^{F*}=1$. Thus, ${T}^{C*}<{T}^{F*}$ under $\frac{v{[\beta +\left(1-\beta \right)v]}^{3}}{{32\beta }^{2}}<k$. □

Proof of coordination

Under the two-part tariff contract, the retailer’s profit is ${\pi }_{r}^{T}=\left[1-\left(1-\beta \right)T\right]\left(p-w\right)D+\left(1-\beta \right)T\left(vm-w\right)D-\left(1-\beta \right){T}^{2}-F$, where $D=1-\frac{\left[1-\left(1-\beta \right)T\right]p}{\beta m}$. Similar to the proof of Lemma 2, the retailer’s best response is: (1) When $m<\frac{4\beta }{\left(1-\beta \right){v}^{2}}$, if $\underset{\_}{w}\le w<\beta m$, then ${T}^{T}=\frac{\beta mv-vw}{4\beta -\left(1-\beta \right)m{v}^{2}}$, ${p}^{T}=\frac{2{\beta }^{2}m-\beta \left(1-\beta \right){m}^{2}{v}^{2}+2\beta w}{4\beta -\left(1-\beta \right)m{v}^{2}-\beta \left(1-\beta \right)mv+\left(1-\beta \right)vw}$, ${D}^{T}=\frac{2\beta m-2w}{4\beta m-\left(1-\beta \right){m}^{2}{v}^{2}}$, and ${\pi }_{r}^{T}=\frac{{(\beta m-w)}^{2}}{[4\beta -\left(1-\beta \right)m{v}^{2}]m}-F$; if $w<\underset{\_}{w}$, then ${T}^{T}=1$, ${p}^{T}=\frac{\beta m-\left(1-\beta \right)mv+w}{2\beta }$, ${D}^{T}=\frac{\beta m+\left(1-\beta \right)mv-w}{2\beta m}$, and ${\pi }_{r}^{T}=\frac{{[\beta m+\left(1-\beta \right)mv-w]}^{2}}{4\beta m}-F$. (2) When $m>\frac{4\beta }{\left(1-\beta \right){v}^{2}}$, if $w<\overline{w}$, then ${T}^{T}=1$, ${p}^{T}=\frac{\beta m-\left(1-\beta \right)mv+w}{2}$, ${D}^{T}=\frac{\beta m+\left(1-\beta \right)mv-w}{2\beta m}$, and ${\pi }_{r}^{T}=\frac{{[\beta m+\left(1-\beta \right)mv-w]}^{2}}{4\beta m}-F$. Where $\underset{\_}{w}=\frac{\beta mv-4\beta +\left(1-\beta \right)m{v}^{2}}{v}$ and $\overline{w}=\frac{2\beta mv-4\beta +\left(1-\beta \right)m{v}^{2}}{2v}$.

The manufacturer’s profit under the two-part tariff contract is ${\pi }_{m}^{T}=wD-k{m}^{2}-F$. From the retailer’s best response, the manufacturer decides the optimal fixed fee and wholesale price under each case. (1) When $m<\frac{4\beta }{\left(1-\beta \right){v}^{2}}$: (a) if $\underset{\_}{w}\le w<\beta m$, ${F}^{T}=\frac{{(\beta m-w)}^{2}}{[4\beta -\left(1-\beta \right)m{v}^{2}]m}$ and ${\pi }_{m}^{T}=\frac{{\beta }^{2}{m}^{2}-{w}^{2}}{4\beta m-\left(1-\beta \right){m}^{2}{v}^{2}}-k{m}^{2}$. Thus, if $m<\frac{4\beta }{\beta v+\left(1-\beta \right){v}^{2}}$, then the optimal wholesale price ${w}^{T*}=0$; (b) if $w<\underset{\_}{w}$, ${F}^{T}=\frac{{[\beta m+\left(1-\beta \right)mv-w]}^{2}}{4\beta m}$ and ${\pi }_{m}^{T}=\frac{{[\beta +\left(1-\beta \right)v]}^{2}{m}^{2}-{w}^{2}}{4\beta m}-\left(1-\beta \right)-k{m}^{2}$. Thus, if $\frac{4\beta }{\beta v+\left(1-\beta \right){v}^{2}}<m$, then ${w}^{T*}=0$. (2) When $m>\frac{4\beta }{\left(1-\beta \right){v}^{2}}$, if $w<\overline{w}$, ${F}^{T}=\frac{{[\beta m+\left(1-\beta \right)mv-w]}^{2}}{4\beta m}$ and ${\pi }_{m}^{T}=\frac{{[\beta +\left(1-\beta \right)v]}^{2}{m}^{2}-{w}^{2}}{4\beta m}-\left(1-\beta \right)-k{m}^{2}$. Thus, the optimal wholesale price ${w}^{T*}=0$. To sum up, the equilibrium solutions under the two-part tariff contract are as follow: (1) if $m<\frac{4\beta }{\beta v+\left(1-\beta \right){v}^{2}}$, then ${T}^{T*}=\frac{\beta mv}{4\beta -\left(1-\beta \right)m{v}^{2}}$, ${p}^{T*}=\frac{2{\beta }^{2}m-\beta \left(1-\beta \right){m}^{2}{v}^{2}}{4\beta -\left(1-\beta \right)m{v}^{2}-\beta \left(1-\beta \right)mv}$, ${F}^{T*}=\frac{2\beta }{4\beta -\left(1-\beta \right)m{v}^{2}}$, ${w}^{T*}=0$, ${\pi }_{m}^{T*}=\frac{{\beta }^{2}m}{4\beta -\left(1-\beta \right)m{v}^{2}}-k{m}^{2}$, and ${\pi }_{r}^{T*}=0$; (2) if $\frac{4\beta }{\beta v+\left(1-\beta \right){v}^{2}}<m$, then ${T}^{T*}=1$, ${p}^{T*}=\frac{\beta m-\left(1-\beta \right)mv}{2\beta }$, ${F}^{T*}=\frac{{\left[\beta m+\left(1-\beta \right)mv\right]}^{2}}{4\beta }-\left(1-\beta \right)$, ${w}^{T*}=0$, ${\pi }_{m}^{T*}=\frac{{[\beta +\left(1-\beta \right)v]}^{2}m}{4\beta }-\left(1-\beta \right)-k{m}^{2}$, and ${\pi }_{r}^{T*}=0$. □